Известия РАН. Механика жидкости и газа, 2019, № 2, стр. 38-47

Анализ гипотез Колмогорова в сжимаемом турбулентном потоке

А. Н. Секундов^a, К. Я. Якубовский^a, *

^a Центральный институт авиационного моторостроения им. П.И. Баранова
Москва, Россия

Поступила в редакцию 24.07.2018
После доработки 18.10.2018
Принята к публикации 18.10.2018

DOI: 10.1134/S0568528119020117

Аннотация

Численными методами исследуются структурные функции в однородной изотропной турбулентности. Рассматривается как одномерная, так и трехмерная турбулентность. Анализируются методы построения сжимаемой турбулентности.

Ключевые слова: однородная, изотропная турбулентность, спектр, структурная функция

Особенности турбулентности можно описать, например, с помощью структурных функций S(r) и спектров E(k) [1, 2]. В работах А.Н. Колмогорова для этих функций были предложены следующие полуэмпирические соотношения

(0.1)

$S(r) \approx {{(\varepsilon \times r)}^{{2/3}}},\quad E(k) \approx C \times {{\varepsilon }^{{2/3}}} \times {{k}^{{ - 5/3}}}$

Как показывают эксперименты и прямые численные расчеты [1], эти соотношения выполняются, если расстояние между точками “r” удовлетворяет неравенствам: $\eta \ll r \ll L$, где η – масштаб Колмогорова, L – интегральный масштаб турбулентности, жидкость несжимаемая и число Рейнольдса Re достаточно большое (Re > 10⁵).

Соотношения (0.1) универсальны и тестировались на множестве примеров. Однако в некоторых исследованиях [3, 4] отмечается, что в сжимаемых турбулентных потоках известный закон Колмогорова о наклоне в спектре “–5/3” нарушается и предлагается такая его модификация, которая содержит число Маха

(0.2)

$E(k,\varepsilon ,{\text{M}}) = C \times {{k}^{{ - 11/3}}} \times {{\varepsilon }^{{2/3}}} \times {{{\text{M}}}^{{2/3}}}$

Таким образом, утверждается, что в сжимаемой турбулентности спектры могут существенно отличаться от гипотез Колмогорова, и наклон спектра мощности скорости, к примеру, “–11/3” по сравнению с “–5/3” в несжимаемой жидкости.

Плотность среды может изменяться не только за счет изменения скорости, но также и из-за изменения температуры, например, в атмосфере или при горении. В этом случае, как утверждается в исследовании [5], выражение для S в (0.1) также может изменяться, а показатель степени “p” в (0.3) может отличаться от 2/3

(0.3)

$\frac{S}{{{{{\langle u{{{\text{'}}}^{2}}\rangle }}^{{3/2}}}}} \approx {{\left( {\frac{{\varepsilon \times r}}{{{{{\langle u{{{\text{'}}}^{2}}\rangle }}^{{3/2}}}}}} \right)}^{p}}$

В цитируемой статье [2] предлагается расширение феноменологии Колмогорова, которое учитывает сжимаемость среды путем масштабирования в спектре мощности и в структурных функциях скорости взвешенной по плотности V = uρ^1/3.

У авторов статьи есть определенные сомнения в справедливости некоторых утверждений цитируемых работ. В частности, очевидно, что предлагаемое масштабирование не удовлетворяет соображениям размерности, а соотношение (0.3) не удовлетворяет принципу Галилея. В данной статье сделана попытка проверки расчетными методами предложенных в [2–4] соотношений, их справедливости при вариации числа Маха от 0 до 1.5. На примере одномерной турбулентности и вырождения однородной изотропной турбулентности в кубе с периодичными граничными условиями проанализированы соотношения (0.1).

Основные расчеты выполнены с помощью метода моделирования крупных вихрей LES. В качестве подсеточной модели в методе LES использовалась модель Смагоринского с постоянной С_s = 0.1. Кратко этот метод и его слабые стороны описаны, например, в статье [6].

Основная цель проводимых расчетов – выявить, от каких параметров может зависеть (кроме числа Маха) структурная функция для однородной и (в трехмерном случае) изотропной турбулентности.

1. ОДНОМЕРНАЯ ТУРБУЛЕНТНОСТЬ

В случае однородной изотропной турбулентности принципиальной разницы между одномерным и трехмерным случаями нет. Поэтому имеет смысл начать анализ с одномерного случая. Вводится однородная случайная функция [7]

(1.1)

$x(n) = {{k}_{1}} \times e(n) + {{k}_{2}} \times x(n - 1),\quad {{k}_{1}} = \sqrt {D \times (1 - k_{2}^{2})} ,\quad {{k}_{2}} = \exp ( - a)$

где e(n) – значения дискретного белого гауссовского шума с нулевым математическим ожиданием и единичной дисперсией. Такое распределение x(n) (1.1) соответствует корреляционной функции вида

(1.2)

$R(m) = D \cdot \exp ( - a \times m)$

Параметрами модели в данном случае являются дисперсия выходного моделируемого процесса D = 1 и параметр a, который определяет статистическую связь соседних случайных отсчетов.

Следует отметить, что корреляционная функция (1.2) неплохо описывает турбулентность для средних значений расстояний r между точками. Но поведение R(m) при малых r функция (1.2) описывает неточно. Для описания поведения R(m) на малых расстояниях между точками требуются более сложные соотношения, которые в данной работе не использовались.

В одномерном случае расчетное исследование проведено в следующем порядке. Синтезировано одномерное распределение пульсационной скорости U′(n), соответствующее корреляционной функции (1.2) с помощью выражений (1.1). Параметр $a$ в этой функции подобран для получения нормального вида спектра плотности энергии турбулентности. По полученному распределению рассчитана структурная функция, вид которой для участка $\eta \ll r \ll L$ затем сравнивается с аппроксимацией Колмогорова. При этом число Рейнольдса Re_t = k²/(ε × ν) = 3 × 10⁵, здесь k – энергия турбулентности.

Распределение случайной функции e(n) для N = 10⁵ отсчетов было получено с использованием несложного алгоритма на основе известных функций и здесь не приводится. Такое количество отсчетов определяется следующими требованиями. Масштаб Колмогорова и интегральный масштаб турбулентности могут отличаться на 3–4 порядка (рис. 1). Пространственный и временной шаги между отсчетами должны быть достаточно малыми, чтобы описать участок высоких частот спектра энергии пульсационной скорости, соответствующий интервалу $\eta \ll r \ll L$, и одновременно необходимо достаточное представительство низких частот, т.е. продолжительность выборки, для правильного вида соответствующего “источникового” участка спектра. Кроме того, при построении структурной функции в окрестности $\eta \ll r \ll L$ для хорошего осреднения необходимо достаточно большое значение отношения N/N_z, где N – количество отсчетов в выборке, а N_z – длина выборки в окрестности $\eta \ll r \ll L$, для которой строится структурная функция.

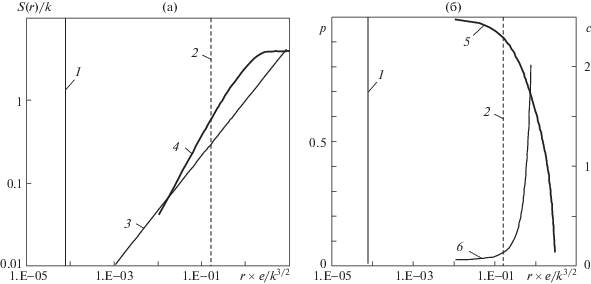
Рис. 1.

Синтетическая одномерная турбулентность ($a = 0.01$): (а) – сравнение значений левой и правой частей уравнения Колмогорова; (б) – степень p и коэффициент С в аппроксимации C × (ε × r)^p; 1 – масштаб Колмогорова; 2 – интегральный масштаб $L = C_{\mu }^{{3/4}} \times {{k}^{{3/2}}}{\text{/}}\varepsilon $, C_μ = 0.09; 3 – аппроксимация Колмогорова (ε × r)^2/3; 4 – структурная функция S(r); 5, 6 – p и C

Используя выражения (1.1), генерируется одномерное распределение пульсационной скорости U′(n), удовлетворяющее корреляционной функции (1.2).

Затем вычисляется энергия турбулентных пульсаций k = 〈U′²〉/2 как среднее арифметическое половины квадратов пульсационных скоростей во всех точках выборки. Далее проводится расчет зависимости безразмерной структурной функции S/k от r.

Шаг по пространству Δx = 7 × 10^–4 м и масштаб пульсации скорости $U_{{rms}}^{'} \approx 100$ м/с выбраны для удобства сопоставления с результатами трехмерных расчетов, выполненных для куба с ребром длиной 10^–2 м (описываются ниже). Для построения спектра распределения энергии турбулентности по частотам вихрей каждому отсчету U'(n) приписано время с шагом Δt = 10^–4 с, что может имитировать получение данных о пульсации скорости с помощью термоанемометра с относительной скоростью Δx/Δt движения в турбулентном потоке. Выбор шага по времени не имеет особого значения, так как не изменяет характер спектра энергии турбулентности, а только смещает диапазон частот.

Значение диссипации ε непосредственно не получить из такого синтетического одномерного распределения U'(n), не сделав предположения о равновесии порождения и диссипации. Значение параметра $a$ = 0.01 было подобрано так (рис. 2), чтобы спектр плотности энергии турбулентности имел требуемые характерные области, в частности, наклон инерционного диапазона соответствовал закону “–5/3”, и чтобы начало структурной функции попадало в диапазон $\eta \ll r \ll L$ (рис. 1а), и на этом участке S(r) была близка к (ε × r)^2/3. При $a = 0.1$ высокочастотный участок мало представлен – начало структурной функции лежит вне диапазона $\eta \ll r \ll L$.

Рис. 2.

Синтетическая одномерная турбулентность и линейная интерполяция промежуточных значений (9 дополнительных отсчетов): (а) – одномерное распределение пульсационной скорости; (б) – спектр плотности энергии турбулентности; 1 – исходное распределение ($a = 0.01$, k = 4727 м²/с²); 2 – линейная интерполяция; 3 – спектр распределения 2; 4 – аппроксимация “–5/3”; PSD – спектральная плотность энергии турбулентности

Значение диссипации ε = 5 × 10⁶ м²/с³ подобрано так, чтобы в интервале $\eta \ll r \ll L$ левая и правая части уравнения Колмогорова (0.1) были близки, что оказалось возможным. Однако степень “p” в аппроксимации C × (ε × r)^p в этом диапазоне “r” не равна 2/3 и монотонно меняется. Соответственно и С отличается от 1 и становится переменной в зависимости от r. Степень p на рис. 1б получена по двум соседним точкам S(r) и S(r + Δx) из следующих соображений: S(r) = C × (ε × r)^p, S(r + Δx) = C × (ε×(r + Δx))^p, тогда степень p находится как p(r) = lg(S(r)/S(r + Δx))/lg(r/(r + Δx)), а значение C – как C(r) = S(r)/(ε × r)^p.

Графики аппроксимации Колмогорова и структурной функции (рис. 1а) имеют пересечение в диапазоне $\eta \ll r \ll L$, однако степень в точке пересечения больше 2/3 (рис. 1б) и близка к 1, а множитель С ≈ 0.06.

Как уже отмечалось, корреляция (1.2) плохо описывает поведение турбулентности на малых расстояниях. С целью исследования поведения структурной функции в ближайшей окрестности r ≈ η, где η – масштаб Колмогорова, исходное распределение U' = f(x) методом линейной интерполяции дополнено 9-ю промежуточными значениями U' (шаг по пространству и времени уменьшен в 10 раз). Такой подход не меняет скоррелированности данных при сохранении неизменным шага сбора данных, однако позволяет проанализировать поведение структурной функции вблизи η, а также степени p и множителя С в аппроксимации С × (ε × r)^p.

На рис. 1 и 3 значения масштабов: Колмогорова η = (ν³/ε)^1/4, интегральный масштаб L = = $C_{\mu }^{{3/4}} \times {{k}^{{3/2}}}{\text{/}}\varepsilon $, где C_μ = 0.09. Благодаря введению дополнительных точек в спектре рис. 2б появился участок, похожий на участок вязкой диссипации мелких вихрей. Степень в ближайшей окрестности масштаба Колмогорова приблизилась к 2 (рис. 3б).

Рис. 3.

Синтетическая одномерная турбулентность при $a = 0.01$, k = 4727 м²/с²: (а) – структурная функция, левая и правая части уравнения Колмогорова; (б) – изменение степени в правой части уравнения Колмогорова; 1 – масштаб Колмогорова; 2 – интегральный масштаб; 3 – аппроксимация Колмогорова (ε × r)^2/3; 4 – структурная функция S(r); 5 – степень p для исходного распределения, 6 – степень p для дополненного распределения

Вернемся к стандартной корреляции (1.2). Проварьируем в расчетах параметры $a$ и ε. Эти результаты приведены на рис. 4 и 5 .

Рис. 4.

Одномерная турбулентность и влияние показателя $a$ на вид структурной функции S(r)/k и на степень p в аппроксимации S(r)/k ∼ r^p: 1–4 – a = 1.1; 0.535; 0.1; 0.01

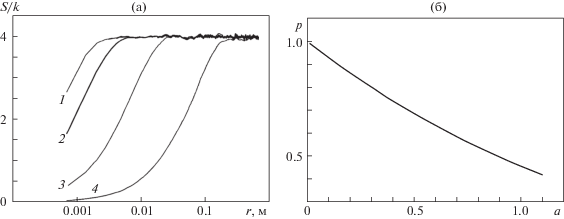
Рис. 5.

Влияние значения диссипации ε на вид аппроксимации структурной функции: (а, б ) – ε = 10⁸; 10⁹ м³/с²; 1 – масштаб Колмогорова, 2 – интегральный масштаб, 3 – аппроксимация Колмогорова; 4 – структурная функция S(r); 5 – p = 2/3

Степень p = 2/3 реализуется при $a = 0.535$. В случае одномерной синтетической турбулентности обезразмерить расстояние r × ε/k^3/2 не удается, так как отсутствует информация об ε. Подобрать ε для попадания начала структурной функции в интервал $\eta \ll r \ll L$ можно, но тогда ε будет иметь свое значение для каждой кривой по величине $a$.

Можно подобрать показатель $a = 0.535$ так, чтобы степень на ближайшей к интервалу $\eta \ll r \ll L$ границе кривой S(r), вычисленная по уравнению p(r) = lg[S(r)/S(r + Δx)]/lg[r/(r + Δx)], была равна p = 2/3 (рис. 5). Однако при этом не удается подобрать ε такой, чтобы S(r)/k была близка к аппроксимации Колмогорова (ε × r)^2/3 внутри диапазона $\eta \ll r \ll L$. Это удается сделать только в диапазоне r > L и при ε = 10⁹ м²/с³ (рис. 5б).

Графики на рис. 1, 3–5 свидетельствуют о том, что степень p = 2/3 не универсальна и при сравнительно небольших (умеренных) числах Рейнольдса существенно зависит от показателя $a$, который в свою очередь определяет особенность поведения турбулентности (вид корреляционной функции) при умеренных и малых расстояниях между точками.

2. ТРЕХМЕРНЫЙ СЛУЧАЙ

Выполнена серия трехмерных нестационарных расчетов для сжимаемого вязкого газа методом LES для разных значений среднего пульсационного числа Маха и для нескольких уровней качества расчетной сетки. По результатам расчетов строились распределения структурной функции S(r) и выполнялось сравнение с аппроксимацией Колмогорова внутри и вблизи диапазона масштабов $\eta \ll r \ll L$.

Расчетная область представляет собой куб с ребром 0.01 м, состоящий из одинаковых кубических расчетных ячеек. Каждая грань куба соединяется с противоположной гранью с помощью граничных условий периодичности. Начальное поле получается как суперпозиция случайных нескоррелированных флуктуаций скорости, среднее значение которой соответствует заданному пульсационному числу Маха. Начальное поле пульсации скорости в сжимаемом вязком потоке быстро самопроизвольно затухает, поэтому необходимо ее поддержание. Поддержание среднего пульсационного числа Маха осуществлялось двумя способами:

– пропорциональной коррекцией скорости через каждые 10 временных слоев – умножением всех компонент скорости во всех ячейках на отношение М_t/М_c, где М_t – целевое значение пульсационного числа Маха, а М_c – текущее его среднее по объему значение;

– с помощью дополнительного постоянно действующего источникового члена в уравнении движения, значение которого также пропорционально текущему отношению М_t/М_c. Оба метода дали близкие результаты.

Из-за вязких эффектов происходит разогрев куба, который компенсируется с помощью источникового члена в уравнении энергии для поддержания постоянным среднего значения температуры.

Среднее турбулентное число Рейнольдса в расчетах находилось в диапазоне Re_t = 9.83 × 10³–9.8 × 10⁴, что меньше, чем в одномерном варианте.

Система уравнений решается матрично. Используются дискретизация третьего порядка по пространству и неявная схема второго порядка по времени. На каждом временном слое выполняется по 10 итераций, за которые решение хорошо устанавливается (сходится на 3–4 порядка на каждом временном слое). Максимальное локальное число Куранта не превышает 0.4–0.5.

Вычислять структурную функцию в ограниченном расчетном объеме можно, используя два подхода. В первом после получения квазиустановившегося решения (когда после переходного процесса параметры потока начинают колебаться около своего среднего значения) используется мгновенное поле скорости, а структурная функция S(r) получается в результате осреднения по объему. Такой подход дает хорошие результаты в случае большого размера расчетной сетки и когда интегральный масштаб турбулентности много меньше длины стороны куба, тогда вид структурной функции не зависит от выбора момента для осреднения. Однако, как показали реальные расчеты, для небольших сеток 25 × 25 × 25 средние по объему значения параметров существенно пульсируют по времени (рис. 6). В таком случае используется второй подход с осреднением по времени, особенно для определения среднего значения диссипации (для последующей оценки масштабов Колмогорова и интегрального масштаба турбулентности).

Рис. 6.

Изменение среднего по объему значения диссипации турбулентной энергии в кубе 25 × 25 × 25

При втором подходе на квазиустановившемся режиме происходит накопление статистики для вычисления структурной функции S(r), энергии турбулентности k и диссипации ε. Причем сбор статистики происходит не на всех, а только на каждом 10-м временном слое непосредственно перед процедурой восстановления среднего числа Маха, при этом вычисляются и суммированием накапливаются следующие параметры потока:

1) энергия турбулентных пульсаций: k_t = (U² + V² + W²)/2 – на текущем временном слое, k_Σt = k_Σt–1 + k_t – накопление суммы для осреднения.

2) диссипация энергии турбулентности как: ε = (k_t–1 – k_t)/Δt, где Δt – шаг по времени, ${{k}_{{t - 1}}} = (U_{{t - 1}}^{2} + V_{{t - 1}}^{2} + W_{{t - 1}}^{2}){\text{/}}2$ – энергия турбулентных пульсаций на предыдущем временном слое, ε_Σt = ε_Σt–1 + ε – накопление суммы для осреднения.

3) вычисляется левая часть уравнения Колмогорова для всех ячеек куба относительно центральной точки куба: S = [((x – x_с) × (U – U_c) + (y – y_с) × (V – V_c) + (z – z_c) × (W – W_c))/r]² – левая часть уравнения Колмогорова для текущей ячейки относительно центральной ячейки куба, где (U_c, V_c, W_c) – компоненты скорости в центральной ячейке куба, (x_c, y_c, z_c) – координаты центра куба, r – длина радиус-вектора, соединяющего центр текущей ячейки с центральной ячейкой куба, S_Σt = S_Σt–1 + S – накопление суммы для осреднения.

После накопления достаточной статистики и окончания счета суммы k_Σ, ε_Σ и S_Σ во всех ячейках делятся на количество временных слоев осреднения, а затем значения k и ε осредняются по объему куба. В этом случае все вычисления комплекса S выполняются относительно только одной точки куба потому, что в противном случае количество вычислений драматически возрастает. Для сетки размерности N × N × N для полного перебора сочетаний радиус-вектора и проекции разности скоростей на него, т.е. для полного осреднения S по объему, в отношении всех ячеек потребуется N⁶ вычислений комплекса S, а для вычисления относительно одной точки потребуется только N³ вычислений, что допустимо выполнять в ходе решения.

После получения осредненного по времени поля значений S в каждой ячейке куба необходимо получить зависимость структурной функции S(r) от r. Для этого необходимо выполнить осреднение для всех ячеек по расстоянию от центра куба. Так как сетка используется равномерная, то множество возможных расстояний от центра куба до ячеек будет ограниченным и содержать не более 3 × N² дискретных значений. При этом все ячейки, для которых выражение m = (i – i_c)² + (j – j_c)² + (k – k_c)² имеет одинаковое значение, расположены точно на одинаковом расстоянии от центра куба, что делает строгим и упрощает процедуру осреднения S(r) по r. Здесь i, j, k – индексы ячеек в структурированной равномерной сетке, а i_c, j_c, k_c – индексы центральной ячейки куба. Тогда для всех ячеек, имеющих одинаковое значение m, выполняются суммирование и арифметическое осреднение значения S. Таким образом, создается одномерное распределение S = f(m), а из него получается S = f(r), где r = Δx × √m, Δ x= Δy = Δz – шаг сетки.

Как и для одномерного случая, для ориентировки вычисляются и наносятся на график значения масштаба Колмогорова и интегрального масштаба турбулентности.

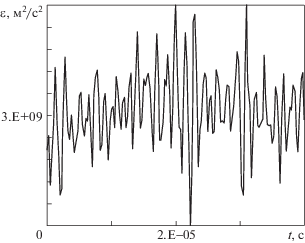
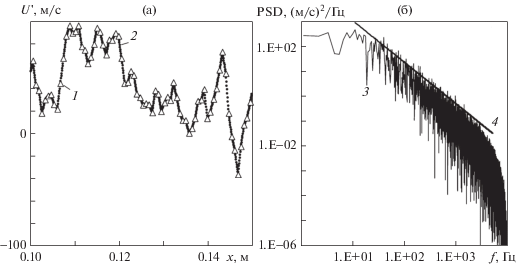
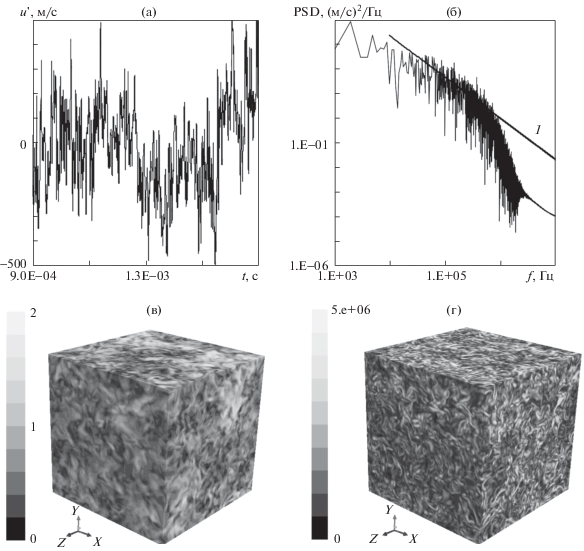
Спектр плотности энергии турбулентности (рис. 7б), построенный по осциллограмме продольной компоненты скорости U' = f(t) для центральной точки куба, при средней пульсационной скорости, соответствующей М ≈ 0.8, имеет слабо выраженный инерционный участок, который плохо соотносится с законом “–5/3”. Вероятно, это связано с ограниченностью расчетного объема и соответственно с неправильным описанием низкочастотной составляющей спектра, а также недостаточно большим числом Рейнольдса (Re_t = 4.74 × 10⁴). Возможно, причина и в высоком значении среднего пульсационного числа Маха ≈ 0.8, влияющем на распределение энергии по масштабам вихрей.

Рис. 7.

Трехмерный расчет для куба 200 × 200 × 200, М ≈ 0.8: (а) – осциллограмма компоненты u пульсационной скорости в центре куба (k = 4.5 × 10⁴ м²/с²), (б) – спектр плотности энергии турбулентности (1 – аппроксимация “–5/3”), (в) – мгновенное поле числа Маха на гранях куба, г – мгновенное поле модуля завихренности на гранях куба, PSD – спектральная плотность энергии турбулентности

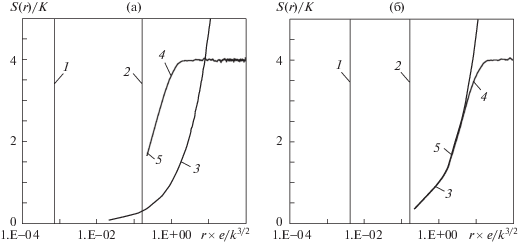
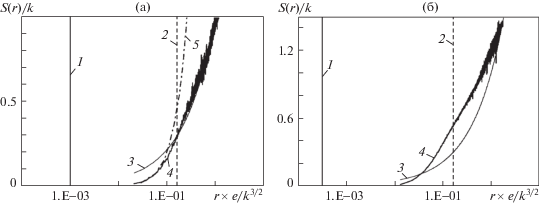
На рис. 8 структурная функция построена двумя методами – осреднением по времени (4 на рис. 8) и по пространству (5 на рис. 8). Интересно, что несмотря на существенные пульсации средних параметров потока (рис. 6), оказалось возможным хорошее соответствие S(r), полученное по двум этим подходам, если для каждого использовать свое значение средней энергии турбулентности: в первом случае – полученное осреднением по времени на достаточном количестве временных слоев (k_T = 4727 м²/с²), во втором – мгновенное для текущего поля скорости (k_V = 4039 м²/с²), для которого строилась S(r). Однако, как и в одномерном случае (рис. 1 и 3 ), графики структурной функции и аппроксимации Колмогорова при М ≈ 0.28 (рис. 8а) хоть и пересекаются у интервала $\eta \ll r \ll L$, но имеют существенно разные наклоны. Внутри диапазона $\eta \ll r \ll L$ степень p от начала кривой S(r) (4 и 5 на рис. 8а) плавно изменяется от 1.86 до 1.6 к правой границе интервала.

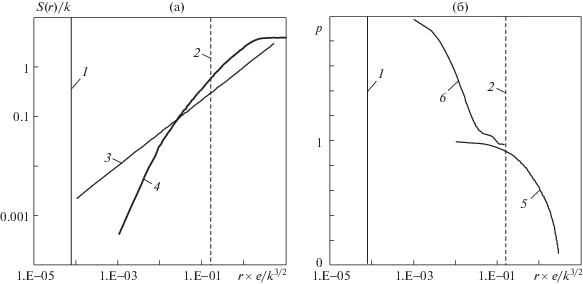
Рис. 8.

Анализ структурной функции для сжимаемого потока для куба 25 × 25 × 25: (а, б) – М ≈ 0.28, Re_t = = 2.4 × 10⁴; 1.5, 9.8 × 10⁴; 1 – масштаб Колмогорова; 2 – интегральный масштаб; 3 – аппроксимация Колмогорова; 4 – структурная функция S(r), осреднение по времени для центра куба; 5 – S(r), осреднение по пространству по мгновенному полю

С увеличением числа Маха от 0.28 до 1.5 пересечение графиков аппроксимации Колмогорова (ε × r)^2/3 и структурной функции S(r) выходит за диапазон $\eta \ll r \ll L$ в сторону больших масштабов, однако при этом наклоны аппроксимации (ε × r)^2/3 и S(r) сближаются (рис. 8б).

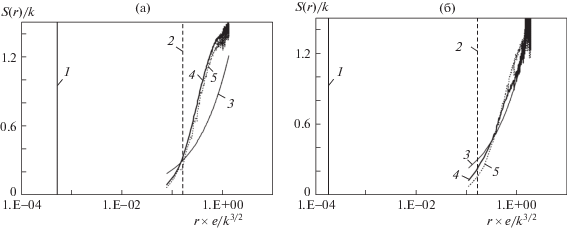
Графики на рис. 8 и 9 позволяют сопоставить результаты расчета структурных функций при разных числах ячеек (25 и 200) на ребрах куба. Видно разное влияние числа Маха. Так, если для куба 25 × 25 × 25 (рис. 8а и 8б) рост числа Маха сближает расчетную зависимость с гипотезой Колмогорова, то для куба 200 × 200 × 200 (рис. 9а и 9б) наблюдается более сложная зависимость – пересечение кривых с увеличением числа Маха смещается внутрь диапазона $\eta \ll r \ll L$, однако усиливается рассогласование наклона кривых.

Рис. 9.

Анализ структурной функции для сжимаемого потока для куба 200 × 200 × 200: (а) М ≈ 0.28, Re_t = 9.83 × 10³, k = 5056, ε = 1.52 × 10⁸; (б) М ≈ 0.8, Re_t = 4.74 × 10⁴, k = 44700 м²/с², ε = 2.47 × 10⁹ м³/с²; 1–4 как на рис. 8; 5 – структурная функция S(r), одномерная модель (1.1), (1.2) при a = 0.535, k = 5056 м²/с²

3. РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ

В расчетах обнаружены влияние на вид структурной функции S(r) и степень p в ее аппроксимации (0.3), по крайней мере, трех параметров:

1) показателя $a$ в экспоненциальной зависимости для корреляционной функции (1.2);

2) числа Маха, определенного по пульсационной скорости M = U′/c;

3) числа Рейнольдса Re_t = k²/(ε × ν).

Одномерные расчеты свидетельствуют о том, что степень p = 2/3 в аппроксимации структурной функции (0.3) не вполне универсальна и при сравнительно небольших (умеренных) числах Рейнольдса (10⁴–10⁵) существенно зависит от показателя a, который в свою очередь определяет особенность поведения турбулентности (вид корреляционной функции) при умеренных расстояниях между точками.

Расчетное значение p = 2/3 обнаруживается только в определенных узких диапазонах параметра $a$ и расстояний между точками r × ε/k^3/2.

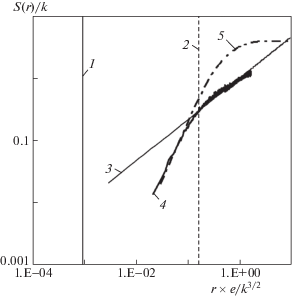
Результаты одномерного и 3D-расчета, в части поведения S(r) в интервале $\eta \ll r \ll L$, совпадают (рис. 10), если в одномерном расчете использовать корреляцию (1.2) с показателем $a = 0.535$ и ввести дополнительные промежуточные точки для описания турбулентности на малых расстояниях. Вне интервала $\eta \ll r \ll L$ результаты 3D-расчета совпадают с аппроксимацией Колмогорова.

Рис. 10.

Анализ структурной функции для сжимаемого потока (куб 200 × 200 × 200): М ≈ 0.28, Re_t = 9.83 × 10³, k = 5056 м²/с², ε = 1.52 × 10⁸ м³/с² (обозначения как на рис. 9)

ЗАКЛЮЧЕНИЕ

На примере одномерной турбулентности и вырождения однородной изотропной турбулентности проанализировано выполнение соотношений Колмогорова при вариации пульсационного числа Маха от 0 до 1.5. Численно с использованием одномерного подхода и трехмерно методом LES исследованы структурные функции в однородной изотропной турбулентности. Выявлено влияние на вид структурной функции показателя a в экспоненциальной зависимости для корреляционной функции, а также пульсационного числа Маха и турбулентного числа Рейнольдса. Внутри интервала масштабов $\eta \ll r \ll L$ результаты одномерного и 3D-расчетов совпадают, а вне этого интервала 3D-расчет совпадает с аппроксимацией Колмогорова. Показатель степени в аппроксимации Колмогорова соответствует значению 2/3 только в определенных узких пределах расстояний и степени связности колебаний.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (Проект № 16-01-00035).

Список литературы

Монин А.С., Яглом А.М. Статистическая гидромеханика. Ч. 1. М.: Наука, 1965.
Юшков В.П. Гипотезы Колмогорова: возможность доказательства. Физика Земли, атмосферы и гидросферы // ВМУ. Сер. 3. Физика. Астрономия. 2014. № 5. С. 55.
Kritsuk A.G., Rick Wagner, and Michael L. Norman. Energy cascade and scaling in supersonic isothermal turbulence // J. Fluid Mech. Publ. online: 22, July, 2013.
Ingenito A., Bruno C. Physics and Regimes of Supersonic Combustion // AIAA. 2010.V. 48. № 3.
Богушевич А.Я. Наблюдаемые нарушения закона “2/3” в экспериментальных спектрах турбулентных флуктуаций температуры и условия их возникновения. Институт мониторинга климатических и экологических систем СО РАН. e-mail: bay@imces.ru
Секундов А.Н. Некоторые проблемы моделирования турбулентных течений. Germany: Lan-Publ., 2014, 144 с.
Бакалов В.П. Цифровое моделирование случайных процессов. 2002. Вып. 4. 88 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал