1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 3, 2019

Известия РАН. Механика жидкости и газа, 2019, № 3, стр. 70-82

МОДЕЛИРОВАНИЕ И РАСЧЕТ НЕСТАЦИОНАРНОЙ ФИЛЬТРАЦИИ СУСПЕНЗИИ В ТУПИКОВОМ И ОТКРЫТОМ КАНАЛАХ С УЧЕТОМ ДИФФУЗИИ ДИСПЕРСНЫХ ЧАСТИЦ И ОСАДКООБРАЗОВАНИЯ

Т. Р. Аманбаев a, b, *

a Южно-Казахстанский государственный университет им. М. Ауэзова
Шымкент, Казахстан

b Институт математики и математического моделирования
Алматы, Казахстан

* E-mail: tulegen_amanbaev@mail.ru

Поступила в редакцию 19.03.2018
После доработки 24.07.2018
Принята к публикации 19.10.2018

Полный текст (PDF)

Аннотация

В рамках диффузионного приближения построена одномерная модель фильтрации суспензии в канале с учетом диффузии дисперсного компонента и осадкообразования. Система уравнений приведена к уравнению конвективной диффузии в интегро-дифференциальной форме. Полученное уравнение проинтегрировано численным методом. Установлены определяющие параметры поставленной задачи. Обсуждаются некоторые результаты расчетов, иллюстрирующие влияние диффузионных потоков частиц и определяющих параметров на динамику суспензии в канале. Анализируется поведение зависимости среднего потока фильтрата от времени при разных значениях определяющих параметров.

Ключевые слова: канал, суспензия, фильтрация, осадкообразование, диффузия, диффузионное приближение, число Пекле

Во многих практических задачах возникает необходимость изучения процессов, происходящих при фильтрации суспензии через пористый слой [1–7]. Так, например, проблемы осветления и стерилизации фармацевтических и биологических жидкостей, лекарственных препаратов, получения стерильного воздуха, тонкой очистки газовых сред, микробиологической стабилизации вин, осветления различных алкогольных и безалкогольных напитков, фильтрации бутилированной и минеральной воды решаются при помощи микро- и ультрафильтрационного оборудования [8]. Движение дисперсной смеси в канале при наличии фильтрации жидкой фазы через стенки часто встречается в различных областях современной техники, например, как отмечено в [9], при разделении суспензии в трубчатых и половолоконных мембранных элементах [10, 11] и аппаратах с тангенциальной фильтрацией [12]. Подобные задачи также возникают при изучении течений суспензий в трещинах гидроразрыва в нефтеносных пластах [13–15], анализе проблемы снижения проводимости прискважинной зоны пласта за счет проникновения в него фильтрата промывочной жидкости [16] и образования корки на стенках при бурении скважин [6, 17] и др.

На фильтрацию суспензии существенное влияние оказывает процесс осадкообразования на стенках канала. Кроме того, в случаях мелкодисперсных (например, нанодисперсных) смесей следует учесть диффузию дисперсной фазы. Задача о фильтрации суспензии в каналах с учетом указанных эффектов весьма сложна и к настоящему времени подробно не исследована. В [9] данная задача рассмотрена в упрощенной постановке без привлечения динамических уравнений, а также без учета диффузии дисперсной фазы.

Отметим, что соотношение между конвективным и диффузионным переносом вещества характеризуется числом Пекле Pe = Lu/D, где D – коэффициент диффузии, u, L – характерные скорость среды и длина канала. При больших числах Пекле преобладает конвективный перенос, а при значениях Pe $ \lesssim $ 10 существенным становится диффузионный перенос частиц. В большинстве случаев числа Пекле достаточно велики. Однако для малых частиц (порядка нанометра), которые используются в ряде технологических процессов (очистка наносуспензий от примесей и т.п.) при достаточно малых скоростях движения дисперсной смеси число Pe может принимать значения порядка 10–100. Например, согласно [18] при нормальных условиях для частиц радиусом порядка 1 нм (10–9 м) коэффициент диффузии с учетом поправки Каннингема–Милликена (~102, при размерах частиц менее 1 мкм в коэффициенте диффузии необходимо учитывать поправочный множитель Каннингема–Милликена [18, 19]) имеет порядок D ~ 10–4 м2/с. Тогда при характерных длине канала L = 1 м и скоростях движения среды u ~ 10–3–10–2 м/с (характерны для каналов из-за фильтрации через проницаемые стенки) число Пекле оценивается диапазоном от 10 до 100. Указанная ситуация характерна для ультрафильтрационного процесса разделения дисперсных смесей. Таким образом, в некоторых технологических процессах возникает необходимость учета диффузионных потоков дисперсной фазы.

Целью данной работы являются математическое моделирование и расчет процесса нестационарной фильтрации суспензии в тупиковом и открытом каналах с учетом диффузионных потоков дисперсных частиц и осадкообразования в рамках одномерной модели. Результаты и выводы работы могут быть полезны, в частности, при проектировании фильтрационных установок, а также для оценки и проверки адекватности более сложных (например, двумерных или двухскоростных и т.п.) моделей фильтрования дисперсных смесей.

1. ПОСТРОЕНИЕ МОДЕЛИ И ПОСТАНОВКА ЗАДАЧИ

Рассмотрим движение в канале дисперсной смеси (суспензии), состоящей из жидкой (несущей) и твердой (дисперсной) фаз. Вещества несущей и дисперсной фаз полагаются несжимаемыми. На внутренней боковой поверхности канала с постоянным поперечным сечением имеется фильтрующая перегородка (мембрана), через которую протекает чистая жидкость (фильтрат) из-за перепада давления на внутренней и внешней сторонах мембраны. Поток фильтрата зависит от гидравлических сопротивлений фильтрующей перегородки и слоя осадка на ее поверхности. Отметим, что вопросы кольматации (захвата мелких частиц в порах мембраны) и сжимаемости осадка не рассматриваются. При наличии кольматации проницаемость фильтра может оказаться изменяющейся как во времени, так и по пространству. Следует подчеркнуть, что кольматация является достаточно сложным процессом, и в данное время исследование этого явления еще не полностью завершено (некоторые модели кольматации обсуждаются в [20]). Изменением поперечного сечения канала за счет образования осадка на стенках пренебрегается. Задача рассматривается в одномерной постановке – все параметры смеси зависят от времени и одной пространственной (продольной) координаты. В рамках данной постановки все параметры смеси являются осредненными параметрами по поперечному сечению канала. Для адекватного описания движения суспензии в рамках одномерной модели с оттоком жидкости через стенки канала полагается, что компонент скорости потока в направлении стенок намного меньше продольного компонента скорости смеси. Кроме того, канал считается достаточно длинным по сравнению с характерным размером поперечного сечения, что позволяет пренебречь краевыми эффектами на входе в канал: в частности, длина трубы должна намного превышать длину входного участка, где пограничные слои на стенках канала постепенно смыкаются. Ниже приведено обоснование справедливости двух последних допущений.

Уравнения неразрывности для составляющих суспензии и уравнение импульса смеси запишем в диффузионном приближении (в этом случае составляющие смеси принято называть компонентами), когда можно пренебречь инерцией относительного движения компонентов смеси [21, 22]. Уравнения неразрывности при наличии диффузии вещества можно представить в виде

(1.1)
$\frac{{\partial {{\rho }_{1}}}}{{\partial t}} + \nabla \cdot {{\rho }_{1}}{\mathbf{v}} = - \nabla \cdot {{{\mathbf{J}}}_{1}},\quad \frac{{\partial {{\rho }_{2}}}}{{\partial t}} + \nabla \cdot {{\rho }_{2}}{\mathbf{v}} = - \nabla \cdot {{{\mathbf{J}}}_{2}}$
${{{\mathbf{J}}}_{1}} + {{{\mathbf{J}}}_{2}} = 0$, $\rho {\mathbf{v}} = {{\rho }_{1}}{{{\mathbf{v}}}_{1}} + {{\rho }_{2}}{{{\mathbf{v}}}_{2}}$
$\rho = {{\rho }_{1}} + {{\rho }_{2}}$, ${{\rho }_{1}} = (1 - c)\rho _{1}^{ \circ }$, ${{\rho }_{2}} = c\rho _{{\text{2}}}^{^\circ }$, ($\rho _{{\text{1}}}^{^\circ }$, $\rho _{{\text{2}}}^{^\circ }$ = const)

Здесь ρ, v – плотность и среднемассовая (барицентрическая) скорость смеси; ${{\rho }_{i}}$ и $\rho _{{\text{i}}}^{^\circ }$ – приведенные и истинные плотности; ${{{\mathbf{v}}}_{i}}$ – векторы скорости несущей (i = 1) и дисперсной (i = 2) компонентов; c – объемная концентрация дисперсной примеси; ${{{\mathbf{J}}}_{1}}$, ${{{\mathbf{J}}}_{2}}$ – векторы потоков диффузии; $(\nabla \cdot )$ – оператор дивергенции; t – время.

Сложение уравнений системы (1.1) дает уравнение неразрывности для смеси в целом

(1.2)
$\frac{{\partial \rho }}{{\partial t}} + \nabla \cdot \rho {\mathbf{v}} = 0$

Для получения одномерного уравнения неразрывности несущей жидкости в канале при наличии фильтрации выделим элементарный объем V, ограниченный поверхностью Σ, которая состоит из двух близко расположенных поперечных сечений с координатами x и x + dx (ось x направлена вдоль канала в направлении движения суспензии) и отсеченной ими боковой поверхности канала, и проинтегрируем по этому объему первое уравнение системы (1.1). Далее, применяя формулу Гаусса-Остроградского к объемному интегралу от дивергенции, получим уравнение материального баланса по жидкости в интегральной форме

(1.3)
$\int\limits_V {\frac{{\partial {{\rho }_{1}}}}{{\partial t}}d\tau = - \int\limits_\Sigma {{{\rho }_{1}}{\mathbf{v}} \cdot {\mathbf{n}}d\sigma - \int\limits_\Sigma {{{{\mathbf{J}}}_{1}} \cdot {\mathbf{n}}d\sigma } } } $
где n – внешняя нормаль к поверхности Σ, а точка между векторами обозначает их скалярное произведение. Данное уравнение означает, что изменение плотности жидкости в выделенном объеме будет происходить за счет конвективной и диффузионной потоков массы через поверхность Σ, ограничивающей этот объем. Далее, полагая все параметры смеси осредненными по поперечному сечению канала и учитывая малость dx, из (1.3) придем к уравнению материального баланса жидкости в объеме V = Sdx (S – площадь поперечного сечения канала)

(1.4)
$\frac{{\partial {{\rho }_{1}}}}{{\partial t}}Sdx = - \left[ {{{\rho }_{1}}u} \right]S - {{\rho }_{1}}q{{S}_{w}} - \left[ {{{J}_{1}}} \right]S$

Здесь величина q представляет собой объемный поток фильтрата через единицу площади боковой поверхности (имеет размерность скорости); u, ${{J}_{1}}$ – скорость суспензии и поток диффузии вдоль оси x; ${{S}_{w}}$ = Λdx – площадь боковой поверхности, заключенной между выбранными сечениями; Λ – периметр поперечного сечения канала; квадратными скобками обозначены разность величин на длине dx. Разделив обе части (1.4) на Sdx и устремляя dx к нулю, получим уравнение сохранения массы жидкого компонента в дифференциальной форме

(1.5)
$\frac{{\partial {{\rho }_{1}}}}{{\partial t}} + \frac{{\partial {{\rho }_{1}}u}}{{\partial x}} = - {{\rho }_{1}}q\frac{\Lambda }{S} - \frac{{\partial {{J}_{1}}}}{{\partial x}}$

Из второго уравнения системы (1.1) аналогичным образом вытекает уравнение сохранения массы дисперсного компонента в канале в одномерном приближении

(1.6)
$\frac{{\partial {{\rho }_{2}}}}{{\partial t}} + \frac{{\partial {{\rho }_{2}}u}}{{\partial x}} = - {{\rho }_{2}}q\frac{\Lambda }{S} - \frac{{\partial {{J}_{2}}}}{{\partial x}}$

Сложение последних двух уравнений дает уравнение сохранения массы для смеси в целом (с учетом того, что ${{J}_{1}} + {{J}_{2}} = 0$)

(1.7)
$\frac{{\partial \rho }}{{\partial t}} + \frac{{\partial \rho u}}{{\partial x}} = - \rho q\frac{\Lambda }{S}$
которое может заменить одно из уравнений (1.5), (1.6). В уравнение (1.7) не входит явно слагаемое, ответственное за диффузию компонентов смеси.

Полагая, что диффузия мелких частиц происходит за счет их броуновского движения, для величины потока диффузии вдоль канала J2 имеем [23, 24]

(1.8)
${{J}_{2}} = - \rho _{{\text{2}}}^{^\circ }D\frac{{\partial c}}{{\partial x}},\quad D = \frac{{kT}}{{3\pi \mu d}}{{K}_{C}}$
где D – коэффициент броуновской диффузии частиц, определяемый формулой Эйнштейна [23] с поправочным коэффициентом Каннингема-Милликена ${{K}_{C}}$ [18]; k – постоянная Больцмана; T, μ – температура и вязкость жидкости; d – диаметр частиц. Коэффициент ${{K}_{C}}$ всегда больше или равен единице, его следует учитывать при размерах частиц менее 1 мкм.

В объемных концентрациях уравнения (1.5), (1.6) с учетом (1.8) примут вид

(1.9)
$\frac{{\partial (1 - с )}}{{\partial t}} + \frac{{\partial (1 - с )u}}{{\partial x}} = - \frac{\Lambda }{S}(1 - с )q - \frac{{\rho _{{\text{2}}}^{^\circ }}}{{\rho _{{\text{1}}}^{^\circ }}}D\frac{{{{\partial }^{2}}с }}{{\partial {{x}^{2}}}},\quad \frac{{\partial с }}{{\partial t}} + \frac{{\partial с u}}{{\partial x}} = - \frac{\Lambda }{S}с q + D\frac{{{{\partial }^{2}}с }}{{\partial {{x}^{2}}}}.$

Складывая между собой уравнения системы (1.9), получим

(1.10)
$\frac{{\partial u}}{{\partial x}} = - \frac{\Lambda }{S}q + \left( {1 - \frac{{\rho _{{\text{2}}}^{^\circ }}}{{\rho _{{\text{1}}}^{^\circ }}}} \right)D\frac{{{{\partial }^{2}}c}}{{\partial {{x}^{2}}}}$

Полученное уравнение может заменить одно из уравнений системы (1.9). Отметим, что в отличие от (1.7) уравнение (1.10) имеет диффузионную составляющую в правой части. Подставляя (1.10) в любое из уравнений системы (1.9) (после раскрытия производной по x в левых частях), придем к уравнению конвективной диффузии

(1.11)
$\frac{{\partial с }}{{\partial t}} + u\frac{{\partial c}}{{\partial x}} = \frac{\rho }{{\rho _{{\text{1}}}^{^\circ }}}D\frac{{{{\partial }^{2}}с }}{{\partial {{x}^{2}}}}$

Отметим, что в уравнении (1.11) отсутствует слагаемое, ответственное за фильтрацию жидкости через стенки канала. Это объяснимо, поскольку в левой части уравнения стоит субстанциональная производная. Другая отличительная особенность уравнения состоит в том, что перед диффузионной составляющей имеется множитель $\rho {\text{/}}\rho _{{\text{1}}}^{^\circ }$, зависящий, вообще говоря, от объемной концентрации c. При такой форме записи уравнения конвективной диффузии влияние фильтрации через боковую поверхность проявляется через скорость u, которая определяется, например, по (1.10). В целом уравнение (1.11) является нелинейным.

Для учета влияния сил давления и трения о стенки канала на динамику суспензии следует привлечь уравнение импульсов. С этой целью рассмотрим уравнение количества движения среды, занимающей вышеупомянутый элементарный объем V. В предположении отсутствия внешних массовых сил имеем [22]

$\int\limits_V {\rho \frac{{d{\mathbf{v}}}}{{dt}}d\tau = \int\limits_\Sigma {{{{\mathbf{p}}}_{n}}d\sigma } } $
где поверхностный интеграл в правой части представляет собой сумму внешних поверхностных сил, действующих на среду в объеме V; ${{{\mathbf{p}}}_{n}}$ – вектор напряжения, приложенный на площадку dσ с нормалью n. Проецируя подынтегральные выражения на ось x, а затем, раскрывая субстанциональную производную в левой части и приведя ее к дивергентному виду с помощью (1.2) и далее применяя формулу Гаусса–Остроградского к объемному интегралу с дивергенцией, получим

$\int\limits_V {\frac{{\partial \rho u}}{{\partial t}}d\tau + \int\limits_\Sigma {\rho u{\mathbf{v}} \cdot {\mathbf{n}}d\sigma = \int\limits_\Sigma {{{p}_{{nx}}}d\sigma } } } $

Отсюда, полагая все параметры смеси осредненными по поперечному сечению канала и учитывая, что ${{p}_{{nx}}} = - p$ на поперечных сечениях и ${{p}_{{nx}}} = - {{\tau }_{w}}$ на боковой поверхности канала, где p и ${{\tau }_{w}}$ – давление и сила (приходящаяся на единицу площади) вязкого трения о стенки канала, придем к уравнению сохранения количества движения в объеме V = Sdx

$\frac{{\partial \rho u}}{{\partial t}}Sdx + [\rho {{u}^{2}}]S + \rho uq{{S}_{w}} = - \left[ p \right]S - {{\tau }_{w}}{{S}_{w}}$

Здесь прямые скобки имеют тот же смысл, что и ранее для (1.4). Разделив обе части полученного соотношения на Sdx и устремляя dx к нулю, получим уравнение импульсов смеси в дифференциальной форме

$\frac{{\partial \rho u}}{{\partial t}} + \frac{{\partial \rho {{u}^{2}}}}{{\partial x}} = - \frac{{\partial p}}{{\partial x}} - {{\tau }_{w}}\frac{\Lambda }{S} - \rho uq\frac{\Lambda }{S}$
которое с учетом (1.7) можно привести к более удобному виду

(1.12)
$\rho \left( {\frac{{\partial u}}{{\partial t}} + u\frac{{\partial u}}{{\partial x}}} \right) = - \frac{{\partial p}}{{\partial x}} - {{\tau }_{w}}\frac{\Lambda }{S}$

Отметим, что в отличие от уравнений неразрывности, в уравнении импульсов наличие диффузионных потоков никак не проявляется (в соответствии с диффузионным приближением [21]). Кроме того, в уравнении (1.12) отсутствует слагаемое, обусловленное фильтрацией жидкости, что объясняется присутствием в левой части субстанциональной производной (как в случае с уравнением конвективной диффузии, рассмотренном выше). В такой форме уравнение импульсов одномерного движения смеси в трубе встречается в [25]. Силу трения жидкости о поверхность стенки определим как

${{\tau }_{w}} = {{K}_{f}}\frac{1}{2}\rho {{u}^{2}}$

Коэффициент трения ${{K}_{f}}$ зависит, например, от вязкости среды, шероховатости поверхности; как правило, используются его эмпирические оценки.

Следует подчеркнуть, что система уравнений (1.9), (1.12) фактически представляет собой односкоростную (или одножидкостную) модель дисперсной смеси [21].

Уравнение для толщины h несжимаемого слоя осадка на стенках канала получается из материального баланса твердого вещества в цилиндре с единичным основанием и элементом высоты dh: (1 – ε)dh = c(x, t)q(x, t)dt, здесь ε – пористость слоя осадка частиц (считается постоянной), dt – отрезок времени, в течение которого образуется слой осадка высотой dh. Интегрируя обе части приведенного соотношения в предположении отсутствия осадка на стенках канала в начальный момент времени, получим уравнение для толщины слоя осадка в интегральной форме [9]

(1.13)
$h(x,t) = \frac{1}{{1 - \varepsilon }}\int\limits_0^t {c(x,\tau )q(x,\tau )d\tau } $

Для потока фильтрата имеем уравнение [1]

$q(x,t) = \frac{{\Delta p(x,t)}}{{\mu \left[ {{{G}_{m}}{{h}_{m}} + Gh(x,t)} \right]}}$, $\Delta p = p - {{p}_{e}}$
где ${{h}_{m}}$, ${{G}_{m}}$ – толщина и гидравлическое сопротивление фильтрующей мембраны; G – гидравлическое сопротивление осадка; ${{p}_{e}}$ – давление на внешней стороне боковой фильтрующей перегородки (считается постоянным). Параметры ${{G}_{m}}$ и G в теории фильтрации именуют также обратными проницаемостями веществ мембраны и осадка [1]. При постоянном перепаде давления (Δp = const) и отсутствии осадка на стенках канала (h = 0) имеем q = const. В этом случае из (1.10) следует, что при отсутствии диффузии (или при его наличии в равноплотной суспензии, когда $\rho _{1}^{ \circ }$ = $\rho _{2}^{ \circ }$) скорость смеси линейно зависит от координаты.

Уравнение для q удобно переписать в виде

(1.14)
$q = {{q}_{0}}P{{\left( {1 + \frac{h}{{{{h}_{c}}}}} \right)}^{{ - 1}}}$
${{q}_{0}} = \frac{{\Delta {{p}_{0}}}}{{\mu {{G}_{m}}{{h}_{m}}}}$, ${{h}_{c}} = \frac{{{{G}_{m}}{{h}_{m}}}}{G}$, $P = \frac{{\Delta p}}{{\Delta {{p}_{0}}}}$, $\Delta {{p}_{0}} = {{p}_{0}} - {{p}_{e}}$

Здесь ${{q}_{0}}$ – максимальный поток фильтрата (при t = 0); ${{h}_{c}}$ – характерная толщина осадка; ${{p}_{0}}$ – давление на входе в канал; P – безразмерный перепад давления, который используется ниже при обезразмеривании уравнения импульсов.

Таким образом, имеем замкнутую систему уравнений (1.10)–(1.14) для неизвестных величин u, c, p, h, q, представляющую математическую модель исследуемого процесса. Отметим, что в [9] использованы уравнение неразрывности для дисперсного компонента (второе уравнение системы (1.9)) и уравнение (1.10) без диффузионных слагаемых, а вместо уравнения импульсов (1.12) принято условие постоянства перепада давления (Δp = const).

Дадим оценку параметров канала, при которых выполняются основные допущения настоящего раздела. При наличии оттока жидкости через стенки канала необходимо установить условия малости компонента скорости потока в направлении стенок. С этой целью возьмем отношение максимального потока фильтрата ${{q}_{0}}$ и соответствующей ему продольной скорости суспензии ${{u}_{0}} = L{{q}_{0}}{\text{/}}a$, где L – длина канала, $a = S{\text{/}}\Lambda $ – характерный поперечный размер или гидравлический радиус [25] канала. Имеем ${{q}_{0}}$/${{u}_{0}}$ = a/L. При a/L $ \ll $ 1 или для достаточно длинных по сравнению с характерным поперечным размером каналов можно принять малым компонент скорости потока в направлении стенок по сравнению с продольным компонентом. Для типичного фильтровального канала [9] с параметрами L = 1 м, a = 10–2 м это условие довольно хорошо выполняется.

Кроме того, канал должен быть настолько длинным, чтобы можно было пренебречь краевыми эффектами на входе в канал. Если пренебречь эффектами неодномерности из-за оттока жидкости через стенки, то для трубы круглого сечения длина входного участка, на протяжении которого погранслойное течение переходит в пуазейловское по оценкам [27], составляет величину порядка 0.1rRe, где r – радиус трубы, Re – число Рейнольдса, рассчитанное по диаметру трубы. Таким образом, для исключения эффектов входного участка должно выполняться условие 0.1rRe/L $ \ll $ 1. Например, для воды, движущейся со скоростью ${{u}_{0}}$ ~ 10–2 м/с в трубе с вышеприведенными типичными параметрами указанное условие имеет место.

Введем безразмерные переменные

$T = \frac{{t{{u}_{0}}}}{L}$, $X = \frac{x}{L}$, $U = \frac{u}{{{{u}_{0}}}}$, $C = \frac{c}{{{{c}_{0}}}}$, $Q = \frac{q}{{{{q}_{0}}}}$, $H = \frac{h}{a}$, $P = \frac{{\Delta p}}{{\Delta {{p}_{0}}}}$
где ${{q}_{0}}$, ${{u}_{0}}$ – максимальный поток фильтрата и соответствующая ему скорость суспензии; ${{c}_{0}}$ – объемная концентрация частиц на входе в канал. Отметим, что поскольку в уравнение для q входит перепад давления Δp, то за масштаб давления удобно взять характерное значение перепада давления $\Delta {{p}_{0}} = {{p}_{0}} - {{p}_{e}}$. В уравнении импульсов вместо давления p используем перепад давления $\Delta p = p - {{p}_{e}}$.

Уравнение конвективной диффузии (1.11) и уравнение для скорости суспензии (1.10) в безразмерных переменных примут форму

(1.15)
$\frac{{\partial C}}{{\partial T}} = - U\frac{{\partial C}}{{\partial X}} + \frac{{1 + \gamma C}}{{{\text{Pe}}}}\frac{{{{\partial }^{2}}C}}{{\partial {{X}^{2}}}}$
(1.16)
$\frac{{\partial U}}{{\partial x}} = - Q - \frac{\gamma }{{{\text{Pe}}}}\frac{{{{\partial }^{2}}C}}{{\partial {{X}^{2}}}}$
${\text{Pe}} = \frac{{L{{u}_{0}}}}{D}$, $\gamma = {{c}_{0}}\left( {\frac{{\rho _{{\text{2}}}^{^\circ }}}{{\rho _{{\text{1}}}^{^\circ }}} - 1} \right)$

Здесь Pe – характерное число Пекле; γ > 0 – параметр, характеризующий состав суспензии ($\rho _{{\text{2}}}^{^\circ }$ > $\rho _{{\text{1}}}^{^\circ }$).

В безразмерных переменных уравнение импульсов (1.12) запишется в виде

(1.17)
$\begin{gathered} \frac{{\partial P}}{{\partial X}} = - \frac{{1 + \gamma C}}{\varphi }\left( {\frac{{\partial U}}{{\partial T}} + U\frac{{\partial U}}{{\partial X}} + \psi {{U}^{2}}} \right) \\ \varphi = \frac{{\Delta {{p}_{0}}}}{{\rho _{{\text{1}}}^{^\circ }u_{0}^{2}}},\quad \psi = {{K}_{f}}\frac{L}{{2a}} \\ \end{gathered} $

Оценки показали, что параметр φ обычно принимает достаточно большие значения, а коэффициент γ мал из-за малости ${{c}_{0}}$ (параметр γ может оказаться малым также при $\rho _{{\text{2}}}^{^\circ }$ ~ $\rho _{{\text{1}}}^{^\circ }$). Например, когда $\Delta {{p}_{0}}$ ~ 0.1 МПа, $\rho _{{\text{1}}}^{^\circ }$ ~ 103 кг/м3, ${{u}_{0}}$ ~ 10–2 м/с, L ~ 1 м, a ~ 10–2 м (порядки величин совпадают с приведенными в [9] данными для типичного фильтровального процесса), получим φ ~ 106. Оценки коэффициента трения по численным [28] и экспериментальным [29] результатам дают ${{K}_{f}}$ ~ 10–3 (наличие осадка на стенках канала не приводит к существенному изменению коэффициента трения), так что параметр ψ~10–1. Проведенные оценки говорят о том, что изменением давления вдоль канала, определяемым уравнением (1.17), можно пренебречь и считать давление в канале однородным. Далее примем, что $\Delta p = \Delta {{p}_{0}}$ (тогда P = 1), при этом уравнение импульсов можно исключить из дальнейшего рассмотрения.

Начальное и граничные условия для объемной концентрации C и скорости U примем в следующем виде

(1.18)
$\begin{gathered} C(X,{\text{ }}0) = 0,\quad C(0,{\text{ }}T) = {\text{1}},\quad \frac{{\partial С }}{{\partial X}}(1,{\text{ }}T) = 0,\quad U({\text{1}},T){\text{ }} = {{U}_{L}} \\ {{U}_{L}} = \frac{{{{u}_{L}}}}{{{{u}_{0}}}} \\ \end{gathered} $
где ${{u}_{L}}$ – скорость среды на выходе из канала; в первом приближении ее можно считать постоянной. В случае тупикового канала при закрытом правом конце ${{U}_{L}}$ = 0.

В начальный момент времени имеем скачок концентрации на входе в канал. Предпоследнее соотношение в (1.18) вытекает из условия, что на твердой границе должно обращаться в нуль нормальный к поверхности компонент диффузионного потока [24]. Для открытого канала это равенство обеспечивает непрерывность концентрации на выходе из канала. При отсутствии диффузионного слагаемого (Pe → ∞) в (1.15), согласно решению гиперболического уравнения переноса, первоначальный скачок концентрации будет перемещаться вдоль канала, не меняя своей формы. Отметим, что если в начальный момент времени C = 1 на всем протяжении канала [9], то в рамках принятой одножидкостной модели концентрация частиц таковой останется и в дальнейшем.

С учетом начального условия Q(X,0) = 1 и принятого выше равенства P = 1 для безразмерных потока фильтрата и толщины осадка имеем

(1.19)
$Q(X,T) = {{\left( {1 + 2\kappa \int\limits_0^T {Cd\tau } } \right)}^{{ - 1/2}}}$
(1.20)
$H(X,T) = \frac{1}{{{{C}_{d}}}}\delta (X,T),\quad \delta (X,T) = \frac{1}{\kappa }({{Q}^{{ - 1}}} - 1)$
$\kappa = \frac{1}{{{{C}_{d}}}}\frac{a}{{{{h}_{c}}}}$, ${{C}_{d}} = \frac{{{{c}_{d}}}}{{{{c}_{0}}}}$

Здесь ${{c}_{d}} = 1 - \varepsilon $ – объемная доля твердого вещества в осадке.

Отметим, что уравнение (1.15) с учетом (1.16), (1.19) представляет собой нелинейное интегро-дифференциальное уравнение, для решения которого используются численные методы.

Для проведения расчетов уравнение для скорости (1.16) удобно один раз проинтегрировать и получить с учетом (1.19) и краевых условий (1.18) следующее соотношение

(1.21)
$U(X,T) = {{U}_{L}} + \int\limits_X^1 {{{{\left( {1 + 2\kappa \int\limits_0^T {Cd\tau } } \right)}}^{{ - 1/2}}}d\chi } - \frac{\gamma }{{{\text{Pe}}}}\frac{{\partial C}}{{\partial X}}$

Видно, что в случае тупикового канала скорость суспензии на входе в канал X = 0 ограничена интенсивностью оттока жидкости через боковую фильтрующую поверхность, определяемой вторым слагаемым в (1.21) (третье слагаемое мало из-за малости γ), а в случае с открытым правым концом еще и скоростью на выходе из канала UL.

Средний поток фильтрата $\bar {Q}(T)$ можно вычислить при известных значениях потока вдоль канала Q(X, T) по формуле

$\bar {Q}(T) = \int\limits_0^1 {Q(X,T)dX} $

Определяющими параметрами поставленной задачи являются следующие пять параметров

κ, Pe, ${{C}_{d}}$, γ, ${{U}_{L}}$

В случае тупикового канала параметр ${{U}_{L}}$ отпадает, а параметр γ достаточно мал. Последнее обстоятельство позволяет представить систему (1.15) (1.16) в приближенном виде

(1.22)
$\frac{{\partial C}}{{\partial T}} = - U\frac{{\partial C}}{{\partial X}} + \frac{1}{{{\text{Pe}}}}\frac{{{{\partial }^{2}}C}}{{\partial {{X}^{2}}}}$
(1.23)
$\frac{{\partial U}}{{\partial x}} = - Q$

Вместо уравнения (1.23) можно использовать (1.21) без последнего слагаемого. В случае отсутствия осадкообразования G = 0 (${{c}_{0}}$ ≠ 0, т.к. при ${{c}_{0}}$ = 0 имеем только несущую жидкость) или при κ = 0 получим Q = 1 и U = ${{U}_{L}}$ + (1–X); для тупикового канала U = 1–X.

Отметим, что при U = const применение известных методов математической физики [30] позволяет получить аналитическое решение уравнения (1.22). При U = 1 это решение с учетом граничного и начального условий (1.18) запишется в форме

(1.24)
$\begin{gathered} C(X,T) = \left[ {\left( {1 - \frac{X}{{1 + 2\beta }}} \right)\exp \left( {\frac{T}{{4\beta }}} \right) + \sum\limits_{n = 1}^\infty {{{\theta }_{n}}(T)\sin ({{\lambda }_{n}}X)} } \right]\exp \left( {\frac{{X - 0.5T}}{{2\beta }}} \right) \\ {{\theta }_{n}}(T) = {{a}_{n}}\left\{ {\exp ( - \beta \lambda _{n}^{2}T) + \frac{1}{{1 + 4{{\beta }^{2}}\lambda _{n}^{2}}}\left[ {\exp \left( {\frac{T}{{4\beta }}} \right) - \exp ( - \beta \lambda _{n}^{2}T)} \right]} \right\} \\ {{a}_{n}} = - \frac{2}{{{{\lambda }_{n}} - \sin {{\lambda }_{n}}\cos {{\lambda }_{n}}}}\left[ {1 - \cos {{\lambda }_{n}} - \frac{{\sin {{\lambda }_{n}} - {{\lambda }_{n}}\cos {{\lambda }_{n}}}}{{{{\lambda }_{n}}(1 + 2\beta )}}} \right],\quad \beta = \frac{1}{{{\text{Pe}}}} \\ \end{gathered} $

Здесь ${{\lambda }_{n}}$ – положительные корни трансцендентного уравнения tgλ + 2βλ = 0.

При U = 0 решение уравнения диффузии (1.22), удовлетворяющее условиям (1.18), имеет вид

(1.25)
$\begin{gathered} C(X,T) = 1 - \sum\limits_{n = 1}^\infty {\frac{2}{{{{\lambda }_{n}}}}\exp ( - \beta \lambda _{n}^{2}T)\sin ({{\lambda }_{n}}X)} \\ {{\lambda }_{n}} = \frac{{1 + 2n}}{2}\pi \\ \end{gathered} $

Соотношения (1.24), (1.25) используются для проверки компьютерного алгоритма численного решения поставленной задачи. Решение приближенного уравнения (1.22) будет располагаться между этими аналитическими решениями.

Предельному значению концентрации C = 1 соответствуют следующие выражения для параметров суспензии

(1.26)
${{U}_{ * }}(X,T) = {{\left( {1 + 2\kappa T} \right)}^{{ - 1/2}}}(1 - X),\quad {{Q}_{ * }} = {{\bar {Q}}_{ * }} = {{(1 + 2\kappa T)}^{{ - 1/2}}},\quad {{\delta }_{ * }} = \frac{1}{\kappa }[{{(1 + 2\kappa T)}^{{1/2}}} - 1]$
которые ограничивают в каждый момент времени действительные распределения в канале (поскольку в рассматриваемой постановке всегда C ≤ 1)

$U \geqslant {{U}_{ * }}$, $Q \geqslant {{Q}_{ * }}$, $\bar {Q} \geqslant {{\bar {Q}}_{ * }}$, $\delta \leqslant {{\delta }_{ * }}$

Учитывая предельное (с ростом времени) значение объемной концентрации в канале C = 1, из (1.26) следуют приближенные зависимости, описывающие асимптотическое поведение параметров смеси в канале при сколь угодно больших временах T $ \gg $ 1

(1.27)
$U(X,T) \cong {{(2\kappa T)}^{{ - 1/2}}}(1 - X),\quad \bar {Q} \cong {{(2\kappa T)}^{{ - 1/2}}},\quad \delta \cong {{\left( {\frac{2}{\kappa }T} \right)}^{{1/2}}}$

Согласно этим зависимостям скорость и средний поток фильтрата с течением времени ведут себя как ${{T}^{{ - 1/2}}}$, тогда как толщина осадка меняется как ${{T}^{{1/2}}}$. Соотношения (1.27) можно использовать для получения простых связей между характеризующими исследуемый процесс параметрами при больших временах, в частности, δ$\bar {Q} \cong $ 1/κ.

2. РЕЗУЛЬТАТЫ РАСЧЕТОВ

Интегро-дифференциальное уравнение (1.15) для C с учетом соотношений (1.19), (1.21) для Q и U и начально-краевых условий (1.18) решалось численным методом конечных разностей с контролем необходимой точности и условий устойчивости расчетов. Толщина осадка вычислялась по формуле (1.20) при известных значениях Q. Во всех расчетах принималось γ = 10–3. Расчеты показали, что использование вместо уравнений (1.15), (1.16) приближенных соотношений (1.22), (1.23) дает практически одинаковые результаты.

На рис. 1 представлены распределения безразмерной скорости U, относительной объемной концентрации дисперсного компонента смеси C, безразмерного потока фильтрата Q, а также параметра δ, характеризующего безразмерную толщину осадка на стенке при κ = 1, Pe = 10, вдоль тупикового канала (${{U}_{L}}$ = 0).

Рис. 1.

Распределения параметров суспензии вдоль тупикового канала в разные моменты времени при κ = 1, Pe = 10, ${{U}_{L}}$ = 0: 1 – 8 – T=0.25, 0.50, 0.75, 1.0, 1.25, 1.50, 1.75, 2.0; сплошные кривые – с диффузией и осадкообразованием; штриховые – без учета диффузии (Pe → ∞); штрихпунктирные – без учета осадкообразования (κ = 0); пунктирные – предельные решения, рассчитанные по (1.24) и соответствующие моментам времени T = 0.25, 0.50, 1.0

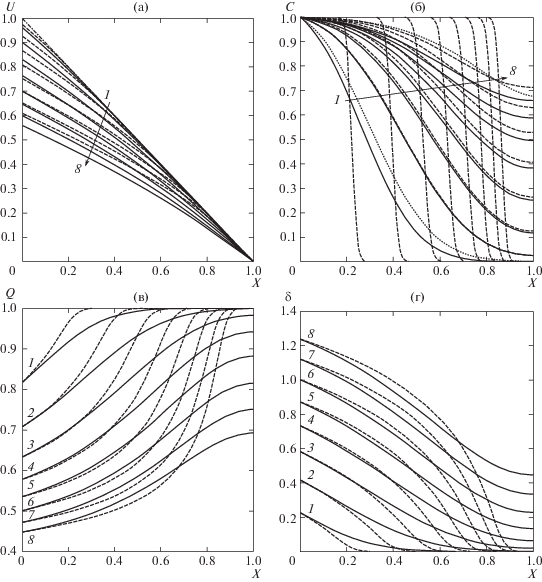
Из приведенных на рис. 1 зависимостей следует, что скорость движения суспензии в канале с течением времени из-за увеличения толщины осадка постепенно уменьшается, причем наличие процессов осадкообразования и диффузии приводит к снижению скорости суспензии. С течением времени различие в распределении скорости суспензии вдоль канала при наличии и отсутствии диффузии увеличивается. На начальной стадии при T $ \lesssim $ 0.5 распределения C(X), соответствующие наличию (сплошные кривые) и отсутствию (штрихпунктирные кривые) осадкообразования особо не различаются, поскольку в эти моменты на стенках канала сколько-нибудь существенного осадка не образуется. Заметное различие между этими случаями имеет место в более поздние моменты времени. Отметим, что рассчитанное по (1.24) и численное распределения объемной концентрации вначале отличаются незначительно, но с течением времени различие между ними увеличивается и, начиная с некоторого момента времени T $ \gtrsim $ 0.5, оно становится существенным (рис. 1б).

Поток фильтрата принимает минимальное значение на входе в канал и растет вдоль канала, достигая максимального значения на правом конце канала, причем с течением времени он снижается. Отметим некоторую особенность поведения распределения потока фильтрата Q вдоль канала при наличии и отсутствии диффузии (рис. 1в). До момента времени T $ \cong $ 0.75 наличие диффузии приводит к уменьшению потока фильтрата по всей длине канала. Однако с течением времени эффект диффузии частиц проявляется на разных участках канала по-разному: на начальном участке, простирающемся от входа до некоторой критической точки, наличие процесса диффузии приводит к росту потока фильтрата, тогда как во втором участке, занимающем отрезок от упомянутой критической точки до правого конца канала, диффузия приводит, наоборот, к снижению величины Q.

Толщина осадка вдоль канала постепенно уменьшается, достигая своего минимального значения на правом конце канала (рис. 1г). Отметим, что особенность, аналогичная для потока фильтрата, наблюдается и в процессе формирования осадка на стенке канала: до момента времени T $ \cong $ 0.75 наличие диффузионных потоков влечет собой увеличение толщины осадка на стенке канала, тогда как при T $ \gtrsim $ 0.75 длину канала можно разбить на два характерных участка, на первом из которых диффузия приводит к уменьшению толщины осадка, а на втором – к ее росту.

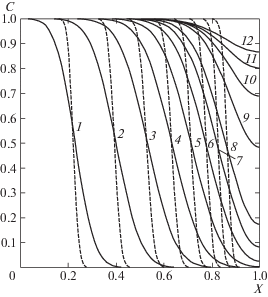
Для определения влияния числа Пекле на поведение суспензии на рис. 2 показано распределение объемной концентрации частиц C вдоль канала при Pe = 100 (аналогично рис. 1). Штриховые кривые соответствуют отсутствию диффузионных потоков (Pe → ∞). Сравнивая рис. 2 с рис. 1б, можно заметить сильное различие в поведении зависимости C(X) при разных значениях параметра Pe: при большем значении Pe из-за уменьшения интенсивности процесса диффузии профиль концентрации частиц расплывается вдоль канала намного слабее. Расчеты также показали, что с ростом Pe толщина осадка в окрестности закрытого конца канала уменьшается, при этом поток фильтрата в этой зоне увеличивается.

Рис. 2.

Распределения объемной концентрации суспензии вдоль тупикового канала в разные моменты времени при κ = 1, Pe = 100, ${{U}_{L}}$ = 0: кривые 1–8 соответствуют тем же моментам времени, что на рис. 1; 9 –12 – T = 2.75, 3.50, 4.25, 5.0; штриховые кривые – без учета диффузии (Pe → ∞)

Расчетами установлено, что рост параметра κ приводит к существенному уменьшению потока фильтрата и соответственно к уменьшению скорости суспензии в канале; данный вывод основан на сравнении результатов, отвечающих значению κ = 0, с расчетными данными для κ = 1.

Результаты расчетов для канала с открытым правым концом при ${{U}_{L}}$ = 0.5 свидетельствуют, что по сравнению с тупиковым каналом концентрация дисперсной фазы значительно быстрее достигает своего предельного значения 1 вдоль всего канала (рис. 3). Это приводит, в свою очередь, к заметному росту толщины осадка вдоль трубы при уменьшении потока фильтрата.

Рис. 3.

Распределения объемной концентрации суспензии вдоль открытого канала в разные моменты времени при κ = 1, Pe = 100, ${{U}_{L}}$ = 0.5: 1 –7 – T = 0.25, 0.50, 0.75, 1.0, 1.25, 1.50, 1.75

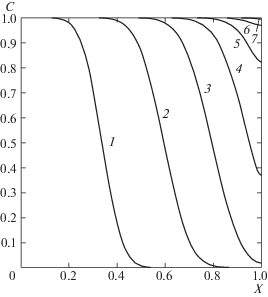
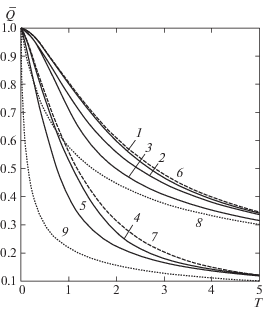
Рисунок 4 иллюстрирует поведение зависимости среднего потока фильтрата $\bar {Q}$ от времени при разных значениях определяющих параметров. Видно, что с уменьшением числа Ре, также как и при увеличении параметра κ, средний поток фильтрата уменьшается, причем изменение κ влияет на поведение зависимости $\bar {Q}(T)$ намного сильнее, чем изменение Ре. Открытый правый конец канала также приводит к уменьшению $\bar {Q}$. Следует отметить, что в рассматриваемом диапазоне изменения определяющих параметров наличие диффузии дисперсной примеси практически не сказывается на среднем потоке фильтрата, хотя с уменьшением числа Пекле влияние диффузии на $\bar {Q}$ заметно усиливается. Для каждого заданного значения κ кривые $\bar {Q}(T)$, получающиеся при варьировании параметров Ре и UL, располагаются между соответствующими данному значению κ пунктирной и штриховой линиями.

Рис. 4.

Зависимость среднего потока фильтрата от времени: 1 – κ = 1, Pe = 100, ${{U}_{L}}$ = 0; 2 – κ = 1, Pe = 10, ${{U}_{L}}$ = 0; 3 – κ = 1, Pe = 100, ${{U}_{L}}$ = 0.5; 4 – κ = 10, Pe = 100, ${{U}_{L}}$ = 0; 5 – κ = 10, Pe = 10, ${{U}_{L}}$ = 0; 6 и 7 –отсутствие диффузии (Pe → ∞) при κ = 1 и 10 (${{U}_{L}}$ = 0); 8 и 9 – формула (1.26) для ${{\bar {Q}}_{ * }}$ при тех же значениях κ

ЗАКЛЮЧЕНИЕ

На основе построенной одномерной модели проведены расчеты фильтрации суспензии в канале с учетом диффузии мелкодисперсной фазы и осадкообразования на стенках канала. Показано, что в исследованном диапазоне изменения определяющих параметров давление внутри канала можно принимать однородным.

Получены приближенные формулы, характеризующие асимптотическое поведение параметров рассматриваемого процесса при больших временах. Проведено сравнение найденного приближенного аналитического решения с численным решением задачи. Проанализировано влияние процесса диффузии дисперсных частиц, а также определяющих параметров на течение суспензии в тупиковом и открытом каналах.

Расчеты показали, что до определенного момента времени наличие диффузии приводит к уменьшению потока фильтрата по всей длине канала. В более поздние моменты диффузия влияет на поток фильтрата неравномерно: на начальном участке канала из-за диффузии поток фильтрата растет, а на участке ближе к концу канала, – наоборот, существенно падает. Установлено, что по сравнению с тупиковым каналом в открытом канале средний поток фильтрата уменьшается.

За рамками построенной модели остались эффекты кольматации мембраны и сжимаемости осадка, приводящие к снижению их проницаемости, и которые могут быть учтены при дальнейшем развитии предлагаемой модели.

Работа выполнена при финансовой поддержке Министерства образования и науки Республики Казахстан (грант № 3486/ГФ4).

Список литературы

  1. Жужиков В.А. Фильтрование. Теория и практика разделения суспензий. М.: Химия, 1971. 156 с.

  2. Coussy O. Poromechanics. Chichester: Wiley, 2004. 315 p.

  3. Шехтман Ю.М. Фильтрация малоконцентрированных суспензий. М.: Изд-во АН СССР, 1961. 212 с.

  4. Ершин Ш.А. Гидроаэродинамика. Алматы: Изд-во КазНУ им. Аль-Фараби, 2013. 354 с.

  5. Леонтьев Н.Е. Точные решения задачи о фильтрации суспензии с замедлением скачка концентрации в рамках нелинейной двухскоростной модели // Изв. РАН. МЖГ. 2017. № 1. С. 168–174. https://doi.org/10.7868/S0568528117010108

  6. Димов C.В., Кузнецов В.В., Рудяк В.Я., Тропин Н.М. Экспериментальное изучение фильтрации микросуспензии в высокопроницаемой пористой среде // Изв. РАН. МЖГ. 2012. № 2. С. 47–56.

  7. Ахмадиев Ф.Г., Ибятов Р.И., Киямов Х.Г. Математическое моделирование процесса разделения суспензии в барабанном вакуум-фильтре со сходящей рабочей лентой // Теорет. основы хим. технологии. 1998. Т. 32. № 2. С. 188–194.

  8. Давыдова Е.Б. Средства и модели мембранной микрофильтрации промышленных жидких сред в автоматизированных технологических комплексах: Автореф. дис. … канд. тех. наук: 05.13.06. Владимир, 2013. 16 с.

  9. Давыдова Е.Б., Ильин М.И., Тарасов А.В. Моделирование нестационарного процесса фильтрации суспензий в тупиковом канале // Теорет. основы хим. технологии. 2013. Т. 47. № 3. С. 352–354. https://doi.org/10.7868/S0040357113030032

  10. Дытнерский Ю.И. Обратный осмос и ультрафильтрация. М.: Химия, 1978. 352 с.

  11. Поляков Ю.С. Ультра- и микрофильтрация в половолоконных аппаратах с образованием осадка на поверхности мембран: Дис. … канд. тех. наук: 05.17.08. М., 2004. 150 с.

  12. Ильин М.И., Федотов Ю.А., Яманов Ю.И., Тарасов А.В. Мембранный фильтрующий модуль. Пат. 2194566 С1 Ru. 2002.

  13. Асмолов Е.С., Лебедева Н.А., Осипцов А.A. Инерционная миграция осаждающихся частиц при течении суспензии в ячейке Хеле–Шоу // Изв. РАН. МЖГ. 2009. № 3. С. 85–101.

  14. Jackson R. The dynamics of fluidized particles. Cambridge: Cambridge University Press, 2000. 339 p.

  15. Hammond P.S. Settling and slumping in a Newtonian slurry, and implications for proppant placement during hydraulic fracturing of gas wells // Chem. Eng. Sci. 1995. V. 50. № 20. P. 3247–3260.

  16. Михайлов Н.Н. Изменение физических свойств горных пород в околоскважинных зонах. М.: Недра, 1987. 151 с.

  17. Иванников В.И., Кучеренко Э.И., Михлин Л.П. Аналитическое исследование процесса фильтрации бурового раствора из скважины в пласт // Докл. АН СССР. 1986. Т. 290. №5. С. 1072–1076.

  18. Фукс А.Н. Механика аэрозолей. М.: Изд-во АН СССР, 1955. 353 с.

  19. Стечкина И.Б., Кирш А.А. Диффузионный метод определения размеров взвешенных в газе наночастиц // Коллоид. журнал. 2013. Т. 75. № 4. С. 538–540. https://doi.org/10.7868/S0023291213040137

  20. Капранов Ю.И. Модели кольматации пористых сред // Математические модели фильтрации и их приложения. Новосибирск: Институт гидродинамики им. М.А. Лаврентьева, 1999. С. 89–97.

  21. Нигматулин Р.И. Динамика многофазных сред. Ч. 1. М.: Наука, 1987. 464 с.

  22. Седов Л.И. Механика сплошной среды. Т. 1. М.: Наука, 1983. 528 с.

  23. Einstein A. Investigations on the theory of Brownian movement. New York: Dover, 1956. 144 p.

  24. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. VI. Гидродинамика. М.: Наука, 1988. 736 с.

  25. Уоллис Г. Одномерные двухфазные течения. М.: Мир, 1972. 440 с.

  26. Лойцянский Л.Г. Механика жидкости и газа. М.: Наука, 1987. 840 с.

  27. Левич В.Г. Физико-химическая гидродинамика. М.: Гос. издат. физ.-матем. литер., 1959. 700 с.

  28. Батенко С.Р., Терехов В.И. Трение и теплообмен в ламинарном отрывном потоке за прямоугольным уступом при наличии пористого вдува или отсоса // Прикл. мех. и техн. физ. 2006. Т. 47. № 1. С. 18–28.

  29. Бойко А.В., Корнилов В.И. Измерение локального коэффициента поверхностного трения с помощью термоанемометра // Теплофизика и аэромеханика. 2010. Т. 17. № 4. С. 613–623.

  30. Тихонов А.Н., Самарский А.А. Уравнения математической физики. М.: Изд-во МГУ, 1999. 735 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал