Известия РАН. Механика жидкости и газа, 2019, № 3, стр. 58-69

ВЛИЯНИЕ ПРИМЕСИ НЕИСПАРЯЮЩИХСЯ КАПЕЛЬ НА СТРУКТУРУ ТЕЧЕНИЯ И ТЕМПЕРАТУРУ АДИАБАТИЧЕСКОЙ СТЕНКИ В СЖИМАЕМОМ ДВУХФАЗНОМ ПОГРАНИЧНОМ СЛОЕ

И. В. Голубкина^a, *, А. Н. Осипцов^a, **

^a МГУ им. М.В. Ломоносова, Научно-исследовательский институт механики
Москва, Россия

^* E-mail: giv-mm@mail.ru
^** E-mail: osiptsov@imec.msu.ru

Поступила в редакцию 18.10.2018
После доработки 18.10.2018
Принята к публикации 19.10.2018

DOI: 10.1134/S0568528119030046

Аннотация

Построена математическая модель и проведены численные расчеты задачи продольного обтекания плоской теплоизолированной пластины высокоскоростным стационарным потоком вязкого теплопроводного газа с примесью жидких капель, температура которых отличается от температуры несущей фазы. Рассматривается диапазон параметров течения, в котором испарением капель можно пренебречь, при этом внутри пограничного слоя температура капель может существенно изменяться. Математическая модель двухфазного пограничного слоя модифицирована с учетом неоднородности температуры по радиусу капель, что потребовало, наряду с решением макроуравнений двухжидкостной модели, находить решение уравнения теплопроводности внутри капель. На основании параметрических расчетов исследованы режимы течения с образованием жидкой пленки за счет осаждающихся на стенку капель. Определены параметры подобия и найден диапазон определяющих параметров, в котором за счет теплообмена с жидкой фазой в пограничном слое происходит заметное снижение температуры адиабатической стенки даже при очень малых исходных концентрациях капель.

Ключевые слова: капли, газокапельная смесь, пограничный слой, теплоизолированная стенка, безмашинное энергоразделение, равновесная температура

Ранее, в работах [1–3], обтекание пластины сверхзвуковым газокапельным потоком рассматривалось в диапазоне очень высоких температур стенки, когда либо на самой пластине, либо в пристеночной области пограничного слоя происходит быстрое испарение капель, что и определяет тепловой баланс между двухфазным потоком и адиабатической стенкой. В настоящей работе рассматривается диапазон невысоких температур стенки, когда испарением капель можно пренебречь, но за счет осаждения капель под действием боковых сил Сэфмана на стенке может формироваться тонкая жидкая пленка. Целью исследования является количественная оценка равновесной температуры адиабатической стенки с учетом наличия жидкой пленки при различных исходных температурах жидкой и газовой фаз в набегающем потоке.

Рассматриваемая задача является ключевым элементом проблемы безмашинного энергоразделения газовых потоков по схеме А.И. Леонтьева [4], представляющей альтернативу известному способу безмашинного энергоразделения газовых потоков с помощью вихревых трубок Ранка-Хилша [5]. При относительной эффективности энергоразделения, трубки Ранка-Хилша обладают существенным недостатком, обусловленным их большим гидравлическим сопротивлением. Схема безмашинного энергоразделения газового потока, предложенная в [4], лишена указанного недостатка. Указанная схема [4] основана на теплообмене между до- и сверхзвуковым потоками, имеющими одинаковые параметры торможения и разделенными тонкой перегородкой с низким тепловым сопротивлением. В настоящее время обсуждаются различные возможные способы повышения эффективности схемы [4], в том числе: применение перфорированных перегородок [6], использование щелевого и распределенного вдува или отсоса газа, создание рельефа на разделяющей перегородке [7] и др. В [1–3] обсуждалась возможность использования примеси конденсированной жидкой фазы в сверхзвуковом потоке для интенсификации теплообмена на разделительной перегородке. В [1] рассмотрен предельный случай горячей стенки и относительно крупных капель, для которых в пограничном слое пластины существенна боковая сила Сэфмана [8], обусловленная локальным градиентом скорости потока на масштабе капли. Под действием указанной силы капли выносятся на обтекаемую горячую поверхность, где и происходит их испарение. В [2] рассматривается другой предельный случай достаточно мелких капель, которые не попадают на стенку, поскольку успевают испариться еще в области пограничного слоя. Как показано в [3], повышение эффективности энергоразделения газового потока по схеме [4] обусловлено, по сути, уменьшением температуры восстановления на стенке в сверхзвуковом пограничном слое. Поэтому параметрическое исследование задачи о ламинарном газокапельном пограничном слое в высокоскоростном стационарном двухфазном потоке на адиабатической плоской пластине и выяснение диапазона параметров, в котором капли приводят к заметному снижению равновесной температуры стенки, представляют существенный интерес.

В качестве основы математической модели ниже используются основные положения теории двухфазного ламинарного пограничного слоя при малой объемной концентрации капель [9–11]. Дисперсная фаза описывается уравнениями континуума, лишенного собственных напряжений, столкновениями и броуновским движением капель пренебрегается. Объемная концентрация капель считается пренебрежимо малой, а массовая концентрация капель конечна, но достаточно мала. В рассматриваемом ниже случае потребовалось значительное усложнение модели двухфазного пограничного слоя в связи с необходимостью учета неоднородности температуры внутри капель, а также наличия жидкой пленки, формирующейся за счет выпадающих на стенку капель. Указанные обстоятельства потребовали, наряду с решением макроуравнений двухконитуального приближения, решать уравнения теплопроводности внутри отдельных капель и рассматривать уравнения жидкой пленки на обтекаемой поверхности.

Исследования влияния капель на структуру пограничного слоя и теплообмен с обтекаемой поверхностью имеют уже значительную историю. Обзоры литературы можно найти, например, в [11, 12]. Подчеркнем лишь, что в данной работе существенно новыми элементами постановки задачи о течении в двухфазном сжимаемом пограничном слое являются: учет неоднородности температуры внутри капель и формирование жидкой пленки на обтекаемой поверхности за счет капель, выносимых на стенку боковой силой Сэфмана [8].

1. ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ

Рассматривается стационарное обтекание полубесконечной плоской пластины сверхзвуковым ламинарным потоком газокапельной смеси. Декартова система координат (Oxy) связана с началом пластины. Несущая фаза – сжимаемый совершенный теплопроводный газ с постоянными теплоемкостями. Вязкость и теплопроводность несущей фазы зависят от температуры по степенному закону: λ/λ_∞ = μ/μ_∞ = (T/T_∞)^ω; индекс ∞ относится к параметрам набегающего потока. Среда частиц описывается в континуальном приближении уравнениями “холодного” (лишенного собственных напряжений) континуума с постоянной массой и радиусом капель:

(1.1)

$\begin{gathered} {\text{div}}({{n}_{s}}{{{\mathbf{V}}}_{s}}) = 0,\quad m({{{\mathbf{V}}}_{s}}\nabla ){{{\mathbf{V}}}_{s}} = {{{\mathbf{f}}}_{s}} \\ {{c}_{s}}m({{{\mathbf{V}}}_{s}}\nabla )\left\langle {{{T}_{s}}} \right\rangle = {{q}_{s}},\quad \left\langle {{{T}_{s}}} \right\rangle = \frac{1}{\sigma }\int\limits_0^\sigma {{{T}_{s}}} (r)dr \\ \end{gathered} $

Здесь n_s – числовая плотность капель, имеющих радиус σ и массу m, V_s – скорость капель, c_s – теплоемкость вещества капель, $\left\langle {{{T}_{s}}} \right\rangle $ – температура вещества капли, осредненная по ее объему, f_s – сумма сил аэродинамического сопротивления капли и подъемной силы Сэфмана [8, 10], q_s – приток тепла к поверхности капли со стороны газовой фазы. Считается, что капли обтекаются в режиме сплошной среды при достаточно малых числах Рейнольдса, поэтому можно использовать выражения для f_s и q_s, справедливые для стационарного обтекания сферы радиуса σ локально сдвиговым потоком:

(1.2)

${{{\mathbf{f}}}_{s}} = 6\pi \sigma \mu ({\mathbf{V}} - {{{\mathbf{V}}}_{s}}) + 6.46{{\sigma }^{2}}{{\left( {\mu \rho \frac{{\partial u}}{{\partial y}}} \right)}^{{1/2}}}\left( {u - {{u}_{s}}} \right){\mathbf{j}},\quad {{q}_{s}} = 4\pi \sigma \lambda (T - {{T}_{{sw}}})$

где V, T, μ, ρ и ∂u/∂y – скорость, температура, вязкость, плотность и градиент скорости несущей фазы в точке, где находится капля, T_sw – температура поверхности капли, j – единичный орт оси ординат.

В стандартной модели “запыленного газа” [9] обычно предполагается, что температуру внутри капли можно считать однородной, и тогда ${{T}_{{sw}}} = \left\langle {{{T}_{s}}} \right\rangle $. Такое предположение справедливо для большинства твердых материалов, имеющих высокую температуропроводность. В случае испаряющихся капель [1–3] температура их поверхностей T_sw предполагалась постоянной во всем поле течения, что также существенно упрощало численные расчеты.

В случае, рассматриваемом в настоящей работе, приходится учитывать неоднородность температуры по радиусу капель (и отличие T_sw от $\left\langle {{{T}_{s}}} \right\rangle $), поскольку температуропроводность воды невысока. Этот факт следует из соотношения характерных времен установления однородной температуры внутри капли τ = c_sσ²ρ$_{s}^{0}$/λ_s и скоростной релаксации капли ${{\tau }_{\text{v}}}$ = m/6πσμ = 2σ²ρ$_{s}^{0}$/9μ (здесь λ_s и ρ$_{s}^{0}$ – теплопроводность и плотность вещества капель). Для водяных капель при нормальных условиях эти времена имеют одинаковый порядок величины: τ/${{\tau }_{\text{v}}}$ = 9c_sμ/2λ_s ≈ 0.57, поэтому, вместо последнего уравнения (1.1), следует решать уравнение теплопроводности внутри капли (r – радиальная координата, отсчитываемая от центра капли, t – время) в системе отсчета, связанной с центром капли:

(1.3)

${{c}_{s}}{{\rho }_{s}}\frac{{\partial {{T}_{s}}}}{{\partial t}} = {{\lambda }_{s}}\frac{1}{{{{r}^{2}}}}\frac{\partial }{{\partial r}}\left( {{{r}^{2}}\frac{{\partial {{T}_{s}}}}{{\partial r}}} \right)$

Граничные условия: непрерывность тепловых потоков на поверхности капли и отсутствие источников или стоков тепла в ее центре

(1.4)

$\begin{gathered} r = 0{\text{:}}\,\,\frac{{\partial {{T}_{s}}}}{{\partial r}} = 0 \\ r = \sigma {\text{:}}\,\,{{\lambda }_{s}}\frac{{\partial {{T}_{s}}}}{{\partial r}} = \frac{\lambda }{\sigma }(T - {{T}_{{sw}}}) \\ \end{gathered} $

Таким образом, в принятой континуальной модели температура дисперсной фазы T_s является функцией трех переменных: эйлеровых координат (x, y) и внутренней радиальной координаты r, отсчитываемой от центра частицы, находящейся в рассматриваемой точке пространства.

Уравнения несущей фазы с учетом притоков импульса и энергии со стороны дисперсной фазы записываются в виде [7]

(1.5)

$\begin{gathered} {\text{div}}(\rho {\mathbf{V}}) = 0 \\ \rho ({\mathbf{V}}\nabla ){\mathbf{V}} = - \nabla p + {{\nabla }_{j}}{{\tau }^{{ij}}}{{{\mathbf{e}}}_{j}} - {{n}_{s}}{{{\mathbf{f}}}_{s}} \\ {{c}_{p}}\rho ({\mathbf{V}}\nabla )T = ({\mathbf{V}}\nabla )p + {\text{div}}(\lambda \nabla T) + {{\tau }^{{ij}}}{{\varepsilon }_{{ij}}} - {{n}_{s}}{{q}_{s}} + {{n}_{s}}{{{\mathbf{f}}}_{s}}({\mathbf{V}} - {{{\mathbf{V}}}_{s}}) \\ p = \rho RT,\quad {{\tau }^{{ij}}} = 2\mu {{\varepsilon }^{{ij}}} - \frac{2}{3}\mu {{\delta }^{{ij}}}{\text{div}}({\mathbf{V}}),\quad {{\varepsilon }_{{ij}}} = \frac{1}{2}({{\nabla }_{i}}{{\text{v}}_{j}} + {{\nabla }_{j}}{{\text{v}}_{i}}) \\ \end{gathered} $

Здесь ρ и p – плотность и давление несущей фазы, τ_ij – компоненты тензора касательных напряжений, ε_ij – компоненты тензора скоростей деформации, δ^ij – символы Кронекера, e_j – базисные векторы системы координат, c_p – теплоемкость газа при постоянном давлении, R – газовая постоянная. Поскольку рассматриваются достаточно высокие (как правило, сверхзвуковые) скорости набегающего потока, эффектами силы тяжести пренебрегается.

В качестве граничных условий следует задать условия в набегающем потоке, условие прилипания для скорости несущей фазы на пластине, а также условие адиабатичности (нулевого суммарного потока тепла) на поверхности пластины.

Под действием силы Сэфмана капли осаждаются на поверхность пластины и формируют жидкую пленку. Упростим постановку (1.1)–(1.5), считая, что характерные числа Рейнольдса течения на интересующем нас масштабе длины велики, а массовая концентрация капель конечна, но достаточно мала. В качестве характерного масштаба длины удобно взять длину скоростной релаксации стоксовской капли [10, 11], посчитанную по параметрам внешнего потока (индекс ∞ здесь и далее относится к параметрам начального сечения внешнего потока): ${{l}_{\text{v}}} = m{{U}_{\infty }}{\text{/}}6\pi \sigma {{\mu }_{\infty }}$.

Сформулируем асимптотическую постановку задачи, следующую из (1.1)–(1.5) при Re = = ρ_∞U_∞${{l}_{\text{v}}}$/μ_∞ → ∞. Для реальных приложений представляет интерес диапазон размеров капель σ = 10^–6–10^–5 м и скоростей U_∞ = 350–1650 м/с. Тогда для микронных водяных капель при нормальных условиях во внешнем воздушном потоке имеем ${{l}_{\text{v}}}$ ≈ 0.005–0.015 м; Re ≈ (1.167–3.5) × 10⁴, а для десятимикронных капель ${{l}_{\text{v}}}$ ≈ 0.5–1.5 м; Re ≈ (1.167–3.5) × 10⁶.

2. УРАВНЕНИЯ ВНЕШНЕГО НЕВЯЗКОГО ТЕЧЕНИЯ

Вдали от стенки, вне пограничного слоя, в главном приближении при больших числах Рейнольдса течение двухфазной среды является одномерным. Безразмерные переменные введем следующим образом (звездочкой здесь и ниже обозначены размерные переменные)

$x = \frac{{x{\text{*}}}}{{{{l}_{\text{v}}}}},\quad u = \frac{{u{\text{*}}}}{{{{U}_{\infty }}}},\quad \rho = \frac{{\rho {\text{*}}}}{{{{\rho }_{\infty }}}},\quad T = \frac{{T{\text{*}}}}{{{{T}_{\infty }}}},\quad p = \frac{{p{\text{*}}}}{{\rho _{\infty }^{{}}RT_{\infty }^{{}}}},\quad \mu = \frac{{\mu *}}{{{{\mu }_{\infty }}}},\quad \lambda = \frac{{\lambda {\text{*}}}}{{{{\lambda }_{\infty }}}}$

${{u}_{s}} = \frac{{u_{s}^{*}}}{{{{U}_{\infty }}}},\quad {{T}_{s}} = \frac{{T_{s}^{*}}}{{{{T}_{\infty }}}},\quad {{n}_{s}} = \frac{{n_{s}^{*}}}{{{{n}_{{s\infty }}}}},\quad r = \frac{{r{\text{*}}}}{\sigma }$

При Re → ∞ из системы (1.1)–(1.5) в безразмерных переменных, введенных выше, получаем следующую систему уравнений, описывающих течение во внешней (невязкой) области течения над пластиной

$\frac{{d\rho u}}{{dx}} = 0,\quad \frac{{d{{n}_{s}}{{u}_{s}}}}{{dx}} = 0,\quad {{u}_{s}}\frac{{d{{u}_{s}}}}{{dx}} = \mu \left( {u - {{u}_{s}}} \right)$

(2.1)

$\rho u\frac{{du}}{{dx}} = - \frac{1}{{\gamma {{{\text{M}}}^{2}}}}\frac{{dp}}{{dx}} - \alpha \mu {{n}_{s}}\left( {u - {{u}_{s}}} \right),\quad p = \rho T,\quad \lambda = \mu = {{T}^{\omega }}$

$\rho u\frac{{dT}}{{dx}} = u\frac{{\gamma - 1}}{\gamma }\frac{{dp}}{{dx}} + \frac{{2\alpha }}{{3\Pr }}{{n}_{s}}\lambda \left( {{{T}_{{sw}}} - T} \right) + \alpha (\gamma - 1){{{\text{M}}}^{2}}{{n}_{s}}\mu {{(u - {{u}_{s}})}^{2}}$

${{u}_{s}}\frac{{\partial {{T}_{s}}}}{{\partial x}} = A\left( {\frac{{{{\partial }^{2}}{{T}_{s}}}}{{\partial {{r}^{2}}}} + \frac{2}{r}\frac{{\partial {{T}_{s}}}}{{\partial r}}} \right),\quad A = \frac{{2{{\lambda }_{s}}}}{{9{{c}_{s}}{{\mu }_{\infty }}}},\quad \alpha = \frac{{mn_{{s\infty }}^{{}}}}{{\rho _{\infty }^{{}}}}$

Данная система содержит следующие независимые параметры подобия: показатель адиабаты газа γ, число Маха набегающего потока М, посчитанное по параметрам несущей фазы, число Прандтля газовой фазы Pr, относительную массовую концентрацию дисперсной фазы α, параметр A, характеризующий скорость прогрева капли, и показатель степени ω. Поскольку способы введения жидкой фазы в газовый поток могут быть различными, будем рассматривать общую ситуацию, когда имеется рассогласование температур фаз в области над носиком пластины. Для системы (2.1) следует задать условия в начальном сечении

(2.2)

$x = 0{\text{:}}\,\,u = 1,\quad T = 1,\quad \rho = 1,\quad {{u}_{s}} = 1,\quad {{n}_{s}} = 1,\quad {{T}_{s}} = {{T}_{{sw}}} = {{T}_{{s0}}}$

Для уравнения теплопроводности внутри капли из (2.1) справедливо также граничное условие на поверхности капли

(2.3)

$r = 1{\text{:}}\,\,\frac{{\partial {{T}_{s}}}}{{\partial r}} = BT_{{sw}}^{\omega }(T - {{T}_{{sw}}}),\quad B = \frac{{{{\lambda }_{\infty }}}}{{{{\lambda }_{s}}}}$

Температура всех капель в начальном сечении x = 0 для простоты считается однородной по радиусу капли. Видно, что граничное условие содержит еще один параметр подобия B. В последующих разделах параметры течения, найденные из решения задачи (2.1)–(2.3), будут называться параметрами внешнего потока и снабжаться индексом e.

3. УРАВНЕНИЯ ДВУХФАЗНОГО ПОГРАНИЧНОГО СЛОЯ

Для вывода уравнений пограничного слоя введем «растянутую» координату

$y = \frac{{y{\text{*}}\sqrt {{\text{Re}}} }}{{{{l}_{\text{v}}}}}$

и соответствующим образом “растянутые” нормальные скорости фаз

$\text{v} = \frac{{\text{v}{\text{*}}\sqrt {\operatorname{Re} } }}{{{{U}_{\infty }}}},\quad {{\text{v}}_{s}} = \frac{{\text{v}_{s}^{*}\sqrt {\operatorname{Re} } }}{{{{U}_{\infty }}}}$

Остальные безразмерные переменные вводятся так же, как в разд. 2. Переписывая исходные уравнения модели двухфазного течения в безразмерных растянутых переменных, переходя к пределу Re → ∞ и сохраняя главные члены, получаем уравнения двухфазного пограничного слоя (более детально процедура вывода уравнений двухфазного пограничного методом сращиваемых асимптотических разложений описана в [11]

(3.1)

$\begin{gathered} \frac{{\partial \rho u}}{{\partial x}} + \frac{{\partial \rho \text{v}}}{{\partial y}} = 0 \\ \rho \left( {u\frac{{\partial u}}{{\partial x}} + \text{v}\frac{{\partial u}}{{\partial y}}} \right) = - \frac{1}{{\gamma {{{\text{M}}}^{2}}}}\frac{{d{{p}_{e}}}}{{dx}} + \frac{\partial }{{\partial y}}\left( {\mu \frac{{\partial u}}{{\partial y}}} \right) - \alpha \mu {{n}_{s}}\left( {u - {{u}_{s}}} \right) \\ \end{gathered} $

$\begin{gathered} \rho \left( {u\frac{{\partial T}}{{\partial x}} + \text{v}\frac{{\partial T}}{{\partial y}}} \right) = u\frac{{\gamma - 1}}{\gamma }\frac{{d{{p}_{e}}}}{{dx}} + \frac{1}{{\Pr }}\frac{\partial }{{\partial y}}\left( {\mu \frac{{\partial T}}{{\partial y}}} \right) + (\gamma - 1){{{\text{M}}}^{2}}\mu {{\left( {\frac{{\partial u}}{{\partial y}}} \right)}^{2}} + \\ + \;\frac{{2\alpha }}{{3\Pr }}{{n}_{s}}\lambda \left( {{{T}_{{sw}}} - T} \right) + \alpha (\gamma - 1){{{\text{M}}}^{2}}{{n}_{s}}\mu {{(u - {{u}_{s}})}^{2}} \\ \end{gathered} $

$p = \rho T,\quad \lambda = \mu = {{T}^{\omega }}$

$\frac{{\partial {{n}_{s}}{{u}_{s}}}}{{\partial x}} + \frac{{\partial {{n}_{s}}{{\text{v}}_{s}}}}{{\partial y}} = 0,$

${{u}_{s}}\frac{{\partial {{u}_{s}}}}{{\partial x}} + {{\text{v}}_{s}}\frac{{\partial {{u}_{s}}}}{{\partial y}} = \mu \left( {u - {{u}_{s}}} \right)$

${{u}_{s}}\frac{{\partial {{\text{v}}_{s}}}}{{\partial x}} + {{\text{v}}_{s}}\frac{{\partial {{\text{v}}_{s}}}}{{\partial y}} = \mu \left( {\text{v} - {{\text{v}}_{s}}} \right) + \kappa \left( {u - {{u}_{s}}} \right)\sqrt {\mu \rho \left| {\frac{{\partial u}}{{\partial y}}} \right|} ,$

${{u}_{s}}\frac{{\partial {{T}_{s}}}}{{\partial x}} + {{\text{v}}_{s}}\frac{{\partial {{T}_{s}}}}{{\partial y}} = A\left( {\frac{{{{\partial }^{2}}{{T}_{s}}}}{{\partial {{r}^{2}}}} + \frac{2}{r}\frac{{\partial {{T}_{s}}}}{{\partial r}}} \right),$

$\alpha = \frac{{m{{n}_{{s\infty }}}}}{{{{\rho }_{\infty }}}},\quad {\text{M}} = \frac{{{{U}_{\infty }}}}{{{{a}_{\infty }}}},\quad \Pr = \frac{{{{c}_{p}}{{\mu }_{\infty }}}}{{{{\lambda }_{\infty }}}},\quad \kappa = \frac{{6.46}}{{12\pi \sqrt 6 }}{{\left( {\frac{{2\sigma \rho _{\infty }^{{}}{{U}_{\infty }}}}{{\mu _{\infty }^{{}}}}} \right)}^{{3/2}}}{{\left( {\frac{{2\rho _{s}^{{}}}}{{\rho _{\infty }^{{}}}}} \right)}^{{1/4}}}$

Здесь c_p – теплоемкость газа при постоянном давлении, a_∞ – скорость звука газа в набегающем потоке, p_e(x) – распределение давления во внешнем потоке, найденное из решения системы (2.1). В добавление к параметрам подобия, упоминавшимся выше, в (3.1) появляется параметр κ, характеризующий вклад силы Сэфмана в межфазный обмен импульсом. Следует отметить, что роль силы Сэфмана в рассматриваемых условиях течения очень существенна, поскольку даже для малых капель микронного размера в сверхзвуковом пограничном слое величина параметра κ достигает величин порядка 10³.

Сформулируем теперь граничные условия для системы (3.1). Поскольку подсистема уравнений несущей фазы в (3.1) является параболической, для параметров газа требуется задать профили скорости и температуры в начальном сечении, условия сращивания скорости и температуры газа с внешним решением, найденным из (2.1), вдали от пластины, а также условия прилипания и адиабатичности на поверхности пластины. Подсистема уравнений дисперсной фазы является гиперболической, ее характеристики – траектории частиц, поэтому требуется задать все параметры дисперсной фазы лишь в начальном сечении при x = 0.

Итак, в начальном сечении следует задать:

(3.2)

$x = 0,\quad y > 0{\text{:}}\,\,u = 1,\quad T = 1,\quad {{n}_{s}} = 1,\quad {{u}_{s}} = 1,\quad {{T}_{s}} = {{T}_{{sw}}} = {{T}_{{s0}}},\quad {{\text{v}}_{s}} = 0$

Условия сращивания с внешним потоком таковы:

(3.3)

$y \to \infty {\text{:}}\,\,u \to {{u}_{e}}(x),\quad T \to {{T}_{e}}(x)$

Для уравнения теплопроводности внутри капли, решаемого для каждого узла расчетной сетки, используется граничное условие (2.3). Поскольку под действием боковой силы капли могут осаждаться на обтекаемой поверхности и формировать жидкую пленку, возникают определенные сложности с математической формулировкой граничных условий на поверхности пластины. В [13, 14] развита теория двухфазного пограничного слоя с учетом образования жидкой пленки из осаждающихся на стенку капель, однако рассматривались лишь течения с несжимаемой несущей фазой и заданной температурой стенки. Согласно классификации [13], течение в пленке описывается либо уравнениями пограничного слоя (так называемое “быстрое течение”, при значительных потоках массы осаждающихся капель), либо – при малых значениях потока массы осаждающихся капель – уравнениями ползущего течения (стоксовой пленки). В последнем случае характерная скорость жидкости в пленке много меньше скорости внешнего невязкого потока, толщина пленки много меньше толщины пограничного слоя, а градиент температуры по нормали к обтекаемой поверхности в пленке равен нулю. В следующем разделе на основе подробного асимптотического анализа уравнений пленки показано, что в случае, рассматриваемом в настоящей работе, как правило, реализуется именно второй случай. Это позволяет значительно упростить процедуру задания граничных условий. Пренебрегая толщиной пленки на масштабе пограничного слоя и скоростью жидкости в пленке, нижнее граничное условие для (3.1) можно записать в виде

(3.4)

$y = 0:\quad u = 0,\quad \text{v} = 0,\quad {{q}_{\Sigma }} = 0$

Здесь q_Σ – суммарный безразмерный тепловой поток от несущей фазы и осаждающихся капель

(3.5)

${{q}_{\Sigma }} = {{\left. {\frac{{\partial T}}{{\partial y}}} \right|}_{{y = 0}}} + {{\left. {\alpha \frac{{{{c}_{s}}}}{{{{c}_{p}}}}\Pr \left[ {{{n}_{{sw}}}{{v}_{{sw}}}\frac{{T - \left\langle {{{T}_{s}}} \right\rangle }}{{{{T}^{\omega }}}}} \right]} \right|}_{{y = 0}}}$

Здесь, как и ранее, угловые скобки обозначают температуру, осредненную по объему капли, кинетической энергией капель пренебрегается ввиду ее очевидной малости по сравнению с тепловой энергией. В выражение (3.5) вошел новый независимый безразмерный параметр χ = c_s/c_p. Теперь постановка задачи (3.1)–(3.5) является полностью замкнутой.

4. УРАВНЕНИЯ ПЛЕНОЧНОГО ТЕЧЕНИЯ

Перейдем к описанию пленочного течения, формирующегося за счет выпадения капель, и выведем асимптотические уравнения пленки и граничные условия на ее границе. Характерную длину, как и ранее, примем равной l_v. Характерная толщина $h_{0}^{*}$ и скорость пленки U_f заранее неизвестны, они будут определены ниже. Безразмерные переменные, описывающие течение в пленке, удобно ввести следующим образом (индекс f относится к параметрам течения в пленке):

$x = \frac{{x{\text{*}}}}{{{{l}_{\text{v}}}}},\quad \eta = \frac{{y{\text{*}}}}{{{{l}_{\text{v}}}\varepsilon }},\quad {{u}_{f}} = \frac{{u_{f}^{*}}}{{{{U}_{f}}}},\quad {{\text{v}}_{f}} = \frac{{\text{v}_{f}^{*}}}{{{{U}_{f}}\varepsilon }},\quad \varepsilon = \frac{{h_{0}^{*}}}{{{{l}_{\text{v}}}}},\quad {{T}_{f}} = \frac{{T_{f}^{*}}}{{{{T}_{\infty }}}},\quad {{p}_{f}} = \frac{{p_{f}^{{}}}}{{\rho _{\infty }^{{}}RT_{\infty }^{{}}}}$

Из условия баланса массы в пленке имеем

(4.1)

$\rho _{s}^{{}}{{U}_{f}}h_{0}^{*}\sim \rho _{s}^{{}}{{\varphi }_{{s0}}}{{U}_{\infty }}{{l}_{\text{v}}}{\text{/}}\sqrt {\operatorname{Re} } $

Здесь ${{\varphi }_{{s\infty }}} = \alpha \rho _{\infty }^{{}}{\text{/}}\rho _{s}^{{}}$ – характерная объемная доля капель во внешнем потоке. Из (4.1) можно положить

(4.2)

$\frac{{h_{0}^{*}}}{{{{l}_{v}}}} = \varepsilon = \frac{{{{\varphi }_{{s\infty }}}}}{{\sqrt {\operatorname{Re} } }}\frac{{{{U}_{\infty }}}}{{{{U}_{f}}}}$

Предполагая, что пленка вовлекается в движение в основном касательным напряжением, действующим на ее границе со стороны газовой фазы, имеем баланс касательной компоненты импульса

$\mu _{\infty }^{*}\frac{{{{U}_{\infty }}\sqrt {\operatorname{Re} } }}{{{{l}_{\text{v}}}}}\sim \mu _{s}^{*}\frac{{{{U}_{f}}}}{{h_{0}^{*}}}$

Теперь из (4.2) и (4.1) можем выразить характерные значения толщины пленки и скорости течения в ней через известные параметры

$h_{0}^{*} = {{l}_{v}}\sqrt {\frac{{{{\varphi }_{{s\infty }}}}}{{\operatorname{Re} }}\frac{{\mu _{s}^{*}}}{{\mu _{\infty }^{*}}}} = \delta \sqrt {{{\varphi }_{{s\infty }}}\frac{{\mu _{s}^{*}}}{{\mu _{\infty }^{*}}}} ,\quad {{U}_{f}} = {{U}_{\infty }}\sqrt {{{\varphi }_{{s\infty }}}\frac{{\mu _{\infty }^{*}}}{{\mu _{{s\infty }}^{*}}}} $

Здесь буквой $\delta = {{l}_{\text{v}}}{\text{/}}\sqrt {\operatorname{Re} } $ обозначена характерная толщина пограничного слоя на рассматриваемом масштабе длины. В приложениях, представляющих интерес, характерная объемная доля дисперсной фазы φ_s∞ в набегающем потоке мала (порядка 10^–5), а отношение вязкостей фаз $\mu _{\infty }^{*}{\text{/}}\mu _{{s\infty }}^{*}\sim {{10}^{{ - 2}}}$. Тогда из (4.1) имеем: $h_{0}^{*}\sim \delta {\text{/}}30$, а скорость течения в пленке U_f ∼ 3 × 10^–4U_∞. Данные оценки оправдывают снос граничных условий на поверхность пластины и пренебрежение скоростью пленки в (3.5). Выведем теперь асимптотические уравнения пленки и покажем, что градиентом температуры в пленке по нормали к обтекаемой поверхности можно пренебречь.

Запишем уравнения Навье–Стокса и притока тепла для стационарного течения в пленке в безразмерных переменных, введенных в начале раздела

(4.3)

$\frac{{\partial u_{f}^{{}}}}{{\partial x}} + \frac{{\partial \text{v}_{f}^{{}}}}{{\partial \eta }} = 0$

$\alpha {{({{\varphi }_{{s\infty }}}\mu _{\infty }^{*}{\text{/}}\mu _{s}^{*})}^{{1/2}}}\left( {u_{f}^{{}}\frac{{\partial u_{f}^{{}}}}{{\partial x}} + \text{v}_{f}^{{}}\frac{{\partial u_{f}^{{}}}}{{\partial \eta }}} \right) = \frac{{{{{({{\varphi }_{{s\infty }}}\mu _{s}^{*}{\text{/}}\mu _{\infty }^{*})}}^{{1/2}}}}}{{\gamma {{{\text{M}}}^{2}}}}\frac{{\partial {{p}_{f}}}}{{\partial x}} + {{\varepsilon }^{2}}\frac{{{{\partial }^{2}}u_{f}^{{}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}u_{f}^{{}}}}{{\partial {{\eta }^{2}}}}$

$\alpha {{\varepsilon }^{2}}{{({{\varphi }_{{s\infty }}}\mu _{\infty }^{*}{\text{/}}\mu _{s}^{*})}^{{1/2}}}\left( {u_{f}^{{}}\frac{{\partial \text{v}_{f}^{{}}}}{{\partial x}} + \text{v}_{f}^{{}}\frac{{\partial \text{v}_{f}^{{}}}}{{\partial \eta }}} \right) = \frac{{{{{({{\varphi }_{{s\infty }}}\mu _{s}^{*}{\text{/}}\mu _{\infty }^{*})}}^{{1/2}}}}}{{\gamma {{{\text{M}}}^{2}}}}\frac{{\partial {{p}_{f}}}}{{\partial \eta }} + {{\varepsilon }^{4}}\frac{{{{\partial }^{2}}{{\text{v}}_{f}}}}{{\partial {{x}^{2}}}} + {{\varepsilon }^{2}}\frac{{{{\partial }^{2}}\text{v}_{f}^{{}}}}{{\partial {{\eta }^{2}}}}$

$\begin{gathered} \alpha {{({{\varphi }_{{s\infty }}}\mu _{\infty }^{*}{\text{/}}\mu _{s}^{*})}^{{1/2}}}{\text{P}}{{{\text{r}}}_{f}}\left( {{{u}_{f}}\frac{{\partial {{T}_{f}}}}{{\partial x}} + {{\text{v}}_{f}}\frac{{\partial {{T}_{f}}}}{{\partial \eta }}} \right) = {{\varepsilon }^{2}}\frac{{{{\partial }^{2}}{{T}_{f}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}{{T}_{f}}}}{{\partial {{\eta }^{2}}}} + \\ + \frac{{{{c}_{p}}}}{{{{c}_{s}}}}(\gamma - 1){{{\text{M}}}^{2}}{{\Pr }_{f}}({{\varphi }_{{s\infty }}}\mu _{\infty }^{*}{\text{/}}\mu _{s}^{*})\left[ {{{{\left( {\frac{{\partial {{u}_{f}}}}{{\partial \eta }} + {{\varepsilon }^{2}}\frac{{\partial {{\text{v}}_{f}}}}{{\partial x}}} \right)}}^{2}} + 2{{\varepsilon }^{2}}{{{\left( {\frac{{\partial {{u}_{f}}}}{{\partial x}}} \right)}}^{2}} + 2{{\varepsilon }^{2}}{{{\left( {\frac{{\partial {{\text{v}}_{f}}}}{{\partial \eta }}} \right)}}^{2}}} \right] \\ \end{gathered} $

Учитывая, что относительная толщина пленки ε, а также величины ${{({{\varphi }_{{s\infty }}}\mu _{\infty }^{*}{\text{/}}\mu _{s}^{*})}^{{1/2}}}$ и ${{({{\varphi }_{{s\infty }}}\mu _{s}^{*}{\text{/}}\mu _{\infty }^{*})}^{{1/2}}}{\text{/}}\gamma {{{\text{M}}}^{2}}$ достаточно малы в рассматриваемых условиях (характерные значения объемной доли капель и отношения вязкостей фаз приводились выше), пренебрежем соответствующими членами в (4.3) и получим асимптотические уравнения пленочного течения

(4.4)

$\frac{{\partial {{u}_{f}}}}{{\partial x}} + \frac{{\partial {{\text{v}}_{f}}}}{{\partial \eta }} = 0,\quad \frac{{{{\partial }^{2}}{{u}_{f}}}}{{\partial {{\eta }^{2}}}} = 0,\quad \frac{{{{\partial }^{2}}{{T}_{f}}}}{{\partial {{\eta }^{2}}}} = 0,\quad \frac{{\partial {{p}_{f}}}}{{\partial \eta }} = 0$

При выводе (4.4) учтено также, что ${{\varepsilon }^{2}}{\text{/}}{{({{\varphi }_{{s\infty }}}\mu _{s}^{*}{\text{/}}\mu _{\infty }^{*})}^{{1/2}}} \ll 1$. Таким образом, в рассматриваемых условиях течение в пленке описывается уравнениями теории смазки (или стоксовой пленки), которые нужно решать в слое заранее неизвестной толщины. На поверхности пластины задаются условия прилипания и адиабатичности. Как следует из последнего уравнения (4.4) для адиабатической стенки, на которой $\partial T_{f}^{{}}{\text{/}}\partial y = 0$, температура жидкости в пленке зависит только от продольной координаты, что оправдывает снесение граничного условия равенства нулю суммарного теплового потока на внешнюю границу пленки (условия (3.4)–(3.5)).

Сформулируем теперь граничные условия на внешней границе пленки. Из равенства потоков массы по нормали к внешней границе пленки при $y* = h{\text{*}}(x*)$ (здесь $h{\text{*}}(x*)$ − форма поверхности пленки) можно записать

(4.5)

$mn_{s}^{*}(\text{v}_{s}^{*} - u_{s}^{*}h_{x}^{{*'}}) = \rho _{s}^{*}(\text{v}_{f}^{*} - u_{f}^{*}h_{x}^{{*'}})$

Штрихом здесь и далее обозначена производная по продольной координате. Условие баланса касательной компоненты импульса на границе тонкой пленки имеет вид:

(4.6)

$\mu {\text{*}}\frac{{\partial u{\text{*}}}}{{\partial y{\text{*}}}} - mn_{s}^{*}(\text{v}_{s}^{*} - u_{s}^{*}h_{x}^{{*'}})u_{s}^{*} = \mu _{s}^{*}\frac{{\partial u_{f}^{*}}}{{\partial y{\text{*}}}} - \rho _{s}^{*}(\text{v}_{f}^{*} - u_{f}^{*}h_{x}^{{*'}})u_{f}^{*}$

В (4.5), (4.6) при вычислении нормальных к поверхности пленки компонент скорости учитывается, что $h_{x}^{{*'}} \ll 1$, и пренебрегается некоторыми очевидно малым членами, имеющими порядок отношений нормальной и продольной скоростей в пограничном слое и пленке. Переходя в (4.5), (4.6) к безразмерным переменным и используя масштабы обезразмеривания, принятые в пограничном слое и пленке, и пренебрегая малыми величинами, которые уже были опущены при выводе уравнений пленки (4.4), получаем граничные условия в безразмерном виде

(4.7)

$\begin{gathered} \eta = h(x){\text{:}}\quad u_{f}^{{}}h_{x}^{'} - \text{v}_{f}^{{}} = j(x),\quad \frac{{\partial {{u}_{f}}}}{{\partial \eta }} = \tau (x) \\ j(x) = - \alpha n_{{sw}}^{{}}(x)\text{v}_{{sw}}^{{}}(x),\quad \tau (x) = T_{w}^{\omega }{{\left. {\frac{{\partial u}}{{\partial y}}} \right|}_{{y = 0}}} - \alpha n_{{sw}}^{{}}(x)u_{{sw}}^{{}}(x)\text{v}_{{sw}}^{{}}(x) \\ \end{gathered} $

Из закона сохранения нормальной компоненты потока импульса на поверхности пленки в рассматриваемом приближении получается тривиальное условие непрерывности давления, а из условия однородности температуры по толщине пленки, как уже отмечалось выше, условие адиабатичности стенки сносится на внешнюю границу пленки (3.4)–(3.5). Правые части в соотношениях (4.7) – потоки массы и касательного импульса дисперсной фазы – должны быть предварительно рассчитаны из решения уравнений двухфазного пограничного слоя.

Уравнения пленочного течения можно проинтегрировать и получить распределение скоростей в пленке

${{u}_{f}}(x,\eta ) = \tau (x)\eta ,\quad {{\text{v}}_{f}}(x,\eta ) = - \frac{{\tau {\text{'}}(x)}}{2}{{\eta }^{2}}$

Из первого условия (4.7) получаем

(4.8)

$h(x) = \sqrt {\frac{2}{{\tau (x)}}\int\limits_o^x {j(s)ds} } $

Как видно из анализа, проведенного в данном разделе, задача о пленочном течении отделяется от задачи о двухфазном пограничном слое и не влияет на определение равновесной температуры адиабатической стенки.

5. О ЧИСЛЕННОМ МЕТОДЕ

Для численного решения краевой задачи (3.1)–(3.5) использовалась неявная разностная схема на декартовой сетке с первым порядком аппроксимации по продольной координате и вторым порядком – по поперечной. Производные по поперечной координате аппроксимировались центральными разностями на следующем слое по x, а по продольной координате – направленными разностями. При переходе на следующий слой для нахождения граничных условий на верхней границе расчетной области и значения градиента давления сначала решается система обыкновенных дифференциальных уравнений (2.5). Учитывая порядок аппроксимации по продольной координате внутри расчетной области, для решения системы (2.5) был выбран метод Эйлера первого порядка точности.

Для нахождения температуры поверхности капель ${{T}_{{sw}}}(x,y)$ в каждой точке расчетной области решается уравнение теплопроводности с граничными условиями (2.3). Радиальная координата в капле используется в качестве переменной прогонки, а в качестве маршевой переменной выступает продольная координата x. Прогонка в капле производится до тех пор, пока не будут выполнены граничные условия (2.3) в центре капли и на межфазной границе, в результате чего находятся распределения температуры как внутри капель, так и на поверхности капель на новом слое по x.

Для нахождения распределения величин u, T, u_s, v_s, n_s на следующем слое также используется метод прогонки. Распределение плотности находится из уравнения состояния, а поперечная скорость несущей фазы определяется из уравнения неразрывности, при этом значение интеграла от производной по продольной координате вычисляется методом трапеций.

6. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Численные расчеты проводились для различных значений безразмерного коэффициента при силе Сэфмана κ и относительной массовой концентрации капель в набегающем потоке α, при этом значения других определяющих параметров фиксированы: M = 3, Pr = 0.72, γ = 1.4, ω = 1, B = 0.04, χ = 4. Тепловые параметры взяты из предположения, что рассматривается двухфазная смесь “воздух–капли воды”.

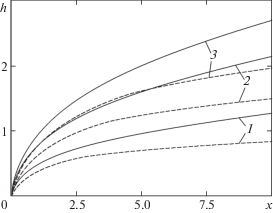
Для того, чтобы убедиться в целесообразности решения уравнения теплопроводности внутри капель в каждой точке расчетной области, были произведены тестовые расчеты течения без учета градиента температуры внутри капли (в предположении, что жидкость в капле прогревается мгновенно) и с учетом такового. На рис. 1 показано распределение температур газовой и дисперсной фазы во внешнем потоке, параллельном пластине, при α = 0.03, T_s0 = 0.1. Видно, что во втором случае газ охлаждается сильнее, поскольку передача тепла от несущей фазы внутрь капель и прогревание вещества по объему капли происходит достаточно медленно.

Рис. 1.

Распределение температуры газа (сплошные линии) и температура поверхности капель (пунктирные линии) во внешнем потоке в случае однородного (1) и неоднородного (2) поля температур внутри капли.

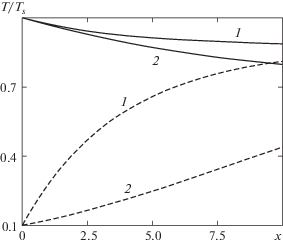
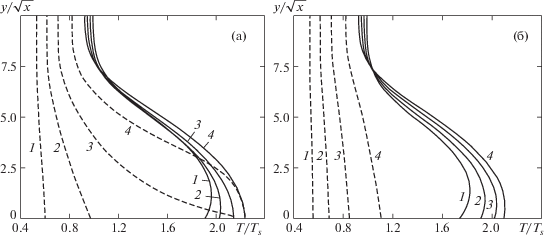
На рис. 2 показаны характерные картины распределения траекторий капель внутри пограничного слоя. Траектории, а также профили параметров фаз, приведенные на рис. 3 и рис. 4, рассчитаны для значений коэффициента κ =100 (а), 1000 (б) при T_s0 = 0.5 и α = 0.03. На рис. 2а, который соответствует случаю малоинерционных частиц, капли выпадают на поверхность только до некоторого значения x (при данном наборе параметров x ≈ 4), а дальше двигаются вдоль стенки подобно несущей фазе. В случае более крупных частиц (рис. 2б), все они (в пределах расчетной области) осаждаются на поверхность пластины. На рис. 3 изображены профили числовой концентрации частиц как функции величины y/x^1/2, которая является автомодельной переменной при решении аналогичной задачи в чистом газе. Профили на рис. 3а соответствуют случаю κ = 100. Видно, что в области, где осаждения капель не происходит, числовая концентрация при малых значениях y/x^1/2 сильно возрастает, поскольку дисперсные частицы накапливаются вблизи стенки. Если происходит быстрое выпадение капель (рис. 3б, κ = 1000), то концентрация n_s с приближением к стенке значительно уменьшается. На рис. 4 показаны профили температур газа и поверхности капель. Видно, что в случае κ = 1000 (рис. 4б) выравнивание температур фаз происходит значительно медленнее, чем при κ = 100 (рис. 4а).

Рис. 2.

Траектории капель: M = 3, α = 0.03, T_s0= 0.5; κ = 100 (а), 1000 (б).

Рис. 3.

Профили числовой концентрации капель: x = 0.5, 2, 4, 8 (1–4); M = 3, α = 0.03, T_s0 = 0.5; κ = 100 (а), 1000 (б).

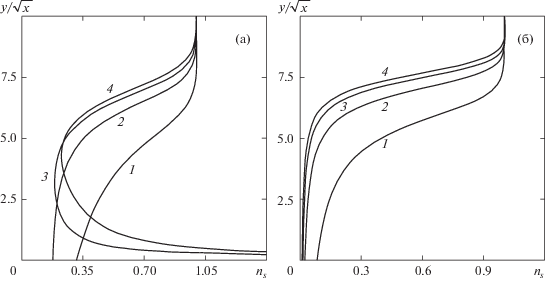
Рис. 4.

Профили безразмерной температуры несущей фазы: x = 0.5, 2, 4, 8 (1–4); M = 3, α = 0.03, T_s0 = 0.5; κ = 100 (а), 1000 (б); сплошные линии – температура газа, пунктирные – температура поверхности капель.

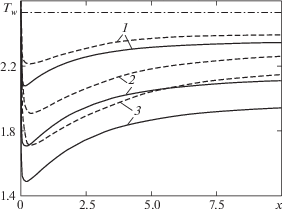
Распределение безразмерной равновесной температуры адиабатической стенки T_w вдоль оси x для различных значений определяющих параметров представлено на рис. 5. Для сравнения там же приведена равновесная температура стенки в чистом газе. С возрастанием значений массовой концентрации капель степень охлаждения поверхности пластины заметно увеличивается. Например, при начальных значениях массовой концентрации капель около процента наблюдается снижение температуры стенки примерно на 10%, для массовой концентрации α = 0.05 уменьшение T_w уже более 20%. Кроме того, снижению уровня кривых T_w способствует увеличение вклада подъемной силы Сэфмана (параметра κ).

Рис. 5.

Распределение равновесной температуры стенки: κ = 100 (пунктирные линии), 1000 (сплошные линии); ${{T}_{{s0}}}$ = 0.5. α = 0.01 (1), 0.03 (2), 0.05 (3); штрихпунктирная линия – значение равновесной температуры стенки в чистом газе.

На рис. 6 изображена безразмерная толщина пленки h, посчитанная по формуле (4.8). Видно, что чем выше значения параметров κ и α, тем сильнее возрастает толщина пленки с увеличением x.

Рис. 6.

Форма поверхности пленки: T_s0 = 0.5; κ = 100 (пунктирные линии), 1000 (сплошные линии); α = 0.01 (1), 0.03 (2), 0.05 (3).

ЗАКЛЮЧЕНИЕ

На основании численных расчетов обтекания теплоизолированной пластины высокоскоростным газокапельным потоком в условиях, когда испарением капель можно пренебречь, исследованы динамические и тепловые характеристики газовой и дисперсной фаз в пограничном слое. Показано, что для корректного расчета межфазного теплообмена в пограничном слое необходимо учитывать неоднородность температурного поля внутри капель. Произведены расчеты параметров пленки, образующейся в результате осаждения капель на поверхность, и показано, что в рассматриваемом диапазоне параметров наличие пленки не влияет на равновесную температуру адиабатической стенки. Получена количественная оценка снижения равновесной температуры стенки, обусловленная осаждением относительно холодных капель на обтекаемую поверхность. Установлено, что при исходных значениях массовой концентрации капель порядка нескольких процентов происходит снижение температуры стенки на десятки процентов. Другим важным параметром, оказывающим влияние на интенсивность осаждения частиц, является коэффициент, характеризующий величину силы Сэфмана: чем выше значение этого коэффициента, тем сильнее охлаждение поверхности пластины.

Полученные результаты показывают, что добавление даже небольшой концентрации неиспаряющихся жидких капель в сверхзвуковой поток может быть использовано как способ повышения эффективности схемы безмашинного энергоразделения газовых потоков [4].

Список литературы

Леонтьев А.И., Осипцов А.Н., Рыбдылова О.Д. Пограничный слой на пластине в сверхзвуковом газокапельном потоке. Влияние испаряющихся капель на температуру адиабатической стенки // Теплофизика высоких температур. 2015. Т. 53. № 6. С. 910–917.
Азанов Г.М., Осипцов А.Н. Влияние мелких испаряющихся капель на температуру адиабатической стенки в сжимаемом двухфазном пограничном слое // Изв. РАН. МЖГ. 2016. № 4. С. 67–74.
Azanov G.M., Osiptsov A.N. The efficiency of one method of mashineless temperature stratification in a gas flow // Int. J. Heat Mass Transfer. 2017. V. 106. P. 1125–1133.
Леонтьев А.И. Газодинамический метод энергоразделения газовых потоков // Теплофизика высоких температур. 1997. Т. 35. № 1. С. 157–159.
Eiasma-ard S., Promvonge P. Review of Ranque-Hilsch effects in vortex tubes // Renewable and Sustainable Energy Rev. 2008. V. 12. № 7. P. 1822–1842.
Здитовец А.Г., Виноградов Ю.А., Стронгин М.М. Экспериментальное исследование температурной стратификации воздушного потока, протекающего через сверхзвуковой канал с центральным телом в виде пористой проницаемой трубки // Изв. РАН. МЖГ. 2013. № 5. С. 134–145.
Leontiev A.I., Kiselev N.A., Vinogradov Yu.A., Strongin M.M., Zditovets A.G., Burtsev S.A. Experimental investigation of heat transfer and drag on surfaces coated with dimples of different shape // Int. J. Thermal Sciences. 2017. V. 118. P. 152–167.
Saffman P.G. The lift on a small sphere in a slow shear flow // J. Fluid Mech. 1965. V. 22. P. 385. Corrigendum: J. Fluid Mech. 1968. V. 31. P. 628.
Marble F.E. Dynamics of dusty gases // Annu. Rev. Fluid Mech. 1970. V. 2. P. 397–446.
Osiptsov A.N., Shapiro E.G. Heat transfer in the boundary layer of a “gas-evaporating drops” two-phase mixture // Int. J. Heat Mass Transfer. 1993. V. 36. № 1. P. 71–78.
Osiptsov A.N. Mathematical modeling of dusty-gas boundary layers // Appl. Mech. Rev. 1997. V. 50. P. 357–370.
Терехов В.И., Пахомов М.А. Тепломассоперенос и гидродинамика в газокапельных потоках. Новосибирск.: Наука, 2008. 283 с.
Осипцов А.Н., Шапиро Е.Г. Обтекание поверхности аэродисперсным потоком с образованием жидкой пленки из осаждающихся частиц // Изв. АН СССР. МЖГ. 1989. № 4. С. 85–92.
Наумов В.А. Расчет газодисперсного ламинарного пограничного слоя на пластине с учетом образующейся жидкой пленки // Изв. РАН. МЖГ. 1992. № 2. С. 179–181.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал