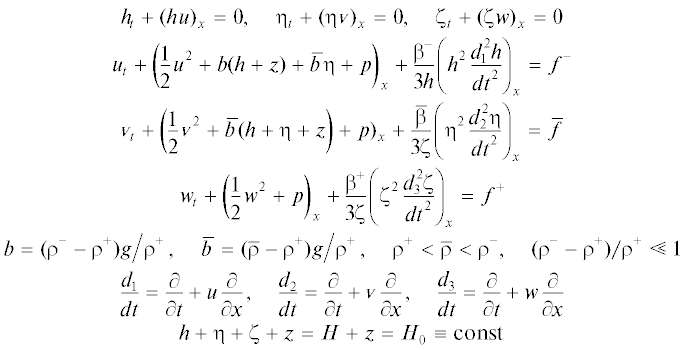Известия РАН. Механика жидкости и газа, 2019, № 3, стр. 38-47
НЕЛИНЕЙНЫЕ ВНУТРЕННИЕ ВОЛНЫ В ШЕЛЬФОВОЙ ЗОНЕ МОРЯ
В. Ф. Кукарин a, *, В. Ю. Ляпидевский b, c, **, Ф. Ф. Храпченков d, ***, И. О. Ярощук d, ****
a Институт неорганической химии им. А.В. Николаева СО РАН
Новосибирск, Россия
b Институт гидродинамики им. М.А. Лаврентьева СО РАН
Новосибирск, Россия
c Воронежский государственный университет
Воронеж, Россия
d Тихоокеанский океанологический институт им. В.И. Ильичева, ДВО РАН
Владивосток, Россия
* E-mail: kukarin@niic.nsc.ru
** E-mail: liapid@hydro.nsc.ru
*** E-mail: fedi@poi.dvo.ru
**** E-mail: yaroshchuk@poi.dvo.ru
Поступила в редакцию 12.07.2018
После доработки 18.10.2018
Принята к публикации 18.10.2018
Аннотация
Рассматривается проблема распространения внутренних волн в прибрежной зоне. На основе математической модели трехслойной мелкой воды построены решения, описывающие эволюцию нелинейных волн над шельфом. Анализ полученных решений дает возможность установить основные закономерности трансформации уединенных волн и нелинейных волновых пакетов большой амплитуды в шельфовой зоне моря. В работе обсуждаются новые возможности применения аналитических и численных решений для интерпретации натурных экспериментов.
Внутренние волны в прибрежной зоне морей и больших водоемов наблюдаются повсеместно. Необходимым условием генерации и распространения волн является вертикальная плотностная стратификация водоема, связанная с неоднородностью распределения температуры и солености. Особенностью распространения внутренних волн в шельфовой зоне является смена полярности (трансформация волн понижения в волны повышения), существенное уменьшение периода и увеличение амплитуды при выходе на берег. Для описания структуры внутренних волн большой амплитуды необходимо использовать модели теории мелкой воды, учитывающие совместное влияние нелинейных и дисперсионных эффектов. Далее под волнами большой амплитуды будем понимать возмущения поля плотности, амплитуда которых существенно превосходит начальную толщину одного из квазиоднородных слоев перед фронтом волны (приповерхностного слоя для волн понижения и придонного слоя для волн повышения).
Приповерхностные и придонные волны большой амплитуды наблюдаются как в южных, так и северных морях и являются объектом интенсивных исследований [1–4]. Результаты лабораторного и прямого численного моделирования нелинейных волновых процессов в шельфовой зоне представлены в [5–8]. Эффективным инструментом исследования нестационарных волновых процессов в прибрежной зоне является использование математических моделей многослойной мелкой воды для описания динамики внутренних волн большой амплитуды [9–14]. Полностью нелинейные и слабо нелинейные модели распространения внутренних волн с достаточной точностью представляют структуру уединенных внутренних волн. Одной из нерешенных проблем является расчет в рамках этих моделей пространственно-временной эволюции реальных нелинейных волновых пакетов короткопериодных внутренних волн, наблюдаемых в прибрежных водах.
В настоящей работе изучается возможность применения упрощенных математических моделей многослойной мелкой воды для интерпретации реальных данных о распространении придонных внутренних волн большой интенсивности в шельфовой зоне Японского моря.
1. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
Уравнения многослойной мелкой воды с учетом нелинейности и негидростатичности распределения давления в слоях выведены в [9]. В данной работе рассматривается трехслойная модель и ее подмодели, позволяющие описывать эволюцию внутренних волн большой амплитуды в придонном и приповерхностном слоях.
В приближении Буссинеска уравнения трехслойного течения слабо стратифицированной по плотности жидкости в поле силы тяжести принимают вид (второе приближение мелкой воды)
Здесь x – пространственная переменная; t – время; $w,v,u$ – скорость верхнего, среднего, нижнего слоя соответственно; ${{\rho }^{ + }},\bar {\rho },{{\rho }^{ - }}$ – плотности в слоях; $\zeta ,\,\eta ,\,h$ – толщина слоев; $g$ – ускорение свободного падения; $p$ – модифицированное давление; z = z(x) – форма дна. Правая часть (1.1), задающая трение на внутренних и внешних границах течения, будет представлена ниже.
Следствием (1.1) для несжимаемой жидкости является зависимость полного расхода через произвольное сечение канала только от времени
Параметр $\beta $ при старших производных в (1.1) характеризует влияние вертикального ускорения жидкости в том или ином слое на форму внутренней волны. Вертикальные ускорения слоев, связанные с формой дна, в этой модели не учитываются, т.е. предполагается, что форма дна меняется плавно, и производными ${{z}_{x}},\,\,{{z}_{{xx}}}$ в уравнениях второго приближения мелкой воды можно пренебречь [10].
Величина $Q(t)$ считается известной в силу граничных условий. Поэтому после исключения переменных $\eta ,v,p$ система (1.1) сводится к четырем уравнениям для функций $h,\,\zeta ,\,u,\,w.$ Но и получаемая система достаточно сложна для построения частных решений и численного исследования нестационарных волновых процессов.
Дальнейшее упрощение (1.1) состоит в использовании условия гидростатичности распределения давления в одном или двух слоях. Условие гидростатичности в прослойке $(\bar {\beta } = 0)$ связано с развитием мелкомасштабных волновых движений, генерируемых сдвигом скорости во внешних слоях. Модель (1.1) с $\bar {\beta } = 0$ пригодна для описания эволюции внутренних волн конечной амплитуды, включая придонные и приповерхностные, а также прослоечные волны. Модель верифицирована в [11–13] с использованием данных натурных и лабораторных экспериментов. Эта модель описывает нелинейное взаимодействие первой и второй мод при деформации внутренней волны над шельфом [11], однако обладает сравнительно малым запасом точных решений.
Важным объектом изучения океанических течений являются придонные и приповерхностные волны большой амплитуды. Этот термин применяется к волнам, амплитуда которых существенно превышает начальную толщину одного из внешних слоев, поверхностного или придонного. Волны большой амплитуды известны также под названием волн с “захваченным ядром”, так как для этого класса возмущений средняя скорость частиц жидкости в соответствующем слое близка к скорости волны и, как следствие, в этом слое членами, представляющими вертикальное ускорение, можно пренебречь (${{\beta }^{ + }} = 0$ или ${{\beta }^{ - }} = 0$) в случае, когда волна распространяется с постоянной скоростью. Таким образом, для приповерхностных волн большой амплитуды будет использоваться модель (1.1) при ${{\beta }^{ + }} = \bar {\beta } = 0,\,\,{{\beta }^{ - }} = 1,$ а для придонных волн большой амплитуды – та же модель при ${{\beta }^{ - }} = \bar {\beta } = 0,\,\,{{\beta }^{ + }} = 1.$
Для построения точных решений и численного анализа нестационарных процессов уравнения придонных и приповерхностных волн большой амплитуды удобно представить в следующем дивергентном виде [12]
(1.2)
$\begin{gathered} {{h}_{t}} + {{(hu)}_{x}} = 0,\quad {{\zeta }_{t}} + {{(\zeta w)}_{x}} = 0 \\ {{K}_{t}} + {{\left( {Ku - \frac{1}{2}{{u}^{2}} + b(h + z) + \bar {b}\eta + p - \frac{{{{\beta }^{ - }}}}{2}{{h}^{2}}u_{x}^{2}} \right)}_{x}} = {{f}^{ - }} \\ {{R}_{t}} + {{\left( {Rw - \frac{1}{2}{{w}^{2}} + p - \frac{{{{\beta }^{ + }}}}{2}{{\zeta }^{2}}w_{x}^{2}} \right)}_{x}} = {{f}^{ + }} \\ {{v}_{t}} + {{\left( {\frac{1}{2}{{v}^{2}} + \bar {b}(h + \eta + z) + p} \right)}_{x}} = \bar {f} \\ R = w - \frac{{{{\beta }^{ + }}}}{{3\zeta }}{{({{\zeta }^{3}}{{w}_{x}})}_{x}},\quad K = u - \frac{{{{\beta }^{ - }}}}{{3h}}{{({{h}^{3}}{{u}_{x}})}_{x}} \\ \eta = H - h - \zeta ,\quad v = \frac{{Q(t) - hu - \zeta w}}{\eta } \\ \end{gathered} $Заметим, что модель (1.2) при $\eta \equiv \,0$ и ${{\beta }^{{\, - }}} = \,\,{{\beta }^{{\, + }}} = 1$ совпадает с уравнениями двухслойного течения, выведенными в [14]. Там же представлена слабонелинейная модель, сводящаяся к уравнению Кортевега-де-Вриза с постоянными коэффициентами, полученными для фиксированного стационарного двухслойного течения. Эта модель пригодна для описания волн умеренной амплитуды и малоэффективна для волн большой амплитуды и волновых боров, существенно изменяющих при их прохождении среднее течение. Ниже будет использован вариант двухслойной слабонелинейной модели, примененной в [12] для расчета эволюции придонных волновых боров в шельфовой зоне моря.
Двухслойная слабонелинейная модель получается из (1.2) при $\eta \equiv \,0$ заменой полных производных вдоль соответствующих траекторий частными производными по времени в членах, содержащих старшие производные. Кроме того, в предположении малости скоростей $u,\,\,w$ имеем
После исключения давления уравнения (1.2) принимают вид [12]
(1.3)
$\begin{gathered} {{h}_{t}} + {{(hu)}_{x}} = 0 \\ {{M}_{t}} + {{\left( {Mw + S(u - w) - \frac{1}{2}{{u}^{2}} + \frac{1}{2}{{w}^{2}} + b(h + z)} \right)}_{x}} = f \\ \zeta = H - h,\quad w = \frac{{Q - hu}}{\zeta },\quad f = - \frac{{cH(u - w{\text{)}}\left| {u - w} \right|}}{{h\zeta }},\quad c = {\text{const}} \\ S = \frac{1}{H}\left( {hM + (H - h)u + hw - \frac{2}{3}Hh{{h}_{x}}{{u}_{x}}} \right) \\ \end{gathered} $(1.4)
$M = u\, - \,w\,\, - \,\,\frac{1}{{3h}}{{({{h}^{3}}{{u}_{x}})}_{x}} - \frac{1}{{3\zeta }}{{({{(H - h)}^{2}}h\,{{u}_{x}})}_{x}}$Особенностью модели (1.3) является то, что все входящие в уравнения величины являются явными функциями от искомых переменных h и $u$, а также их производных, причем в выражение для $S$ и $M$, кроме h и известной функции $H = H(x)$, входят производные ${{h}_{x}},\,\,{{u}_{x}},\,\,{{u}_{{xx}}}.$ Поэтому для расчета нестационарных волн, задаваемых уравнениями (1.3), может быть применен численный метод, разработанный в [15] для уравнений Грина–Нагди. Основная идея этого метода состоит в том, что величины h, M рассматриваются как эволюционные, а скорость $u(t,x)$ восстанавливается на каждом шаге по времени как решение краевой задачи для обыкновенного дифференциального уравнения (1.4) с заданными функциями $h,\,\,{{h}_{x}},\,M.$
Ниже уравнения (1.3) будут использованы для расчета эволюции нелинейного пакета внутренних волн в шельфовой зоне и сравнения полученных решений с данными натурных наблюдений. Конечно, реальная стратификация в прибрежных водах достаточно сложна. Тем не менее аппроксимация профиля температуры двухслойным ступенчатым профилем позволяет применить модель (1.3) для расчета основных характеристик пакета внутренних волн первой моды, таких как амплитуда, фаза, а также описать их нелинейное взаимодействие.
2. БЕГУЩИЕ ВОЛНЫ
В течениях над ровным дном $(H \equiv {\text{const}})$ можно рассмотреть класс решений, которые являются стационарными в некоторой системе координат, движущейся со скоростью $D$ относительно неподвижной системы, т.е. решения вида $h = h(\xi ),\,\,\zeta = \zeta (\xi ),\,\,u = u(\xi ),\,\,w = w(\xi ),\,\,\xi = x - Dt.$ Анализ таких решений сводится к соответствующей системе обыкновенных дифференциальных уравнений. Заметим, что в силу галилеевой инвариантности (1.2) можно ограничиться рассмотрением стационарных решений, т.е. достаточно построить решения следующей системы уравнений
(2.1)
$\begin{gathered} hu = {{Q}^{ - }}\quad \zeta w = {{Q}^{ + }}\quad \eta = H - h - \zeta \quad v = \frac{{Q - {{Q}^{ - }} - {{Q}^{ + }}}}{\eta } \\ ({{J}^{ - }}){\text{'}} = {{f}^{ - }}\quad ({{J}^{ + }}){\text{'}} = {{f}^{ + }}\quad (\bar {J}){\text{'}} = \bar {f} \\ \end{gathered} $(2.2)
$\begin{gathered} {{J}^{ - }} = \frac{1}{2}{{u}^{2}} + bh + \bar {b}\eta + p - \frac{{{{\beta }^{ - }}}}{3}u({{h}^{2}}u'){\text{'}} - \frac{{{{\beta }^{ - }}}}{6}{{h}^{2}}{{(u')}^{2}} \\ {{J}^{ + }} = \frac{1}{2}{{w}^{2}} + p - \frac{{{{\beta }^{ + }}}}{3}w({{\zeta }^{2}}w'){\text{'}} - \frac{{{{\beta }^{ + }}}}{6}{{\zeta }^{2}}{{(w')}^{2}} \\ \bar {J} = \frac{1}{2}{{v}^{2}} + \bar {b}(h + \eta ) + p \\ \end{gathered} $В случае, когда диссипативными эффектами можно пренебречь, т.е. ${{f}^{ - }} = \,\,{{f}^{ + }} = \bar {f} = 0,$ уравнения (2.1) при ${{J}^{ \pm }} \equiv \,\,{\text{const}},\,\,\bar {J} \equiv {\text{const}}$ допускают решения в виде уединенных волн со следующими условиями при $\left| x \right|\, \to \infty $:
(2.3)
$\begin{gathered} h \to {{h}_{0}}\quad \zeta \to {{\zeta }_{0}}\quad u \to {{u}_{0}}\quad w \to {{w}_{0}} \hfill \\ h' \to 0\quad h'' \to 0\quad \zeta ' \to 0\quad \zeta '' \to 0 \hfill \\ \end{gathered} $Однако для ${{\beta }^{ + }} > 0,\,\,{{\beta }^{ - }} > 0$ такие решения могут быть найдены только для дискретных значений определяющих параметров [13]. В то же время в [13] показано, что уравнения приповерхностных $(\,{{\beta }^{ + }} = \bar {\beta } = 0,\,\,{{\beta }^{ - }} > 0)$ и придонных волн $(\,{{\beta }^{ - }} = \bar {\beta } = 0,\,\,{{\beta }^{ + }} > 0)$ допускают однопараметрическое семейство уединенных волн, форма которых находится в квадратурах. Эти решения используются для интерпретации натурных и лабораторных экспериментов. Нетрудно показать, что и для однородной системы (1.3), (1.4) решения, представляющие уединенные волны, также могут быть найдены в квадратурах.
Другим важным классом решений модели (1.1), описывающим эволюцию волновых пакетов в трехслойной жидкости, являются волновые боры. В бездиссипативной среде $({{f}^{ - }} = \,\,{{f}^{ + }} = \bar {f} = 0)$ такие решения существенно нестационарны и в процессе эволюции распадаются на серию уединенных волн. Но в слабодиссипативных средах волновой бор может быть представлен бегущей волной. При этом вид правой части, моделирующей диссипативные процессы в течениях со сдвигом скорости в слоях, определяет структуру внутреннего волнового бора.
В качестве примера рассмотрим структуру придонного внутреннего бора, полученную из решения системы уравнений (2.1), (2.2) при ${{\beta }^{ - }} = 0,\,\,{{\beta }^{ + }} = 1.$ Условие (2.3) реализуется на левой границе течения при $x \to - \infty .$ Если правая часть представляет трение на внутренних и внешних границах течения в следующем виде
(2.4)
$\begin{gathered} {{f}^{ - }} = - \frac{{{{c}_{w}}u\left| u \right| + {{c}_{i}}(u - v)\left| {u - v} \right|}}{h},\quad \bar {f} = - \frac{{{{c}_{i}}(v - u)\left| {v - u} \right| + {{c}_{i}}(v - w)\left| {v - w} \right|}}{\eta }, \\ {{f}^{ + }} = - \frac{{{{c}_{i}}(w - v)\left| {w - v} \right|}}{\zeta } - \upsilon {{w}_{{xx}}}, \\ \end{gathered} $Рис. 1.
Структура стационарного волнового бора: (a) цуг волн, близкий к периодическому при H0 = 42 м, ${{c}_{w}} = {{c}_{i}} = 2 \cdot \,{{10}^{{ - 3}}},\,\,\upsilon = 0$; (б) цуг с монотонно убывающей амплитудой волн с учетом поправки (2.5) при $\upsilon = 0.2$ м2/с.
На рис. 1б изображен волновой бор $(\upsilon = 0.2$ м2/с), для которого учтена поправка (2.5). Параметры построенных решений (амплитуда, период и т.д.) характерны для наблюдаемых значений при прохождении волнового бора в прибрежной зоне, что будет показано ниже. Заметим, что волновые пакеты внутренних волн, обусловленные прохождением внутреннего бора в натурных условиях, являются существенно нестационарными. Поэтому стационарная структура внутреннего бора, изображенного на рис. 1, является лишь некоторой аппроксимацией наблюдаемой волновой картины.
3. ФОРМИРОВАНИЕ ВНУТРЕННЕГО БОРА НАД СКЛОНОМ
Рассмотрим возможность применения моделей (1.2) и (1.3) для расчета нестационарного процесса выхода уединенной волны понижения в шельфовую зону моря и связанного с ним формирования пакета интенсивных внутренних волн. Этот процесс регулярно наблюдается в прибрежных водах и играет важную роль в массообмене в шельфовой зоне [11]. В рамках слабонелинейных двухслойных моделей, сводящихся к уравнениям Кордевега-де-Вриза или Гарднера, в которых коэффициенты определяются начальной невозмущенной стратификацией, трансформация волны при выходе на берег приводит к смене “полярности” волны, т.е. преобразованию ее в волну повышения [16]. Существенно нелинейные модели демонстрируют более сложный процесс выполаживания переднего фронта и укручения заднего фронта достаточно длинной внутренней волны, приводящий к формированию волнового бора [8, 13].
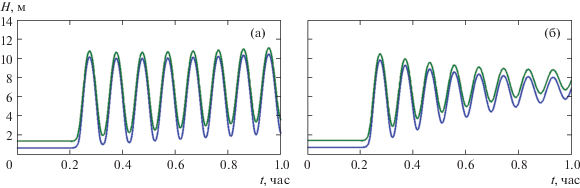
Эволюция внутренней уединенной волны понижения, распространяющейся над склоном с учетом реальной стратификации жидкости, показана на рис. 2. Картина течения построена на основе двумерной численной модели развития нелинейных возмущений в стратифицированной жидкости, включающей турбулентный массообмен [8]. Тонкими сплошными линиями на рис. 2 изображены линии постоянной плотности с интервалом 0.5 кг/м3. В качестве начальных данных выбрана уединенная волна понижения в достаточно глубокой части канала так, чтобы влияние дна на начальном участке распространения симметричной волны было минимальным [8]. Несмотря на то что рассматриваемая стратификация далека от двухслойного или трехслойного распределения плотности, математические модели многослойной мелкой воды, учитывающие нелинейные и дисперсионные эффекты, являются достаточно эффективными. В работе [17] сравнение проводилось с двухслойной моделью (1.2) при отсутствии верхнего слоя $(\zeta \equiv 0,{{\beta }^{ - }}$ = 1), а в [13] тот же расчет использован для верификации модели (1.2) с ${{\beta }^{ \pm }} = 1.$ Для того, чтобы убедиться в возможности использования трехслойной модели (1.2) при ${{\beta }^{ + }} = 0,\,\,{{\beta }^{ - }} = 1$ (приповерхностные внутренние волны большой амплитуды), а также двухслойной слабонелинейной модели (1.3), для описания процесса формирования придонного волнового бора, в рамках указанных моделей проведены соответствующие расчеты. Начальная стратификация, соответствующая трехслойной схеме течения, выбрана следующим образом: H = 300 м, h0 = 230 м, η0 = 30 м, $b = 6 \cdot {{10}^{{ - 2}}}\,{{\text{м }} \mathord{\left/ {\vphantom {{\text{м }} {{{{\text{с }}}^{{\text{2}}}}{\text{,}}\,}}} \right. \kern-0em} {{{{\text{с }}}^{{\text{2}}}}{\text{,}}\,}}\bar {b} = 0.25\,b$ (см. [13]). Уединенная волна движется слева направо с начальной скоростью 2.1 м/с. Внешние жирные линии на рис. 2 показывают положение границ слоев трехслойного течения (уравнения (1.2)), внутренняя пунктирная линия – двухслойного течения (уравнения (1.3)). Наклон дна постоянный (zx = 0.05). Положение волны относительно дна можно определить на рис. 2б. Проведенные расчеты показывают, что модели (1.2) и (1.3) могут быть использованы для расчета эволюции достаточно длинных волн в шельфовой зоне моря.
Рис. 2.
Расчет эволюции длинных волн в шельфовой зоне: (a) приповерхностная уединенная волна; (б) – формирование волнового бора над склоном (положение волны относительно дна). Тонкие сплошные линии – линии постоянной плотности. Внешние жирные линии – границы слоев трехслойного течения (1.2); пунктирная линия – граница двухслойного течения (1.3).
4. СТРУКТУРА ВНУТРЕННЕГО БОРА В ШЕЛЬФОВОЙ ЗОНЕ ЯПОНСКОГО МОРЯ
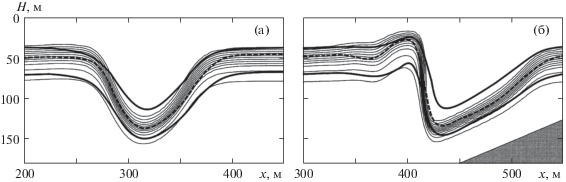
Рассмотрим структуру нелинейных волновых пакетов придонных внутренних волн, генерируемых при формировании внутреннего бора, на основе экспериментальных данных, полученных на гидрофизическом полигоне ТОИ ДВО РАН в 2013 г. Методика проведения экспериментов изложена в [18]. На рис. 3 изображено взаимное расположение автономных донных станций для измерения вертикального профиля температуры, расположенных на различной глубине вдоль нормали к фронту внутренней волны, генерируемой в окрестности границы шельфовой зоны. Распространение возмущений вдоль выбранного направления можно считать двумерным и использовать представленные выше математические модели для анализа наблюдаемых волновых пакетов.
Рис. 3.
Расположение автономных донных станций для измерения вертикального профиля температуры в шельфовой зоне Японского моря.
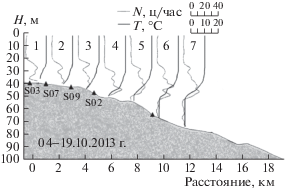
Ограничимся рассмотрением одного события 7.10.2013 – прохождение через станции S07 и S03 волнового бора. Станция S07 располагалась на глубине 42 метра и была оснащена цепочкой термисторов (12 датчиков на расстоянии трех метров друг от друга), начиная с одного метра от дна. Параметры станции S03 – 36 датчиков через 1 м, начиная с 1 м от дна. Расстояние между станциями – 840 метров.
На рис. 4 представлена зависимость температуры на различных горизонтах от времени, полученная на станции S03 и показывающая прохождение волнового бора через два часа после начала измерений. Приведенные данные позволяют четко выделить интенсивные волновые процессы в стратифицированной по температуре жидкости, но для численного анализа волнового пакета удобнее рассчитать деформацию изотерм при прохождении внутренней волны. На рис. 5 показаны изотермы от 5 до 15°С с интервалом в 1°С, соответствующие волновому пакету, изображенному на рис. 4 (тонкие линии). Жирные линии – границы стационарного трехслойного течения, построенного в рамках модели (1.2). Отметим, что наблюдаемый волновой пакет является существенно нестационарным, поэтому стационарное решение характеризует усредненные свойства волнового бора.
Рис. 4.
Зависимость температуры на различных горизонтах от времени, полученные на станции S03 при прохождении волнового бора 7.10.2013 г.
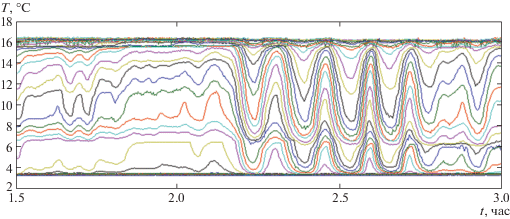
Рис. 5.
Изотермы от 5 до 15°C с интервалом в 1°C, соответствующие волновому пакету на рис. 4 (тонкие линии). Жирные линии – границы стационарного трехслойного течения, рассчитанные по модели (1.2).
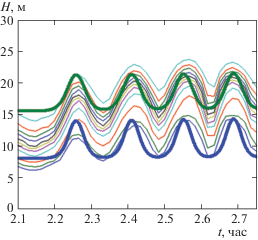
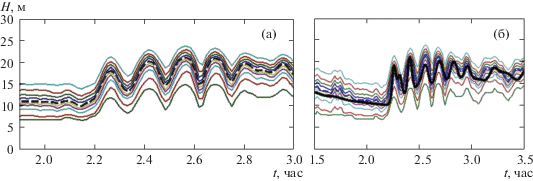
Одной из нерешенных проблем динамики прибрежных вод является построение математической модели, позволяющей восстановить поля температуры и скорости, связанные с прохождением пакетов нелинейных внутренних волн, по данным непрерывного зондирования с использованием системы поверхностных или донных станций. В двумерной постановке проблема формулируется следующим образом: по данным колебаний профиля температуры на более глубоководной станции восстановить амплитудно-частотные характеристики волнового пакета, распространяющегося в сторону берега и, в частности, сравнить их с записью аналогичных характеристик на более мелководной станции. В работе [19] такой подход реализован с использованием одного эволюционного уравнения. При этом, из-за слишком большого расстояния между соседними станциями, добиться хорошего совпадения по фазам и амплитудам рассчитанных и измеренных волн на контрольной станции не удалось.
В работе [12] аналогичная постановка реализована для станций S07 и S03 в октябре 2012 г. В качестве расчетной модели использовалась слабонелинейная двухслойная модель (1.3). В качестве моделируемого события рассматривалось прохождение через эти станции волнового бора. Получено соответствие фазовых и амплитудных характеристик нескольких лидирующих волн между расчетными данными и данными измерений деформации изотерм. Поскольку такой расчет является единичным, в данной работе такая постановка задачи реализована для натурных наблюдений в октябре 2013 г. Выбор участка измерений, связанного с прохождением волнового бора, определялся следующими обстоятельствами. Во-первых, достаточно простыми начальными условиями в численном расчете, так как перед внутренним бором наблюдается период “затишья” и можно в качестве начальных данных рассматривать стационарное течение, в частности, состояние покоя. Во-вторых, в рассматриваемой группе волн отдельные волны на различных станциях легко идентифицируются. На рис. 6, а приведена запись изотерм на станции S07. Пунктиром обозначена изотерма, выбранная в качестве границы раздела однородных слоев в двухслойной модели (1.3). Зависимость положения этой границы от времени использовалась в качестве граничных условий для системы (1.3) на левой границе расчетной области, достаточно большой для того, чтобы рассматриваемые возмущения не дошли до правой границы. На рис. 6, б приведена запись аналогичных изотерм, сделанная на станции S03. Жирная сплошная линия представляет собой результат численного расчета по двухслойной модели (1.3). Пунктирная линия – измеренная изотерма 10°C, положение которой сравнивается с результатом численного расчета. Из рисунка видно достаточно хорошее совпадение между численными и измеренными положениями изотерм для основных волн в пакете. Заметим, что в 2013 г. начальная стратификация перед волновым бором существенно отличалась от двухслойной. Тем не менее двухслойная модель воспроизвела основные особенности распространения волнового пакета, по крайней мере на расстояниях, десятикратно превышающих среднюю длину волн в волновом боре.
Рис. 6.
Внутренний бор, зарегистрированный 7.10.2013 г. на станциях S07 (а) и S03 (б). Тонкие сплошные линии – изотермы с интервалом 1°C. Пунктир (изотерма 10°C) – граница раздела однородных слоев в двухслойной модели (1.3); жирная сплошная линия – результат численного расчета по двухслойной модели.
ЗАКЛЮЧЕНИЕ
Проведенные исследования уединенных волн большой амплитуды, распространяющихся в приповерхностных и придонных слоях, продемонстрировали возможность применения основной модели и ее подмоделей для расчета нестационарных волновых процессов и выяснения основных закономерностей трансформации уединенных волн и нелинейных волновых пакетов большой амплитуды в шельфовой зоне моря.
Показано, что упрощенные модели двухслойной и трехслойной мелкой воды с учетом негидростатичности распределения давления в одном или нескольких слоях применимы для описания эволюции нелинейных волновых пакетов в прибрежных водах с достаточно сложной плотностной стратификацией.
Список литературы
Helfrich K.R., Melville W.K. Long nonlinear internal waves // Ann. Rev. Fluid Mech. 2006. V. 38. P. 395–425. https://doi.org/10.1146/annurev.fluid.38.050304.092129
Scotti A., Pineda J. Observation of very large and steep internal waves of elevation near the Massachusetts coast // Geophys. Res. Let. 2004. V. 31. L22307. P. 1–5. https://doi.org/10.1029/2004GL021052
Lien R.-Ch., Henyey F., Ma B., Yang Y.J. Large-amplitude internal solitary waves observed in the northern South China sea: properties and energetic // J. Phys. Oceanography. 2014. V. 44. №. 4. P. 1095–1115. https://doi.org/10.1175/JPO-D-13-088.1
Кукарин В.Ф., Ляпидевский В.Ю., Навроцкий В.В., Храпченков Ф.Ф. Эволюция внутренних волн большой амплитуды в шельфовой зоне моря // Фундаментальная и прикладная гидрофизика. 2013. Т. 6. № 2. С. 35–45.
Гаврилов Н.В., Ляпидевский В.Ю., Ляпидевская З.А. Влияние дисперсии на распространение внутренних волн в шельфовой зоне // Фундаментальная и прикладная гидрофизика. 2013. Т. 6. № 2. С. 25–34.
Moore Ch.D., Koseff J.R., Hult E.L. Characteristics of bolus formation and propagation from breaking internal waves on shelf slopes // J. Fluid Mech. 2016. V. 791. P. 260–283. https://doi.org/10.1017/jfm.2016.58
Lamb K.G. Shoaling solitary internal waves: on a criterion for the formation of waves with trapped cores // J. Fluid Mech. 2003. V. 478. P. 81–100. https://doi.org/10.1017/S0022112002003269
Vlasenko V., Hutter K. Numerical experiments on the breaking of solitary internal waves over a slope-shelf topography // J. Phys. Oceanography. 2002. V. 32. P. 1779–1793.
Choi W. Modeling of strongly nonlinear internal gravity waves // Proc. Fourth Inter. Conf. Hydrodynamics / Eds. Y. Goda, M. Ikehata, K. Suzuki. 2000. P. 453–458.
Gavrilyuk S.L., Liapidevskii V.Yu., Chesnokov A.A. Spilling breakers in shallow water: applications to Favre waves and to the shoaling and breaking of solitary waves // J. Fluid Mech. 2016. V. 808. P. 441–468. https://doi.org/10.1017/jfm.2016.662
Гаврилов Н.В., Ляпидевский В.Ю., Ляпидевская З.А. Трансформация внутренних волн большой амплитуды над шельфом // Фундаментальная и прикладная гидрофизика. 2015. Т. 8. № 3. С. 32–43.
Ляпидевский В.Ю., Новотрясов В.В., Храпченков Ф.Ф., Ярощук И.О. Внутренний волновой бор в шельфовой зоне моря // ПМТФ. 2017. Т. 58. № 5. С. 60–71. https://doi.org/10.15372/PMTF20170506
Liapidevskii V., Gavrilov N. Large Internal Solitary Waves in Shallow Waters // The Ocean in Motion: Circulation, Waves, Polar Oceanography. Editors: Manuel G. Velarde, Roman Yu. Tarakanov, Alexey V. Marchenko. Springer Oceanography. 2018. P. 87–108. https://doi.org/10.1007/978-3-319-71934-4_9
Choi W., Camassa R. Fully nonlinear internal waves in a two-fluid system // J. Fluid Mech. 1999. V. 386. P. 1–36. https://doi.org/10.1017/S0022112099005820
Le Metayer O., Gavrilyuk S., Hank S. A numerical scheme for the Green-Naghdi model // J. Comput. Phys. 2010. V. 229. P. 2034–2045. https://doi.org/10.1016/j.jcp.2009.11.021
Серебряный А.Н., Пао К.П. Прохождение нелинейной внутренней волны через точку переворота на шельфе // Докл. АН. 2008. Т. 420. № 4. С. 543–547.
Gavrilov N., Liapidevskii V., Gavrilova K. Mass and momentum transfer by solitary internal waves in a shelf zone // Nonlin. Processes Geophys. 2012. V. 19. P. 265–272. https://doi.org/10.5194/npg-19-265-2012
Леонтьев А.П., Ярощук И.О., Смирнов С.В., Кошелева А.В., Пивоваров А.А., Самченко А.Н., Швырев А.Н. Пространственно-распределенный измерительный комплекс для мониторинга гидрофизических процессов на океаническом шельфе // Приборы и техника эксперимента. 2017. № 1. С. 128–135. https://doi.org/10.7868/S0032816216060227
Талипова Т.Г., Пелиновский Е.Н., Куркин А.А., Куркина О.Е. Моделирование динамики интенсивных внутренних волн на шельфе // Изв. РАН. Физика атмосферы и океана. 2014. Т. 50. № 6. С. 714–722. https://doi.org/10.7868/S0002351514060169
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика жидкости и газа