Известия РАН. Механика жидкости и газа, 2019, № 3, стр. 98-112
Теплообмен и теплофизика дозвуковых струй диссоциированного воздуха, обтекающих цилиндрические модели в индукционном ВЧ-плазмотроне
С. А. Васильевский a, А. Н. Гордеев a, А. Ф. Колесников a, *
a Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия
* E-mail: koles@ipmnet.ru
Поступила в редакцию 08.08.2018
После доработки 18.10.2018
Принята к публикации 18.10.2018
Аннотация
Проведено экспериментальное и численное исследование теплообмена дозвуковых течений высокоэнтальпийного воздуха в индукционном плазмотроне ВГУ-4 для трех вариантов секционированного разрядного канала с диаметром выходного сечения 30, 40 и 50 мм. В качестве модели использовался цилиндр с плоским торцом диаметром 20 мм. По экспериментальным данным численно восстановлены энтальпия he и скорость на оси струи с помощью программы Gamma. Предложен метод приближенного определения энтальпии he на основе экспериментальных данных и формулы Фэя-Риддела для теплового потока. Введен эффективный безразмерный радиус модели reff, учитывающий зависимость потока на внешней границе пограничного слоя от геометрии модели и разрядного канала и режима работы плазмотрона. Проведены расчеты reff для режимов работы плазмотрона ВГУ-4 с простым цилиндрическим разрядным каналом и секционированным каналом. Проведено сравнение расчетов энтальпии he с помощью “точного” и приближенного методов. Максимальное различие в значениях he составило 6%.
Индукционные ВЧ-плазмотроны широко используются для аэрофизических исследований, в том числе для моделирования аэродинамического нагрева, испытаний образцов теплозащитных материалов с целью определения их термохимической стойкости и каталитических свойств их поверхности по отношению к гетерогенной рекомбинации атомов азота и кислорода [1–7]. Известно, что в наземных установках невозможно полностью моделировать натурные условия входа затупленного тела в атмосферу, однако возможно локальное моделирование условий теплопередачи от пограничного слоя к критической точке на поверхности [8, 9]. Для такого локального моделирования необходимо одновременное выполнение трех условий: 1) давление торможения в критической точке модели, испытываемой в плазмотроне, должно быть равно давлению торможения p0 в критической точке на поверхности тела; 2) энтальпия he на оси струи на внешней границе пограничного слоя перед моделью должна быть равна полной энтальпии в натурных условиях; 3) должны быть равны градиенты скорости β на внешней границе пограничного слоя перед моделью и перед критической точкой затупленного тела.
В дозвуковых струях высокоэнтальпийного воздуха давление вблизи критической точки модели близко к давлению у стенки испытательной камеры pc, которое достаточно легко и точно измеряется в процессе эксперимента. Для локального моделирования натурного теплообмена и подбора режимов испытаний образцов материалов ключевыми являются вопросы, связанные с определением энтальпии и градиента скорости на внешней границе пограничного слоя.
Прямое измерение энтальпии дозвуковой струи диссоциированного воздуха возможно с помощью специально разработанного датчика – энтальпиемера [10], но это практически невозможно сделать в потоках частично диссоциированного углекислого газа. Измерение энтальпии с помощью энтальпиемера требует проведения специальных экспериментов, является длительным и трудоемким делом, и в ряде случаев может давать значительную погрешность. С учетом этого на практике энтальпия и характерная скорость дозвуковой струи восстанавливаются по экспериментальным данным (по тепловому потоку к высококаталитичному эталонному материалу и скоростному напору) с помощью численных решений уравнений неравновесного пограничного слоя.
В данной работе предлагается новый метод приближенного и быстрого определения энтальпии дозвуковой воздушной струи по тепловому потоку на основе известной формулы Фэя-Риддела [11, 12] для теплового потока от пограничного слоя к абсолютно каталитической поверхности в критической точке затупленного тела. В формулу Фэя–Риддела входит градиент скорости β. Этот параметр удобно заменить на безразмерный эффективный радиус модели reff = (1/β)Vs/Rm, где Rm и Vs – радиус модели и характерное значение скорости набегающего потока. Параметр reff отражает влияние на тепловой поток к критической точке модели внешнего по отношению к пограничному слою течения, включая влияние завихренности набегающей дозвуковой струи. Существенной особенностью предлагаемого подхода является предварительный расчет эффективного радиуса модели с помощью программ численного расчета течения в разрядном канале (Alpha) и дозвукового обтекания модели (Beta). Отметим, что вычисление эффективного радиуса модели необходимо также для определения условий локального моделирования теплопередачи [8, 9].
1. ЭКСПЕРИМЕНТЫ НА ВЧ-ПЛАЗМОТРОНЕ
Эксперименты по теплообмену в дозвуковых струях высокоэнтальпийного воздуха проведены на 100-киловаттном индукционном ВЧ-плазмотроне ВГУ-4 (ИПМех РАН) для трех конфигураций секционированного разрядного канала, состоящего из кварцевой трубки длиной 400 мм и водоохлаждаемого конического сопла в конце канала с углом полураствора 30 градусов. Диаметры выходных сечений насадков для трех конфигураций: D = 30, 40 и 50 мм. Использовалась модель – цилиндр с плоским торцом диаметром dm = 20 мм, причем расстояние от среза канала до модели было равно диаметру выходного сечения сопла: Lzm = D. Во всех экспериментах статическое давление в испытательной камере pc = 100 гПа, расход воздуха G = 2.4 г/с, мощность ВЧ-генератора по анодному питанию Nap менялась от 20 до 75 кВт.
Экспериментальная диагностика включала измерения статического давления pc у стенки испытательной камеры; определение динамического давления pdyn на оси струи, натекающей на модель, с помощью водоохлаждаемой трубки Пито; измерения теплового потока qwc к медному водоохлаждаемому калориметру, встроенному в модель, – цилиндр с плоским торцом диаметром dm = 20 мм. Для определения мощности, вкладываемой в плазму Npl = Napζ, использовались экспериментальные данные для к.п.д. ζ = ζ(Nap), полученные ранее. Значения полученных в экспериментах параметров qwc и pdyn для трех серий экспериментов с использованием разрядного канала с тремя величинами диаметра выходного сечения D приведены в таблицах: D = 30 (табл. 1), 40 (2) и 50 мм (3). Значения qwc и pdyn использовались далее при расчетном восстановлении энтальпии на внешней границе пограничного слоя he и характерной скорости дозвукового потока Vs для условий экспериментов. Полученные величины he и Vs приведены в соответствующих табл. 1–3.
Таблица 1.
| Nap, кВт | qwc, Вт/см2 | pdyn, Пa | he, МДж/кг | Vs, м/с | reff |
|---|---|---|---|---|---|
| 20 | 211 | 800 | 13.65 | 553.4 | 1.69 |
| 25 | 280 | 950 | 17.51 | 648.0 | 1.76 |
| 30 | 335 | 1060 | 20.68 | 718.7 | 1.84 |
| 35 | 386 | 1160 | 23.46 | 782.6 | 1.87 |
| 40 | 430 | 1250 | 25.87 | 839.8 | 1.91 |
| 45 | 472 | 1340 | 28.17 | 897 | 1.95 |
| 50 | 512 | 1420 | 30.30 | 949 | 1.98 |
| 55 | 549 | 1480 | 32.34 | 996 | 2.00 |
| 60 | 581 | 1580 | 33.99 | 1053 | 2.04 |
| 65 | 619 | 1650 | 36.07 | 1111 | 2.08 |
| 70 | 649 | 1710 | 37.40 | 1153 | 2.08 |
| 75 | 675 | 1770 | 38.84 | 1207 | 2.12 |
Таблица 2.
| Nap, кВт | qwc, Вт/см2 | pdyn, Пa | he, МДж/кг | Vs, м/с | reff |
|---|---|---|---|---|---|
| 20 | 154 | 260 | 13.25 | 314.4 | 1.68 |
| 25 | 204 | 310 | 16.8 | 368.7 | 1.72 |
| 30 | 245 | 350 | 19.65 | 410.7 | 1.72 |
| 35 | 285 | 390 | 22.16 | 449.7 | 1.74 |
| 40 | 323 | 430 | 24.72 | 489.7 | 1.77 |
| 45 | 356 | 460 | 26.85 | 521.4 | 1.79 |
| 50 | 387 | 480 | 28.94 | 547.4 | 1.80 |
| 55 | 418 | 500 | 31.16 | 575.5 | 1.83 |
| 60 | 448 | 520 | 33.19 | 603.8 | 1.85 |
| 65 | 476 | 540 | 35.04 | 632.9 | 1.86 |
| 70 | 502 | 560 | 36.9 | 666.8 | 1.91 |
| 75 | 528 | 580 | 38.6 | 703.6 | 1.94 |
Таблица 3.
| Nap, кВт | qwc, Вт/см2 | pdyn, Пa | he, МДж/кг | Vs м/с | reff |
|---|---|---|---|---|---|
| 20 | 105 | 102 | 11.6 | 191 | 1.68 |
| 25 | 139 | 117 | 14.8 | 220 | 1.71 |
| 30 | 185 | 139 | 18.7 | 258 | 1.72 |
| 35 | 218 | 156 | 21.5 | 285 | 1.74 |
| 40 | 251 | 172 | 24.3 | 312 | 1.77 |
| 45 | 282 | 180 | 26.9 | 331 | 1.78 |
| 50 | 308 | 192 | 29.0 | 351 | 1.78 |
| 55 | 333 | 204 | 31.0 | 373 | 1.82 |
| 60 | 357 | 219 | 32.8 | 396 | 1.84 |
| 65 | 380 | 226 | 34.6 | 415 | 1.85 |
| 70 | 402 | 232 | 36.5 | 440 | 1.91 |
| 75 | 425 | 240 | 37.9 | 470 | 1.94 |
2. ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ТЕЧЕНИЙ ПЛАЗМЫ В РАЗРЯДНОМ КАНАЛЕ И ДОЗВУКОВЫХ СТРУЙ ВЫСОКОЭНТАЛЬПИЙНОГО ВОЗДУХА
Настоящая методика численного моделирования основана на разбиении всего поля течения в плазмотроне ВГУ-4 на три характерные области [13–15]:
1) течение равновесной плазмы в разрядном канале (расчет по программе Alpha на основе уравнений Навье–Стокса и упрощенных уравнений Максвелла);
2) течение в высокоэнтальпийной равновесной струе диссоциированного воздуха, истекающей из канала и обтекающей модель (расчет по программе Beta на основе уравнений Навье–Стокса);
3) течение в неравновесном пограничном слое в окрестности критической точки на поверхности модели (расчет по программе Gamma на основе уравнений пограничного слоя конечной толщины).
В данном разделе рассмотрено численное моделирование течений в первых двух областях. Численное моделирование дозвукового течения плазмы в разрядном канале проводится на основе уравнений Навье–Стокса и упрощенных уравнений Максвелла в предположении, что индукционная плазма воздуха является термически и химически равновесной, это предположение является достаточно точным при p0 > 50 гПа. Предполагается также, что значения мощности Npl, вкладываемой в плазму, не слишком велики, так что можно пренебречь потерями энергии, связанными с излучением плазмы [16, 17]. Течение в цилиндрическом канале считается стационарным, ламинарным и осесимметричным с закруткой потока в азимутальном направлении. Для расчета используются полные уравнения Навье–Стокса, записанные в цилиндрической системе координат (z, r) с учетом трех компонент скорости – аксиальной, радиальной и азимутальной. В полную систему уравнений входит упрощенное уравнение Максвелла для усредненной по времени тангенциальной компоненты комплексной амплитуды вихревого электрического поля Eθ [13, 14]. Уравнения включают источниковые члены, учитывающие влияние электромагнитного поля: Fz, Fr – аксиальная и радиальная компоненты силы Лоренца (так называемое магнитное давление), а также QJ – джоулево тепло.
Граничные условия для данной задачи: 1) во входном сечении задаются три компоненты скорости, определяемые условиями эксперимента, – заданным массовым расходом газа и закруткой потока; 2) нулевые значения для компонент скорости и значения температуры Tw = 300 K задаются на всех твердых поверхностях; 3) условия симметрии используются на оси канала; 4) “мягкие” граничные условия (равенство нулю производных от газодинамических параметров) используются в выходном сечении канала.
Для вычисления источниковых членов необходимо определить модель электромагнитных явлений в индукционном плазмотроне. Считается, что индуктор состоит из отдельных бесконечно тонких круговых витков, перпендикулярных оси симметрии, с одинаковым током в каждом витке. Переменный внешний ток порождает монохроматическое электрическое и магнитное поля с комплексными амплитудами E(z, r), H(z, r).
Электромагнитное поле внутри индуктора определяется двумерным уравнением Максвелла для амплитуды тангенциальной компоненты электрического поля Eθ(z, r). Это уравнение приведено в [13] и является довольно сложным для решения, т.к. требует задания отдельной расчетной области большого диаметра, чтобы на внешней границе этой области можно было положить электрическое поле равным нулю.
Используя особенность разрядного канала плазмотрона ВГУ-4, который является относительно тонким, можно принять дополнительное предположение, что электрическое поле меняется в продольном направлении значительно меньше, чем поперек канала. Используя это предположение, можно существенно упростить двумерные уравнения и свести их к квазиодномерному приближению для уравнений Максвелла [13–15]
(1.1)
$\tfrac{d}{{dr}}\left( {\tfrac{1}{r}\tfrac{d}{{dr}}\left( {r{{E}_{\theta }}} \right)} \right) = - i\omega {{\mu }_{0}}\sigma {{E}_{\theta }}{\text{,}}\quad i\omega {{\mu }_{0}}{{H}_{z}} = \tfrac{1}{r}\tfrac{d}{{dr}}\left( {r{{E}_{\theta }}} \right)$Полученное квазиодномерное приближение позволяет определить комплексную амплитуду электрического поля Eθ(z, r) в результате решения краевой задачи для обыкновенного дифференциального уравнения (1.1); продольная координата z в этой задаче является параметром, т.к. Eθ зависит от z только через граничное условие на стенке канала:
(1.2)
${\text{ }}r = {{R}_{c}}:\;\frac{1}{r}\frac{d}{{dr}}\left( {r{{E}_{\theta }}} \right) = i\omega {{\mu }_{0}}{{H}_{{zc0}}}{\text{(}}z{\text{)}}$Численный метод решения уравнений Навье–Стокса основан на методе конечных объемов и алгоритме SIMPLE Патанкара–Сполдинга с применением шахматной сетки [19], сильно неравномерной как в аксиальном, так и в радиальном направлении.
Коэффициенты переноса (вязкость, полная теплопроводность, электропроводность) определялись в процессе расчета с помощью интерполяции по заранее рассчитанным таблицам. Таблицы коэффициентов переноса рассчитывались по разработанной ранее программе SoVA [20]. Такой подход позволяет использовать достаточно точные значения коэффициентов переноса с минимальным увеличением времени счета.
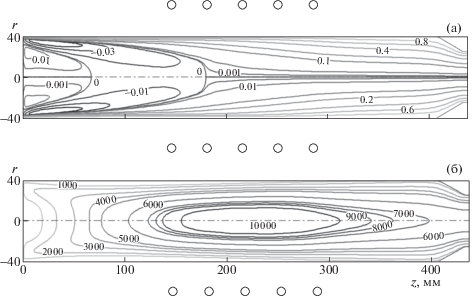
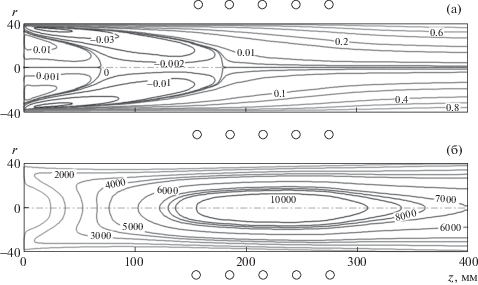
С помощью описанного метода по программе Alpha проведены расчеты течения воздушной плазмы в простом цилиндрическом разрядном канале и в каналах с коническими насадками для следующего характерного режима ВГУ-4: давление p0= 100 гПа, мощность по анодному питанию Nap = 45 кВт, соответствующая мощность, вкладываемая в плазму Npl = 29 кВт, массовый расход воздуха G = 2.4 г/с. На рис. 1 показаны результаты расчета – изолинии безразмерной функции тока (а) и изотермы (б) для простого разрядного канала без конического насадка с диаметром выходного сечения D = 80 мм. Аналогичные результаты для того же режима ВГУ-4 показаны на рис. 2 для секционированного канала с коническим насадком с диаметром выходного сечения D = 50 мм.
Рис. 1.
Изолинии в простом разрядном канале D = 80 мм: (а) – безразмерная функция тока, (б) – изотермы.
Расчет течения во второй области – в испытательной камере плазмотрона, где истекающая из разрядного канала дозвуковая струя высокоэнтальпийного воздуха обтекает модель, проводится по программе Beta также на основе полных уравнений Навье–Стокса, записанных в цилиндрической системе координат (z, r). Влияние электромагнитного поля в этой области не учитывается. Основное внимание уделяется ядру струи вблизи передней критической точки модели, включая пограничный слой, где используется более мелкая подробная сетка. В целом расчетная сетка во второй области является существенно неравномерной по обоим направлениям.
Для численного решения уравнений Навье–Стокса во второй области используется тот же численный метод Патанкара–Сполдинга [19], что и в канале. В качестве граничных условий на входе здесь задаются на срезе разрядного канала параметры газа, полученные на предыдущем этапе из расчета по программе Alpha. На твердых поверхностях скорость газа равна нулю и температура Tw = 300 K. На выходной границе области используются мягкие граничные условия, которые можно применять, если длина области течения достаточно превышает ее ширину, что накладывает ограничение на длину расчетной области ${{L}_{{v{\text{ }}}}} \geqslant {\text{ 1}}.{\text{5}} \times {{D}_{v}}$, т.е. длина расчетной области должна быть больше, чем полтора диаметра камеры.
В ядре дозвуковой струи, истекающей из канала, давление и температура меняются слабо, и в этой области при не слишком низких давлениях реализуется модель химически равновесного течения. Поэтому расчет во второй области, так же как и в первой, проводится в предположении термически и химически равновесного течения. Область ядра струи перед моделью представляет основной практический интерес, тогда как расчет на периферии струи и вниз по потоку от переднего торца модели проводится только для того, чтобы “замкнуть” задачу, используя граничные условия на стенке барокамеры и на правой границе расчетной области.
По описанному методу с помощью программы Beta проведены расчеты обтекания модели дозвуковой струей для экспериментальных условий, указанных выше: p0 = 100 гПа, Npl = 29 кВт, G = 2.4 г/с. Расстояние Lzm от среза разрядного канала до модели равно 100 мм. Геометрия модели – цилиндр с плоским торцом диаметром dm, который в этих расчетах варьировался от 20 до 140 мм. Для сравнения был проведен также расчет обтекания Евромодели – цилиндра диаметром 50 мм с закругленной кромкой, радиус закругления 11 мм.
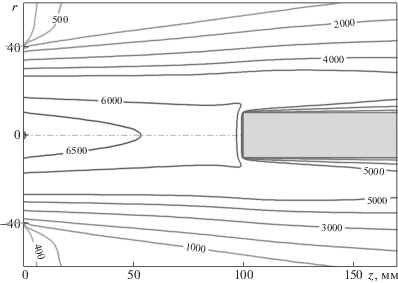
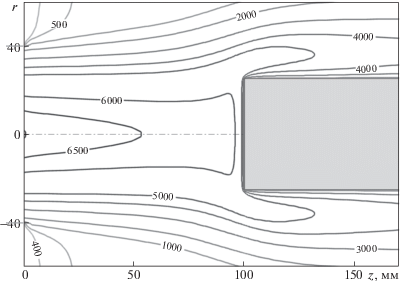
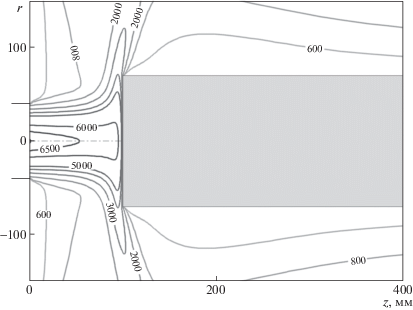
На рис. 3–5 показаны рассчитанные изотермы для обтекания моделей – плоских цилиндров диаметром dm = 20, 50 и 140 мм. Все эти расчеты проведены для случая истечения дозвуковой струи из простого цилиндрического канала без насадка, D = 80 мм.
На рис. 3–5 представлена не вся расчетная область, а область ядра струи, т.к. практический интерес представляет течение между срезом разрядного канала и лобовой поверхностью модели, включая относительно тонкий пограничный слой вблизи переднего торца модели.
Основным результатом расчета по программе Beta являются не только параметры потока газа в ядре струи перед моделью, но и вычисляемые по этим параметрам безразмерные величины, характеризующие толщину пограничного слоя и завихренность потока на внешней границе пограничного слоя перед моделью. Четыре безразмерные величины определяются в результате расчета по программе Beta по следующим формулам: Δ = δ/Rm – безразмерная толщина пограничного слоя; u(Ze, 0)/U0 – безразмерная скорость; u1e = u1(Ze) – безразмерная производная радиальной скорости; параметр, характеризующий завихренность потока
Здесь нижний индекс “e” обозначает значение функции на внешней границе пограничного слоя, δ – размерная толщина пограничного слоя, Rm – радиус модели; Ze – продольная координата, соответствующая положению внешней границы пограничного слоя; U0 – характерная скорость, равная здесь скорости потока на срезе разрядного канала плазмотрона на оси симметрии, u(z, r) – компонента скорости струи в продольном направлении вдоль оси симметрии, z – координата вдоль оси симметрии, r – радиальная координата, т.е. расстояние от оси симметрии струи. Все указанные параметры определяются на внешней границе пограничного слоя на оси струи, z = Ze, r = 0. Безразмерная производная радиальной скорости u1(z) определяется следующей формулой:
Внешняя граница пограничного слоя z = Ze определяется по результатам расчета обтекания модели дозвуковой струей воздуха из условия максимума производной от u1(z) на оси струи du1(z)/dz = max. Это условие эквивалентно обращению в ноль второй производной от u1(z). Касательная к u1(z), проведенная через точку (Ze, u1(Ze)), имеет максимальный наклон к оси z. Эта касательная является локальной асимптотикой слабо вязкого течения, на которую выходит расчет по программе Gamma вблизи внешней границы пограничного слоя за счет постановки соответствующих граничных условий.
Указанные выше четыре безразмерные величины были рассчитаны для различных вариантов, в том числе для различных значений диаметра модели, и использовались далее для расчета безразмерного эффективного радиуса модели.
3. РАСЧЕТ БЕЗРАЗМЕРНОГО ГРАДИЕНТА СКОРОСТИ И ЭФФЕКТИВНОГО РАДИУСА МОДЕЛИ
Расчет безразмерного градиента скорости u1w и эффективного радиуса reff = 1/u1w проводится с помощью программы Beta следующим образом. Сначала градиент скорости u1e вычисляется по известному распределению радиальной скорости $v\left( {z,r} \right)$ на внешней границе пограничного слоя с помощью формулы
(3.1)
${{u}_{{1e}}} = \frac{{{{R}_{m}}}}{{{{V}_{s}}}}{{\left[ {\frac{{\partial v{\text{(}}z{\text{,}}r{\text{)}}}}{{\partial r}}} \right]}_{{z = {{Z}_{e}},r = 0}}}$Получить сразу из решения уравнений Навье–Стокса нужный градиент скорости u1w на поверхности модели нельзя, он просто равен нулю в рамках уравнений Навье–Стокса. Параметр u1w определяется путем экстраполяции значения u1(z) с внешней границы пограничного слоя на стенку, т.е. по формуле
(3.2)
${{u}_{{1w}}} = {{u}_{{1e}}} + {\Delta }{{R}_{m}}{{\left[ {\frac{{\partial {{u}_{1}}\left( z \right)}}{{\partial z}}} \right]}_{{z = {{Z}_{e}},r = 0}}}$Производные $\partial v\left( {z,r} \right){\text{/}}\partial r$ и ∂u1/∂z вычисляются численно. Расчет reff для всех режимов испытаний на плазмотроне требует проведения многопараметрических расчетов по программам Alpha и Beta и занимает много времени. Поэтому вместо точного расчета параметра reff для каждого режима испытаний предлагается использовать аппроксимационные формулы, выражающие зависимость reff от существенных параметров эксперимента, например от мощности плазмотрона Nap при заданных значениях dm, или просто зависимость reff от диаметра модели dm, полученную для некоторого базового режима работы плазмотрона.
В качестве первого примера получим зависимость reff от dm при неизменных прочих параметрах. Как показали предварительные вспомогательные расчеты, reff сильнее всего зависит именно от диаметра и геометрии модели. Зависимость reff от давления p, мощности Nap, массового расхода воздуха G оказывается существенно слабее.
Для получения зависимости reff от dm проведена серия расчетов по программам Alpha и Beta для простого цилиндрического разрядного канала длиной 400 мм и диаметром 80 мм, без конического насадка, для часто используемых в экспериментах базовых значений параметров, определяющих режим работы плазмотрона ВГУ-4: давление p0 = 100 гПа, мощность Nap = 45 кВт, массовый расход воздуха G = 2.4 г/с. Расчеты выполнены для моделей простой геометрии – цилиндров с плоским торцом диаметром dm от 20 мм до 140 мм. Расстояние от среза разрядного канала до модели во всех вариантах было неизменным: Lzm = 100 мм. По программе Alpha рассчитывалось течение плазмы в канале для заданного базового режима, затем по программе Beta проводилась серия расчетов для различных значений диаметра модели dm для заданного базового режима работы ВГУ-4. По результатам этих расчетов по формулам (3.1), (3.2) определялись градиент скорости u1w и эффективный радиус модели reff.
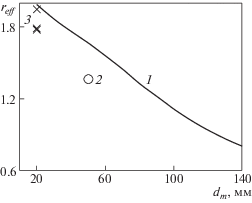
На рис. 6 кривой (1) показаны рассчитанные значения reff(dm) для моделей – цилиндров с плоским торцом разного диаметра, обтекаемых дозвуковой струей воздуха из простого цилиндрического канала. Для оценки влияния геометрии модели на рис. 6 показано рассчитанное значение reff для Евромодели – цилиндра диаметром dm = 50 мм с закругленной кромкой (точка 2). Для сравнения показаны также значения reff, рассчитанные для модели – цилиндра с плоским торцом dm = 20 мм для секционированного канала с D = 30, 40, 50 мм при Nap = 45 кВт – точки 3 (см. также табл. 1–3).
Рис. 6.
Эффективный радиус reff (dm) для различной геометрии модели и канала: 1 – цилиндры с плоским торцом различного диаметра dm, простой канал D = 80 мм; 2 – Евромодель dm = 50 мм, простой канал D = 80 мм; 3 – цилиндр с плоским торцом dm = 20 мм, секционированный канал D = 30, 40, 50 мм.
Полученная зависимость reff(dm) для моделей – цилиндров с плоским торцом и цилиндрического канала диаметром D = 80 мм аппроксимирована комбинацией линейной функции и полинома 2-го порядка
(3.3)
$\begin{gathered} {{r}_{{eff}}} = - 0.010613{{d}_{m}} + 2.1906,\quad 20 \leqslant {{d}_{m}} < 70 \\ {{r}_{{eff}}} = 2.5734 - 0.019524{{d}_{m}} + 0.000048957d_{m}^{2},\quad 70 \leqslant {{d}_{m}} < 140 \\ \end{gathered} $В формулах (3.3) значение dm в мм, а reff – безразмерное. Отличие аппроксимации (3.3) от расчета по программе Beta не превышает 1%.
Как видно из рис. 6, при значениях диаметра модели, меньших диаметра среза разрядного канала D = 80 мм, зависимость reff(dm) близка к линейной, но при dm, больших 80 мм, характер зависимости меняется, т.к. фактически характерным размером для задачи обтекания вместо диаметра модели становится диаметр канала.
В качестве второго примера были проведены расчеты обтекания цилиндрической модели с плоским торцом при давлении 100 гПа и расходе 2.4 г/с для трех вариантов геометрии секционированного разрядного канала с диаметрами выходного сечения D = 30, 40 и 50 мм в диапазоне Nap = 20–75 кВт. Для всех вариантов рассчитан reff и в результате получены следующие линейные аппроксимации reff:
(3.4)
$\begin{gathered} {{r}_{{eff}}} = {\text{1}}.{\text{598}} + 0.00{\text{7286}}{{N}_{{ap}}},\quad D = {\text{3}}0\;{\text{м м }} \hfill \\ {{r}_{{eff}}} = {\text{1}}.{\text{592}} + 0.00{\text{441}}0{{N}_{{ap}}},\quad D = {\text{4}}0\;{\text{м м }} \hfill \\ {{r}_{{eff}}} = {\text{1}}.{\text{588}} + 0.00{\text{4365}}{{N}_{{ap}}},\quad D = {\text{5}}0\;{\text{м м }} \hfill \\ \end{gathered} $4. ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ТЕЧЕНИЯ И ТЕПЛОПЕРЕДАЧИ В НЕРАВНОВЕСНОМ ПОГРАНИЧНОМ СЛОЕ ДИССОЦИИРОВАННОГО ВОЗДУХА ВБЛИЗИ КРИТИЧЕСКОЙ ТОЧКИ МОДЕЛИ
Третья расчетная область – пограничный слой конечной толщины на оси симметрии струи вблизи переднего торца модели. Поверхность модели имеет заданную температуру Tw и характеризуется эффективным коэффициентом каталитической рекомбинации атомов γw.
Пограничный слой для условий эксперимента на ВЧ-плазмотроне ВГУ-4 является обычно существенно неравновесным, а при низких давлениях – замороженным. Численное моделирование течения и теплопередачи от химически неравновесного пограничного слоя к критической точке модели реализовано в компьютерной программе Gamma. Важная особенность программы Gamma, позволяющая получать достаточно точные результаты, – тесная интеграция с надежными экспериментальными данными: тепловым потоком qwc, измеренным в критической точке модели с помощью водоохлаждаемого медного калориметра, и динамическим давлением pdyn, измеренным с помощью трубки Пито. Подробное описание методов измерений приведено в [21].
Программа Gamma основана на численном решении уравнений пограничного слоя на оси симметрии потока с учетом каталитических реакций рекомбинации атомов O и N на поверхности модели. Модель течения в третьей области построена на основе системы одномерных уравнений пограничного слоя конечной толщины, в которой учитывается завихренность потока на его внешней границе, а численное решение уравнений Навье–Стокса используется как внешнее решение [14]. Используется 5-ти компонентная модель диссоциированного воздуха: N2, O2, NO, N и O.
Некоторые обозначения, используемые в данном разделе, отличаются от использовавшихся в предыдущих разделах, в силу специфики третьей расчетной области и используемых здесь уравнений пограничного слоя. Вместо координат цилиндрической системы (z, r) здесь используются координаты: x – расстояние вдоль торца модели от ее критической точки, y – расстояние по нормали от торца модели в сторону набегающей струи. Компонента скорости V в обозначениях данного раздела соответствует обозначению u из предыдущих разделов, Vs – характерное значение скорости потока вдоль оси симметрии. Компонента скорости U в направлении x (т.е. перпендикулярно оси симметрии) равна нулю на оси симметрии, и в уравнения входит градиент этой компоненты скорости u1. В уравнения пограничного слоя входят безразмерные параметры, полученные ранее из расчета обтекания модели с помощью программы Beta: Δ = δ/Rm – безразмерная толщина пограничного слоя, здесь δ – размерная толщина пограничного слоя; Rm – радиус модели; ${{v}_{e}}$ – безразмерная скорость на внешней границе пограничного слоя (т.е. размерная скорость Ve, отнесенная к характерной скорости Vs); u1e – безразмерная производная радиальной скорости на внешней границе пограничного слоя; [∂u1/∂y]e – безразмерный параметр, характеризующий завихренность потока на внешней границе пограничного слоя; y – безразмерная координата поперек пограничного слоя.
Для уравнений сохранения импульса и энергии использовались граничные условия прилипания и заданная температура поверхности Tw. При постановке граничных условий для уравнений диффузии компонент на внешней границе пограничного слоя предполагается, что течение во внешнем потоке равновесное
Здесь индекс “eq” обозначает равновесные значения параметров на внешней границе пограничного слоя. Равновесные концентрации компонент Cieq вычисляются с помощью уравнений химического равновесия для заданных значений давления и температуры (или энтальпии) на внешней границе пограничного слоя.
Используется простая однопараметрическая модель рекомбинации атомов N и O, полученная в рамках следующих предположений: 1) каталитическая рекомбинация атомов N и O на поверхности (S) описывается реакциями 1-го порядка
2) концентрация молекул NO мала и можно пренебречь их участием в каталитических реакциях на поверхности; 3) вероятность рекомбинации атомов N, O на поверхности одинакова и равна эффективному коэффициенту γw: γw = γwO = γwN. 4) диффузионные потоки к поверхности пропорциональны только концентрации соответствующей компоненты, что в рассматриваемом случае дает следующие выражения для массовых диффузионных потоков атомов Ji: – Ji = ρKwiCi, (i = N, O); 5) для диффузионных потоков химических компонентов используется простая модель бинарной диффузии.
Здесь Ci – массовая концентрации i-й компоненты, ρ – плотность смеси, Kwi – константа скорости гетерогенной рекомбинации i-й компоненты, которая определяется через коэффициенты γwN и γwO [21]
Расчет уравнений химически неравновесного пограничного слоя конечной толщины производится с помощью разностной схемы [22] 4-го порядка аппроксимации. Полная система уравнений решается итерациями, для обеспечения сходимости итераций применяется метод нижней релаксации. В результате расчета по программе Gamma определяются профили параметров поперек пограничного слоя – температуры, энтальпии, градиента скорости, концентраций компонент. Основным результатом расчета является значение теплового потока в критической точке модели qw, зависящее от температуры стенки Tw и от заданного значения эффективного коэффициента рекомбинации γw. Расчет qw для заданных экспериментальных условий является основой метода восстановления энтальпии набегающего потока.
5. ОПРЕДЕЛЕНИЕ ЭНТАЛЬПИИ ДОЗВУКОВОГО ПОТОКА ДИССОЦИИРОВАННОГО ВОЗДУХА
Расчетное определение энтальпии с помощью программы Gamma базируется на заданных значениях теплового потока qwc, измеренного к медному водоохлаждаемому калориметру в дозвуковой струе плазмотрона, и динамического давления pdyn, измеренного с помощью трубки Пито, имеющей ту же геометрию, что и модель с калориметром для измерения теплового потока. Энтальпия определяется из условия равенства измеренного теплового потока qwc и теплового потока qw∞, полученного из расчета по программе Gamma для условий эксперимента и абсолютно каталитической стенки. При этом используется предположение, что поверхность химически чистой меди, из которой сделан водоохлаждаемый калориметр, является высококаталитической и для нее можно принять эффективный коэффициент каталитичности γw = 1. Тогда определение энтальпии сводится к решению с помощью программы Gamma методом итераций следующей обратной задачи:
(5.1)
${{q}_{{wc}}} = {{q}_{w}}_{\infty }({{h}_{e}},{{T}_{w}} = {\text{3}}00,{{\gamma }_{w}} = {\text{1}})$(5.2)
${{p}_{{{\text{dyn}}}}} = 0.5{{k}_{p}}{{\rho }_{e}}V_{s}^{2}\;\;{\text{и л и }}\,\;{{V}_{{\text{s}}}} = {{\left( {{{p}_{{dyn}}}{\text{/}}\left( {0.5{{k}_{p}}{{\rho }_{e}}} \right)} \right)}^{{0.5}}}$Значения энтальпии he и характерной скорости потока Vs, рассчитанные по программе Gamma для трех вариантов разрядного канала D = 30, 40, 50 мм, приведены в табл. 1–3. Различная геометрия разрядного канала приводит к большому отличию в скорости потоков на оси струи, но при этом значения энтальпии he при заданной мощности отличаются незначительно.
6. ПРИБЛИЖЕННЫЙ МЕТОД РАСЧЕТА ТЕПЛОВЫХ ПОТОКОВ
Существенным дополнением к “точному” вычислению тепловых потоков с помощью программ Alpha, Beta, Gamma является простой расчет на основе приближенной формулы Фэя–Риддела для теплового потока от равновесного пограничного слоя к критической точке затупленного тела. Формула Фэя–Риддела имеет следующий вид [11, 12]:
(6.1)
$\begin{gathered} {{q}_{{wFR}}} = 0.763{{\Pr }^{{ - 0.6}}}{{\left( {{{{\rho }}_{{\text{e}}}}{{{\mu }}_{{\text{e}}}}} \right)}^{{0.5}}}{{{\beta }}_{{\text{e}}}}^{{0.5}}{{\left( {\frac{{{{{\rho }}_{{\text{w}}}}{{{\mu }}_{{\text{w}}}}}}{{{{{\rho }}_{{\text{e}}}}{{{\mu }}_{{\text{e}}}}}}} \right)}^{{0.1}}}\left( {{{h}_{e}} - {{h}_{w}}} \right) \times \\ \times \;\left[ {1 + ({\text{L}}{{{\text{e}}}^{{0.52}}} - 1)\left( {\frac{{{{C}_{{{\text{O}}e}}}h_{{\text{O}}}^{0} + {{C}_{{{\text{N}}e}}}h_{{\text{N}}}^{0}}}{{{{h}_{e}}}}} \right)} \right] \\ \end{gathered} $где h – энтальпия, β – градиент скорости, ρ – плотность, μ – вязкость, СO и СN – массовые концентрации атомов кислорода и азота; нижние индексы e, w обозначают величины на внешней границе пограничного слоя и на поверхности тела в критической точке; $h_{{\text{O}}}^{0}$, $h_{{\text{N}}}^{0}$ – удельные энтальпии образования атомов O и N; Pr, Le – числа Прандтля и Льюиса, которые полагаются постоянными поперек пограничного слоя. Для упрощения расчетов далее принято Le = 1.
В формуле (6.1) qwFR – тепловой поток к критической точке тела от равновесно диссоциированного пограничного слоя. Эту формулу можно с хорошей точностью использовать и для вычисления теплового потока от химически неравновесного диссоциированного пограничного слоя к идеально каталитической поверхности.
Градиент скорости βe, входящий в (6.1), является ключевым параметром, отражающим влияние на qwFR внешнего по отношению к пограничному слою течения, зависящего от геометрии разрядного канала, формы модели и режима работы плазмотрона. Отметим, что индекс “e” у βe является формальным, поскольку формула (6.1) получена для асимптотически тонкого пограничного слоя. Параметр βe должен определяться экстраполяцией на поверхность тела, т.е. в точке Zw, где Zw – расстояние от среза разрядного канала до поверхности модели
(6.2)
${{{\beta }}_{{\text{e}}}} = {{\left[ {\frac{{\partial v(z,r)}}{{\partial r}}} \right]}_{{z = {{Z}_{w}},r = 0}}}$В (6.2) используется цилиндрическая система координат (z, r), где z – расстояние вдоль струи, т.е. поперек пограничного слоя, $v$ – компонента скорости в радиальном направлении. Далее вместо размерного параметра βe будем использовать безразмерный параметр u1w, определенный выше формулой (3.2), и безразмерный эффективный радиус модели reff = 1/u1w. Размерный эффективный радиус Reff = Rmreff. Тогда, используя приближение Le = 1 и переходя от размерного градиента скорости βe к безразмерному эффективному радиусу reff, формулу (6.1) преобразуем к виду
(6.3)
${{q}_{{wFR}}} = 0.763{\text{P}}{{{\text{r}}}^{{ - 0.6}}}{{\left( {{{{\rho }}_{{\text{e}}}}{{{\mu }}_{{\text{e}}}}} \right)}^{{0.5}}}{{\left( {\frac{{{{V}_{s}}}}{{{{R}_{m}}{{r}_{{eff}}}}}} \right)}^{{0.5}}}{{\left( {\frac{{{{{\rho }}_{{\text{w}}}}{{{\mu }}_{{\text{w}}}}}}{{{{{\rho }}_{{\text{e}}}}{{{\mu }}_{{\text{e}}}}}}} \right)}^{{0.1}}}\left( {{{h}_{e}} - {{h}_{w}}} \right)$7. ПРИБЛИЖЕННЫЙ МЕТОД ОПРЕДЕЛЕНИЯ ЭНТАЛЬПИИ НА ОСНОВЕ ФОРМУЛЫ ФЭЯ-РИДДЕЛА
Восстановление энтальпии с помощью программы Gamma требует численного решения уравнений химически неравновесного пограничного слоя конечной толщины, а в качестве исходных данных для этого расчета требуется набор безразмерных параметров, характеризующих толщину пограничного слоя и завихренность потока на внешней границе пограничного слоя перед моделью. Эти безразмерные параметры определяются в результате расчетов течения в разрядном канале плазмотрона (программа Alpha) и обтекания модели дозвуковой струей (программа Beta), что требует достаточно большого времени.
Альтернативой “точному” методу восстановления энтальпии с помощью программ Alpha, Beta, Gamma является простой расчет на основе приближенной формулы Фэя–Риддела (6.3) для теплового потока от диссоциированного пограничного слоя к абсолютно каталитической стенке в критической точке затупленного тела.
Далее в расчетах принято Pr = 0.71, а значения концентраций компонент диссоциированного воздуха, плотности и вязкости на внешней границе пограничного слоя и вблизи тела определяются с помощью уравнений химического равновесия и приближенного степенного соотношения для вязкости воздуха. Метод приближенного восстановления энтальпии he по заданному измеренному тепловому потоку сводится к решению обратной задачи для следующего уравнения:
где qwFR – тепловой поток, определяемый по формуле (6.3). Эта обратная задача решается методом итераций.С помощью приближенного метода на основе формул (7.1), (6.3) и (5.2) проведены расчеты энтальпии he с использованием аппроксимаций для эффективного радиуса модели reff (3.4) для секционированных каналов с выходными сечениями диаметром D = 30, 40, 50 мм для условий экспериментов: p0 = 100 гПа, G = 2.4 г/с, Nap = 20–75 кВт. Расчеты выполнены для цилиндра с плоским торцом диаметром 20 мм, расстояние от среза канала до поверхности модели равно диаметру выходного сечения канала D. В расчетах по точному и приближенному методам использовались одни и те же экспериментальные данные qwc и pdyn.
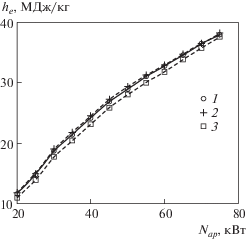
На рис. 7 показано сравнение результатов расчетов he точным методом (сплошные кривые 1) и приближенным методом (7.1), (6.3) (штриховые кривые 2, 3) для диаметра выходного сечения канала D = 50 мм. Как видно из рис. 7, приближенный метод с использованием reff ≈ 2.0, что соответствует аппроксимации reff(dm) (3.3), для этого случая дает достаточно точные значения he, отличающиеся всего на 2% от точных (кривые 2). Использование приближенного метода и аппроксимаций reff(Nap) (3.4) дает погрешность в he, достигающую 6% (3).
Рис. 7.
Сравнение энтальпии he, восстановленной по программе Gamma (1) и рассчитанной по приближенному методу с использованием формул (3.3) и (3.4) для reff (2, 3) для секционированного канала D = 50 мм.
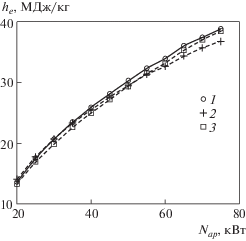
Аналогичное сравнение точных и приближенных значений he для канала с диаметром выходного сечения D = 30 мм показано на рис. 8. В этом случае максимальное различие приближенных и точных значений he составляет 5% для постоянного значения reff ≈ 2.0 и 4% для линейной аппроксимации reff(Nap) (3.4).
Рис. 8.
Сравнение энтальпии he, восстановленной по программе Gamma (1) и рассчитанной по приближенному методу с использованием формул для reff (3.3) и (3.4) (2, 3) для секционированного канала D = 30 мм.
Аналогичное сравнение точных и приближенных значений he проведено также для варианта канала с диаметром выходного сечения D = 40 мм. В этом случае максимальное отличие приближенных и точных значений he составляет 3% для постоянного значения reff ≈ 2.0 и 5% для линейной аппроксимации reff(Nap) (3.4).
ЗАКЛЮЧЕНИЕ
Проведены экспериментальные исследования теплообмена дозвуковых течений высокоэнтальпийного воздуха в индукционном плазмотроне ВГУ-4 для трех вариантов секционированного разрядного канала с диаметром выходного сечения D = 30, 40 и 50 мм. Для каждого варианта геометрии канала эксперименты проведены при давлении p0 = 100 гПа, расходе воздуха G = 2.4 г/с в широком диапазоне мощности ВЧ-генератора Nap = 20–75 кВт. В качестве модели использовался цилиндр с плоским торцом диаметром dm = 20 мм. Проведены измерения теплового потока к водоохлаждаемому медному калориметру qwc в окрестности критической точки и скоростного напора pdyn. По этим измеренным величинам с помощью расчетов по программе Gamma восстановлена энтальпия потока на оси струи he.
Для условий экспериментов проведено численное исследование дозвуковых течений в разрядном канале различной геометрии и обтекания моделей с помощью программ Alpha и Beta. Определены значения эффективного радиуса reff различных моделей, получены простые аппроксимационные формулы двух видов для зависимости reff от диаметра модели reff(dm) и для зависимости от мощности плазмотрона и диаметра выходного сечения секционированного канала с коническими насадками reff(Nap, D).
Предложен метод приближенного определения энтальпии he набегающего дозвукового потока диссоциированного воздуха, обтекающего модель, на основе экспериментальных данных и формулы Фэя–Риддела. Входящий в эту формулу градиент скорости обезразмерен и заменен на обратную величину – эффективный радиус модели reff, учитывающий зависимость потока на внешней границе пограничного слоя от формы модели, геометрии разрядного канала и режима работы плазмотрона.
Проведено сравнение расчетов энтальпии he для условий экспериментов на ВГУ-4 с секционированным разрядным каналом с помощью точного (на основе программ Alpha, Beta и Gamma) и приближенного методов. Максимальное различие в значениях энтальпии he составило 5% при использовании универсальной аппроксимации reff(dm) и 6% – аппроксимаций reff(Nap, D), полученных для условий экспериментов.
Список литературы
Gordeev A.N., Kolesnikov A.F., Yakushin M.I. An Induction Plasma Application to “Buran’s” Heat Protection Tiles Ground Tests // SAMPE J. 1992. 28(3). May/June . P. 29–33.
Гордеев А.Н., Колесников А.Ф. Высокочастотные индукционные плазмотроны серии ВГУ // Актуальные проблемы механики. Физико-химическая механика жидкостей и газов. М.: Наука, 2010. С. 151–177.
Залогин Г.Н., Землянский Б.А., Кнотько В.Б., Мурзинов И.Н., Румынский А.Н., Кузьмин Л.А. Высокочастотный плазмотрон – установка для исследований аэрофизических проблем с использованием высокоэнтальпийных газовых потоков // Космонавтика и ракетостроение. 1994. № 2. С. 22–32.
Жестков Б.Е. Исследование термохимической устойчивости теплозащитных материалов // Уч. зап. ЦАГИ. 2014. Т. XLV. № 5. С. 62–77.
Bottin B., Chazot O., Carbonaro M., Van Der Yaegen V., Paris S. The VKI Plasmatron characteristics and performance // Measurement Techniques for High Enthalpy and Plasma Flows. NATO-RTO-EN-8. 1999.
Herdrich G., Auweter-Kurtz M., Kurtz H., Laux T., Winter M. Operational Behavior of Inductively Heated Plasma Source IPG-3 for Entry Simulations // J. Thermophysics Heat Transfer. 2002. V. 16. № 3.
Dougherty M., Owens W., Meyers J., Fletcher D. Investigations of Surface-Catalyzed Recombination Reactions in Mars Atmosphere // 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition. 4–7 January 2011. Orlando, Florida.
Колесников А.Ф. Условия моделирования в дозвуковых течениях теплопередачи от высокоэнтальпийного потока к критической точке затупленного тела // Изв. РАН. МЖГ. 1993. № 1. С. 172–180.
Колесников А.Ф. Условия локального подобия термохимического взаимодействия высокоэнтальпийных потоков газов с неразрушаемой поверхностью // Теплофизика высоких температур. 2014. Т. 52. № 1. С. 118–125.
Дорошенко В.М., Мысова В.М., Рулев Ю.К., Якушин М.И. Измерение энтальпии в высокотемпературных дозвуковых струях азота и воздуха на индукционном плазмотроне // Инж.-физ. журн. Т. 53. № 3. С. 492–493.
Fay J.A., Riddell F.R. Theory of Stagnation Point Heat Transfer in Dissociated Air // J. Aeronautical Sciences. 1958.V. 25. № 2. P. 73–121.
Дорренс У.Х. Гиперзвуковые течения вязкого газа. М.: Мир, 1966.
Васильевский С.А., Колесников А.Ф. Численное моделирование течений равновесной индукционной плазмы в цилиндрическом канале плазмотрона // Изв. РАН. МЖГ. 2000. № 5. С. 164–173.
Васильевский С.А., Колесников А.Ф. Численное исследование течений и теплообмена в индукционной плазме высокочастотного плазмотрона // Энциклопедия низкотемпературной плазмы. Сер. Б. Т. VII-1. Часть 2. М.: Янус-К. 2008. С. 220–234.
Васильевский С.А., Колесников А.Ф. Численное исследование течения и теплообмена в индукционном плазмотроне и определение каталитической активности материалов // Актуальные проблемы механики. Механика жидкости, газа и плазмы. М.: Наука, 2008. С. 95–123.
Быкова Н.Г., Васильевский С.А., Колесников А.Ф. Влияние излучения на пространственное распределение температуры дозвуковых потоков индукционной плазмы // Теплофизика высоких температур. 2004. Т. 42. № 1. С. 16–22.
Суржиков С.Т. Тепловое излучение газов и плазмы. М.: изд-во МГТУ им. Н.Э. Баумана, 2004.
Vanden Abeele D., Vasil’evskii S.A., Kolesnikov A.F., Degrez G., Bottin B. Code-to-Code Validation of Inductive Plasma Computations // Progress in Plasma Processing of Materials (Eds P. Fauchais and J. Amouroux). Begell House, N.Y. 1999. P. 245–250.
Patankar S. Numerical heat transfer and fluid flow. Hemisphere Publishing Corp. N.Y. 1980.
Васильевский С.А., Соколова И.А., Андриатис А.В. Описание пакета программ SoVA, предназначенного для расчета равновесного состава и коэффициентов переноса низкотемпературной плазмы в высших приближениях метода Чепмена-Энскога // Электронный журн. “Физико-химическая кинетика в газовой динамике”. 2005. http://chemphys.edu.ru/media/published/2005-06-14-001.pdf
Колесников А.Ф., Якушин М.И. Об определении эффективных вероятностей гетерогенной рекомбинации атомов по тепловым потокам к поверхности, обтекаемой диссоциированным воздухом // Матем. моделирование. 1989. Т. 1. № 3. С. 44–60.
Петухов И.В. Численный расчет двумерных течений в пограничном слое // Численные методы решения дифференциальных и интегральных уравнений и квадратурные формулы. М.: Наука, 1964. С. 304–325.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика жидкости и газа