1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 4, 2019

Известия РАН. Механика жидкости и газа, 2019, № 4, стр. 19-26

Трехмерные течения во вращающемся цилиндре при наличии турбулентных пограничных слоев на торцевых дисках

В. Д. Борисевич a, *, Е. П. Потанин a, b, **

a Национальный исследовательский ядерный университет “МИФИ”
Москва, Россия

b Национальный исследовательский центр “Курчатовский институт”
Москва, Россия

* E-mail: VDBorisevich@mephi.ru
** E-mail: Potanin_EP@nrcki.ru

Поступила в редакцию 01.10.2018
После доработки 18.12.2018
Принята к публикации 18.12.2018

Полный текст (PDF)

Аннотация

Представлена аналитическая модель расчета гидродинамических характеристик потока вязкой несжимаемой жидкости во вращающемся цилиндре при наличии тормозящей крышки в случае образования на торцевых поверхностях турбулентных пограничных слоев. Анализ выполнен с учетом всех нелинейных инерционных членов в уравнениях движения в рамках интегральных соотношений Лойцянского. Приближенные профили скоростей в пограничных слоях задаются в соответствии с эмпирическим 1/7 – законом. Основной поток разделяется на невязкое квазитвердое ядро и боковой слой, в котором сосредоточена практически вся восходящая часть циркуляционного потока. Неизвестные величины угловой скорости ядра и его границы по радиусу оцениваются из баланса моментов сил трения, действующих на основной вращающийся поток, и условия неразрывности циркуляционного течения.

Ключевые слова: вращающиеся потоки, турбулентные пограничные cлои, вязкая жидкость, ядро потока

Вращательное движение жидких и газообразных сред находит широкое применение во многих приложениях – центробежное разделение газовых и жидких смесей [1], получение изотопомодифицированных материалов (газовые центрифуги) [2], очистка воздуха от жидкости и пыли [3], газотурбинные установки [4], насосные агрегаты [5] и др. Для многих прикладных задач важной модельной проблемой является изучение трехмерной гидродинамики вязкого газа во вращающемся цилиндре при наличии тормозящих элементов в верхней его части [6]. Последние вызывают нарушение равновесия между центробежной силой и градиентом давления в торцевых зонах и, как следствие, возникновение вторичного циркуляционного течения. Указанная задача непосредственно связана с газодинамикой центробежных разделительных устройств [2].

Интерес к изучению течений в быстро вращающемся цилиндре при наличии тормозящей крышки обусловлен тем, что такая система качественно моделирует течение в центрифуге с механическим возбуждением циркуляции [2]. Если скорость вращения разделяемой смеси в объеме определяет радиальный эффект разделения, то вторичные циркуляционные потоки, связанные с тормозящим влиянием неподвижного торца, ответственны за умножение первичного эффекта разделения по высоте аппарата. В [6] рассмотрено трехмерное движение газа во вращающемся цилиндре с тормозящей крышкой и рассчитан циркуляционный поток, вызванный тормозящим действием крышки в случае ламинарного течения в торцевых пограничных слоях. При больших числах Рейнольдса на вращающемся дне и неподвижной крышке возможно образование турбулентных пограничных слоев [7, 8]. Известно, что в газовых центрифугах для разделения изотопов, при увеличении длины ротора интенсивность циркуляционного течения падает [9]. В связи с этим приходится искать пути увеличения интенсивности циркуляции (например, увеличивать градиент температуры на боковой стенке ротора), что требует дополнительных энергозатрат и увеличивает стоимость получаемого продукта [10, 11]. Отсюда следует важность оценок влияния турбулизации течения в приторцевых пограничных слоях на интенсивность осевой циркуляции.

В настоящей работе исследуется трехмерное движение вязкой сплошной среды во вращающемся с постоянной угловой скоростью ${{\omega }_{0}}$ цилиндре в случае турбулентного характера течения в пограничных слоях на верхней тормозящей крышке и нижнем торце цилиндра.

1. ТУРБУЛЕНТНЫЙ ПОГРАНИЧНЫЙ СЛОЙ НА БЕСКОНЕЧНО ПРОТЯЖЕННОМ ДИСКЕ

Рассмотрим сначала вращающийся с угловой скоростью ${{\omega }_{0}}$ диск бесконечного радиуса при наличии внешнего потока вращающегося с угловой скоростью ${{\omega }_{1}} < {{\omega }_{0}}$.

Для расчета турбулентного пограничного слоя на диске воспользуемся интегральными соотношениями, полученными в результате интегрирования уравнений Навье–Стокса в проекции на радиальное и азимутальное направления [12]

(1.1)
$\frac{d}{{dr}}\left( {r\int\limits_0^\delta {{{u}^{2}}dz} } \right) - \int\limits_0^\delta {{{\text{v}}^{2}}dz} = - r\frac{{{{\tau }_{r}}}}{\rho } - \int\limits_0^\delta {r\frac{{\partial p}}{{\partial r}}} dz$
(1.2)
$\frac{d}{{dr}}\left( {{{r}^{2}}\int\limits_o^\delta {u\text{v}dz} } \right) - {{\omega }_{1}}{{r}^{2}}\frac{d}{{dr}}\left( {r\int\limits_0^\delta u dz} \right) = - {{r}^{2}}\frac{{{{\tau }_{\varphi }}}}{\rho }$
где $u$ и $v$ – радиальная и азимутальные компоненты скорости среды, $p$ – давление рабочего газа, $r$ – радиальная координата; $z$ – осевая координата, отсчитываемая от поверхности диска, ${{\tau }_{r}}$ и ${{\tau }_{\varphi }}$ – соответствующие компоненты вязких напряжений на диске. Отметим, что подобные соотношения без учета второго члена в левой части уравнения (1.2) впервые использовал Карман [13], а в дальнейшем – Окайя и Хасегава [14].

Зададим величины $u$ и $v$ в пограничном слое в виде (1.3)–(1.4), воспользовавшись эмпирическим законом “1/7”. Однако, в отличие от работы [14], используем симметричный профиль радиальной скорости

(1.3)
$u = \alpha r\left( {{{\omega }_{0}} - {{\omega }_{1}}} \right){{\left( {\frac{z}{\delta }} \right)}^{{1/7}}}\left[ {1 - {{{\left( {\frac{z}{\delta }} \right)}}^{{1/7}}}} \right]$
(1.4)
$\text{v} = r\left( {{{\omega }_{1}} - {{\omega }_{0}}} \right){{\left( {\frac{z}{\delta }} \right)}^{{1/7}}} + r{{\omega }_{0}}$
где $\delta $ – толщина пограничного слоя на диске, $\alpha $ – неизвестная постоянная, которая наряду с $\delta $ подлежит определению.

Вблизи диска ($z \to 0$) справедливы зависимости

$\frac{{\text{v} - r{{\omega }_{0}}}}{{r\left( {{{\omega }_{0}} - {{\omega }_{1}}} \right)}} = - {{\left( {\frac{z}{\delta }} \right)}^{{1/7}}},\quad \frac{u}{{r\left( {{{\omega }_{0}} - {{\omega }_{1}}} \right)}} = \alpha {{\left( {\frac{z}{\delta }} \right)}^{{1/7}}}$
вследствие чего $\alpha $ представляет собой отношение радиальной и азимутальной составляющих напряжений трения ${{\tau }_{r}}$ и ${{\tau }_{\varphi }}$ (${{\tau }_{r}} = - \alpha {{\tau }_{\varphi }}$) на диске.

Для определения ${{\tau }_{\varphi }}$ и ${{\tau }_{r}}$ используем полуэмпирические соотношения [7, 14]

(1.5)
${{\tau }_{\varphi }} = - 0.0225\rho {{r}^{{7/4}}}{{\left( {{{\omega }_{0}} - {{\omega }_{1}}} \right)}^{{7/4}}}{{\left( {\frac{\nu }{\delta }} \right)}^{{1/4}}}{{(1 + {{\alpha }^{2}})}^{{3/8}}}$
(1.6)
${{\tau }_{r}} = 0.0225\alpha \rho {{r}^{{7/4}}}{{\left( {{{\omega }_{0}} - {{\omega }_{1}}} \right)}^{{7/4}}}{{\left( {\frac{\nu }{\delta }} \right)}^{{1/4}}}{{(1 + {{\alpha }^{2}})}^{{3/8}}}$
где $\nu $ – коэффициент кинематической вязкости среды.

Будем предполагать, что полученные решения для протяженного диска справедливы при условии ${{10}^{5}} \leqslant \operatorname{Re} \leqslant {{10}^{6}}$ [7].

В пограничном слое радиальный градиент давления равен градиенту давления во внешнем потоке [6, 15]

(1.7)
$\frac{{\partial p}}{{\partial r}} = \rho \omega _{1}^{2}r$

Полагая согласно [14] $\delta = \gamma {{r}^{{3/5}}}$ и используя (1.1)–(1.7), получим следующие уравнения:

(1.8)
$M{{\alpha }^{2}}\gamma {{\left( {1 - m} \right)}^{2}} + \left( {m - 1} \right)\left( {1 + 8m} \right) = - N\alpha {{(1 + {{\alpha }^{2}})}^{{3/8}}}{{\left( {1 - m} \right)}^{{7/4}}}$
(1.9)
$R\alpha \gamma [23{{(1 - m)}^{2}} + 50m\left( {1 - m} \right)] = N\alpha {{(1 + {{\alpha }^{2}})}^{{3/8}}}{{\left( {1 - m} \right)}^{{7/4}}}$
где $m = {{{{\omega }_{1}}} \mathord{\left/ {\vphantom {{{{\omega }_{1}}} {{{\omega }_{0}}}}} \right. \kern-0em} {{{\omega }_{0}}}}$; $M = 504{\text{/}}275$; $N = 1{\text{/}}44$; $R = 7{\text{/}}1800$.

Решение системы (1.8)–(1.9) приводит к следующему результату:

(1.10)
${{\alpha }^{2}} = \frac{{(1 + 7m - 8{{m}^{2}})}}{{\left( {1 - m} \right)\left[ {S\left( {1 - m} \right) + 7m} \right]}},\quad \gamma = {{\left\{ {\frac{{N{{{(1 + {{\alpha }^{2}})}}^{{3/8}}}{{{\left( {1 - m} \right)}}^{{7/8}}}}}{{R\alpha [23{{{\left( {1 - m} \right)}}^{2}} + 50m\left( {1 - m} \right)]}}} \right\}}^{{4/5}}}$
где $S = 2779{\text{/}}550$.

Определив на основании (1.5) и (1.10) напряжение ${{\tau }_{\varphi }}$, можно рассчитать коэффициент момента сил трения, действующих на одну сторону диска

(1.11)
${{C}_{M}} = \frac{{2M}}{{\rho {{\omega }^{2}}R_{0}^{5}}}$
где $M = 2\pi \int_0^{{{R}_{0}}} {{{r}^{2}}{{\tau }_{\varphi }}} dr$

Отметим важность учета в левой части уравнения для проекции азимутального импульса второго члена, описывающего ускорение среды

$A = - {{\omega }_{1}}{{r}^{2}}\frac{d}{{dr}}\left( {r\int\limits_0^\delta u dz} \right)$

Дело в том, что знак этого члена противоположен инерционному ускорению, описываемому первым членом в уравнении (1.2), при радиальном потоке, направленном к периферии, и совпадает с ним при обратном направлении этого потока. По этой причине в случае вращения среды над неподвижным основанием и диска, вращающегося в движущейся среде (при ${{\omega }_{0}} > {{\omega }_{1}}$), когда направление радиального потока изменяется на противоположное, инерционные ускорения имеют противоположные знаки, по-разному влияя на циркуляционный поток. Важно отметить, что при учете в (1.2) ускорения A и одновременном использовании несимметричного профиля радиальной скорости [14] решение задачи в случае вращения среды над неподвижным основанием отсутствует.

Рассмотрим подробнее частный случай торможения вращающегося над неподвижным основанием азимутального потока ${{\omega }_{1}} \ne 0$, ${{\omega }_{0}} = 0$.

На рис. 1 линией 1 показана определенная согласно (1.11) зависимость ${{C}_{M}}$ от величины $\operatorname{Re} _{1}^{{0.2}}$, где ${{\operatorname{Re} }_{1}} = {{\omega }_{{\text{1}}}}R_{{\text{1}}}^{{\text{2}}}{\text{/}}\nu $ – число Рейнольдса, рассчитанное по угловой скорости ${{\omega }_{1}}$. Пунктирной линией 2 показаны результаты расчета, полученные без учета второго члена в левой части уравнения (2) [14]. Как следует из расчета, выполненного с использованием формул (1.5)–(1.11), выражение для коэффициента момента сил трения принимает вид

(1.12)
${{C}_{M}} = 0.034{{\operatorname{Re} }^{{ - 0.2}}}$
Рис. 1.

Зависимости коэффициента момента сил трения о поверхность неподвижного диска при наличии внешнего вращающегося потока: 1 – расчет с использованием формул (1.5)–(1.11); 2 – результаты [14] без учета второго члена в левой части уравнения (1.2) в случае несимметричного профиля радиальной скорости.

Отметим, что полученная зависимость (1.12) учитывает как упомянутый выше инерционный член, так и изменение второго члена в скобках для профиля радиальной скорости.

Аналогичное соотношение по результатам [14] имеет вид

(1.13)
${{C}_{M}} = 0.038{{\operatorname{Re} }^{{ - 0.2}}}$

Воспользуемся теперь общими соотношениями (1.10) для расчета случая вращения диска в неподвижной среде (${{\omega }_{1}} = 0$, ${{\omega }_{0}} \ne 0$).

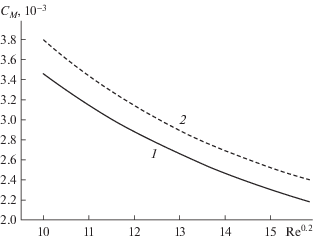
На рис. 2 приведены зависимости коэффициента момента сил трения от числа Рейнольдса для диска, вращающегося в неподвижной среде, полученные расчетным путем и экспериментально. Сплошная линия 1 описывает зависимость ${{C}_{M}}$от $\lg \operatorname{Re} $, где число Рейнольдса определено по угловой скорости вращения диска ${{\omega }_{0}}$. Пунктирной линией 2 показаны результаты расчета из работы [14] для турбулентного пограничного слоя на протяженном диске, вращающемся в неподвижной среде. Также показаны экспериментальные данные 3 работы [16]. Видно, что влияние инерционного члена A не проявляется, однако симметризация профиля способствует лучшему согласованию результатов эксперимента и расчета.

Рис. 2.

Зависимости коэффициента момента сил трения от числа Рейнольдса при вращении диска в неподвижной среде: 1 – расчет с использованием формул (1.5), (1.10) и (1.11); 2 – результаты расчета, полученные в [14]; 3 – экспериментальные данные [16].

2. ТРЕХМЕРНОЕ ТЕЧЕНИЕ ВО ВРАЩАЮЩЕМСЯ ЦИЛИНДРЕ ПРИ НАЛИЧИИ ТОРМОЗЯЩЕЙ КРЫШКИ

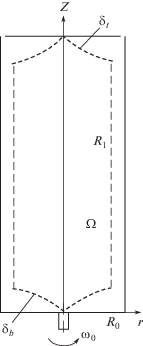
Исследуем поле скоростей во вращающемся с угловой скоростью ${{\omega }_{0}}$ прямом круговом цилиндре при наличии неподвижного верхнего торца, воспользовавшись предложенной в [6] приближенной методикой учета влияния пограничных слоев на торцах вращающегося цилиндра. Предположим, что на обеих торцевых поверхностях образуются тонкие турбулентные пограничные слои. Будем также предполагать, что полученные решения для протяженного диска в условиях неперекрывающихся пограничных слоев справедливы при условии ${{10}^{5}} \leqslant \operatorname{Re} \leqslant {{10}^{6}}$ [7]. Отсутствие перекрытия слоев ($L \gg {{\delta }_{t}}(R) + {{\delta }_{b}}(R)$) при $\operatorname{Re} = {{10}^{6}}$ приводит к неравенству $L \gg {{10}^{{ - 2}}}$ м. Назовем основным объемом всю область потока за исключением торцевых пограничных слоев. Предположим, что в центральной части основного объема возникает ламинарное квазитвердое невязкое ядро с исчезающе малой радиальной скоростью, а к боковой поверхности примыкает вязкий ламинарный слой, в котором доминирует восходящий осевой поток – рис. 3.

Рис. 3.

Области течения во вращающемся цилиндре с неподвижной крышкой.

Пусть ядро радиуса ${{R}_{1}}$ вращается с некоторой неизвестной угловой скоростью $\Omega $. Эти характеристики ядра вместе с толщинами пограничных слоев ${{\delta }_{t}}$, ${{\delta }_{b}}$, а также параметрами циркуляционного течения подлежат определению. Следуя [6], будем предполагать, что в основном объеме отсутствуют изменения окружной и осевой компонент скорости по высоте цилиндра $\partial {{V}_{\varphi }}{\text{/}}\partial z = \partial {{W}_{z}}{\text{/}}\partial z = 0$.

Предположим, что полученное выше решение для бесконечно протяженных дисков приближенно справедливо до радиуса $r = {{R}_{1}}$. Решение для окружной скорости в слое на боковой поверхности ${{\text{v}}^{s}}$ найдем сшиванием на границе двух областей при $r = {{R}_{1}}$.

Решение для $\text{v}_{{}}^{s}$ будем искать в виде

(2.1)
${{\text{v}}^{s}} = \Omega r - \frac{{(\Omega - {{\omega }_{0}}){{R}_{0}}}}{{{{{({{R}_{0}} - {{R}_{1}})}}^{2}}}}{{(r - {{R}_{1}})}^{2}}$

Осевой перепад давления определим из баланса центробежных сил, действующих в пограничных слоях на нижнем и верхнем дисках $\Delta {{p}_{z}} \approx Q{{r}^{2}}$, где

$Q = \frac{{\rho \omega _{0}^{2}}}{{72}}\left( {1 + 7{{m}_{\Omega }}} \right),\quad {{m}_{\Omega }} = \Omega {\text{/}}{{\omega }_{0}}$

Осевую компоненту скорости в слое на боковой поверхности ${{w}^{s}}(r)$ определим из баланса вязких сил и сил давления

(2.2)
$\eta \frac{1}{r}\frac{d}{{dr}}r\frac{{d{{w}^{s}}}}{{dr}} = - \frac{{Q{{r}^{2}}}}{L}$

Уравнение (2.2) следует решать при следующих граничных условиях

(2.3)
${{w}^{s}}({{R}_{1}}) = - {{w}^{c}}({{R}_{1}}),\quad {{w}^{s}}({{R}_{0}}) = 0$

Здесь ${{w}^{c}}({{R}_{1}}) = \frac{7}{{36}}\Omega \alpha \gamma (\Omega ){{\left( {\nu {\text{/}}\Omega } \right)}^{{0.2}}}R_{1}^{{0.6}}$ – абсолютная величина осевой скорости в ядре на радиусе ${{R}_{1}}$.

Интегрируя (2.2) с условиями (2.3), получим

(2.4)
${{w}^{s}}(r) = \frac{D}{{16}}(R_{0}^{4} - {{r}^{4}}) + \left( {\frac{{(R_{0}^{4} - R_{1}^{4})D}}{{16}} + {{w}^{c}}({{R}_{1}})} \right)\frac{{\ln (r{\text{/}}{{R}_{0}})}}{{\ln ({{R}_{0}}{\text{/}}{{R}_{1}})}}$
где $D = \frac{{\rho \omega _{0}^{2}}}{{72\eta L}}\left( {1 + 7{{m}_{\Omega }}} \right)$.

Для определения неизвестных ${{R}_{1}}$ и ${{m}_{\Omega }}$, входящих в (2.4), воспользуемся балансами сил трения, действующих на вращающийся основной объем [6, 15], и неразрывностью циркуляционного потока

(2.5)
${{M}_{0}} + {{M}_{s}} = {{M}_{1}},$
(2.6)
$\int\limits_0^{{{R}_{1}}} {{{w}^{c}}(r)2\pi rdr} = \int\limits_{{{R}_{1}}}^{{{R}_{0}}} {{{w}^{s}}(r)2\pi rdr} .$

Здесь ${{M}_{0}}$, ${{M}_{s}}$ – вращающие моменты сил трения, действующие со стороны нижнего основания и боковой поверхности цилиндра, ${{M}_{1}}$ – тормозящий момент со стороны неподвижного торца. Аналогично [6] из (2.5)–(2.6) с учетом (1.5), (2.1) и (2.4) получим приближенные соотношения для определения ${{R}_{1}}$ и $\Omega $

(2.7)
$\frac{1}{{207}}{{\left( {2d} \right)}^{{3/20}}}\left[ {\frac{{m_{\Omega }^{{9/8}}{{{(1 + \alpha _{t}^{2})}}^{{3/8}}}}}{{\gamma _{t}^{{1/4}}}} - \frac{{{{{\left( {1 - {{m}_{\Omega }}} \right)}}^{{7/4}}}}}{{\gamma _{b}^{{1/4}}}}} \right] = \frac{{{{l}^{2}}\left( {1 - {{m}_{\Omega }}} \right)\left( {1 + {{x}_{1}}} \right)}}{{\left( {1 - {{x}_{1}}} \right){{{\operatorname{Re} }}_{L}}}}$
(2.8)
$\frac{7}{{78}}Mx_{1}^{{13/5}} = \left\{ {\frac{{(1 - x_{1}^{2})dc}}{{32}} - \frac{{(1 - x_{1}^{6})c}}{{96}} + \left[ {\frac{{(1 - x_{1}^{4})dc}}{{16\ln {{x}_{1}}}} + \frac{7}{{36\ln {{x}_{1}}}}Mx_{1}^{{3/5}}} \right]\left( {\frac{1}{4} + \frac{{x_{1}^{2}}}{2}\ln {{x}_{1}} - \frac{{x_{1}^{2}}}{4}} \right)} \right\}$
где ${{x}_{1}} = \frac{{{{R}_{1}}}}{{{{R}_{0}}}}$, $l = \frac{L}{{{{R}_{0}}}}$, ${{\operatorname{Re} }_{L}} = \frac{{{{\omega }_{0}}{{L}^{2}}}}{\nu }$, $d = \frac{{\omega _{0}^{2}{{R}_{0}}^{4}}}{{2{{\nu }^{2}}}}$, $c = \frac{{1 + 7{{m}_{\Omega }}}}{{36}}$, $M = \frac{{m_{\Omega }^{{4/5}}{{{\operatorname{Re} }}_{L}}}}{{{{{\left( {2d} \right)}}^{{1/10}}}l}}{{\alpha }_{t}}{{\gamma }_{t}}$, ${{\alpha }_{t}} = \alpha ({{m}_{\Omega }} = 0)$, αb = $\alpha ({{m}_{\Omega }})$, ${{\gamma }_{t}} = \gamma ({{m}_{\Omega }} = 0)$, ${{\gamma }_{b}} = \gamma ({{m}_{\Omega }})$.

Отметим, что при рассмотрении вращательного течения в длинном прямом круговом цилиндре условия образования турбулентных пограничных слоев могут отличаться от случаев, исследованных в ранних работах [16, 17] с неподвижным кожухом, поскольку действие вращающейся боковой поверхности может затягивать процесс турбулизации. По этой причине трудно оценить степень выполнения предположения о характере течения в пограничных слоях на торцах. В работе [6], в частности, использована гипотеза о ламинарности пограничных слоев даже при больших числах Рейнольдса. Ниже проводится сравнение результатов расчетов при обоих вышеуказанных предположениях.

Выполним расчет для воздуха при нормальных условиях. Если предположить, что на дисках развиваются турбулентные пограничные слои, то в рассматриваемом диапазоне чисел Рейнольдса сила трения вращательного потока на дисках возрастает по сравнению со случаем ламинарного течения [7]. Поэтому можно было бы предположить, что существенно больший момент сил трения в случае турбулентного пограничного слоя должен приводить к заметному увеличению циркуляционного потока. Однако результаты расчетов свидетельствуют о том, что в случае турбулентных пограничных слоев расширяется область слоя на боковой стенке цилиндра (см. рис. 4).

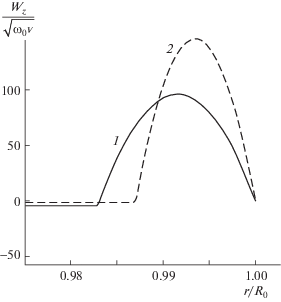
Рис. 4.

Профили осевой скорости в торцевых пограничных слоях: 1 – расчет в предположении, что на дисках развиваются турбулентные пограничные слои; 2 – расчет в предположении ламинарности течения в пограничных слоях [6].

При этом турбулизация течения в пограничных слоях не приводит к заметному увеличению циркуляционного потока. Полученный результат можно объяснить тем обстоятельством, что силы трения увеличиваются не только для вращательного потока, но и для радиального течения в пограничном слое, компенсируя увеличение момента сил азимутального трения.

На рис. 4 сплошной линией 1 показаны профили осевой скорости, рассчитанные в предположении о развитии турбулентных торцевых пограничных слоев, полученные в результате численного решения системы уравнений (2.7), (2.8) для следующих значений параметров: ${{\omega }_{0}} = {{10}^{3}}$ 1/с, $L = 0.1$ м, ${{R}_{0}} = 0.05$ м, $\nu = 1.5 \times {{10}^{{ - 5}}}$ м2/с; рабочая среда – воздух при нормальном давлении $P = {{10}^{5}}$ Па и комнатной температуре $T = 300$ K. Пунктирная кривая 2 соответствует случаю ламинарных пограничных слоев на торцах.

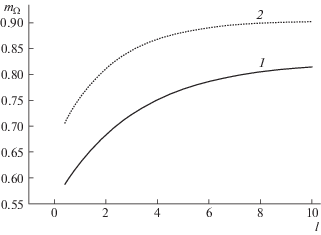
Зависимость безразмерной угловой скорости вращения ядра потока от отношения длины цилиндра к его радиусу $l$ показана на рис. 5 сплошной линией 1. Пунктирной линией 2 приведены результаты расчета в случае ламинарного течения [6]. Как видно, турбулентность течения в пограничных слоях способствует уменьшению скорости вращения невязкого ядра.

Рис. 5.

Зависимость безразмерной угловой скорости вращения ядра m от отношения l высоты цилиндра к его радиусу: 1 – результаты расчета в предположении турбулентности пограничных слоев; 2 – расчет при допущении ламинарности пограничных слоев [6].

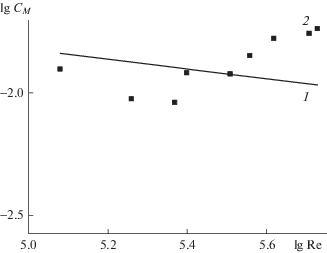
На рис. 6 приведены результаты расчета коэффициента момента сил трения, действующих на газ со стороны вращающегося дна цилиндра в случае l → 0, когда можно не учитывать влияние боковых стенок. Также показаны экспериментальные результаты 2, полученные в работе [17] для шероховатого диска.

Рис. 6.

Зависимости коэффициента момента сил трения от числа Рейнольдса: 1 – результаты расчета в случае $l \to 0$; 2 – экспериментальные результаты [17].

ЗАКЛЮЧЕНИЕ

На основе интегральных соотношений рассчитаны турбулентные пограничные слои на вращающихся и неподвижных дисках с учетом нелинейных инерционных членов в уравнениях движения.

Результаты, полученные для протяженных дисков, использованы для расчета гидродинамических характеристик течения во вращающемся цилиндре с неподвижной крышкой в предположении об образовании невязкого ядра потока.

Показано, что возбуждение турбулентности в пограничных слоях на торцах приводит к уменьшению угловой скорости невязкого ядра потока из-за возрастания момента сил трения тормозящей крышки. Однако при этом не происходит существенного увеличения скорости осевой циркуляции в роторе.

Работа выполнена при поддержке Программы повышения конкурентоспособности Национального исследовательского ядерного университета МИФИ (контракт № 02.a03.21.0005 от 27 августа 2013).

Список литературы

  1. Минакер В.Е., Джинчарадзе Е.К. Центробежный аппарат для разделения смеси, состоящей из двух жидких и одной твердой фракций, Патент RU 2032470, 1995.

  2. Борисевич В.Д., Борман В.Д., Сулаберидзе Г.А., Тихомиров А.В., Токманцев В.И. Физические основы разделения изотопов в газовой центрифуге // М: Изд. дом МЭИ, 2011. 275 с.

  3. Исакссон Р., Торвид П. Центробежный сепаратор и ротор, Патент RU 2523817, 2014.

  4. Поршаков Б.П., Апостолов А.А., Никишин В.И. Газотурбинные установки на газопроводах. М: Нефть и газ, 2003. 240 с.

  5. Кишкин A.A., Краев М.В., Жуйков Д.А., Мелкозёров М.Г., Черненко Д.В. Расчет течения в конической щели с внутренним вращающимся диском. Программа для ЭВМ. РОСПАТЕНТ, св-во об офиц. регистрации № 2001611149 от 06.09. 2001 г.

  6. Потанин Е.П. Трехмерное движение газа во вращающемся цилиндре с тормозящей крышкой // Изв. РАН. МЖГ. 2013. № 1. С. 78–87.

  7. Дорфман Л.А. Гидродинамическое сопротивление и теплоотдача вращающихся тел. М.: ФИЗМАТГИЗ, 1960. 260 с.

  8. Imayama Sh., Alfredsson P.H., Lingwood R.J. Experimental study of rotating-disk boundary-layer flow with surface roughness // J. Fluid Mech. 2016. V. 786. P. 5–28.

  9. Gu Z.Y., Jiang D.J., Zeng S., Borisevich V.D. A homotopy algorithm to solve the problems of flows under strong rotation // J. Phys.: Conf. Ser. 2018. 1099. 012010.

  10. Борисевич В.Д., Наумочкин В.В., Смаков Б.М. Механическое и тепловое возбуждение течения газа во вращающемся цилиндре // Изв. АН СССР. МЖГ. 1987. № 4. С. 24–28.

  11. Белоцерковский О.М., Бетелин В.Б., Борисевич В.Д. Денисенко В.В., Ериклинцев И.В., Козлов С.А., Конюхов А.В., Опарин А.М., Трошкин О.В. К теории противотока во вращающемся вязком теплопроводном газе // Журн. вычисл. матем. и матем. физ. 2011. Т. 51(2). С. 222–236.

  12. Лойцянский Л.Г. Ламинарный пограничный слой. М.: ГИФМЛ, 1962.

  13. Karman Th.V. Laminare and turbulente reibung // ZAMM. 1921. V. 1. P. 233–252.

  14. Okaya T., Hasegawa M. On the friction to the disc rotating in cylinder // Jpn. J. Phys. 1939. V. 13. № 1. P. 78–91.

  15. Borisevich V.D., Potanin E.P., Whichello J. Circulation control in MHD rotating flows // J. Fluid Mech. 2017. V. 829. P. 328–244.

  16. Schmidt W. Ein einfaches Messverfahren für Drehmomente // Z. VDI. 1921. № 65. P. 441–444.

  17. Theodorsen Th., Regier A. Experiments on drag of revolving discs, cylinders and streamline rods at high speeds. NACA Report. 1944. № 793.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал