1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 4, 2019

Известия РАН. Механика жидкости и газа, 2019, № 4, стр. 42-48

ЦИРКУЛЯЦИОННЫЕ ЭФФЕКТЫ ПРИ ДВИЖЕНИИ ОБЪЕКТОВ В МОРСКОЙ СРЕДЕ И АТМОСФЕРЕ

И. Ю. Владимиров a, b, *, Н. Н. Корчагин a, b, **

a Институт океанологии им. П.П. Ширшова РАН
Москва, Россия

b Московский государственный технический университет им. Н.Э. Баумана
Москва, Россия

* E-mail: iyuvladimirov@rambler.ru
** E-mail: e-niknik@mail.ru

Поступила в редакцию 26.09.2018
После доработки 18.10.2018
Принята к публикации 18.10.2018

Полный текст (PDF)

Аннотация

Получены выражения для гидродинамической нагрузки на диполь при его циркуляционном обтекании потоком стратифицированной (двухслойной) жидкости конечной глубины. Исследованы зависимости волнового сопротивления и подъемной силы от скорости потока и циркуляции. Показано, что учет циркуляции может существенно изменить величину гидродинамической реакции на диполь. Обнаружен эффект резкого (реверсивного) изменения направления действия подъемной силы в относительно узком диапазоне скорости обтекания моделируемого диполем фрагмента трубопровода. Обсуждается возможность проявления подобного эффекта при движении самоходных подводных объектов и летательных аппаратов.

Ключевые слова: стратифицированные течения, волновое сопротивление, подъемная сила, циркуляционное обтекание

Морская поверхность – поверхность, на которой проявляются, с одной стороны, воздействия солнечного излучения и атмосферных явлений, с другой – процессы в толще воды. При этом следные структуры глубинных возмущений могут, во-первых, представляться в качестве индикаторов источников возмущений – это физические процессы (внутренние волны), неоднородности рельефа дна и искусственные объекты. Во-вторых, эти структуры могут идентифицировать подобные источники глубинных возмущений, что является важной задачей при мониторинге и контроле морских акваторий.

При возведении в морской среде инженерных конструкций необходимо оценивать силовые нагрузки, возникающие под действием стратифицированных течений. Наряду с вязким сопротивлением препятствие в таком потоке испытывает гидродинамические реакции волновой природы, обусловленные развитием внутренних волн. Примером таких воздействий являются взвесенесущие потоки, возникающие в придонных слоях при перемешивании потока с микро- и мелкозернистыми частицами грунта, что приводит к избытку плотности таких потоков и формированию резкого пикноклина на границе таких потоков [1].

Придонные слои океана порой представляют области интенсивных течений. Среди них – придонные потоки холодных более плотных вод, стекающие с материковых склонов (например, Антарктиды) и растекающиеся по дну Мирового океана. В 80-х годах прошлого века были обнаружены так называемые “придонные шторма” – периоды резкой интенсификации придонных течений продолжительностью до 1–2 нед. При этом скорости таких течений могут достигать значений до 1 м/с [2]. Кроме того, необходимо принять во внимание, что обтекание препятствий может происходить с определенной циркуляцией скорости, которая вносит дополнительный, не учитываемый ранее вклад в силовое воздействие среды на препятствие.

Ранее авторами рассмотрена модель [3] поперечного обтекания двухслойным стратифицированным течением горизонтально протяженного технического элемента (например, транспортного трубопровода или подобного фрагмента подводного сооружения). Цель исследования – гидродинамическая реакция на возмущения, возникающие при обтекании подводных препятствий.

Модель представлена в виде двух совмещенных гидродинамических особенностей: диполя с моментом $m = 2\pi V{{R}^{2}}$, моделирующего поперечное обтекание цилиндра радиуса R, и точечного вихря интенсивности $\Gamma $, обеспечивающего заданную циркуляцию. Здесь $V$ – скорость набегающего потока [4]. Толщина верхнего слоя ${{H}_{1}}$, нижнего – ${{H}_{2}}$, а плотности соответственно ${{\rho }_{1}}$ и ${{\rho }_{2}}$ (${{\rho }_{1}} < {{\rho }_{2}}$). Начало координат расположено на невозмущенной границе между слоями жидкости, ось x направлена вдоль этой границы, ось y – вертикально вверх. Вихрь и диполь локализованы в точке ($0, - h$). Далее представляем модель в краткой постановочной форме и исследуем обтекание диполя в нижнем слое под скачком плотности воды.

В отличие от предыдущей работы [3] ниже исследуется зависимость силового воздействия на препятствие от важной характеристики морской среды – относительного перепада плотности между слоями $\varepsilon = ({{\rho }_{2}} - {{\rho }_{1}}){\text{/}}{{\rho }_{2}}$.

Комплексно-сопряженная скорость возмущенного диполем двухслойного потока представляется в виде ${{\mu }_{k}}(z) = V + {{U}_{k}}(z)$, где $z = x + iy$, $k = 1,2$. Для вычисления гидродинамических сил, действующих на диполь, выполняется переход к безразмерным переменным

$X = \frac{x}{R},\quad Y = \frac{y}{R},\quad Z = \frac{z}{R} = X + iY,\quad \delta = \frac{{{{\rho }_{1}}}}{{{{\rho }_{2}}}},\quad {{h}_{1}} = \frac{{{{H}_{1}}}}{R},\quad {{h}_{2}} = \frac{{{{H}_{2}}}}{R}$
$h = \frac{H}{R},\quad {{u}_{k}} = \frac{{{{U}_{k}}}}{V},\quad \gamma = \frac{\Gamma }{{2\pi VR}},\quad E = \frac{{gR}}{{{{V}^{2}}}} = \frac{1}{{{\text{F}}{{{\text{r}}}^{2}}}}$

Здесь $g$ – ускорение свободного падения, ${\text{Fr}}$ – число Фруда по радиусу цилиндра. Тогда задача об отыскании возмущений комплексно-сопряженной скорости ${{u}_{k}}$, вносимых в поток диполем и вихрем, локализованными под скачком плотности, формулируется таким образом: требуется найти аналитические функции ${{u}_{1}}(Z)$ и ${{u}_{2}}(Z)$, удовлетворяющие граничным условиям

(1.1)
${\text{Im}}\left[ {i\frac{{d{{u}_{1}}}}{{dZ}} - E{{u}_{1}}} \right] = 0\quad {\text{п р и }}\quad Y = {{h}_{1}}$
(1.2)
$\delta {\text{Im}}\left[ {i\frac{{d{{u}_{1}}}}{{dZ}} - E{{u}_{1}}} \right] = {\text{Im}}\left[ {i\frac{{d{{u}_{2}}}}{{dZ}} - E{{u}_{2}}} \right] = 0\quad {\text{п р и }}\quad Y = 0$
(1.3)
${\text{Im }}{{u}_{1}} = {\text{Im }}{{u}_{2}}\quad {\text{п р и }}\quad Y = 0$
(1.4)
${\text{Im }}{{u}_{2}} = 0\quad {\text{п р и }}\quad Y = - {{h}_{2}}$
причем ${{u}_{1}}(Z)$ должна быть регулярна в полосе $ - \infty < X < + \infty $, $0 < Y < {{h}_{1}}$, а ${{u}_{2}}(Z)$ – в полосе $ - \infty < X < + \infty $, $ - {{h}_{2}} < Y < 0$ всюду за исключением точки $Z = - ih$, в которой она имеет полюс второго порядка
${{u}_{2}}(Z) = - \frac{1}{{{{{(Z + ih)}}^{2}}}} + \frac{\gamma }{i}\frac{1}{{Z + ih}} + f(Z)$
где $f(Z)$ – регулярная функция (см. ниже).

Граничное условие (1.1) описывает постоянство давления на свободной поверхности, (1.2) – непрерывность давления при переходе границы раздела слоев, (1.3) определяет отсутствие потока жидкости через эту границу, а (1.4) является условием непротекания на дне (вывод (1.1)–(1.4), см. в [5]).

В силу линейности задачи представим искомую комплексно-сопряженную скорость в виде суммы возмущений комплексно-сопряженной скорости, вносимых в поток точечным вихрем и диполем: ${{u}_{k}}(Z) = u_{k}^{\gamma }(Z) + u_{k}^{m}(Z)$ ($k = 1,2$).

Для функций $u_{k}^{\gamma }(Z)$ и $u_{k}^{m}(Z)$ получаем граничные условия, аналогичные (1.1)–(1.4), причем

(1.5)
$u_{2}^{\gamma }(Z) = \frac{\gamma }{i}\frac{1}{{Z + ih}} + {{f}_{\gamma }}(Z)$
(1.6)
$u_{2}^{m}(Z) = - \frac{1}{{{{{(Z + ih)}}^{2}}}} + {{f}_{m}}(Z)$
где ${{f}_{\gamma }}(Z)$ и ${{f}_{m}}(Z)$ – функции, регулярные в полосе $ - \infty < X < + \infty $, $ - {{h}_{2}} < Y < 0$, и f(Z) = fγ(Z) + fm(Z).

Скорости $u_{1}^{\gamma }(Z)$ и ${{f}_{\gamma }}(Z)$, а также $u_{1}^{m}(Z)$ и ${{f}_{m}}(Z)$ ищем в виде их разложения в интеграл Фурье по волновым числам

(1.7)
$u_{1}^{\gamma }(Z) = \gamma \int\limits_0^\infty [{{A}_{\gamma }}(\xi ){{e}^{{i\xi Z}}} + {{B}_{\gamma }}(\xi ){{e}^{{ - i\xi Z}}}]d\xi $
(1.8)
${{f}_{\gamma }}(Z) = \gamma \int\limits_0^\infty [{{C}_{\gamma }}(\xi ){{e}^{{i\xi Z}}} + {{D}_{\gamma }}(\xi ){{e}^{{ - i\xi Z}}}]d\xi $
(1.9)
$u_{1}^{m}(Z) = \int\limits_0^\infty \xi [{{A}_{m}}(\xi ){{e}^{{i\xi Z}}} + {{B}_{m}}(\xi ){{e}^{{ - i\xi Z}}}]d\xi $
(1.10)
${{f}_{m}}(Z) = \int\limits_0^\infty \xi [{{C}_{m}}(\xi ){{e}^{{i\xi Z}}} + {{D}_{m}}(\xi ){{e}^{{ - i\xi Z}}}]d\xi $
где функции ${{A}_{\gamma }}(\xi )$, ${{B}_{\gamma }}(\xi )$, ${{C}_{\gamma }}(\xi )$, ${{D}_{\gamma }}(\xi )$ и ${{A}_{m}}(\xi )$, ${{B}_{m}}(\xi )$, ${{C}_{m}}(\xi )$, ${{D}_{m}}(\xi )$ подлежат определению.

Далее, из (1.5), (1.8) получим выражения для $u_{2}^{\gamma }(Z)$ в областях нижнего слоя, находящихся выше и ниже горизонта локализации вихря и диполя

(1.11)
$u_{2}^{\gamma }(Z) = \left\{ \begin{gathered} \gamma \int\limits_0^\infty [( - {{e}^{{ - \xi h}}} + {{C}_{\gamma }}(\xi )){{e}^{{i\xi Z}}} + {{D}_{\gamma }}(\xi ){{e}^{{ - i\xi Z}}}]d\xi ,\quad {\text{е с л и }}\quad Y > - h \hfill \\ \gamma \int\limits_0^\infty [{{C}_{\gamma }}(\xi ){{e}^{{i\xi Z}}} + ({{e}^{{\xi h}}} + {{D}_{\gamma }}(\xi )){{e}^{{ - i\xi Z}}}]d\xi ,\quad {\text{е с л и }}\quad Y < - h \hfill \\ \end{gathered} \right.$

Аналогично из (1.6) и (1.10) можно получить интегральное представление для $u_{2}^{m}(Z)$

(1.12)
$u_{2}^{m}(Z) = \left\{ {\begin{array}{*{20}{c}} {\int\limits_0^\infty \xi [({{e}^{{ - \xi h}}} + {{C}_{m}}(\xi )){{e}^{{i\xi Z}}} + {{D}_{m}}(\xi ){{e}^{{ - i\xi Z}}}]d\xi ,\quad {\text{е с л и }}\quad Y > - h} \\ {\int\limits_0^\infty \xi [{{C}_{m}}(\xi ){{e}^{{i\xi Z}}} + ({{e}^{{\xi h}}} + {{D}_{m}}(\xi )){{e}^{{ - i\xi Z}}}]d\xi ,\quad {\text{е с л и }}\quad Y < - h} \end{array}} \right.$

Далее, опуская процедуру нахождения подынтегральных функций в (1.7)–(1.10) из условий (1.1)–(1.4), получим аналитические выражения этих функций [3], а также $f(Z)$

(1.13)
$\begin{gathered} f(Z) = \mathop {lim}\limits_{{{\varepsilon }_{1}} \to 0} \left\{ {\gamma \left[ {\int\limits_{ - i{{\varepsilon }_{1}}}^{ - i{{\varepsilon }_{1}} + \infty } {{C}_{\gamma }}(\xi ){{e}^{{i\xi Z}}}d\xi + \int\limits_{i{{\varepsilon }_{1}}}^{i{{\varepsilon }_{1}} + \infty } {{D}_{\gamma }}(\xi ){{e}^{{ - i\xi Z}}}d\xi } \right]} \right. + \\ + \;\left. {\left[ {\int\limits_{ - i{{\varepsilon }_{1}}}^{ - i{{\varepsilon }_{1}} + \infty } \xi {{C}_{m}}(\xi ){{e}^{{i\xi Z}}}d\xi + \int\limits_{i{{\varepsilon }_{1}}}^{i{{\varepsilon }_{1}} + \infty } \xi {{D}_{m}}(\xi ){{e}^{{ - i\xi Z}}}d\xi } \right]} \right\} \\ \end{gathered} $

Для вычисления коэффициента комплексно-сопряженной гидродинамической нагрузки на цилиндр $С {\text{*}}$ воспользуемся формулой Чаплыгина [4], согласно которой

$C* = \frac{{{{F}_{X}} - i{{F}_{Y}}}}{{{{\rho }_{2}}{{V}^{2}}R}} = \frac{i}{2}\int\limits_K^{} {{{{(1 + {{u}_{2}}(Z))}}^{2}}dZ} $

Здесь ${{F}_{X}}$ – волновое сопротивление, ${{F}_{Y}}$ – подъемная сила диполя (размерные), а интегрирование осуществляется по произвольному контуру $K$, расположенному в нижнем слое и охватывающему рассматриваемые диполь и вихрь. Поскольку

${{u}_{2}}(Z) = - \frac{1}{{{{{(Z + ih)}}^{2}}}} + \frac{\gamma }{i}\frac{1}{{Z + ih}} + f(Z)$
и функция $f(Z)$ регулярна в области, занятой нижней частью потока жидкости, то подынтегральная функция ${{(1 + {{u}_{2}}(Z))}^{2}}$ имеет в этой области единственную особую точку $Z = - ih$. Применяя теорему о вычетах, находим $C* = 2\pi i\gamma + 2\pi i\gamma f( - ih) + 2\pi f{\text{'}}( - ih)$.

В дальнейшем исследуется комплексный коэффициент $\Delta С $ добавочной силы к обобщенной силе Жуковского, действующей на цилиндр [4], и его составляющие ${{C}_{X}}$ и $\Delta {{C}_{Y}}$. Очевидно, что

(1.14)
$\Delta C* = {{C}_{X}} - i\Delta {{C}_{Y}} = 2\pi i\gamma f( - ih) + 2\pi f{\text{'}}( - ih)$

Далее, из (1.13) с помощью интегральной теоремы Коши находим

$\begin{gathered} f( - ih) = \gamma \int\limits_0^{ + \infty } [{{C}_{\gamma }}(\xi ){{e}^{{\xi h}}} + {{D}_{\gamma }}(\xi ){{e}^{{ - \xi h}}}]d\xi + \int\limits_0^{ + \infty } \xi [{{C}_{m}}(\xi ){{e}^{{\xi h}}} + {{D}_{m}}(\xi ){{e}^{{ - \xi h}}}]d\xi + \\ + \;\pi i\gamma \sum\limits_{j = 1}^s {\mathop {{\text{res}}}\limits_{\xi = {{\xi }_{j}}} } \{ {{C}_{\gamma }}(\xi ){{e}^{{\xi h}}} - {{D}_{\gamma }}(\xi ){{e}^{{ - \xi h}}}\} + \pi i\sum\limits_{j = 1}^s {\mathop {{\text{res}}}\limits_{\xi = {{\xi }_{j}}} } \{ \xi [{{C}_{m}}(\xi ){{e}^{{\xi h}}} - {{D}_{m}}(\xi ){{e}^{{ - \xi h}}}]\} \\ \end{gathered} $$\begin{gathered} f{\text{'}}( - ih) = i\gamma \int\limits_0^{ + \infty } \xi [{{C}_{\gamma }}(\xi ){{e}^{{\xi h}}} - {{D}_{\gamma }}(\xi ){{e}^{{ - \xi h}}}]d\xi + i\int\limits_0^{ + \infty } {{\xi }^{2}}[{{C}_{m}}(\xi ){{e}^{{\xi h}}} - {{D}_{m}}(\xi ){{e}^{{ - \xi h}}}]d\xi - \\ - \pi \gamma \sum\limits_{j = 1}^s {\mathop {{\text{res}}}\limits_{\xi = {{\xi }_{j}}} } \;\{ \xi [{{C}_{\gamma }}(\xi ){{e}^{{\xi h}}} + {{D}_{\gamma }}(\xi ){{e}^{{ - \xi h}}}]\} - \pi \sum\limits_{j = 1}^s {\mathop {{\text{res}}}\limits_{\xi = {{\xi }_{j}}} } \;\{ {{\xi }^{2}}[{{C}_{m}}(\xi ){{e}^{{\xi h}}} + {{D}_{m}}(\xi ){{e}^{{ - \xi h}}}]\} \\ \end{gathered} $

Отсюда из (1.14) имеем

(1.15)
$\begin{gathered} \Delta C* = 2\pi i\int\limits_0^{ + \infty } \{ (\gamma + \xi )\left[ {\xi {{C}_{m}}(\xi ) + \gamma {{C}_{\gamma }}(\xi )} \right]{{e}^{{\xi h}}} + (\gamma - \xi )\left[ {\xi {{D}_{m}}(\xi ) + \gamma {{D}_{\gamma }}(\xi )} \right]{{e}^{{ - \xi h}}}\} d\xi + \\ + 2{{\pi }^{2}}\sum\limits_{j = 1}^s {\mathop {{\text{res}}}\limits_{\xi = {{\xi }_{j}}} } \;\{ - (\gamma + \xi )\left[ {\xi {{C}_{m}}(\xi ) + \gamma {{C}_{\gamma }}(\xi )} \right]{{e}^{{\xi h}}} + (\gamma - \xi )\left[ {\xi {{D}_{m}}(\xi ) + \gamma {{D}_{\gamma }}(\xi )} \right]{{e}^{{ - \xi h}}}\} \\ \end{gathered} $

Интеграл в (1.15) понимается в смысле главного значения по Коши, а вычеты берутся по всем $s$ полюсам ${{\xi }_{j}}$ соответствующей функции, расположенным на положительной действительной оси. Из (1.12) видно, что эти полюса являются положительными корнями уравнения

(1.16)
${{\xi }^{2}} + [\delta {{\xi }^{2}} + (1 - \delta ){{E}^{2}}]th\xi {{h}_{1}}th\xi {{h}_{2}} - \xi E\left( {th\xi {{h}_{1}} + th\xi {{h}_{2}}} \right) = 0$

Из проведенного авторами анализа [5] следует, что уравнение (1.16) имеет два положительных корня при выполнении условия

(1.17)
${\text{Fr}} < {\text{Fr}}_{{cr}}^{{в н }} = \sqrt {\frac{{\beta + 1 - \sqrt {{{{(\beta + 1)}}^{2}} - 4\varepsilon \beta } }}{2}} $
и один положительный корень, если

(1.18)
${\text{Fr}}_{{cr}}^{{в н }} < {\text{Fr}} < {\text{Fr}}_{{cr}}^{{п о в }} = \sqrt {\frac{{\beta + 1 + \sqrt {{{{(\beta + 1)}}^{2}} - 4\varepsilon \beta } }}{2}} $

При ${\text{Fr}} > {\text{Fr}}_{{cr}}^{{п о в }}$ положительных решений нет. Здесь $\beta = {{H}_{2}}{\text{/}}{{H}_{1}}$. С физической точки зрения критические числа Фруда ${\text{Fr}}_{{cr}}^{{в н }}$ и ${\text{Fr}}_{{cr}}^{{п о в }}$ означают максимальное число Фруда, при котором в потоке за обтекаемым цилиндром образуются волны, обусловленные соответственно наличием слоя скачка и свободной поверхности (т.е. внутренние и поверхностные моды).

Выделяя в (1.15) вещественную и мнимую части, окончательно получаем следующие выражения для коэффициентов волнового сопротивления и подъемной силы

(1.19)
$\begin{gathered} {{C}_{X}} = 2{{\pi }^{2}}\sum\limits_{j = 1}^s {\mathop {{\text{res}}}\limits_{\xi = {{\xi }_{j}}} } \{ - (\gamma + \xi )\left[ {\xi {{C}_{m}}(\xi ) + \gamma {{C}_{\gamma }}(\xi )} \right]{{e}^{{\xi h}}} + (\gamma - \xi )\left[ {\xi {{D}_{m}}(\xi ) + \gamma {{D}_{\gamma }}(\xi )} \right]{{e}^{{ - \xi h}}}\} \\ \Delta {{C}_{Y}} = - 2\pi i\int\limits_0^{ + \infty } \{ (\gamma + \xi )[\xi {{C}_{m}}(\xi ) + \gamma {{C}_{\gamma }}(\xi )]{{e}^{{\xi h}}} + (\gamma - \xi )[\xi {{D}_{m}}(\xi ) + \gamma {{D}_{\gamma }}(\xi )]{{e}^{{ - \xi h}}}\} d\xi \\ \end{gathered} $
где вычеты вычисляются по известным формулам [6]. Отметим, что в выражение для коэффициента подъемной силы не включена сила Архимеда.

В аналогичной постановке исследуется задача о гидродинамической реакции при циркуляционном обтекании моделируемого точечным диполем цилиндра, расположенного в верхнем слое потока (над скачком). Затем после использованных выше преобразований получаем выражения для коэффициентов волнового сопротивления и добавочной подъемной силы. Опуская громоздкие выкладки (см. [3]), числено рассчитываем конечные результаты модели с представлением их в графическом виде.

РАСЧЕТЫ СИЛОВОГО ВОЗДЕЙСТВИЯ

Расчеты силового воздействия на обтекаемый цилиндр проводились для реальных значений характеристик морской среды по формулам $\Delta {{F}_{Y}} = {{\rho }_{2}}{{V}^{2}}R\Delta {{C}_{Y}}$ (нижний слой), $\Delta {{F}_{Y}} = {{\rho }_{1}}{{V}^{2}}R\Delta {{C}_{Y}}$ (верхний слой), где коэффициенты $\Delta {{C}_{Y}}$ выражены через (1.19), а также (2.2) из [3]. Плотность в верхнем слое ${{\rho }_{1}} = 1024$ кг/м3, а относительный перепад плотности между нижним и верхним слоями варьирует в диапазоне ${{\rho }_{2}}{\text{/}}{{\rho }_{1}} = 1.001\, - \,1.005$. В придонном слое перепад ${{\rho }_{2}}{\text{/}}{{\rho }_{1}}$ может изменяться в пределах 1.01–1.05, что соответствует взвесенесущему потоку в нижнем слое. В первом случае это относительно слабый взвесенесущий поток, во втором – взмученный поток, проявляющийся вблизи дна на склонах подводных возвышенностей [1]. Общая толщина потока 60 м, толщина верхнего слоя ${{H}_{1}} = 50$ м, радиус цилиндра (трубопровода) $R = 0.71$ м. Диполь локализован в нижнем или верхнем слое на расстоянии h = 2 м от границы раздела. Безразмерная циркуляция определялась как $\gamma = \Gamma {\text{/}}(2\pi VR)$, где V – скорость потока, $\Gamma $ – размерная циркуляция. В силу равнозначности положительной и отрицательной завихренностей в потоке при анализе изменчивости подъемной силы можно выбрать любую ${{\gamma }^{ \pm }}$: $\Delta F_{Y}^{ + }$ – при положительной, а $\Delta F_{Y}^{ - }$ – при отрицательной циркуляциях. Отметим, что поскольку в [3] относительно полно проведены исследования изменчивости силы сопротивления FX, то ниже рассматривается задача об изменчивости лишь подъемной силы $\Delta F_{Y}^{ \pm }$.

Анализ модельных решений в [3, 7] показал, что усиление воздействия потока на препятствие обусловлено увеличением мощности скачка плотности $\varepsilon $, и вместе с расстоянием $h$ они являются основными параметрами рассматриваемой задачи. На рис. 1 приведены зависимости силовых воздействий на диполь от относительного перепада плотности $\varepsilon $. Здесь диполем моделируется фрагмент трубопровода.

Рис. 1.

Зависимость подъемной силы диполя от относительного перепада плотности между слоями; модель трубопровода. Диполь над (а) и под (б) скачком плотности при $V{\text{ }} = {\text{ }}0.7$ м/с: 1–4 – γi = 0, 0.1, 0.2, 0.3.

Как видно на рис. 1, кривые с однонаправленными положительными циркуляциями $\Delta F_{Y}^{ + }$ в зависимости от локализации относительно скачка плотности существенно отличаются между собой как по форме, так и по значениям величин. Представленные кривые по разные стороны скачка по характеру изменчивости противоположны между собой. Согласно [3] отличия представленных на рис. 1 графиков $\Delta F_{Y}^{ + }$ и построенных вблизи, но по разные стороны границы раздела слоев обусловлены разнонаправленностью циркуляции, что приводит в одних случаях к увеличению скорости обтекания (между скачком и цилиндром), в других – к ее уменьшению. Подобное изменение $\Delta F_{Y}^{{}}$ характерно как для положительной, так и отрицательной завихренностей.

Таким образом, дополнительно возникающие при наличии циркуляции скорости силовые нагрузки разнонаправленно действуют вдоль участка трубопроводной линии. В этом случае, несмотря на свою незначительность, но действуя в течение продолжительного времени, они могут приводить к деформации трубопровода, а в дальнейшем – к возможному его повреждению. Поэтому подобные эффекты необходимо учитывать при прокладке подводных коммуникаций и трубопроводных линий. Отметим, что выявленные в модели изменения подъемной силы в зависимости от величины циркуляции ${{\gamma }_{i}}$ в подобных исследованиях ранее не учитывались.

В продолжение анализа результатов модельной задачи представляет интерес исследовать характерную особенность в изменчивости подъемной силы и ее соответствующую интерпретацию. В этой связи перейдем от рассмотренной выше неподвижно обтекаемой точечной модели к кинематически подобной физической модели поступательно движущегося объекта. Не нарушая общности рассматриваемой модельной задачи, ограниченный фрагмент трубопровода можно представить в виде сигарообразного (или овоидного) тела, по форме моделирующего определенный тип самоходного подводного объекта. При этом для адекватного сопоставления конструкции (геометрии) модельного овоида с первоначальной точечной моделью необходимо в качестве силового воздействия на подводный объект выделить боковую компоненту вектора силы, распределенную по длине корпуса физической модели.

Исходя из такого преобразования первоначальной модели, гипотетически можно воспользоваться расчетами зависимости подъемной силы расположенного под скачком плотности диполя от скорости потока, рис. 2. Здесь диполь моделирует обтекание подводного объекта овоидной формы, что наглядно представляет реверсивные изменения направления подъемной силы $\Delta F_{Y}^{ + }$(V) на соответствующих интервалах скоростей обтекания.

Рис. 2.

Зависимость подъемной силы диполя, расположенного под скачком плотности, от скорости потока при ${{\rho }_{2}}{\text{/}}{{\rho }_{1}} = 1.005$, H1 = 100 м, H2 = 200 м, h = 6 м, R = 3.5 м; модель подводного объекта: 1–4 – γ = 0.0, 0.1, 0.2, 0.3. Черные стрелки указывают на интервалы с реверсивным изменением кривых $\Delta F_{Y}^{ + }$(V).

С целью гипотетического преобразования точечной модели в соответствующую форму овоидного объекта можно сослаться на характерный пример из морской практики – случаи относительно быстрого и опасного погружения подводного объекта на десять и более метров вглубь [3]. Такой эффект принято объяснять наличием внутренних волн, генерируемых на скачках плотности среды. Однако параметры внутренних волн, зависящих от мощности скачка плотности $\varepsilon $ (с минимальным периодом порядка десяти минут и длиной в сотни метров), отражают более медленную динамику внутренней волны по сравнению с относительно резким опусканием самого объекта. При этом подобный эффект может проявляться либо при изменении направления движения объекта с возникновением боковой составляющей потока, либо вариациях направления самого течения (также с выделенным боковым компонентом к корпусу объекта). И как показали расчеты, выделение боковой составляющей потока с ненулевой циркуляцией может привести к возникновению дополнительной силы, направленной вертикально вниз – рис. 2. Отметим, что наблюдаемый здесь разрыв кривых в окрестности точки V ≈ 2 м/с обусловлен существованием максимальной скорости потока, при которой за обтекаемым объектом образуются внутренние волны (границей между внутренней и поверхностной модой) – см. формулы (1.17) и (1.18).

Подобный эффект при циркуляционном обтекании объекта может проявляться и в атмосфере, например, во время полета самолета. В этом случае конфигурация (геометрия) такого объекта в целом также представляется в форме овоида. Тогда его обтекание воздушным потоком приводит к возникновению силы, направленной вертикально вниз, что согласно результатам модели может оказаться причиной неожиданно резкого и опасного снижения высоты летательного аппарата. При этом подобный эффект действительно проявляется в полете. Поэтому использование здесь модельных результатов при исследовании полета самолета, по-видимому, представляется правомерным.

Уравнения гидро- и аэродинамики (без учета в последних сжимаемости воздуха) тождественны. А в случае обтекания со скоростью не более 1/5 скорости звука (или скорости полета до 250 км/ч) наличием сжимаемости воздуха вообще можно пренебречь [8]. Однако здесь, как и для подводного объекта, рассчитанные модельные параметры принимаются гипотетически и должны рассматриваться лишь как качественные оценки.

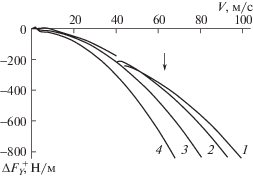
На рис. 3 в графическом виде наглядно представлено относительно мощное силовое воздействие на летательный аппарат, возникающее при его посадке с понижением скорости полета в пределах 300–400 км/ч. Резкое увеличение модуля вертикальной силы $\Delta F_{Y}^{ \pm }$ для всех γi на этих графиках указывает на риск резкого снижения (провала) траектории самолета. Можно предположить, что резкие провалы самолета обусловлены механизмом силового воздействия циркуляции скорости и возникновением дополнительной вертикальной силы, которая может реверсивно изменять свое направление в отличие от подъемной силы Жуковского.

Рис. 3.

Зависимость подъемной силы диполя, расположенного под слоем скачка, от скорости потока при ${{\rho }_{2}} = 1.26$ кг/м3, ${{\rho }_{2}}{\text{/}}{{\rho }_{1}} = 1.3$, H1 = 1000 м, H2 = 2000 м, h = 6 м, R = 3.5 м: 1–4 – γ = 0.0, 0.1, 0.2, 0.3.

В итоге суммарное воздействие одинаковых по природе сил, но приложенных к разным частям самолета – крыльям и фюзеляжу – в зависимости от направления каждой из них, может приводить к резким вертикальным колебаниям траектории полета, что и не редко проявляется в летной практике.

Список литературы

  1. Жмур В.В., Сапов Д.А. Катастрофические взвесенесущие гравитационные потоки в придонном слое океана // Мировой океан. Т. 1. Геология и тектоника океана. Катастрофические явления в океане. М.: Научный мир, 2013. С. 499–524.

  2. Kontar E.A., Sokov A.V. A benthic storm in the northeastern tropical Pacific over the fields of manganese nodules // Deep-Sea Res. 1994. V. 41. № 7. P. 1069–1089.

  3. Владимиров И.Ю., Корчагин Н.Н., Савин А.С. Волновая реакция диполя при циркуляционном обтекании двухслойным потоком конечной глубины // Изв. РАН. МЖГ. 2016. № 2. С. 90–99.

  4. Лойцянский Л.Г. Механика жидкости и газа. М.: Наука, 1978. 736 с.

  5. Владимиров И.Ю., Корчагин Н.Н., Савин А.С. Поверхностные возмущения при обтекании препятствий стратифицированным потоком конечной глубины // Океанология. 2012. Т. 52. № 6. С. 825–835.

  6. Сидоров Ю.В., Федорюк М.В., Шабунин М.И. Лекции по теории функций комплексного переменного. М.: Наука, 1976. 408 с.

  7. Владимиров И.Ю., Корчагин Н.Н., Савин А.С. Волновое воздействие взвесенесущего потока на обтекаемое препятствие // Докл. РАН. 2015. Т. 461. № 2. С. 223–227.

  8. Седов Л.И. Механика сплошной среды. Т. 2. М.: Наука, 1973. 584 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал