Известия РАН. Механика жидкости и газа, 2019, № 4, стр. 72-81
О РЕШЕНИИ ЗАДАЧИ РИМАНА, ОПИСЫВАЮЩЕЙ ЗАКАЧКУ НАГРЕТОГО РАСТВОРА СОЛИ В ВОДОНАСЫЩЕННЫЙ ПЛАСТ
А. А. Афанасьев a, *, А. А. Чернова a, **
a МГУ им. М.В. Ломоносова, Научно-исследовательский институт механики
Москва, Россия
* E-mail: afanasyev@imec.msu.ru
** E-mail: anya_chernova_2504@mail.ru
Поступила в редакцию 07.11.2018
После доработки 17.12.2018
Принята к публикации 18.12.2018
Аннотация
Решена автомодельная задача о распаде произвольного разрыва применительно к процессам неизотермической фильтрации соленой жидкости. Учитывается возможность выпадения в пористой среде осадка в виде твердой фазы соли и сопутствующее снижение проницаемости. В предположении несжимаемой среды и пренебрежении теплопроводностью предложен геометрический метод решения задачи на плоскости. Показано, что решение необходимо строить только из сильных разрывов и областей однородного распределения параметров, а центрированные волны Римана невозможны. Исследованы возможные типы решений задачи. Продемонстрировано, что при высокой температуре закачиваемого раствора соли в пласт распространяются три сильных разрыва, из которых только на внутреннем рвется температура.
Формирование месторождений цветных металлов часто связывают с фильтрацией водных растворов солей, нагретых до температур выше 400°C. Подобные растворы, богатые полезными химическими элементами, выделяются из вулканических очагов при дегазации магмы [1]. Далее раствор поднимается к поверхности с глубин 5 и более км, фильтруясь через геологические породы [2, 3]. При этом достигаются условия термодинамического равновесия пар–жидкость, при которых раствор расслаивается на фазы жидкости и пара, причем пар, как более легкая фаза, быстро поднимается к поверхности. Так как концентрация соли в паре мала, то это процесс сопровождается увеличением концентрации соли и других растворенных веществ в жидкости, т.е. раствор “выкипает”. В результате на глубинах 1–2 км образуются линзы концентрированного раствора соли, из которых формируются порфировые месторождения.
Образование линзы, в случае если нагретый раствор быстро поднимается по узкому высокопроницаемому вулканическому каналу, сопровождается выпадением на скелет породы осадка в виде твердой фазы соли [3, 4]. В результате канал перекрывается, а нагретый раствор растекается в горизонтальном направлении на глубинах 1–2 км. Таким образом, происходит внедрение, т.е. закачка, нагретого раствора соли из канала вулкана в окружающие породы, насыщенные более холодной и пресной водой. На качественном уровне, пренебрегая неоднородностями проницаемой геологической среды и трехмерным характером течения, данный процесс описывается решением одномерной задачи о распаде произвольного разрыва. С одной стороны от разрыва находится нагретый раствор соли, а с другой – холодная пресная вода.
Закачка соленой воды в пористые среды с учетом выпадения осадка соли рассматривалась ранее в работах многих авторов. В [5] исследованы процессы выпадения растворенных солей в осадок при испарении грунтовых вод. В [6] разработаны методы численного моделирования многофазной фильтрации соленой жидкости, которые в [7] использовались для исследования образования осадка при отборе жидкости из геотермального резервуара. Показано, что при испарении воды концентрация соли в жидкости растет, что приводит к насыщению раствора, образованию осадка и, при определенных параметрах, полной закупорке пористой среды.
В настоящей работе исследуется процесс закачки нагретого раствора соли в холодный водонасыщенный пласт. Причем рассматриваются параметры, при которых водяной пар не образуется. Учитывается, что растворимость соли в воде есть функция температуры, а выпадение осадка обусловлено тем, что при снижении температуры раствор становится насыщенным. Эти процессы качественно отличаются от процессов, рассмотренных в работах [5, 7, 8], где выпадение соли связано с испарением воды и сопутствующим увеличением солености жидкости, которое достигает равновесного значения. В отличие от [7, 8], где исследован отбор пара из геотермального резервуара, в данной работе, наоборот, рассмотрена закачка соленой воды в пласт.
1. ОСНОВНЫЕ УРАВНЕНИЯ
Одномерная неизотермическая фильтрация двухкомпонентной жидкости – соленой воды (например, бинарной смеси NaCl–H2O) – описывается следующей системой уравнений [4, 9]:
(1.1)
$\frac{\partial }{{\partial t}}\left( {\phi \left( {{{\rho }_{l}}c\left( {1 - s} \right) + {{\rho }_{s}}s} \right)} \right) + \frac{\partial }{{\partial x}}\left( {{{\rho }_{l}}cw} \right) = 0$(1.2)
$\frac{\partial }{{\partial t}}\left( {\phi {{\rho }_{l}}\left( {1 - c} \right)\left( {1 - s} \right)} \right) + \frac{\partial }{{\partial x}}\left( {{{\rho }_{l}}\left( {1 - c} \right)w} \right) = 0$(1.3)
$\frac{\partial }{{\partial t}}\left( {\phi \left( {{{\rho }_{l}}{{h}_{l}}\left( {1 - s} \right) + {{\rho }_{s}}{{h}_{s}}s} \right) + \left( {1 - \phi } \right){{\rho }_{r}}{{h}_{r}}} \right) + \frac{\partial }{{\partial x}}\left( {{{\rho }_{l}}{{h}_{l}}w} \right) = 0$Здесь $\phi $ – пористость среды, $\rho $ – плотность, c – массовая концентрация соли в жидкости, $s$ – насыщенность твердой фазы соли, $w$ – скорость фильтрации жидкости, $h$ – энтальпия. Индексы $r$, $l$, $s$ отвечают параметрам скелета пористой среды, жидкости и твердой фазы соли соответственно.
Уравнения (1.1) и (1.2) – законы сохранения массы соли (NaCl) и воды (H2O) соответственно, а уравнение (1.3) – закон сохранения энергии насыщенной пористой среды, записанный в терминах энтальпии [10] и в пренебрежении теплопроводностью. В системе (1.1)–(1.3) предполагается, что жидкость может расслаиваться на две фазы – жидкую фазу соленой воды и твердую фазу соли, а температура ниже температуры кипения воды, т.е. газовая фаза водяного пара не образуется.
Введем “объемную” концентрацию соли в жидкой фазе $\tau $ следующим образом:
(1.4)
${{\rho }_{l}} = {{\rho }_{w}}\left( {1 - \tau } \right) + {{\rho }_{d}}\tau ,\quad {{\rho }_{l}}{{h}_{l}} = {{\rho }_{w}}{{h}_{w}}\left( {1 - \tau } \right) + {{\rho }_{d}}{{h}_{d}}\tau $(1.5)
$c = \frac{{{{\rho }_{d}}\tau }}{{{{\rho }_{w}}\left( {1 - \tau } \right) + {{\rho }_{d}}\tau }}$Соотношения (1.4), (1.5) подразумевают, что жидкая фаза l состоит из двух “псевдофаз” w и d с объемными концентрациями $\tau $ и $1 - \tau $ соответственно.
Кривая термодинамического равновесия между жидкостью и твердой фазой соли задается соотношением
где ${{\tau }_{ * }}(T)$ – монотонно возрастающая функция температуры [11]. Для дальнейших рассуждений конкретное математическое выражение для ${{\tau }_{ * }}(T)$ не существенно. Если соленость жидкости ниже равновесного значения ($\tau < {{\tau }_{ * }}$), то твердая фаза не образуется, а соль полностью растворена в жидкости. При увеличении солености и достижения ею равновесного значения ($\tau = {{\tau }_{ * }}$) возможно выпадение осадка соли. Соленость жидкости не может быть выше значения ${{\tau }_{ * }}$.Далее сделаем упрощающее допущение, что все фазы – несжимаемые среды, а их энтальпии – линейные функции температуры:
(1.7)
$\phi ,{{\rho }_{j}} = {\text{const;}}\quad {{h}_{j}} = {{C}_{j}}T + {{h}_{{j0}}};\quad j = w,s,r,d$С учетом соотношений (1.5)–(1.8) система уравнений (1.1)–(1.3) сведется к виду
(1.10)
$\frac{\partial }{{\partial t}}\left( {\phi \left( {\tau \left( {1 - s} \right) + s} \right)} \right) + w\frac{{\partial \tau }}{{\partial x}} = 0$(1.11)
${{\left( {\rho C} \right)}_{m}}\frac{{\partial T}}{{\partial t}} + {{\left( {\rho C} \right)}_{l}}w\frac{{\partial T}}{{\partial x}} = 0$Здесь ${{(\rho С )}_{m}}$ – объемная теплоемкость насыщенной пористой среды, а ${{(\rho С )}_{l}}$ – объемная теплоемкость двухкомпонентной (NaCl–H2O) многофазной смеси.
Введем полную, т.е. просуммированную по жидкой и твердой фазам, объемную концентрацию соли
Тогда при $\xi \leqslant {{\tau }_{ * }}$, т.е. ниже прямой 1 на рис. 1, смесь находится в однофазном состоянии жидкости, а при $\xi > {{\tau }_{ * }}$, т.е. выше прямой 1 – в двухфазном состоянии жидкость–соль.
Рис. 1.
Фазовая плоскость $\left\{ {{{\tau }_{*}},\xi } \right\}$. Прямая 1 – линия термодинамического равновесия ($\xi = {{\tau }_{ * }}$ или $s = 0$), 2 – $s = 1$, а штриховые прямые – линии уровня $s = {\text{const}}$. Область I – p = 1, а II – p = 2
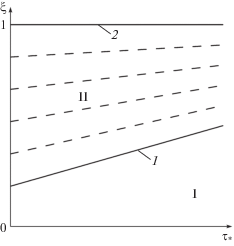
Согласно (1.5), массовая концентрация есть известная функция объемной концентрации, т.е. $с (\tau )$, а согласно (1.12) насыщенность выражается через $\tau $ и $\xi $, т.е. $s(\tau ,\xi )$. Тогда, учитывая предположения (1.7), (1.8), законы сохранения (1.9)–(1.11) есть система трех уравнений относительно четырех неизвестных $\tau $, $\xi $, $T$, $w$ (вместо $T$ можно выбрать переменную ${{\tau }_{ * }}$), а для замыкания системы необходимо дополнительное соотношение. В областях однофазной фильтрации система замыкается условием s = 0 или $\xi = \tau $, причем выполняется неравенство $\tau \leqslant {{\tau }_{ * }}$, а в областях двухфазной фильтрации – условием $\tau = {{\tau }_{ * }}(T)$, причем $\xi > \tau $.
2. УРАВНЕНИЯ В БЕЗРАЗМЕРНОМ ВИДЕ
Введем безразмерные параметры в виде
(2.1)
$x{\text{'}} = {x \mathord{\left/ {\vphantom {x {\bar {x}}}} \right. \kern-0em} {\bar {x}}},\quad t{\text{'}} = {t \mathord{\left/ {\vphantom {t {\bar {t}}}} \right. \kern-0em} {\bar {t}}},\quad w{\text{'}} = {w \mathord{\left/ {\vphantom {w {\bar {w}}}} \right. \kern-0em} {\bar {w}}},\quad T{\text{'}} = {T \mathord{\left/ {\vphantom {T {\bar {T}}}} \right. \kern-0em} {\bar {T}}},\quad \bar {x} = \frac{1}{\phi }\int\limits_0^{\bar {t}} {w(t)dt} $(2.3)
$\frac{{\partial \xi }}{{\partial t{\text{'}}}} + \frac{{\partial \tau }}{{\partial x{\text{'}}}} = 0$(2.4)
$A\left( \xi \right)\frac{{\partial {{\tau }_{ * }}}}{{\partial t{\text{'}}}} + B\left( \tau \right)\frac{{\partial {{\tau }_{ * }}}}{{\partial x{\text{'}}}} = 0$(2.5)
$A\left( \xi \right) = \left( {1 - \xi } \right){{\Phi }_{w}} + \xi {{\Phi }_{s}} + 1,\quad B\left( \tau \right) = \left( {1 - \tau } \right){{\Phi }_{w}} + \tau {{\Phi }_{s}}$(2.6)
${{\Phi }_{w}} = \frac{{\phi {{\rho }_{w}}{{C}_{w}}}}{{\left( {1 - \phi } \right){{\rho }_{r}}{{C}_{r}}}},\quad {{\Phi }_{s}} = \frac{{\phi {{\rho }_{s}}{{C}_{s}}}}{{\left( {1 - \phi } \right){{\rho }_{r}}{{C}_{r}}}}$Согласно (2.2), скорость фильтрации является функцией времени. Не ограничивая общности в уравнениях (2.3) и (2.4) предполагаем, что эта функция $w(t) \equiv \bar {w}(t)$ задана, а $w{\text{'}} \equiv 1$. Тогда уравнение (2.2) выполняется тождественно, а в системе (2.2)–(2.4) число законов сохранения сокращается до двух уравнений (2.3) и (2.4) на $\xi $, $\tau $, ${{\tau }_{ * }}$. Согласно (2.4) по известному ${{\tau }_{ * }}$ можно восстановить значение температуры $T$. В областях однофазной фильтрации система (2.3), (2.4) замыкается условием $\xi = \tau $, $\tau \leqslant {{\tau }_{*}}$, а в области двухфазной фильтрации – условием $\tau = {{\tau }_{*}}$, $\xi > \tau $.
Осаждение соли может приводить к снижению проницаемости пористой среды [5, 7, 8] и, в соответствии с законом Дарси, к увеличению градиента давления. Однако, согласно (2.2), полный расход жидкости сохраняется вдоль x, поэтому изменение проницаемости не влияет на распределения $\xi $, $\tau $, ${{\tau }_{ * }}$.
В дальнейшем у безразмерных параметров (1.13) штрих опускается.
3. О МАЛЫХ ВОЗМУЩЕНИЯХ И СИЛЬНЫХ РАЗРЫВАХ
Определим характеристические скорости в областях однофазной и двухфазной фильтрации. Для этого рассмотрим распространение малых возмущений на фоне однородного распределения параметров течения. Ищем решение системы (2.3), (2.4) в виде простых гармонических волн
где k – волновое число, $\omega $ – частота, ${{u}_{0}} = {\text{const}}$ – фоновое распределение параметров, $\delta u \to 0$ – малые амплитуды возмущения, а i – мнимая единица. Подставляя (3.1) в систему (2.3), (2.4), учитывая (1.12) и пренебрегая слагаемыми второго порядка малости, получим дисперсионное соотношение(3.2)
$(\omega - {{a}_{\xi }}k)(\omega - {{a}_{T}}k) = 0,\quad {{a}_{\xi }} = 2 - p,\quad {{a}_{T}} = \frac{B}{A}$(3.3)
$\omega = {{a}_{\xi }}k{\text{:}}\quad \delta \xi \ne 0,\quad \delta {{\tau }_{ * }} = \tau _{*}^{'}\delta T = 0$При этом, когда p = 1 возмущения концентрации “вморожены” в жидкость, т.е. ${{a}_{\xi }} = 1$. При p = 2 скорость распространения возмущений концентрации равна нулю, ${{a}_{\xi }} = 0$, так как твердая фаза соли неподвижна.
В областях p = 1 со второй характеристикой (${{a}_{T}} = {B \mathord{\left/ {\vphantom {B A}} \right. \kern-0em} A}$) распространяются только возмущения ${{\tau }_{ * }}$ (т.е. температуры T)
(3.4)
$p = 1{\text{:}}\quad \omega = \frac{{B(\tau )}}{{A(\tau )}}k,\quad \delta \xi = \delta \tau = 0,\quad \delta {{\tau }_{ * }} = \tau _{*}^{'}\delta T \ne 0$(3.5)
$p = 2{\text{:}}\quad \omega = \frac{{B({{\tau }_{ * }})}}{{A(\xi )}}k,\quad \delta \xi \ne 0,\quad \delta T \ne 0,\quad A\delta {{\tau }_{ * }} = A\tau _{*}^{'}\delta T = B\delta \xi $Из законов сохранения (1.1)–(1.3), записанных в интегральной форме, следуют условия на сильных разрывах, которые сразу приведем в безразмерных переменных
где W – скорость разрыва, верхним индексом ± обозначены параметры перед и за разрывом соответственно, а квадратными скобками – скачок соответствующей величины на разрыве (например, $\left[ w \right] = {{w}^{ + }} - {{w}^{ - }}$). Согласно уравнению (3.6), скорость фильтрации непрерывна на разрыве. Учитывая, что $w \equiv 1$, условие (3.6) выполняется тождественно.В соответствии с (3.8) возможны разрывы двух различных типов. На разрывах первого типа температура непрерывна $\left[ {{{\tau }_{ * }}} \right] = 0$ (или $\left[ T \right] = 0$), а скорость W имеет значение, удовлетворяющее соотношению (3.7)
Данным разрывам на фазовой плоскости соответствует ветвь адиабаты ${{\theta }_{\xi }}$, представляющая собой вертикальную прямую (рис. 2). Эта ветвь – геометрическое место точек $({{\tau }_{ * }},\xi )$ возможных состояний за (или перед) разрывом первого типа при заданном состоянии перед (или за) разрывом, которому соответствует точка $O_{p}^{ + }$ (или $O_{p}^{ - }$), p = 1, 2.
Рис. 2.
Адиабаты разрыва при заданном начальном состоянии за $O_{p}^{ - }$ (a) или перед $O_{p}^{ + }$ (б) разрывом в областях однофазного (p = 1) и двухфазного (p = 2) состояния. Сплошными и штриховыми линиями показаны эволюционные и неэволюционные отрезки ветвей адиабаты. Прямая 1 – линия термодинамического равновесия $\xi = {{\tau }_{ * }}$
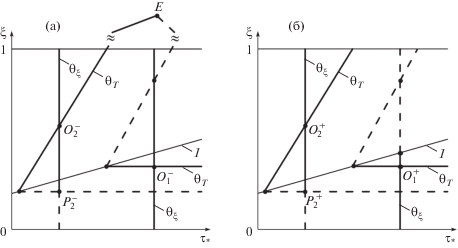
Разрывы второго типа, на которых $\left[ {{{\tau }_{ * }}} \right] \ne 0$, распространяются с характеристической скоростью ${{a}_{T}}$, причем эта скорость на разрыве непрерывна
Данным разрывам на фазовой плоскости соответствует ветвь адиабаты ${{{\theta }}_{T}}$, которая в областях p = 1 есть отрезок прямой $\xi = {\text{const}}$, а в областях p = 2 – отрезок прямой
Подставляя (2.5) в (3.9), получим уравнение этой прямой в виде
(3.10)
$\xi = \gamma ({{\tau }_{ * }} - {{\psi }_{\tau }}) + {{\psi }_{\xi }},\quad {{\psi }_{\tau }} = \frac{{{{\Phi }_{w}}}}{{{{\Phi }_{w}} - {{\Phi }_{s}}}},\quad {{\psi }_{\xi }} = \frac{{{{\Phi }_{w}} + 1}}{{{{\Phi }_{w}} - {{\Phi }_{s}}}}$Для эволюционности сильного разрыва необходимо потребовать, чтобы от него уходило на единицу меньше малых возмущений, чем число заданных на нем условий [12]. Так как на сильном разрыве выполняется два невырожденных условия (3.7) и (3.8), то он эволюционен, если от него уходит ровно одна характеристика (3.3) или (3.4) (или (3.5)). Для определения эволюционных отрезков ветвей ${{\theta }_{\xi }}$ и ${{\theta }_{T}}$ адиабаты (рис. 2), необходимо сравнить скорость разрыва W с характеристическими скоростями ${{a}_{\xi }}$ и ${{a}_{T}}$.
Для различных положений точки O эволюционные отрезки адиабаты ${{\theta }_{\xi }}$ и ${{\theta }_{T}}$ изображены на рис. 2. Если точка O соответствует однофазному состоянию за разрывом $O = O_{1}^{ - }$, то эволюционными являются вся ветвь ${{\theta }_{\xi }}$ и весь отрезок ветви ${{\theta }_{T}}$, расположенный в области $p = 1$. Когда же $O = O_{1}^{ + }$, то эволюционными являются отрезки ветвей ${{\theta }_{\xi }}$ и ${{\theta }_{T}}$, расположенные в области p = 1. Если точка O соответствует двухфазному состоянию перед или за разрывом $O = O_{2}^{ \pm }$, то эволюционны отрезок ветви ${{\theta }_{\xi }}$, лежащий выше точки $P_{2}^{ \pm }$, и весь отрезок ветви ${{\theta }_{T}}$, расположенный в области p = 2.
4. ПОСТАНОВКА ЗАДАЧИ РИМАНА
Рассмотрим одномерную задачу неизотермической фильтрации смеси соленой жидкости в области $x \in [0, + \infty )$. В начальный момент времени (t = 0) пористая среда насыщена водой с малой соленостью ${{\tau }_{0}} = {{\xi }_{0}}$ при температуре ${{T}_{0}}$. При t = 0 через границу x = 0 в область $x > 0$ начинает закачиваться соленая вода с объемной концентрацией соли ${{\tau }_{i}} = {{\xi }_{i}}$, температурой ${{T}_{i}}$ и постоянным объемным расходом ${{w}_{i}} = 1$. Согласно (2.2) и (3.6) закачка жидкости приведет к мгновенному установлению однородного распределения скорости $w = {{w}_{i}}$ во всей области течения $x \geqslant 0$. Также закачка приведет к распространению от границы x = 0 в область x > 0 центрированных в точке x = 0, t = 0 возмущений температуры и концентрации соли $\xi $ (и $\tau $). По постановке данная задача аналогична классической задаче Баклея–Леверетта в теории фильтрации [13].
Решение сформулированной задачи в общем случае должно строиться из сильных разрывов, центрированных волн Римана и областей однородного распределения параметров [12]. Однако у системы (2.3) и (2.4) не существует решений в виде центрированных волн Римана. Действительно, волна не может быть связана с центрированным пучком характеристик (3.3) или (3.4), скорости которых принимают дискретные, но постоянные значения 1 или 0 соответственно. В возмущениях (3.4) $\delta {{a}_{T}}(\tau ) = 0$ и, согласно (2.5), в возмущениях (3.5)
характеристическая скорость не изменяется, поэтому центрированные волны, связанные с данной характеристикой, тоже невозможны. Таким образом, решение сформулированной задачи нужно строить только из сильных разрывов и областей однородного распределения параметров.5. ИССЛЕДОВАНИЕ РЕШЕНИЙ ЗАДАЧИ
Начальному распределению параметров в водонасыщенном пласте поставим в соответствие на фазовой плоскости точку $R$, а параметрам закачиваемой жидкости точку $I$ в области p = 1 (рис. 3). Точка $R$, соответствующая холодной пресной воде, расположена при $\xi = 0$ и малых значениях ${{\tau }_{ * }}$, т.е., согласно (1.6), малых температурах T. Точка $I$, соответствующая нагретой соленой жидкости, расположена при $\xi > 0$ и больших значениях ${{\tau }_{ * }}$. Для решения поставленной задачи необходимо найти путь на фазовой плоскости, соединяющий точки $I$ и $R$, отдельные отрезки которого соответствуют только эволюционным отрезками адиабат разрывов. Причем при возрастании пространственной координаты $x$ каждый следующий разрыв должен распространяться быстрее предыдущего.
Рис. 3.
Траектории, соответствующие решению задачи на фазовой плоскости, при различных положениях точек $I$ и $R$. Показаны траектории, соответствующие решению первого (а) и второго (б) типов. При фиксированных ${{R}_{1}}$ (или ${{I}_{2}}$) заштрихованы области параметров (а) (или (б)), соответствующие решению второго типа
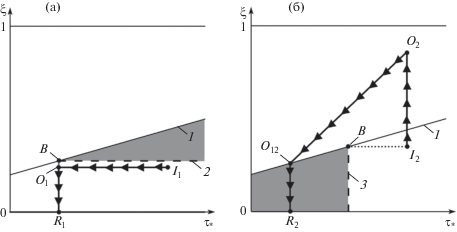
Рассмотрим “элементарные” решения системы уравнений (2.3), (2.4) для того, чтобы на фазовой плоскости было удобно сравнивать скорости двух последовательно распространяющихся разрывов и проверять их эволюционность. Под элементарным решением имеется в виду решение, которое содержит последовательность двух эволюционных разрывов, распространяющихся в положительном направлении оси x со скоростями ${{W}_{1}}$ и ${{W}_{2}}$. При этом разрыв, расположенный при большей координате, x распространяется быстрее, т.е. ${{W}_{1}} < {{W}_{2}}$ (рис. 4). За разрывом $1$, между разрывами и перед разрывом 2 все параметры имеют однородное распределение, которым на фазовой плоскости соответствуют точки ${{O}^{ - }}$, O и ${{O}^{ + }}$ соответственно. Таким образом, на фазовой плоскости элементарному решению можно поставить в соответствие траекторию из ${{O}^{ - }}$ в ${{O}^{ + }}$, проходящую через точку O. Траектория составляется только из эволюционных отрезков адиабаты разрыва, выпущенной из точки O, с учетом ограничения на скорости разрыва ${{W}_{1}} < {{W}_{2}}$.
Рис. 4.
Схематическое изображение последовательности двух разрывов в “элементарном” решении. Точки $O$ обозначают состояния перед и за разрывом
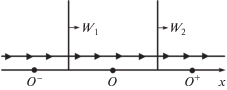
Для различных положений точки O возможные элементарные решения изображены на рис. 5. Стрелки показывают направление движения вдоль траекторий при возрастании $x$. Таким образом, решение задачи сводится к определению последовательности точек (${{O}_{i}}$, $i = 1,2,\; \ldots $) на фазовой плоскости и соответствующих им элементарных решений, соединяющих точки $I$ и $R$. Причем в решении $i$ выполняются условия $O = {{O}_{i}}$, ${{O}^{ + }} = {{O}_{{i + 1}}}$, а в решении $i + 1$ – $O = {{O}_{{i + 1}}}$, ${{O}^{ - }} = {{O}_{i}}$ (рис. 4).
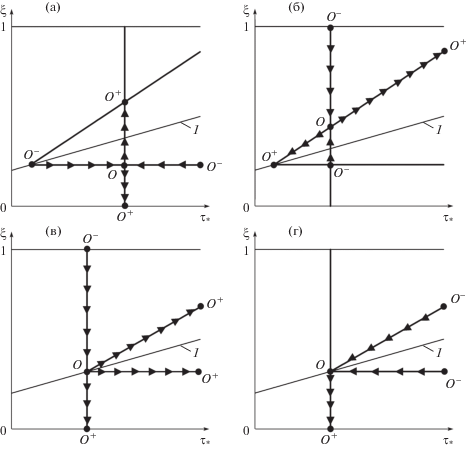
Рис. 5.
Элементарные решения при различных положениях точки $O$ в области однофазного (а) и двухфазного (б) состояния смеси, а также на линии термодинамического равновесия (в, г)
Предположим, что граничным и начальным условиям задачи соответствуют точки ${{I}_{1}}$ и ${{R}_{1}}$ на рис. 3а. То есть, пусть на фазовой плоскости точка ${{O}_{1}}$ – вершина прямоугольника, образованного ${{I}_{1}}$ и ${{R}_{1}}$, – лежит ниже линии термодинамического равновесия $\xi = {{\tau }_{ * }}$. В этом случае существует единственная траектория, соединяющая ${{I}_{1}}$ и ${{R}_{1}}$. Она образована элементарным решением на рис. 5а, в котором ${{O}^{ - }} = {{I}_{1}}$, $O = {{O}_{1}}$, а ${{O}^{ + }} = {{R}_{1}}$. В данном решении первого типа с быстрым разрывом 3 (${{W}_{3}} = {{a}_{\xi }} = 1$) распространяются возмущения солености (рис. 6а). Быстрый фронт ограничивает объем пористой среды ($x < {{W}_{3}}{{t}_{ * }}$), насыщенный концентрированным раствором соли, который закачан в пласт к моменту времени ${{t}_{ * }}$. С медленным разрывом (${{W}_{2}} = {{a}_{T}} < 1$) распространяются возмущения температуры $T$ (или ${{t}_{ * }}$), которые отстают от возмущений $\xi $ из-за теплообмена между жидкостью и неподвижной породой. За медленным фронтом $T = {{T}_{i}}$, а перед ним – $T = {{T}_{0}}$. При этом осадок соли не образуется, а течение остается однофазным (s = 0).
Рис. 6.
Решения первого (а) и второго (б) типов. Показаны волновые картины и распределения $\xi $, ${{\tau }_{*}}$ и $s$ в момент времени $t = {{t}_{ * }}$. На волновых картинах сплошные прямые 1, 2 и 3 – траектории разрывов, заштрихована область двухфазного течения, а стрелки показывают направление распространения характеристических скоростей
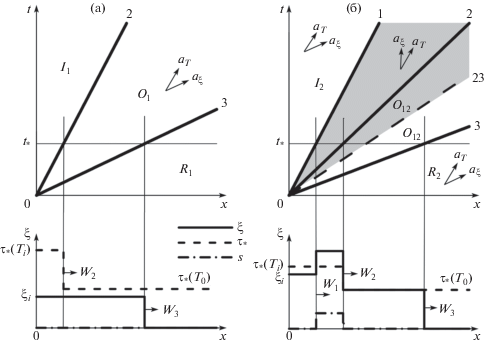
Теперь предположим, что условиям задачи соответствуют точки ${{I}_{2}}$ и ${{R}_{2}}$ на рис. 3б. То есть, пусть линия термодинамического равновесия $\xi = {{\tau }_{ * }}$ пересекает прямоугольник, образованный точками ${{I}_{2}}$ и ${{R}_{2}}$. В этом случае не существует решения задачи первого типа, так как не существует элементарного решения из ${{I}_{2}}$ в ${{R}_{2}}$, проходящего через точку ${{O}_{2}}$ (рис. 5б). Анализ возможных решений показывает, что существует единственная траектория из ${{I}_{2}}$ в ${{R}_{2}}$ (рис. 3б), составленная из элементарных решений {${{O}^{ - }} = {{I}_{2}}$, $O = {{O}_{2}}$, ${{O}^{ + }} = {{O}_{{12}}}$} (рис. 5б) и {${{O}^{ - }} = {{O}_{2}}$, $O = {{O}_{{12}}}$, ${{O}^{ + }} = {{R}_{2}}$} (рис. 5г). В данном решении задачи второго типа от области закачки (x = 0) в пласт (x > 0) распространяются три сильных разрыва. С самым быстрым разрывом, как и в решении первого типа, распространяются возмущения концентрации. Причем за разрывом течет насыщенный раствор соли: $\xi = \tau = {{\tau }_{ * }}({{T}_{0}})$. Далее между медленными разрывами 1 и 2 (${{W}_{1}}{{t}_{ * }} \leqslant x \leqslant {{W}_{2}}{{t}_{ * }}$, ${{W}_{1}} < {{a}_{T}}$, ${{W}_{2}} = {{a}_{T}}$) распространяется область двухфазного течения. В ней насыщенность твердой фазы больше нуля (s > 0). При этом концентрации $\xi > {{\tau }_{ * }}({{T}_{i}})$ и $\tau > {{\tau }_{ * }}({{T}_{i}})$ ($\xi > \tau $) достигают максимальных значений, превышающих ${{\xi }_{i}}$ и ${{\tau }_{i}}$. За самым медленным разрывом 1, $x < {{W}_{1}}{{t}_{ * }}$, происходит течение нагнетаемого раствора соли (${{\xi }_{i}} > {{\tau }_{i}}$). Фазовые превращения сконцентрированы на разрывах: на фронте 1 соль растворяется и вместе с жидкостью переносится далее в пласт, выпадая в осадок на фронте 2. В решении второго типа температура рвется только на внутреннем разрыве. Так как точка ${{O}_{{12}}}$ лежит на линии термодинамического равновесия (рис. 3б), то граница между областями двухфазного и однофазного течения между разрывами 2 и 3 строго не определена. На волновой картине этой границе может соответствовать любая прямая 23, выпущенная из начала координат и расположенная между прямыми линиями 2 и 3 (рис. 6б). Предполагая, что она не совпадает с прямыми линиями 2 и 3, получим, что все разрывы в построенном решении эволюционные. Действительно, от разрыва 1 уходит характеристика $a_{T}^{ + } > {{W}_{1}}$, от разрыва 2 – $a_{\xi }^{ - } < {{W}_{2}}$ и от 3 – $a_{T}^{ - } < {{W}_{3}}$ (рис. 6б).
Ограничим на фазовой плоскости области параметров, соответствующих решениям различного типа. Сначала зафиксируем начальные параметры в пласте, т.е. положение точки ${{R}_{1}}$ (рис. 3а). Тогда, если точка ${{I}_{1}}$, соответствующая параметрам нагнетаемой в пласт смеси, находится ниже горизонтальной штриховой прямой 2, пересекающая линию термодинамического равновесия 1 в точке $B$, то реализуется решение первого типа. Если же ${{I}_{1}}$ находится выше данной прямой, то реализуется решение второго типа. Таким образом, при фиксированном состоянии ${{R}_{1}}$ область параметров, соответствующая решению второго типа, ограничена прямыми 1 и 2 правее и выше точки $B$, а остальная подобласть ниже прямой 1 соответствует решению первого типа. Теперь зафиксируем параметры закачиваемой жидкости – состояние ${{I}_{2}}$ (рис. 3б). Тогда, если состояние ${{R}_{2}}$ находится левее вертикальной штрихованной прямой 3, пересекающей линию термодинамического равновесия в точке $B$, то реализуется решение второго типа, а правее – решение первого типа. Таким образом, при фиксированном состоянии ${{I}_{2}}$ область параметров, соответствующая решению второго типа, ограничена прямыми 1 и 3 левее и ниже точки $B$, а остальная подобласть ниже прямой 1 соответствует решению первого типа.
ЗАКЛЮЧЕНИЕ
Решена задача Римана, описывающая закачку нагретого раствора соли в холодный водонасыщенный пласт. Показано, что если нагнетаемый раствор достаточно недонасыщен (${{\xi }_{i}} \ll {{\tau }_{ * }}({{T}_{i}})$), то реализуется решение задачи первого типа, содержащее только два разрыва – быстрый фронт концентрации и медленный фронт температуры. Если же нагнетаемый раствор близок к состоянию насыщения (${{\xi }_{i}} \to {{\tau }_{ * }}({{T}_{i}})$), то реализуется решение задачи второго типа, содержащее три разрыва, из которых два самых медленных ограничивают область осаждения соли, а температура изменяется только на внутреннем разрыве. Показано, что решение задачи определяется двумя параметрами подобия. Разработан геометрический метод, позволяющий на фазовой плоскости ограничить области различных типов решений и определить тип и количественные характеристики распределений параметров для заданных значений параметров подобия. Исследовано поведение решений задачи на фазовой плоскости и показано, что возможны только два описанных типа решения задачи, причем для любых начальных и граничных условий существует не более одного решения.
Список литературы
Blundy J., Mavrogenes J., Tattitch B., Sparks S., Gilmer A. Generation of porphyry copper deposits by gas–brine reaction in volcanic arcs // Nat. Geosci. 2015. V. 8. P. 235–240. https://doi.org/10.1038/ngeo2351
Weis P. The dynamic interplay between saline fluid flow and rock permeability in magmatic–hydrothermal systems // Geofluids 2015. V. 15. P. 350–371. https://doi.org/10.1111/gfl.12100
Afanasyev A., Blundy J., Melnik O., Sparks S. Formation of magmatic brine lenses via focused fluid-flow beneath volcanoes // Earth Planet. Sci. Lett. 2018. V. 486. P. 119–128. https://doi.org/10.1016/j.epsl.2018.01.013
Афанасьев А.А., Мельник О.Э. Численное моделирование формирования линзы концентрированного рассола при дегазации магматического очага // Изв. РАН. МЖГ. 2017. № 3. С. 88–95. https://doi.org/10.7868/S0568528117030100
Цыпкин Г.Г. Накопление и выпадение солей в осадок при испарении и движении грунтовых вод // Изв. РАН. МЖГ. 2003. № 6. С. 84–93.
Battistelli A., Calore C., Pruess K. The simulator TOUGH2/EWASG for modelling geothermal reservoirs with brines and noncondensible gas // Geothermics. 1997. V. 26. P. 437–464. https://doi.org/10.1016/S0375-6505(97)00007-2
Калоре К., Цыпкин Г.Г. Численное моделирование образования осадка при кипении раствора соли в геотермальном резервуаре // Изв. РАН. МЖГ. 2015. № 4. С. 110–118.
Tsypkin G.G., Woods A.W. Precipitate formation in a porous rock through evaporation of saline water // J. Fluid. Mech. 2005. V. 537. P. 35–53. https://doi.org/10.1017/S0022112005005124
Афанасьев A.А. Математическая модель неизотермической многофазной фильтрации бинарной смеси // Изв. РАН. МЖГ. 2011. № 1. С. 104–115.
Beek W.J., Mutzall M.K., Van Heuven J.W. Transport Phenomena / 2nd ed. N.Y.: Wiley, 1999. 342 p.
Driesner T. The system H2O–NaCl. Part II: Correlations for molar vol-ume, enthalpy, and isobaric heat capacity from 0 to 1000°C, 1 to 5000 bar, and 0 to 1 XNaCl // Geochim. Cosmochim. Acta 2007. V. 71. P. 4902–4919. https://doi.org/10.1016/j.gca.2007.05.026
Куликовский А.Г., Свешникова Е.И. Нелинейные волны в упругих средах. М.: Моск. лицей, 1998. 412 с.
Buckley S.E., Leverett M.C. Mechanism of fluid displacement in sands // Trans. AIME. 1942. V. 146. P. 107–116.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика жидкости и газа


