1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 4, 2019

Известия РАН. Механика жидкости и газа, 2019, № 4, стр. 111-118

ОТРАЖЕНИЕ ПОТОКА РАЗРЕЖЕННОГО ГАЗА ОТ СТЕНКИ С ОТВЕРСТИЕМ И ИСТЕЧЕНИЕ ГАЗА В ВАКУУМ

В. А. Титарев a, *, А. А. Фролова a, **, Е. М. Шахов a, ***

a ФИЦ Информатика и управление РАН
Москва, Россия

* E-mail: titarev@ccas.ru
** E-mail: aafrolova@yandex.ru
*** E-mail: shakhov@ccas.ru

Поступила в редакцию 26.06.2018
После доработки 16.01.2019
Принята к публикации 16.01.2019

Полный текст (PDF)

Аннотация

На основе кинетической S-модели решается двумерная нестационарная задача об отражении равномерного сверхзвукового потока разреженного газа, падающего нормально на стенку с отверстием и истечение газа через отверстие (щель и канал) в вакуум. Изучается влияние щели на характер отражения, на скорость отраженной ударной волны от стенки и на формирование струи газа, истекающего в вакуум, в зависимости от скорости падающего потока, степени разреженности газа и от условий на стенке. Исследуется также влияние толщины стенки, то есть длины канала, через который происходит истечение. В качестве основной интегральной характеристики рассчитывается расход газа через отверстие. Прослеживается выход процесса истечения на стационарный режим отражения. Кинетическое уравнение решается численно консервативным методом конечных разностей второго порядка аппроксимации по всем переменным.

Ключевые слова: разреженный газ, кинетическая S-модель, ударная волна, истечение в вакуум, схема Колгана

В последние годы значительно возрос интерес к нестационарным течениям разреженного газа, в частности, в связи с возможностью создания высокоскоростных молекулярных пучков импульсного типа с использованием малогабаритных бездиафрагменных ударных труб [1]. Первые попытки численного моделирования течений в установках подобного типа [2, 3] были предприняты почти сразу после опубликования экспериментальных результатов [1]. Однако результаты численного анализа [2, 3] лишь отдаленно и качественно отражают черты процессов, регистрируемых в опытах. Отмечается сильное затухание ударных волн, распространяющихся по газу, в связи с чем исследования ограничивались каналами и трубами сравнительно небольшой длины, порядка десяти, в лучшем случае нескольких десятков калибров. По-видимому, по этой причине вопросы истечения газа через отверстие в задней стенке трубы вообще не рассматривались в цитированных работах. Между тем эксперименты проводились в трубах длиной в сотни калибров. Столь сильного затухания ударных волн не наблюдалось, число Маха головной волны почти всюду было постоянным на основном участке трубы и слабо затухающим на заключительном ее интервале.

Рассогласование результатов численного анализа и измерений в опытах побуждает к более детальному изучению процессов в ударной трубе периодического действия методами вычислительной математики. Некоторые аспекты этих процессов изучались в работах [4–7]. Отметим также, что начало исследованиям двумерных течений, возникающих вследствие распада разрыва давления в покоящемся газе, расположенном в пространстве между двумя параллельными пластинами, было положено в [8, 9].

Данная работа посвящена изучению заключительной стадии одного периода периодического процесса, а именно, процессу истечения газа через отверстие в задней стенке трубы в вакуум после отражения падающей ударной волны от этой стенки с отверстием. Задача решается в упрощенной постановке. Предполагается, во-первых, что на стенку падает равномерный поток, соответствующий равномерному потоку за падающей ударной волной нулевой толщины. Во-вторых, считается, что боковые стенки трубы отсутствуют. Второе допущение оправдано для начальной фазы истечения, когда возмущения от боковых стенок еще не влияют на характер истечения, и премлемо для не слишком больших времен от начала процесса. Более существенным является первое допущение. В дальнейшем планируется снять оба ограничения.

Цель работы состоит в том, чтобы проследить влияние отверстия на характер отражения потока от стенки и на характер формирования истекающей струи в вакуум в зависимости от скорости и температуры набегающего потока, точнее, от отношения давления перед падающей ударной волной к давлению в камере высокого давления по теории идеальной ударной трубы и от степени разреженности газа, то есть от числа Кнудсена. В случае стенки ненулевой толщины вместо щели рассматривается короткий канал. Наличие канала и профиля его стенок вносит свои особенности в картину истечения. В работе изучается влияние толщины стенки в простейшем варианте, когда канал образован двумя пластинами, параллельными скорости набегающего потока. В этом случае возникает еще один параметр задачи, длина канала. Влияние этого параметра также исследуется в работе.

1. ФОРМУЛИРОВКА ЗАДАЧИ

Рассматривается нестационарное двумерное течение одноатомного разреженного газа, возникающее при отражении равномерного сверхзвукового потока, набегающего на стенку с отверстием. Поток направлен против нормали к стенке.

В начальный момент t = 0 газ занимает полупространство $ - \infty < x < 0$ и имеет постоянные параметры ${{n}_{{II}}}$, ${{u}_{{II}}}$, ${{p}_{{II}}}$, ${{T}_{{II}}}$ (числовая плотность, скорость, давление и температура соответственно) за падающей ударной волной, отвечающие параметрам газа ${{n}_{I}}$, ${{u}_{I}} = 0$, ${{p}_{I}}$, ${{T}_{I}}$ перед ударной волной. При этом ударная волна возбуждена распадом разрыва в покоящемся газе с параметрами ${{n}_{I}}$, ${{p}_{I}}$, ${{T}_{I}}$ и ${{n}_{{IV}}}$, ${{p}_{{IV}}}$, ${{T}_{{IV}}} = {{T}_{I}}$, с отношением давления ${{p}_{{IV}}}{\text{/}}{{p}_{I}}$. Таким образом, за начальный момент времени принят момент, когда ударная волна достигла плоскости x = 0.

Стенка толщины L расположена между плоскостями $0 < x < L$ и имеет отверстие шириной $2h$ в виде канала $ - h < y < h$ или щели при L = 0. Первоначально в канале и в полупространстве $x > L$ газа нет, пустота (вакуум). При x = 0 располагается диафрагма, отделяющая газ от вакуума. В момент t = 0 диафрагма убирается и начинается процесс истечения газа в вакуум. Одновременно происходит отражение потока от стенки. Взаимодействие этих двух процессов и является предметом исследования. Исследуются выход на стационарный режим истечения и формирование газовой струи, истекающей в вакуум.

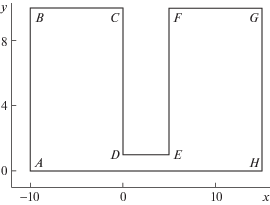
При решении задачи используется симметрия течения в плоскости $xy$ и строится решение в полуплоскости $y \geqslant 0$. Окончательная геометрия задачи представлена на рис. 1. Состояние разреженного газа в точке $(x,y)$ плоскости xOy в момент времени $t$ определяется функцией распределения молекул по скоростям $f(t,x,y,{\mathbf{\xi }})$, где ${\mathbf{\xi }} = ({{\xi }_{x}},{{\xi }_{y}},{{\xi }_{z}})$ компоненты вектора молекулярной скорости по направлениям $(x,y,z)$ соответственно. В дальнейшем вводятся безразмерные величины. В качестве масштабов длины, скорости, времени, плотности, температуры, потока тепла, функции распределения и вязкости используются величины в покоящемся газе перед падающей ударной волной

$h,\quad {{\beta }_{I}},\quad \frac{h}{{{{\beta }_{I}}}},\quad {{n}_{I}},\quad {{T}_{I}},\quad m{{n}_{I}}\beta _{I}^{3},\quad {{n}_{I}}\beta _{I}^{{ - 3}},\quad {{\mu }_{I}} = \frac{5}{{16}}m{{n}_{I}}\sqrt \pi {{\beta }_{I}}{{\lambda }_{I}}$
Рис. 1.

Геометрия задачи в плоскости xy.

Здесь ${{\beta }_{I}} = \sqrt {2R{{T}_{I}}} $ – наиболее вероятная скорость молекул, ${{\lambda }_{I}}$ – средняя длина свободного пробега, соответствующая параметрам покоящегося газа ${{n}_{I}}$, ${{T}_{I}}$. Ниже все безразмерные величины обозначены теми же буквами, что и размерные.

Предполагается, что функция распределения удовлетворяет уравнению Больцмана с оператором столкновений в форме S-модели [10]

(1.1)
$\begin{array}{*{20}{c}} {\frac{{\partial f}}{{\partial t}} + {{\xi }_{x}}\frac{{\partial f}}{{\partial x}} + {{\xi }_{y}}\frac{{\partial f}}{{\partial y}} = J,\quad J = \nu ({{f}^{ + }} - f),\quad \nu = {{\delta }_{I}}\frac{P}{\mu }} \\ {{{f}^{ + }} = {{f}_{M}}\left( {1 + \frac{8}{5}(1 - Pr){{S}_{\alpha }}{{c}_{\alpha }}\left( {{{c}^{2}} - \frac{5}{2}} \right)} \right),\quad {{f}_{M}} = \frac{n}{{{{{(\pi T)}}^{{3/2}}}}}\exp ( - {{c}^{2}})} \\ {{\mathbf{S}} = \frac{q}{{n{{T}^{{3/2}}}}},\quad {\mathbf{c}} = \frac{{\mathbf{v}}}{{\sqrt T }},\quad {\mathbf{v}} = {\mathbf{\xi }} - {\mathbf{u}}} \end{array}$

Индексы 1, 2, 3 соответствуют направлениям осей $x$, $y$, $z$. Предполагается суммирование по повторяющимся греческим индексам. Параметр разреженности δI, входящий в модельный интеграл столкновений, обратно пропорционален числу Кнудсена Kn, определенному по длине свободного пробега λI

${{\delta }_{I}} = \frac{{h{{p}_{I}}}}{{\mu ({{T}_{I}}){{\beta }_{I}}}} = \frac{8}{{5\sqrt \pi }}\frac{1}{{{\text{Kn}}}}$

Входящие в уравнение (1.1) макроскопические величины, такие как числовая плотность $n$, температура T, давление p, средняя скорость газа ${\mathbf{u}} = ({{u}_{1}},{{u}_{2}},{{u}_{3}})$ и поток тепла ${\mathbf{q}} = ({{q}_{1}},{{q}_{2}},{{q}_{3}})$, выражаются через функцию распределения в виде интегралов по пространству молекулярных скоростей

$\left( {n,n{\mathbf{u}},\frac{3}{2}nT + n{{u}^{2}},{\mathbf{q}}} \right) = \int {\left( {1,{\mathbf{\xi }},{{\xi }^{2}},\frac{1}{2}{\mathbf{v}}{{v}^{2}}} \right)} fd{\mathbf{\xi }},\quad p = nT$

Начальные условия имеют вид

$\begin{array}{*{20}{c}} {f(0,x,y,{\mathbf{\xi }}) = \frac{{{{n}_{{II}}}}}{{{{{(\pi {{T}_{{II}}})}}^{{3/2}}}}}exp\left( { - \frac{{{{{({\mathbf{\xi }} - {{{\mathbf{u}}}_{{II}}})}}^{2}}}}{{{{T}_{{II}}}}}} \right),}&{x < 0} \\ {f(0,x,y,{\mathbf{\xi }}) = 0,}&{x \geqslant 0} \end{array}$

Постановка граничных условий имеет следующий вид. На горизонтальной границе y = 0 (сегмент AH) ставится условие зеркального отражения молекул. На стенке канала (сегмент DE), а также на вертикальных стенках обоих резервуаров (CD и EF) используется граничное условие диффузного отражения молекул при полной тепловой аккомодации с температурой стенок ${{T}_{w}}$. При этом температура стенок полагается постоянной и равной начальной температуре газа ${{T}_{w}} = {{T}_{I}} \equiv 1$

${{f}_{w}}(t,x,y,{\mathbf{\xi }}) = \frac{{{{n}_{w}}}}{{{{{(\pi )}}^{{3/2}}}}}exp( - {{\xi }^{2}}),\quad {{\xi }_{n}} > 0\quad {{n}_{w}} = 2\sqrt \pi {{N}_{i}},\quad {{N}_{i}} = - \int\limits_{{{\xi }_{n}} < 0} {{\xi }_{n}}fd{\mathbf{\xi }}$

Здесь ${{n}_{w}}(t,{\mathbf{x}})$ – плотность отраженных молекул (определяется условиями непротекания), ξn – проекция вектора скорости молекулы ξ на внешную единичную нормаль к поверхности.

При численном счете на достаточно удаленных внешних контурах области задается функция распределения для молекул, входящих в расчетную область. При $x,y \to \infty $ (сегменты FG, GH) полагается f = 0. На границах AB, BC ($x \to - \infty $, $y \to \infty $) задается локально-максвелловская функция с параметрами набегаюшего потока ${{n}_{{II}}}$, ${{u}_{{II}}}$, ${{T}_{{II}}}$.

Интегральной характеристикой течения является зависимость от времени расхода массы через отверстие. Удобно использовать нормированное значение расхода, которое в безразмерных переменных определим следующим образом

(1.2)
$Q = \frac{{\dot {M}(t)}}{{{{{\dot {M}}}_{\infty }}}},\quad \dot {M}(t) = \int\limits_0^1 \rho (t,0,y){{u}_{x}}(t,0,y)dy,\quad {{\dot {M}}_{\infty }} = {{n}_{{II}}}{{u}_{{II}}}$

2. РЕЗУЛЬТАТЫ

Задача решалась численно с помощью квазимонотонного явного метода второго порядка аппроксимации кинетического уравнения [11, 12]. Детали приложения данного метода к нестационарным плоским задачам могут быть найдены в [7] и здесь не приводятся. Расчеты проводились с помощью параллельного трехмерного кода “Несветай-3Д” [13], разработанного ранее первым автором. Использовалась трехмерная пространственная сетка, в которой по направлению z вводилось разбиение из 4 расчетных точек и выставлялись граничные условия зеркального отражения молекул в направление оси Oz. Единственным существенным отличием от предыдущих работ является использование ограничителя наклонов типа minmod, предложенного в [14]. Данная версия ограничителя показала себя более надежной для расчета истечения в вакуум на неравномерной пространственной сетке, чем более поздние модификации других авторов.

Решение задачи зависит от длины канала $L{\text{/}}h$, параметра разреженности покоящегося газа ${{\delta }_{I}}$ и отношения начальных давлений ${{p}_{I}}{\text{/}}{{p}_{{IV}}}$. Приводимые ниже численные результаты получены для $\mu = \sqrt T $, что соответствует молекулам-шарам. Расчеты проводились для ${{p}_{I}}{\text{/}}{{p}_{{IV}}} = 100$. При этом число Маха возникающей ударной волны ${{M}_{s}} = 2.195$, безразмерные параметры газа за фронтом ${{n}_{{II}}} = 2.465$, ${{u}_{{II}}} = 1.191$, ${{T}_{{II}}} = 2.341$. Рассматривалось четыре варианта геометрии: $L{\text{/}}h$ = 0 (щель), 1, 5 и одномерное отражение газа от плоской стенки x = 0 при отсутствии отверстия.

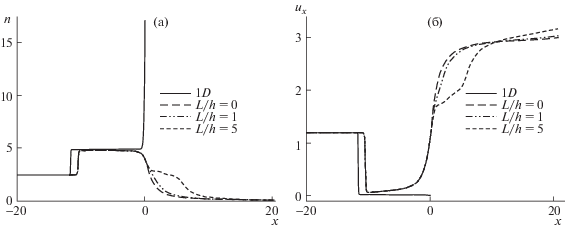
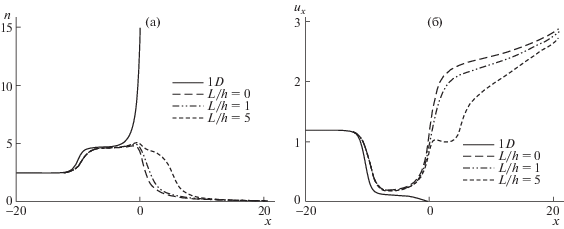
Анализ результатов начнем с рассмотрения влияния правого резервуара на скорость отраженной ударной волны. На рис. 2 и рис. 3 представлено распределение плотности и скорости газа по оси $Ox$ для момента времени t = 10 и всех четырех вариантов геометрии. В одномерном случае наблюдается типичная картина отражения ударной волны от холодной стенки [15]. При этом скорость отраженной волны в кинетическом решении заметно меньше, чем в решении уравнений Эйлера. При наличии правого резервуара скорость отраженной волны на оси симметрии заметно падает. Величина скорости волны не зависит от длины канала $L{\text{/}}h$: при x < 0 кривые зависимости макроскопических величин от координаты $x$ практически совпадают. При этом в правом резервуаре имеет место заметное торможение потока стенками канала для $L{\text{/}}h = 5$. Особенно хорошо оно видно в профиле скорости. При большем значении параметра разреженности ${{\delta }_{I}} = 100$ режим течения в левом резервуаре близок к сплошной среде. Одномерное решение кинетического уравнения состоит из кусочно-постоянных значений вплоть до пристеночного слоя, в котором видны большие градиенты макроскопических величин. Различия кривых плотности и скорости для двухмерного решения с отверстием/каналом становятся более заметными. Так, стенки канала заметно тормозят поток уже для $L{\text{/}}h = 1$. Для $L{\text{/}}h = 5$ внутри канала формируется профиль волны, напоминающий ударную. Таким образом, длина канала оказывает существенное влияние на картину течения в правом резервуаре, но практически не меняет скорость отраженной волны.

Рис. 2.

Распределение плотности (а) и скорости газа вдоль оси ox (б) для t = 10, δI = 1 и различных значений L/h. Кривая 1D относится к одномерному решению.

Рис. 3.

То же, что на рис. 2, но δI = 100.

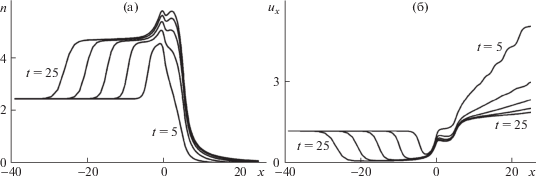
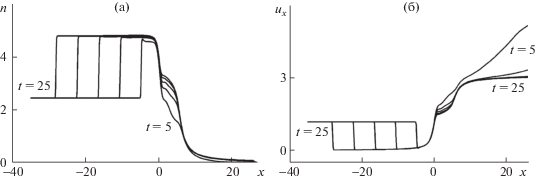
На рис. 4 представлены кривые распределения плотности и скорости газа вдоль оси канала для $L{\text{/}}h = 5$, моментов времени $t = 5$, 10, 15, 20, 25 и параметра разреженности ${{\delta }_{I}} = 1$. В профилях видна отраженная ударная волна, бегущая по левому резервуару, и распространяющаяся в вакуум волна разрежения. Торможение газа стенками канала проявляется в горизонтальных участках профилей скорости при $0 \leqslant x \leqslant 5$. В области правого резервуара имеет место разгон газа до сверхзвуковых скоростей. Аналогичные кривые для ${{\delta }_{I}} = 100$ представлены на рис. 5. Фронт ударной волны становится более крутым и приближается к газодинамическому; его разрешение ограничено разрешением расчетной сетки. В правом резервуаре с ростом времени значения макропараметров быстро выходят на стационарный режим и при $t \geqslant 15$ совпадают.

Рис. 4.

Плотность (а) и скорость (б) газа: t = 5, 10, 15, 20, 25; δI = 1, L/h = 5.

Рис. 5.

То же, что на рис. 4: δI = 100 и L/h = 5.

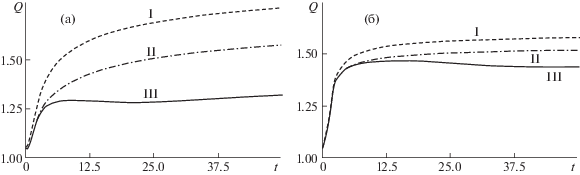
На рис. 6 представлены кривые зависимости расхода массы $Q$ через отверстие (см. формулу 1.2) от времени для обоих значений параметра разреженности ${{\delta }_{I}} = 1$, 100. Видно, что для истечения через достаточно длинный канал $L{\text{/}}h = 5$ расход массы имеет четко выраженный максимум на умеренных временах, после чего стремится к стационарному значению. Для режима ${{\delta }_{I}} = 100$ такое значение достигается при $t \approx 35$, в то время как для ${{\delta }_{I}} = 1$ имеет место очень медленный рост даже для $t = 50$. В другом предельном случае – истечения через щель $L{\text{/}}h = 0$ – значение расхода устанавливается со временем гораздо медленнее, монотонно возрастая с ростом значения t. При истечении через короткий канал $L{\text{/}}h = 1$ расход массы ведет себя качественно как в случае истечения через щель.

Рис. 6.

Зависимость расхода Q (см. формулу 1.2) от времени: δI = 1 (а), 100 (б); L/h = 0 (I), 1 (II), 5 (III).

В заключение рассматривается картина поля течения для случая $L{\text{/}}h = 5$, момента времени $t = 20$ и ${{\delta }_{I}} = 100$. На рис. 7 представлены линии уровня плотности газа и потока массы $n{{u}_{x}}$ вблизи канала. Хорошо видны отраженная ударная волна, а также сложная картина течения в канале и вблизи его границ.

Рис. 7.

Плотность (а) и поток массы nux (б): t = 20, δI = 100, L/h = 5.

ЗАКЛЮЧЕНИЕ

Представлено численное исследование на основе кинетической $S$-модели задачи об отражении равномерного сверхзвукового потока разреженного газа, падающего нормально на стенку с отверстием и истечение газа через отверстие (щель и канал) в вакуум. Показано, что присутствие отверсия снижает скорость отражения ударной волны от диффузной стенки, при этом длина канала влияет только на картину течения в области первоначального вакуума. Присутствие канала (стенки) приводит к снижению расхода массы и более быстрому выходу процесса истечения на стационарный режим.

Работа выполнена при финансовой поддержке РФФИ, проект 16-01-00489.

Список литературы

  1. Miyoshi N., Nagata S., Kinefuchi I., Shimizu K., Takagi S., Matsumoto Y. Development of ultra small shock tube for high energy molecular beam source // 26th Internat. Symp. Rarefied Gas Dynamics. AIP Conf. Proc. 1084., P. 557–562. Melville, New York, 2009.

  2. Zeitoun D.E., Graur I.A., Burtschell Y., Ivanov M.S., Kudrayvtsev A.N., Bondar Ye.A. Continuum and kinetic simulation of shock wave propagation in long microchannel // 26th Internat. Symp. Rarefied Gas Dynamics. AIP Conf. Proc. 1084., P. 964–969. Melville, New York, 2009.

  3. Клосс Ю.Ю., Черемисин Ф.Г., Шувалов П.В. Решение уравнения Больцмана для нестационарных течений с ударными волнами в узких каналах // Журн. вычисл. матем. и матем. физ. 2010. Т. 50. № 6. С. 1148–1158.

  4. Конопелько Н.А., Титарев В.А., Шахов Е.М. Торможение разреженного газа в микроканале при расширении в вакуум // Изв. РАН. МЖГ. 2015. № 2. С. 129–141.

  5. Конопелько Н.А., Титарев В.А., Шахов Е.М. Нестационарное течение разреженного газа в микроканале из-за распада разрыва давления // Журн. вычисл. матем. и матем. физ. 2016. V. 56. № 3. С. 476–489.

  6. Конопелько Н.А., Шахов Е.М. Развитие и установление истечения разреженного газа из резервуара через плоский канал в вакуум // Журн. вычисл. матем. и матем. физ. 2017. V. 57. № 10. С. 1722–1733.

  7. Титарев В.А., Шахов Е.М. Нестационарное течение разреженного газа с ударной волной в канале // Изв. РАН. МЖГ. 2018. № 1. С. 147–155.

  8. Ларина И.Н., Рыков В.А., Шахов Е.М. Развитие течения разреженного газа между параллельными пластинами из-за начального разрыва давления // Докл. Академии наук. 1995. Т. 343. № 4. С. 482–485.

  9. Ларина И.Н., Рыков В.А., Шахов Е.М. Нестационарные течения разреженного газа между параллельными пластинами // Изв. РАН. МЖГ. 1997. № 2. С. 165–173.

  10. Шахов Е.М. Об обобщении релаксационного кинетического уравнения Крука // Изв. АН СССР. МЖГ. 1968. № 5. С. 142–145.

  11. Титарев В.А. Неявный численный метод расчета пространственных течений разреженного газа на неструктурированных сетках // Журн. вычисл. матем. и матем. физ. 2010. Т. 50. № 10. С. 1811–1826.

  12. Titarev V.A. Efficient deterministic modelling of three-dimensional rarefied gas flows // Commun. Comput. Phys. 2012. V. 12. № 1. P. 161–192.

  13. Титарев В.А. Программный комплекс моделирования трехмерных течений одноатомного разреженного газа Несветай-3Д / Свидетельство о государственной регистрации программы для ЭВМ 2017613138 от 06.06.2017. 2017.

  14. Колган В.П. Применение принципа минимальных значений производной к построению конечно-разностных схем для расчета разрывных течений газовой динамики // Учен. зап. ЦАГИ. 1972. Т. 3. № 6. С. 68–77.

  15. Кудиш И.И., Рыков В.А. Отражение ударной волны от твердой стенки // Журн. вычисл. матем. и матем. физ. 1973. Т. 13. № 5. С. 1288–1297.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал