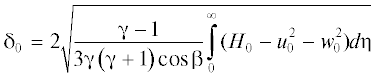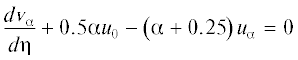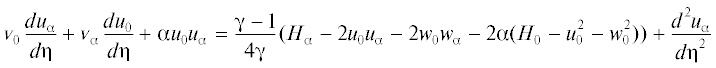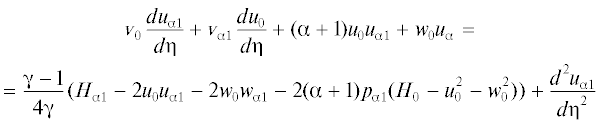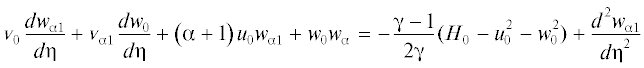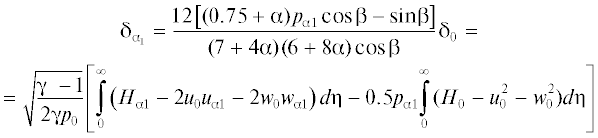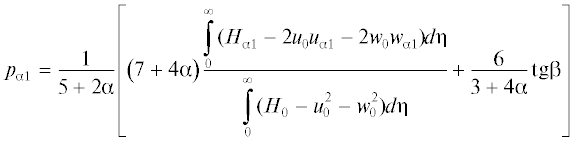Известия РАН. Механика жидкости и газа, 2019, № 5, стр. 59-69

О влиянии температурного фактора на распространение возмущений при гиперзвуковом обтекании скользящей пластины

Г. Н. Дудин^a, *, В. Я. Нейланд^a

^a Центральный аэрогидродинамический институт им. проф. Н.Е. Жуковского
Московская обл., Жуковский, Россия

Поступила в редакцию 13.12.2018
После доработки 18.12.2018
Принята к публикации 18.12.2018

DOI: 10.1134/S0568528119040042

Аннотация

Рассмотрено течение в пространственном ламинарном пограничном слое на скользящей пластине конечной длины на режиме сильного вязко-невязкого взаимодействия с гиперзвуковым потоком. В окрестности передней кромки проведены разложения функций течения в ряды в предположении, что на задней кромке пластины задается донное давление, величина которого зависит от поперечной координаты. Установлено, что в полученные разложения входит неопределенная функция и ее производная по поперечной координате. Сформулированы и численно решены соответствующие краевые задачи, найдены собственные числа и показано, что показатель степени в третьем члене разложения отличается от второго только на единицу. Исследовано влияние температуры поверхности пластины на характеристики течения и на индуцирование трехмерных возмущений.

Ключевые слова: пространственный пограничный слой, скользящая пластина, сильное взаимодействие, температурный фактор

Впервые автомодельное решение для течения около полубесконечной пластины на режиме сильного взаимодействия пограничного слоя с гиперзвуковым потоком получено в [1] с использованием формулы “касательного клина”. В более точной постановке исследование, учитывающее течение в ударном слое, было проведено в [2]. Автомодельное решение для режима сильного взаимодействия на полубесконечной скользящей пластине было найдено в [3]. Исследования двумерных течений в пограничном слое на пластине, оканчивающейся донным срезом, показали, что в случае сильного вязко-невязкого взаимодействия разложение функций течения в окрестности передней кромки не является единственным, а содержит некоторую константу [4–6]. При этом предполагалось, что задаваемое донное давление не изменяется по поперечной координате. В [4], где впервые была установлена неединственность, для вычисления индуцированного давления была использована формула касательного клина, а в [6] – решалась краевая задача с учетом ударного слоя. Существование неединственности решения на передней кромке объясняет возможность распространения возмущений против потока на всю длину пластины. Влияние определяющих параметров на значение собственного числа в случае двумерных течений изучено в [7]. В [8] было показано, что решение задачи вблизи передней кромки скользящей пластины также может быть не единственным. В [9, 10] было впервые исследовано течение в пограничном слое на пластине для режима сильного взаимодействия в случае, когда дополнительное условие на задней кромке зависит от поперечной координаты. Установлено, что в этом случае решение в окрестности передней кромки пластины не является единственным, а разложения для давления, энтальпии, продольной и нормальной компонент скорости в ряды зависят от некоторой, вообще говоря, произвольной функции, зависящей от поперечной координаты. Краевые задачи для определения членов разложения для поперечной компоненты скорости отделяются от основных систем уравнений, так как показатель степени для первого члена разложения равен собственному числу плюс единица, а для второго – удвоенному собственному числу плюс единица. При этом поперечный компонент скорости оказывается пропорциональным производной от указанной выше произвольной функции по поперечной координате. Показано, что в этом случае происходит перестройка двумерного пограничного слоя в трехмерный, но важно отметить, что образующееся поперечное течение не оказывает влияние на индуцированное давление, энтальпию, продольный и нормальный компоненты скорости. Совершенно иная картина течения в пограничном слое реализуется при обтекании скользящей пластины конечной длины, когда течение изначально является трехмерным. Первые результаты исследования обтекания скользящей пластины, когда дополнительное условие на ее задней кромке не является постоянным, а изменяется по размаху, кратко представлены в [11], где сформулированы и решены краевые задачи только для первых двух членов разложения и исследовано влияние угла скольжения на характеристики течения на теплоизолированной пластине.

В настоящей работе дополнительно сформулирована и решена краевая задача для третьих членов разложения. Установлено, что показатель степени этих членов разложения, причем для всех функций течения, на единицу больше, чем предыдущего, а множитель при этих членах разложения пропорционален производной от указанной выше произвольной функции по поперечной координате. Следовательно, наличие угла скольжения принципиально изменяет характер распространения возмущений в пространственном пограничном слое на пластине. В частности, в сечениях, в которых возмущение давления равно нулю, а градиент давления по размаху пластины не равен нулю, распространение возмущений будет определяться только третьими членами разложения. Следовательно, при достаточно больших значениях этих градиентов давления, именно они могут играть определяющую роль в распространении возмущений против потока.

1. ПОСТАНОВКА ЗАДАЧИ

Рассматривается обтекание при наличии угла скольжения бесконечной по размаху пластины заданной длины L на режиме сильного вязко-невязкого взаимодействия при постоянной температуре поверхности T_w. Газ считается совершенным с отношением удельных теплоемкостей γ = c_p/${{c}_{{v}}}$ и коэффициентом вязкости, линейно зависящим от температуры µ⁰/µ_∞ = c_∞T⁰/T_∞, где c_∞ = const, а индекс ∞ обозначает параметры в невозмущенном потоке. Компоненты вектора скорости u⁰, ${{{v}}^{0}}$, w⁰ в пространственном ламинарном пограничном слое направлены соответственно вдоль осей x⁰, y⁰, z⁰ декартовой системы координат, начало которой расположено на передней кромке пластины. Ось x⁰ направлена перпендикулярно передней кромки, а ось z⁰ – вдоль нее. Угол скольжения β – это угол между направлением невозмущенного потока и осью x⁰. Считается, что на задней кромке пластины при x⁰ = L задано распределение донного давления p$_{d}^{0}$(z⁰), которое зависит от поперечной координаты z⁰, причем характерный размер области изменения давления по поперечной координате порядка L₁. Отношение характерных линейных масштабов – N = L/L₁. Предполагается, что для проекции числа Маха на нормаль к передней кромке выполняется условие M_n = M_∞cosβ ≫ 1. Рассматривается предельный случай, когда в невозмущенном потоке V_∞ – скорость, ρ_∞ – плотность и H_∞ – энтальпия стремятся к постоянным значениям, а число Маха M_∞ → ∞. Тогда параметры в невозмущенном потоке: p_∞ – давление, a_∞ – скорость звука и T_∞ – температура стремятся к нулю.

Согласно гиперзвуковой теории малых возмущений [12] при M_n ≫ 1 и безразмерной толщине ламинарного пограничного слоя δ ≪ 1 в случае выполнения предположения о сильном взаимодействии M_nδ ≫ 1 индуцированное давление, создаваемое толщиной вытеснения, имеет порядок p⁰ ∼ p_∞${\text{M}}_{n}^{2}$δ². Так как температура газа внутри пограничного слоя порядка температуры торможения T₀, тогда из уравнения состояния получаем оценку для плотности ρ⁰ ∼ ρ_∞δ².

Исходя из равенства порядков главных инерционных и вязких членов уравнения импульса вдоль оси x⁰, получаем оценку для δ ∼ (Re₀)^–1/4, где Re₀ = ρ_∞V_∞L/μ₀ – число Рейнольдса, μ₀ – динамический коэффициент вязкости при температуре торможения. При обтекании скользящей пластины масштаб поперечного компонента скорости: w⁰ ∼ V_∞sinβ. Нормальный компонент скорости в данном случае – ${{{v}}^{0}}$ ∼ V_∞δ. Заметим, что при β = 0 скорость поперечного течения будет определяться только градиентом индуцированного давления по размаху пластины [9, 10].

При выполнении условия M_nδ ≫ 1 для определения индуцированного давления, создаваемого толщиной вытеснения, используется приближенная формула “касательного клина” [12]. В соответствии с оценками для ламинарного пространственного пограничного слоя в гиперзвуковом потоке [5, 12] вводятся следующие безразмерные переменные:

(1.1)

${{x}^{0}} = Lx,\quad {\text{ }}{{y}^{0}} = {\delta }Ly,\quad {{z}^{0}} = {{L}_{1}}z,\quad {{{\mu }}^{0}} = {{{\mu }}_{0}}{\mu }$

${\delta }_{e}^{0} = L{\delta }{{{\delta }}_{e}},\quad {{{\rho }}^{0}} = {{{\rho }}_{\infty }}{{{\delta }}^{2}}{\rho },\quad {{p}^{0}} = {{{\rho }}_{\infty }}V_{\infty }^{2}{{{\delta }}^{2}}{{p}_{*}},\quad p_{{^{d}}}^{0} = {{{\rho }}_{\infty }}V_{\infty }^{2}{{{\delta }}^{2}}{{p}_{{d*}}}$

${{u}^{0}} = {{V}_{\infty }}u,\quad {{w}^{0}} = {{V}_{\infty }}w,\quad {{{v}}^{0}} = {{V}_{\infty }}\delta {{{v}}_{*}},\quad {{H}^{0}} = 0.5V_{\infty }^{2}H,\quad H_{w}^{0} = 0.5V_{\infty }^{2}{{H}_{w}}$

Здесь H⁰ – полная энтальпия. Далее применяется преобразование А.А. Дородницына

(1.2)

${\lambda } = \int\limits_0^y {{\rho }dy} ,\quad {{{v}}_{{\delta }}} = {\rho }{{{v}}_{*}} + u\frac{{\partial {\lambda }}}{{\partial x}} + Nw\frac{{\partial {\lambda }}}{{\partial z}}$

Учитывая особенности поведения функций течения в окрестности передней кромки пластины, вводится преобразование переменных

(1.3)

${\lambda } = {{x}^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}}{\lambda *},\quad {{p}_{*}} = {{x}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}p\left( {x,z} \right),\quad {{p}_{{d*}}}\left( z \right) = {{p}_{d}}\left( z \right)$

${\rho } = {{x}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\rho {\text{*}}\left( {x,{\lambda *},z} \right),\quad {{{\delta }}_{{e*}}} = {{x}^{{{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4}}}}{{{\delta }}_{e}}(x,z),\quad {{{v}}_{\delta }} = {{x}^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 4}} \right. \kern-0em} 4}}}}\left( {{v}{\text{*}} - xu\frac{{\partial {\lambda *}}}{{\partial x}}} \right)$

В переменных (1.1)–(1.3) система уравнений ламинарного пространственного пограничного слоя принимает вид

(1.4)

$x\frac{{\partial u}}{{\partial x}} + \frac{{\partial {v}{\text{*}}}}{{\partial {\lambda *}}} + Nx\frac{{\partial w}}{{\partial z}} + \frac{u}{4} = 0$

$xu\frac{{\partial u}}{{\partial x}} + {v}{\text{*}}\frac{{\partial u}}{{\partial {\lambda *}}} + Nxw\frac{{\partial u}}{{\partial z}} = \frac{{{\gamma } - 1}}{{2{\gamma }}}(H - {{u}^{2}} - {{w}^{2}})\left( {\frac{1}{2} - \frac{x}{p}\frac{{\partial p}}{{\partial x}}} \right) + \frac{{2{\gamma }p}}{{{\gamma } - 1}}\frac{{{{\partial }^{2}}u}}{{\partial {\lambda }{{{\text{*}}}^{2}}}}$

$xu\frac{{\partial w}}{{\partial x}} + {v}{\text{*}}\frac{{\partial w}}{{\partial {\lambda *}}} + Nxw\frac{{\partial w}}{{\partial z}} = - N\frac{{{\gamma } - 1}}{{2{\gamma }}}(H - {{u}^{2}} - {{w}^{2}})\frac{x}{p}\frac{{\partial p}}{{\partial z}} + \frac{{2{\gamma }p}}{{{\gamma } - 1}}\frac{{{{\partial }^{2}}w}}{{\partial {\lambda }{{{\text{*}}}^{2}}}}$

$xu\frac{{\partial H}}{{\partial x}} + {v}{\text{*}}\frac{{\partial H}}{{\partial {\lambda *}}} + Nxw\frac{{\partial H}}{{\partial z}} = \frac{{2{\gamma }p}}{{{\gamma } - 1}}\left[ {\frac{1}{{\sigma }}\frac{{{{\partial }^{2}}H}}{{\partial {\lambda }{{{\text{*}}}^{2}}}} - \frac{{1 - {\sigma }}}{{\sigma }}\frac{{{{\partial }^{2}}({{u}^{2}} + {{w}^{2}})}}{{\partial {\lambda }{{{\text{*}}}^{2}}}}} \right]$

${\text{ }}p = \frac{{{\gamma } + 1}}{2}{{\left[ {\left( {\frac{3}{4}{{{\delta }}_{e}} + x\frac{{\partial {{{\delta }}_{e}}}}{{\partial x}}} \right)\cos {\beta }\,{\text{ + }}\,Nx\frac{{\partial {{{\delta }}_{e}}}}{{\partial z}}\sin {\beta }} \right]}^{2}}$

${{{\delta }}_{e}} = \frac{{{\gamma } - 1}}{{2{\gamma }p}}\int\limits_0^\infty {(H - {{u}^{2}} - {{w}^{2}})} d{\lambda *},\quad p\left( {x = 1,z} \right) = {{p}_{d}}\left( z \right)$

$\begin{gathered} {\lambda *} = 0{\text{: }}u = w = {v}* = 0,\quad H = {{H}_{w}} \\ {\lambda *} \to \infty {\text{: }}u \to \cos {\beta },\quad w \to \sin {\beta },\quad H \to 1\quad \left( {0 \leqslant x \leqslant 1,\left| z \right| < \infty } \right) \\ \end{gathered} $

Здесь σ – число Прандтля, H_w – полная энтальпия на поверхности пластины, а p_d(z) – безразмерное давление на задней кромке пластины. На передней кромке при x = 0 данная система трехмерных уравнений в частных производных вырождается в систему обыкновенных дифференциальных уравнений и ее решение позволяет найти начальные условия для решения системы (1.4). В результате получаем систему для нахождения автомодельного решения на полубесконечной скользящей пластине [3]. Краевая задача (1.4), определяющая течение на всем крыле и зависящая от параметров N, H_w, σ, γ и β может быть решена численно конечно-разностным методом [13]. Заметим, что в уравнения (1.4) в частности входит вторая производная ∂²δ_e/∂x², следовательно, данная система уравнений не является системой параболического типа. Следствием наличия этой второй производной является то, что возмущения, задаваемые на задней кромке пластины, могут распространяться вверх по потоку вплоть до передних кромок.

2. РАЗЛОЖЕНИЕ В ОКРЕСТНОСТИ ПЕРЕДНЕЙ КРОМКИ

Для исследования поведения функций течения в окрестности x = 0 можно преобразовать краевую задачу (1.4) и ввести новые переменные

(2.1)

${\lambda }* = \sqrt {\frac{{2{\gamma }}}{{{\gamma } - 1}}p\left( {x,z} \right)} { \eta },\quad {v}* = \sqrt {\frac{{2{\gamma }}}{{{\gamma } - 1}}p\left( {x,z} \right)} \left[ {{v} + \frac{{x{\eta }}}{{2p}}\left( {u\frac{{\partial p}}{{\partial x}} + Nw\frac{{\partial p}}{{\partial z}}} \right)} \right]$

После такого преобразовании в уравнениях переноса и неразрывности давление в знаменателе останется только при производной от индуцированного давления, что удобно при проведении в дальнейшем разложений. После подстановки (2.1) в краевую задачу (1.4) она приводится к виду

(2.2)

$x\frac{{\partial u}}{{\partial x}} + \frac{{\partial {v}}}{{\partial {\eta }}} + Nx\frac{{\partial w}}{{\partial z}} + \frac{x}{2}\left( {\frac{u}{p}\frac{{\partial p}}{{\partial x}} + N\frac{w}{p}\frac{{\partial p}}{{\partial z}}} \right) + \frac{u}{4} = 0$

$xu\frac{{\partial u}}{{\partial x}} + {v}\frac{{\partial u}}{{\partial {\eta }}} + Nxw\frac{{\partial u}}{{\partial z}} = \frac{{{\gamma } - 1}}{{2{\gamma }}}(H - {{u}^{2}} - {{w}^{2}})\left( {\frac{1}{2} - \frac{x}{p}\frac{{\partial p}}{{\partial x}}} \right) + \frac{{{{\partial }^{2}}u}}{{\partial {{{\eta }}^{2}}}}$

$xu\frac{{\partial w}}{{\partial x}} + {v}\frac{{\partial w}}{{\partial {\eta }}} + Nxw\frac{{\partial w}}{{\partial z}} = - N\frac{{{\gamma } - 1}}{{2{\gamma }}}(H - {{u}^{2}} - {{w}^{2}})\frac{x}{p}\frac{{\partial p}}{{\partial z}} + \frac{{{{\partial }^{2}}w}}{{\partial {{{\eta }}^{2}}}}$

$xu\frac{{\partial H}}{{\partial x}} + {v}\frac{{\partial H}}{{\partial {\eta }}} + Nxw\frac{{\partial H}}{{\partial z}} = \frac{1}{{\sigma }}\frac{{{{\partial }^{2}}H}}{{\partial {{{\eta }}^{2}}}} - \frac{{1 - {\sigma }}}{{\sigma }}\frac{{{{\partial }^{2}}({{u}^{2}} + {{w}^{2}})}}{{\partial {{{\eta }}^{2}}}}$

${\text{ }}p = \frac{{{\gamma } + 1}}{2}{{\left[ {\left( {\frac{3}{4}{{{\delta }}_{e}} + x\frac{{\partial {{{\delta }}_{e}}}}{{\partial x}}} \right)\cos {\beta } + Nx\frac{{\partial {{{\delta }}_{e}}}}{{\partial z}}\sin {\beta }} \right]}^{2}}$

${{{\delta }}_{e}} = \sqrt {\frac{{{\gamma } - 1}}{{2{\gamma }p}}} \int\limits_0^\infty {(H - {{u}^{2}} - {{w}^{2}})} d{\eta ,}\quad p\left( {x = 1,z} \right) = {{p}_{d}}\left( z \right)$

$\begin{gathered} {\eta } = 0{\text{: }}u = w = {v} = 0,\quad H = {{H}_{w}} \\ {\eta } \to \infty {\text{:}}\quad u \to \cos {\beta },\quad w \to \sin {\beta },\quad H \to 1\quad \left( {0 \leqslant x \leqslant 1,\left| z \right| < \infty } \right) \\ \end{gathered} $

Так как поперечное течение в пространственном пограничном слое при β ≠ 0 существует изначально, то, как показали детальные предварительные исследования, решение в окрестности передней кромки пластины можно искать в виде

(2.3)

$p\left( {x,z} \right) = {{p}_{0}} + {{p}_{{\alpha }}}\left( z \right){{x}^{{\alpha }}} + N\frac{{d{{p}_{{\alpha }}}\left( z \right)}}{{dz}}{{p}_{{{\alpha 1}}}}{{x}^{{{\alpha } + 1}}} + \ldots $

${{{\delta }}_{e}}\left( {x,z} \right) = {{{\delta }}_{0}} + {{{\delta }}_{{\alpha }}}\frac{{{{p}_{{\alpha }}}\left( z \right)}}{{{{p}_{0}}}}{{x}^{{\alpha }}} + \frac{N}{{{{p}_{0}}}}\frac{{d{{p}_{{\alpha }}}\left( z \right)}}{{dz}}{{\delta }_{{{\alpha 1}}}}{{x}^{{{\alpha } + 1}}} + \ldots $

$u(x,{\eta },z) = {{u}_{0}}({\eta }) + {{u}_{{\alpha }}}\left( {\eta } \right)\frac{{{{p}_{{\alpha }}}\left( z \right)}}{{{{p}_{0}}}}{{x}^{{\alpha }}} + \frac{N}{{{{p}_{0}}}}\frac{{d{{p}_{{\alpha }}}\left( z \right)}}{{dz}}{{u}_{{{\alpha 1}}}}\left( {\eta } \right){{x}^{{{\alpha } + 1}}} + \ldots $

$H(x,{\eta },z) = {{H}_{0}}({\eta }) + {{H}_{{\alpha }}}\left( {\eta } \right)\frac{{{{p}_{{\alpha }}}\left( z \right)}}{{{{p}_{0}}}}{{x}^{{\alpha }}} + \frac{N}{{{{p}_{0}}}}\frac{{d{{p}_{{\alpha }}}\left( z \right)}}{{dz}}{{H}_{{{\alpha 1}}}}\left( {\eta } \right){{x}^{{{\alpha } + 1}}} + \ldots $

${v}(x,{\eta },z) = {{{v}}_{0}}({\eta }) + {{{v}}_{{\alpha }}}\left( {\eta } \right)\frac{{{{p}_{{\alpha }}}\left( z \right)}}{{{{p}_{0}}}}{{x}^{{\alpha }}} + \frac{N}{{{{p}_{0}}}}\frac{{d{{p}_{{\alpha }}}\left( z \right)}}{{dz}}{{{v}}_{{{\alpha 1}}}}\left( {\eta } \right){{x}^{{{\alpha } + 1}}} + \ldots $

$w(x,{\eta },z) = {{w}_{0}}({\eta }) + {{w}_{{\alpha }}}\left( {\eta } \right)\frac{{{{p}_{{\alpha }}}\left( z \right)}}{{{{p}_{0}}}}{{x}^{{\alpha }}} + \frac{N}{{{{p}_{0}}}}\frac{{d{{p}_{{\alpha }}}\left( z \right)}}{{dz}}{{w}_{{{\alpha 1}}}}\left( {\eta } \right){{x}^{{{\alpha } + 1}}} + \ldots $

где индексом 0 обозначены члены разложений, соответствующие автомодельному решению для полубесконечной скользящей пластины [3], и предполагается, что собственное число α > 0. Заметим, что опущенные члены разложений имеют порядки О(x^{α + 2}), О(x^{α + 3}) и т.д., а также – О(x^2α), О(x^{2α + 1}) и т.д. Вид разложений (2.3) принципиально отличается от случая обтекания пластины при отсутствии угла скольжения. Во-первых, как показано в [9, 10], в разложении для поперечной компоненты скорости w(x, η, z) первые два коэффициента разложения (2.3) оказываются тождественно равными нулю, во-вторых – для остальных функций течения показатель степени в третьих членах разложения равен 2α, а в качестве множителя в них входит величина (p_α(z)/p₀)². Следовательно, при наличии угла скольжения третьи члены разложения (2.3) ∼ ~ x^{α + 1}dp_α(z)/dz могут существенно влиять на передачу возмущений против потока, особенно в тех сечениях z = const, где p_α(z) достаточно мало. Заметим также, что величина собственного числа α уменьшается с увеличением угла скольжения [11]. В общем случае, при поиске вида разложений (2.3), предполагалось, что коэффициенты для всех функций течения при членах, содержащих собственное число α и в следующих членах, являются функциями от двух переменных η и z. Но оказалось, что эти коэффициенты зависят только от координаты η и краевые задачи для определения собственного числа и для третьих членов разложения представляют собой системы обыкновенных дифференциальных уравнений.

Подставляя разложения (2.3) в систему уравнений и граничные условия (2.2) и собирая члены одного порядка, получаем соответствующие краевые задачи. Для первых членов разложения получается следующая система (автомодельная часть):

(2.4)

${{{v}}_{0}}\frac{{d{{u}_{0}}}}{{d{\eta }}} = \frac{{{\gamma } - 1}}{{4{\gamma }}}({{H}_{0}} - u_{0}^{2} - w_{0}^{2}) + \frac{{{{d}^{2}}{{u}_{0}}}}{{d{{{\eta }}^{2}}}}$

${{{v}}_{0}}\frac{{d{{H}_{0}}}}{{d{\eta }}} = \frac{1}{{\sigma }}\frac{{{{d}^{2}}{{H}_{0}}}}{{d{{{\eta }}^{2}}}} - \frac{{1 - {\sigma }}}{{\sigma }}\frac{{{{d}^{2}}(u_{0}^{2} + w_{0}^{2})}}{{d{{{\eta }}^{2}}}}$

${{{v}}_{0}}\frac{{d{{w}_{0}}}}{{d{\eta }}} = \frac{{{{d}^{2}}{{w}_{0}}}}{{d{{{\eta }}^{2}}}},\quad \frac{{d{{{v}}_{0}}}}{{d{\eta }}} + 0.25{{u}_{0}} = 0$

${{p}_{0}} = \frac{3}{4}\sqrt {\frac{{\left( {{\gamma } + 1} \right)\left( {{\gamma } - 1} \right)}}{{2{\gamma }}}} \cos {\beta }\int\limits_0^\infty {({{H}_{0}} - u_{0}^{2} - w_{0}^{2})} d{\eta }$

$\begin{gathered} {\eta } = 0{\text{:}}\,\,\,{{u}_{0}} = {{w}_{0}} = {{{v}}_{0}} = 0,\quad {{H}_{0}} = {{H}_{w}}{\text{;}} \\ {\eta } \to \infty {\text{:}}\,\,\,{{u}_{0}} \to \cos {\beta ,}\quad {{w}_{0}} \to \sin {\beta },\quad {{H}_{0}} \to 1 \\ \end{gathered} $

Краевая задача (2.4) имеет автомодельное решение, которое впервые при числе Прандтля σ = 1 получено в [3] и описывает течение около полубесконечной скользязщей пластины на режиме сильного взаимодействия или около скользящей пластины конечной длины, если на ее задней кромке задано донное давление, соответствующее местному давлению для автомодельного решения.

Соответственно для вторых членов разложения получаем краевую задачу, решение которой позволяет найти и собственное число α (неавтомодельная часть)

(2.5)

${{{v}}_{0}}\frac{{d{{H}_{{\alpha }}}}}{{d{\eta }}} + {{{v}}_{{\alpha }}}\frac{{d{{H}_{0}}}}{{d{\eta }}} + {\alpha }{{u}_{0}}{{H}_{{\alpha }}} = \frac{1}{{\sigma }}\frac{{{{d}^{2}}{{H}_{{\alpha }}}}}{{d{{{\eta }}^{2}}}} - 2\frac{{1 - {\sigma }}}{{\sigma }}\frac{{{{d}^{2}}\left( {{{u}_{0}}{{u}_{{\alpha }}} + {{w}_{0}}{{w}_{{\alpha }}}} \right)}}{{d{{{\eta }}^{2}}}}$

${{{v}}_{0}}\frac{{d{{w}_{{\alpha }}}}}{{d{\eta }}} + {{{v}}_{{\alpha }}}\frac{{d{{w}_{0}}}}{{d{\eta }}} + {\alpha }{{u}_{0}}{{w}_{{\alpha }}} = \frac{{{{d}^{2}}{{w}_{{\alpha }}}}}{{d{{{\eta }}^{2}}}}$

${{{\delta }}_{{\alpha }}} = \frac{3}{{6 + 8{\alpha }}}{{{\delta }}_{0}} = \sqrt {\frac{{{\gamma } - {\text{ 1}}}}{{2{\gamma }{{p}_{0}}}}} \left[ {\int\limits_0^\infty {\left( {{{H}_{{\alpha }}} - 2{{u}_{0}}{{u}_{{\alpha }}} - 2{{w}_{0}}{{w}_{{\alpha }}}} \right)d{\eta } - {\text{0}}{\text{.5}}\int\limits_0^\infty {({{H}_{0}} - u_{0}^{2} - w_{0}^{2})d{\eta }} } } \right]$

$\frac{{\left( {2{\alpha } + 3} \right)}}{{\left( {4{\alpha } + 3} \right)}}\int\limits_0^\infty {({{H}_{0}} - u_{0}^{2} - w_{0}^{2})} d{\eta } = \int\limits_0^\infty {\left( {{{H}_{{\alpha }}} - 2{{u}_{0}}{{u}_{{\alpha }}} - 2{{w}_{0}}{{w}_{{\alpha }}}} \right)d{\eta }} $

${\eta } = 0{\text{:}}\,\,\,{{u}_{{\alpha }}} = {{w}_{{\alpha }}} = {{{v}}_{{\alpha }}} = {{H}_{{\alpha }}} = 0;\quad {\eta } \to \infty {\text{:}}\,\,\,{{u}_{{\alpha }}} \to 0,\quad {{w}_{{\alpha }}} \to 0,\quad {{H}_{{\alpha }}} \to 0$

В краевой задаче (2.5) интегральное соотношение для определения собственного числа α получено из разложений (2.3) для давления p и толщины вытеснения δ_e. Заметим, что система (2.5) существенно отличается от соответствующей системы [9], так как в ней уравнение для w_α(η) уже не отделилось. Для заданных значений определяющих параметров H_w, σ, γ и β решение системы уравнений (2.4) позволяет найти все функции течения u₀(η), w₀(η), ${{{v}}_{0}}$(η), H₀(η), p₀, δ₀ на передней кромке пластины. Затем из решения краевой задачи (2.5) с тривиальными граничными условиями определяется собственное число α, если оно существует, и соответствующие ему коэффициенты разложений u_α(η), w_α(η), ${{{v}}_{\alpha }}$(η), H_α(η), δ_α. Важно отметить, что так как параметр p_α(z) в разложениях (2.3) оказывается произвольным, то решение в окрестности передней кромки не является единственным. В каждом сечении z = const имеется, в отличие от [8], свое однопараметрическое семейство решений. Подбор параметра p_α(z), в принципе, позволяет (в рассматриваемом пока двухчленном разложении) удовлетворить дополнительному условию на задней кромке пластины, или придти в особую точку на ней, если имеет место отрыв и трение обращается в ноль. Таким образом, в данном случае для течения в пространственном пограничном справедлива теория полос вдоль оси x, перпендикулярной передней кромке пластины.

Для третьих членов разложения получаем следующую краевую задачу:

(2.6)

$\frac{{d{{{v}}_{{{\alpha 1}}}}}}{{d{\eta }}} + \left( {{\alpha } + 1.25} \right){{u}_{{{\alpha 1}}}} + {{w}_{{\alpha }}} + {\text{0}}{\text{.5}}\left( {{{w}_{0}} + \left( {{\alpha } + {\text{1}}} \right){{p}_{{{\alpha 1}}}}{{u}_{0}}} \right) = 0$

${{{v}}_{0}}\frac{{d{{H}_{{{\alpha 1}}}}}}{{d{\eta }}} + {{{v}}_{{{\alpha 1}}}}\frac{{d{{H}_{0}}}}{{d{\eta }}}{\text{ + }}\left( {{\alpha } + {\text{1}}} \right){{u}_{0}}{{H}_{{{\alpha 1}}}} + {{w}_{0}}{{H}_{{\alpha }}} = \frac{1}{{\sigma }}\frac{{{{d}^{2}}{{H}_{{{\alpha 1}}}}}}{{d{{{\eta }}^{2}}}} - 2\frac{{1 - {\sigma }}}{{\sigma }}\frac{{{{d}^{2}}\left( {{{u}_{0}}{{u}_{{{\alpha 1}}}} + {{w}_{0}}{{w}_{{{\alpha 1}}}}} \right)}}{{d{{{\eta }}^{2}}}}$

${\eta } = 0{\text{:}}\,\,\,{{u}_{{{\alpha 1}}}} = {{w}_{{{\alpha 1}}}} = {{{v}}_{{{\alpha 1}}}} = {{H}_{{{\alpha 1}}}} = 0;\quad {\eta } \to \infty {\text{:}}\,\,\,{{u}_{{{\alpha 1}}}} \to 0,\quad {{w}_{{{\alpha 1}}}} \to 0,\quad {{H}_{{{\alpha 1}}}} \to 0$

Система уравнений (2.6) является линейной и неоднородной с нулевыми граничными условиями. Вид этой системы подтверждает, что коэффициенты разложений u_α1(η), w_α1(η), ${{{v}}_{{\alpha 1}}}$(η), H_α1(η), δ_α1 действительно не зависят от поперечной координаты z. Полученная система содержит параметр p_α1, значение которого однозначно определяется из интегрального соотношения, полученного в результате разложения в ряды индуцированного давления и толщины вытеснения, причем коэффициент p_α1 также не зависит от координаты z. Сформулированные краевые задачи (2.4), (2.5) и (2.6) принципиально отличаются от соответствующих краевых задач для случая обтекания пластины при отсутствии угла скольжения [10], в которых уравнения для определения коэффициентов разложения для поперечной компоненты скорости отделялись от основной системы уравнений. Учитывая, что и сами разложения (2.3) принципиально отличаются от случая, когда скольжение отсутствует, возникает вопрос, что происходит, если в краевых задачах (2.4)–(2.6) полагать β = 0. Если в краевых условиях системы (2.4) положить β = 0, то уравнение для определения первого члена разложения для поперечной компоненты скорости имеет единственное решение w₀(η) = 0, а следовательно, dw₀(η)/dη = 0. Тогда уравнение для определения второго члена разложения для поперечной компоненты скорости в системе (2.5) станет однородным, а его решение w_α(η) = 0. Заметим, что системы (2.4) и (2.5) после этого точно совпадут с соответствующими краевыми задачами, приведенными в [9], где рассмотрено обтекание пластины при отсутствии угла скольжения. Если теперь рассмотреть систему (2.6) при условиях, что β = 0, w₀(η) = 0 и w_α(η) = 0, то в этой системе только уравнение для определения w_α1(η) останется неоднородным и совпадающим с уравнением, приведенным в [9]. Остальные уравнения станут однородными, а их решения соответственно: u_α1(η) = 0, ${{{v}}_{{\alpha 1}}}$(η) = 0, H_α1(η) = 0, δ_α1 = 0 и p_α1 = 0. Заметим, что при этом и вид разложений (2.3) изменится и точно совпадет с разложениями [9]. Можно показать (системы уравнений из-за громоздкости не приведены), что решения краевых задач для опущенных членов разложений, имеющих порядки О(x^{α + 2}), О(x^{α + 3}), …, О(x^{α +}ⁿ), до тех пор, пока показатели степени α + n < 2α, если в них положить β = 0, являются тривиальными, первое нетривиальное решение получится для системы порядка О(x^2α), а сама краевая задача примет вид, приведенный в [10], причем уравнение для определения соответствующей компоненты поперечной компоненты скорости отделится от основной системы.

3. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ

В настоящей работе численные исследования проведены только при значениях числа Прандтля σ = 1, показателя адиабаты γ = 1.4 и параметра N = 1. Основное внимание уделено изучению температурного фактора H_w и угла скольжения β на характеристики течения. Краевые задачи (2.4)–(2.6) решались численно с помощью метода прогонки. Для вычисления определенных интегралов использовалась формула Симпсона. Размер шага по нормальной координате равнялся Δη = 0.01, а количество узлов по нормали к поверхности до N_η = 1351. Значение собственного числа считалось вычисленным, если интегральное условие в краевой задаче (2.5) выполнялось с точностью |ε| ≤ 0.0002. Такое же требование ставилось при вычислении интеграла для определения параметра p_α1 при решении краевой задачи (2.6).

Результаты расчетов профилей коэффициентов разложений (2.3) u₀(η) (кривые 1–3), w₀(η) (4–6), H₀(η) (7–9), полученных в результате решения краевой задачи (2.4), в зависимости от температурного фактора H_w = 0.75 (2, 5, 8), 1 (1, 4, 7), 1.25 (3, 6, 9) при β = 45° приведены на рис. 1. Увеличение энтальпии H_w от 0.75 до 1.25 приводит к качественному изменению профиля энтальпии, профиль продольной компоненты скорости u₀(η) становится более наполненным, но его максимальные изменения не превышают 15%, а профиль w₀(η) практически не зависит от температурного фактора. Это автомодельное решение [3]. Далее представлены результаты, полученные при решения краевых задач (2.5) и (2.6). Зависимости профилей коэффициентов разложения для продольной компоненты скорости u_α(η) (кривые 1–3) и u_α1(η) (4–6) от температурного фактора H_w = 0.75 (2, 5), 1 (1, 4), 1.25 (3, 6) при σ = 1, γ = 1.4, β = 45° приведены на рис. 2. Все приведенные профили являются отрицательными по величине, причем максимальные по модулю значения u_α(η), примерно, в два раза меньше, чем u_α1(η). Заметим, что увеличение энтальпии поверхности пластины H_w влияет на данные профили в противоположных направлениях, а именно, приводит к небольшому наполнению профиля u_α(η), но значительно уменьшает u_α1(η). Зависимости профилей коэффициентов разложения для поперечной компоненты скорости w_α(η) (кривые 1–3) и w_α1(η) (4–6) от температурного фактора H_w = 0.75 (2, 5), 1 (1, 4), 1.25 (3, 6) при β = 45° представлены на рис. 3. В этом случае увеличение энтальпии поверхности пластины H_w, наоборот, уменьшает максимальные значения профиля w_α(η) и значительно увеличивает – w_α1(η), но при этом максимальные по модулю значения w_α1(η) примерно в два раза превышают – w_α(η). Зависимости профилей коэффициентов разложений полной энтальпии H_α(η) (кривые 2, 3), H_α1(η) (5, 6) от температурного фактора H_w = 0.75 (2, 5), 1.25 (3, 6) при β = 45° приведены на рис. 4.

Рис. 1.

Зависимости профилей коэффициентов разложений u₀(η) (1–3), w₀(η) (4–6), H₀(η) (7–9) от температурного фактора H_w = 0.75 (2, 5, 8), 1.0 (1, 4, 7), 1.25 (3, 6, 9) при σ = 1, γ = 1.4, β = 45°

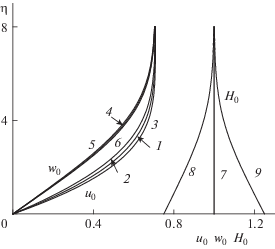
Рис. 2.

Зависимости профилей коэффициентов разложения u_α(η) (1–3), u_α1(η) (4–6) от температурного фактора H_w = 0.75 (2, 5), 1.0 (1, 4), 1.25 (3, 6) при σ = 1, γ = 1.4, β = 45°

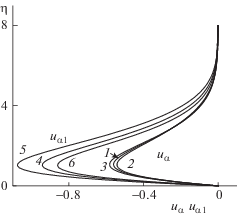
Рис. 3.

Зависимости профилей коэффициентов разложения w_α(η) (1–3), w_α1(η) (4–6) от температурного фактора H_w = 0.75 (2, 5), 1.0 (1, 4), 1.25 (3, 6) при σ = 1, γ = 1.4, β = 45°

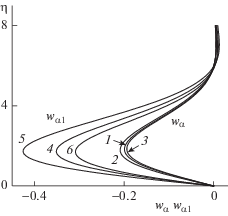
Рис. 4.

Зависимости профилей коэффициентов разложений H_α(η) (2, 3), H_α1(η) (5, 6) от температурного фактора H_w = 0.75 (2, 5), 1.25 (3, 6) при σ = 1, γ = 1.4, β = 45°

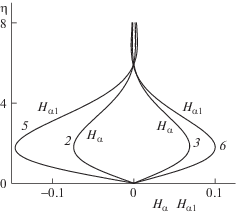
Следует отметить, что профили коэффициента H_α(η) и H_α1(η) являются немонотонными функциями, и во внешней части пограничного слоя при η > 5.5 меняют знак на противоположный. Профили коэффициентов при H_w = 1 не приведены, так как в рассматриваемом случае, при числе Прандтля σ = 1, H_α(η) = 0 и H_α1(η) = 0. Отметим, что максимальные по модулю значения профиля H_α1(η) примерно в полтора-два раза превышают H_α(η). Зависимости коэффициентов разложения для индуцированного давления: p₀ (кривые 1–3), параметра p_α1 (4–6) и собственного числа α × 10^–1 (7–9) от угла скольжения β при значениях температурного фактора H_w = 0.75 (2, 5, 8), 1 (1, 4, 7), 1.25 (3, 6, 9) представлены на рис. 5. Увеличение β приводит к существенному уменьшению значения собственного числа α, а это означает, что с ростом угла скольжения значительно усиливается интенсивность передачи возмущений против потока. Причем наиболее сильно собственные числа уменьшаются для случая обтекания охлаждаемой пластины (кривая 8). Величина угла скольжения также влияет на значения автомодельного давления p₀ и параметра p_α1, вычисляемого при решении краевой задачи (2.6), причем этот параметр обращается в ноль, когда пластина обтекается без угла скольжения. Следует отметить, что параметр p_α1 быстрее растет при охлаждении поверхности пластины (кривая 5), чем при ее нагреве (6).

Рис. 5.

Зависимости коэффициентов разложения p₀ (1–3), p_α1 (4–6) и собственного числа α × 10^–1 (7–9) от угла скольжения β при значениях температурного фактора H_w = 0.75 (2, 5, 8), 1 (1, 4, 7), 1.25 (3, 6, 9) при σ = 1, γ = 1.4

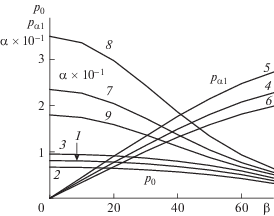
Используя приведенные данные для рассмотренных определяющих параметров и задавая произвольную функцию p_α(z), можно с помощью разложений (2.3) построить возмущенное течение на пластине. Далее, в качестве примера, рассматривается случай, когда произвольная функция, входящая в разложения (2.3), имеет вид p_α(z) = С × cos⁶(πz), причем экстремальные значения модуля ее производной dp_α(z)/dz на порядок больше самой функции. Для значений параметров β = 45° и H_w = 1.25 разложение (2.3) для давления при двухчленном разложении имеет вид: p(2) = p(x, z) = 0.75734 + p_α(z)x^α, а при трехчленном – p(3) = p(x, z) = 0.75734 + p_α(z)x^α + + 1.457dp_α(z)/dzx^{α + 1}, где соответствующее собственное число α = 9.964. Коэффициент в выражении p_α(z) выбран равным С = 0.025, так как при значениях, больших этой величины, коэффициент трения в продольном направлении du/dη на задней кромке пластины обращается в ноль и возникает отрыв.

На рис. 6 приведена зависимость коэффициента, пропорционального тепловому потоку dH(2)/dy = dH₀/dη + p_α(z)/p₀dH_α/dηx^α (двухчленное разложение) на части поверхности пластины (0.6 ≤ x ≤ 1) при p_α(z) = 0.025cos⁶(πz), β = 45° и H_w = 1.25, где автомодельное индуцированное давление p₀ = 0.75734. Экстремальные значения тепловых потоков совпадают с максимальными значениями функции p_α(z) = 0.025cos⁶(πz), модули тепловых потоков уменьшаются, но их изменения не превышают 3%. Совершенно иное распределение тепловых потоков получается, если учесть третий член разложения.

Рис. 6.

Зависимость коэффициента dH(2)/dy на поверхности пластины (0.6 ≤ x ≤ 1) при p_α(z) = 0.025cos⁶(πz), σ = 1, γ = 1.4, β = 45° и H_w = 1.25

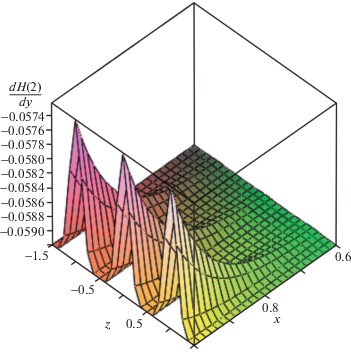
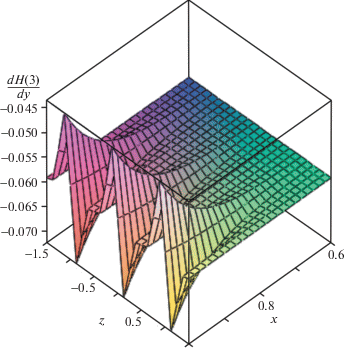
На рис. 7 приведена зависимость коэффициента dH(3)/dy = dH₀/dη + p_α(z)/p₀dH_α/dηx^α + + N/p₀dp_α(z)/dzdH_α1/dηx^{α + 1} (трехчленное разложение) на поверхности пластины при тех же определяющих параметрах. Следует отметить, что, во-первых, максимумы смещаются, во-вторых, появляются области, в которых тепловые потоки растут, а в третьих, и это самое главное, их изменение достигает 25%. Таким образом, показано, что при наличии угла скольжения необходимо обязательно учитывать третий член разложений (2.3), если на задней кромке пластины могут появиться достаточно большие градиенты давления по ее размаху.

Рис. 7.

Зависимость коэффициента dH(3)/dy на поверхности пластины (0.6 ≤ x ≤ 1) при p_α(z) = 0.025cos⁶(πz), σ = 1, γ = 1.4, β = 45° и H_w = 1.25

ЗАКЛЮЧЕНИЕ

Построены трехчленные разложения для функций течения в окрестности передней кромки скользящей пластины конечной длины в случае, когда на задней кромке задается распределение давления, зависящее от поперечной координаты. В результате решения краевой задачи для второго члена разложения найдены собственные значения. Показано, что в результате решения системы уравнений для третьего члена разложения однозначно определяется сомножитель в третьем члене разложения для индуцированного давления. Выявлено сильное влияние угла скольжения и температурного фактора на характеристики пространственного течения в пространственном пограничном слое. Показано, что наличие угла скольжения принципиально изменяет передачу возмущений против потока, по сравнению с обтеканием пластины при отсутствии скольжения. Установлено, что при наличии угла скольжения необходимо обязательно учитывать третий член разложений, если на задней кромке пластины появляются достаточно большие градиенты давления по поперечной координате. Все это может приводить к большим пикам тепловых потоков.

Работа выполнена при поддержке гранта РФФИ (№ 18-01-00211).

Список литературы

Lees L. On the boundary-layer equations in hypersonic flow and their approximate solutions // J. Aeronaut. Sci. 1953. № 20(20). P. 143–145.
Stewartson K. On the motion of a flat plate at high speed in a viscous compressible fluid. II Steady motion // J. Aeronaut. Sci. 1955. № 22(5). P. 303–309.
Whalen R.J. Boundary-layer interaction on a yawed infinit wing in hypersonic flow // JASS. 1959. V. 26. № 12. P. 839–841.
Нейланд В.Я. Распространение возмущений вверх по течению при взаимодействии гиперзвукового потока с пограничным слоем // Изв. АН СССР. МЖГ. 1970. № 4. С. 40–49.
Нейланд В.Я., Боголепов В.В., Дудин Г.Н., Липатов И.И. Асимптотическая теория сверхзвуковых течений вязкого газа. М.: Физматлит, 2003. 456 с.
Brown S.N., Stewartson K. A non-uniqueness of the hypersonic boundary layer // Q. J. Mech. Appl. Math. 1975. V. XXVIII. Pt. 1. P. 75–90.
Коваленко А.А. Исследование отрыва пограничного слоя при сильном взаимодействии с гиперзвуковым потоком газа // Уч. зап. ЦАГИ. 1974. Т. V. № 6. С. 39–47.
Козлова И.Г., Михайлов В.В. О сильном вязком взаимодействии на треугольном и скользящем крыльях // Изв. АН СССР. МЖГ. 1970. № 4. С. 94–99.
Дудин Г.Н., Нейланд В.Я. Об индуцировании трехмерных возмущений в пограничном слое при сильном взаимодействии с гиперзвуковым потоком // Изв. РАН. МЖГ. 2018. № 1. С. 89–96.
Дудин Г.Н., Нейланд В.Я. Влияние температуры поверхности пластины на распространение возмущений при гиперзвуковом обтекании // Уч. зап. ЦАГИ. 2018. Т. XLIX. № 5. С. 3–16.
Дудин Г.Н., Нейланд В.Я. О распространении возмущений на скользящей пластине на режиме сильного взаимодействия // ДАН 2018. Т. 483. № 1. С. № 1. С. 33–36.
Hayes W.D., Probstein R.F. Hypersonic flow theory. N.Y.; L.: Acad. Press, 1959.
Дудин Г.Н. Треугольные крылья в вязком гиперзвуковом потоке. М.: МФТИ, 2011. 258 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал