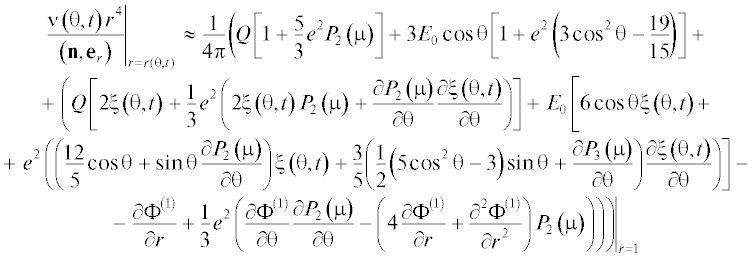Известия РАН. Механика жидкости и газа, 2019, № 5, стр. 70-82

КВАДРУПОЛЬНОЕ ЭЛЕКТРОМАГНИТНОЕ ИЗЛУЧЕНИЕ ЗАРЯЖЕННОЙ КАПЛИ, ОСЦИЛЛИРУЮЩЕЙ В СУПЕРПОЗИЦИИ КОЛЛИНЕАРНЫХ ГРАВИТАЦИОННОГО И ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЕЙ

А. И. Григорьев^a, *, Н. Ю. Колбнева^a, С. О. Ширяева^a

^a Ярославский государственный университет им. П.Г. Демидова
Ярославль, Россия

Поступила в редакцию 15.01.2019
После доработки 11.02.2019
Принята к публикации 04.03.2019

DOI: 10.1134/S0568528119050049

Аннотация

В аналитических расчетах первого порядка малости по безразмерной амплитуде осцилляций заряженной электропроводной капли, неподвижной в суперпозиции гравитационного и электростатического полей, найдено аналитическое выражение для квадрупольного момента капли, обусловленного наличием собственного и индуцированного зарядов на ее поверхности. Во втором порядке малости по квадрату отношения характерного линейного размера капли к длине излучаемой волны оценена интенсивность электромагнитного излучения от капли, генерируемого изменением во времени величины ее квадрупольного момента.

Ключевые слова: заряженная капля, электростатическое поле, осцилляции, квадруполь, излучение

Уже из курса общей физики известно, что ускоренно движущийся электрический заряд теряет энергию на электромагнитное излучение [1–3]. С подобной ситуацией приходится сталкиваться и при колебаниях заряженной поверхности жидкости, в частности при осцилляциях заряженной капли воды [4].

Электромагнитное излучение системы ускоренно движущихся зарядов согласно мультипольным представлениям [5, 6] состоит из суперпозиции дипольной, квадрупольной и магнитно-дипольной компонент. Разделение общего излучения на мультипольные компоненты ведется по малому параметру η – квадрату отношения характерного линейного размера системы (в нашем случае капли) к длине излучаемой волны [5, 6].

В случае осциллирующей капли проводящей жидкости (например, воды), несущей собственный и индуцированный заряды, естественно использовать еще один малый параметр ε – безразмерную амплитуду осцилляций, равную отношению амплитуды к характерному линейному размеру капли.

В качестве примера, имеющего практические значимые приложения [7–10], возьмем дождевую воду. Проблема наличия радиоизлучения от осциллирующей облачной капли была впервые сформулирована в [4]. Там же был предложен способ оценивания интенсивности радиоизлучения от осциллирующей заряженной капли идеальной жидкости на основе решения электрогидродинамической задачи об осцилляциях заряженной капли и закона сохранения энергии. В дальнейшем на основе тех же идей были проведены расчеты в [11, 12].

В [13] была рассмотрена задача о расчете дипольной компоненты полного излучения от осциллирующей заряженной капли в электростатическом поле [13]. В работе [14] изучалось квадрупольное излучение от осциллирующей сферической заряженной капли. В настоящей работе проведено исследование интенсивности квадрупольного излучения сфероидальной заряженной капли, подвешенной в суперпозиции гравитационного и электростатического полей.

1. ФИЗИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ

Рассмотрим задачу об электромагнитном излучении сфероидальной капли первоначального радиуса R, несущей заряд Q, идеальной несжимаемой идеально проводящей жидкости с массовой плотностью ρ, коэффициентом поверхностного натяжения σ, неподвижно висящей в грозовом облаке в суперпозиции гравитационного g и однородного электростатического E₀ полей. Причем электростатическое поле направлено коллинеарно гравитационному так, что E₀ || g, а центр масс капли неподвижен.

Наличие внешнего электростатического поля приводит к появлению на поверхности капли индуцированных зарядов и, как следствие, к искажению равновесной сферической формы капли. В линейном приближении по величине стационарной деформации равновесная форма капли может считаться сфероидальной, вытянутой по полю [15, 16].

Предполагаем, что на поверхности капли существует капиллярное волновое движение, возникающее в силу теплового движения молекул жидкости, приводящее к искажению равновесной в поле сфероидальной формы. Амплитуда таких волновых движений весьма мала: ~(κT/σ)^1/2, где κ – постоянная Больцмана, T – абсолютная температура [17]. Под действием внешних силовых воздействий амплитуда непрерывно осциллирующей капли может принимать значения до десятков процентов от радиуса капли [18, 19].

Собственный и индуцированный внешним электростатическим полем заряды распределяются по возмущенной капиллярным волновым движением поверхности проводящей капли. При этом капиллярные осцилляции заряженной поверхности сфероидальной капли (находящейся во внешнем поле) при ускоренном движении зарядов приводят к излучению электромагнитных волн.

Согласно общей теории излучения электромагнитных волн интенсивность квадрупольного излучения для ускоренно движущейся системы зарядов вычисляется по формуле [5, 6]

(1.1)

$I = \frac{1}{{180{{c}^{5}}}}\sum\limits_{\alpha ,\beta = 1}^3 {{{{\left( {\frac{{{{\partial }^{3}}}}{{\partial {{t}^{3}}}}{{D}_{{\alpha \beta }}}} \right)}}^{2}}} $

полученной во втором порядке малости по η. Тензор квадрупольного момента ${{D}_{{\alpha \beta }}}$ определяется в виде

(1.2)

${{D}_{{\alpha \beta }}}\left( t \right) = \iiint\limits_V {\gamma ({\mathbf{r}},t)(3{{x}_{\alpha }}(t){{x}_{\beta }}(t) - {{\delta }_{{\alpha \beta }}}{{r}^{2}}(t))dV}$

γ(r, t) – объемная плотность заряда, δ_αβ – дельта-символ Кронекера, x_α(t) и x_β(t) – координаты радиус-вектора r(t) в декартовой системе координат (x, y, z) для точки, лежащей в объеме капли V.

Ограничим рассмотрение осесимметричными осцилляциями поверхности капли. Все расчеты задачи будем проводить в сферической системе координат (r, θ, φ) с началом в центре масс капли в безразмерных переменных, в которых R = ρ = σ = 1. Остальные величины задачи будут выражены в долях своих характерных значений

$\left[ Q \right] = {{R}^{{3/2}}}{{\sigma }^{{1/2}}},\quad \left[ {{{E}_{0}}} \right] = {{R}^{{ - 1/2}}}{{\sigma }^{{1/2}}},\quad \left[ t \right] = {{R}^{{3/2}}}{{\rho }^{{1/2}}}{{\sigma }^{{ - 1/2}}}$

$\left[ V \right] = {{R}^{{ - 1/2}}}{{\rho }^{{ - 1/2}}}{{\sigma }^{{1/2}}},\quad \left[ r \right] = R,\quad \left[ P \right] = {{R}^{{ - 1}}}\sigma $

2. МАТЕМАТИЧЕСКАЯ ФОРМУЛИРОВКА ЗАДАЧИ

Пусть в начальный момент времени t = 0 равновесная сфероидальная форма капли r(θ) претерпевает осесимметричное тепловое возмущение ξ(θ, t) с амплитудой осцилляций ε, причем ε $ \ll $ R. Форму возмущенной поверхности капли в системе координат, начало которой совпадает с положением центра масс капли, в безразмерных переменных представим в виде

(2.1)

$r(\theta ,t) = r(\theta ) + \xi (\theta ,t);\quad \left| \xi \right| \ll 1$

Примем, что волновое движение жидкости в капле является потенциальным. Поле скоростей течения жидкости в капле V(r, t) = gradψ(r, t), связанное с осцилляциями ее поверхности, полностью определяется гидродинамическим потенциалом ψ(r, t) [20]. Оно имеет тот же порядок малости (в безразмерных переменных), что и безразмерная амплитуда осцилляций поверхности капли ψ(r, t) ~ ξ(θ, t) ~ ε. Электрическое поле вокруг капли будем характеризовать потенциалом Φ(r, t).

Математическая формулировка задачи о капиллярных осцилляциях заряженной капли неподвижной в суперпозиции гравитационного и внешнего однородного электростатического полей имеет вид

$\Delta \psi (r,\theta ,t) = 0;\quad \Delta \Phi (r,\theta ,t) = 0$

$r \to 0{\text{:}}\,\psi (r,\theta ,t) \to 0,\quad r \to \infty {\text{:}}\,\Phi (r,\theta ,t) \to - {{E}_{0}}r\cos \theta $

$r = r(\theta ) + \xi (\theta ,t){\text{:}}\,\frac{{\partial \xi \left( {\theta ,t} \right)}}{{\partial t}} = \frac{{\partial \psi \left( {r,\theta ,t} \right)}}{{\partial r}} - \frac{1}{{{{r}^{2}}}}\frac{{\partial \psi \left( {r,\theta ,t} \right)}}{{\partial \theta }}\left( {\frac{{\partial r\left( \theta \right)}}{{\partial \theta }} + \frac{{\partial \xi \left( {\theta ,t} \right)}}{{\partial \theta }}} \right) \equiv $

$ \equiv P\left( {r,\theta ,t} \right) + {{P}_{E}}\left( {r,\theta ,t} \right) + {{P}_{g}}\left( {r,\theta ,t} \right) = {{P}_{\sigma }}\left( {r,\theta ,t} \right);\quad \Phi (r,\theta ,t) = {{\Phi }_{s}}(t)$

(2.2)

$t = 0{\text{:}}\,\xi \left( \theta \right) = \varepsilon \sum\limits_{j\, \in \,\Xi } {{{h}_{j}}} {{P}_{j}}\left( \mu \right);\quad \sum\limits_{j\, \in \,\Xi } {{{h}_{j}}} = 1;\quad \varepsilon \ll 1;\quad \frac{{\partial \xi \left( \theta \right)}}{{\partial t}} = 0$

где h_j – коэффициенты, определяющие парциальный вклад j-й колебательной моды в суммарное начальное возмущение, Ξ – множество значений номеров изначально возбужденных колебательных мод, P_j(μ) полином Лежандра j-го порядка, j – целое число, μ ≡ cosθ.

Исходя из общефизических соображений, для замыкания выписанной системы уравнений сформулируем дополнительные интегральные условия: постоянства объема капли, неподвижности ее центра масс и сохранения полного заряда капли

$\int\limits_V {{{r}^{2}}dr\sin \theta d\theta d\varphi = \frac{4}{3}\pi } ;\quad \int\limits_V {{\mathbf{r}} \cdot {{r}^{2}}dr\sin \theta d\theta d\varphi = 0} $

$V = [0 \leqslant r \leqslant r(\theta ) + \xi (\theta ,t),0 \leqslant \theta \leqslant \pi ,0 \leqslant \varphi \leqslant 2\pi ]$

(2.3)

$ - \frac{1}{{4\pi }}\oint\limits_S {({\mathbf{n}}({\mathbf{r}},t),\nabla \Phi ({\mathbf{r}},t))dS} = Q;\quad S = [r = r(\theta ) + \xi (\theta ,t),0 \leqslant \theta \leqslant \pi ,0 \leqslant \varphi \leqslant 2\pi ]$

Здесь Φ_s(t) – постоянное вдоль поверхности капли значение ее электрического потенциала; P(r, t) = P₀ – ∂ψ(r, t)/∂t – гидродинамическое давление, P₀ – постоянное давление внутри капли в состоянии равновесия, P_q(r, t) = (gradΦ(r, t))²/8π – давление электрического поля, P_g = g[r(0) – – (r(θ) + ξ(θ, t))μ] – давление гравитационного поля на поверхности капли, P_σ = divn(r, t) – капиллярное давление, n(r, t) – единичный вектор нормали, определяемый в виде [21]:

(2.4)

${\mathbf{n}}\left( {{\mathbf{r}},t} \right) = {{\left. {\frac{{\nabla \left( {r - r\left( {\theta ,t} \right)} \right)}}{{\left| {\nabla \left( {r - r\left( {\theta ,t} \right)} \right)} \right|}}} \right|}_{{r = r\left( {\theta ,t} \right)}}}$

Искомые величины разложим по порядкам малости безразмерной амплитуды осцилляций ε [22]

${\xi }({\theta },t) = {{{\xi }}^{{\left( 1 \right)}}}({\theta },t) + {\rm O}({{{\varepsilon }}^{2}});\quad {{\psi }_{j}}({\mathbf{r}},t) = \psi _{j}^{{\left( 1 \right)}}({\mathbf{r}},t) + {\rm O}({{\varepsilon }^{2}})$

$P({\mathbf{r}},t) = {{P}^{{\left( 0 \right)}}}({\mathbf{r}}) + {{P}^{{\left( 1 \right)}}}({\mathbf{r}},t) + {\rm O}({{\varepsilon }^{2}});\quad {{P}_{E}}({\mathbf{r}},t) = P_{E}^{{\left( 0 \right)}}({\mathbf{r}}) + P_{E}^{{\left( 1 \right)}}({\mathbf{r}},t) + {\rm O}({{\varepsilon }^{2}})$

${{P}_{g}}({\mathbf{r}},t) = P_{g}^{{\left( 0 \right)}}({\mathbf{r}}) + P_{g}^{{\left( 1 \right)}}({\mathbf{r}},t) + {\rm O}({{\varepsilon }^{2}});\quad {{P}_{\sigma }}({\mathbf{r}},t) = P_{{^{\sigma }}}^{{\left( 0 \right)}}({\mathbf{r}}) + P_{{^{\sigma }}}^{{\left( 1 \right)}}({\mathbf{r}},t) + {\rm O}({{\varepsilon }^{2}})$

(2.5)

$\Phi ({\mathbf{r}},t) = {{\Phi }^{{\left( 0 \right)}}}({\mathbf{r}}) + {{\Phi }^{{\left( 1 \right)}}}({\mathbf{r}},t) + {\rm O}({{\varepsilon }^{2}})$

где Ф⁽⁰⁾(r, θ) – электрический потенциал в окрестности равновесного заряженного сфероида во внешнем электростатическом поле, Ф⁽¹⁾(r, t) – поправка первого порядка малости к электрическому потенциалу, связанная с возмущением поверхности капли. Верхний индекс означает порядок малости по ε.

Подставим разложения (2.5) в (2.2)–(2.3). Выделим задачу нулевого порядка для нахождения равновесной формы поверхности капли r(θ) и равновесного электрического потенциала Ф⁽⁰⁾(r, θ). Также выделим и задачу первого порядка для нахождения формы возмущенной поверхности капли r(θ, t) и электрического потенциала Ф⁽¹⁾(r, t) – добавки, возникающей в окрестности возмущенного заряженного сфероида во внешнем поле.

3. ЗАДАЧА НУЛЕВОГО ПОРЯДКА ПО ε

Математическая формулировка задачи нулевого порядка малости по ε имеет вид

$\Delta {{\Phi }^{{\left( 0 \right)}}}({\mathbf{r}}) = 0$

$r \to \infty {\text{:}}\,{{\Phi }^{{\left( 0 \right)}}}({\mathbf{r}}) \to - {{E}_{0}}r\cos \theta $

$r = r(\theta ){\text{:}}\,{{\Phi }^{{\left( 0 \right)}}}({\mathbf{r}}) = {\text{const;}}\quad {{P}^{{\left( 0 \right)}}} + P_{q}^{{\left( 0 \right)}} + P_{g}^{{\left( 0 \right)}} = P_{\sigma }^{{\left( 0 \right)}}$

$\int\limits_V {{{r}^{2}}dr\sin \theta d\theta d\varphi = \frac{4}{3}\pi } ;\quad \int\limits_V {{\mathbf{r}} \cdot {{r}^{2}}dr\sin \theta d\theta d\varphi = 0} $

$V = [0 \leqslant r \leqslant r(\theta ),0 \leqslant \theta \leqslant \pi ,0 \leqslant \varphi \leqslant 2\pi ]$

(3.1)

$ - \frac{1}{{4\pi }}\oint\limits_S {({{{\mathbf{n}}}_{0}}(r,\theta ),\nabla {{\Phi }^{{\left( 0 \right)}}}(r,\theta ))dS} = Q;\quad S = [r = r(\theta ),0 \leqslant \theta \leqslant \pi ,0 \leqslant \varphi \leqslant 2\pi ]$

где n₀(r) – единичный вектор нормали к невозмущенной поверхности сфероидальной капли, вычисляемый по формуле (2.4) при r = r(θ).

В итоге решение задачи (3.1) примет следующий вид:

${{\Phi }^{{\left( 0 \right)}}}(r,\theta ) = \frac{Q}{r}\left( {1 + \frac{1}{{3{{r}^{2}}}}{{e}^{2}}{{P}_{2}}\left( \mu \right)} \right) + $

(3.2)

$ + {{E}_{0}}\left( {r{{P}_{1}}\left( \mu \right)\left( {\frac{1}{{{{r}^{3}}}} - 1} \right) + \frac{2}{5}\frac{1}{{{{r}^{2}}}}{{e}^{2}}\left( {{{P}_{1}}\left( \mu \right) + \frac{3}{2}\frac{1}{{{{r}^{2}}}}{{P}_{3}}\left( \mu \right)} \right)} \right)$

${{P}^{{\left( 0 \right)}}}(r,\theta ) = {{P}_{0}};\quad P_{q}^{{\left( 0 \right)}}(r,\theta ) = {{{{{(\nabla {{\Phi }^{{\left( 0 \right)}}})}}^{2}}} \mathord{\left/ {\vphantom {{{{{(\nabla {{\Phi }^{{\left( 0 \right)}}})}}^{2}}} {8\pi }}} \right. \kern-0em} {8\pi }};\quad P_{g}^{{\left( 0 \right)}} = g\left( {1 - {{P}_{1}}\left( \mu \right)} \right)$

$P_{\sigma }^{{\left( 0 \right)}}(r,\theta ) = 2 - \frac{1}{3}{{e}^{2}}\left( {2 + {{L}_{\theta }}} \right){{P}_{2}}\left( \mu \right);\quad {{L}_{\theta }} \equiv \frac{1}{{\sin \theta }}\frac{\partial }{{\partial \theta }}\left( {\sin \theta \frac{\partial }{{\partial \theta }}} \right)$

(3.3)

$r(\theta ) \approx 1 + {{e}^{2}}h(\theta ) + {\rm O}({{e}^{4}}) \equiv 1 + \frac{1}{3}{{e}^{2}}{{P}_{2}}\left( \mu \right) + {\rm O}({{e}^{4}})$

(3.4)

${{e}^{2}} = \frac{{9w}}{{1 - W}};\quad w = \frac{{E_{0}^{2}}}{{16\pi }};\quad W = \frac{{{{Q}^{2}}}}{{16\pi }};\quad g = 12\sqrt {Ww} $

где выражение равновесной поверхности капли (3.3) с точностью до квадрата эксцентриситета e² совпадает с уравнением вытянутого сфероида [16]. Решение (3.2) является разложением точного решения, приведенного в [23].

4. ЗАДАЧА ПЕРВОГО ПОРЯДКА ПО $\varepsilon $

Приведем математическую формулировку задачи первого порядка малости по $\varepsilon $ в виде

(4.1)

$\Delta \psi (r,\theta ,t) = 0;\quad \Delta {{\Phi }^{{\left( 1 \right)}}}(r,\theta ,t) = 0$

(4.2)

$r \to 0{\text{:}}\,\psi (r,\theta ,t) \to 0;\quad r \to \infty {\text{:}}\,{{\Phi }^{{\left( 1 \right)}}}(r,\theta ,t) \to 0$

(4.3)

(4.4)

${{P}^{{\left( 1 \right)}}}\left( {r,\theta ,t} \right) + P_{q}^{{\left( 1 \right)}}\left( {r,\theta ,t} \right) + P_{g}^{{\left( 1 \right)}}\left( {r,\theta ,t} \right) = P_{\sigma }^{{\left( 1 \right)}}\left( {r,\theta ,t} \right)$

(4.5)

$\Phi (r,\theta ,t) = {{\Phi }_{s}}(t)$

(4.6)

$\int\limits_V {{{r}^{2}}dr\sin \theta d\theta d\varphi = 0} ;\quad \int\limits_V {{\mathbf{r}} \cdot {{r}^{2}}dr\sin \theta d\theta d\varphi = 0} $

$V = [0 \leqslant r \leqslant r(\theta ),0 \leqslant \theta \leqslant \pi ,0 \leqslant \varphi \leqslant 2\pi ]$

(4.7)

$\oint\limits_S {\left( {{\mathbf{n}}\left( {\mathbf{r}} \right),\nabla \Phi \left( {\mathbf{r}} \right)} \right)dS} = 0;\quad S = [r = r(\theta ),0 \leqslant \theta \leqslant \pi ,0 \leqslant \varphi \leqslant 2\pi ]$

Решения уравнений Лапласа (4.1) для гидродинамического ψ(r, t) и электрического Ф⁽¹⁾(r, t) потенциалов, удовлетворяющие граничным условиям (4.2), а также возмущение равновесной формы поверхности капли ξ(θ, t) запишем в виде рядов по полиномам Лежандра:

(4.8)

$\psi \left( {r,\theta ,t} \right) = \varepsilon \sum\limits_{n = 0}^\infty {{{H}_{n}}} \left( t \right){{r}^{n}}{{P}_{n}}\left( \mu \right)$

(4.9)

${{\Phi }^{{\left( 1 \right)}}}\left( {r,\theta ,t} \right) = \varepsilon \sum\limits_{n = 0}^\infty {{{F}_{n}}} \left( t \right){{r}^{{ - \left( {n + 1} \right)}}}{{P}_{n}}\left( \mu \right)$

(4.10)

$\xi \left( {\theta ,t} \right) = \varepsilon \sum\limits_{n = 0}^\infty {{{M}_{n}}} \left( t \right){{P}_{n}}\left( \mu \right)$

Выражения для поправок к давлениям, вызванных возмущением поверхности капли ξ(θ, t), принимают следующий вид:

${{P}^{{\left( 1 \right)}}}\left( {r,\theta ,t} \right) = - \left( {\frac{{\partial \psi \left( {r,\theta ,t} \right)}}{{\partial t}} + {{e}^{2}}\frac{{{{\partial }^{2}}\psi \left( {r,\theta ,t} \right)}}{{\partial r\partial t}}h\left( \theta \right)} \right)$

$\begin{gathered} P_{q}^{{\left( 1 \right)}}\left( {r,\theta ,t} \right) = - \frac{1}{{4\pi }}\left( {2\left( {4{{Q}^{2}}{{e}^{2}}h\left( \theta \right) + \frac{1}{3}{{{\left( {Q + 3{{E}_{0}}\cos \theta } \right)}}^{2}}} \right)\xi \left( {\theta ,t} \right) + \left( {Q + 3{{E}_{0}}\cos \theta } \right)\frac{{\partial {{\Phi }^{{\left( 1 \right)}}}}}{{\partial r}} + } \right. \\ \left. { + \;Q{{e}^{2}}\left( { - \frac{{\partial h\left( \theta \right)}}{{\partial \theta }}\frac{{\partial {{\Phi }^{{\left( 1 \right)}}}}}{{\partial \theta }} + h\left( \theta \right)\left( {\frac{{\partial {{\Phi }^{{\left( 1 \right)}}}}}{{\partial r}} + \frac{{{{\partial }^{2}}{{\Phi }^{{\left( 1 \right)}}}}}{{\partial {{r}^{2}}}}} \right)} \right)} \right) \\ \end{gathered} $

$P_{g}^{{\left( 1 \right)}}\left( {r,\theta ,t} \right) = - g\xi \left( {\theta ,t} \right)\cos \theta $

$P_{\sigma }^{{\left( 1 \right)}}\left( {r,\theta ,t} \right) = - \left( {2 + {{L}_{\theta }}} \right)\xi \left( {\theta ,t} \right) + 2{{e}^{2}}\left( {\xi \left( {\theta ,t} \right){{L}_{\theta }}h\left( \theta \right) + h\left( \theta \right)\left( {2 + {{L}_{\theta }}} \right)\xi \left( {\theta ,t} \right)} \right)$

Подставляя (4.8)–(4.9) и (4.10) в граничные условия (4.3), (4.5)–(4.7), найдем соотношения, связывающие коэффициенты H_n(t) и F_n(t) в (4.9) и (4.10) с амплитудами возмущения M_n(t) в виде:

(4.11)

$\begin{gathered} {{H}_{n}}\left( t \right) = \frac{1}{n}\left( {\frac{{\partial {{M}_{n}}\left( t \right)}}{{\partial t}}\left( {1 - \frac{1}{{3n}}{{e}^{2}}\left( {n\left( {n - 1} \right){{K}_{{2,n,n}}} - {{\alpha }_{{2,n,n}}}} \right)} \right) - } \right. \\ - \;\frac{{{{e}^{2}}}}{3}\left( {\frac{{\partial {{M}_{{n - 2}}}\left( t \right)}}{{\partial t}}\frac{{\left( {\left( {n - 2} \right)\left( {n - 3} \right){{K}_{{2,n - 2,n}}} - {{\alpha }_{{2,n - 2,n}}}} \right)}}{{\left( {n - 2} \right)}} + } \right. \\ \left. {\left. { + \;\frac{{\partial {{M}_{{n + 2}}}\left( t \right)}}{{\partial t}}\frac{{\left( {\left( {n + 2} \right)\left( {n + 1} \right){{K}_{{2,n + 2,n}}} - {{\alpha }_{{2,n + 2,n}}}} \right)}}{{\left( {n + 2} \right)}}} \right)} \right);\quad \left( {n \geqslant 0} \right) \\ \end{gathered} $

(4.12)

$\begin{gathered} {{F}_{n}}\left( t \right) = \Phi _{s}^{{\left( 1 \right)}}{{\delta }_{{n,0}}} + {{E}_{0}}[3(\mu _{{n - 1}}^{ + }{{M}_{{n - 1}}}\left( t \right) + \mu _{{n + 1}}^{ - }{{M}_{{n + 1}}}\left( t \right)) + \\ + \;{{e}^{2}}\left( {{{M}_{{n - 3}}}\left( t \right){{l}_{1}} + {{M}_{{n - 1}}}\left( t \right){{l}_{2}} + {{M}_{{n + 1}}}\left( t \right){{l}_{3}} + {{M}_{{n + 3}}}\left( t \right){{l}_{4}}} \right)] + \\ + \;Q[{{M}_{n}}\left( t \right) + {{e}^{2}}\left( {{{M}_{{n - 2}}}\left( t \right){{l}_{5}} + {{M}_{n}}\left( t \right){{l}_{6}} + {{M}_{{n + 2}}}\left( t \right){{l}_{7}}} \right)];\quad (n \geqslant 0) \\ \end{gathered} $

$\Phi _{s}^{{\left( 1 \right)}} = \frac{1}{{35}}{{e}^{2}}\left( {6{{E}_{0}}{{M}_{3}}\left( t \right) + 14Q{{M}_{2}}\left( t \right)} \right)$

${{M}_{0}}(t) = - \frac{2}{3}{{e}^{2}}{{M}_{2}}(t);\quad {{M}_{1}}(t) = - \frac{3}{5}{{e}^{2}}{{M}_{3}}(t)$

$\mu _{n}^{ + } = \frac{{n + 1}}{{2n + 1}};\quad \mu _{n}^{ - } = \frac{n}{{2n + 1}}$

${{K}_{{m,k,n}}} = {{[C_{{k0,m0}}^{{n0}}]}^{2}};\quad {{\alpha }_{{m,k,n}}} = - \sqrt {m(m + 1)k(k + 1)} C_{{m0,k0}}^{{n0}} \cdot C_{{m - 1,k1}}^{{n0}}$

где $C_{{mk,lp}}^{{nq}}$ – коэффициенты Клебша–Гордана [24], отличные от нуля, только когда индексы удовлетворяют соотношениям |m – k| ≤ n ≤ m + k, m + k + n – четное и k + p = q. Коэффициенты l_j, зависящие только от номера моды n, не приводятся, чтобы не загромождать изложение тривиальными выражениями.

Подставляя полученные выражения в динамическое граничное условие (4.4) с учетом (4.11), запишем неоднородное дифференциальное уравнение второго порядка (эволюционное уравнение) для нахождения амплитудных коэффициентов M_n(t)

(4.13)

$\begin{gathered} \frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}{{M}_{n}}\left( t \right) + \omega _{n}^{2}{{M}_{n}}\left( t \right) = \\ \; = {{e}^{2}}\left( {\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}{{M}_{{n - 2}}}(t){{\chi }_{1}} + {{M}_{{n - 2}}}(t){{\chi }_{2}} + \frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}{{M}_{{n + 2}}}(t){{\chi }_{3}} + {{M}_{{n + 2}}}(t){{\chi }_{4}}} \right) + \\ \; + \frac{1}{{4\pi }}({{Q}^{2}}{{e}^{2}}\left( {{{M}_{{n - 2}}}(t){{\chi }_{5}} + {{M}_{{n + 2}}}(t){{\chi }_{6}}} \right) + Q{{E}_{0}}({{M}_{{n - 1}}}(t){{\chi }_{7}} + {{M}_{{n + 1}}}(t){{\chi }_{8}})) \\ \end{gathered} $

χ_n – коэффициенты, зависящие только от номера моды, приведены в приложении; частота осцилляций n-й моды ω_n определяется в виде:

$\begin{gathered} \omega _{n}^{2} = n\left( {\left( {n - 1} \right)\left( {n + 2} \right) - {{e}^{2}}\frac{{(2{{n}^{5}} + 23{{n}^{4}} + 21{{n}^{3}} - 17{{n}^{2}} - 7n - 2)}}{{\left( {2n - 1} \right)\left( {2n + 1} \right)\left( {2n + 3} \right)}} + } \right. \\ \left. {\; + 4W\left( {{{e}^{2}}\frac{{(4{{n}^{4}} + 6{{n}^{3}} - 2{{n}^{2}} - 2n - 1)}}{{\left( {2n - 1} \right)\left( {2n + 1} \right)\left( {2n + 3} \right)}} - \left( {n - 1} \right)} \right)} \right) \\ \end{gathered} $

Будем искать решение получившегося эволюционного уравнения (4.9) в виде суммы общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения.

Полагая, что зависимость от времени амплитуд возмущения M_n(t) является экспоненциальной, решение однородного уравнения представим в следующем виде:

(4.14)

${{M}_{n}}{{\left( t \right)}_{{одн}}} = {{a}_{n}}\exp \left( {i\left( {{{\omega }_{n}}t + {{b}_{n}}} \right)} \right) + {\text{к}}{\text{.с}}{\text{.;}}\quad \left( {n \geqslant 0} \right)$

где a_n и b_n – вещественные константы, определяемые из начальных условий; аббревиатурой “к.с.” обозначены слагаемые, комплексно сопряженные к выписанным.

Частное решение неоднородного уравнения можно найти, используя метод последовательных приближений по e².

Общее решение эволюционного уравнения с учетом (4.14) имеет вид:

(4.15)

$\begin{gathered} {{M}_{n}}\left( t \right) = 2\left( {{{a}_{n}}\cos ({{\omega }_{n}}t + {{b}_{n}}) + {{e}^{2}}({{a}_{{n - 2}}}{{\alpha }_{1}}(n)\cos ({{\omega }_{{n - 2}}}t + {{b}_{{n - 2}}}) + {{a}_{{n + 2}}}{{\alpha }_{2}}(n)\cos ({{\omega }_{{n + 2}}}t + {{b}_{{n + 2}}}))\mathop + \limits_{} } \right. \\ \left. {\; + \frac{3}{{4\pi }}Q{{E}_{0}}({{a}_{{n - 1}}}{{\alpha }_{3}}(n)\cos ({{\omega }_{{n - 1}}}t + {{b}_{{n - 1}}}) + {{a}_{{n + 1}}}{{\alpha }_{4}}(n)\cos ({{\omega }_{{n + 1}}}t + {{b}_{{n + 1}}}))} \right) \\ \end{gathered} $

Удовлетворяя начальным условиям (2.2), получим вещественные константы a_n и b_n в виде:

${{a}_{n}} = \frac{1}{2}{{h}_{j}}\left( {{{\delta }_{{j,n}}} + {{e}^{2}}\left( {{{\delta }_{{j,n - 2}}}{{\alpha }_{5}}\left( n \right) + {{\delta }_{{j,n}}}{{\alpha }_{6}}\left( n \right) + {{\delta }_{{j,n + 2}}}{{\alpha }_{7}}\left( n \right)} \right) - \frac{3}{{4\pi }}Q{{E}_{0}}\left( {{{\delta }_{{j,n - 1}}}{{\alpha }_{1}}\left( n \right) + {{\delta }_{{j,n + 1}}}{{\alpha }_{2}}\left( n \right)} \right)} \right)$

(4.16)

${{b}_{n}} = 0;\quad (j \in \Xi ,n = 2,\,\,3,\,\,4...)$

где δ_j,_n – символ Кронекера. Выражения для коэффициентов α₁(n) – α₇(n), зависящих от значения индекса n и от физического параметра W, определенного (3.4), не приводятся в виду их чрезвычайной громоздкости.

В итоге, подставляя полученные соотношения (4.16) в общее решение неоднородного эволюционного уравнения (4.15), определим уравнение r(θ, t), описывающее форму возмущенной поверхности заряженной капли, осциллирующей в суперпозиции гравитационного и электростатического полей, с точностью до слагаемых первого порядка по каждому из малых параметров ε и e² в виде

(4.17)

$r(\theta ,t) = 1 + {{e}^{2}}h\left( \theta \right) + \varepsilon \sum\limits_{j\, \in \,\Xi } {{{M}_{j}}\left( t \right){{P}_{j}}\left( \mu \right)} $

где амплитудные коэффициенты M_n(t) имеют следующий вид:

(4.18)

$\begin{gathered} {{M}_{j}}\left( t \right) = \left( {{{h}_{j}} + {{S}_{1}}\left( j \right)} \right)\cos \left( {{{\omega }_{j}}t} \right) + {{S}_{2}}\left( j \right)\left( {\cos \left( {{{\omega }_{{j - 2}}}t} \right) - \cos \left( {{{\omega }_{j}}t} \right)} \right) + \\ \; + {{S}_{3}}\left( j \right)\left( {\cos \left( {{{\omega }_{j}}t} \right) - \cos \left( {{{\omega }_{{j + 2}}}t} \right)} \right) + {{S}_{4}}\left( j \right)\cos \left( {{{\omega }_{{j - 1}}}t} \right) + {{S}_{5}}\left( j \right)\cos \left( {{{\omega }_{{j + 1}}}t} \right) \\ \end{gathered} $

где S_i(j) – коэффициенты, зависящие от начальных амплитуд h_j, h_{j ± 1}, h_{j ±} ₂, от физических параметров W, w и e², определенных (3.4), от значения индекса j. Аналитический вид коэффициентов не приводится в силу громоздкости. Заметим, что S₁(j), S₄(j), S₅(j) имеют величину порядка ~ QE₀, а S₂(j), S₃(j) ~ e². В отсутствие внешнего электрического коэффициенты S_i(j) обращаются в ноль, и амплитуды возмущения M_n(t) будут определяться лишь слагаемым с частотой ${{\omega }_{j}}$: M_j(t) = h_j·cos(ω_jt)_.

Подставляя в (4.9) соотношения (4.12) и (4.18) для коэффициентов F_n(t) и M_j(t), найдем поправку к электрическому потенциалу, связанную с возмущением поверхности капли, в виде

(4.19)

$\begin{gathered} {{\Phi }^{{\left( 1 \right)}}}\left( {{\mathbf{r}},t} \right) = \varepsilon \left( {\frac{1}{{35r}}{{e}^{2}}\left( {6{{E}_{0}}{{M}_{3}}\left( t \right) + 14Q{{M}_{2}}\left( t \right)} \right) + \sum\limits_{j \in \Xi } {\{ {{E}_{0}}[3(\mu _{{j - 1}}^{ + }{{M}_{{j - 1}}}\left( t \right) + \mu _{{j + 1}}^{ - }{{M}_{{j + 1}}}\left( t \right)) + } } \right. \\ \; + {{e}^{2}}\left( {{{M}_{{j - 3}}}\left( t \right){{l}_{1}}\left( j \right) + {{M}_{{j - 1}}}\left( t \right){{l}_{2}}\left( j \right) + {{M}_{{j + 1}}}\left( t \right){{l}_{3}}\left( j \right) + {{M}_{{j + 3}}}\left( t \right){{l}_{4}}\left( j \right)} \right)] + \\ \left. {_{{_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}}\, + Q[{{M}_{j}}\left( t \right) + {{e}^{2}}({{M}_{{j - 2}}}\left( t \right){{l}_{5}}\left( j \right) + {{M}_{j}}\left( t \right){{l}_{6}}\left( j \right) + {{M}_{{j + 2}}}\left( t \right){{l}_{7}}\left( j \right))]\} {{r}^{{ - \left( {j + 1} \right)}}}{{P}_{j}}\left( \mu \right)} \right) \\ \end{gathered} $

5. ПОВЕРХНОСТНАЯ ПЛОТНОСТЬ ЗАРЯДА

Найдем поверхностную плотность ν(r, t) собственного и индуцированного внешним электростатическим полем зарядов, распределенных по возмущенной поверхности идеально проводящей капли, по известной формуле:

(5.1)

$\nu \left( {{\mathbf{r}},t} \right) = {{\left. {\frac{{{{E}_{n}}({\mathbf{r}},t)}}{{4\pi }}} \right|}_{{r = r(\theta ,t)}}} = {{\left. { - \frac{1}{{4\pi }}\left( {{\mathbf{n}}\left( {{\mathbf{r}},t} \right),\nabla \Phi \left( {{\mathbf{r}},t} \right)} \right)} \right|}_{{r = r\left( {\theta ,t} \right)}}}$

где r(θ, t) определяется соотношением (4.17).

Используя разложение (2.5) для электрического потенциала и вектор нормали к возмущенной поверхности сфероида в виде:

(5.2)

${\mathbf{n}}\left( {{\mathbf{r}},t} \right) = \left( {1 - \frac{1}{3}{{e}^{2}}\frac{{\partial {{P}_{2}}\left( \mu \right)}}{{\partial \theta }}\frac{{\partial \xi \left( {\theta ,t} \right)}}{{\partial \theta }}} \right){{{\mathbf{e}}}_{r}} - \left( {\frac{{\partial \xi \left( {\theta ,t} \right)}}{{\partial \theta }} + \frac{1}{3}{{e}^{2}}\left( {\left( {1 - \xi \left( {\theta ,t} \right)} \right)\frac{{\partial {{P}_{2}}\left( \mu \right)}}{{\partial \theta }} - {{P}_{2}}\left( \mu \right)\frac{{\partial \xi \left( {\theta ,t} \right)}}{{\partial \theta }}} \right)} \right){{{\mathbf{e}}}_{\theta }}$

и используя (5.1), выпишем поверхностную плотность заряда (собственного и индуцированного внешним электростатическим полем) на возмущенной капле $r(\theta ,t)$ с точностью до слагаемых порядка E₀e²ε $\sim E_{0}^{3}\varepsilon $

(5.3)

$\begin{gathered} \nu \left( {{\mathbf{r}},t} \right) = \frac{1}{{4\pi }}\left( {Q\left[ {1 + \frac{1}{3}{{e}^{2}}{{P}_{2}}\left( \mu \right)} \right] + 3{{E}_{0}}\left[ {{{P}_{1}}\left( \mu \right) + \frac{2}{5}{{e}^{2}}{{P}_{3}}\left( \mu \right)} \right]\mathop {\mathop - \limits^{} }\limits_{} } \right. \\ \; - 2\left( {Q[1 + {{e}^{2}}{{P}_{2}}\left( \mu \right)] + {{E}_{0}}\left[ {3{{P}_{1}}\left( \mu \right) + \frac{1}{5}{{e}^{2}}\left( {{{P}_{1}}\left( \mu \right) + 15{{P}_{3}}\left( \mu \right)} \right)} \right]} \right)\xi \left( {\theta ,t} \right) - \\ {{\left. {\left. {\; - \frac{{\partial {{\Phi }^{{\left( 1 \right)}}}}}{{\partial r}} + \frac{1}{3}{{e}^{2}}\left( {\frac{{\partial {{\Phi }^{{\left( 1 \right)}}}}}{{\partial \theta }}\frac{{\partial {{P}_{2}}\left( \mu \right)}}{{\partial \theta }} - \frac{{{{\partial }^{2}}{{\Phi }^{{\left( 1 \right)}}}}}{{\partial {{r}^{2}}}}{{P}_{2}}\left( \mu \right)} \right)} \right)} \right|}_{{r = 1}}} \\ \end{gathered} $

Здесь функции ξ(θ, t) и Ф⁽¹⁾(r, t) имеют первый порядок малости по $\varepsilon $. В (5.2) e_r и e_θ – орты сферической системы координат.

Учитывая возмущение равновесной формы поверхности капли из (4.17) и решение (4.19) для поправки первого порядка к электрическому потенциалу, определим поверхностную плотность заряда в виде разложения по полиномам Лежандра

(5.4)

$\begin{gathered} \nu \left( {{\mathbf{r}},t} \right) = \frac{1}{{4\pi }}\left( {Q\left[ {1 + \frac{1}{3}{{e}^{2}}{{P}_{2}}\left( \mu \right)} \right] + 3{{E}_{0}}\left[ {{{P}_{1}}\left( \mu \right) + \frac{2}{5}{{e}^{2}}{{P}_{3}}\left( \mu \right)} \right] + \varepsilon \sum\limits_{j \in \Xi } {\left\{ {Q{{M}_{j}}\left( t \right){{k}_{0}}\mathop + \limits_{}^{} } \right.} } \right. \\ \; + {{E}_{0}}\left[ {{{M}_{{j - 1}}}\left( t \right){{k}_{1}} + {{M}_{{j + 1}}}\left( t \right){{k}_{2}}} \right] + {{e}^{2}}\left( {Q\left[ {{{M}_{{j - 2}}}\left( t \right){{k}_{3}} + {{M}_{j}}\left( t \right){{k}_{4}} + {{M}_{{j + 2}}}\left( t \right){{k}_{5}}} \right]\mathop + \limits_{}^{} } \right. \\ \left. {\left. {\left. {\;\mathop + \limits_{}^{} {{E}_{0}}\left[ {{{M}_{{j - 3}}}\left( t \right){{k}_{6}} + {{M}_{{j - 1}}}\left( t \right){{k}_{7}} + {{M}_{{j + 1}}}\left( t \right){{k}_{8}} + {{M}_{{j + 3}}}\left( t \right){{k}_{9}}} \right] + \left( {\frac{2}{5}Q{{M}_{2}}\left( t \right) + \frac{6}{{35}}{{E}_{0}}{{M}_{3}}\left( t \right)} \right){{\delta }_{{j,0}}}} \right)} \right\}{{P}_{j}}\left( \mu \right)} \right) \\ \left( {j \in \Xi } \right) \\ \end{gathered} $

где коэффициенты k₀– k₉, зависящие лишь от значения индекса j, приведены в приложении. Из вида выражения (5.4) следует, что поверхностная плотность заряда представлена в виде суперпозиции поверхностных плотностей собственного и индуцированного зарядов, распределенных по возмущенной поверхности заряженной капли, осциллирующей в электростатическом поле.

6. КВАДРУПОЛЬНЫЙ МОМЕНТ

Для вычисления интенсивности квадрупольного излучения от электропроводной капли рассчитаем тензор ее электрического квадрупольного момента D_αβ(t) в сферической системе координат с началом в центре масс капли, учитывая формальное соотношение, связывающее объемную плотность заряда γ = γ(t) с поверхностной $\nu = \nu (\theta ,t)$ на проводящей осесимметричной капле:

$\gamma (r,\theta ,t) \equiv \nu \left( {\theta ,t} \right)\delta \left( {r - r(\theta ,t)} \right)$

где δ(r – r(θ, t)) – дельта-функция Дирака [5], в сферической системе координат с началом в центре капли. Наличие дельта-функции в выше записанных выражениях позволяет перейти от интегрирования по объему капли в (1.2) к интегрированию по возмущенной поверхности капли. В результате, аналогично тому, как это было проделано в [14], компоненты тензора квадрупольного момента запишутся в виде:

${{D}_{{12}}} = {{D}_{{21}}} = {{D}_{{13}}} = {{D}_{{31}}} = {{D}_{{23}}} = {{D}_{{32}}} = 0$

(6.1)

$\begin{gathered} {{D}_{{11}}}\left( t \right) = {{D}_{{22}}}\left( t \right) = - \frac{1}{2}{{D}_{{33}}}\left( t \right) = \pi \int\limits_0^\pi {\frac{{\nu \left( {\theta ,t} \right)}}{{\left( {{\mathbf{n}}\left( {{\mathbf{r}},t} \right),{{{\mathbf{e}}}_{r}}} \right)}}{{r}^{4}}\left( {\theta ,t} \right)(1 - 3{{{\cos }}^{2}}\theta )\sin \theta d\theta } = \\ \; = - 2\pi \int\limits_0^\pi {\frac{{\nu \left( {\theta ,t} \right)}}{{\left( {{\mathbf{n}}\left( {{\mathbf{r}},t} \right),{{{\mathbf{e}}}_{r}}} \right)}}{{r}^{4}}\left( {\theta ,t} \right){{P}_{2}}\left( \mu \right)\sin \theta d\theta } \\ \end{gathered} $

Используя поверхностную плотность заряда (5.3) и вектор нормали (5.2) к возмущенной поверхности капли (2.1), запишем подынтегральное выражение в (6.1) с точностью до слагаемых ~E₀e²ε:

(6.2)

Подставляя (6.2) в (6.1) и учитывая вид функции $\xi \left( {\theta ,t} \right)$, выражение (4.19) для Ф⁽¹⁾(r, t), используя ортогональность полиномов Лежандра, выражение (4.18) и переходя к размерным переменным, получим диагональные компоненты D_αβ в окончательном виде с точностью до слагаемых порядка ~E₀e²ε:

(6.3)

$\begin{gathered} {{D}_{{11}}}\left( t \right) = {{D}_{{22}}}\left( t \right) = - \frac{1}{2}{{D}_{{33}}}\left( t \right) = - \left( {\frac{1}{3}Q{{R}^{2}}{{e}^{2}} + \varepsilon \left( {\left( {Q{{R}^{2}}{{h}_{2}} + \frac{{72}}{{77}}{{E}_{0}}{{R}^{4}}W{{h}_{3}}} \right)\cos \left( {{{\omega }_{2}}t} \right) + } \right.} \right. \\ + \;\frac{9}{7}{{E}_{0}}{{R}^{4}}\left( {1 - \frac{8}{{11}}W} \right){{h}_{3}}\cos \left( {{{\omega }_{3}}t} \right) + {{e}^{2}}\left( {(Q{{R}^{2}}{{f}_{0}} + {{E}_{0}}{{R}^{4}}{{f}_{1}})\cos \left( {{{\omega }_{2}}t} \right)\mathop + \limits^{} } \right. \\ \left. {\left. {\left. {\mathop + \limits^{} \;(Q{{R}^{2}}{{f}_{2}} + {{E}_{0}}{{R}^{4}}{{f}_{3}})\cos \left( {{{\omega }_{3}}t} \right) + (Q{{R}^{2}}{{f}_{4}} + {{E}_{0}}{{R}^{4}}{{f}_{5}})\cos \left( {{{\omega }_{4}}t} \right) + {{E}_{0}}{{R}^{4}}{{f}_{6}}\cos \left( {{{\omega }_{5}}t} \right)} \right)} \right)} \right) \\ \end{gathered} $

Выражения для коэффициентов f₀ – f₆, зависящих от начальных амплитуд h₂, h₃, h₄, h₅ и от физического параметра W, определенного (3.4), приведены в приложении ввиду их громоздкости.

7. ИНТЕНСИВНОСТЬ КВАДРУПОЛЬНОГО ИЗЛУЧЕНИЯ

Для того, чтобы рассчитать интенсивность квадрупольного излучения, найдем максимальное значение суммы в (1.1), используя компоненты тензора квадрупольного момента согласно (6.1) и (6.3):

$\begin{gathered} \sum\limits_{\alpha ,\beta = 1}^3 {\left( {\frac{{{{\partial }^{3}}}}{{\partial {{t}^{3}}}}{{D}_{{\alpha \beta }}}\left( t \right)} \right)_{{\max }}^{2}} = 6{{\varepsilon }^{2}}\left( {\left( {Q{{R}^{2}}{{h}_{2}} + \frac{{72}}{{77}}{{E}_{0}}{{R}^{4}}W{{h}_{3}}} \right)\omega _{2}^{3} + } \right. \\ + \;\frac{9}{7}{{E}_{0}}{{R}^{4}}\left( {1 - \frac{8}{{11}}W} \right){{h}_{3}}\omega _{3}^{3} + {{e}^{2}}((Q{{R}^{2}}{{k}_{0}} + {{E}_{0}}{{R}^{4}}{{k}_{1}})\omega _{2}^{3} + \\ {{\left. {\mathop + \limits^{} (Q{{R}^{2}}{{k}_{2}} + {{E}_{0}}{{R}^{4}}{{k}_{3}})\omega _{3}^{3} + (Q{{R}^{2}}{{k}_{4}} + {{E}_{0}}{{R}^{4}}{{k}_{5}})\omega _{4}^{3} + {{E}_{0}}{{R}^{4}}{{k}_{6}}\omega _{5}^{3})} \right)}^{2}} \\ \end{gathered} $

В итоге аналитическое выражение для интенсивности квадрупольного излучения электропроводной сфероидальной заряженной капли, осциллирующей в суперпозиции гравитационного и электростатического полей, примет следующий вид:

(7.1)

$\begin{gathered} I = \frac{1}{{30{{c}^{5}}}}{{\varepsilon }^{2}}\left( {\left( {Q{{R}^{2}}{{h}_{2}} + \frac{{72}}{{77}}{{E}_{0}}{{R}^{4}}W{{h}_{3}}} \right)\omega _{2}^{3} + \frac{9}{7}{{E}_{0}}{{R}^{4}}\left( {1 - \frac{8}{{11}}W} \right){{h}_{3}}\omega _{3}^{3} + } \right. \\ {{\left. { + \;{{e}^{2}}((Q{{R}^{2}}{{k}_{0}} + {{E}_{0}}{{R}^{4}}{{k}_{1}})\omega _{2}^{3} + (Q{{R}^{2}}{{k}_{2}} + {{E}_{0}}{{R}^{4}}{{k}_{3}})\omega _{3}^{3}\mathop + \limits_{}^{} (Q{{R}^{2}}{{k}_{4}} + {{E}_{0}}{{R}^{4}}{{k}_{5}})\omega _{4}^{3} + {{E}_{0}}{{R}^{4}}{{k}_{6}}\omega _{5}^{3})} \right)}^{2}} \\ \end{gathered} $

Из вида выражения (7.1) следует, что квадрупольное излучение обусловлено капиллярными осцилляциями заряженной капли в поле на второй, третьей, четвертой и пятой модах, если форма возмущенной поверхности капли обнаружена в расчетах первого порядка по каждому из малых параметров ε и e².

Используя (7.1), можно оценить величину интенсивности фонового шумового электромагнитного излучения от различных жидкокапельных систем искусственного и естественного происхождения, например таких, как конвективные облака. Возможный источник электромагнитного излучения связан с осцилляциями конечной амплитуды мелких капель из диапазона наиболее часто встречающихся в облаке размеров от 3 мкм до 30 мкм. Концентрация $n$ таких капель в облаке ~10³ см³ [25]. Осцилляции большой амплитуды облачных капель могут быть вызваны различными причинами: коагуляцией; дроблением на более мелкие в результате процессов столкновения или в результате реализации электростатической неустойчивости; гидродинамическим и электрическим взаимодействием близко пролетающих капель; аэродинамическим взаимодействием с развитой мелкомасштабной турбулентностью, характерной для грозовых облаков. Амплитуды колебаний облачных капель, согласно данным натурных наблюдений [18, 19], могут достигать десятков процентов от радиуса капли.

Проведем оценку интенсивности фонового квадрупольного электромагнитного излучения единичной слабо заряженной капли, осциллирующей в электростатическом поле. Для численных оценок примем [26]: ε = 0.1, h₂ = h₃ = h₄ = h₅ = 0.25, σ = 73 дин/см, ρ = 1 г/см³, Q = 1 × 10^–6 СГСЭ (~4 × 10^–3Q_кр (Q_кр – критическое значение заряда) при R = 3 мкм и ~1 × 10^–4Q_кр при R = = 30 мкм), E₀= 0.17 СГСЭ (E₀= 50 В/см) (~5 × 10^–5E_0кр (E_0кр – критическое значение напряженности поля) при R = 3 мкм и ~2 × 10^–4E_0кр при R = 30 мкм), R = 30 мкм. Тогда из (7.1) несложно получить I ~ 2 × 10^–46 эрг/с. В проведенной оценке принято, что величина собственного заряда капли совпадает с величиной индуцированного внешним электростатическим полем заряда: Q = q = 0.75E₀·R². Для капли радиусом R = 8 мкм получим значение интенсивности излучения I ~ 2 × 10^–45 эрг/с. Для капли размером R = 3 мкм получим оценку I ~ 1 × 10^–43 эрг/с. Результаты расчетов приведены на рис. 1 (кривая 1).

Рис. 1.

Зависимость интенсивности квадрупольного электромагнитного излучения единичной заряженной капли, осциллирующей в однородном электростатическом поле, от радиуса равновеликой сферической капли: ε = 0.1, h₂ = h₃ = h₄ = h₅ = 0.25, σ = 73 дин/см, ρ = 1 г/см³, кривая 1 соответствует Q = 1 × 10^–6 СГСЭ (~4 × × 10^–3Q_кр (R = 3 мкм) и ~1 × 10^–4Q_кр (R = 30 мкм)), E₀= 0.17 СГСЭ (E₀= 50 В/см) (~5 × 10^–5E_0кр (R = 3 мкм) и ~2 × 10^–4E_0кр (R = 30 мкм)), кривая 2 – Q = 1 × 10^–6 СГСЭ, E₀= 0, кривая 3 – Q = 0, E₀= 0.17 СГСЭ (E₀= 50 В/см).

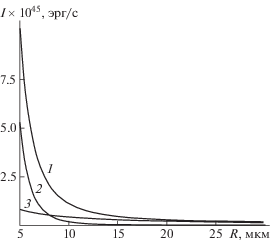
Видно, что с увеличением размера капли интенсивность излучения быстро снижается: при увеличении радиуса капли на порядок (от R = 3 мкм до R = 30 мкм) интенсивность излучения уменьшается в 600 раз. Это соответствует аналитической зависимости (7.1), при учете того обстоятельства, что ω = ω(R), а также W = W(R).

Для сравнения зависимостей величины интенсивности излучения от размера капель, на рис. 1 проиллюстрированы зависимостями интенсивности излучения при отсутствии заряда на капле Q = 0 (кривая 2) и при отсутствии внешнего электрического поля E₀= 0 (кривая 3).

Расчеты показывают (см. кривую 2), что в случае слабо заряженной капли (~3 × 10^–3·Q_кр при R = 3 мкм и ~1 × 10^–4Q_кр при R = 30 мкм), осциллирующей в отсутствии электрического поля, с увеличением размера капли интенсивность излучения убывает быстро: при увеличении радиуса на порядок (от R = 3 мкм до R = 30 мкм) интенсивность электромагнитного излучения уменьшается в 10⁵ раз.

Для незаряженной капли, осциллирующей в электростатическом поле (~5 × 10^–5E_0кр при R = = 3 мкм и ~2 × 10^–4E_0кр при R = 30 мкм), расчеты показывают (см. кривую 3), что при изменении радиуса капли на порядок (от R = 3 мкм до R = 30 мкм) интенсивность излучения убывает лишь на порядок.

Из рис. 1 видно, что простое сложение кривых 2 и 3 не дает кривой 1. Это связано с тем, что выражение (7.1) содержит заряд Q и напряженность электростатического поля E₀ в виде произведений (с учетом зависимости W от Q), и при обращении ноль E₀ или Q качественный вид зависимости (7.1) меняется.

Интенсивность электромагнитного излучения из облака будет в N раз больше по сравнению с одиночной каплей (N – число капель в облаке), если принять для оценки по порядку величины, что все капли имеют одинаковый размер и осциллируют синфазно. Это может иметь место при разряде молнии в случае резкого изменения величины напряженности поля за характерное время, меньшее периода осцилляций капель. Если капли осциллируют независимо друг от друга, с произвольными фазами, то интегральная мощность излучения из облака будет в корень квадратный из N раз больше, чем интенсивность излучения единичной капли [12].

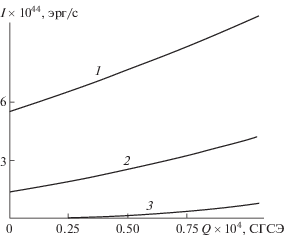
На рис. 2 представлены зависимости интенсивности излучения от величины собственного заряда для одиночной капли. Кривые 1 и 2 построены при конечном значении напряженности электростатического поля. Видно, что с ростом величины заряда на капле на порядок, интенсивность излучения увеличивается примерно в два раза. Кривой 3 нанесена такая же зависимость, рассчитанная при E₀= 0. Из кривых 1–3 видно, что интенсивность излучения снижается по величине при уменьшении величины напряженности внешнего поля. Уменьшается и скорость прироста интенсивности при увеличении собственного заряда, что вызвано, по-видимому, исчезновением слагаемых в (7.1), содержащих произведения QE₀.

Рис. 2.

Зависимость интенсивности квадрупольного электромагнитного излучения единичной заряженной капли, осциллирующей в однородном электростатическом поле, от величины ее заряда, рассчитанного при тех же прочих значениях физических величин, что на рис. 1 и R = 30 мкм. Кривая 1 соответствует E₀= 3.4 СГСЭ (E₀= 1000 В/см~ 3 × 10^–3E_0кр), кривая 2 – E₀= 1.7 СГСЭ (E₀= 500 В/см~2 × 10^–3E_0кр), кривая 3 – E₀= 0.

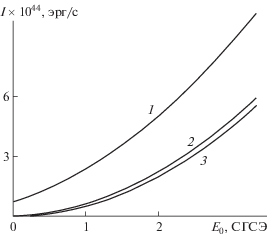
На рис. 3 приведены зависимости интенсивности излучения от величины напряженности электростатического поля. Видно, что как в случае заряженной капли (кривые 1 и 2), так и в случае незаряженной (кривая 3), интенсивность излучения быстро увеличивается с ростом E₀. В частности, видно, что в отсутствие заряда зависимость интенсивности излучения от величины напряженности E₀ сохраняет качественный вид, снижаясь по абсолютной величине. Снижается и скорость увеличения интенсивности с ростом E₀, что вызвано, по-видимому, исчезновением слагаемых в (7.1), содержащих произведения QE₀.

Рис. 3.

Зависимость интенсивности квадрупольного электромагнитного излучения единичной заряженной капли, осциллирующей в однородном электростатическом поле, от величины напряженности внешнего электростатического поля, рассчитанного при тех же прочих значениях физических величин, что на рис. 1 и R = 30 мкм. Кривая 1 соответствует ~1 × 10^–4 СГСЭ ~ 1 × 10^–2Q_кр, кривая 2 – Q = 1 × 10^–5 СГСЭ ~1 × 10^–3Q_кр , кривая 3 – Q = 0.

ЗАКЛЮЧЕНИЕ

В рамках электрогидродинамического расчета найдено аналитическое выражение для зависящего от времени квадрупольного момента заряженной капли, осциллирующей в суперпозиции гравитационного и электростатического полей. Оценена интенсивность электромагнитного излучения от такой капли, обусловленного изменением во времени величины ее квадрупольного момента.

Список литературы

Крауфорд Ф. Волны. Берклеевский курс физики. Т. 3. М.: Наука, 1976. 528 с.
Астахов А.В., Широков Ю.М. Курс физики. Т. 2. Электромагнитное поле. М.: Физматгиз, 1980. 360 с.
Сивухин Д.В. Общий курс физики. Т. 3. Электричество. Часть вторая. М.: Наука, 1996. 320 с.
Калечиц В.И., Нахутин И.Е., Полуэктов П.П. О возможном механизме радиоизлучения конвективных облаков // ДАН СССР. 1982. Т. 262. № 6. С. 1344–1347.
Левич В.Г. Курс теоретической физики. Т. 1. М.: Физматгиз, 1969. 910 с.
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. 2. Теория поля. М.: Наука, 1973. 504 с.
Белоцерковский А.В., Дивинский Л.И. Активно-пассивная радиолокация грозовых и грозоопасных очагов в облаках / Под ред. Качурина Л.Г. и Дивинского Л.И. СПб: Гидрометеоиздат, 1992. 286 с.
Качурин Л.Г. Физические основы воздействия на атмосферные процессы. Л.: Гидрометеоиздат, 1990. 463 с.
Горелик А.Г., Козлов А.И., Стерлядкин В.В. Рассеяние радиоволн на несферических и осциллирующих дождевых каплях // Науч. вест. МГТУ ГА. 2012. № 176. С. 25–30.
Френкель Я.И. Теория явлений атмосферного электричества. Л–М.: Гостехтеориздат, 1949. 155 с.
Григорьев А.И., Ширяева С.О. Электромагнитное излучение осциллирующей заряженной капли конечной проводимости // Изв. РАН. МЖГ. 2002. № 5. С. 74–80.
Богатов Н.А. Электромагнитное поле, генерируемое капиллярными колебаниями капель // Сборник тезисов докладов VI Международной конференции “Солнечно-земные связи и физика предвестников землетрясений”. Петропавловск-Камчатский, ДВО РАН, 2013. С. 10–11.
Григорьев А.И., Колбнева Н.Ю., Ширяева С.О. Дипольное электромагнитное излучение заряженной капли, осциллирующей в однородном электростатическом поле // Изв. РАН. МЖГ. 2018. № 2. С. 62–76.
Григорьев А.И., Колбнева Н.Ю., Ширяева С.О. Квадрупольное электромагнитное излучение осциллирующей заряженной капли // ЖТФ. 2017. Т. 87. Вып. 6. С. 914–920.
Abbas M.A., Latham J. The disintegration and electrification of charged water drops falling in an electric field // Quart. J. Roy. Met. Soc. 1969. V. 95. P. 63–76.
Григорьев А.И., Ширяева С.О., Белавина Е.И. Равновесная форма заряженной капли в электрическом и гравитационном полях // Журн. техн. физики. 1989 Т. 59. Вып. 6. С. 27–34.
Френкель Я.И. К теории Тонкса о разрыве поверхности жидкости постоянным электрическим полем в вакууме // ЖЭТФ. 1936. Т. 6. № 4. С. 348–350.
Beard K.V., Tokay A.A. The field study of small raindrop oscillation // Geophysical Research Letters. 1991. El. № 12. P. 2257–2260.
Стерлядкин В.В. Натурные измерения колебаний капель осадков // Изв. АН СССР. ФАО. 1988. Т. 24. № 6. С. 613–621.
Ландау Л.Д., Лифшиц Е.М. Гидродинамика. М.: Наука, 1986. 733 с.
Hendrics C.D., Schneider J.M. Stability of conducting droplet under the influence of surface tension and electrostatic forces // J. Amer. Phys. 1963. V. 1. № 6. P. 450–453.
Найфе А.Х. Методы возмущений. М.: Мир, 1976. 455 с.
Ландау Л.Д., Лифшиц Е.М. Электродинамика сплошных сред. М.: Наука, 1982. 621 с.
Варшалович Д.А., Москалев А.Н., Херсонский В.К. Квантовая теория углового момента. Л.: Наука, 1975. 436 с.
Мазин И.П., Шметер С.М. Облака. Строение и физика образования. Л.: Гидрометеоиздат, 1983. 280 с.
Мазин И.П., Хргиан А.Х., Имянитов И.М. Облака и облачная атмосфера. Справочник. Л.: Гидрометеоиздат, 1989. 647 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал