Известия РАН. Механика жидкости и газа, 2019, № 5, стр. 125-134
Исследование сингулярности течения в тройной точке стационарного нерегулярного маховского отражения ударной волны в плоском канале
Е. И. Васильев *
Волгоградский государственный университет
Волгоград, Россия
* E-mail: vasilev@volsu.ru
Поступила в редакцию 04.02.2019
После доработки 06.03.2019
Принята к публикации 06.03.2019
Аннотация
В рамках модели Эйлера рассмотрена задача стационарного маховского отражения ударной волны в плоском канале с акцентом на исследование параметров течения в тройной точке. В аналитическом исследовании использована локальная теория для криволинейных ударных волн. Получено условие на исходные данные задачи, при которых в тройной точке реализуется сингулярность. В условиях сингулярности градиенты параметров течения и кривизна фронтов ударных волн и тангенциального разрыва в тройной точке обращаются в бесконечность. В численном исследовании использован разностный метод Годунова второго порядка и новая технология стягивающейся к тройной точке сетки в сочетании с выделением разрывов. Расчеты подтвердили аналитически предсказанную границу сингулярности. Дополнительные численные эксперименты показали, что граница сингулярности сохраняется при введении искусственных источников в уравнение энергии. Эти результаты позволяют выдвинуть гипотезу, что сингулярность в тех же границах реализуется и для других двумерных течений с нерегулярным отражением ударных волн.
Впервые на возможность существования сингулярности в тройной точке конфигурации Маха указал Гудерлей [1] на основании исследований в приближении потенциального течения. Согласно его результатам кривизна отраженного фронта, фронта Маха и линии тока при подходе к тройной точке либо уменьшается до нуля, либо стремится к бесконечности. Бесконечная кривизна фронтов ударных волн приводит к бесконечным градиентам параметров течения в точке их пересечения. В работе [2] результаты теоретического анализа в окрестности тройной точки сравнивались с результатами экспериментов. Сделан вывод, что причиной расхождения при дозвуковых течениях за отраженным фронтом является сингулярность в тройной точке. В интерпретации работы [3] пограничные режимы возникновения сингулярности в области исходных данных должны находиться в промежутке между режимами с максимальным углом поворота линии тока в отраженном фронте и режимами с числом Маха, равным 1 за отраженным фронтом. Значительно позже в работе [4] с помощью локальной теории исследовано влияние источников тепла на градиенты поля течения в тройной точке. Сделан вывод, что для плоских стационарных отражений при отсутствии источников тепла градиенты параметров течения должны быть нулевыми, а кривизна фронтов ударных волн должна стремиться к нулю. В работе [5] проведены подобные исследования для осесимметричных и неоднородных течений. Построены зависимости градиентов течения от входящих неоднородностей. Возможное наличие сингулярности в тройной точке в работах [4, 5] не учитывалось. Ясно, что локальная теория не может ответить на вопрос реализуемости решений с сингулярностью, но если она существует, то значительная часть результатов работ [4, 5] вызывает сомнение. Для выяснения этого вопроса необходимо проводить решение в полной постановке. Недавно в [6] с применением численного моделирования высокого разрешения в полной постановке для плоского течения было показано, что сингулярность в тройной точке имеет место не только в регионе парадокса Неймана [7, 8], но также и для региона маховского отражения. Расчеты показали, что логарифмическая сингулярность существует вплоть до перехода в регулярное отражение для слабых ударных волн по крайне мере до чисел Маха набегающего потока М0 < 2. Более точную границу существования сингулярности в [6] установить не удалось. В данной работе устраняется этот пробел.
Рассматривается задача стационарного отражения косой ударной волны с углом наклона β в плоском сверхзвуковом потоке идеального совершенного газа с числом Маха M0 (рис. 1). Фрагмент диаграммы возможных конфигураций тройной точки (Т-конфигурации) в плоскости исходных данных M0 и β для небольшого диапазона умеренно слабых ударных волн в газе с показателем адиабаты γ = 5/3 изображен на рис. 2. В области ниже кривой 1 не существует падающего скачка, так как ${{{\text{M}}}_{0}}\sin {\beta } < 1$. Выше кривой 2 располагается так называемый регион парадокса Неймана, существование сингулярности в котором установлено как численно [7, 8], так и экспериментально [9]. Ниже кривой 2 расположены области, в которых существуют решения в виде трехударной (MR) и двухударной (RR между 3 и 1) конфигураций. Последняя конфигурация соответствует регулярному отражению без тройной точки. Эти области перекрываются, что говорит о возможной неоднозначности решения. В области между 3 и 1 конфигурация Маха существует либо в виде прямой, либо в виде инверсной конфигурации (iMR). В последней угол между фронтом Маха и контактным разрывом больше 90°. Кривая 5 соответствует Т-конфигурациям, в которых поток в отраженной ударной волне имеет максимально возможный угол отклонения. Правее кривой 4 реализуются течения, в которых поток за отраженным фронтом является сверхзвуковым. Заметим, что участки кривых 4 и 5 в RR-области построены для iMR. Прямое MR в данной окрестности решения не имеет. Расчеты, выполненные в [6–8], для серии точек между кривыми 2 и 3 для M0 < 2 показали присутствие сингулярности. Цель данной работы состоит в более точном определении границы существования сингулярности при M0 > 2.
Рис. 1.
Стационарное нерегулярное отражение ударной волны в плоском канале. Изолинии числа Маха для варианта с не максимальной высотой фронта Маха: 1 – фронт падающей ударной волны с углом наклона β к набегающему потоку с числом Маха M0; 2, 3, 4, 5 – стенки канала; L – высота узкой части канала.
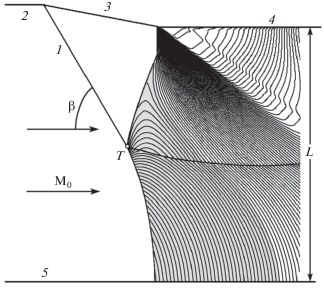
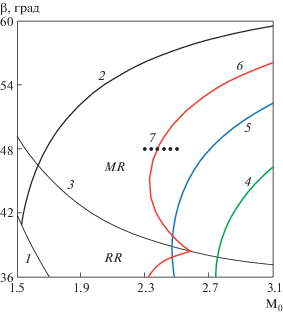
Рис. 2.
Фрагмент диаграммы областей трехударной конфигурации (γ = 5/3); регулярное отражение (RR) 1–3; 2 – нулевой угол отклонения в отраженном скачке; регион Маха (MR) ниже кривой 2; 4 – M = 1 за отраженным скачком; 5 – максимальный угол отклонения в отраженном скачке; 6 – граница сингулярности (2.13); 7 – множество рассчитанных вариантов.
1. ПОСТАНОВКА ЗАДАЧИ И МЕТОД ЧИСЛЕННОГО РЕШЕНИЯ
Рассматривается стационарное сверхзвуковое течение идеального совершенного газа в плоском канале с прямолинейным клином. Конфигурация течения изображена на рис. 1, где представлены изолинии числа Маха для демонстрационного расчета. Порождаемая клином падающая ударная волна 1 отражается нерегулярным образом от нижней стенки канала. В тройной точке T прямолинейный фронт падающей волны расщепляется на фронт отраженной волны (выше точки T), и фронт Маха (ниже точки T). В общем случае оба этих фронта являются криволинейными. Кроме ударных волн, из точки T выходит контактный разрыв, который разделяет потоки, прошедшие по разные стороны от тройной точки. На кромке отражающего клина формируется веер центрированной волны разрежения, который пересекается с отраженным фронтом. Для слабых ударных волн непосредственно за фронтом Маха и отраженной волной реализуется дозвуковое течение (затененная область на рис. 1). Однако ниже по течению волна разрежения переводит поток в сверхзвуковой. Сверхзвуковой режим на выходе из канала является необходимым условием реализуемости такого стационарного течения.
Исходными данными задачи являются число Маха набегающего потока M0 и угол наклона фронта падающего скачка β. При фиксированных размерах клина течение зависит также и от высоты L узкой части канала. Для реализуемости такого течения необходимо, чтобы высота канала L была больше некоторого минимального размера Lm. Стационарное течение возможно лишь в случаях L ≥ Lm, при которых отраженная волна приходит на верхнюю стенку правее центра волны разрежения. Чтобы уменьшить количество исходных данных, в данной работе рассматривались конфигурации с минимальным значением высоты L = Lm, т.е. такие конфигурации, при которых отраженная ударная волна проходит бесконечно близко от центра волны разрежения. Это несколько усложняет технологию численного моделирования, но сужает количество исходных данных до двух: M0 и β. В таких конфигурациях высота фронта Маха имеет максимальное значение.
В численных расчетах стационарное течение отыскивалось как предельное установившееся по времени нестационарное течение.
Двумерное нестационарное течение невязкого совершенного газа с постоянными теплоемкостями описывается дифференциальными уравнениями
(1.1)
$\begin{gathered} \frac{{\partial {\mathbf{a}}}}{{\partial t}} + \frac{\partial }{{\partial x}}{\mathbf{F}}({\mathbf{a}}) + \frac{\partial }{{\partial y}}{\mathbf{G}}({\mathbf{a}}) = {\mathbf{H}} \\ {\mathbf{a}} = \left[ {\begin{array}{*{20}{c}} {\rho } \\ {{\rho }u} \\ {{\rho }v} \\ e \end{array}} \right],\quad {\mathbf{F}}({\mathbf{a}}) = \left[ {\begin{array}{*{20}{c}} {{\rho }u} \\ {p + {\rho }{{u}^{2}}} \\ {{\rho }uv} \\ {(e + p)u} \end{array}} \right],\quad {\mathbf{G}}({\mathbf{a}}) = \left[ {\begin{array}{*{20}{c}} {{\rho }v} \\ {{\rho }uv} \\ {p + {\rho }{{v}^{2}}} \\ {(e + p)v} \end{array}} \right],\quad {\mathbf{H}} = \left[ {\begin{array}{*{20}{c}} 0 \\ 0 \\ 0 \\ S \end{array}} \right] \\ e = \frac{p}{{{\gamma } - 1}} + \frac{1}{2}{\rho }({{u}^{2}} + {{v}^{2}}) \\ \end{gathered} $Здесь x – координата вдоль нижней отражающей плоскости, y – ортогональная к x координата, ρ и p – плотность и давление, u и $v$ – компоненты скорости вдоль осей x и y соответственно, e – полная энергия единицы объема, показатель адиабаты γ = 5/3, S – источник тепла, который в основной модели отсутствует. Он будет описан дополнительно по мере появления.
Граничными условиями являются условия непротекания на стенках канала и условия Ренкина-Гюгонио на ударных волнах. Обезразмеривание величин проводилось по высоте узкой части канала, плотности и скорости звука набегающего потока.
Технология численных расчетов в целом совпадает с [6]. Для численного решения использовался базовый метод [10], адаптированный для криволинейных подвижных сеток, с алгоритмом выделения и отслеживания фронтов ударных волн и контактного разрыва.
Методика расчета состояла из двух этапов: расчет полного стационарного течения, и более точный расчет потока в окрестности тройной точки. На первом этапе для заданных значений M0 и β проводился расчет полного течения с L = Lm. Подвижными границами расчетной области являлись фронт Маха, фронт отраженной волны и внутренняя сеточная линия, исходящая из тройной точки, которая подстраивалась под форму контактного разрыва. Кромка отражающего клина с центром веера волны разрежения всегда располагалась на фронте отраженной волны. Стационарное решение достигалось установлением по времени.
На втором этапе расчет продолжается на подвижной сетке, непрерывно стягивающейся к тройной точке. Сетка стягивается с сохранением геометрического подобия. Скорость стягивания подбирается таким образом, чтобы скорости движения нижней, верхней и правой границ были сверхзвуковыми относительно газа. Такой подход позволяет избежать проблем с граничными условиями на границе сетки, стягивающейся к тройной точке. В каждый момент времени стягивающаяся сетка характеризуется фактором стягивания Fz, который непрерывно уменьшался от 1 до 10–8. На этапе стягивания также применяются процедуры выделения ударных волн и контактного разрыва, что позволяет получать с высокой точностью количественную информацию о геометрии поверхностей разрывов на всех масштабах стягивания. Основное отличие от [6] состояло в использовании расширенного формата “база + смещение” для представления параметров поля течения в оперативной памяти. В качестве базы использовались параметры потока в тройной точке, вычисленные по локальной трехударной теории. Такой подход в сочетании с частичным программированием на ассемблере позволил существенно повысить точность расчетов на заключительных этапах стягивания.
2. ТЕОРЕТИЧЕСКОЕ ИССЛЕДОВАНИЕ
Выше описанная вычислительная технология слишком ресурсоемка для поиска границы сингулярности только с помощью большой серии расчетов. Предварительное аналитическое исследование может уменьшить объем и повысить надежность вычислительных результатов. Далее для оценки градиентов параметров в тройной точке используем известный подход хорошо развитой локальной теории [11], но в более компактном изложении.
2.1. Градиенты для одиночного криволинейного скачка
Законы сохранения массы, импульса и энергии для косого скачка (рис. 3, а ) приводят к четырем уравнениям для параметров по разные стороны от фронта ударной волны
(2.2)
${{p}_{0}} + {{{\rho }}_{0}}q_{0}^{2}{{\sin }^{2}}{\beta } = p + {\rho }{{q}^{2}}{{\sin }^{2}}{\theta }$(2.4)
$(p - {{p}_{0}})({\gamma } + 1) = 2({{{\rho }}_{0}}q_{0}^{2}{{\sin }^{2}}{\beta } - {\gamma }{{p}_{0}})$(2.5)
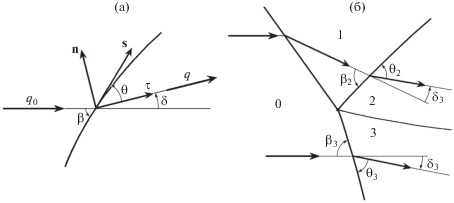
${{p}_{s}} + {{({\rho }{{q}^{2}})}_{s}}{{\sin }^{2}}{\theta } = \rho {{q}^{2}}{{{\delta }}_{s}}\sin 2{\theta }$Рис. 3.
Обозначения угловых параметров потока для одиночной ударной волны (а) и для тройной конфигурации (б); β – угол входа, θ – угол выхода, δ – угол отклонения
Для нахождения (ρq2)s продифференцируем произведение уравнений (2.1) и (2.3) с аналогичным последующим исключением параметров входного потока. В результате получим после несложных преобразований
(2.6)
${\rho }{{q}^{2}}{{{\delta }}_{s}}\cos 2{\theta } - \frac{{\sin 2{\delta }}}{{\sin 2{\beta }}}{\rho }{{q}^{2}}{{{\beta }}_{s}} = {{({\rho }{{q}^{2}})}_{s}}\sin {\theta }\cos {\theta }$Аналогичные действия после дифференцирования уравнения (2.4) приведут к
После исключения из последних трех уравнений (2.5), (2.6) и (2.7) величин (ρq2)s и βs получим
(2.8)
${{p}_{s}}\left( {1 - \frac{{{\gamma } + 1}}{4}\frac{{\sin 2{\delta }}}{{\sin 2{\beta }{{{\cos }}^{2}}{\theta }}}} \right) = {\rho }{{q}^{2}}{{{\delta }}_{s}}\tan {\theta }$Дальнейшие действия связаны с привлечением дифференциальных уравнений движения за фронтом ударной волны. Используем уравнения стационарного течения в переменных годографа q и φ, которые являются следствием системы (1.1) при S = 0. Здесь φ – угол наклона вектора скорости к оси x. В криволинейных ортогональных координатах τ, n, связанных с линиями тока уравнения имеют компактный вид
(2.9)
$\begin{gathered} {{({\rho }q)}_{{\tau }}} + {\rho }q{{{\varphi }}_{n}} = 0,\quad {\rho }q{{q}_{{\tau }}} + {{p}_{{\tau }}} = 0 \\ {\rho }{{q}^{2}}{{{\varphi }}_{{\tau }}} + {{p}_{n}} = 0,\quad {\rho }{{p}_{{\tau }}} - {\gamma }p{{{\rho }}_{{\tau }}} = 0 \\ \end{gathered} $Предполагаем, что (2.9) выполняются не только в области течения, но и на границе, т.е. на заднем фронте ударной волны. Исключим в (2.9) производные ρτ и qτ. В полученных двух уравнениях выразим производные по нормали n через производные вдоль фронта и вдоль линии тока, используя простые соотношения (см. рис. 3а)
В результате получим два уравнения, связывающие производные pτ, ps, φτ, φs.
(2.10)
$\begin{gathered} (1 - {{M}^{2}}){{p}_{\tau }}\sin {\theta } + {\rho }{{q}^{2}}{{{\varphi }}_{\tau }}\cos {\theta } - {\rho }{{q}^{2}}{{{\varphi }}_{s}} = 0 \\ {{p}_{\tau }}\cos {\theta } - {\rho }{{q}^{2}}{{{\varphi }}_{\tau }}\sin {\theta } - {{p}_{s}} = 0 \\ \end{gathered} $Здесь M – локальное число Маха. С учетом того, что для однородного потока перед ударной волной φs = δs, три уравнения (2.8) и (2.10) сводятся к одному уравнению для производных вдоль линии тока
(2.11)
$\begin{gathered} {{p}_{{\tau }}}B + {{{\varphi }}_{{\tau }}}A{\rho }{{q}^{2}}\tan {\theta } = 0 \\ B = 1 - {{M}^{2}}{{\sin }^{2}}{\theta } - A,\quad A = 2{{\cos }^{2}}{\theta } - \frac{{{\gamma } + 1}}{4}\frac{{\sin 2{\delta }}}{{\sin 2{\beta }}} \\ \end{gathered} $Используя (2.11) не сложно выразить и все остальные градиенты через кривизну линии тока φτ.
2.2. Тройная точка (точка ветвления)
Схема течения около тройной точки с обозначениями направлений отсчета углов в классической трехударной теории изображена на рис. 3б. Уравнение (2.11) справедливо как для отраженного фронта, так и для фронта Маха. Для отраженного фронта отсчет углов совпадает с принятыми при выводе уравнения (2.11), но для фронта Маха нужно сделать замену β → (π – β), θ → → (π – θ) и δ → – δ. По свойству тангенциального разрыва производные pτ и φτ в секторах 2 и 3 на рис. 3б должны быть одинаковыми. В результате получим систему
(2.12)
$\begin{gathered} {{B}_{2}}{{p}_{{\tau }}} + {{C}_{2}}{{{\varphi }}_{{\tau }}} = 0 \hfill \\ {{B}_{3}}{{p}_{{\tau }}} - {{C}_{3}}{{{\varphi }}_{{\tau }}} = 0 \hfill \\ \end{gathered} $Однородная система (2.12) имеет конечное ненулевое решение, если определитель системы равен нулю
На рис. 2 изображена красная кривая 6, которая разделяет области исходных данных с отрицательными и положительным значениями определителя Δ. Точка излома на кривой 6 является границей между прямой и инверсной конфигурациями Маха. На кривой 6 существует конечное ненулевое решение системы (2.12), а вне этой кривой градиенты и кривизна либо нуль, либо бесконечность (как было предсказано Гудерлеем). Для разрешения этого вопроса были выполнены расчеты в полной постановке для исходных данных, отмеченных точками (7) на рис. 2.
3. РЕЗУЛЬТАТЫ РАСЧЕТОВ И ОБСУЖДЕНИЕ
Расчеты были выполнены для совершенного газа (γ = 5/3) для случаев с входными данными β = 48° и M0 = 2.3, 2.34, 2.38, 2.42, 2.46, 2.5. На диаграмме рис. 2 они отмечены жирными точками (7), расположенными по разные стороны от кривой 6. Значение 2.38 попадает на кривую 6. Используемая сетка содержала 640 × 800 ячеек.
Обычно для маховского отражения в плоском канале выпуклость фронта Маха направлена по потоку, а выпуклость отраженного фронта направлена навстречу потоку. При этом давление за ударными волнами при перемещении снизу вверх монотонно уменьшается. Выпуклость контактного разрыва обычно направлена вниз, т.е. к плоскости отражения. Знаки кривизны разрывов в таких ситуациях будем считать положительными. Это означает, что в ранее принятых обозначениях под кривизной фронта Маха κM, отраженного фронта κR и контактного разрыва κС понимаем
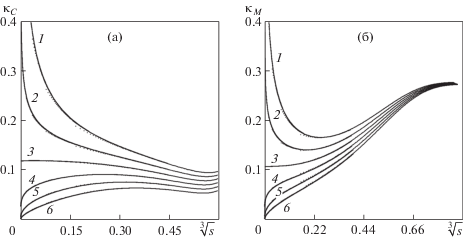
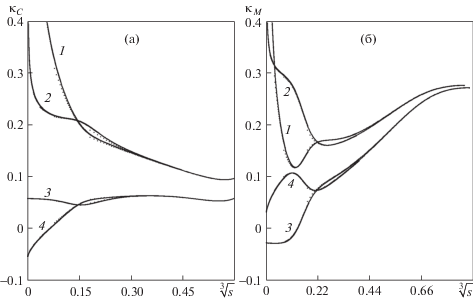
На рис. 4 изображены расчетные зависимости кривизны контактного разрыва и фронта Маха как функции натурального параметра вдоль фронтов от тройной точки. Кривые составлены из результатов девяти последовательных расчетов с различными значениями Fz = 1 → 10–8. Сетки этих расчетов частично перекрывают друг друга. Несмотря на то что результат от каждой ячейки изображается в виде дискретной точки, вся совокупность точек выглядит как жирная кривая. Можно заметить отклонения дискретных точек в переходных зонах, иллюстрирующих процесс уточнения решения при уменьшении Fz. Для более подробного изображения около нуля ось ординат растянута заменой аргумента на s1/3. Графики показывают неограниченное возрастание кривизны, т.е. градиентную сингулярность при M0 < 2.38 (кривые 1 и 2). При M0 = 2.38 (кривая 3) кривизна около нуля выходит на конечное ненулевое значение, а при M0 > 2.38 (кривые 4–6) кривизна стремится к нулю, т.е. сингулярное поведение первых частных производных параметров течения и кривизны фронтов исчезает, но сохраняется особенность во вторых производных. Таким образом, графики на рис. 4 подтверждают предположение о том, что формула (2.13) описывает границу существования сингулярности в плоскости исходных данных.
Рис. 4.
Кривизна тангенциального разрыва (а) и фронта Маха (б) как функции нормированного натурального параметра s от тройной точки: β = 48°; M0 = 2.3, 2.34, 2.38, 2.42, 2.46 и 2.50 (1–6).
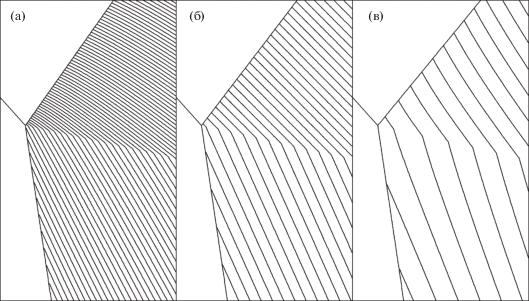
На рис. 5 изображены изобары фрагментов поля давления в окрестности тройной точки для трех из выше упомянутых вариантов: M0 = 2.30 (а), 2.38 (б), 2.46 (в) при факторе стягивания Fz = 10–3. Вертикальный размер фрагментов составляет 6 × 10–4 высоты канала. Фрагменты содержат приблизительно 300 × 600 ячеек расчетной сетки. Изобары для всех вариантов изображены с одинаковым шагом дискретности Δp = 10–5 . Изломы изобар указывают на местоположение тангенциального разрыва. По плотности расположения изобар хорошо видно различие в величине градиентов давления для вариантов с сингулярностью (а) и без сингулярности (в). Наблюдается различие в выпуклости и в тенденции сгущения изобар к тройной точке за фронтом отраженной ударной волны. В пограничном варианте (б) изобары почти прямолинейны с одинаковым шагом. В вариантах (а) и (в) прогиб изобар прямо противоположный, что говорит о разных знаках вторых производных поля давления.
Рис. 5.
Изолинии фрагментов поля давления около тройной точки для β = 48° и различных M0 = 2.30 (а), 2.38 (б), 2.46 (в); Fz = 10–3, шаг изолиний Δp = 10–5.
В случае осесимметричного течения система (2.12) будет неоднородной. Члены в правой части могут возникать как из-за неоднородности набегающего потока, так и из-за источниковых членов в уравнениях движения. В этих случаях ситуация с решением системы (2.12) изменяется. Везде, за исключением найденной границы (2.13), будет существовать ненулевое решение. Для выяснения вопроса о реализуемости таких решений был проведен численный эксперимент с искусственным источником S в уравнении энергии в системе (1.1). Вставленный источник тепла действовал вблизи тройной точки только в секторе между фронтом Маха и тангенциальным разрывом в малой ограниченной области размером порядка 1% от характерного размера задачи L
Источник повлияет на формулы локальной теории через четвертое уравнение (2.9), которое примет вид
Опуская повторный вывод формул, выпишем для этого случая итоговый результат аналога системы (2.12) в безразмерной форме
(3.1)
$\begin{gathered} {{B}_{2}}{{p}_{\tau }} + {{C}_{2}}{{{\varphi }}_{\tau }} = 0 \\ {{B}_{3}}{{p}_{\tau }} - {{C}_{3}}{{{\varphi }}_{\tau }} = - K{{\sin }^{2}}{{{\theta }}_{3}}M_{3}^{2}({\gamma } - 1)q_{3}^{{ - 1}} \\ \end{gathered} $Через решение системы (3.1) выражаются кривизны отраженного фронта и фронта Маха в тройной точке (κС = φτ):
(3.2)
${{\kappa }_{R}} = \frac{{\gamma + 1}}{4}\left( {\frac{{{{{\varphi }}_{\tau }}}}{{{\text{cos}}{{{\theta }}_{2}}}} - \frac{{{{p}_{\tau }}}}{{{{{\rho }}_{2}}q_{2}^{2}{\text{sin}}{{{\theta }}_{2}}}}} \right),\quad {{\kappa }_{M}} = \frac{{\gamma + 1}}{4}\left( {\frac{{{{{\varphi }}_{\tau }}}}{{{\text{cos}}{{{\theta }}_{3}}}} + \frac{{{{p}_{\tau }}}}{{{{{\rho }}_{3}}q_{3}^{2}{\text{sin}}{{{\theta }}_{3}}}}} \right)$На рис. 6 изображены расчетные зависимости кривизны контактного разрыва и фронта Маха как функции натурального параметра вдоль фронтов от тройной точки для двух вариантов источника с константой K = 2 и K = –2. Существенное влияние источника на кривизну фронтов проявляется лишь на расстоянии s < 0.01 от тройной точки. Видно, что при M0 = 2.3 (кривые 1 и 2) сингулярность сохранилась, а при M0 = 2.5 (кривые 3 и 4) реализуется конечное значение кривизны в тройной точке. В последнем случае (M0 = 2.5) кривизна фронтов в тройной точке хорошо согласуется с локальной теорией (3.1–3.2), согласно которой при положительном K = 2 кривизны κС = 0.0573 и κM = –0.0284 . При K = –2 величины такие же, но с обратным знаком. Теоретические кривизны при M0 = 2.3 (κС = $ \mp $0.1652, κM = $ \mp $0.2551 при K = ±2) совсем не согласуются с результатами расчетов, включая расхождения по знаку при K = 2. Причиной расхождения является сингулярность. Сам вывод аналитических формул предполагает существование конечных предельных градиентов в тройной точке, что в условиях сингулярности не выполняется.
Рис. 6.
Кривизна тангенциального разрыва (а) и фронта Маха (б) как функции натурального параметра s в расчетах с искусственным источником в секторе за фронтом Маха: β = 48°; M0 = 2.3, K = ±2 (1, 2); M0 = 2.5, K = ±2 (3, 4).
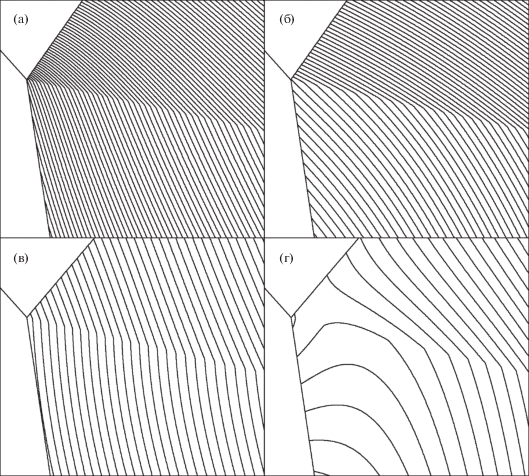
На рис. 7 изображены изобары фрагментов поля давления в окрестности тройной точки для этих четырех вариантов. Вертикальный размер фрагментов составляет 6 × 10–3 высоты канала, т.е. в 10 раз больше, чем на рис. 5. Изобары для всех фрагментов также изображены с одинаковым, но увеличенным шагом дискретности Δp = 10–4 . На нижних фрагментах (в) и (г) сингулярность отсутствует. Константа K заметно влияет на расположение изобар. На фрагменте (в) видна изобара, которая касается фронта Маха. Это означает, что при подходе к тройной точке вдоль фронта Маха давление повышается, и кривизна фронта становится отрицательной. На фрагменте (г) наблюдается локальный минимум давления в тройной точке. Это означает, что выше тройной точки кривизна отраженного фронта становится отрицательной. Таким образом, расчеты при M0 = 2.5 количественно и качественно согласуются с локальной теорией. При M0 = 2.3 (фрагменты (а) и (б)) картина иная. Расположение изолиний мало отличается от того, что было на рис. 5а. Источник не сильно влияет на величину градиентов. При подводе тепла (K > 0) градиенты увеличиваются, а при отводе тепла (K < 0) уменьшаются, но в целом расположение изобар и сингулярность сохраняются.
Рис. 7.
Изолинии фрагментов поля давления в расчетах с источником за фронтом Маха для различных (M0, K): (а) (2.3, 2), (б) (2.3, –2), (в) (2.5, 2), (г) (2.5, –2); Fz = 10–2, шаг изолиний Δp = 10–4.
На основании этих расчетов можно сделать вывод, что источниковые члены конечной интенсивности не могут привести к устранению сингулярности. Аналогичным свойством должны обладать и другие вариации в постановке задачи, не приводящие к дополнительным особенностям частных производных решения в тройной точке, например, неоднородное или осесимметричное течение. Можно выдвинуть гипотезу, что найденная граница сингулярности имеет универсальный характер.
Заметим, что утверждение работы [3] о том, что граница возникновения сингулярности должна находиться в промежутке между кривыми 4 и 5 на рис. 2, справедливо лишь в узкой пограничной зоне между прямыми и инверсными конфигурациями Маха. Излом на границе 6 в точности совпадает с точкой Крокко, которая соответствует возникновению бесконечной кривизны присоединенного скачка на острие клина в сверхзвуковом потоке [1]. Нижняя часть границы 6 соответствует инверсным конфигурациям, которые в принятой постановке задачи с прямолинейным отражающим клином не существуют, но могут быть реализованы при изменении геометрии отражающего клина или граничных условий на верхней стенке канала [12]. Для течений в плоском канале непрерывный переход по исходным данным от прямого маховского отражения к инверсному обычно не реализуется. Поэтому существование сингулярности в инверсных конфигурациях Маха нуждается в дополнительном подтверждении.
ЗАКЛЮЧЕНИЕ
С привлечением локальной трехударной теории криволинейных волн построена возможная граница в области исходных данных для существования градиентной сингулярности в тройной точке конфигураций Маха. Справедливость границы подтверждена высокоточным численным моделированием в полной постановке для стационарного маховского отражения в плоском канале. Дополнительные вычислительные эксперименты с искусственными источниками показали устойчивость сингулярности к подобным вариациям уравнений движения. Полученные результаты позволяют сделать вывод, что сингулярность в тех же границах существует и в других геометриях течения. Наличие сингулярности необходимо учитывать как в интерпретации результатов экспериментов, так и в использовании простых моделей, основанных на локальной трехударной теории.
Список литературы
Guderley K.G. Considerations of the structure of mixed subsonic-supersonic flow patterns // Wright Field Report F-TR-2168-ND. 1947. P. 144–149.
Kawamura R., Saito H. Reflection of shock waves – 1. Pseudo-stationary case // J. Phys. Soc. Jpn. 1956. V. 11. P. 584.
Sternberg J. Triple-shock-wave intersections // Phys. Fluids. 1959. V. 2. № 2. P. 179–206.
Hornung H.G. Gradients at a curved shock in reacting flow // Shock Waves. 1998. V. 8. P. 11–21.
Uskov V.N., Mostovykh P.S. The flow gradient in the vicinity of triple points // Proceedings of 21st Intl. Shock Interact. Symp. Latvia, 3-8 August 2014. Riga: Univ. Latvia. 2014. P. 57–62.
Васильев Е.И. Характер сингулярности тройной точки при стационарном отражении слабых ударных волн // Изв. РАН. МЖГ. 2016. № 6. С. 91–100.
Васильев Е.И., Крайко А.Н. Численное моделирование дифракции слабых скачков на клине в условиях парадокса Неймана // Журн. вычисл. математики и матем. физики. 1999. Т. 39. № 8. С. 1393–1404.
Васильев Е.И. Четырехволновая схема слабого маховского взаимодействия ударных волн в условиях парадокса Неймана // Изв. РАН. МЖГ. 1999. № 3. С. 144–152.
Skews B.W., Li G., Paton R. Experiments on Guderley Mach reflection // Shock Waves. 2009. V. 19. P. 95–102.
Васильев Е.И. W-модификация метода С.К. Годунова и ее применение для двумерных нестационарных течений запыленного газа // Журн. вычисл. математики и матем. физики. 1996. Т. 36. № 1. С. 122–135.
Molder S. Curved shock theory // Shock Waves. 2016. V. 26. P. 337–353.
Ben-Dor G., Elperin T., Li H., Vasiliev E. The influence of the downstream pressure on the shock wave reflection phenomenon in steady flows // J. Fluid Mech. 1999. V. 386. P. 213–232.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика жидкости и газа


