Известия РАН. Механика жидкости и газа, 2020, № 1, стр. 9-21
Колебания жидкости в цилиндрических баках с продольными демпфирующими перегородками
a Центральный научно-исследовательский институт машиностроения
Московская обл., Королев, Россия
* E-mail: dd5556@tsniimash.ru
Поступила в редакцию 24.02.2019
После доработки 29.03.2019
Принята к публикации 20.04.2019
Аннотация
Представлен асимптотический метод исследования малых колебаний жидкости в цилиндрических баках с продольными демпфирующими перегородками. Подробно исследовано влияние количества и ширины перегородок на гидродинамические параметры и коэффициенты демпфирования колебаний жидкости в круговой цилиндрической полости с плоским днищем. Численные результаты получены методом конечных элементов. Основываясь на асимптотической теории вихревого сопротивления, для перегородок малой относительной ширины предложен метод возмущений, применимый для определения демпфирования колебаний жидкости в баках произвольной формы.
Появление, начиная со второй половины прошлого века, многочисленных публикаций по колебаниям жидкости со свободной поверхностью в баках связано с потребностями ракетно-космической техники (РКТ) [1, 2]. Подвижность больших масс жидкости в топливных баках оказывает существенное влияние на движение ракет-носителей, разгонных блоков и космических аппаратов и может приводить к динамической неустойчивости их движения [3]. На активных участках полета относительное движение жидкости в топливных баках происходит при больших числах Рейнольдса и Бонда – силами поверхностного натяжения можно пренебрегать, а влияние вязкости жидкости проявляется в тонком пограничном слое на стенках баков и установленных в них внутренних устройств.
Демпфирование колебаний жидкости, обусловленное диссипацией энергии в пограничном слое, чрезвычайно мало [4]. Поэтому для обеспечения динамической устойчивости движения объектов РКТ и улучшения качества переходных процессов в топливные баки устанавливают различные конструктивные устройства. Чаще всего применяются поперечные и продольные демпфирующие перегородки, частично перекрывающие объем жидкости [5].
Задачи определения демпфирования колебаний жидкости в баках и сопротивления пластинок в периодическом потоке жидкости тесно связаны. Двумерная проблема определения сил, действующих на плоскую пластинку в периодическом потоке жидкости, экспериментально исследована в [6]. Установлено, что при больших числах Рейнольдса коэффициент сопротивления не зависит от числа Рейнольдса и определяется некоторым параметром Kc, обратно пропорциональным амплитуде колебаний потока, который по имени исследователей назван числом Келегана-Карпентера. В [7] эти экспериментальные данные для коэффициента сопротивления были аппроксимированы степенной зависимостью от амплитуды колебаний с показателем –1/2, и полученная зависимость применена для определения демпфирования колебаний жидкости в баках с кольцевой перегородкой небольшой относительной ширины. По-видимому, впервые правильное асимптотическое значение показателя степени –1/3 для малых амплитуд колебаний, представляющих основной практический интерес, указано в [8].
Общая асимптотическая теория вихревого сопротивления колебаний в жидкости тел с острыми кромками, двугранный угол которых меньше $\pi $, или обтекания таких тел периодическим потоком жидкости предложена в [9, 10]. Она основана на введении коэффициента интенсивности скоростей (КИС), определяющего потенциальное движение жидкости в “дальней” окрестности кромки. С самих кромок происходит периодический сход образующихся вихрей, и в малой ближней окрестности кромок движение жидкости вихревое. КИС аналогичны коэффициентам интенсивности напряжений в линейной механике трещин деформируемого твердого тела [11], введенных в [12]. Определение сопротивления при колебаниях в жидкости пластинок произвольной пространственной формы сведено к нахождению КИС и некоторой универсальной при больших числах Рейнольдса постоянной. Решения ряда задач о сопротивлении пластинок при колебаниях в жидкости получены в [13].
В [14] асимптотическая теория вихревого сопротивления применена к определению демпфирования малых колебаний жидкости в баках с произвольными перегородками. Полости топливных баков объектов РКТ образуются поверхностями вращения. Общий алгоритм численного исследования методом конечных элементов колебаний и демпфирования колебаний жидкого топлива в таких баках с поперечными перегородками, сохраняющими осевую симметрию полости, представлен в [15]. Подробные результаты приведены для колебаний жидкости в цилиндрическом баке с кольцевой демпфирующей перегородкой.
Результаты исследований колебаний жидкости в горизонтальной прямоугольной полости с плоским днищем и плоскими вертикальными перегородками и полуцилиндрическими вставками на стенках представлены в [16–19]. Отличительная особенность этих работ состоит в рассмотрении колебаний жидкости при малом отношении ее глубины к длине волны первой моды колебаний. В настоящей статье рассматриваются колебания жидкости в произвольной прямой цилиндрической полости с плоским днищем с продольными перегородками любой формы. Основное внимание уделяется колебаниям глубокой жидкости в длинных цилиндрических баках нижних ступеней ракет-носителей, так как днища топливных баков объектов РКТ не бывают плоскими.
1. ПОСТАНОВКА ЗАДАЧИ И ОСНОВНЫЕ ЗАВИСИМОСТИ
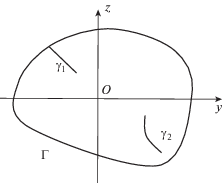
Рассматриваются малые колебания несжимаемой жидкости в прямой цилиндрической полости с плоским днищем. Возможная форма поперечного сечения полости с контуром $\Gamma $ ее стенок показана на рис. 1. С полостью связывается прямоугольная система координат $Oxyz$, ось Ox которой направлена параллельно образующей полости против вектора кажущегося ускорения массовых сил ${{{\mathbf{g}}}_{ * }}$. Начало системы координат располагается на свободной поверхности жидкости. В полости может находиться любое число продольных перегородок, частично перекрывающих объем жидкости от дна до свободной поверхности. Форма каждой из перегородок от координаты $x$ не зависит. Рассматриваются перегородки, толщина которых во много раз меньше характерного поперечного размера полости, поэтому их удобно считать бесконечно тонкими. Линиями ${{\gamma }_{1}}$ и ${{\gamma }_{2}}$ на рис. 1 показаны контуры двух перегородок.
Рис. 1.
Поперечное сечение прямой цилиндрической полости с контуром $\Gamma $ ее стенок и контурами ${{\gamma }_{1}}$, ${{\gamma }_{2}}$, находящихся в полости продольных перегородок
Числа Рейнольдса и Бонда определяются по характерному поперечному размеру полости ${{R}_{0}}$, частоте колебаний жидкости $\omega $, коэффициенту кинематической вязкости жидкости $\nu $, кажущемуся ускорению ${{{\mathbf{g}}}_{ * }}$, плотности жидкости $\rho $ и коэффициенту поверхностного натяжения $\sigma $
При колебаниях жидкости с острых кромок перегородок происходит сход пограничного слоя с периодическим образованием вихрей. Принимается, что существенное вихревое движение жидкости локализуется в тонких пограничных слоях и в малых окрестностях острых кромок перегородок, а в основном объеме полости движение жидкости потенциальное.
Потенциал скоростей жидкости относительно полости представляем разложением по собственным формам колебаний
Как известно [20], собственные формы колебаний являются решениями краевой задачи на собственные значения для уравнения Лапласа с граничными условиями на неподвижных поверхностях и свободной поверхности жидкости
(1.2)
$\Delta \varphi = 0;\quad {{\left. {\partial \varphi {\text{/}}\partial {v}} \right|}_{S}} = 0;\quad {{\left. {\partial \varphi {\text{/}}\partial x} \right|}_{\Sigma }} = \kappa {{\varphi }_{\Sigma }}$Применяя для решения задачи (1.2) метод разделения переменных, положив φ(x, y, z) = = $X(x) \cdot \phi (y,z)$, удовлетворяя граничному условию ${{\left. {X{\text{'}}} \right|}_{{x = - h}}} = 0$ на дне полости и условию нормировки ${{\left. {X{\text{'}}} \right|}_{{x = 0}}} = 1$ на свободной поверхности, находим
где h – глубина жидкости, а определение $ \cdot \phi (y,z)$) сводим к решению двумерного уравнения(1.3)
$\frac{{{{\partial }^{2}}\phi }}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}\phi }}{{\partial {{z}^{2}}}} + {{k}^{2}}\phi = 0$Если собственные функции ${{\phi }_{n}}(y,z)$ и собственные значения $k_{n}^{2}$ двумерной краевой задачи (1.3), (1.4) определены, то
(1.5)
${{X}_{n}}(x) = \frac{{ch\left[ {{{k}_{n}}(x + h)} \right]}}{{{{k}_{n}}sh({{k}_{n}}h)}};\quad {{\varphi }_{n}}(x,y,z) = {{X}_{n}}(x){{\phi }_{n}}(y,z)$Удовлетворяя граничному условию на свободной поверхности жидкости в (1.2), находим значения частотных параметров
Собственные функции ${{\phi }_{n}}(y,z)$ нормируем условием $\max \left| {{{\phi }_{n}}(y,z)} \right| = 1$. Тогда обобщенная скорость ${{\dot {s}}_{n}}$(t) в (1.1) есть скорость частиц жидкости на свободной поверхности по нормали к ней в максимуме формы колебаний.
Важными характеристиками колебаний жидкости являются кинетическая энергия E ее движения, а также сила F и момент M, действующие на бак [21]
(1.7)
$E = \frac{1}{2}\sum {{{\mu }_{n}}} \dot {s}_{n}^{2};\quad {{\mu }_{n}} = \rho \int\limits_\Sigma {{{\varphi }_{n}}\frac{{\partial {{\varphi }_{n}}}}{{\partial \nu }}} dS = \rho {{\kappa }_{n}}\int\limits_\Sigma {\varphi _{n}^{2}dS} $(1.8)
$F = - \sum {{{\lambda }_{n}}} {{\ddot {s}}_{n}};\quad {{\lambda }_{n}} = \rho \int\limits_\Sigma r \frac{{\partial {{\varphi }_{n}}}}{{\partial \nu }}dS = \rho {{\kappa }_{n}}\int\limits_\Sigma {r{{\varphi }_{n}}dS} $(1.9)
$M = - \sum {({{\lambda }_{{On}}}} {{\ddot {s}}_{n}} + {{g}_{ * }}\, \times {{\lambda }_{n}}{{s}_{n}});\quad {{\lambda }_{{On}}} = \rho \int\limits_{S + \Sigma } {(r \times \nu ){{\varphi }_{n}}dS} $Колебания жидкости при движении бака описываются уравнениями [21]
(1.10)
$F = - \sum {{{m}_{n}}} {{\ddot {r}}_{n}};\quad {{m}_{n}} = \lambda _{n}^{2}{\text{/}}{{\mu }_{n}}$Масса эквивалентного осциллятора ${{m}_{n}}$ не зависит от нормировки собственных форм, и ее величина является важной динамической характеристикой колебаний жидкости.
Учет демпфирования необходим на резонансных режимах колебаний жидкости. Рассматривая вынужденные колебания на одной из собственных частот ${{\omega }_{n}}$, полагаем ${{\dot {s}}_{n}}(t) = {{{v}}_{0}}\sin {{\omega }_{n}}t$ и записываем потенциал скоростей (1.1) в виде $\phi (t,r) = {{{v}}_{0}}{{\phi }_{n}}(r)\sin {{\omega }_{n}}t$, пренебрегая влиянием всех других тонов колебаний. В локальной цилиндрической системе координат $xr\vartheta $, полярная ось которой направлена по линии острой кромки какой-либо демпфирующей перегородки, а полярный угол отсчитывается от одной стороны кромки к другой ее стороне, главная сингулярная часть потенциала скоростей имеет вид [10]
(1.11)
$\phi (t,x,r,\vartheta ) = \left[ {{{K}_{{v}}}(x)\sqrt {\frac{{2r}}{\pi }} \cos \frac{\vartheta }{2} + O(r)} \right]\sin \omega t)$(1.12)
$\frac{{\partial \phi }}{{\partial r}} = \left[ {\frac{{{{K}_{{v}}}(x)}}{{\sqrt {2\pi r} }}\cos \frac{\vartheta }{2} + O(1)} \right]\sin \omega t;\quad \frac{{\partial \phi }}{{r\partial \vartheta }} = \left[ { - \frac{{{{K}_{{v}}}(x)}}{{\sqrt {2\pi r} }}\sin \frac{\vartheta }{2} + O(1)} \right]\sin \omega t$Для того, чтобы представления (1.11), (1.12) имели место, необходимо выполнение условия [10]
(1.13)
${{\delta }_{ * }}{\text{/}}{{R}_{0}} \ll {{d}_{ * }}{\text{/}}{{R}_{0}} \ll 1;\quad {{\delta }_{ * }} = {{(\nu {\text{/}}\omega )}^{{1/2}}};\quad {{d}_{ * }} = {{({{K}_{{v}}}{\text{/}}\omega )}^{{2/3}}}$Линейный масштаб ${{\delta }_{ * }}$ определяет характерную толщину периодического пограничного слоя, а линейный масштаб ${{d}_{ * }}$ – характерный размер области существенного вихревого движения в окрестности острых кромок.
При выполнении условия (1.13) логарифмический декремент колебаний жидкости для выбранного тона определяется по формуле [15]
(1.14)
$\delta = K{{\left( {\frac{{{{{v}}_{0}}}}{{{{R}_{0}}\omega }}} \right)}^{{2/3}}};\quad {{K}_{i}} = 2\frac{{\rho R_{0}^{3}}}{\mu }{{\int\limits_{ - h}^0 {\left( {\frac{{K_{{v}}^{2}(x)}}{{{{R}_{0}}{v}_{0}^{2}}}} \right)} }^{{4/3}}}\frac{{dx}}{{{{R}_{0}}}}$Нелинейное вихревое демпфирование даже при относительно малых амплитудах колебаний жидкости может на 2 порядка превышать демпфирование, обусловленное диссипацией энергии в пограничных слоях [5].
2. МЕТОД РЕШЕНИЯ
Для определения гидродинамических параметров и коэффициентов нелинейного вихревого демпфирования колебаний жидкости необходимо получить решение краевой задачи на собственные значения (1.3), (1.4). Основывая численное решение на применении метода конечных элементов (МКЭ), перейдем к вариационной формулировке краевой задачи введением функционала
(2.1)
$I(\phi ) = \frac{1}{2}\int\limits_\Sigma {{{{(\nabla \phi )}}^{2}}dS} - \frac{1}{2}{{k}^{2}}\int\limits_\Sigma {{{\phi }^{2}}dS} $Из равенства вариации функционала нулю следует, что решения краевой задачи доставляют этому функционалу стационарные значения, причем граничное условие (1.4) является естественным.
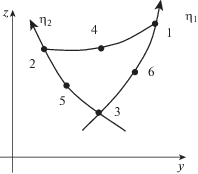
Область $\Sigma $ невозмущенной плоской свободной поверхности жидкости представляется треугольными конечными элементами квадратичного порядка [22]. Общий вид конечного элемента показан на рис. 2; цифрами обозначены номера узлов. Срединные узлы сторон конечного элемента, сходящихся в острой кромке перегородки, сдвигаются на 1/4 длины соответствующей стороны к узлу острой кромки, чтобы обеспечить требуемую особенность (1.12) скорости жидкости в ее окрестности.
Рис. 2.
Общий вид треугольного конечного элемента квадратичного порядка. Цифрами обозначены номера узлов элемента
Внутри конечного элемента i координаты y, z и функция $\phi (y,z)$ выражаются квадратичными функциями однородных треугольных координат
(2.2)
$y = \sum\limits_{k = 1}^6 {y_{k}^{i}} {{f}_{k}} = {{\{ f\} }^{T}}\{ {{y}^{i}}\} ;\quad z = \sum\limits_{k = 1}^6 {z_{k}^{i}} {{f}_{k}} = {{\{ f\} }^{T}}\{ {{z}^{i}}\} $Координата ${{\eta }_{3}}$ в этих функциях не является независимой переменной: ${{\eta }_{1}} + {{\eta }_{2}} + {{\eta }_{3}} = 1$.
Для вычисления двойных интегралов определяем якобиан преобразований координат (2.2) в области конечного элемента
(2.4)
$J = \left[ {\begin{array}{*{20}{c}} {\partial y{\text{/}}\partial {{\eta }_{1}}}&{\partial z{\text{/}}\partial {{\eta }_{1}}} \\ {\partial y{\text{/}}\partial {{\eta }_{2}}}&{\partial z{\text{/}}\partial {{\eta }_{2}}} \end{array}} \right] = B\left[ {\begin{array}{*{20}{c}} {{\text{\{ }}{{{\text{y}}}^{i}}{\text{\} }}}&{{\text{\{ }}{{{\text{z}}}^{i}}{\text{\} }}} \end{array}} \right]$Используя выражения (2.3), (2.4), находим
(2.5)
$\iint\limits_{{{S}_{i}}} {[{{{(\partial \phi {\text{/}}\partial y)}}^{2}}} + {{(\partial \phi {\text{/}}\partial z)}^{2}}]\,dydz = {{{\text{\{ }}{{\phi }^{i}}{\text{\} }}}^{T}}\,\left( {\int\limits_0^1 {\int\limits_0^{1 - {{\eta }_{2}}} {{{C}^{{\text{т}}}}C\left| J \right|d{{\eta }_{1}}d{{\eta }_{2}}} } } \right){\text{\{ }}{{\phi }^{i}}{\text{\} }}$(2.6)
$\iint\limits_{{{S}_{i}}} {{{\phi }^{2}}dydz} = {{{\text{\{ }}{{\phi }^{i}}{\text{\} }}}^{T}}\left( {\int\limits_0^1 {\int\limits_0^{1 - {{\eta }_{2}}} {{\text{\{ }}f{\text{\} \{ }}f{{{\text{\} }}}^{{\text{т}}}}\left| J \right|d{{\eta }_{1}}d{{\eta }_{2}}} } } \right){\text{\{ }}{{\phi }^{i}}{\text{\} }}$Интегралы в (2.5), (2.6) вычисляются по специальной квадратурной формуле гауссова типа с четырьмя узлами [23]. Координаты узлов $\eta _{k}^{i}$ и веса $w_{ * }^{i}$ квадратурной формулы приведены в табл. 1.
Таблица 1.
Координаты узлов и веса квадратурной формулы для вычисления интегралов по треугольной области
| i | $\eta _{1}^{i}$ | $\eta _{2}^{i}$ | $\eta _{3}^{i}$ | $w_{ * }^{i}$ |
|---|---|---|---|---|
| 1 | 1/3 | 1/3 | 1/3 | –9/32 |
| 2 | 3/5 | 1/5 | 1/5 | 25/96 |
| 3 | 1/5 | 3/5 | 1/5 | 25/96 |
| 4 | 1/5 | 1/5 | 3/5 | 25/96 |
Суммируя выражения (2.5) и (2.6) по всем конечным элементам, приходим к дискретной форме функционала (2.1)
где w – вектор-столбец значений функции $\phi (y,z)$ в узлах всех элементов. Условие экстремума этого функционала приводит к линейной алгебраической задаче на собственные значенияЗадача на собственные значения (2.7) решается методом итераций в подпространстве [24]. Процесс итераций повторяется до достижения требуемой точности низших собственных значений.
После решения краевой задачи (1.3), (1.4), применяя общие зависимости (1.7), (1.8), вычисляем коэффициенты обобщенных масс
(2.8)
${{\mu }_{n}} = \frac{\rho }{{{{\kappa }_{n}}}}\sum\limits_i {{{{{\text{\{ }}w_{n}^{i}{\text{\} }}}}^{T}}} \left( {\int\limits_0^1 {\int\limits_0^{1 - {{\eta }_{2}}} {{\text{\{ }}f{\text{\} \{ }}f{{{\text{\} }}}^{T}}\left| J \right|d{{\eta }_{1}}d{{\eta }_{2}}} } } \right){\text{\{ }}w_{n}^{i}{\text{\} }}$(2.9)
${{\lambda }_{{n2}}} = \rho \sum\limits_i {{{{{\text{\{ }}{{y}^{i}}{\text{\} }}}}^{T}}} \left( {\int\limits_0^1 {\int\limits_0^{1 - {{\eta }_{2}}} {{\text{\{ }}f{\text{\} \{ }}f{{{\text{\} }}}^{T}}\left| J \right|d{{\eta }_{1}}d{{\eta }_{2}}} } } \right){\text{\{ }}w_{n}^{i}{\text{\} }}$(2.10)
${{\lambda }_{{n3}}} = \rho \sum\limits_i {{{{{\text{\{ }}{{z}^{i}}{\text{\} }}}}^{T}}} \left( {\int\limits_0^1 {\int\limits_0^{1 - {{\eta }_{2}}} {{\text{\{ }}f{\text{\} \{ }}f{{{\text{\} }}}^{T}}\left| J \right|d{{\eta }_{1}}d{{\eta }_{2}}} } } \right){\text{\{ }}w_{n}^{i}{\text{\} }}$Здесь ${\text{\{ }}w_{n}^{i}{\text{\} }}$ – вектор-столбец значений функции ${{\phi }_{n}}(y,z)$ в узлах i-конечного элемента. Интегралы находятся по квадратурной формуле, значения координат и весов которой приведены в табл. 1 . Суммирование проводится по всем элементам на свободной поверхности жидкости.
Поскольку выполняется условие неразрывности, то из (1.8) следует ${{\lambda }_{{n1}}} = 0$, поэтому главный вектор гидродинамических сил F параллелен свободной поверхности жидкости. Проекции вектора ${{\lambda }_{{On}}}$ на оси координат Oy и Oz
Коэффициенты нелинейного вихревого демпфирования колебаний жидкости вычисляются с использованием интегрального соотношения [15]
(2.11)
$\int\limits_\lambda {K_{{v}}^{2}} \delta n(\lambda )d\lambda = - \delta \kappa \int\limits_\Sigma {{{\varphi }^{2}}} dS$Зависимость (2.11) выполняется для любого тона колебаний жидкости. Из нее следует важный вывод, что увеличение площади перегородок приводит к уменьшению собственных частот колебаний жидкости.
Так как коэффициенты интенсивности скоростей ${{K}_{{v}}}$ пропорциональны скорости жидкости, то из зависимостей (1.5), (1.12) следует, что вдоль линии острой кромки любой перегородки
где ${{K}_{{{v}0}}}$ – неопределенный коэффициент, R0 – характерный поперечный размер полости, в качестве которого для круговой цилиндрической полости удобно взять ее радиус. Как и выше, здесь и далее для упрощения записи номер тона колебаний жидкости в индексах ${{K}_{{v}}}(x)$, ${{K}_{{{v}0}}}$ и k опускается.Подставляя выражение (2.12) в левую часть интегрального соотношения (2.11), в котором полагаем $\delta n(x) = {\text{const}}$, находим
(2.13)
$\frac{{K_{{{v}0}}^{2}}}{{{{R}_{0}}{v}_{0}^{2}}}\frac{1}{{2{{k}^{3}}R_{0}^{3}}}\left( {\frac{{ch(kh)}}{{sh(kh)}} + \frac{{kh}}{{s{{h}^{2}}(kh)}}} \right) = - \frac{{\delta \kappa }}{{\kappa \delta n{\text{/}}{{R}_{0}}}}\frac{\mu }{{\rho R_{0}^{3}}}$Вычисляя путем решения краевой задачи собственные значения $\kappa = {{k}_{n}}th({{k}_{n}}h)$ и коэффициенты присоединенных масс $\mu = {{\mu }_{n}}$, а затем изменения собственных значений $\delta \kappa $ при вариациях ширины δn перегородки, можно определить по формуле (2.13) безразмерный коэффициент $K_{{{v}0}}^{2}{\text{/}}({{R}_{0}}{v}_{0}^{2})$. При этом для получения надежных результатов краевую задачу необходимо решать несколько раз при различных значениях вариации δn ширины демпфирующей перегородки вдоль линии острой кромки.
Принимая во внимание зависимость (2.12), для одной острой кромки перегородки коэффициент Ki в (1.14) определяется следующим образом:
(2.14)
$K = 2\frac{{\rho R_{0}^{3}}}{\mu }{{\left( {\frac{{K_{{{v}0}}^{2}}}{{{{R}_{0}}{v}_{0}^{2}}}} \right)}^{{4/3}}}{{\int\limits_{ - h}^0 {\left( {\frac{{ch[k(x + h)]}}{{k{{R}_{0}}sh(kh)}}} \right)} }^{{8/3}}}d\frac{x}{{{{R}_{0}}}}$Общий коэффициент K в зависимости декремента колебаний от амплитуды должен определяться суммой коэффициентов Ki для всех острых кромок перегородок.
Согласно принятому условию нормировки величина ${{{v}}_{0}}{\text{/}}\omega = {{s}_{0}}$ есть амплитуда жидкости по нормали к свободной поверхности в точке максимума формы соответствующего тона колебаний. Однако в уравнениях возмущенного движения объектов РКТ [25], как правило, используется обобщенная координата перемещений массы эквивалентного осциллятора rn. Из (1.14), учитывая связь обобщенных координат ${{s}_{n}} = {{\lambda }_{n}}{{r}_{n}}{\text{/}}{{\mu }_{n}}$, находим
(2.15)
$\delta = K{{({{s}_{0}}{\text{/}}{{R}_{0}})}^{{2/3}}} = {{K}_{r}}{{({{r}_{0}}{\text{/}}{{R}_{0}})}^{{2/3}}};\quad {{K}_{r}} = {{(\lambda {\text{/}}\mu )}^{{2/3}}}K$Днища топливных баков объектов РКТ не бывают плоскими, поэтому основной практический интерес представляет случай “глубокой” жидкости в удлиненных цилиндрических баках нижних ступеней ракеты-носителя. Если $h \to \infty $, то интеграл в правой части (2.14) вычисляется аналитически
Влиянием днища можно пренебрегать, и применять эту зависимость при $h{\text{/}}{{R}_{0}} \geqslant 1.5$.
3. ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ РАСЧЕТОВ
Расчеты проведены по программе HDTB_C [26], написанной на языке FORTRAN. Сначала приведем решение задачи о колебаниях жидкости в круговой цилиндрической полости без демпфирующих перегородок. Учитывая наличие двух плоскостей симметрии, конечно-элементная сетка задавалась только на четверти свободной круговой поверхности жидкости.
Результаты расчетов для трех антисимметричных относительно плоскости Oz и симметричных относительно плоскости Oy тонов колебаний жидкости представлены в табл. 2. В ней приняты следующие обозначения: N – количество конечных элементов, R0 – радиус цилиндрической полости, ${{m}_{n}}(\infty ){\text{/}}(\rho R_{0}^{3})$ – безразмерные массы эквивалентных осцилляторов при $h \to \infty $. Отметим, что для жидкости конечной глубины для любой цилиндрической полости с плоским днищем справедливо соотношение ${{m}_{n}}(h) = {{m}_{n}}(\infty )th({{k}_{n}}h)$.
Таблица 2.
Сравнение результатов расчетов методом конечных элементов с аналитическим решением для круговой цилиндрической полости
| N | 4 | 16 | 64 | 256 | Аналитическое решение |
|---|---|---|---|---|---|
| ${{k}_{1}}{{R}_{0}}$ | 1.8424 | 1.8413 | 1.8412 | 1.8412 | 1.8412 |
| ${{m}_{1}}(\infty ){\text{/}}(\rho R_{0}^{3})$ | 1.4289 | 1.4281 | 1.4279 | 1.4279 | 1.4278 |
| ${{k}_{2}}{{R}_{0}}$ | 4.3804 | 4.2144 | 4.2021 | 4.2012 | 4.2012 |
| ${{m}_{2}}(\infty ){\text{/}}(\rho R_{0}^{3})$ | 0 | 0 | 0 | 0 | 0 |
| ${{k}_{3}}{{R}_{0}}$ | 5.6861 | 5.3652 | 5.3339 | 5.3316 | 5.3314 |
| ${{m}_{3}}(\infty ){\text{/}}(\rho R_{0}^{3})$ | 0.0460 | 0.0434 | 0.0430 | 0.04296 | 0.04297 |
Как видно, достаточная для практических приложений точность по всем параметрам обеспечивается уже при 16 конечных элементах. Как правило, практическое значение имеет только первый тон колебаний, и в данном случае для него высокая точность достигается при применении всего 4 конечных элементов.
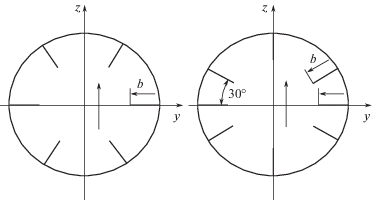
Приведем решение задачи о колебаниях жидкости в круговой цилиндрической полости с равномерно расположенными в ней продольными перегородками. Угол между плоскостями смежных перегородок $\alpha = 2\pi {\text{/}}N$, N – количество перегородок. Гидродинамические параметры определялись для бесконечно глубокой жидкости при наличии в полости 4, 6 и 8 перегородок различной ширины. На рис. 3 показаны поперечные сечения полости, в которой установлены 6 перегородок. Стрелками обозначено направление колебаний жидкости.
Рис. 3.
Цилиндрическая полость с шестью продольными перегородками; стрелками показано направление колебаний жидкости: слева – перпендикулярно плоскости пары противоположных перегородок; справа – под углом $\alpha {\text{/}}2 = 30^\circ $ к плоскости смежных перегородок
При проведении расчетов учитывалось наличие двух плоскостей симметрии, и конечно-элементная сетка задавалась на четверти свободной поверхности жидкости. В данном случае получение приемлемых результатов потребовало намного больше конечных элементов, чем для полости без демпфирующих перегородок. Результаты расчетов частотного параметра и массы эквивалентного осциллятора для первого тона колебаний жидкости представлены на рис. 4. Как выяснилось, эти параметры слабо зависят от количества перегородок, а при небольшой ширине $b{\text{/}}R \leqslant 0.2$ слабо зависят также и от их ширины, что полностью согласуется с экспериментальными данными [5]. При малых амплитудах колебаний вихревое движение жидкости в окрестности острых кромок перегородок не оказывает сколь-нибудь заметного влияния на инерционные гидродинамические параметры.
Рис. 4.
Зависимость частотного параметра (I) и массы осциллятора (II) колебаний глубокой жидкости в круговой цилиндрической полости от ширины перегородок. Число перегородок: 4 – □, 6 – ∆, 8 – ○
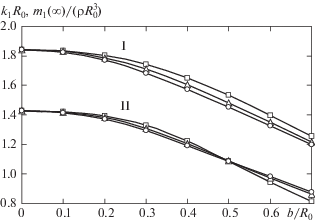
В табл. 3 представлены полученные расчетом значения коэффициентов $K$ и ${{K}_{r}}$ в зависимости (2.15) демпфирования от амплитуды колебаний для варианта 1 направления колебаний жидкости. Если $b{\text{/}}{{R}_{0}} < 0.3$, то наибольшее демпфирование обеспечивается при установке в полости 8 перегородок, а при ширине перегородок $b{\text{/}}{{R}_{0}} = 0.3$ оно практически одинаковое для всех рассматриваемых случаев. Если $b{\text{/}}{{R}_{0}} > 0.3$, то 4 перегородки обеспечивают более высокое демпфирование, чем 6 перегородок, а 6 перегородок – более высокое, чем 8 перегородок. Взаимное влияние перегородок проявляется эффектом затенения и приводит к снижению величины демпфирования.
Таблица 3.
Зависимость демпфирования колебаний жидкости от количества перегородок и их ширины в круговой цилиндрической полости, направление колебаний жидкости перпендикулярно плоскости пары противоположных перегородок
| $b{\text{/}}{{R}_{0}}$ | 4 перегородки | 6 перегородок | 8 перегородок | |||
|---|---|---|---|---|---|---|
| K | Kr | K | Kr | K | Kr | |
| 0.1 | 0.0676 | 0.0896 | 0.0985 | 0.1311 | 0.1325 | 0.1755 |
| 0.2 | 0.2450 | 0.3166 | 0.2876 | 0.3784 | 0.3335 | 0.4303 |
| 0.3 | 0.5335 | 0.6540 | 0.5282 | 0.6756 | 0.5580 | 0.6873 |
| 0.4 | 0.9150 | 1.0285 | 0.7715 | 0.9400 | 0.7578 | 0.8771 |
| 0.5 | 1.4283 | 1.4335 | 0.9948 | 1.1343 | 0.9230 | 0.9941 |
В табл. 4 представлены значения коэффициентов K и Kr для варианта 2 направления колебаний жидкости. Как видно из сравнения с представленными выше результатами, для полости, в которой 4 перегородки, величина демпфирования существенно зависит от направления колебаний. При любой ширине перегородок демпфирование ниже, чем в полости, в которой 6 перегородок. Демпфирование колебаний жидкости в полости, в которой 6 перегородок, слабо зависит от направления колебаний. Расчеты показывают, что еще слабее демпфирование зависит от направления колебаний, если в полости 8 перегородок.
Таблица 4.
Зависимость демпфирования колебаний жидкости от количества перегородок и их ширины в круговой цилиндрической полости, направление колебаний жидкости под углом $\alpha {\text{/}}2$ к плоскости смежных перегородок
| $b{\text{/}}{{R}_{0}}$ | 4 перегородки | 6 перегородок | ||
|---|---|---|---|---|
| K | Kr | K | Kr | |
| 0.1 | 0.0614 | 0.0818 | 0.1018 | 0.1349 |
| 0.2 | 0.1817 | 0.2405 | 0.3085 | 0.3988 |
| 0.3 | 0.3860 | 0.5007 | 0.5682 | 0.6999 |
| 0.4 | 06210 | 0.7712 | 0.8538 | 0.9809 |
| 0.5 | 0.9273 | 1.0741 | 1.1245 | 1.1887 |
Полученные результаты находятся в удовлетворительном согласии с экспериментальными данными [5] и имеют большое практическое значение. Для обеспечения наивысшей величины демпфирования колебаний жидкости в топливные баки необходимо устанавливать 6 продольных перегородок шириной $b{\text{/}}{{R}_{0}} > 0.3$. Если в баке находятся 6 продольных перегородок шириной $b{\text{/}}{{R}_{0}} = 0.3$, то при амплитуде колебаний жидкости ${{s}_{0}}{\text{/}}{{R}_{0}} = 0.1$ логарифмический декремент $\delta \approx 0.11$. В баке без перегородок при характерных числах Рейнольдса ${\text{Re}}$ порядка 107 величина логарифмического декремента δ согласно [5] может быть порядка 10–3. Наличие перегородок приводит к некоторому увеличению этого демпфирования, обусловленного диссипацией энергии в пограничном слое также и на их поверхности.
4. МЕТОД ВОЗМУЩЕНИЙ
В методе возмущений принимается, что каждый участок перегородки малой ширины находится в плоском периодическом потоке жидкости. При таком допущении коэффициенты интенсивности скоростей на острых кромках перегородки определяются простой формулой [10]
где b – ширина перегородки, ${v}$ – амплитуда скорости жидкости по нормали к перегородке в месте ее расположения, когда она отсутствует.Для продольных перегородок малой ширины скорость ${v}$ можно брать на стенке бака. Используя аналитическое решение задачи о колебаниях жидкости в цилиндрическом баке с плоским днищем без перегородок [5], находим
(4.2)
$\frac{{K_{{v}}^{2}(x,\theta )}}{{{{R}_{0}}{v}_{0}^{2}}} = \frac{{\pi b}}{{\xi _{1}^{2}{{R}_{0}}}}\frac{{c{{h}^{2}}[{{\xi }_{1}}(x + h){\text{/}}{{R}_{0}}]}}{{s{{h}^{2}}({{\xi }_{1}}h{\text{/}}{{R}_{0}})}}{{\cos }^{2}}\theta $Выясним, насколько приближенная формула (4.2), основанная на зависимости (4.1), в рассматриваемом частном случае согласуется с результатами вычисления МКЭ коэффициентов интенсивности скоростей. Так как в решении МКЭ зависимость от продольной координаты x такая же, то достаточно сравнить значения на свободной поверхности жидкости. Ограничимся таким сравнением для перегородки, расположенной под углом θ = 0. Полагая в (4.2) x = 0, θ = 0, для достаточно глубокой жидкости получим зависимость
Для сравнения в табл. 5 приведены результаты, получаемые МКЭ и по формуле (4.3). Для перегородок шириной $b{\text{/}}{{R}_{0}} = 0.1$ значения $K_{{v}}^{2}{\text{/}}({{R}_{0}}{v}_{0}^{2})$, определенные методом возмущений, на 15–20% ниже. Это может быть связано как с некоторой погрешностью вычислений МКЭ, так и с тем, что в методе возмущений не учитывается кривизна стенки бака. Такая погрешность для практических приложений считается допустимой [5]. Для перегородок шириной $b{\text{/}}{{R}_{0}} = 0.2$ и $b{\text{/}}{{R}_{0}} = 0.3$ результаты, получаемые методом возмущений и МКЭ, отличаются весьма сильно, причем наблюдается существенное взаимное влияние перегородок, которое в методе возмущений никак не учитывается.
Таблица 5.
Значения безразмерного квадрата коэффициента интенсивности скоростей $K_{{v}}^{2}{\text{/}}({{R}_{0}}{v}_{{\text{0}}}^{{\text{2}}})$ на свободной поверхности для перегородки, расположенной под углом θ = 0, в цилиндрическом баке с продольными перегородками, полученные методом конечных элементов и методом возмущений
| Метод | $b{\text{/}}{{R}_{0}} = 0.1$ | $b{\text{/}}{{R}_{0}} = 0.2$ | $b{\text{/}}{{R}_{0}} = 0.3$ |
|---|---|---|---|
| МКЭ, 4 перегородки | 0.106 | 0.288 | 0.547 |
| МКЭ, 6 перегородок | 0.113 | 0.252 | 0.392 |
| МКЭ, 8 перегородок | 0.115 | 0.231 | 0.347 |
| Метод возмущений | 0.0927 | 0.185 | 0.278 |
Общий вывод, который может быть сделан, состоит в том, что метод возмущений применим для перегородок, ширина которых $b{\text{/}}{{R}_{0}} \leqslant 0.1$. При этом для баков с полостями вращения R0 – наименьший радиус поперечного сечения бака с продольными перегородками.
Некоторые результаты, наглядно характеризующие демпфирование колебаний жидкости в цилиндрическом баке с продольными перегородками, приведены в виде графических зависимостей на рис. 5: сплошные линии – МКЭ, штриховые линии – метод возмущений. Результаты представлены для первого тона колебаний глубокой жидкости, когда влиянием днища можно пренебречь. Направление колебаний жидкости перпендикулярно плоскости пары перегородок. В (1.14) при вычислении методом возмущений величины K коэффициент обобщенной массы колебаний жидкости определялся для бака без перегородок по формуле [5]
Рис. 5.
Зависимости логарифмических декрементов от амплитуды колебаний жидкости в баке с шестью продольными перегородками. Сплошные линии – метод конечных элементов, штриховые линии – метод возмущений: 1, 2 – $b{\text{/}}{{R}_{0}} = 0.1,\;0.2$
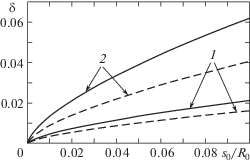
Ограниченность применения метода возмущений условием $b{\text{/}}{{R}_{0}} \leqslant 0.1$ обусловлена тем, что в нем не учитывается кривизна стенок бака, конечность объема жидкости и взаимное влияние перегородок. Достоинством метода является то, что он может применяться тогда, когда решена задача на собственные значения и получено распределение скоростей жидкости в баке произвольной формы с гладкими стенками.
ЗАКЛЮЧЕНИЕ
Представлен метод определения гидродинамических параметров и вихревого демпфирования колебаний жидкости в прямой цилиндрической полости произвольной формы с любыми продольными перегородками. Проведены расчеты для круговой цилиндрической полости с продольными демпфирующими перегородками, имеющие практическую значимость для объектов ракетно-космической техники. Установлено, что с увеличением ширины перегородок до 0.7 радиуса демпфирование монотонно возрастает. Величина демпфирования в баках, содержащих четыре перегородки, существенно зависит от направления колебаний. Увеличение ширины перегородок более выгодно, чем увеличение их числа. В баках, содержащих шесть и восемь перегородок, ширина которых 0.3 радиуса, демпфирование почти одинаковое. При ширине перегородок больше 0.3 радиуса демпфирование в баках, содержащих шесть перегородок, выше, чем в баках, содержащих восемь перегородок. Таким образом, показано, что каждой ширине перегородок отвечает некоторое их оптимальное число. Если необходимо обеспечить максимально возможное демпфирование, то перегородок должно быть шесть. Для определения вихревого демпфирования колебаний жидкости в баках произвольной формы с любыми перегородками малой относительной ширины предложен метод возмущений.
Список литературы
Abramson H.N. (Ed). The Dynamic Behavior of Liquids in Moving Containers // NASA-SP 106. 1966. 467 p.
Ibrahim R.A. Liquid sloshing dynamics: theory and application. Cambridge: Univ. Press, 2005. 948 p.
Рабинович Б.И. Введение в динамику ракет-носителей космических аппаратов. М.: Машиностроение, 1975. 416 с.
Черноусько Ф.Л. Движение твердого тела с полостями, содержащими вязкую жидкость. М.: ВЦ АН СССР, 1968. 230 с.
Микишев Г.Н. Экспериментальные методы в динамике космических аппаратов. М.: Машиностроение, 1978. 247 с.
Keulegan G.H. and Carpenter L.H. Forces on cylinders and plates in an oscillating fluid. J. Res. Bur. Stand. 1958. V. 80. P. 423–440.
Miles J.W. Ring damping of free surface oscillations in a circular tank // J. Appl. Mech. 1958. V. 25. № 2. P. 274–276.
Graham J.M.R. The forces on sharp-edged cylinders in oscillatory flow at low Keulegan–Carpenter numbers // J. Fluid Mech. 1980. V. 97. Pt. 2. P. 331–346.
Бужинский В.А. Энергия вихреобразования при колебаниях в жидкости тела с острыми кромками // Докл. АН СССР. 1990. Т. 313. № 5. С. 1072–1074.
Бужинский В.А. Вихревое сопротивление пластинки при колебаниях в маловязкой жидкости // ПММ. 1990. Т. 54. Вып. 2. С. 233–238.
Черепанов Г.П. Механика хрупкого разрушения. М.: Наука, 1974. 640 с.
Irwin G.R. Analysis of stresses and strains near the end of a crack traversing a plate // J. Appl. Mech. 1957. V. 24. № 3. P. 361–364.
Бужинский В.А., Мельникова И.М. Определение сопротивления колеблющихся пластин в жидкости // ПММ. 1991. Т. 55. Вып. 2. С. 264–274.
Бужинский В.А. Колебания жидкости в резервуарах, содержащих конструктивные элементы с острыми кромками // Докл. АН. 1998. Т. 363. № 1. С. 53–55.
Бужинский В.А. Вихревое демпфирование колебаний жидкости в резервуарах с перегородками // ПММ. 1998. Т. 62. Вып. 2. С. 235–243.
Калиниченко В.А., Со А.Н., Чашечкин Ю.Л. Вихревое демпфирование колебаний жидкости в прямоугольном сосуде // Изв. РАН. МЖГ. 2015. № 5. С. 28–40.
Со А.Н., Сысоева Е.Я. Затухание волн в сосуде с пластинами-демпферами // Изв. РАН. МЖГ. 2016. № 1. С. 3–8.
Калиниченко В.А., Со А.Н., Чашечкин Ю.Л. Картины циркуляционных течений в волнах Фарадея при наличии пластин-демпферов // Изв. РАН. МЖГ. 2016. № 5. С. 64–71.
Калиниченко В.А., Нестеров С.В., Со А.Н. Стоячие поверхностные волны в прямоугольном сосуде с локальными нерегулярностями стенок и дна // Изв. РАН. МЖГ. 2017. № 2. С. 65–74.
Моисеев Н.Н., Румянцев В.В. Динамика тела с полостями, содержащими жидкость. М.: Наука, 1965. 439 с.
Нариманов Г.С. О движении твердого тела, полость которого частично заполнена жидкостью // ПММ. 1956. Т. 20. Вып. 1. С. 21–38.
Brebbia C.A., Telles J.C.F., Wrobel L.C. Boundary Element Techniques. Theory and Application in Engineering. Springer-Verlag. Berlin–Heidelberg–New York–Tokyo, 1984. = Бреббия К., Теллес Ж., Вроубел Л. Методы граничных элементов. М.: Мир, 1987. 524 с.
Strang G., Fix G.J. An analysis of the finite element method. Prentige-Hall Inс. 1973 = Стренг Г., Фикс Дж. Теория метода конечных элементов. М.: Мир, 1977. 349 с.
Hammer P.C., Marlowe O.J., Stroud A.H. Numerical integration over simplexes and cones. Math. Tables Other Aids Comput. 1956. № 10. P. 130–139.
Колесников К.С. Динамика ракет. М: Машиностроение, 2003. 519 с.
Бужинский В.А. Вычисление коэффициентов демпфирования колебаний жидкости в цилиндрических баках с продольными перегородками методом конечных элементов: Программа для ЭВМ // Св-во о гос. регистрации № 2012661056, 6 декабря 2012 г.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика жидкости и газа


