Известия РАН. Механика жидкости и газа, 2020, № 1, стр. 91-103

Моделирование потерь давления на трение в призабойной зоне трещины ГРП

И. К. Гималтдинов^a, b, *, А. М. Ильясов^c, **

^a Уфимский государственный нефтяной технический университет
Уфа, Россия

^b Академия наук Республики Башкортостан
Уфа, Россия

^c Уфимский государственный авиационный технический университет
Уфа, Россия

^* E-mail: iljas_g@mail.ru
^** E-mail: amilyasov67@gmail.com

Поступила в редакцию 10.04.2019
После доработки 10.07.2019
Принята к публикации 12.07.2019

DOI: 10.31857/S0568528120010053

Полный текст (PDF)

Аннотация

Предложена математическая модель, описывающая изменение давления в трещине гидравлического разрыва пласта (ГРП) после остановки закачки жидкости гидроразрыва и учитывающая потери на трение в призабойной зоне скважины вследствие искривления траектории трещины и наличия перфорационных отверстий. Получены аналитические решения для давления в трещине ГРП после остановки закачки жидкости гидроразрыва при монотонном и колебательном режимах течения в трещине, а также аналитические выражения для падения давления в призабойной зоне скважины. Выполнено параметрическое исследование полученных решений.

Ключевые слова: трещина гидроразрыва пласта, монотонный и осцилляционный режимы течения, потери давления на трение

Для приложений представляет интерес задача о полных потерях давления на трение во время закачки жидкости ГРП. Эти потери складываются из потерь давления в насосно-компрессорных трубах (НКТ) в скважине, потерь в перфорационных отверстиях и потерь в трещине. Если известны реологические свойства жидкости ГРП, то потери давления в НКТ и в большей части трещины ГРП известны. Однако потери давления в призабойной зоне трещины заранее не известны и могут быть существенными. Эти потери возникают из-за наличия перфорационных отверстий и искривления траектории трещины ГРП при ее развитии. Основные потери давления в перфорационных отверстиях будут происходить в перфорационных отверстиях, вовлеченных в развитие трещины ГРП.

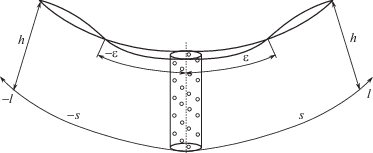
При формировании вертикальной трещины ГРП ее траектория стремится отклониться в направлении максимального горизонтального напряжения, рис. 1. В результате траектория трещины становится криволинейной. Актуальной задачей при моделировании процесса развития трещины ГРП является адекватный учет потерь давления в такой криволинейной трещине. Эти потери давления складываются из потерь на вязкое трение, потерь в перфорационных отверстиях скважины и потерь вследствие искривления траектории трещины ГРП после выхода из перфорационных каналов. Последние возникают из-за дополнительных потерь (по сравнению с потерями в трещине с прямолинейной траекторией) на вязкое трение и потерь, связанных с тем, что на некотором расстоянии ε от скважины после поворота траектории трещины из-за падения давления образуется самое узкое, исключая край трещины, поперечное сечение трещины – своеобразный “клапан”, который создает дополнительные потери давления [1]. Если за пространственную координату s принять естественную координату – дугу траектории трещины, то для симметричной относительно скважины трещины ГРП при |s| > ε траектория трещины становится практически прямолинейной, а потери на трение определяются только вязким трением, рис. 1.

Рис. 1.

Схема к постановке задачи.

В приложениях потери давления из-за вязкого трения в прямолинейной трещине рассчитываются по обычным гидравлическим формулам [2]. Потери давления в перфорационных отверстиях определяются согласно [3]:

$\Delta {{p}_{{per}}} = \rho {{({{v}_{{per}}}{\text{/}}{{C}_{d}})}^{2}}{\text{/}}2$

где ρ – плотность жидкости; C_d– коэффициент сжатия струи; ${{v}_{{per}}}$ – скорость жидкости в перфорационных отверстиях.

Потери давления вследствие кривизны траектории трещины ГРП рассчитываются согласно формуле [1]:

$\Delta {{p}_{c}} = K{{v}^{\beta }}$

где K – коэффициент пропорциональности, $v$ – скорость жидкости в трещине, а параметр β принадлежит интервалу 0.25 ≤ β ≤ 1.

Однако для каждой операции ГРП (скважины) потери давления на трение индивидуальны, поскольку, во-первых, неизвестно число перфорационных отверстий, вовлеченных в процесс развития трещины, от которого зависит скорость течения ${{v}_{{per}}}$ в перфорационных отверстиях. Во-вторых, в зависимости от направлений перфорационных каналов, а также минимального и максимального горизонтального напряжений в призабойной зоне скважины зависит кривизна траектории трещины ГРП в этой зоне. Как следствие, являются неизвестными коэффициент K и показатель степени β.

Одним из способов оценки потерь на трение в прискважинной зоне является использование данных забойных датчиков давления после остановки закачки жидкости гидроразрыва. На практике динамика падения забойного давления после остановки насоса представлена двумя основными режимами – монотонным и колебательным. Монотонный режим падения забойного давления в трещине ГРП без проппанта можно описать уравнениями параболического типа, например, уравнением Перкинса–Керна-Нордгрена (ПКН) [4, 5]. Классическая модель ПКН использует гидравлическое приближение, приближение теории смазки и решение Снеддона [6] о раскрытии трещины в плоскости, находящейся в состоянии плоской деформации, на берега которой действуют нормальные напряжения. В классической модели ПКН жидкость гидроразрыва является ньютоновской. Имеются обобщения этой модели, когда в качестве жидкости ГРП рассматриваются неньютоновские жидкости [1]. В недавних работах [7, 8] для закрепленной проппантом полубесконечной трещины ГРП на основе уравнения пъезопроводности выведено интегро-дифференциальное уравнение для давления в трещине и получены его автомодельные решения в виде бегущих волн давления, когда трещину и пласт насыщают ньютоновские жидкости, а на скважине задан гармонический сигнал.

Однако для трещин ГРП конечной длины колебательный режим падения давления при стационарных граничных условиях можно описать только уравнениями гиперболического типа. В работе [9] выполнено обобщение классической модели ПКН с учетом инерционных слагаемых. В результате параболическая система уравнений изменяет свой тип, преобразуясь в систему уравнений строго гиперболического типа. В работе [10] на базе модели, развитой в работе [9], предложена математическая модель для описания изменения давления после остановки закачки жидкости гидроразрыва в прямолинейной симметричной трещине ГРП без учета влияния скважины.

В данной работе предпринята попытка оценить потери давления на трение в призабойной зоне трещины ГРП (по первой амплитуде в колебательном режиме и по полному падению в монотонном режиме) во время закачки жидкости гидроразрыва по данным забойных датчиков давления после остановки закачки жидкости гидроразрыва в “тестовом” ГРП. Для этой цели предлагается обобщение модели [10] и решается прямая задача об изменении давления в призабойной зоне трещины после остановки насоса с учетом перфорационных отверстий и кривизны траектории трещины. В свою очередь, это решение можно использовать для решения обратной задачи по данным забойных манометров после остановки насоса.

1. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

Как было отмечено во введении, описание течения в трещине ГРП основано на обобщении модели ПКН гиперболического типа [9].

Путем линеаризации модели, предложенной в работе [9], получена математическая модель, описывающая течение жидкости в прямолинейной трещине ГРП после остановки закачки жидкости гидроразрыва [10]

(1.1)

$\frac{{\partial w{\kern 1pt} '}}{{\partial t}} + {{w}_{0}}\frac{{\partial v{\kern 1pt} '}}{{\partial x}} = 0$

(1.2)

$\frac{{\partial {\kern 1pt} v{\kern 1pt} '}}{{\partial t}} + \frac{b}{\rho }\frac{{\partial w{\kern 1pt} '}}{{\partial x}} = - \frac{{12\mu v{\kern 1pt} '}}{{\rho w_{0}^{2}}}$

где w' – возмущения раскрытия трещины; $v{\kern 1pt} '$ – возмущения скорости течения жидкости ГРП в трещине; ρ – постоянная плотность жидкости ГРП в трещине; b = 4G/(πh(1 – ν)) > 0 – жесткость трещины, где h – постоянная высота трещины, а G, ν – соответственно модуль сдвига и коэффициент Пуассона породы; μ – вязкость жидкости.

Возмущенные поля раскрытия трещины и скорости течения рассматриваются относительно стационарного “фонового” решения системы уравнений ПКН гиперболического типа без учета утечек жидкости через стенки трещины. Это фоновое решение подчиняется системе уравнений

$\begin{gathered} {{v}_{0}}\frac{{\partial {\kern 1pt} {{w}_{0}}}}{{\partial x}} + {{w}_{0}}\frac{{\partial {\kern 1pt} {{v}_{0}}}}{{\partial x}} = 0 \\ \frac{b}{\rho }{\kern 1pt} \frac{{\partial {{w}_{0}}}}{{\partial x}} + {{v}_{0}}\frac{{\partial {{v}_{0}}}}{{\partial x}} = - \frac{{12\mu {{v}_{0}}}}{{\rho w_{0}^{2}}} \\ \end{gathered} $

Величину w₀ = const можно трактовать как эффективное раскрытие трещины, на фоне которого происходят ее собственные колебания с нулевой скоростью частиц жидкости ${{v}_{0}}$ = 0.

Рассмотрим, например, правое “крыло” симметричной трещины ГРП, рис. 1. Как было сказано во введении, на расстоянии ε вдоль траектории трещины от перфорационных отверстий траектория трещины становится прямолинейной. При х > ε потери давления в трещине определяются только вязким трением. Разумеется, в интервале 0 ≤ x ≤ ε также действует вязкое трение, как и для прямолинейной трещины, но в интервале 0 ≤ x ≤ ε еще имеются дополнительные потери давления, которые определяются кривизной траектории трещины и наличием “клапана” в точке с координатой х = ε.

Обозначим через (Δp)₁ перепад давления за счет вязкого трения в прямолинейной трещине в интервале 0 ≤ x ≤ ε. Просуммируем дополнительные потери давления в этом интервале за счет кривизны и перфорационных отверстий и обозначим соответствующий перепад давления через (Δp)₂. Поставим прямую задачу определения введенных перепадов после остановки закачки жидкости ГРП. При этом будем опираться на уравнения (1.1), (1.2) модели течения в прямолинейной трещине ГРП без учета скважины.

Для учета суммарного гидравлического сопротивления в прискважинном интервале трещины ГРП (–ε ≤ x ≤ ε) за счет потерь в перфорационных отверстиях и поворота трещины ГРП при выходе из перфорационных каналов систему уравнений из работы [9] необходимо модифицировать (здесь не приведена). Для этого добавим в уравнение импульсов дополнительное линейное слагаемое, отвечающее за указанные потери давления. Тогда система уравнений для возмущенного течения примет вид

(1.3)

$\frac{{\partial w{\kern 1pt} '}}{{\partial t}} + {{w}_{0}}\frac{{\partial v{\kern 1pt} '}}{{\partial x}} = 0$

(1.4)

$\frac{{\partial {\kern 1pt} v{\kern 1pt} '}}{{\partial t}} + \frac{b}{\rho }\frac{{\partial w{\kern 1pt} '}}{{\partial x}} = - \frac{{12\mu v{\kern 1pt} '}}{{\rho w_{0}^{2}}} - {{K}_{c}}v{\kern 1pt} '$

где K_c– коэффициент трения, имеющий в системе единиц СИ размерность c^–1. Последнее слагаемое в (1.4) действует не на всей длине симметричной трещины ГРП, а только в некотором интервале (–ε ≤ x ≤ ε) призабойной зоны. При этом в правой части уравнения движения фонового решения появится аналогичное линейное слагаемое $ - {{K}_{c}}{{v}_{0}}$, но указанное выше стационарное решение останется таким же, как и в работе [10]. Линейное представление потерь давления на дополнительное трение в призабойной зоне является модельным допущением.

Дифференцируя уравнение (1.3) по времени, а уравнение (1.4) по пространственной координате, получим уравнение для возмущений раскрытия трещины в рассматриваемом случае

(1.5)

$\frac{{{{\partial }^{2}}w{\kern 1pt} '}}{{\partial {{t}^{2}}}} - a_{0}^{2}\frac{{{{\partial }^{2}}w{\kern 1pt} '}}{{\partial {{x}^{2}}}} + {{b}_{0}}\frac{{\partial w{\kern 1pt} '}}{{\partial t}} = f(x,t) = - {{K}_{c}}\frac{{\partial w{\kern 1pt} '}}{{\partial t}},\quad a_{0}^{2} = \frac{{b{{w}_{0}}}}{\rho },\quad {{b}_{0}} = \frac{{12\mu }}{{\rho w_{0}^{2}}}$

2. НАЧАЛЬНЫЕ И ГРАНИЧНЫЕ УСЛОВИЯ

Предлагается постановка начально-краевой задачи о собственных колебаниях трещины ГРП после остановки насоса, рассмотренная в работе [10]. Найти решение уравнения (1.5) для возмущений раскрытия трещины при следующих граничных и начальных условиях (края трещины фиксированы)

(2.1)

$w{\kern 1pt} '( - l,t) = w{\kern 1pt} '(l,t) = 0$

(2.2)

$w{\kern 1pt} '(x,0) = \left\{ \begin{gathered} \frac{{w_{{\max }}^{'}}}{l}(x + l),\quad x \in [ - l,0] \hfill \\ \frac{{w_{{\max }}^{'}}}{l}(l - x),\quad x \in [0,l] \hfill \\ \end{gathered} \right.,\quad w_{t}^{'}(x,0) = 0$

Условия (2.1) и (2.2) означают, что возмущения граничных условий равны нулю, после остановки закачки жидкости ГРП возмущение раскрытия трещины линейно распределено вдоль трещины (первое начальное условие) и скорость возмущения раскрытия трещины равна нулю (второе начальное условие).

3. АНАЛИТИЧЕСКОЕ РЕШЕНИЕ

Сделаем замену переменных

(3.1)

$x{\kern 1pt} ' = (x + l){\text{/}}2$

Тогда в новых переменных уравнение (1.5) примет вид

(3.2)

$\frac{{{{\partial }^{2}}w{\kern 1pt} '}}{{\partial {{t}^{2}}}} - \frac{{a_{0}^{2}}}{4}\frac{{{{\partial }^{2}}w{\kern 1pt} '}}{{\partial {{x}^{2}}}} + {{b}_{0}}\frac{{\partial w{\kern 1pt} '}}{{\partial t}} = f(x,t) = - {{K}_{c}}\frac{{\partial w{\kern 1pt} '}}{{\partial t}}$

где у независимой пространственной переменной штрихи опущены, а слагаемое в правой части уравнения (3.2) действует на интервале (l – ε)/2 ≤ x ≤ (l + ε)/2.

Граничные и начальные условия (2.1) в новых переменных примут вид

(3.3)

$w{\kern 1pt} '(0,t) = w{\kern 1pt} '(l,t) = 0$

(3.4)

$\varphi (x) = w{\kern 1pt} '(x,0) = \left\{ \begin{gathered} \frac{{2w_{{\max }}^{'}x}}{l},\quad x \in [0,l{\text{/}}2] \hfill \\ \frac{{2(l - x)w_{{\max }}^{'}}}{l},\quad x \in [l{\text{/}}2,l] \hfill \\ \end{gathered} \right.,\quad \psi (x) = w_{t}^{'}(x,0) = 0$

В работе [10] получено аналитическое решение уравнения (3.2) без правой части при начально-краевых условиях (3.3), (3.4). Показано, что возможны два основных типа решения для поведения давления (раскрытия) в трещине после остановки насоса –монотонное и колебательное.

Монотонное решение реализуется для гармоник с преобладанием инерционных сил над вязкими силами и в новых переменных (3.1) имеет вид

(3.5)

$\begin{gathered} b_{0}^{2} > a_{0}^{2}{{\left( {\frac{{{\pi }n}}{l}} \right)}^{2}},\quad n = 1,...,m,\quad {{\omega }_{n}} = \sqrt {\frac{{b_{0}^{2} - {\lambda }_{n}^{2}a_{0}^{2}}}{4}} ,\quad {{\lambda }_{n}} = \frac{{{\pi }n}}{l} \\ w_{1}^{'}(x,t) = \exp ( - {{b}_{0}}t{\text{/}}2)\sum\limits_1^\infty {\left( {{{A}_{n}}\exp ({{{\omega }}_{{\text{n}}}}t) + {{B}_{n}}\exp ( - {{\omega }_{n}}t)} \right)} \sin \left( {\frac{{{\pi }nx}}{l}} \right) \\ {{b}_{0}} = \frac{{12{\mu }}}{{{\rho }w_{0}^{2}}},\quad a_{0}^{2} = \frac{{b{{w}_{0}}}}{\rho },\quad {{A}_{n}} = \frac{{{{b}_{n}}({{\omega }_{n}} + {{b}_{0}}{\text{/}}2)}}{{2{{\omega }_{n}}}} \\ {{B}_{n}} = \frac{{{{b}_{n}}({{\omega }_{n}} - {{b}_{0}}{\text{/}}2)}}{{2{{\omega }_{n}}}},\quad {{b}_{n}} = \frac{{8w_{{\max }}^{'}}}{{{{{\left( {{\pi }n} \right)}}^{2}}}}\sin \left( {\frac{{{\pi }n}}{2}} \right) \\ \end{gathered} $

Колебательное решение реализуется для гармоник с преобладанием вязких сил над силами инерции и в новых переменных (3.1) имеет вид

(3.6)

$\begin{gathered} b_{0}^{2} < a_{0}^{2}{{\left( {\frac{{\pi n}}{l}} \right)}^{2}},\quad n = m + 1,...\quad {{\omega }_{n}} = \sqrt {\frac{{\lambda _{n}^{2}a_{0}^{2} - b_{0}^{2}}}{4}} \\ w_{2}^{'}(x,t) = \exp ( - {{b}_{0}}t{\text{/}}2)\sum\limits_1^\infty {\left( {{{A}_{n}}\cos ({{\omega }_{n}}t) + {{B}_{n}}\sin ({{\omega }_{n}}t)} \right)} \sin \left( {\frac{{\pi nx}}{l}} \right) \\ {{A}_{n}} = {{b}_{n}},\quad {{B}_{n}} = \frac{{{{b}_{0}}{{b}_{n}}}}{{2{{\omega }_{n}}}} \\ \end{gathered} $

Допустим, что для уравнения (3.2) при начально-краевых условиях (3.3), (3.4) решение для раскрытия трещины в интервале (l – ε)/2 ≤ x ≤ (l + ε)/2 будет иметь тот же вид (3.5) или (3.6), что и в случае собственных колебаний трещины ГРП без учета наличия скважины и кривизны ее траектории.

Дифференцирование по времени решения (3.5) дает вид слагаемого в правой части уравнения (1.5), отвечающего за дополнительные потери давления на трение из-за кривизны трещины и потерь в перфорационных отверстиях в призабойной зоне трещины ГРП в случае монотонного режима течения в трещине:

(3.7)

$\begin{gathered} f(x,t) = - {{K}_{c}}\exp ( - {{b}_{0}}t{\text{/}}2)\sum\limits_1^\infty {\left( {{{\alpha }_{m}}\exp ({{{\omega }}_{m}}t) - {{{\gamma }}_{m}}\exp ( - {{\omega }_{m}}t)} \right)} \sin \left( {\frac{{\pi mx}}{l}} \right) \\ {{\alpha }_{m}} = {{A}_{m}}({{\omega }_{m}} - {{b}_{0}}{\text{/}}2),\quad {{\gamma }_{m}} = {{B}_{m}}({{\omega }_{m}} + {{b}_{0}}{\text{/}}2) \\ \end{gathered} $

Дифференцирование по времени решения (3.6) дает вид аналогичного слагаемого в правой части уравнения (1.5) в случае колебательного режима течения в трещине:

(3.8)

$\begin{gathered} f(x,t) = {{K}_{c}}\exp ( - {{b}_{0}}t{\text{/}}2)\sum\limits_1^\infty {\left( {{{{\alpha }}_{m}}{\text{cos}}({{\omega }_{m}}t) + {{{\gamma }}_{m}}{\text{sin}}({{\omega }_{m}}t)} \right)} \sin \left( {\frac{{\pi mx}}{l}} \right) \\ {{\alpha }_{m}} = {{A}_{m}}{{b}_{0}}{\text{/}}2 - {{B}_{m}}{{\omega }_{m}} = 0,\quad {{\gamma }_{m}} = {{B}_{m}}{{b}_{0}}{\text{/}}2 + {{\omega }_{m}}{{A}_{m}} \\ \end{gathered} $

Первое равенство во второй строке (3.8) следует из двух последних соотношений (3.6).

Для нахождения аналитического решения задач (3.2)–(3.4), (3.7) или (3.2)–(3.4), (3.8) применим метод разделения переменных [11]. Будем искать решение этой задачи в виде разложения в ряд Фурье по синусам

(3.9)

$w{\kern 1pt} '(x,t) = \sum\limits_1^\infty {{{w}_{n}}(t)} \sin \left( {\frac{{\pi nx}}{l}} \right)$

Очевидно, что представление (3.9) удовлетворяет граничным условиям (3.3). Также представим в виде рядов Фурье функцию f(x, t) и начальные условия φ(x) и ψ(x):

(3.10)

$f(x,t) = \sum\limits_1^\infty {{{f}_{n}}(t)} \sin \left( {\frac{{\pi nx}}{l}} \right),\quad {{f}_{n}}(t) = \frac{2}{l}\int\limits_0^l {f(\xi ,t)} \sin \left( {\frac{{\pi n\xi }}{l}} \right)d\xi $

(3.11)

$\varphi (x) = \sum\limits_1^\infty {{{\varphi }_{n}}} \sin \left( {\frac{{\pi nx}}{l}} \right),\quad {{\varphi }_{n}} = \frac{2}{l}\int\limits_0^l {\varphi (\xi )} \sin \left( {\frac{{\pi n\xi }}{l}} \right)d\xi $

(3.12)

$\psi (x) = \sum\limits_1^\infty {{{\psi }_{n}}} {\text{sin}}\left( {\frac{{\pi nx}}{l}} \right),\quad {{\psi }_{n}} = \frac{2}{l}\int\limits_0^l {\psi (\xi )} \sin \left( {\frac{{\pi n\xi }}{l}} \right)d\xi $

Из выражений (3.9), (3.11) и (3.12) следуют равенства

(3.13)

${{w}_{n}}(0) = {{\varphi }_{n}},\quad {{\dot {w}}_{n}}(0) = \frac{{d{{w}_{n}}(0)}}{{dt}} = {{\psi }_{n}}$

Подстановка выражений (3.9) и (3.10) в уравнение (3.2) приводит к уравнению

(3.14)

${{\ddot {w}}_{n}}(t) + {{b}_{0}}{{\dot {w}}_{n}}(t) + \frac{{a_{0}^{2}}}{4}{{\left( {\frac{{\pi n}}{l}} \right)}^{2}},\quad {{w}_{n}}(t) = {{f}_{n}}(t)$

По принципу суперпозиции решение уравнения (3.14) можно представить в виде суммы решения однородной задачи $w_{n}^{{(1)}}$ сданными начальными условиями (3.4) и решения неоднородной задачи $w_{n}^{{(2)}}$ с однородными начальными условиями

(3.15)

${{w}_{n}} = w_{n}^{{(1)}} + w_{n}^{{(2)}}$

Монотонное решение однородного уравнения (3.14) имеет вид

(3.16)

$w_{n}^{{(1)}}(t) = \exp ( - {{b}_{0}}t{\text{/}}2)\left( {{{A}_{n}}\exp ({{\omega }_{n}}t) + {{B}_{n}}\exp ( - {{\omega }_{n}}t)} \right)$

а колебательное решение однородного уравнения (3.14) имеет вид

(3.17)

$w_{n}^{{(1)}}(t) = \exp ( - {{b}_{0}}t{\text{/}}2)\left( {{{A}_{n}}\cos ({{\omega }_{n}}t) + {{B}_{n}}\sin ( - {{\omega }_{n}}t)} \right)$

Решение неоднородной задачи $w_{n}^{{(2)}}$ с однородными начальными условиями представляется в виде [11]:

(3.18)

$w_{n}^{{(2)}}(t) = \int\limits_0^t {w_{n}^{{(1)}}(t - \tau )} {{f}_{n}}(\tau )d\tau $

где решение $w_{n}^{{(1)}}$ удовлетворяет начальным условиям

(3.19)

$w_{n}^{{(1)}}(0) = 0,\quad \frac{{dw_{n}^{{(1)}}(0)}}{{dt}} = 1$

Из уравнений (3.16)–(3.19) находятся решения неоднородного уравнения в случае монотонного движения в трещине

(3.20)

$w_{n}^{{(2)}}(t) = \int\limits_0^t {\frac{{{{e}^{{ - {{b}_{0}}(t - \tau )/2}}}}}{{{{\omega }_{n}}}}sh({{\omega }_{n}}(t - \tau )} ){{f}_{n}}(\tau )d\tau $

и в случае колебательного движения

(3.21)

$w_{n}^{{(2)}}(t) = \int\limits_0^t {\frac{{{{e}^{{ - {{b}_{0}}(t - \tau )/2}}}}}{{{{\omega }_{n}}}}\sin ({{\omega }_{n}}(t - \tau )} ){{f}_{n}}(\tau )d\tau $

Вычисление коэффициентов f_n(t) согласно (3.10), (3.7) и (3.8) дает следующие выражения. Для монотонного течения

(3.22)

${{f}_{n}}(t) = - \frac{{2{{K}_{c}}}}{l}\exp ( - {{b}_{0}}t{\text{/}}2)\sum\limits_1^\infty {\left( {{{\alpha }_{m}}\exp ({{\omega }_{m}}t) - {{{\gamma }}_{m}}\exp ( - {{\omega }_{m}}t)} \right)} {{z}_{{nm}}}$

а для колебательного течения

(3.23)

${{f}_{n}}(t) = \frac{{2{{K}_{c}}}}{l}\exp ( - {{b}_{0}}t{\text{/}}2)\sum\limits_1^\infty {{{\gamma }_{m}}\sin ({{\omega }_{m}}t)} {{z}_{{nm}}}$

где коэффициенты z_nm определяются по формуле

(3.24)

${{z}_{{nm}}} = \left[ \begin{gathered} \varepsilon - \frac{l}{{2\pi n}}\sin \frac{{\pi n\varepsilon }}{l}\cos (\pi n),\quad n = m \hfill \\ \frac{l}{{\pi (n - m)}}\sin \frac{{\pi (n - m)\varepsilon }}{{2l}}\cos \frac{{\pi (n - m)}}{2} - \hfill \\ \, - \frac{l}{{\pi (n + m)}}\sin \frac{{\pi (n + m)\varepsilon }}{{2l}}\cos \frac{{\pi (n + m)}}{2},\quad n \ne m \hfill \\ \end{gathered} \right.$

Подстановка (3.22) и (3.23) соответственно в (3.20) и (3.21), применение принципа суперпозиции (3.15) и разложения (3.9) дает следующие решения для возмущенного раскрытия трещины ГРП после остановки насоса. В случае монотонного течения в “старых” переменных имеем решение

(3.25)

$\begin{gathered} w_{1}^{'}(x,t) = \exp ( - {{b}_{0}}t{\text{/}}2)\sum\limits_{n = 1}^\infty {\left( {{{A}_{n}}\exp ({{\omega }_{n}}t) + {{B}_{n}}\exp ( - {{\omega }_{n}}t)} \right)} \sin \left( {\frac{{\pi n(x + l)}}{{2l}}} \right) - \\ \, - \frac{{{{K}_{c}}}}{l}\exp ( - {{b}_{0}}t{\text{/}}2)\sum\limits_{n = 1}^\infty {\sum\limits_{m = 1}^\infty {\frac{{{{z}_{{nm}}}}}{{{{\omega }_{n}}}}} \left( {{{\alpha }_{m}}{{\beta }_{{nm}}}(t) - {{\gamma }_{m}}{{\delta }_{{nm}}}(t)} \right)} \sin \left( {\frac{{\pi n(x + l)}}{{2l}}} \right) \\ \end{gathered} $

где α_m, γ_m выражаются через константы A_m, B_m согласно двум последним формулам (3.7), а функции времени β_nm(t) и δ_nm(t) равны соответственно

(3.26)

${{\beta }_{{nm}}}(t) = \left[ \begin{gathered} t\exp ({{\omega }_{n}}t) - \frac{1}{{{{\omega }_{n}}}}{\text{sh}}({{\omega }_{n}}t),\quad n = m \hfill \\ \frac{1}{{{{\omega }_{m}} - {{\omega }_{n}}}}\left( {{\text{exp}}({{\omega }_{m}}t) - {\text{exp}}({{\omega }_{n}}t)} \right) - \frac{1}{{{{\omega }_{m}} + {{\omega }_{n}}}}\left( {{\text{exp}}({{\omega }_{m}}t) - {\text{exp}}( - {{\omega }_{n}}t)} \right),\quad n \ne m \hfill \\ \end{gathered} \right.$

(3.27)

${{\delta }_{{nm}}}(t) = \left[ \begin{gathered} \frac{1}{{{{\omega }_{n}}}}{\text{sh}}({{\omega }_{n}}t) - t{\text{exp}}( - {{\omega }_{n}}t),\quad n = m \hfill \\ \frac{1}{{{{\omega }_{m}} + {{\omega }_{n}}}}\left( {{\text{exp}}({{\omega }_{n}}t) - {\text{exp}}( - {{\omega }_{m}}t)} \right) - \hfill \\ \, - \frac{1}{{{{\omega }_{n}} - {{\omega }_{m}}}}\left( {{\text{exp}}( - {{\omega }_{m}}t) - {\text{exp}}( - {{\omega }_{n}}t)} \right),\quad n \ne m \hfill \\ \end{gathered} \right.$

В случае колебательного течения в “старых” переменных решение имеет вид

(3.28)

$\begin{gathered} w_{2}^{'}(x,t) = \exp ( - {{b}_{0}}t{\text{/}}2)\sum\limits_{n = 1}^\infty {\left( {{{A}_{n}}\cos ({{\omega }_{n}}t) + {{B}_{n}}\sin ({{\omega }_{n}}t)} \right)} \sin \left( {\frac{{\pi n(x + l)}}{{2l}}} \right) + \\ \, + \frac{{2{{K}_{c}}}}{l}\exp ( - {{b}_{0}}t{\text{/}}2)\sum\limits_{n = 1}^\infty {\sum\limits_{m = 1}^\infty {\frac{{{{z}_{{nm}}}}}{{{{\omega }_{n}}}}} {{\gamma }_{m}}{{\beta }_{{nm}}}(t)} \sin \left( {\frac{{\pi n(x + l)}}{{2l}}} \right) \\ \end{gathered} $

где γ_m выражается через константы A_m, B_m согласно последней формуле (3.8), а функция времени β_nm(t) равна

(3.29)

${{\beta }_{{nm}}}(t) = \left[ \begin{gathered} \frac{1}{{2{{\omega }_{n}}}}\sin ({{\omega }_{n}}t) - \frac{t}{2}\cos ({{\omega }_{n}}t),\quad n = m \hfill \\ \frac{1}{{2({{\omega }_{m}} + {{\omega }_{n}})}}\left( {\sin ({{\omega }_{n}}t) - \sin ({{\omega }_{m}}t)} \right) - \hfill \\ \, - \frac{1}{{2({{\omega }_{m}} - {{\omega }_{n}})}}\left( {\sin ({{\omega }_{m}}t) - \sin ({{\omega }_{n}}t)} \right),\quad n \ne m \hfill \\ \end{gathered} \right.$

В решениях (3.25) и (3.28) выполнена обратная замена пространственной переменной (3.1).

Согласно допущениям модели ПКН изменение давления в трещине подчиняется уравнению [10]

(3.30)

$p{\kern 1pt} (x,t) = \sigma + b{\kern 1pt} {{w}_{0}} + bw{\kern 1pt} '(x,t)$

где σ – постоянное минимальное горизонтальное напряжение в окрестности стенок трещины ГРП. Для монотонного и колебательного режимов течения после остановки закачки жидкости ГРП в последнее слагаемое в правой части (3.30) нужно подставить решения (3.25) и (3.28) соответственно.

4. ПОТЕРИ ДАВЛЕНИЯ НА ТРЕНИЕ В ПРИСКВАЖИННОЙ ОБЛАСТИ

Дифференцирование (3.25) по времени, подстановка в уравнение (1.3) и последующее интегрирование полученного уравнения по пространственной координате дают поле возмущенной скорости в трещине при монотонном течении

(4.1)

$\begin{gathered} v_{1}^{'}(x,t) = {{v}_{1}} + {{v}_{2}} \\ {{v}_{1}} = \frac{{\exp ( - {{b}_{0}}t{\text{/}}2)}}{{{{w}_{0}}}}\sum\limits_{n = 1}^\infty {\left( {{{\alpha }_{n}}\exp ({{\omega }_{n}}t) - {{\gamma }_{n}}\exp ( - {{\omega }_{n}}t)} \right)} \frac{{2l}}{{\pi n}}\cos \left( {\frac{{\pi n(x + l)}}{{2l}}} \right) \\ {{v}_{2}}{{e}^{{({{b}_{0}}t{\text{/}}2)}}} = \frac{{{{K}_{c}}}}{{{{w}_{0}}l}}\sum\limits_{n = 1}^\infty {\sum\limits_{m = 1}^\infty {\frac{{{{z}_{{nm}}}}}{{{{\omega }_{n}}}}} \text{[}{{\alpha }_{m}}({{\beta }_{{nm}}}(t){{b}_{0}}{\text{/}}2 - \beta _{{nm}}^{'}(t)) + {{\gamma }_{m}}(\delta _{{nm}}^{'}(t) - {{\delta }_{{nm}}}(t){{b}_{0}}{\text{/}}2)]\frac{{2l}}{{\pi n}}} \cos \left( {\frac{{\pi n(x + l)}}{{2l}}} \right) \\ \end{gathered} $

В формуле (4.1) введены обозначения

(4.2)

$\beta _{{nm}}^{'}(t) = \left[ \begin{gathered} {\text{exp}}({{\omega }_{n}}t) + {{\omega }_{n}}t{\text{exp}}({{\omega }_{n}}t) - {\text{ch}}({{\omega }_{n}}t),\quad n = m \hfill \\ \frac{1}{{{{\omega }_{m}} - {{\omega }_{n}}}}\left( {{{\omega }_{m}}{\text{exp}}({{\omega }_{m}}t) - {{\omega }_{n}}{\text{exp}}({{\omega }_{n}}t)} \right) - \hfill \\ \, - \frac{1}{{{{\omega }_{m}} + {{\omega }_{n}}}}\left( {{{\omega }_{m}}{\text{exp}}({{\omega }_{m}}t) + {{\omega }_{n}}{\text{exp}}( - {{\omega }_{n}}t)} \right),\quad n \ne m \hfill \\ \end{gathered} \right.$

(4.3)

$\delta _{{nm}}^{'}(t) = \left[ \begin{gathered} {\text{ch}}({{\omega }_{n}}t) - {\text{exp}}( - {{\omega }_{n}}t) + {{\omega }_{n}}t{\text{exp}}( - {{\omega }_{n}}t),\quad n = m \hfill \\ \frac{1}{{{{\omega }_{m}} + {{\omega }_{n}}}}\left( {{{\omega }_{n}}{\text{exp}}({{\omega }_{n}}t) + {{\omega }_{m}}{\text{exp}}( - {{\omega }_{m}}t)} \right) - \hfill \\ \, - \frac{1}{{{{\omega }_{n}} - {{\omega }_{m}}}}\left( {{{\omega }_{n}}{\text{exp}}( - {{\omega }_{n}}t) - {{\omega }_{m}}{\text{exp}}( - {{\omega }_{m}}t)} \right),\quad n \ne m \hfill \\ \end{gathered} \right.$

Дифференцирование (3.28) по времени, подстановка в уравнение (1.3) и интегрирование полученного уравнения по пространственной координате дают поле возмущенной скорости в трещине при колебательном течении

(4.4)

$\begin{gathered} v_{2}^{'}(x,t) = {{v}_{1}} + {{v}_{2}} \\ {{v}_{1}} = - \frac{{\exp ( - {{b}_{0}}t{\text{/}}2)}}{{{{w}_{0}}}}\sum\limits_{n = 1}^\infty {\left( {{{\alpha }_{n}}\cos ({{\omega }_{n}}t) + {{\gamma }_{n}}\sin ({{\omega }_{n}}t)} \right)} \frac{{2l}}{{\pi n}}\cos \left( {\frac{{\pi n(x + l)}}{{2l}}} \right) \\ {{v}_{2}} = \frac{{2{{K}_{c}}\exp ( - {{b}_{0}}t{\text{/}}2)}}{{{{w}_{0}}l}}\sum\limits_{n = 1}^\infty {\sum\limits_{m = 1}^\infty {\frac{{{{z}_{{nm}}}}}{{{{\omega }_{n}}}}} {{\gamma }_{m}}(\beta _{{nm}}^{'}(t) - {{\beta }_{{nm}}}(t){{b}_{0}}{\text{/}}2)\frac{{2l}}{{\pi n}}} \cos \left( {\frac{{\pi n(x + l)}}{{2l}}} \right) \\ \end{gathered} $

где введено обозначение

(4.5)

$\beta _{{nm}}^{'}(t) = \left[ \begin{gathered} {{\omega }_{n}}\frac{t}{2}\sin ({{\omega }_{n}}t) - \frac{1}{2}\cos ({{\omega }_{n}}t),\quad n = m \hfill \\ \frac{1}{{2({{\omega }_{m}} + {{\omega }_{n}})}}\left( {{{\omega }_{n}}\cos ({{\omega }_{n}}t) - {{\omega }_{m}}\cos ({{\omega }_{m}}t)} \right) - \hfill \\ \, - \frac{1}{{2({{\omega }_{m}} - {{\omega }_{n}})}}\left( {{{\omega }_{m}}\cos ({{\omega }_{m}}t) - {{\omega }_{n}}\cos ({{\omega }_{n}}t)} \right),\quad n \ne m \hfill \\ \end{gathered} \right.$

Часть поля скорости ${{v}_{1}}$ в трещине не учитывает наличие скважины и кривизну траектории трещины. Эта часть всегда присутствует в симметричной прямолинейной трещине. Дополнительная часть поля скорости v₂ связана с кривизной траектории трещины и потерями на трение в перфорационных отверстиях.

Наконец, перепад давления Δp(t) в призабойной зоне симметричной трещины можно определить по формуле

(4.6)

$\Delta p(t) = \frac{{12\mu }}{{w_{0}^{2}}}\int\limits_0^\varepsilon {\left| {{{v}_{1}}(x,t)} \right|dx} + {{K}_{c}}\rho \int\limits_0^\varepsilon {\left| {{{v}_{2}}(x,t)} \right|dx} $

Подстановка (4.1)–(4.3) в уравнение (4.6) дает величину перепада давления в ε окрестности скважины как функцию времени для монотонного режима течения в трещине

(4.7)

$\begin{gathered} \Delta p(t) = {{(\Delta p)}_{1}}(t) + {{(\Delta p)}_{2}}(t) \\ {{(\Delta p)}_{1}} = \frac{{12\mu }}{{w_{0}^{3}}}\left| {\exp ( - {{b}_{0}}t{\text{/}}2)\sum\limits_{n = 1}^\infty {\left( {{{\alpha }_{n}}\exp ({{\omega }_{n}}t) - {{\gamma }_{n}}\exp ( - {{\omega }_{n}}t)} \right)} {{{\left( {\frac{{2l}}{{\pi n}}} \right)}}^{2}}\left( {\sin \frac{{\pi n(\varepsilon + l)}}{{2l}} - \sin \frac{{\pi n}}{2}} \right)} \right| \\ {{(\Delta p)}_{2}} = \frac{{K_{c}^{2}\rho }}{{{{w}_{0}}l}}\left| {\exp ( - {{b}_{0}}t{\text{/}}2)\sum\limits_{n = 1}^\infty {\sum\limits_{m = 1}^\infty {\frac{{{{z}_{{nm}}}}}{{{{\omega }_{n}}}}} {{g}_{{nm}}}} {{{\left( {\frac{{2l}}{{\pi n}}} \right)}}^{2}}\left( {\sin \frac{{\pi n{\kern 1pt} (\varepsilon + l)}}{{2l}} - \sin \frac{{\pi n}}{2}} \right)} \right| \\ {{g}_{{nm}}} = {{\alpha }_{m}}({{\beta }_{{nm}}}(t){{b}_{0}}{\text{/}}2 - \beta _{{nm}}^{'}(t)) + {{\gamma }_{m}}(\delta _{{nm}}^{'}(t) - {{\delta }_{{nm}}}(t){{b}_{0}}{\text{/}}2) \\ \end{gathered} $

Подстановка (4.4) и (4.5) в (4.6) дает величину перепада давления в ε-окрестности скважины как функцию времени при колебательном режиме течения в трещине

(4.8)

$\begin{gathered} \Delta p(t) = {{(\Delta p)}_{1}}(t) + {{(\Delta p)}_{2}}(t) \\ {{(\Delta p)}_{1}} = \frac{{12\mu }}{{w_{0}^{3}}}\left| {\exp ( - {{b}_{0}}t{\text{/}}2)\sum\limits_{n = 1}^\infty {{{\gamma }_{n}}\sin ({{\omega }_{n}}t)} {{{\left( {\frac{{2l}}{{\pi n}}} \right)}}^{2}}\left( {\sin \frac{{\pi n(\varepsilon + l)}}{{2l}} - \sin \frac{{\pi n}}{2}} \right)} \right| \\ {{(\Delta p)}_{2}} = \frac{{2K_{c}^{2}\rho }}{{{{w}_{0}}l}}\left| {\exp ( - {{b}_{0}}t{\text{/}}2)\sum\limits_{n = 1}^\infty {\sum\limits_{m = 1}^\infty {\frac{{{{z}_{{nm}}}}}{{{{\omega }_{n}}}}} {{\gamma }_{m}}(\beta _{{nm}}^{'}(t) - {{\beta }_{{nm}}}(t){{b}_{0}}{\text{/}}2)} {{{\left( {\frac{{2l}}{{\pi n}}} \right)}}^{2}}\left( {\sin \frac{{\pi n(\varepsilon + l)}}{{2l}} - \sin \frac{{\pi n}}{2}} \right)} \right| \\ \end{gathered} $

где введено обозначение

(4.9)

$\beta _{{nm}}^{'}(t) = \left[ \begin{gathered} {{\omega }_{n}}\frac{t}{2}\sin ({{\omega }_{n}}t) - \frac{1}{2}{\kern 1pt} \cos ({{\omega }_{n}}t),\quad n = m \hfill \\ \frac{1}{{2({{\omega }_{m}} + {{\omega }_{n}})}}\left( {{{\omega }_{n}}\cos ({{\omega }_{n}}t) - {{\omega }_{m}}\cos ({{\omega }_{m}}t)} \right) - \hfill \\ \, - \frac{1}{{2({{\omega }_{m}} - {{\omega }_{n}})}}\left( {{{\omega }_{m}}\cos ({{\omega }_{m}}t) - {{\omega }_{n}}\cos ({{\omega }_{n}}t)} \right),\quad n \ne m \hfill \\ \end{gathered} \right.$

В формулах (4.7) и (4.8) перепад давления (Δp)₁ в призабойной зоне возникает из-за вязкости жидкости гидроразрыва пласта и не учитывает кривизну трещины и наличие перфорационных каналов. Перепад давления (Δp)₂ в призабойной зоне порождается кривизной траектории трещины и потерями давления на трение в перфорационных каналах.

Если K_c → 0, а ε ≠ 0.l, то выражения (4.7) и (4.8) определяют изменение по времени перепада давления в призабойной зоне трещины протяженностью ε одного крыла симметричной прямолинейной трещины ГРП. Если K_c → 0, а ε → l, то выражения (4.7) и (4.8) определяют изменение по времени перепада давления в одном крыле симметричной прямолинейной трещины ГРП длиной l. Если K_c ≠ 0, а ε → 0, то, как и следовало ожидать, перепад давления стремится к нулю Δp → 0. Если K_c ≠ 0, а ε ≠ 0, l, то выражения (4.7) и (4.8) определяют изменение по времени перепада давления в призабойной зоне протяженностью ε одного крыла симметричной криволинейной трещины ГРП с учетом потерь в перфорационных отверстиях эксплуатационной колонны. И, наконец, если K_c ≠ 0, а ε → l, то выражения (4.7) и (4.8) определяют изменение по времени перепада давления на всем крыле протяженностью l симметричной криволинейной трещины ГРП с учетом потерь в перфорационных отверстиях эксплуатационной колонны.

При выводе формул (4.7) и (4.8) неоднократно использовались операции почленного дифференцирования и интегрирования рядов Фурье. Вопросы обоснования таких процедур, а также сходимости функциональных однократных рядов, рассмотрены в работах [12, 13], а двукратных рядов – в работе [13]. На практике рассматриваются не бесконечные ряды, а конечные суммы, поэтому вопрос обоснования операций их почленного интегрирования, дифференцирования и т.д. не стоит. Однако может стоять вопрос о неустойчивом нарастании малых возмущений при суммировании конечных сумм с большим количеством членов [12].

5. РЕЗУЛЬТАТЫ РАСЧЕТОВ

На рис. 2–7 представлены результаты расчетов по полученным решениям. При вычислениях были использованы следующие параметры: ρ = 1000 кг/м³, μ = 0.001 Па с, w₀ = 0.0023 м, l = 100 м, h = 10.0 м, $w_{{\max }}^{'}$ = 0.0001 м, G = 10¹⁰ Па, ν = 0.25. Используемая вязкость соответствует вязкости воды при замещении скважинной жидкости линейным гелем. Это один из вариантов тестового ГРП.

Рис. 2.

Тестовый расчет. Сплошная линия – n = m = 60, штриховая – n = m = 80.

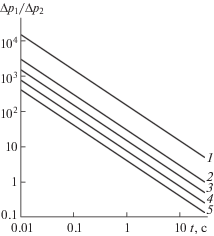
Рис. 3.

Отношение перепадов давления (Δp)₁/(Δp)₂ при монотонном режиме течения в трещине от времени для различных протяженностей области поворота ε при K_с = 0.1 с^–1. Линии 1–5 соответствуют ε=1, 5, 10, 20, 40 (м).

Рис. 4.

То же, что на рис. 3: K_с = 1 с^–1.

Рис. 5.

То же, что на рис. 2: K_с = 20 с^–1.

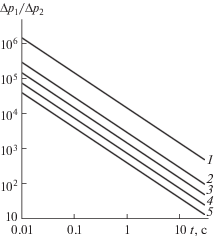
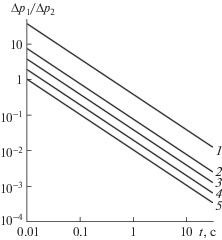
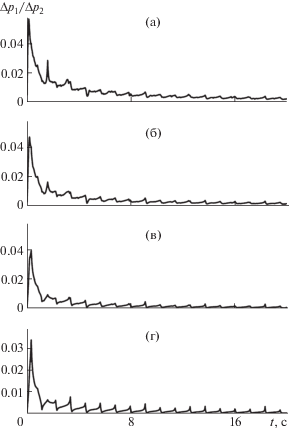
Рис. 6.

Динамика отношений перепадов давления (Δp)₁/(Δp)₂ для колебательного режима течения при K_с = 1 с^–1: (a), (б), (в), (г) отвечают протяженностям области поворота ε = 10, 20, 40 и 60 м соответственно.

Рис. 7.

То же, что на рис. 6: K_с = 20 с^–1.

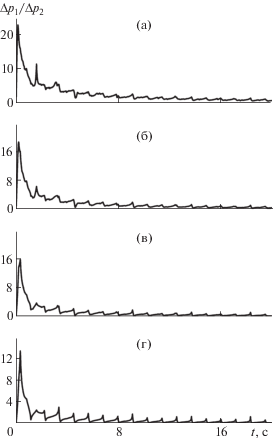
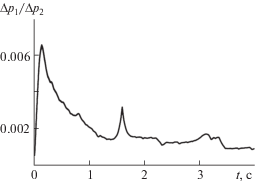
На рис. 2 показаны графики отношений перепадов давления (Δp)₁/(Δp)₂ в колебательном режиме течения после остановки насоса при указанных выше параметрах. Непрерывная кривая соответствует количеству членов ряда n = 60, m = 60. Штриховая кривая соответствует количеству членов ряда n = 80, m = 80. Дополнительные параметры равны K_с = 20 1/с, ε = 10 м. Интервал времени равен 4 с. Из фиг. 2 видно полное совпадение графиков. Далее расчеты для колебательного режима проводились при n = 60, m = 60.

Для монотонного режима течения при рассматриваемых параметрах во всех расчетах берется только один член ряда в формуле (4.7), согласно ограничению на параметры монотонного течения – первая формула (3.5).

На рис. 3–5 показано отношение перепадов давления (Δp)₁/(Δp)₂ при монотонном режиме течения в трещине после остановки закачки жидкости ГРП в логарифмических координатах. На рис. 3 показано отношение перепадов давления (Δp)₁/(Δp)₂при K_с = 0.1 с^–1 для различных значений размеров области поворота ε. Видно, что перепад давления (Δp)₁ за счет вязкости жидкости на порядки превосходит перепад (Δp)₂. На рис. 4 показано отношение перепадов давления (Δp)₁/(Δp)₂ при K_с = 1 1/с для различных значений ε. Отношение перепадов давлений (Δp)₁/(Δp)₂ многократно уменьшается по сравнению с предыдущим случаем. На рис. 5 показано отношение перепадов давления (Δp)₁/(Δp)₂ при K_с = 20 с^–1 для различных значений ε. В этом случае перепад давления (Δp)₁ на порядки превосходит перепад (Δp)₂ только в начальный момент времени, далее доля потерь давления за счет кривизны и перфорационных отверстий на порядки начинает превосходить перепад давления (Δp)₁ за счет вязкости жидкости. Также из рис. 3–5 видно, что с увеличением размеров области поворота ε доля потерь давления из-за поворота потока и потерь в перфорационных отверстиях увеличивается. Наоборот, с уменьшением размеров области поворота ε вклад потерь давления из-за вязкого трения увеличивается.

На рис. 6–7 показано отношение перепадов давления (Δp)₁/(Δp)₂ при осцилляционном режиме течения в трещине после остановки закачки жидкости ГРП. На рис. 6 показано отношение перепадов давления (Δp)₁/(Δp)₂ при K_с = 1 с^–1для различных значений размеров области поворота ε. Видно, что так же как и в монотонном режиме течения после остановки насоса перепад давления (Δp)₁ за счет вязкости жидкости на порядки превосходит перепад (Δp)₂. Только при K_с = 20 с^–1(рис. 7) вклад перепада давления(Δp)₂ за счет перфораций и кривизны траектории трещины ГРП на порядки превышает вклад перепада давления (Δp)₁ за счет вязкости жидкости. Как видно из рис. 6 – рис. 7 как и в монотонном режиме течения в трещине ГРП после остановки насоса, в колебательном режиме течения вклад перепада давления (Δp)₂ при фиксированном значении коэффициента пропорциональности K_с увеличивается с увеличением области поворота ε.

Нужно отметить, что порядок формально введенной величины K_c заранее не известен. Если имеются данные забойных датчиков давления после остановки закачки жидкости ГРП, то используя решение (3.28) при x = 0 и уравнение (3.30), можно решить обратную “коэффициентную” задачу, чтобы оценить постоянную K_c, эффективное значение величины ε и коэффициенты уравнения (3.28).

Формулы (4.7) или (4.8) для вычисления потерь давления за счет кривизны трещины и перфорационных отверстий могут быть использованы для оценки полного перепада давления в основной операции ГРП при закачке жидкости гидроразрыва, после определения коэффициента K_c по данным забойных манометров в тесте на мини ГРП с проппантом. При использовании представленной модели для основного ГРП вместо динамической вязкости ньютоновской жидкости следует, например, использовать эффективную вязкость псевдопластичной жидкости, в которой учитывается присутствие гранул проппанта. Корреляционные зависимости вязкости суспензий от объемного содержания проппанта и вязкости жидкости гидроразрыва, используемые при моделировании образования и развития трещины ГРП, представлены в обзорной главе работы [14].

ЗАКЛЮЧЕНИЕ

В работе представлена математическая модель для описания течения в криволинейной трещине ГРП, с учетом вклада перфорационных отверстий скважины, после остановки насоса. Получены аналитические решения для возмущений раскрытия трещины в монотонном и колебательном режимах течения в трещине. На основе этих решений получены формулы для определения полных потерь давления на трение в прискважинной области трещины после остановки закачки жидкости ГРП. Полные потери давления включают в себя потери на вязкое трение, потери в перфорационных отверстиях и дополнительные потери вследствие искривления траектории трещины ГРП в некоторой окрестности скважины.

Работа частично поддержана грантом Академии Наук Республики Башкортостан № 0301200057819000040_104987.“Создание теоретических основ разработки трудноизвлекаемых запасов и нетрадиционных ресурсов углеводородов (высоковязкие нефти, низкопроницаемые пласты) из пластов, подверженных ГРП с помощью горизонтальных скважин”.

Список литературы

Economides M.J., Nolte K.G. Reservoir Stimulation. NY and Chichester.: Wiley, 2000. 750 p.
Идельчик И.Е. Справочник по гидравлическим сопротивлениям. М.: Машиностроение, 1992. 672 с.
Economides M.J., Martin T. Modern fracturing. Enhancing natural gas production. Houston, TX. USA: Energy Tribune Publ. Inc., 2007. 509 p.
Perkins T.K., Kern L.R. Width of hydraulic fractures // J. Petroleum Technology. 1961. V. 13. № 4. P. 937949.
Nordgren R.P. Propogation of a vertical hydraulic fracture // Society of Petroleum Engineers J. 1972. V. 12. № 4. P. 306–314.
Sneddon J.N., Berry D.S. The Classical Theory of Elasticity. Berlin etc.: Springer, 1958 = Снеддон И.Н., Берри Д.С. Классическая теория упругости. М.: Физматгиз, 1961. 219 с.
Шагапов В.Ш., Нагаева З.М. К теории фильтрационных волн давления в трещине, находящейся в пористой проницаемой среде // Прикладная механика и техническая физика. 2017. Т. 58. № 5 (345). С. 121–130.
Нагаева З.М., Шагапов В.Ш. Об упругом режиме фильтрации в трещине, расположенной в нефтяном или газовом пласте // Прикладная математика и механика. 2017. Т. 81. № 3. С. 319–329.
Ильясов А.М., Булгакова Г.Т. Квазиодномерная модель гиперболического типа гидроразрыва пласта // Вестн. Сам. гос. техн. ун-та. Сер. Физ.-мат. науки. 2016.Т. 20. № 4. С. 739–754. https://doi.org/10.14498/vsgtu1522
Байков В.А., Булгакова Г.Т., Ильясов А М., Кашапов Д.В. К оценке геометрических параметров трещины гидроразрыва пласта// Изв. РАН. МЖГ. 2018. № 5. С. 64–75. DOI: 1031857/S05682810001790-0.
Тихонов А.Н., Самарский А.А. Уравнения математической физики. М.: Наука, 1977. 735 с.
Будак Б.М., Фомин С.В. Кратные интегралы и ряды. М.: Наука, 1965. 608 с.
Воробьев Н.Н. Теория рядов. М.: Наука, 1979. 408 с.
Осипцов А.А. Модели механики многофазных сред для технологии гидроразрыва пласта: Дис. … док. физ.-мат. наук: 01.02.05. М., 2017. 310 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал