Известия РАН. Механика жидкости и газа, 2020, № 1, стр. 45-56

Управление поперечным течением в пограничном слое на скользящем крыле с помощью пристеночной объемной силы

С. В. Мануйлович^*

Центральный аэрогидродинамический институт им. Н.Е. Жуковского
Московская обл., Жуковский, Россия

Поступила в редакцию 29.04.2019
После доработки 25.06.2019
Принята к публикации 25.06.2019

DOI: 10.31857/S0568528120010090

Аннотация

В рамках системы уравнений Навье–Стокса рассмотрена задача об ослаблении поперечного течения в пограничном течении на скользящем крыле периодической по размаху пристеночной объемной силой, моделирующей воздействие системы плазменных актуаторов. Расчет произведен с помощью разложения искомых решений в ряд Фурье по продольной переменной и конечно-разностной аппроксимации второго порядка точности по вертикальной переменной. Показана роль градиента давления, индуцируемого действием управляющей объемной силы, на процесс формирования возмущенного течения.

Ключевые слова: пограничный слой, поперечное течение, объемная сила, управление

Крылья современных пассажирских самолетов имеют значительную стреловидность и удлинение. Течение в пограничном слое на переднем участке крыла, наряду с разгоном вдоль хорды, испытывает скольжение вдоль размаха. В этих условиях профиль скорости течения в направлении, перпендикулярном передней кромке крыла, обладает большей кривизной, чем профиль в направлении размаха, и течение в пограничном слое носит трехмерный характер. Это означает, что в пограничном слое имеет место поперечное течение – ненулевой профиль скорости в плоскости, перпендикулярной внешней линии тока. Такое течение проявляет неустойчивость невязкого типа, аналогичную неустойчивости затопленной струи.

Неустойчивость поперечного течения – основная причина ламинарно-турбулентного перехода в пограничном слое на стреловидных крыльях современной авиации. Подавление неустойчивости этого типа позволило бы существенно уменьшить сопротивление трения и сократить расход топлива. Неустойчивость поперечного течения тем выше, чем оно интенсивнее. В этой связи снижение интенсивности поперечного течения представляется важной практической задачей.

Широко известный способ подавления неустойчивости поперечного течения – отсос газа через поверхность крыла. Как и в случае подавления неустойчивости Толлмина–Шлихтинга [1], отсос увеличивает наполненность профиля скорости течения в направлении скольжения, что приводит к ослаблению поперечного течения и, как следствие, к снижению его неустойчивости.

Для увеличения наполненности профиля скорости вдоль размаха крыла могут также применяться технологии плазменного разряда [2]. Объемная сила, создаваемая плазменными актуаторами в пристеночной области, создает дополнительный разгон потока, производя эффект, аналогичный действию отсоса. Этот способ уменьшения интенсивности поперечного течения был предложен в [3]. Там теоретически рассматривалась задача управления поперечным течением в пограничном слое на скользящем крыле с помощью пристеночной объемной силы, периодической вдоль размаха. Используемое распределение объемной силы моделировало воздействие, создаваемое последовательностью плазменных актуаторов, расставленных с постоянным шагом вдоль размаха крыла перпендикулярно передней кромке. Расчеты производились в рамках системы уравнений трехмерного пограничного слоя.

Покажем, что использование концепции пограничного слоя в данной ситуации не вполне корректно. С одной стороны, для управления поперечным течением необходимо, чтобы приложенная объемная сила была локализована внутри пограничного слоя. В противном случае профиль течения вдоль размаха приобретет вид струи с точкой перегиба на внешней границе пограничного слоя, а это чревато появлением новых типов неустойчивости. С другой стороны, для оправданного применения уравнений пограничного слоя необходимо, чтобы сила плавно менялась вдоль размаха крыла. Таким образом, продольный размер области приложения силы должен быть порядка характерного масштаба внешнего течения, а поперечный размер – порядка толщины пограничного слоя, т.е. область силового воздействия должна быть сильно вытянута.

Как показано в [4], область силового воздействия, создаваемого диэлектрическим барьерным разрядом, имеет сравнимые продольный и поперечный размеры, что неудивительно, так как сила в конечном счете порождается действием электрического поля, описываемого законами электростатики. В силу этого для описания процесса управления поперечным течением, близкого к практической ситуации, необходимо производить анализ в рамках системы уравнений Навье–Стокса. Этому посвящена данная работа.

1. ПОСТАНОВКА ЗАДАЧИ УПРАВЛЕНИЯ

Рассмотрим задачу управления поперечным течением в ламинарном пограничном слое на скользящем крыле, обтекаемом равномерным потоком с небольшой дозвуковой скоростью. Будем предполагать, что профиль крыла представляет собой гладкую выпуклую фигуру. Обозначим $V_{\infty }^{{^{ \circ }}}$ – скорость набегающего потока, ρ° – его плотность, μ° – коэффициент вязкости (кружками помечаем размерные величины), χ – угол скольжения. Введем криволинейную систему координат с началом в некоторой точке поверхности крыла на разгонном участке течения, ось x° направим вдоль образующей в направлении скольжения, ось y° – по нормали к поверхности крыла. В качестве координаты z° будем использовать расстояние от начала до линии присоединения, отсчитываемое вдоль поверхности крыла в направлении, перпендикулярном образующей (эта координата в дальнейшем играет вспомогательную роль). Соответствующие компоненты вектора скорости обозначим u°, $v^\circ $, w°, давление – p°. Значения параметров течения на внешней границе пограничного слоя будем помечать индексом “e”.

В качестве управляющего силового воздействия будем использовать двумерное распределение объемной силы с компонентами f°, g°, действующей в плоскости x°, y° и не зависящей от z°. Такое распределение моделирует воздействие системы плазменных актуаторов с электродами, перпендикулярными образующей скользящего крыла [3].

В сделанных предположениях параметры течения удовлетворяют системе уравнений Навье–Стокса для несжимаемой жидкости. В криволинейных координатах система имеет вид [5]

$\begin{gathered} \frac{{\partial u^\circ }}{{\partial x^\circ }} + \frac{{\partial v^\circ }}{{\partial y^\circ }} + \frac{1}{H}\frac{{\partial w^\circ }}{{\partial z^\circ }} + \frac{1}{H}\frac{{\partial H}}{{\partial y^\circ }}v^\circ = 0 \\ \rho ^\circ \left( {u^\circ \frac{{\partial u^\circ }}{{\partial x^\circ }} + {{v}^{{^{ \circ }}}}\frac{{\partial u^\circ }}{{\partial y^\circ }} + \frac{1}{H}{{w}^{{^{ \circ }}}}\frac{{\partial u^\circ }}{{\partial z^\circ }}} \right) + \frac{{\partial p^\circ }}{{\partial x^\circ }} = \\ \, = \frac{1}{H}\mu ^\circ \left\{ {\frac{\partial }{{\partial z^\circ }}\left( {\frac{1}{H}\frac{{\partial u^\circ }}{{\partial z^\circ }} - \frac{{\partial w^\circ }}{{\partial x^\circ }}} \right) - \frac{\partial }{{\partial y^\circ }}\left[ {H\left( {\frac{{\partial {v}^\circ }}{{\partial x^\circ }} - \frac{{\partial u^\circ }}{{\partial y^\circ }}} \right)} \right]} \right\} + f^\circ \\ \end{gathered} $

(1.1)

$\rho ^\circ \left( {u^\circ \frac{{\partial {v}^\circ }}{{\partial x^\circ }} + {{v}^{{^{ \circ }}}}\frac{{\partial v^\circ }}{{\partial y^\circ }} + \frac{1}{H}{{w}^{{^{ \circ }}}}\frac{{\partial v^\circ }}{{\partial z^\circ }} - \frac{1}{H}\frac{{\partial H}}{{\partial y^\circ }}{{w}^{{^{ \circ }2}}}} \right) + \frac{{\partial p^\circ }}{{\partial y^\circ }} = $

$\begin{gathered} \, = \frac{1}{H}\mu ^\circ \left\{ {H\frac{\partial }{{\partial x^\circ }}\left( {\frac{{\partial v^\circ }}{{\partial x^\circ }} - \frac{{\partial u^\circ }}{{\partial y^\circ }}} \right) - \frac{\partial }{{\partial z^\circ }}\left[ {\frac{1}{H}\left( {\frac{{\partial Hw^\circ }}{{\partial y^\circ }} - \frac{{\partial v^\circ }}{{\partial z^\circ }}} \right)} \right]} \right\} + g^\circ \\ \rho ^\circ \left( {u^\circ \frac{{\partial w^\circ }}{{\partial x^\circ }} + v^\circ \frac{{\partial w^\circ }}{{\partial y^\circ }} + \frac{1}{H}w^\circ \frac{{\partial w^\circ }}{{\partial z^\circ }} + \frac{1}{H}\frac{{\partial H}}{{\partial y^\circ }}v^\circ w^\circ } \right) + \frac{1}{H}\frac{{\partial p^\circ }}{{\partial z^\circ }} = \\ \, = \mu ^\circ \left\{ {\frac{\partial }{{\partial y^\circ }}\left[ {\frac{1}{H}\left( {\frac{{\partial Hw^\circ }}{{\partial y^\circ }} - \frac{{\partial v^\circ }}{{\partial z^\circ }}} \right)} \right] - \frac{1}{H}\frac{\partial }{{\partial x^\circ }}\left( {\frac{{\partial u^\circ }}{{\partial z^\circ }} - H\frac{{\partial w^\circ }}{{\partial x^\circ }}} \right)} \right\} \\ \end{gathered} $

Единственный не равный 1 метрический коэффициент задается равенством

$H = 1 + \frac{{y^\circ }}{{r^\circ (z^\circ )}}$

где r° – местный радиус кривизны профиля крыла.

В дальнейшем будем использовать две единицы длины – масштаб внешнего течения l° и характерную толщину пограничного слоя δ°

$l^\circ = V_{\infty }^{{^{ \circ }}}{{\left[ {\frac{{dw_{e}^{{^{ \circ }}}}}{{dz^\circ }}(0)} \right]}^{{ - 1}}},\quad \delta ^\circ = \sqrt {\frac{{\mu ^\circ }}{{\rho ^\circ }}{{{\left[ {\frac{{dw_{e}^{{^{ \circ }}}}}{{dz^\circ }}(0)} \right]}}^{{ - 1}}}} $

По самому смыслу концепции пограничного слоя должно быть выполнено

$\frac{{l^\circ }}{{\delta ^\circ }} = \frac{{\rho ^\circ V_{\infty }^{{^{ \circ }}}\delta ^\circ }}{{\mu ^\circ }} = {\text{R}} \gg 1$

Введем безразмерные переменные с помощью соотношений

$\begin{gathered} \left\{ {x^\circ ,y^\circ } \right\} = \delta ^\circ \left\{ {x,y} \right\},\quad z^\circ = l^\circ z,\quad \left\{ {u^\circ ,v^\circ ,w^\circ } \right\} = V_{\infty }^{{^{ \circ }}}\left\{ {u,v,w} \right\} \\ p^\circ = \rho ^\circ V_{\infty }^{{^{ \circ }2}}p,\quad \left\{ {f^\circ ,g^\circ } \right\} = \frac{{\rho ^\circ V_{\infty }^{{^{ \circ }2}}}}{{{{l}^{ \circ }}}}\left\{ {f,g} \right\} \\ \end{gathered} $

и подставим их в (1.1). Пренебрегая членами порядка O(R^-2), получим

(1.2)

$\begin{gathered} \frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} + \frac{1}{{\text{R}}}\frac{{\partial w}}{{\partial z}} + \frac{\sigma }{{\text{R}}}v = 0 \\ u\frac{{\partial u}}{{\partial x}} + v\frac{{\partial u}}{{\partial y}} + \frac{1}{{\text{R}}}w\frac{{\partial u}}{{\partial z}} + \frac{{\partial p}}{{\partial x}} = \frac{1}{{\text{R}}}\left( {\frac{{{{\partial }^{2}}u}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}u}}{{\partial {{y}^{2}}}} + f} \right) \\ u\frac{{\partial v}}{{\partial x}} + v\frac{{\partial v}}{{\partial y}} + \frac{1}{{\text{R}}}w\frac{{\partial v}}{{\partial z}} - \frac{\sigma }{{\text{R}}}{{w}^{2}} + \frac{{\partial p}}{{\partial y}} = \frac{1}{{\text{R}}}\left( {\frac{{{{\partial }^{2}}v}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}v}}{{\partial {{y}^{2}}}} + g} \right) \\ u\frac{{\partial w}}{{\partial x}} + v\frac{{\partial w}}{{\partial y}} + \frac{1}{{\text{R}}}w\frac{{\partial w}}{{\partial z}} + \frac{\sigma }{{\text{R}}}vw + \frac{1}{{\text{R}}}\frac{{\partial p}}{{\partial z}} = \frac{1}{{\text{R}}}\left( {\frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}w}}{{\partial {{y}^{2}}}}} \right) \\ \end{gathered} $

Здесь σ(z) = l°/r° – безразмерная кривизна стенки. Краевые условия для системы (1.2) – условия прилипания и условия сращивания с внешним течением:

(1.3)

$\begin{gathered} u\left( {x,0,z} \right) = v\left( {x,0,z} \right) = w\left( {x,0,z} \right) = 0 \\ u\left( {x,\infty ,z} \right) = {{u}_{e}} = {\text{sin}}\chi ,\quad w\left( {x,\infty ,z} \right) = {{w}_{e}}\left( z \right) \\ \frac{{\partial p}}{{\partial z}}\left( {x,\infty ,z} \right) = - {{w}_{e}}\frac{{\partial {{w}_{e}}}}{{\partial z}} \\ \end{gathered} $

Исходя из феноменологических соображений [6, 7], при иллюстрации управляющего воздействия будем использовать модельное распределение объемной силы вида

(1.4)

$\begin{gathered} f(x,y) = D(x)F(y),\quad g(x,y) = \frac{{dD}}{{dx}}(x)\,G(y) \\ D = \frac{1}{2}\sum\limits_{m = - \infty }^\infty {{\text{exp}}[ - {{{(x - 6{\kern 1pt} m)}}^{2}}]} ,\quad F = {\text{exp}}( - {{y}^{2}}),\quad G = \frac{{\sqrt \pi }}{2}{\text{erfc}}{\kern 1pt} y \\ \end{gathered} $

где erfc y – интеграл вероятностей [8]. Поле силы (1.4) бездивергентное, действие силы сосредоточено внутри пограничного слоя, сила быстро затухает при y → ∞. Распределение (1.4) представляет собой размещенные с периодом Π = 6 единичные области силового воздействия, продольный и поперечный размеры которых относятся как 2:1.

В качестве управляемого течения будем рассматривать пограничный слой на эллиптическом крыле 20%-ной относительной толщины под нулевым углом атаки и углом скольжения χ = π/6. Для удобства при обозначении положения точки на поверхности крыла вместо криволинейной координаты z будем пользоваться декартовой координатой Z, нормированной на длину хорды крыла (0 ≤ Z ≤ 1) и отсчитываемой от носка крыла вдоль хорды перпендикулярно линии растекания.

2. ТЕЧЕНИЕ ПОД ВОЗДЕЙСТВИЕМ ОСРЕДНЕННОЙ СИЛЫ

Рассмотрим вспомогательную задачу о течении, управляемом осредненным по x полем силы (1.4)

(2.1)

${{f}_{0}}\left( y \right) = \frac{{\sqrt \pi }}{{12}}{\text{exp}}( - {{y}^{2}}),\quad {{g}_{0}} \equiv 0$

В этом случае управляемое течение остается однородным по переменной x. Обозначим

(2.2)

$u = U\left( {y,z} \right),\quad v = \frac{1}{{\text{R}}}V\left( {y,z} \right),\quad w = W\left( {y,z} \right),\quad p = P\left( {y,z} \right)$

Подставляя выражения (2.1), (2.2) в систему (1.2) и снова пренебрегая членами порядка O(R^–2), получим

(2.3)

$\begin{gathered} \frac{{\partial V}}{{\partial y}} + \frac{{\partial W}}{{\partial z}} + \frac{\sigma }{{\text{R}}}V = 0 \\ V\frac{{\partial U}}{{\partial y}} + W\frac{{\partial U}}{{\partial z}} = \frac{{{{\partial }^{2}}U}}{{\partial {{y}^{2}}}} + {{f}_{0}} \\ \frac{{\partial P}}{{\partial y}} = \frac{\sigma }{{\text{R}}}{{W}^{2}} \\ V\frac{{\partial W}}{{\partial y}} + W\frac{{\partial W}}{{\partial z}} + \frac{\sigma }{{\text{R}}}VW + \frac{{\partial P}}{{\partial z}} = \frac{{{{\partial }^{2}}W}}{{\partial {{y}^{2}}}} \\ \end{gathered} $

Граничные условия для системы (2.3) аналогичны (1.3). Система (2.3) отличается от обычной системы уравнений для пограничного слоя на скользящем крыле центрифугальными членами порядка O(R^–1). Отсюда следует, что решение краевой задачи для системы (2.3) с точностью до R^–1 совпадает с пограничным слоем Прандтля

(2.4)

$Q = {{Q}_{P}} + O({{{\text{R}}}^{{ - 1}}}),\quad Q = U,V,W,P$

где функции Q_P удовлетворяют классической краевой задаче

$\begin{gathered} {{P}_{P}}\left( {y,z} \right) \equiv {{p}_{e}}\left( z \right) \\ \frac{{\partial {{V}_{P}}}}{{\partial y}} + \frac{{\partial {{W}_{P}}}}{{\partial z}} = 0 \\ \end{gathered} $

(2.5)

$\begin{gathered} {{V}_{P}}\frac{{\partial {{U}_{P}}}}{{\partial y}} + {{W}_{P}}\frac{{\partial {{U}_{P}}}}{{\partial z}} = \frac{{{{\partial }^{2}}{{U}_{P}}}}{{\partial {{y}^{2}}}} + {{f}_{0}} \\ {{V}_{P}}\frac{{\partial {{W}_{P}}}}{{\partial y}} + {{W}_{P}}\frac{{\partial {{W}_{P}}}}{{\partial z}} = {{w}_{e}}\frac{{d{{w}_{e}}}}{{dz}} + \frac{{{{\partial }^{2}}{{W}_{P}}}}{{\partial {{y}^{2}}}} \\ \end{gathered} $

$\begin{gathered} {{U}_{P}}\left( {0,z} \right) = {{V}_{P}}\left( {0,z} \right) = {{W}_{P}}\left( {0,z} \right) = 0 \\ {{U}_{P}}\left( {\infty ,z} \right) = {{u}_{e}},\quad {{W}_{P}}\left( {\infty ,z} \right) = {{w}_{e}}\left( z \right) \\ \end{gathered} $

Структура задачи (2.5) такова, что силовое воздействие позволяет управлять лишь профилем U_P, оставляя без изменений компоненты V_P, W_P.

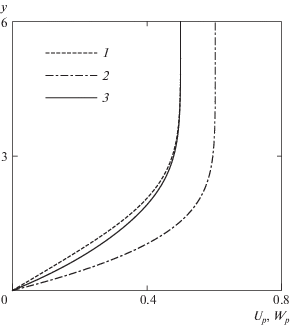
На рис. 1 показаны профили скорости вдоль размаха (1) и вдоль хорды (2) в сечении Z = 0.005 в отсутствие силового воздействия (решение задачи (2.5) при f₀ ≡ 0). Профиль W_P вблизи стенки, в отличие от U_P, значительно искривлен. Воздействие (2.1) увеличивает кривизну профиля U_P (линия 3), не изменяя W_P и тем самым уменьшая интенсивность поперечного течения

(2.6)

${{V}_{{{\text{cf}}}}} = \frac{{{{u}_{e}}{{w}_{e}}}}{{\sqrt {u_{e}^{2} + w_{e}^{2}} }}\left( {\frac{{{{W}_{P}}}}{{{{w}_{e}}}} - \frac{{{{U}_{P}}}}{{{{u}_{e}}}}} \right)$

Рис. 1.

Профили скоростей U_P, W_P в сечении Z = 0.005 в отсутствие воздействия (1, 2); 3 – профиль U_P при силовом воздействии.

На рис. 2 продемонстрировано, как силовое воздействие (2.1) ослабляет амплитуду поперечного течения на участке наибольшей его интенсивности. На рис. 2а показаны профили скорости поперечного течения (2.6) в сечениях Z = {0.1, 0.2, 0.5, 1, 2} × 10^–2 (кривые 1–5) в отсутствие воздействия. Расчеты показывают, что наибольшей амплитуды (V_cf ≈ 0.079) поперечное течение достигает вблизи сечения Z = 0.005. На рис. 2б в тех же сечениях показаны аналогичные профили, измененные под воздействием объемной силы (2.1). Максимальная амплитуда V_cf ≈ 0.056 достигается в том же сечении Z = 0.005. В целом в рассматриваемом диапазоне Z амплитуда поперечного течения уменьшается примерно в полтора раза.

Рис. 2.

Профили скорости поперечного течения при отсутствии управления (а) и при силовом воздействии (б) в сечениях Z = 0.001, 0.002, 0.005, 0.01, 0.02 (1–5).

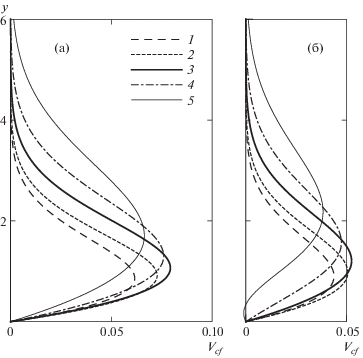
Обратим внимание на то, что в последнем сечении Z = 0.02 скорость V_cf вблизи стенки меняет знак и имеется вторая точка перегиба. Это может привести к появлению еще одной неустойчивой моды, что не является существенным, пока основная мода доминирует.

3. МЕТОД РАСЧЕТА ПЕРИОДИЧЕСКОГО ТЕЧЕНИЯ

Перейдем к анализу решения полной задачи (1.2)–(1.4). Представим его в виде суммы решения вспомогательной задачи для случая действия осредненной силы и поправочных членов:

(3.1)

$u = U + \frac{1}{{\text{R}}}u{\kern 1pt} ',\quad v = \frac{1}{{\text{R}}}V + \frac{1}{{\text{R}}}v{\kern 1pt} ',\quad w = W + \frac{1}{{\text{R}}}w{\kern 1pt} ',\quad p = P + \frac{1}{{\text{R}}}p{\kern 1pt} '$

Подставим (3.1) в систему (1.2). Пренебрегая членами порядка O(R^–2), c учетом (2.3) получим нелинейную систему уравнений для поправочных функций q' в (3.1)

$\begin{gathered} \frac{{\partial u{\kern 1pt} '}}{{\partial x}} + \frac{{\partial v{\kern 1pt} '}}{{\partial y}} = - \frac{1}{{\text{R}}}\left( {\frac{{\partial w{\kern 1pt} '}}{{\partial z}} + \sigma v{\kern 1pt} '} \right) \\ U\frac{{\partial u{\kern 1pt} '}}{{\partial x}} + \frac{{\partial U}}{{\partial y}}v{\kern 1pt} '\; + \frac{{\partial p{\kern 1pt} '}}{{\partial x}} - \frac{1}{{\text{R}}}\left( {\frac{{{{\partial }^{2}}u{\kern 1pt} '}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}u{\kern 1pt} '}}{{\partial {{y}^{2}}}}} \right) - f + {{f}_{0}} = - \frac{1}{{\text{R}}}\left( {V\frac{{\partial u{\kern 1pt} '}}{{\partial y}} + W\frac{{\partial u{\kern 1pt} '}}{{\partial z}} + \frac{{\partial U}}{{\partial z}}w{\kern 1pt} '\; + u{\kern 1pt} '\frac{{\partial u{\kern 1pt} '}}{{\partial x}} + v{\kern 1pt} '\frac{{\partial u{\kern 1pt} '}}{{\partial y}}} \right) \\ \end{gathered} $

(3.2)

$U\frac{{\partial v{\kern 1pt} '}}{{\partial x}} + \frac{{\partial p{\kern 1pt} '}}{{\partial y}} - \frac{1}{{\text{R}}}\left( {\frac{{{{\partial }^{2}}v{\kern 1pt} '}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}v{\kern 1pt} '}}{{\partial {{y}^{2}}}}} \right) - g = - \frac{1}{{\text{R}}}\left( {V\frac{{\partial v{\kern 1pt} '}}{{\partial y}} + W\frac{{\partial v{\kern 1pt} '}}{{\partial z}} + \frac{{\partial V}}{{\partial y}}v{\kern 1pt} '\; - 2{\kern 1pt} \sigma Ww{\kern 1pt} '\; + u{\kern 1pt} '\frac{{\partial v{\kern 1pt} '}}{{\partial x}} + v{\kern 1pt} '\frac{{\partial v{\kern 1pt} '}}{{\partial y}}} \right)$

$U\frac{{\partial w{\kern 1pt} '}}{{\partial x}} + \frac{{\partial W}}{{\partial y}}v{\kern 1pt} '\; - \frac{1}{{\text{R}}}\left( {\frac{{{{\partial }^{2}}w{\kern 1pt} '}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}w{\kern 1pt} '}}{{\partial {{y}^{2}}}}} \right) = - \frac{1}{{\text{R}}}\left( {V\frac{{\partial w{\kern 1pt} '}}{{\partial y}} + W\frac{{\partial w{\kern 1pt} '}}{{\partial z}} + \frac{{\partial W}}{{\partial z}}w{\kern 1pt} '\; + \sigma {\kern 1pt} Wv{\kern 1pt} '\; + u{\kern 1pt} '\frac{{\partial w{\kern 1pt} '}}{{\partial x}} + v{\kern 1pt} '\frac{{\partial w{\kern 1pt} '}}{{\partial y}} + \frac{{\partial p{\kern 1pt} '}}{{\partial z}}} \right)$

Использование соотношений (2.4) показывает, что решение системы (3.2) с точностью R^–1 совпадает с решением линейной системы

(3.3)

$\begin{gathered} \frac{{\partial u{\kern 1pt} '}}{{\partial x}} + \frac{{\partial v{\kern 1pt} '}}{{\partial y}} = 0 \\ {{U}_{P}}\frac{{\partial u{\kern 1pt} '}}{{\partial x}} + \frac{{\partial {{U}_{P}}}}{{\partial y}}v{\kern 1pt} '\; + \frac{{\partial p{\kern 1pt} '}}{{\partial x}} = \frac{1}{{\text{R}}}\left( {\frac{{{{\partial }^{2}}u{\kern 1pt} '}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}u{\kern 1pt} '}}{{\partial {{y}^{2}}}}} \right) + f - {{f}_{0}} \\ {{U}_{P}}\frac{{\partial v{\kern 1pt} '}}{{\partial x}} + \frac{{\partial p{\kern 1pt} '}}{{\partial y}} = \frac{1}{{\text{R}}}\left( {\frac{{{{\partial }^{2}}v{\kern 1pt} '}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}v{\kern 1pt} '}}{{\partial {{y}^{2}}}}} \right) + g \\ {{U}_{P}}\frac{{\partial w{\kern 1pt} '}}{{\partial x}} + \frac{{\partial {{W}_{P}}}}{{\partial y}}v{\kern 1pt} ' = \frac{1}{{\text{R}}}\left( {\frac{{{{\partial }^{2}}w{\kern 1pt} '}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}w{\kern 1pt} '}}{{\partial {{y}^{2}}}}} \right) \\ \end{gathered} $

в которой в качестве коэффициентов использованы параметры управляемого силой (2.1) течения в пограничном слое Прандтля.

Решение системы (3.3) удовлетворяет однородным граничным условиям на стенке и на внешней границе пограничного слоя:

(3.4)

$\begin{gathered} u{\kern 1pt} '\left( {x,0,z} \right) = v{\kern 1pt} '\left( {x,0,z} \right) = w{\kern 1pt} '\left( {x,0,z} \right) = 0 \\ q{\kern 1pt} '\left( {x,\infty ,z} \right) = 0,\quad q = u,v,w,p \\ \end{gathered} $

Несмотря на коэффициент R^–1 при вязких членах в системе (3.3), они сохранены для соответствия порядка системы граничным условиям при y = 0.

Источниковые члены в линейной системе (3.3) не содержат нулевой гармоники, поэтому поправочные члены в (2.1) носят чисто колебательный характер. Задача (3.3), (3.4) не содержит производных искомых функций по переменной z; эта переменная входит лишь в заранее определяемые коэффициенты системы (3.3). Отсюда следует, что функции q' зависят от z как от параметра. Таким образом, для колебательной составляющей решения полной задачи (1.2), (1.3) справедлив закон плоских сечений.

Для расчета решения задачи (3.3), (3.4) будем использовать метод Фурье. Представим компоненты объемной силы и искомые параметры течения в виде рядов

(3.5)

$\begin{gathered} \left\{ {f - {{f}_{0}},g} \right\}\left( {x,y} \right) = \sum\limits_{n = 1}^\infty {\left\{ {{{f}_{n}},{{g}_{n}}} \right\}\,} \left( y \right){\text{exp}}\left( {i{{\alpha }_{n}}x} \right) + {\text{c}}{\text{.c}}{\text{.,}}\quad {{\alpha }_{n}} = \frac{{2\pi n}}{\Pi } \\ q{\kern 1pt} '\left( {x,y{\text{;}}z} \right) = \sum\limits_{n = 1}^\infty {{{q}_{n}}} \left( {y{\text{;}}z} \right){\text{exp}}\left( {i{{\alpha }_{n}}x} \right) + {\text{c}}{\text{.c}}{\text{.,}}\quad q = u,{v},w,p \\ \end{gathered} $

Комплексные амплитуды фурье-гармоник удовлетворяют линейным неоднородным системам обыкновенных дифференциальных уравнений 6-то порядка

(3.6)

$\begin{gathered} i{{\alpha }_{n}}{{u}_{n}} + \frac{{d{{v}_{n}}}}{{dy}} = 0 \\ i{{\alpha }_{n}}{{U}_{P}}{{u}_{n}} + \frac{{d{{U}_{P}}}}{{dy}}{{v}_{n}} + i{{\alpha }_{n}}{{p}_{n}} = \frac{1}{{\text{R}}}\left( {\frac{{{{d}^{2}}{{u}_{n}}}}{{d{{y}^{2}}}} - \alpha _{n}^{2}{{u}_{n}}} \right) + {{f}_{n}} \\ i{{\alpha }_{n}}{{U}_{P}}{{v}_{n}} + \frac{{d{{p}_{n}}}}{{dy}} = \frac{1}{{\text{R}}}\left( {\frac{{{{d}^{2}}{{v}_{n}}}}{{d{{y}^{2}}}} - \alpha _{n}^{2}{{v}_{n}}} \right) + {{g}_{n}} \\ i{{\alpha }_{n}}{{U}_{P}}{{w}_{n}} + \frac{{d{{W}_{P}}}}{{dy}}{{v}_{n}} = \frac{1}{{\text{R}}}\left( {\frac{{{{d}^{2}}{{w}_{n}}}}{{d{{y}^{2}}}} - \alpha _{n}^{2}{{w}_{n}}} \right) \\ \end{gathered} $

Решения систем (3.6) удовлетворяют однородным граничным условиям, являющимся следствием условий прилипания и условий отсутствия модуляции течения на внешней границе пограничного слоя (далее параметр z опускаем)

(3.7)

$\begin{gathered} {{u}_{n}}\left( 0 \right) = {{v}_{n}}\left( 0 \right) = {{w}_{n}}\left( 0 \right) = 0 \\ {{q}_{n}}\left( \infty \right) = 0,\quad q = u,v,w,p \\ \end{gathered} $

Первые три уравнения не содержат функции w_n, поэтому задача (3.6), (3.7) распадается на две неоднородные краевые задачи.

Исключая функции u_n, p_n, получим первую задачу – неоднородное уравнение Орра–Зоммерфельда для функции ${{{v}}_{n}}$ с однородными граничными условиями

(3.8)

$\begin{gathered} {{U}_{P}}\left( {\frac{{{{d}^{2}}{{v}_{n}}}}{{d{{y}^{2}}}} - \alpha _{n}^{2}{{v}_{n}}} \right) - \frac{{{{d}^{2}}{{U}_{P}}}}{{d{{y}^{2}}}}{{v}_{n}} = \frac{1}{{i{{\alpha }_{n}}{\text{R}}}}\left( {\frac{{{{d}^{4}}{{v}_{n}}}}{{d{{y}^{4}}}} - 2\alpha _{n}^{2}\frac{{{{d}^{2}}{{v}_{n}}}}{{d{{y}^{2}}}} + \alpha _{n}^{4}{{v}_{n}}} \right) - \frac{{d{{f}_{n}}}}{{dy}} + i{{\alpha }_{n}}{{g}_{n}} \\ {{v}_{n}}\left( 0 \right) = \frac{{d{{v}_{n}}}}{{dy}}\left( 0 \right) = {{v}_{n}}\left( \infty \right) = 0 \\ \end{gathered} $

Вторая задача – это краевая задача для последнего уравнения системы (3.6)

(3.9)

$\begin{gathered} \frac{1}{{\text{R}}}\left( {\frac{{{{d}^{2}}{{w}_{n}}}}{{d{{y}^{2}}}} - \alpha _{n}^{2}{{w}_{n}}} \right) - i{{\alpha }_{n}}{{U}_{P}}{{w}_{n}} = \frac{{d{{W}_{P}}}}{{dy}}{{v}_{n}} \\ {{w}_{n}}\left( 0 \right) = {{w}_{n}}\left( \infty \right) = 0 \\ \end{gathered} $

Она также неоднородная: дифференциальное уравнение в источниковом члене содержит функцию ${{v}_{n}}$, известную из решения первой задачи.

Для вычисления колебательной составляющей управляемого течения бесконечные суммы в (3.5) заменялись конечными 1 ≤ n ≤ N_h , где N_h – число учитываемых гармоник. При расчете решения задач (3.8), (3.9) полубесконечная область 0 ≤ y < ∞ заменялась конечной 0 ≤ y ≤ y_max и дробилась на N_y равных шагов. В дифференциальных уравнениях производилась конечно-разностная аппроксимация производных второго порядка точности. Условие для $d{{v}_{n}}{\text{/}}dy$ при y = 0 также аппроксимировалось схемой второго порядка с использованием трехточечного шаблона.

При выставлении асимптотических условий для ${{v}_{n}}$ и w_n использовался прием, аналогичный [9]. Анализ показывает, что с учетом быстрого затухания источниковых членов в уравнениях (3.8), (3.9) их решения при y → ∞ имеют вид

$\begin{gathered} {{v}_{n}} = {{C}_{1}}{\text{exp}}\left( { - {{\alpha }_{n}}y} \right) + {{C}_{2}}{\text{exp}}\left( { - {{\lambda }_{n}}y} \right) \\ {{w}_{n}} = {{C}_{3}}{\text{exp}}\left( { - {{\lambda }_{n}}{\kern 1pt} y} \right),\quad {{\lambda }_{n}} = \sqrt {i{{\alpha }_{n}}{\text{R}}{{u}_{e}} + \alpha _{n}^{2}} \\ \end{gathered} $

Составим систему четырех уравнений, последовательно три раза дифференцируя первое равенство, и систему двух уравнений, продифференцировав второе равенство один раз. Избавляясь в полученных системах от членов, явно зависящих от y, получим два смешанных однородных граничных условия для ${{v}_{n}}$ и одно – для w_n

$\begin{gathered} {{v}_{n}} - \frac{{\alpha _{n}^{2} + {{\alpha }_{n}}{{\lambda }_{n}} + \lambda _{n}^{2}}}{{\alpha _{n}^{2}\lambda _{n}^{2}}}\frac{{{{d}^{2}}{{v}_{n}}}}{{d{{y}^{2}}}} - \frac{{{{\alpha }_{n}} + {{\lambda }_{n}}}}{{\alpha _{n}^{2}\lambda _{n}^{2}}}\frac{{{{d}^{3}}{{v}_{n}}}}{{d{{y}^{3}}}} = 0 \\ \frac{{d{{v}_{n}}}}{{dy}} + \frac{{{{\alpha }_{n}} + {{\lambda }_{n}}}}{{{{\alpha }_{n}}{{\lambda }_{n}}}}\frac{{{{d}^{2}}{{v}_{n}}}}{{d{{y}^{2}}}} + \frac{1}{{{{\alpha }_{n}}{{\lambda }_{n}}}}\frac{{{{d}^{3}}{{v}_{n}}}}{{d{{y}^{3}}}} = 0 \\ \frac{{d{{w}_{n}}}}{{dy}} + {{\lambda }_{n}}{{w}_{n}} = 0 \\ \end{gathered} $

которые выполняются с хорошей точностью при сравнительно небольших y = y_max. Эти условия также подвергались конечно-разностной аппроксимации второго порядка точности.

В результате задачи (3.8), (3.9) сводились к линейным алгебраическим системам для N_y + 1 уравнения. Полученные системы решались методом Гаусса. Точность полученного решения контролировалась варьированием параметров дискретизации в промежутках N_y ∈ [500, 1500], y_max ∈ [6, 12 ] , N_h ∈ [5, 10 ] . Ниже приведены результаты расчета колебательной составляющей течения под воздействием поля сил (1.4) в диапазоне одного периода для сечения Z = 0.005, соответствующего максимальной интенсивности поперечного течения.

4. ДАВЛЕНИЕ, ИНДУЦИРУЕМОЕ УПРАВЛЯЮЩИМ ВОЗДЕЙСТВИЕМ

Описание колебательной составляющей течения, управляемого периодической по размаху пристеночной объемной силой, начнем с порождаемого ею возмущения давления. Анализ распределения давления наиболее важен, поскольку именно совместное действие объемной силы и индуцируемого градиента давления позволяет прояснить характер возмущения поля скорости [7]. Иллюстративный расчет выполнен при R = 500.

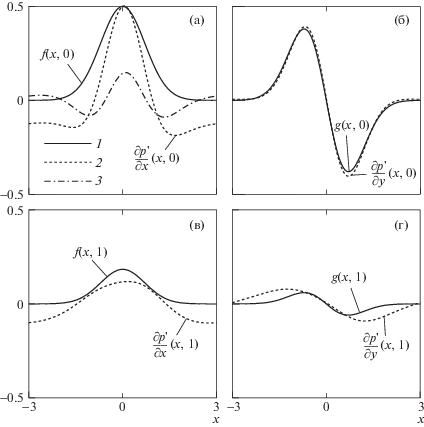
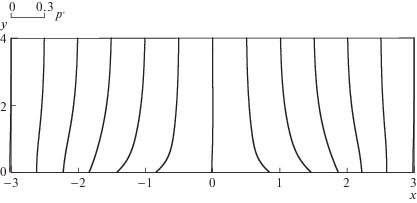
Распределение p'(x, y), вызванное силовым воздействием (1.4), показано на рис. 3. В грубом приближении действие периодической силы вызывает понижение давления выше по потоку от области единичного воздействия, и повышение – ниже по потоку. Для более детального анализа изучим поведение наведенного градиента давления в сравнении с полем объемной силы.

Рис. 3.

Профили возмущения давления при изменении x в диапазоне одного периода с шагом 0.5 (R = 500, Z = 0.005).

На рис. 4 приведены распределения вдоль размаха крыла компонент объемной силы (кривые 1) и индуцированного градиента давления (2) при y = 0 (а, б) и при y = 1 (в, г). Расчеты показывают, что на поверхности крыла максимальное значение тангенциальной компоненты градиента почти совпадает с максимальным значением соответствующей компоненты объемной силы (рис. 4а), а распределение нормальной составляющей градиента практически повторяет форму вертикального силового воздействия (б). На высоте y = 1 демпфирующее действие продольного градиента над серединой области воздействия составляет около 60% от максимального значения продольной компоненты силы (в). Действие вертикальной силы над областью воздействия по-прежнему компенсируется градиентом давления, а на периферийных участках оно приводит к обратному суммарному действию (г).

Рис. 4.

Продольные распределения тангенциальной (а, в), нормальной (б, г) компонент объемной силы (1) и индуцированного ею градиента давления (2): (а, б) – при y = 0, (в, г) – при y = 1; 3 – распределение эффективного градиента давления на стенке (R = 500, Z = 0.005).

5. ВОЗМУЩЕНИЕ ПОЛЯ СКОРОСТИ

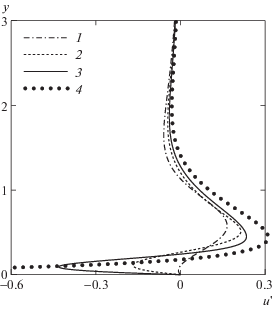
Опишем теперь поле скорости колебательной компоненты управляемого течения. На рис. 5 показаны профили составляющих возмущения скорости в сечениях по x, соответствующих рис. 3.

Рис. 5.

Профили (а, б, в) компонент u', $v{\kern 1pt} '$, w' возмущения скорости (R = 500, Z = 0.005).

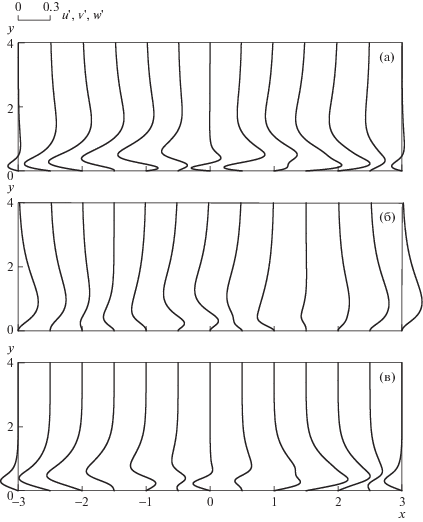
В плоскости x, y (рис. 5а, б) вне области действия силы возмущенное поле скорости имеет сравнительно простую структуру. Над областями единичного силового воздействия возмущенное движение направлено вниз, затем разделяется, отклоняясь к периферийным областям, и, наконец, направляется вверх на равном удалении от областей единичного воздействия.

В узкой пристеночной области, где можно пренебречь конвективным переносом импульса, возмущенное движение вызывается действием эффективного градиента давления

${{\left( {\frac{{\partial p}}{{\partial x}}} \right)}_{{{\text{eff}}}}} = \frac{{\partial p{\kern 1pt} '}}{{\partial x}}\left( {x,0} \right) - f\left( {x,0} \right) + {{f}_{0}}\left( 0 \right)$

Его продольное распределение показано на рис. 4а (линия 3). Пристеночное течение испытывает разгон в областях, где (∂p/∂x)_eff < 0. Это участки слева и справа от области воздействия – соответственно –1.9 < x < –0.6 и 0.8 < x < 2.4 (ср. рис. 4а и рис. 5а). Наоборот, в области, где сила наибольшая, пристеночное течение претерпевает интенсивное торможение. На основном промежутке области силового воздействия возмущенное движение носит сложный характер, поэтому необходим более тщательный анализ.

Для более наглядной иллюстрации поля возмущенной скорости введем функцию тока ψ(x, y) с помощью соотношений

$v{\kern 1pt} ' = - \frac{{\partial \psi }}{{\partial x}},\quad \psi \left( {x,0} \right) = 0$

Подчеркнем, что линии тока возмущенного движения ψ = const не являются траекториями жидких частиц, а лишь указывают направление скорости возмущения течения.

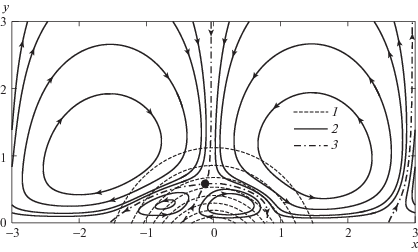
На рис. 6 показаны линии тока возмущенного движения ψ = –0.1, –0.05, –0.02, $ - 0.01$, 0, 0.01, 0.02, 0.05, 0.1. Здесь же кривыми 1 показаны силовые линии воздействия (1.4) – линии уровня функции Φ(x,y) = – D(x)G(y), на которых она принимает значения от –0.8 (внутренняя кривая) до –0.1 с шагом 0.1. Сила действует по часовой стрелке. Бóльшую часть периода занимают два крупных противоположно вращающихся вихря – слева и справа от области силового воздействия. Внутренние линии тока в левом и правом вихрях соответствуют значениям ψ = –0.1 и 0.1 соответственно. Внутри области силового воздействия под действием пристеночного разгона при –1.9 < x < –0.6 и торможения при –0.6 < x < 0.8 формируются два малых вихря. В седловой точке (–0.126, 0.585), отмеченной круглым маркером, скорость возмущенного движения обращается в 0.

Рис. 6.

Схема возмущенного движения в плоскости x, y: 1 – силовые линии объемного воздействия, 2 – линии тока в диапазоне –0.1 ≤ ψ ≤ 0.1, 3 – линия ψ = 0 (R = 500, Z = 0.005).

Возмущенное движение в направлении хорды крыла имеет второстепенное значение и не влияет на движение в плоскости x, y. Форма профилей скорости w' на качественном уровне повторяет форму соответствующих профилей скорости u' (рис. 5а, в).

6. ЗАВИСИМОСТЬ КОЛЕБАТЕЛЬНОЙ КОМПОНЕНТЫ ТЕЧЕНИЯ ОТ ЧИСЛА R

Анализ, проведенный в разд. 3, показывает, что амплитуда колебательной составляющей управляемого течения обратно пропорциональна числу Рейнольдса R, вычисленному по характерной толщине пограничного слоя на разгонном участке течения. Форма возмущений также зависит от R ввиду влияния вязкости, особенно сильного вблизи стенки.

Зависимость формы возмущений продольной скорости от значений R ~ 10²–10³, характерных для области неустойчивости поперечного течения, проиллюстрирована на рис. 7. Расчеты показывают, что с ростом R (кривые 1–3) вблизи стенки формируется вторичный пограничный слой, а во внешней области форма возмущения стремится к предельной кривой 4.

Рис. 7.

Профили возмущения тангенциальной скорости при x = 0.5 для чисел R = 100, 500, 2000, ∞ (1–4) в сечении Z = 0.005.

ЗАКЛЮЧЕНИЕ

Исследована задача управления поперечным течением в пограничном слое на скользящем крыле с помощью пристеночной объемной силы, моделирующей действие периодической вдоль размаха последовательности плазменных актуаторов. Показано, что в главном приближении течение может быть рассчитано в приближении пограничного слоя Прандтля, управляемого осредненной по размаху объемной силой. На примере скользящего крыла эллиптического сечения произведены расчеты, демонстрирующие ослабление поперечного течения на разгонном участке пограничного слоя.

Описание колебательной составляющей управляемого течения допускает линеаризацию по малому параметру – обратному числу Рейнольдса. Выявлена важная роль индуцируемого градиента давления при формировании возмущенного движения. Поле возмущенной скорости представляет собой пару больших противоположно вращающихся вихрей по обеим сторонам от области силового воздействия и пару малых вихрей внутри этой области. Изучена зависимость формы возмущений от числа Рейнольдса.

Список литературы

Шлихтинг Г. Теория пограничного слоя. М.: Наука, 1974. 711 с.
Moreau E. Airflow control by non-thermal plasma actuators // J. Phys. D: Appl. Phys. 2007. V. 40. P. 605–636.
Курячий А.П. Управление поперечным течением в трехмерном пограничном слое с помощью объемного пространственно-периодического силового воздействия // Изв. РАН. МЖГ. 2009. № 2. С. 71–79.
Kriegseis J., Schwarz C., Tropea C., Grundmann S. Velocity-information-based force-term estimation of dielectric-barrier discharge plasma actuators // J. Phys. D: Appl. Phys. 2013. V. 46. 055202. 13 p.
Кочин Н.Е., Кибель И.А., Розе Н.В. Теоретическая гидромеханика. Ч. 2. М.–Л.: ОГИЗ, Гостехиздат, 1948. 612 с.
Мануйлович С.В. Продольно-периодические течения вязкой жидкости, порождаемые пристеночной объемной силой // Изв. РАН. МЖГ. 2015. № 4. С. 59–67.
Мануйлович С.В. Роль градиента давления в течениях, управляемых пристеночной объемной силой // Изв. РАН. МЖГ. 2016. № 4. С. 49–58.
Справочник по специальным функциям с формулами, графиками и математическими таблицами / Под ред. М. Абрамовица и И. Стиган. М.: Наука, 1979. 830 с.
Кузьминский В.А. Матричный метод расчета устойчивости трехмерного пограничного слоя // Уч. зап. ЦАГИ. 2007. Т. 38. № 3–4. С. 44–56.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал