1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 1, 2020

Известия РАН. Механика жидкости и газа, 2020, № 1, стр. 22-32

Модель вертикального перемешивания, вызванного ветровыми волнами

В. Г. Полников *

Институт физики атмосферы им. А.М. Обухова РАН
Москва, Россия

* E-mail: polnikov@mail.ru

Поступила в редакцию 25.10.2018
После доработки 23.04.2019
Принята к публикации 25.06.2019

Полный текст (PDF)

Аннотация

Получены формулы для коэффициента вертикального перемешивания, вызванного ветровыми волнами. Для этого в уравнениях Навье–Стокса скорость течения разлагается на четыре составляющих: средний поток, волновое орбитальное движение, турбулентные флуктуации течения, индуцированные волнами, и фоновые турбулентные флуктуации. Такое разложение позволяет в уравнениях Рейнольдса выделить волновое напряжение Rew как дополнение к фоновому напряжению Reb. Для замыкания Rew используется приближение Прандтля для фоновых турбулентных флуктуаций, приводящее к неявному выражению для индуцированной волнами функции вертикального перемешивания ${{B}_{v}}$. Конечное выражение для ${{B}_{v}}$ определяется с привлечением результатов автора для турбулентной вязкости в зоне волнения, найденного ранее в рамках трехслойной концепции для интерфейса воздух–вода. Явное выражение для функции ${{B}_{v}}(a,{{u}_{*}},z)$ является линейным по амплитуде волны a(z) на глубине z и скорости трения ${{u}_{*}}$ в воздухе. Поскольку амплитуда волны экспоненциально убывает с глубиной, найденный результат для ${{B}_{v}}(a)$ означает возможность усиления воздействия волн на вертикальное перемешивание по сравнению с известной кубической зависимостью ${{B}_{v}}(a)$.

Ключевые слова: турбулентность, напряжения Рейнольдса, вертикальное перемешивание, ветровые волны, граница раздела воздух–вода

Адекватное описание процессов перемешивания в верхнем слое океана важно как с научной, так и с прикладной точек зрения. Об этом свидетельствует огромное число работ в данном направлении, начиная с работ Китайгородского и Ламли [1], дальнейшего их развития в [2–6] и кончая публикациями последних лет [7–9]. Научный интерес к проблеме определяется естественным стремлением исследователей прояснить физику процессов перемешивания в верхнем слое океана. Практическая значимость решения проблемы обусловлена задачами улучшения моделирования океанской циркуляции и прогнозирования изменчивости погоды и климата. Конкретные геофизические приложения таких решений детально описаны в работах [7–9], поэтому далее рассматривается только физический аспект данной задачи.

Традиционный теоретический подход к проблеме основан на использовании многоуровневых схем замыкания статистических моментов для флуктуационных составляющих поля скорости. Для задач динамики верхнего слоя океана указанные схемы в общем виде систематизированы в [4]. При таком подходе рассматриваются полные уравнения Навье–Стокса, содержащие движения разных масштабов изменчивости, строятся цепочки уравнений для моментов различного порядка, и на основе тех или иных гипотез делаются замыкания высших моментов через низшие. Учет множества деталей многомасштабной изменчивости приводит к необходимости введения различных турбулентных переменных (скорости генерации, диффузии и диссипации кинетической энергии турбулентности и т.п.), что характерно для теории турбулентности в целом [10]. В этом направлении достигнут очевидный прогресс и построены многочисленные модели динамики верхнего слоя – см., например, [6–14]. Однако столь общий подход содержит множество физических предположений, гипотез и упрощений. Все эти неопределенности приводят к недооценке вертикального перемешивания в верхнем слое и глубины перемешанного слоя [2, 3, 7, 13].

Указанные недостатки моделирования можно устранить путем учета влияния поверхностных волн на процессы вертикального перемешивания. Эта идея была реализована во многих работах (например, [1, 3, 5, 11–13] и ссылки в них), в которых авторы пытались использовать различные формы вовлечения волновых процессов на границе воздух–вода в традиционные схемы турбулентности. В итоге было показано, что поверхностные волны могут существенно усиливать перемешивание в верхнем слое океана [7–9]. Однако описание процессов перемешивания и их эффективная параметризация пока еще далеки от своего завершения.

Один из успешных результатов решения проблемы перемешивания был получен в работе [5], в которой индуцированная поверхностными волнами турбулентность исследовалась путем прямого замыкания напряжений Рейнольдса. Этот подход основан на концепции существования в верхнем слое воды турбулентности, индуцированной волнами, которая была обоснована и подтверждена в многочисленных экспериментальных [15–21] и теоретических [6, 22] исследованиях. Аналитический подход [5] представляется простейшим, прямым и достаточно эффективным решением рассматриваемой задачи.

Задача волнового перемешивания рассматривалось в [5] путем замыкания непосредственно напряжений Рейнольдса, появляющихся в уравнениях Навье–Стокса после их осреднения по масштабам турбулентных флуктуаций течений [10]. Разлагая флуктуации скорости течений на фоновую турбулентную $u_{i}^{'}$ и флуктуацию $\tilde {u}_{i}^{'}$, индуцированную волновыми движениями, авторы [5] исследовали вопрос замыкания напряжения $\langle \tilde {u}_{i}^{'}u_{j}^{'}\rangle $ (скобки $\left\langle \ldots \right\rangle $ означают статистическое усреднение) в простейшем случае одномерного и однородного среднего потока, U = (U(z), 0, 0). Для напряжения вертикального перемешивания было использовано замыкание

(0.1)
$\langle u_{1}^{'}\tilde {u}_{3}^{'}\rangle = {{B}_{v}}\frac{{dU}}{{d{{x}_{3}}}}$

Здесь индексы (1, 2, 3) обозначают x-, y-, z-компоненты потока, а величина коэффициента ${{B}_{v}}$ интерпретируется как турбулентная диффузия (вязкость) или функция вертикального перемешивания, индуцированная волновыми движениями.

Затем в [5] была принята параметризация величины ${{B}_{v}}$, представленной в виде

(0.2)
${{B}_{v}} = \langle \tilde {\lambda }_{3}^{'}\tilde {u}_{3}^{'}\rangle $

Здесь длина перемешивания Прандтля $\lambda _{3}^{'}$, присущая фоновой турбулентности (неявно введенная в замыкании (0.1)), принята равной масштабу длины перемешивания $\tilde {\lambda }_{3}^{'}$, относящегося к турбулентности, индуцированной волновыми движениями. Затем турбулентная флуктуация течения $\tilde {u}_{3}^{'}$, вызванная волнами, выражается через орбитальные скорости волновых движений $\tilde {u}_{1}^{{}}$ с помощью того же приближения Прандтля: $\tilde {u}_{3}^{'} = \tilde {\lambda }_{3}^{'}(d{{\tilde {u}}_{1}}{\text{/}}dz)$. В итоге выражение для коэффициента вертикального перемешивания Bv приобретает форму, учитывающую только волновые движения

(0.3)
${{B}_{v}} = \langle {{(\tilde {\lambda }_{3}^{'})}^{2}}(d{{\tilde {u}}_{1}}{\text{/}}d{{x}_{3}})\rangle $

С привлечением формул потенциального приближения для поверхностных волн величины $\tilde {\lambda }_{3}^{'}$ и ${{\tilde {u}}_{1}}$ в (0.3) выражаются через спектр волновых чисел $S({\mathbf{k}})$, и функция перемешивания ${{B}_{v}}$, индуцированного волнами, определяется как [5]

(0.4)
${{B}_{v}}(S,z) = \alpha \int {S({\mathbf{k}})\exp (2kz)d{\mathbf{k}}} \frac{{d{{{(\int {{{\omega }^{2}}({\mathbf{k}})S({\mathbf{k}})\exp (2kz)d{\mathbf{k}}} )}}^{{1/2}}}}}{{dz}}$

В (0.4) α – безразмерный подгоночный коэффициент; ω2(k) = g|k| – частота волны, соответствующая волновому вектору k для гравитационных волн; g – ускорение силы тяжести; экспоненты обозначают зависимость спектра поверхностных волн от глубины z, отсчитанной от средней границы раздела сред (ось z направлена вверх).

Основная особенность уравнения (0.4) заключается в кубической зависимости функции ${{B}_{v}}$ от амплитуды волны ${{a}_{0}} = {{\left( {2\int {S({\mathbf{k}})d{\mathbf{k}}} } \right)}^{{1/2}}}$ на поверхности, что приводит к довольно сильному затуханию ${{B}_{v}}$ с глубиной: ${{B}_{v}}(S,z) \propto a_{0}^{3}\exp (3{{k}_{p}}z)$, kp – волновое число, соответствующее пику спектра. Несмотря на столь сильную зависимость от глубины, в [5] отмечено, что “в глобальной модели океанической циркуляции добавление ${{B}_{v}}$ к фоновой вертикальной диффузии дает в численных расчетах структуру температуры в верхнем 100-метровом слое более близкую к климатически наблюдаемой, чем в модели без волнового перемешивания”. Позднее факт значительного воздействия волнового перемешивания на глобальную циркуляцию был подтвержден большой серией работ [7–9, 19, 23, 24].

Согласно сказанному, изложенный подход представляется как перспективное, полуфеноменологическое решение задачи перемешивания, вызванного наличием волн на поверхности моря. Однако, принимая во внимание несколько уязвимых предположений в представленной версии модели перемешивания, вызванного волнением (уравнения 0.2, 0.3), этот подход требует определенной модификации.

Настоящая работа направлена на создание новой версии модели перемешивания, вызванного ветровыми волнами. Отметим, что новая версия обсуждаемой модели приводит к значительно бóльшему влиянию волн на вертикальное перемешивание по сравнению с тем, что дает уравнение (0.4).

1. ПОСТРОЕНИЕ МОДИФИЦИРОВАННОЙ МОДЕЛИ

1.1. Теоретические предпосылки

Воспроизведем некоторые известные аналитические выкладки, входящие в решение рассматриваемой задачи. Эти выкладки проясняют некоторые предположения, которые остались без обсуждения в работе [5] при постулировании ее исходных уравнений. Отметим, рассматриваются движения в верхнем слое воды, расположенном ниже самых глубоких подошв ветровых волн на поверхности жидкости. Предполагается также, что в верхнем слое воды существует определенное фоновое течение жидкости, существующее независимо от поверхностных волн.

Следуя известному подходу теории турбулентности [10, 11], запишем исходные уравнения Навье–Стокса в тензорной форме

(1.1)
$\frac{{\partial {{U}_{i}}}}{{\partial t}} + {{U}_{j}}\frac{{\partial {{U}_{i}}}}{{\partial {{x}_{j}}}} = - \frac{1}{\rho }\frac{{\partial {{P}_{{}}}}}{{\partial {{x}_{i}}}} + \nu \frac{{{{\partial }^{2}}{{U}_{i}}}}{{\partial x_{j}^{2}}}$

Здесь, как и ранее, величина Ui (i = 1, 2, 3) представляет собой x–y–z-составляющую потока жидкости в верхнем слое ниже подошв волн; ρ – плотность воды; P – давление; ν – кинематическая вязкость воды; повторяющиеся индексы означают суммирование по ним. Следуя принятым в [5, 11] подходам, влияние сил Кориолиса в (1.1) не учитывается по причине малости масштабов рассматриваемых движений.

В данной задаче, до выполнения статистических усреднений, очень важно выделить различные виды движений. С этой целью представим разложение полной скорости жидкости при наличии ветровых волн в следующем виде

(1.2)
${{U}_{i}} = \left\langle {{{U}_{i}}} \right\rangle + {{u}_{i}} = ({{\bar {U}}_{i}} + \tilde {U}{{\delta }_{{i,1}}}) + \tilde {u}{}_{i}\; + \;\tilde {u}_{i}^{'} + u_{i}^{'}$

Здесь $\left\langle {{{U}_{i}}} \right\rangle = ({{\bar {U}}_{i}} + \tilde {U}{{\delta }_{{i,1}}})$ – общая, средняя по ансамблю волн скорость, в которой $\bar {U}_{i}^{{}}$ – “фоновая” средняя скорость и $\tilde {U}{{\delta }_{{i,1}}}$ – средняя скорость ветро-волнового дрейфа, наведенная ветром и волновым движениями, направленными по оси Ох (что отражено символом Кронекера ${{\delta }_{{i,1}}}$), а величина ${{u}_{i}}$ является суммарной добавкой к среднему потоку. Добавка ${{u}_{i}}$ включает в себя следующий набор слагаемых: $\tilde {u}{}_{i}$ – орбитальные волновые движения; $\tilde {u}_{i}^{'}$ – индуцированные волнами турбулентные оставляющие; $u_{i}^{'}$ – фоновые турбулентные флуктуации, которые далее называются “фоновой” турбулентностью. Стоксов дрейф, наведенный волнами в силу их нелинейности, включен в общее слагаемое $\tilde {U}{{\delta }_{{i,1}}}$. (Ситуация волн без ветра, когда имеет место только Стоксов дрейф, требует отдельного рассмотрения). Здесь следует отметить, что в разложении (1.2) выполняются следующие условия: 1) орбитальная скорость $\tilde {u}{}_{i}$ не относится к турбулентным флуктуациям скорости; 2) фоновые турбулентные движения $u_{i}^{'}$, по определению, не зависят от вызванных волнами турбулентных движений $\tilde {u}_{i}^{'}$; 3) оба типа флуктуаций, по своей природе, могут статистически коррелировать друг с другом. Последнее замечание очень важно для последующего рассмотрения.

Разложение, аналогичное (1.2), предполагается и для давления Р (без слагаемого дрейфа). Но ниже мы не будем касаться учета вклада слагаемых давления в уравнении (1.1), полагая, что в данной версии наших построений эти слагаемые давления просто “поправляют” введенные выше величины флуктуаций $u_{i}^{'}$ и $\tilde {u}_{i}^{'}$. Поскольку явные выражения для флуктуаций $u_{i}^{'}$ и $\tilde {u}_{i}^{'}$ в нашей модели не потребуются, указанное упрощение системы уравнений представляется вполне оправданным.

Примем следующие известные статистические аппроксимации [10, 11].

1) Все волновые, кроме дрейфа, и турбулентные слагаемые потока в (1.2) при статистическом осреднении по ансамблю волн равны нулю

(1.3а)
$\left\langle {{{{\tilde {u}}}_{i}}} \right\rangle = 0;\quad \langle \tilde {u}_{i}^{'}\rangle = 0;\quad \langle u_{i}^{'}\rangle = 0$

2) Корреляции между средними, орбитальными и турбулентными движениями отсутствуют

(1.3б)
$\left\langle {{{{\bar {U}}}_{i}}{{{\tilde {u}}}_{i}}} \right\rangle = 0,\quad \langle {{\bar {U}}_{i}}\tilde {u}_{i}^{'}\rangle = 0,\quad \langle {{\bar {U}}_{i}}u_{i}^{'}\rangle = 0$

Аналогичное утверждение верно и для дрейфового течения $\tilde {U}{{\delta }_{{i,1}}}$.

3) Корреляции между волновыми орбитальными движениями и турбулентными флуктуациями обоих типов отсутствуют

(1.3в)
$\langle \tilde {u}{}_{i}\tilde {u}_{j}^{'}\rangle = 0,\quad \langle \tilde {u}{}_{i}u_{j}^{'}\rangle = 0$

4) Турбулентные флуктуации, вызванные волнами, и фоновые турбулентные слагаемые коррелируют

(1.3г)
$\langle \tilde {u}_{i}^{'}\tilde {u}_{j}^{'}\rangle \ne 0,\quad \langle \tilde {u}_{i}^{'}u_{j}^{'}\rangle \ne 0,\quad \langle u_{i}^{'}u_{j}^{'}\rangle \ne 0$

Кроме того, для каждой составляющей в (1.2) имеет место условие неразрывности.

Подставляя (1.2) в (1.1), делая усреднение по ансамблю волн и принимая во внимание соотношения (1.3а, б) и условие неразрывности для u, получаем уравнения

(1.4)
$\frac{{\partial \left\langle {{{U}_{i}}} \right\rangle }}{{\partial t}} + \left\langle {{{U}_{j}}} \right\rangle \frac{{\partial \left\langle {{{U}_{i}}} \right\rangle }}{{\partial {{x}_{j}}}} + \frac{{\partial \left\langle {{{u}_{j}}{{u}_{i}}} \right\rangle }}{{\partial {{x}_{j}}}} = \left[ {pressure - terms} \right] + \nu \frac{{{{\partial }^{2}}\left\langle {{{U}_{i}}} \right\rangle }}{{\partial x_{j}^{2}}}$

Здесь $\left\langle {{{U}_{i}}} \right\rangle = {{\bar {U}}_{i}} + {{\tilde {U}}_{i}}{{\delta }_{{i,1}}}$, а третий член в левой части содержит напряжение Рейнольдса Re = $\left\langle {{{u}_{j}}{{u}_{i}}} \right\rangle $. Ввиду принятого разложения (1.2), полное выражение для напряжения Re имеет вид

(1.5)
$\left\langle {{{u}_{j}}{{u}_{i}}} \right\rangle = \left\langle {{{{\tilde {u}}}_{j}}{{{\tilde {u}}}_{i}}} \right\rangle + \langle {{\tilde {u}}_{j}}\tilde {u}_{i}^{'}\rangle + \langle {{\tilde {u}}_{j}}u_{i}^{'}\rangle + \langle \tilde {u}_{j}^{'}{{\tilde {u}}_{i}}\rangle + \langle \tilde {u}_{j}^{'}\tilde {u}_{i}^{'}\rangle + \langle \tilde {u}_{j}^{'}u_{i}^{'}\rangle + \langle u_{j}^{'}{{\tilde {u}}_{i}}\rangle + \langle u_{j}^{'}\tilde {u}_{i}^{'}\rangle + \langle u_{j}^{'}u_{i}^{'}\rangle $

С учетом соотношений (1.3в, г), из (1.5) следует, что

(1.6)
$\left\langle {{{u}_{j}}{{u}_{i}}} \right\rangle = \left\langle {{{{\tilde {u}}}_{j}}{{{\tilde {u}}}_{i}}} \right\rangle + \langle \tilde {u}_{j}^{'}\tilde {u}_{i}^{'}\rangle + \langle \tilde {u}_{j}^{'}u_{i}^{'}\rangle + \langle u_{j}^{'}\tilde {u}_{i}^{'}\rangle + \langle u_{j}^{'}u_{i}^{'}\rangle $

Если волн нет, $\tilde {u}{}_{i}{\text{ = }}\,\,0$ и $\tilde {u}_{i}^{'} = 0$, и напряжение Re приобретает стандартный вид [10]

(1.7)
$\left\langle {{{u}_{j}}{{u}_{i}}} \right\rangle = \langle u_{j}^{'}u_{i}^{'}\rangle $
соответствующий фоновой турбулентности, существующей в отсутствие волн.

В приближении замыкания первого уровня [10], и в случае отсутствия волн, из (1.7) следует

(1.8)
$\left\langle {{{u}_{j}}{{u}_{i}}} \right\rangle = {{K}_{{ji}}}(\partial {{\bar {U}}_{i}}{\text{/}}\partial {{x}_{j}})$
где коэффициент Kji имеет смысл величины турбулентной вязкости (диффузии). Действительно, при постоянном значении Kji = K0 замыкание (1.8) приводит напряжение (1.7) к стандартной форме вязкого члена в уравнении (1.1)

$\frac{{\partial \langle u_{j}^{'}u_{i}^{'}\rangle }}{{\partial {{x}_{j}}}} = \frac{\partial }{{\partial {{x}_{j}}}}{{K}_{{ji}}}(\partial {{\bar {U}}_{i}}{\text{/}}\partial {{x}_{j}}) = {{K}_{0}}\frac{{{{\partial }^{2}}{{{\bar {U}}}_{i}}}}{{{{{(\partial {{x}_{j}})}}^{2}}}}$

Таким образом, выполняя замыкание “волновых” слагаемых в напряжении Re вида (1.6), можно получить искомую функцию вертикального перемешивания, индуцированного волнами.

1.2. Начальная детализация

Для простоты рассмотрим случай постоянного и однородного среднего течения $\left\langle {\mathbf{U}} \right\rangle $ с учетом дрейфа $\tilde {U}$ и с вертикальным сдвигом, направленного вдоль оси OX, т.е.: $\left\langle {\mathbf{U}} \right\rangle = (U(z),0,0)$, и $\partial U{\text{/}}\partial {{x}_{i}}$ = 0 для i = 1, 2.

Ограничиваясь только вертикальными потоками, и полагая, для определенности, в уравнении (10) j = 1 и i = 3, получим для анализа напряжение вида

(1.9)
$\left\langle {{{u}_{1}}{{u}_{3}}} \right\rangle = \left\langle {{{{\tilde {u}}}_{1}}{{{\tilde {u}}}_{3}}} \right\rangle + \langle \tilde {u}_{1}^{'}\tilde {u}_{3}^{'}\rangle + \langle \tilde {u}_{1}^{'}u_{3}^{'}\rangle + \langle u_{1}^{'}\tilde {u}_{3}^{'}\rangle + \langle u_{1}^{'}u_{3}^{'}\rangle $
конечное выражение для которого и следует найти.

Во-первых, полагается, что волновое орбитальное движение является потенциальным. Тогда монохроматическая волна с частотой ω, волновым числом k и амплитудой ${{a}_{0}}$ (при z = 0), распространяющаяся в двумерном (x, z)-пространстве на глубокой воде, может быть описана в линейном приближении следующими формулами [25]. Возвышение поверхности воды имеет вид

(1.10а)
$\eta (x,t) = {{a}_{0}}\cos (kx - \omega t)$

Потенциал скорости задается формулой

(1.10б)
$\phi (x,z,t) = {{a}_{0}}\frac{\omega }{k}\exp (kz)\sin (kx - \omega t)$

Орбитальные скорости задаются соотношениями

(1.10в)
${{\tilde {u}}_{1}} = {{u}_{x}} = {{a}_{0}}\omega \exp (kz)\cos (kx - \omega t)\quad {\text{и}}\quad {{\tilde {u}}_{3}} = {{u}_{z}} = {{a}_{0}}\omega \exp (kz)\sin (kx - \omega t).$
т.е. амплитуда волновых движений затухает с глубиной как $a(k,z) = {{a}_{0}}\exp (kz)$.

Во-вторых, по причине ортогональности осциллирующих функций, из (1.10в) следует, что

(1.11)
$\left\langle {{{{\tilde {u}}}_{1}}{{{\tilde {u}}}_{3}}} \right\rangle = 0$

Используя приближение Прандтля для волновых турбулентных движений в виде

$\tilde {u}_{{1,3}}^{'} = \lambda _{{1,3}}^{'}\partial {{\tilde {u}}_{{1,3}}}{\text{/}}\partial {{x}_{3}}$
аналогично (1.11), можно получить

(1.12)
$\langle \tilde {u}_{1}^{'}\tilde {u}_{3}^{'}\rangle = 0$

В-третьих, исключая в (1.9) фоновую” турбулентность (последнее слагаемое) и используя соотношения (1.11), (1.12), получим следующее индуцированное волнами напряжение

(1.13)
${{\left\langle {{{u}_{1}}{{u}_{3}}} \right\rangle }_{w}} = \langle \tilde {u}_{1}^{'}u_{3}^{'}\rangle + \langle u_{1}^{'}\tilde {u}_{3}^{'}\rangle $

Величина ${{\left\langle {{{u}_{1}}{{u}_{3}}} \right\rangle }_{w}}$ – волновое напряжение, которое аддитивно фоновой турбулентной вязкости, определяемой соотношением вида (1.8). Впервые аналог уравнения (1.13) был постулирован, а затем и проанализирован в работе [5] (см. Введение). Ниже приведена его окончательная детализация.

1.3. Формулы замыкания

Новый подход к замыканию напряжения (1.11) включает следующие шаги.

1) По причине пространственной однородности турбулентности, индуцированной волнами, можно полагать, что оба слагаемых в (1.13) имеют одинаковое значение. Тогда

(1.14)
${{\left\langle {{{u}_{1}}{{u}_{3}}} \right\rangle }_{w}} \cong 2\langle \tilde {u}_{1}^{'}u_{3}^{'}\rangle $

2) Теперь используем стандартное приближение Прандтля для флуктуаций фоновой турбулентности вида

(1.15)
$u_{3}^{'} = \lambda _{3}^{'}\partial U{\text{/}}\partial {{x}_{3}}$
где $\lambda _{3}^{'}$ есть неизвестная, стохастическая длина перемешивания фоновой турбулентности, которая, по определению, не имеет отношения к волновым движениям, поскольку она присуща турбулентности, существующей в отсутствие волн. В итоге основное выражение для дальнейшего анализа приобретает вид

(1.16)
${{\left\langle {{{u}_{1}}{{u}_{3}}} \right\rangle }_{w}} \cong 2\langle \tilde {u}_{1}^{'}\lambda _{3}^{'}\rangle \partial U{\text{/}}\partial {{x}_{3}}$

3) По аналогии с соотношением (1.8), из (1.16) следует неявное выражение для индуцированной волнами турбулентной вязкости ${{B}_{v}}$ вида

(1.17)
${{B}_{v}} \approx 2\langle \tilde {u}_{1}^{'}\lambda _{3}^{'}\rangle $

Остается найти замыкание статистического усреднения в (1.17).

4) Отметим, что соотношение (1.17) для ${{B}_{v}}$ отличается от формулы (0.2), предложенной в [5]. Здесь используется длина перемешивания $\lambda _{3}^{'}$, присущая фоновой турбулентности, которая не может быть выражена через какую-либо часть волновых движений, как обсуждалось выше.

Функция ${{B}_{v}}$ имеет следующие особенности.

${{B}_{v}}$ – это статистический момент, конечное значение которого можно постулировать, что обычно и делается в теории турбулентности [10].

${{B}_{v}}$ есть линейная функция от индуцированной волной турбулентной флуктуации $\tilde {u}_{1}^{'}$, которая, в свою очередь, в приближении Прандтля, также линейна по производной от орбитальной волновой скорости $(d\tilde {u}_{1}^{{}}{\text{/}}d{{x}_{3}})$, т.е. по амплитуде волны – см. формулу (1.10с). Можно ожидать, что на любой фиксированной глубине z величина ${{B}_{v}}$ также должна быть линейной функцией по локальной амплитуде волны a(z), зависящей от глубины z.

5) Далее предлагается не пользоваться приближением Прандтля для волновой турбулентной флуктуации $\tilde {u}_{1}^{'}$ типа (1.15), чтобы потом не искать параметризации для возникающего момента $\langle \tilde {\lambda }_{3}^{'}\lambda _{3}^{'}\rangle $, а выполнить замыкание для ${{B}_{v}}$, путем не прямого, а косвенного определения статистического момента в (1.17), основываясь на недавней теории ветрового дрейфового течения, построенной в работе автора [26].

Согласно этой теории [26, 27] и эмпирическим наблюдениям [28], взволнованная граница раздела воздух–вода имеет трехслойную структуру: приводный слой атмосферы, зону волнения, в которой воздух и вода присутствуют попеременно, и верхний (пограничный) слой воды – рис. 1а. В работе [28] такая структура получена в результате обработки эмпирических наблюдений. Главная особенность указанной трехслойной структуры взволнованной границы раздела состоит в том, что в зоне волнения вертикальный профиль, как средней скорости ветра W(z), так и среднего течения U(z) является линейным по z. Вне зоны волнения эти профили приближаются к логарифмическим [27, 28].

Рис. 1.

Обобщенная картина движений вблизи границы раздела сред. (а) Схема расположения приводного слоя атмосферы, зоны волнения и верхнего слоя воды; кривые линии символизируют ансамбль возвышений поверхности $\eta (t)$ для фиксированной точки пространства; (б) Схематический вид профиля средней скорости течения U(z) (по данным измерения в [28]) и профиля средней скорости ветра W(z) (по расчетам в [27]). Шкала высот z дана в нормировке на длину волны L, соответствующую частоте пика ωp, а средние скорости – в нормировке на ветер W10.

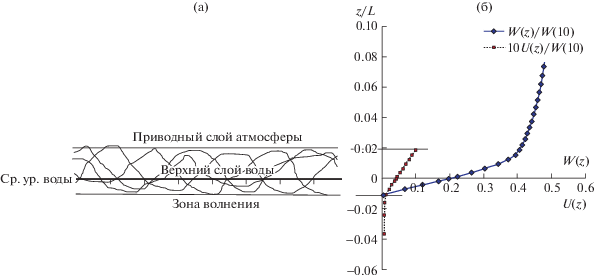
Теоретически факт линейности профиля средней скорости ветра W(z) был получен автором в работе [27] на основе обработки результатов численных экспериментов, описанных в работе [29], что и показано на рис. 1. Для скорости течения в зоне волнения профиль U(z) показан на рис. 1б схематически. Точные результаты измерений U(z) приведены в [28]. Наличие линейного профиля для средних потоков (как ветра, так и течений) означает [10], что зона волнения играет роль вязкого слоя, расположенного между приводным слоем атмосферы и верхним слоем воды. Поэтому, с точки зрения статистической гидродинамики [10], в зоне волнения должны выполняться следующие условия установившегося вязкого сдвигового течения: величина потока импульса τw, индуцированного ветром и направленного вниз, является постоянной; коэффициент турбулентной вязкости Ktw, поддерживающий линейный профиль течения $U(z)$, также является постоянным.

На основании сказанного, согласно классической теории турбулентности [10], в зоне волнения должен выполняться следующий баланс потока импульса

${{\tau }_{w}}{\text{/}}{{\rho }_{w}} = {{K}_{{tw}}}\partial U(z){\text{/}}\partial z$
где в левой части стоит вертикальный поток импульса в воде ${{\tau }_{w}}$, нормированный на плотность воды ${{\rho }_{w}}$. Используя указанный подход, в работе [26] автор установил, что в зоне волнения коэффициент турбулентного перемешивания (вязкости) Ktw имеет вид
(1.18)
${{K}_{{tw}}} = {{\left. {{{c}_{{tw}}}{{u}_{*}}a} \right|}_{{z = 0}}}$
где ctw ~ 10–2 – безразмерный коэффициент, а ${{u}_{*}}$ есть скорость трения в приводном слое атмосферы (подробности см. в Приложении). Уравнение (1.18) означает, что индуцированная волнами турбулентная вязкость Ktw в зоне волнения является линейной функцией по амплитуде волны a.

6) При допущении единства механизма перемешивания в зоне волнения и верхнем слое воды можно предположить, что искомая турбулентная вязкость ${{B}_{v}}$, имеющая место в верхнем слое воды является естественным продолжением турбулентной вязкости Ktw, имеющей место в зоне волнения. Указанное предположение позволяет считать, что параметризация ${{B}_{v}}$ является аналитическим продолжением известной параметризации величины Ktw. Исходя из этого, можно полагать, что на произвольной глубине z будет выполняться соотношение

(1.19)
${{B}_{{v}}}(z) \approx {{K}_{{tw}}}(z)$
где Ktw(z) есть аналитическое продолжение функции Ktw, заданной соотношением (1.18) на невозмущенном уровне воды z = 0. Очевидно, что указанное продолжение реализуется через известную экспоненциальную зависимость от глубины z для амплитуды орбитальных движений каждой спектральной составляющей спектра волн, т.е., согласно (1.10в), a(k, z) = a0exp(kz), где a0 – амплитуда волны на уровне z = 0.

Таким образом, явное, зависящее от амплитуды волны, скорости трения ${{u}_{*}}$ и глубины z выражение для функции ${{B}_{v}}(а,{{u}_{*}},z)$, в случае монохроматической волны на поверхности, принимает вид

(1.20)
${{B}_{v}}(a,{{u}_{*}},z) \approx {{K}_{w}}(z) \approx {{c}_{v}}{{u}_{*}}{{a}_{0}}\exp (kz)$
где ${{c}_{v}}$ ~ 10–2 – безразмерный подгоночный коэффициент. Обобщение соотношения (1.20) на случай спектра поверхностных волн задается формулой
(1.21)
${{B}_{v}}(z) = {{c}_{B}}_{v}{{u}_{*}}{{\left( {\int {S({\mathbf{k}})\exp (2kz)d{\mathbf{k}}} } \right)}^{{1/2}}}$
где ${{c}_{B}}_{v}$ ~ 10–2 – подгоночный коэффициент, аналогичный коэффициенту ${{c}_{v}}$ в (1.20).

1.4. Заключительные замечания

Соотношения (1.20), (1.21) завершают вывод искомой функции вертикального перемешивания ${{B}_{v}}$, индуцированного ветровыми волнами. Как видно из представленных формул, основное различие между (1.21) и результатом (0.4) работы [5] заключается в гораздо более сильной зависимости ${{B}_{v}}$ от локальной амплитуды волны, в силу меньшей степени затухающей экспоненты в уравнении (1.21). Этот результат свидетельствует о возможности реализации существенно большей интенсивности вертикального перемешивания, индуцированного волнами, на глубине z, чем это следует из результата (0.4). В практическом плане полученный результат может приводить к еще более заметному влиянию волнения на процессы в верхнем слое моря и в крупномасштабной циркуляции по сравнению с полученными ранее оценками [5–9].

Для физического понимания процессов в верхнем слое воды представляет интерес верификация полученных зависимостей вида (1.20) и (1.21). Определяемые формулой (1.20) зависимости ${{B}_{v}}({{a}_{0}})$ и ${{B}_{v}}({{u}_{*}})$ могут быть проверены с помощью численного моделирования взволнованной границы раздела воздух–вода по аналогии с [6, 29, 30], а также и в лабораторных экспериментах, подобных [16, 19]. Успешная проверка этих зависимостей позволила бы отдать предпочтение той или иной версии модели, описывающей процессы перемешивания, вызванные волнами. В принципе, возможны и пути аналитической проверки зависимостей ${{B}_{v}}({{a}_{0}})$ и ${{B}_{v}}({{u}_{*}})$, некоторые варианты которых обсуждаются ниже.

2. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Проверим соответствие результата (1.20) некоторым известным эмпирическим зависимостям. Поскольку эмпирические данные по прямому измерению коэффициента турбулентной вязкости ${{B}_{v}}$ в верхнем слое воды автору не известны, нужно выбрать подходящие физические величины, позволяющие выполнить проверку зависимостей ${{B}_{v}}({{a}_{0}})$ и ${{B}_{v}}({{u}_{*}})$ на основе имеющихся данных измерений. Наиболее удобной из таких величин является скорость диссипации кинетической энергии турбулентности ε, величина которой доступна экспериментальным измерениям, например, [11, 16, 17, 31].

Для указанной цели можно использовать соотношение между частью индуцированной волнами скорости диссипации кинетической энергии турбулентности εw и вязкостью ${{B}_{v}}$, записанное в виде [25]

(2.1)
${{\varepsilon }_{w}} \approx {{B}_{v}}{{\left( {\partial {{{\tilde {u}}}_{1}}{\text{/}}\partial {{x}_{3}}} \right)}^{2}}$

В соотношении (2.1) используется вертикальный градиент скорости орбитальных волновых движений как приближение, приемлемое для качественных оценок. Уравнение (2.1) позволяет выполнить аналитическую проверку соответствия соотношений (1.20), (1.21) известным эмпирическим зависимостям εw от амплитуды волны на поверхности ${{a}_{0}}$ и скорости трения ${{u}_{*}}$ в ПСА [11, 16, 31].

Согласно измерениям [16], в случае присутствия на поверхности воды монохроматической волны, имеет место следующая зависимость

(2.2)
${{\varepsilon }_{w}} \propto a_{0}^{3}$

Соответствие между отношениями (1.20) и (2.2) становится очевидным, если учесть, что скорость волны ${{\tilde {u}}_{1}}$ в (2.1) линейна по амплитуде волны – см. (1.10в). Таким образом, аналитическая проверка зависимости ${{\varepsilon }_{w}}({{a}_{0}})$ вполне успешна.

Известная зависимость εw от ${{u}_{*}}$ в верхнем слое воды, согласно измерениям [11, 31], имеет вид

(2.3)
${{\varepsilon }_{w}} \propto u_{*}^{3}$

С использованием соотношений (1.20), (1.21) и (1.10в), формула (2.1) приводит к соотношению

(2.4)
${{\varepsilon }_{w}} \propto {{u}_{*}}a{{({{\omega }_{p}}{{k}_{p}}a)}^{2}} \propto {{u}_{*}}\omega _{p}^{6}{{a}^{3}}$
где $\omega _{p}^{{}}$ – частота пика волнового спектра, а нижний индекс “0” при амплитуде волны опущен для простоты дальнейших записей. Чтобы получить зависимость $\varepsilon ({{u}_{*}})$ из формулы (2.4), можно использовать известные зависимости для безразмерных величин энергии волн $\tilde {E}$ и частоты пика спектра ${{\tilde {\omega }}_{p}}$ от безразмерного разгона волн $\tilde {X}$ для случая установившегося волнения. Согласно многочисленным экспериментальным данным, эти зависимости таковы [32]
(2.5)
$\tilde {E} \equiv \frac{{{{a}^{2}}g}}{{u_{*}^{4}}} \propto \tilde {X} \equiv \frac{{Xg}}{{u_{*}^{2}}}\quad {\text{и}}\quad {{\tilde {\omega }}_{p}} \equiv \frac{{{{\omega }_{p}}{{u}_{*}}}}{g} \propto {{\tilde {X}}^{{ - 1/3}}} \equiv {{\left( {\frac{{Xg}}{{u_{*}^{2}}}} \right)}^{{ - 1/3}}}$
где X – разгон волн в единицах длины, а g – ускорение силы тяжести. Из первого уравнения (2.5) следует, что зависимость (средней) амплитуды волны от скорости трения имеет вид $a(u_{*}^{{}}) \propto u_{*}^{{}}$, а из второго – $\omega _{p}^{{}}(u_{*}^{{}}) \propto {{(u_{*}^{{}})}^{{ - 1/3}}}$. В таком случае соотношение (2.4) приобретает вид
${{\varepsilon }_{w}} \propto {{u}_{*}}\omega _{p}^{6}{{a}^{3}} \propto u_{*}^{2}$
что соответствует эмпирической зависимости (2.3), принимая во внимание неизбежные погрешности оценок для степеней в уравнениях (2.2), (2.3) и (2.5).

Таким образом, обнадеживающие результаты аналитической проверки соответствия соотношений (1.20, 1.21) известным эмпирическим зависимостям (2.2) и (2.3) повышают значимость их экспериментальной проверки. Последнее может быть реализовано путем оценки эмпирических зависимостей ${{B}_{v}}({{a}_{0}})$ и ${{B}_{v}}({{u}_{*}})$ в лотковых экспериментах, аналогичных описанным в [16, 19].

Отметим также, что на наш взгляд, экспериментальные проверки зависимостей ${{B}_{v}}({{a}_{0}})$ и ${{B}_{v}}({{u}_{*}})$ могут выполняться двумя способами. Первый, косвенный путь основан на измерении скорости диссипации кинетической энергии турбулентной εw как функции средней амплитуды волн на поверхности жидкости ${{a}_{0}}$ и скорости трения ${{u}_{*}}$, с последующим использованием правой части соотношения (2.4) для сравнения с теорией, как это представлено выше. Второй, прямой способ может быть реализован путем расчета индуцированной волнами функции вертикального перемешивания ${{B}_{v}}$ (как функции ${{a}_{0}}$ и ${{u}_{*}}$), найденной из измерения скорости пространственного расплывания небольшой капли цветных чернил в слое воды ниже самых глубоких волновых ложбин. Для этой цели можно использовать известную формулу Эйнштейна (${{B}_{v}}\sim {{\left\langle {\Delta z} \right\rangle }^{2}}{\text{/}}\Delta t$, где Δz – размер пятна, Δt – время расплывания пятна), имея в виду физическое тождество между величиной ${{B}_{v}}$ и коэффициентом диффузии пассивных частиц в воде [10]. Соответствующая техника выполнения эксперимента, естественно, нуждается в специальной деталировке, которая при необходимости может быть разработана.

ЗАКЛЮЧЕНИЕ

Построена модель вертикальной функции турбулентного перемешивания, которая предсказывает воздействие ветровых волн на перемешивание в верхнем слое жидкости, более сильное по сравнению с оценками [5]. Модель основана на следующих теоретических положениях.

В уравнениях Навье–Стокса полный поток разлагается на четыре составляющих, включая среднее течение, орбитальные движения волн, турбулентные флуктуации течения, индуцированные волнами и фоновые турбулентные флуктуации. Это позволяет отделить волновое напряжение Рейнольдса Rew от фонового напряжения Reb и получить неявное выражение для индуцированного волнами коэффициента вертикального перемешивания ${{B}_{v}}$.

Выражение для ${{B}_{v}}$ конкретизируется путем привлечения результатов автора [26] для функции турбулентной вязкости Ktw, имеющей место в зоне волнения, расположенной между пограничным слоем атмосферы и верхним слоем воды. Искомая турбулентная вязкость в верхнем слое воды ${{B}_{v}}$ полагается равной аналитическому продолжению функции турбулентной вязкости Ktw, имеющей место в зоне волнения. В конечном счете, ${{B}_{v}}$ задается линейной функцией по амплитуде волны a(z) на глубине z и по скорости трения в воздухе ${{u}_{*}}$, что означает возможность усиления воздействия волн на вертикальное перемешивание по сравнению с известной кубической зависимостью ${{B}_{v}}(a)$, полученной ранее в [5].

Предсказанные аналитические зависимости ${{B}_{v}}({{a}_{0}})$ и ${{B}_{v}}({{u}_{*}})$ могут быть проверены эмпирически, путем их определения по данным измерений в лотковых экспериментах типа [16, 19].

Автор благодарен китайским ученым, профессорам Н. Хуанг (N. Huang) и Д. Дай (D. Dai ) за полезные замечания и советы, которые были сделаны при предварительном обсуждении рассматриваемой проблемы. Работа поддержана Российским фондом фундаментальных исследований (грант № 18-05-00161).

Список литературы

  1. Kitaigorodskii S.A., Lumley J.L. Wave-turbulence interaction in the upper ocean. Pt. I. The Energy Balance in the Interacting Fields of Surface Waves and Wind-Induced Three-Dimensional Turbulence // J. Phys. Oceanogr. 1983. V. 13. P. 1977–1987.

  2. Kantha L.H., Clayson C.A. An improved mixed layer model for geophysical applications // J. Geophys. Res. 1994. V. 99. P. 25,235–25,266.

  3. Ezer T. On the seasonal mixed layer simulated by a basin-scale ocean model and the Mellor-Yamada turbulence scheme // J. Geophys. Res. 2000. V. 105. P. 16843–16855.

  4. Mellor G.L., Yamada T., Development of a turbulence closure model for geophysical fluid problems // Rev. Geophys. Space Phys. 1982. V. 20. P. 851–875.

  5. Qiao F., Yuan Y., Yang Y., Zheng Q., Xia C., and Ma J. Wave-induced mixing in the upper ocean: Distribution and application to a global ocean circulation model // Geophys. Res. Lett. 2004. V. 31, L11303. https://doi.org/10.1029/2004GL019824

  6. Babanin A.V., Chalikov D. Numerical investigation of turbulence generation in non-breaking potential waves // J. Geophys. Res. 2012. V. 117, C00J17. https://doi.org/10.1029/2012JC007929

  7. Qiao F., Yuan Y., Deng J., Dai D., and Song Z. Wave–turbulence interaction-induced vertical mixing and its effects in ocean and climate models // Phil. Trans. R. Soc. 2016. V. A374: 20150201. https://doi.org/10.1098/rsta.2015.0201

  8. Aijaz S., Ghantous M., Babanin A.V., Ginis L., Thomas B., and Wake G. Nonbreaking wave-induced mixing in upper ocean during tropical cyclones using coupled hurricane-ocean-wave modeling // J. Geophys. Res. Oceans. 2017. V. 122. P. 3939–3963. https://doi.org/10.1002/2016JC012219

  9. Wals K., Govekar P., Babanin A.V., Ghantous M., Spence P., and Scoccimarro F. The effect on simulated ocean climate of a parameterization of unbroken wave-induced mixing incorporated into the k-epsilon mixing scheme // J. Adv. Model. Earth Syst. 2017. V. 9. P. 735–758. https://doi.org/10.1002/2016MS000707

  10. Монин А.С., Яглом А.Я. Статистическая гидромеханика. Ч. 2. М.: Наука, 1967. 720 с.

  11. Anis A., Moum J. N. Surface wave–turbulence interactions: Scaling ε(z) near the sea surface // J. Phys. Oceanogr. 1995. V. 25. P. 2025–2045.

  12. Ardhuin F., Jenkins A.D. On the interaction of surface waves and upper ocean turbulence // J. Phys. Oceanogr. 2006. V. 36. P. 551–557. https://doi.org/10.1175/JPO2862.1

  13. Janssen P.E.A.M. Ocean wave effects on the daily cycle in SST // J. Geophys. Res. 2012. V. 117, C00J32. https://doi.org/10.1029/2012JC007943

  14. Craig P.D., Banner M.L. Modelling Wave Enhanced Turbulence in the Ocean Surface Layer // J. Phys. Oceanogr. 1994. V. 24. P. 2547–2559.

  15. Babanin A.V. On a wave-induced turbulence and a wave-mixed upper ocean layer // Geophys. Res. Lett. 2006. V. 33, L20605. https://doi.org/10.1029/2006GL027308

  16. Babanin A.V., Haus B.K. On the existence of water turbulence induced by non-breaking surface waves // J. Phys. Oceanogr. 2009. V. 39. P. 2675–2679. Doi:.https://doi.org/10.1175/2009JPO4202.1

  17. Gemmrich J.R., Farmer D.M. Near-surface turbulence in the presence of breaking waves // J. Phys. Oceanogr. 2004. V. 34. P. 1067–1086.

  18. Gemmrich J.R. Strong turbulence in the wave crest region // J. Phys. Oceanogr. 2010. V. 40. P. 583–595. https://doi.org/10.1175/2009JPO4179.1

  19. Dai D., Qiao F., Sulisz W., Han L., and Babanin A. An Experiment on the Nonbreaking Surface-Wave-Induced Vertical Mixing // J. Phys. Oceanogr. 2010. V. 40. P. 2180–2188.

  20. Pleskachevsky A., Dobrynin M., Babanin A.V., Günther H., and Stanev E. Turbulent mixing due to surface waves indicated by remote sensing of suspended particulate matter and its implementation into coupled modeling of waves, turbulence and circulation // J. Phys. Oceanogr. 2011. V. 41. P. 708–724.

  21. Sutherland P., Melville W.K. Field measurements of surface and near-surface turbulence in the presence of breaking waves // J. Phys. Oceanogr. 2015. V. 45. P. 943–965. https://doi.org/10.1175/JPO-D-14-0133.1

  22. Benilov A.Y. On the turbulence generated by the potential surface waves // J. Geophys. Res. 2012. V. 117, C00J30. https://doi.org/10.1029/2012JC007948

  23. Qiao F., Yuan Y., Ezer T., Xia C., Yang Y., Lü X., and Song Z. A three-dimensional surface wave-ocean circulation coupled model and its initial testing // Ocean Dynamics. 2010. V. 60. P. 1339–1355.

  24. Huang C.J., Qiao F., Dai D., Ma H., and Guo J. Field measurement of upper ocean turbulence dissipation associated with wave-turbulence interaction in the South China Sea // J. Geophys. Res. 2012. V. 17, C00J09. https://doi.org/10.1029/2011JC00780

  25. Yuan Y., Qiao F., Yin X., and Han L. Analytical estimation of mixing coefficient induced by surface wave-generated turbulence based on the equilibrium solution of the second-order turbulence closure model // Science China: Earth Sciences. 2013. V. 56. P. 71–80. https://doi.org/10.1007/s11430-012-4517-x

  26. Polnikov V.G. A Semi-Phenomenological Model for Wind-Induced Drift Currents. Boundary-Layer Meteorol. 2019. V. 172. No, 3. P. 417–433.https://doi.org/10.1007/s10546-019-00456-1

  27. Polnikov V.G. Features of air flow in the trough-crest zone of wind waves. 2010. https://arxiv.org/abs/1006.3621.

  28. Longo S., Chiapponi L., Clavero M., Mäkel T., and Liang D. The study of the turbulence over the air-side and the water-induced boundary waves // Coastal Engineering. 2012. V. 69. P. 67–81.

  29. Chalikov D., Rainchik S. Coupled numerical modelling of wind and waves and theory of the wave boundary layer // Boundary-Layer Meteorol. 2011. V. 138. P. 1–41. https://doi.org/10.1007/s10546-010-9543-7

  30. Skote M., Henningson D.S. Direct numerical simulation of a separated turbulent boundary layer // J. Fluid Mech. 2002. V. 471. No. 1. P. 107–136.

  31. Jones N. L., Monismith S.G. The Influence of Whitecapping Waves on the Vertical Structure of Turbulence in a Shallow Estuarine Embayment // J. Phys. Oceanogr. 2008. V. 38. P. 1563–1580. https://doi.org/10.1175/2007JPO3766.1

  32. Komen G.I., Cavaleri L., Donelan M., Hasselmann K., Hasselmann S., and Janssen P.A.E.M. Dynamics and Modelling of Ocean Waves. Cambridge University Press, 1994. 554 p.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал