Известия РАН. Механика жидкости и газа, 2020, № 1, стр. 33-44
Устойчивость адвективного течения в горизонтальном слое несжимаемой жидкости при наличии условия проскальзывания Навье
К. Г. Шварц a, *, Ю. А. Шварц a, **
a Пермский государственный национальный исследовательский университет
Пермь, Россия
* E-mail: kosch@psu.ru
** E-mail: jul-schwarz@psu.ru
Поступила в редакцию 14.05.2019
После доработки 08.07.2019
Принята к публикации 22.07.2019
Аннотация
Представлено точное решение уравнений Навье-Стокса в приближении Буссинеска, описывающее плоскопараллельное адвективное течение в плоском слое несжимающейся жидкости с горизонтальными границами, на которых задано условие проскальзывания Навье и линейное распределение температуры. Исследуется поведение скорости и температуры с ростом значения параметра проскальзывания. В рамках линейной теории исследуется устойчивость адвективного течения на плоские и спиральные возмущения. В рамках нелинейной постановки задачи изучаются конечно-амплитудные возмущения в надкритической области вблизи минимумов нейтральных кривых.
В горизонтальном слое жидкости при наличии на его границах продольного градиента температуры под действием горизонтальной конвекции возникают адвективные течения [1]. Их специфика состоит в том, что скорость течения перпендикулярна силе плавучести, которая является основной причиной движения. Когда температура на границах слоя является линейной функцией ($T = Ax$, где x – продольная координата, A – постоянный горизонтальный температурный градиент на границах слоя), течение описывается аналитически, являясь точным решением уравнений Навье-Стокса [2, 3]. В случае твердых границ, на которых задано условие прилипания, возникает течение Остроумова-Бириха [4], адвективное термокапиллярное течение, возникающее при наличии свободных границ, описано в [5]. Найдены точные решения, описывающие адвективные течения с усложняющими факторами. В [6] представлено такое течение в вибрационном поле, в [7] описано адвективное течение, возникающее в условиях невесомости под действием линейных высокочастотных колебаний. В [8, 9] описаны адвективные течения, возникающие в магнитном поле. Недавно получено точное решение, описывающее плоскопараллельное адвективное течение в плоском слое несжимающейся жидкости с твердыми границами, на которых задано линейное распределение температуры разных знаков, либо линейный горизонтальный температурный градиент [10] и представлено плоскопараллельное адвективное течение, возникающее при наличии внутреннего линейного относительно горизонтальной координаты источника тепла [11]. Задача о конвекции в плоском горизонтальном слое несжимаемой жидкости с твердыми границами, на нижней из которых температура постоянная, а верхняя граница нагрета параболически, сводится к решению нелинейной системы нестационарных одномерных уравнений [12]. В [13] представлен новый класс адвективных течений, возникающий в горизонтальном слое жидкости. Устойчивость адвективного течения в горизонтальном слое с твердыми границами исследована в [1, 14].
С середины прошлого века сложилось так, что при решении задач с твердыми границами используется условие прилипания на границах соприкосновения жидкостей с твердыми поверхностями [15], на которых скорость равна нулю. В большинстве случаев это справедливо. Однако в работе [16] отмечена особая важность учета эффекта проскальзывания жидкости вдоль границы. При учете скольжения касательная составляющая скорости отлична от нуля и связана с компонентами тензора напряжений. За последние годы проведено много новых исследований, посвященных явлению прилипания/скольжения ньютоновских жидкостей (см. обзоры [17–19]), сделаны аналитические исследования [20, 21], произведено численное исследование устойчивости конвективных течений в наклонном слое при наличии проскальзывания [22].
В данной работе представлена процедура получения нового точного решения уравнений Навье-Стокса в приближении Буссинеска, описывающего плоскопараллельное адвективное течение в горизонтальном слое жидкости с твердыми границами, на которых заданы условия скольжения Навье с целью учета гидродинамики жидкости, протекающей мимо газовых секторов однонаправленных супергидрофобных поверхностей [23]. Изучена устойчивость течения при значении числа Прандтля $Pr = {\text{6}}{\text{.7}}$. Исследовано влияние величины параметра проскальзывания $b$ на характер адвективного течения и его устойчивость.
1. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
Рассмотрим бесконечный горизонтальный слой несжимаемой жидкости с твердыми границами шириной $2h$, помещенный в однородное поле тяжести. Движение жидкости описывается уравнениями конвекции в приближении Буссинеска [1] в декартовой системе координат $Oxyz$ ($z$ – вертикальная координата, x, y – горизонтальные координаты), обезразмерив которые подобно [10, 24], получим
(1.1)
$\frac{{\partial u}}{{\partial t}} + Gr\left[ {u\frac{{\partial u}}{{\partial x}} + {\text{v}}\frac{{\partial u}}{{\partial y}} + w\frac{{\partial u}}{{\partial z}}} \right] = - \frac{{\partial p}}{{\partial x}} + \Delta u$(1.2)
$\frac{{\partial {\text{v}}}}{{\partial t}} + Gr\left[ {u\frac{{\partial {\text{v}}}}{{\partial x}} + {\text{v}}\frac{{\partial {\text{v}}}}{{\partial y}} + w\frac{{\partial {\text{v}}}}{{\partial z}}} \right] = - \frac{{\partial p}}{{\partial y}} + \Delta {\text{v}}$(1.3)
$\frac{{\partial w}}{{\partial t}} + Gr\left[ {u\frac{{\partial w}}{{\partial x}} + {\text{v}}\frac{{\partial w}}{{\partial y}} + w\frac{{\partial w}}{{\partial z}}} \right] = - \frac{{\partial p}}{{\partial z}} + \Delta w + {\kern 1pt} T$(1.4)
$\frac{{\partial u}}{{\partial x}} + \frac{{\partial {\text{v}}}}{{\partial y}} + \frac{{\partial w}}{{\partial z}} = 0$(1.5)
$\frac{{\partial T}}{{\partial t}} + Gr\left[ {u\frac{{\partial T}}{{\partial x}} + {\text{v}}\frac{{\partial T}}{{\partial y}} + w\frac{{\partial T}}{{\partial z}}} \right] = \frac{1}{{\Pr }}\Delta T$На горизонтальных границах слоя задано условие проскальзывания в простейшей формулировке [23] и линейное распределение температуры
(1.6)
$z = \pm 1:\quad \mu \bar {b}\frac{{\partial {\text{u}}}}{{\partial {\text{z}}}} = u,\quad \mu \bar {b}\frac{{\partial {\text{v}}}}{{\partial {\text{z}}}} = v,\quad w = 0,\quad T = {\text{x}}$Здесь ${{\bar {b} = b} \mathord{\left/ {\vphantom {{\bar {b} = b} h}} \right. \kern-0em} h}$ – безразмерная длина скольжения. При этом случай $b = 0$ соответствует условию прилипания, а $b = \infty $ – граничному условию при отсутствии трения.
2. АДВЕКТИВНОЕ ТЕЧЕНИЕ
Учитывая граничное условие (1.6) и условие несжимаемости жидкости (1.4), точное решение системы (1.1)–(1.5) будем искать в следующем виде
(2.1)
$u = {{u}_{0}}(z),\quad {v} \equiv 0,\quad w \equiv 0,\quad T = {{T}_{0}} \equiv x + {{\theta }_{0}}(z),\quad p = {{p}_{0}}\left( {x,z} \right)$Подставив (2.1) в (1.1)–(1.5), получим систему уравнений для скорости, температуры и давления
(2.4)
$Gr{\kern 1pt} Pr{\text{ }}{{u}_{0}}{\text{ }}\left( z \right) = \theta _{0}^{{''}}\left( z \right)$Граничные условия для скорости и температуры имеют вид
(2.5)
$\mu \bar {b}u_{0}^{'}\left( { \pm 1} \right) = {{u}_{0}}\left( { \pm 1} \right),\quad {{\theta }_{0}}( \pm 1) = 0$Отметим, что ${{\theta }_{0}}\left( z \right)$ – это температура жидкости при x = 0. Продифференцируем (2.2) по x, а (2.3) по z. Избавившись от давления, получим уравнение для скорости
К граничным условиям (2.5) добавим условие замкнутости течения
Сначала находим скорость, а затем, с помощью уравнения (2.4), температуру
(2.6)
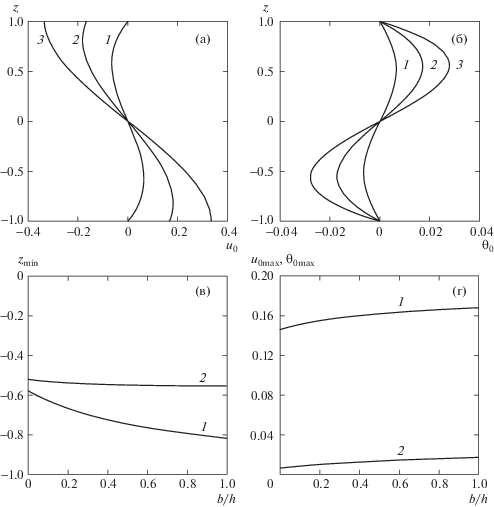
$\begin{gathered} {{u}_{{\text{0}}}}{\text{(}}z{\text{)}} = \frac{{{{z}^{3}} - z}}{6} - \frac{1}{6}\frac{{2\bar {b}}}{{\bar {b} + 1}}z{\text{,}}\quad {{\theta }_{0}}\left( z \right) = \frac{{3{{z}^{5}} - 10{{z}^{3}} + 7z}}{{360}} - \frac{{2\bar {b}}}{{\bar {b} + 1}}\frac{{{{z}^{3}} - z}}{{36}}, \\ {{T}_{0}} = x + GrPr{{\theta }_{0}}\left( z \right) \\ \end{gathered} $Скорость адвективного течения (2.6) – это линейная комбинация течения Остроумова-Бириха и течения Куэтта. Причем вторая производная скорости течения Остроумова-Бириха по $z$ равна скорости течения Куэтта. Профиль скорости и температуры симметричен, рис. 1, a, б. Максимальное и минимальное значение скорости ${{u}_{0}}\left( z \right)$ достигается при ${{z}_{{{\text{ext}}}}} = \pm \sqrt {{{(3\bar {b} + 1)} \mathord{\left/ {\vphantom {{(3\bar {b} + 1)} {(3\bar {b} + 3)}}} \right. \kern-0em} {(3\bar {b} + 3)}}} $ и равно ${{u}_{{{\text{ext}}}}} = \mu \frac{1}{3}{{({{(3\bar {b} + 1)} \mathord{\left/ {\vphantom {{(3\bar {b} + 1)} {(3\bar {b} + 3)}}} \right. \kern-0em} {(3\bar {b} + 3)}})}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}$ (рис. 1, в, г), с ростом коэффициента $\bar {b}$ убывают значения ${{z}_{{{\text{ext}}}}}$ от ${{ - {\text{1}}} \mathord{\left/ {\vphantom {{ - {\text{1}}} {\sqrt {\text{3}} }}} \right. \kern-0em} {\sqrt {\text{3}} }}$ до –1, а максимум скорости растет от ${{\text{1}} \mathord{\left/ {\vphantom {{\text{1}} {({\text{9}}\sqrt {\text{3}} )}}} \right. \kern-0em} {({\text{9}}\sqrt {\text{3}} )}}$ до 1/3. Аналогичным образои меняется максимум температуры. В предельных случаях при $b = 0$ получаем течение [4], а при $b = \infty $ – течение, подобное [5] при отсутствии вращения.
Рис. 1.
Профили (a) скорости ${{u}_{0}}\left( z \right)$ и (б) температуры ${{\theta }_{0}}\left( z \right)$ при $\bar {b} = 0$, 1 и $\infty $ (1 – 3); (в. г) зависимости координаты ${{{\text{z}}}_{{{\text{min}}}}}$ – точки минимального значения и максимального значения скорости (1) и температуры (2) адвективного течения жидкости.
3. ЛИНЕЙНАЯ ТЕОРИЯ
Для исследования устойчивости адвективного течения (2.6) применим метод малых возмущений [14]
(3.1)
${\mathbf{v}} = {{{\mathbf{v}}}_{0}} + V,\quad {{{\mathbf{v}}}_{0}} = \left( {{{u}_{0}},0,0} \right),\quad V = \left( {U,V,W} \right),\quad T = {{T}_{0}} + \theta ,\quad P = {{p}_{0}} + P{\kern 1pt} '$Здесь $V$, $\theta $, $P{\kern 1pt} '$ – малые возмущения. Подставив возмущенные поля скорости, температуры и давления (3.1) в исходную систему (1.1)–(1.5) и граничные условия (1.6), получим следующую задачу
(3.2)
$\begin{gathered} \frac{{\partial V}}{{\partial t}} + Gr\left[ {\left( {V\nabla } \right)V + \left( {V\nabla } \right){{v}_{0}} + \left( {{{v}_{0}}\nabla } \right)V} \right] = - P{\kern 1pt} '\; + \Delta V + \theta {{{\text{e}}}_{{\text{z}}}} \\ {{{\text{e}}}_{{\text{z}}}} = \left( {0{\text{,0,1}}} \right)\quad {\text{div}}V = 0 \\ \end{gathered} $(3.3)
$\frac{{\partial \theta }}{{\partial t}} + Gr\left[ {V\nabla \theta + V\nabla {{T}_{0}} + {{v}_{0}}\nabla \theta } \right] = \frac{1}{{\Pr }}\Delta \theta $(3.4)
$z = \pm 1:\quad \mu \bar {b}\frac{{\partial U}}{{\partial {\text{z}}}} = U,\quad \mu \bar {b}\frac{{\partial {\text{V}}}}{{\partial {\text{z}}}} = V,\quad W = 0,\quad \theta = 0$В рамках линейной теории устойчивости в уравнениях (3.2)–(3.4) пренебрегаем малыми квадратичными по возмущениям $V$ и $\theta $ слагаемыми. Полученная система линейных уравнений имеет решения в виде нормальных возмущений, пропорциональных ${\text{exp}}( - \lambda t + {{k}_{x}}x + {{k}_{y}}y)$, где $\lambda = {{\lambda }_{1}} + i{{\lambda }_{2}}$, – декремент, определяющий временной ход возмущений. Вещественные коэффициенты ${{k}_{x}}$ и ${{k}_{y}}$ – компоненты волнового вектора вдоль осей $X$ и $Y$.
Будем рассматривать два предельных случая: плоские периодические возмущения в виде валов с осью, параллельной оси X, и пространственные спиральные периодические по y возмущения в виде валов с осью, перпендикулярной к оси X.
Случай плоских возмущений
Уравнения возмущений выводятся из линеаризованной системы (3.2)–(3.4) в предположении, что производная по y от всех функций равна нулю (${{k}_{y}} = 0$). Учитывая дивергентность возмущений скорости, введем функцию тока возмущений $\psi (t{\text{,}}x{\text{,}}z)$ и вихря возмущения скорости $\phi (t{\text{,}}x{\text{,}}z)$
Рассмотрим нормальные возмущения вида
В результате задача сведется к решению системы линейных уравнений в частных производных по времени $t$ и переменной $z$
(3.5)
$\frac{{\partial {{\phi }_{1}}}}{{\partial t}} - {{k}_{x}}Gr[{{u}_{0}}(z){{\phi }_{2}} + u_{0}^{{''}}(z){{\psi }_{2}}] = \frac{{{{\partial }^{2}}{{\phi }_{1}}}}{{\partial {{z}^{2}}}} - k_{x}^{2}{{\phi }_{1}} + {{k}_{x}}{{\theta }_{2}}$(3.6)
$\frac{{{{\partial }^{2}}{{\psi }_{\alpha }}}}{{\partial {{z}^{2}}}} - k_{x}^{2}{{\psi }_{\alpha }} + {{\phi }_{\alpha }} = 0\quad (\alpha = 1,2),$(3.7)
$\frac{{\partial {{\phi }_{2}}}}{{\partial t}} + {{k}_{x}}Gr[{{u}_{0}}(z){{\phi }_{1}} + u_{0}^{{''}}(z){{\psi }_{1}}] = \frac{{{{\partial }^{2}}{{\varphi }_{2}}}}{{\partial {{z}^{2}}}} - k_{x}^{2}{{\phi }_{2}} - {{k}_{x}}{{\theta }_{1}}$(3.8)
$\frac{{\partial {{\vartheta }_{1}}}}{{\partial t}} - {{k}_{x}}Gr[{{u}_{0}}(z){{\vartheta }_{2}} + \Pr Gr\theta _{0}^{'}\left( {\text{z}} \right){{\psi }_{2}}] - Gr\frac{{\partial {{\psi }_{1}}}}{{\partial z}} = \frac{1}{{\Pr }}\left[ {\frac{{{{\partial }^{2}}{{\vartheta }_{1}}}}{{\partial {{z}^{2}}}} - k_{x}^{2}{{\vartheta }_{1}}} \right]$(3.9)
$\frac{{\partial {{\vartheta }_{2}}}}{{\partial t}} + {{k}_{x}}Gr[{{u}_{0}}(z){\text{ }}{{\vartheta }_{1}} + \Pr Gr\theta _{0}^{'}\left( {\text{z}} \right){{\psi }_{1}}] - Gr\frac{{\partial {{\psi }_{2}}}}{{\partial z}} = \frac{1}{{\Pr }}\left[ {\frac{{{{\partial }^{2}}{{\vartheta }_{2}}}}{{\partial {{z}^{2}}}} - k_{x}^{2}{{\vartheta }_{2}}} \right]$(3.10)
$z = \pm 1:\quad {{\psi }_{\alpha }} = {{\vartheta }_{\alpha }} = 0,\quad \mu \bar {b}{{\phi }_{\alpha }} = \frac{{\partial {{\psi }_{\alpha }}}}{{\partial z}}\quad (\alpha = 1,2)$В качестве начальных возмущений для неизвестных берем функции, удовлетворяющие граничным условиям (3.10).
Система (3.5)–(3.10) решается по численной методике [24, 25], аналогичной схемам двухполевого метода [26], который используется для решения двухмерных задач в переменных функции тока и вихря скорости. В данном случае функции тока и вихря возмущения скорости зависят от одной пространственной координаты поперек слоя – вторая переменная исчезла в предположении периодичности решения по этой координате. Уравнения для возмущения вихря скорости и функции тока решаются с помощью классической неявной схемы [27], погрешность аппроксимации $O(\Delta t + h_{z}^{2})$, где $\Delta t$ – шаг по времени, ${{h}_{{\text{z}}}}$ – шаг по z. Остальные уравнения системы решаются с помощью схемы Кранка–Николсона [27], погрешность аппроксимации $O(\Delta {{t}^{2}} + h_{z}^{2})$. Учитывая граничные условия (3.10) для функции тока и вихря скорости возмущения для аппроксимации вихря на границах на $(n + 1)$-ом временном слое вместо формулы Тома [26] используются формулы
(3.11)
$\varphi _{{{{\alpha }_{1}}}}^{{n + 1}} = - \frac{{2\psi _{{{{\alpha }_{2}}}}^{{n + 1}}}}{{{{h}_{z}}\left( {{{h}_{z}} + 2\bar {b}} \right)}},\quad \varphi _{{{{\alpha }_{N}}}}^{{n + 1}} = - \frac{{2\psi _{{{{\alpha }_{{N - 1}}}}}^{{n + 1}}}}{{{{h}_{z}}\left( {{{h}_{z}} + 2\bar {b}} \right)}}\quad \left( {\alpha = 1,2} \right)$При построении нейтральной кривой, описывающей зависимость критического числа Грасгофа от волнового числа, для каждого выбранного значения ${{k}_{x}}$ требуется найти такое число Грасгофа, при котором действительная часть декремента возмущений $\lambda = {{\lambda }_{1}} + i{{\lambda }_{2}}$ равна нулю. Иными словами, решается задача о поиске корня ${{\lambda }_{1}} = 0$ для неявной функции ${{\lambda }_{1}}({{k}_{x}}{\text{,}}Gr{\text{,}}\bar {b})$. Эта функция строится дискретно по точкам с помощью многократного решения эволюционной задачи (3.5)–(3.10) методом сеток. Для нахождения действительной части декремента возмущений λ1 прослеживалась эволюция во времени максимумов по модулю неизвестных. В качестве аппроксимации зависимости амплитуд по времени использовалась экспоненциальная формула $C\exp ( - {{\lambda }_{1}}t)$. Неизвестные λ1 и C определяются методом наименьших квадратов [28] по ходу вычислений уравнений системы. Нулевое значение декремента возмущений уточняется методом половинного деления [28]. Характер поведения возмущений от времени существенно зависит от всех параметров задачи; в области неустойчивости все возмущения нарастают, а в области устойчивости затухают.
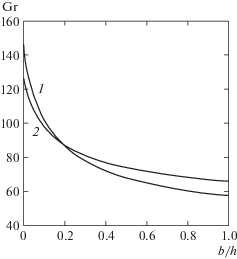
Расчеты показали (рис. 2, а), что при $Pr = {\text{6}}{\text{.7}}$ сохраняется колебательный характер неустойчивости, с ростом параметра $\bar {b}$ критическое число Грасгофа и соответствующее ему волновое число kx убывают
Рис. 2.
Нейтральные кривые адвективного течения для случая плоских (a) и спиральных (б) возмущений: 1 – 3 – $\bar {b} = 0{\text{,}}\;{\text{0}}{\text{.4,}}\;{\text{0}}{\text{.5}}$.
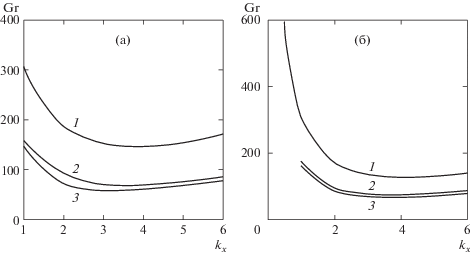
Таким образом, учет проскальзывания Навье делает течение менее устойчивым по сравнению со случаем прилипания на твердых границах.
Случай спиральных возмущений
Уравнения спиральных возмущений выводятся из системы (3.2)–(3.4) в предположении, что производные в ней по $x$ от всех функций равны 0 (${{k}_{x}} = 0$). Имеются три компоненты вектора возмущения скорости и возмущения температуры, которые являются функциями времени $t$ и двух пространственных переменных y, z.
Учитывая дивергентность возмущений скорости, введем функцию тока возмущений $\psi (t{\text{,}}y{\text{,}}z)$ и вихря возмущения скорости $\varphi (t{\text{,}}y{\text{,}}z)$
Рассмотрим нормальные возмущения вида
В результате задача сведется к решению системы линейных уравнений в частных производных по времени $t$ и переменной $z$
(3.12)
$\frac{{\partial {{\varphi }_{1}}}}{{\partial t}} = \frac{{{{\partial }^{2}}{{\varphi }_{1}}}}{{\partial {{z}^{2}}}} - k_{y}^{2}{{\varphi }_{1}} + {{k}_{y}}{{\theta }_{2}}$(3.13)
$\frac{{{{\partial }^{2}}{{\psi }_{\alpha }}}}{{\partial {{z}^{2}}}} - k_{y}^{2}{{\psi }_{\alpha }} + {{\varphi }_{\alpha }} = 0\quad (\alpha = 1,2),$(3.14)
$\frac{{\partial {{\varphi }_{2}}}}{{\partial t}} = \frac{{{{\partial }^{2}}{{\varphi }_{2}}}}{{\partial {{z}^{2}}}} - k_{y}^{2}{{\varphi }_{2}} - {{k}_{y}}{{\theta }_{1}}$(3.15)
$\frac{{\partial {{u}_{1}}}}{{\partial t}} - {{k}_{y}}Gr[u_{0}^{'}(z){{\psi }_{2}}] = \frac{{{{\partial }^{2}}{{u}_{1}}}}{{\partial {{z}^{2}}}} - k_{y}^{2}{{u}_{1}}$(3.16)
$\frac{{\partial {{u}_{2}}}}{{\partial t}} + {{k}_{y}}Gr[u_{0}^{'}(z){{\psi }_{1}}] = \frac{{{{\partial }^{2}}{{u}_{2}}}}{{\partial {{z}^{2}}}} - k_{y}^{2}{{u}_{2}}$(3.17)
$\frac{{\partial {{\theta }_{1}}}}{{\partial t}} - {{k}_{y}}Gr[\Pr Gr\theta _{0}^{'}(z){{\psi }_{2}}] + Gr{{u}_{1}} = \frac{1}{{\Pr }}\left[ {\frac{{{{\partial }^{2}}{{\theta }_{1}}}}{{\partial {{z}^{2}}}} - k_{y}^{2}{{\theta }_{1}}} \right]$(3.18)
$\frac{{\partial {{\theta }_{2}}}}{{\partial t}} + {{k}_{y}}Gr[\Pr Gr\theta _{0}^{'}(z){{\psi }_{1}}] + Gr{{u}_{2}} = \frac{1}{{\Pr }}\left[ {\frac{{{{\partial }^{2}}{{\theta }_{2}}}}{{\partial {{z}^{2}}}} - k_{y}^{2}{{\theta }_{2}}} \right]$(3.19)
$z = \pm 1\quad {{\psi }_{\alpha }} = {{u}_{\alpha }} = {{\theta }_{\alpha }} = 0,\quad \mu \bar {b}{{\varphi }_{\alpha }} = \frac{{\partial {{\psi }_{\alpha }}}}{{\partial z}}\quad (\alpha = 1,2)$Система (3.11)–(3.18) решается по вычислительной схеме аналогично случаю плоских возмущений. В качестве начальных возмущений для неизвестных возьмем функции, удовлетворяющие граничным условиям (3.19).
Также как и для плоских возмущений, с ростом параметра $\bar {b}$ критическое число Грасгофа и соответствующее ему волновое число ky убывают (рис. 2, б), монотонный характер неустойчивости сохраняется
При $\bar {b} < 0.177$ более опасными являются спиральные возмущения (рис. 3), а при $\bar {b} > 0.177$ наиболее опасными являются плоские возмущения.
4. КОНЕЧНО-АМПЛИТУДНЫЕ ВОЗМУЩЕНИЯ
Поведение возмущений конечной амплитуды в надкритической области исследуются на основе нелинейной системы уравнений (3.1)–(3.4).
Случай плоских возмущений
Для плоских периодических по $x$ возмущений система имеет вид
(4.1)
$\frac{{\partial \phi }}{{\partial t}} + Gr\left[ { - \frac{{\partial \psi }}{{\partial {\text{z}}}}\frac{{\partial \phi }}{{\partial x}} + \frac{{\partial \psi }}{{\partial {\text{x}}}}\frac{{\partial \phi }}{{\partial z}} + {{u}_{0}}\left( z \right)\frac{{\partial \phi }}{{\partial x}} + u_{0}^{{''}}\left( z \right)\frac{{\partial \psi }}{{\partial x}}} \right] = \Delta \phi - \frac{{\partial \theta }}{{\partial x}}$(4.3)
$\frac{{\partial \theta }}{{\partial t}} + Gr\left[ { - \frac{{\partial \psi }}{{\partial {\text{z}}}}\frac{{\partial \theta }}{{\partial x}} + \frac{{\partial \psi }}{{\partial {\text{x}}}}\frac{{\partial \theta }}{{\partial z}} + {{{\text{u}}}_{{\text{0}}}}\left( z \right)\frac{{\partial \theta }}{{\partial x}} - \frac{{\partial \psi }}{{\partial {\text{z}}}} + PrGr\theta _{0}^{'}\left( z \right)\frac{{\partial \psi }}{{\partial {\text{x}}}}} \right] = \frac{1}{{\Pr }}\Delta \theta $(4.4)
$z = \pm 1:\quad \mu \bar {b}\phi = \frac{{\partial \psi }}{{\partial {\text{z}}}},\quad \psi = 0,\quad \theta = 0$(4.5)
$\psi \left( {t,0,z} \right) = \psi \left( {t,L,z} \right),\quad \phi \left( {t,0,z} \right) = \phi \left( {t,L,z} \right),\quad \theta \left( {t,0,z} \right) = \theta \left( {t,L,z} \right)$Нелинейная двумерная задача (4.1)–(4.5) решалась численно методом сеток. В рамках двухполевого метода [26] использовалась явная конечно-разностная схема. Уравнение Пуассона (4.2) для функции тока решалось методом последовательной верхней релаксации. Вихрь на горизонтальных границах аппроксимировался по формуле, аналогичной (3.11). Основные расчеты проводились на сетке $101 \times 150$ при $0 \leqslant \bar {b} \leqslant 1$.
Вычисления, сделанные при $\bar {b} = 0$, совпали с результатами [1, 14] для случая твердых границ. Вблизи минимумов нейтральных кривых конечно-амплитудные возмущения температуры $\theta \left( {t,x,z} \right)$ представляют собой систему чередующихся теплых и холодных пятен, а функция тока возмущений $\psi \left( {t,x,z} \right)$ описывает систему вихрей, локализированных и движущихся вдоль горизонтальных границ слоя. С ростом значения параметра $\bar {b}$ характер конечно-амплитудных возмущений качественно не меняетcя (рис. 4), максимум возмущений температуры и скорости возрастает (рис. 5)
Случай спиральных возмущений
Для пространственных периодических по y возмущений система имеет вид
(4.6)
$\begin{gathered} \frac{{\partial U}}{{\partial t}} + Gr\left[ { - \frac{{\partial \Psi }}{{\partial z}}\frac{{\partial U}}{{\partial y}} + \frac{{\partial \Psi }}{{\partial y}}\frac{{\partial U}}{{\partial z}} + {{v}_{0}}(z)\frac{{\partial U}}{{\partial y}} + u_{0}^{'}(z)\frac{{\partial \Psi }}{{\partial y}}} \right] = \Delta U \\ \frac{{\partial \theta }}{{\partial t}} + Gr\left[ { - \frac{{\partial \Psi }}{{\partial z}}\frac{{\partial \theta }}{{\partial y}} + \frac{{\partial \Psi }}{{\partial y}}\frac{{\partial \theta }}{{\partial z}} + {{v}_{0}}(z)\frac{{\partial \theta }}{{\partial y}} + u + \Pr Gr\theta _{0}^{'}(z)\frac{{\partial \Psi }}{{\partial y}}} \right] = \frac{1}{{\Pr }}\Delta \theta \\ \end{gathered} $Нелинейная двумерная задача (4.6) решалась численно методом сеток, аналогично задаче (4.1)–(4.5). Основные расчеты проводились на сетке 101 × 150 при $0 \leqslant \bar {b} \leqslant 1$.
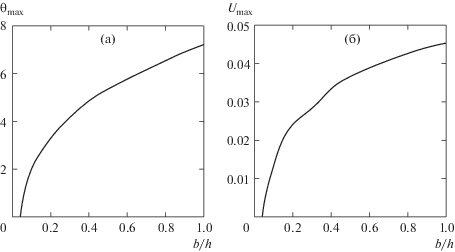
Вычисления, сделанные при $\bar {b} = 0$, совпали с результатами [1, 14] для случая твердых границ. Вблизи границ слоя формируются цепочка теплых и холодных пятен (рис. 6, а). Возмущения функции тока представляют собой структуру, состоящую в плоскости $yOz$ из четырех вихрей. Вихри расположены вблизи горизонтальных границ слоя. Одновременно возмущения первой компоненты скорости описывают в плоскости xOy вихревые движения в центре слоя. С ростом значения параметра $\bar {b}$ характер конечно-амплитудных возмущений качественно не меняется, максимум возмущений температуры и скорости возрастает (рис. 7)
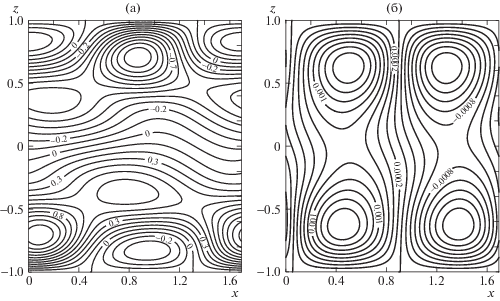
Рис. 6.
Изолинии конечно-амплитудных возмущений (a) температуры $\theta \left( {t,x,z} \right)$, (б) функции тока $\Psi \left( {t,y,z} \right)$ и (в) первой компоненты скорости $U\left( {t,y,z} \right)$ при $\bar {b} = 0.3$, $Gr = 120$, ${{k}_{y}} = 3.76$.
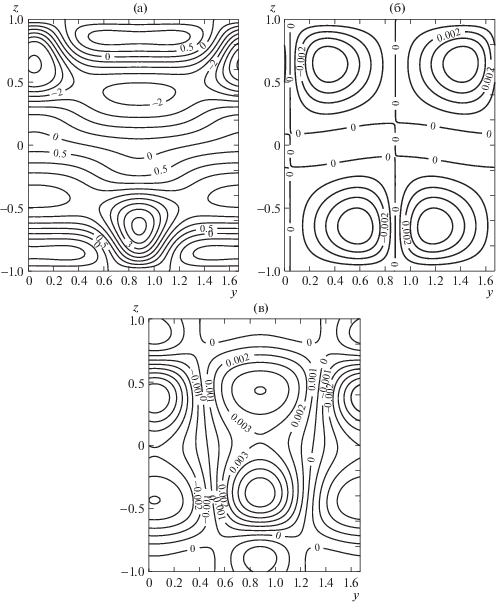
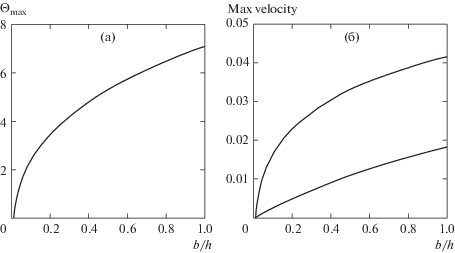
Рис. 7.
Зависимость максимума возмущений температуры (а), возмущений модуля скорости Vmax = = $\max \sqrt {{{U}^{2}} + {{{\left( {\partial \Psi {\text{/}}\partial {\text{y}}} \right)}}^{2}} + {{{\left( {\partial \Psi {\text{/}}\partial {\text{z}}} \right)}}^{2}}} $ (1) и первой компоненты скорости ${{U}_{{\max }}}$ (2) от величины $\bar {b}$ при $Gr = 120$ для случая спиральных возмущений.
ЗАКЛЮЧЕНИЕ
Представлено точное решений уравнений Навье-Стокса, записанное в приближении Обербека-Буссинеска. Описано адвективное течение несжимаемой жидкости в бесконечном горизонтальном слое с условием проскальзывания Навье на границах, при наличии на них линейного распределения температуры. Профили скорости и температуры антисимметричны, показано, что с ростом длины скольжения точки их экстремума сдвигаются к границам горизонтального слоя, максимум и минимум скорости и температуры адвективного течения растут. Линейный анализ устойчивости свидетельствует, что с ростом $\bar {b}$ устойчивость течения падает: уменьшается критическое число Грасгофа. При $\bar {b} < 0.177$ более опасными являются спиральные возмущения, а при $\bar {b} > 0.177$ наиболее опасными являются плоские возмущения. Численное исследование конечно-амплитудных возмущений показало, что с ростом значения параметра проскальзывания $\bar {b}$ характер конечно-амплитудных возмущений качественно не меняетя, максимумы возмущений температуры и скорости возрастают.
Список литературы
Гершуни Г.З., Жуховицкий Е.М., Непомнящий А.А. Устойчивость конвективных течений. М.: Наука, 1989. 320 с.
Остроумов Г.А. Свободная конвекция в условиях внутренней задачи. М.: Гостехтеориздат, 1952. 286 с.
Андреев В.К. Решения Бириха уравнений конвекции и некоторые его обобщения. Препринт СО РАН. ИВМ, № 1–10. Красноярск, 2010.
Бирих Р.В. О термокапиллярной конвекции в горизонтальном слое жидкости // ПМТФ. 1966. № 3. С. 69–72.
Аристов С.Н., Шварц К.Г. Адвективное течение во вращающейся жидкой пленке // Прикладная механика и техническая физика. 2016. Т. 57. № 1(335). С. 216–223. https://doi.org/10.15372/PMTF20160121
Гершуни Г.З., Жуховицкий Е.М. Плоскопараллельные адвективные течения в вибрационном поле // Инженерно-физический журнал. 1989. Т. 56. № 2. С. 238–242.
Бирих Р.В. О вибрационной конвекции в плоском слое с продольным градиентом температуры // Изв. АН СССР. Механика жидкости и газа. 1990. № 4. С. 12–15.
Kaddeche S., Hendry D. and Benhadid H. Magnetic stabilization of the buoyant convection between infinite horizontal walls with a horizontal temperature gradient // J. Fluid Mech. 2003. V. 480. P. 185–216. https://doi.org/10.1017/S0022112002003622
Hudoba A., Molokov S., Aleksandrova S., and Pedcenko A. Linear stability of buoyant convection in a horizontal layer of an electrically conducting fluid in moderate and high vertical magnetic field // Phys. Fluids 2016. V. 28. 094104; https://doi.org/10.1063/1.4962741
Шварц К.Г. Плоскопараллельное адвективное течение в горизонтальном слое несжимаемой жидкости с твердыми границами // Изв.РАН. МЖГ. 2014. № 4. С. 26–30.
Шварц К.Г. Плоскопараллельное адвективное течение в горизонтальном слое несжимаемой жидкости с внутренним линейным источником тепла // Прикладная математика и механика. 2018. Т. 82. Вып. 1. С. 25–30.
Аристов С.Н., Шварц К.Г. Конвективный теплообмен при локализованном нагреве плоского слоя несжимаемой жидкости // Изв. РАН. МЖГ. 2013. № 3. С. 53–58.
Аристов С.Н., Просвиряков Е.Ю. Новый класс точных решений трехмерных уравнений термодиффузии // Теоретические основы химической технологии. 2016. Т. 50. № 3. С. 294–301.
Gershuni G.Z., Laure P., Myznikov V.M., Roux B., Zhukhovitsky E.M. On the stability of plane-parallel advective flows in long horizontal layers // Microgravity Q. 1992. V. 2. № 3. P. 141–151.
Goldstein S. Modern Developments In Fluid Mechanics. Oxford: Oxford Univ. Press, 1938. 330 p.
Раджагопал К.Р. О некоторых нерешенных проблемах нелинейной динамики жидкостей // Успехи математических наук. 2003. Вып. 58. № 2. С. 111–121.
Lauga E., Brenner M.P., Stone H.A. Microfluidics: The no-slip boundary condition / Springer Handbook of Experimental Fluid Mechanics / Ed by Tropea C., Yarin A.L., Foss J.F.). Springer, 2007. 1557 p.
Neto C., Evans D.R., Bonaccurso E., Butt H.-J., Craig V.S.J., Williams D.R.M. Boundary slip in Newtonian liquids: a review of experimental studies // Rep. Prog. Phys. 2005. V. 68. P. 2859–2897.
Granick S., Zhu Y., Lee H. Slippery questions about complex fluids flowing past solids // Nature Materials. 2003. V. 2. P. 221–227.
Шелухин В.В., Христенко У.А. Об одном условии проскальзывания для уравнений вязкой жидкости // ПМТФ. 2013. Т. 54. № 5. С. 101–109.
Борзенко Е.И., Дьякова О.А., Шрагер Г.Р. Исследование явления проскальзывания в случае течения вязкой жидкости в изогнутом канале // Вестн. ТГУ. Механика. 2014. № 2 (28). С. 35–44.
Сагитов Р.В., Шарифулин А.Н. Влияние проскальзывания на бифуркацию конвективных режимов в наклонной замкнутой полости // Пермские гидродинамические научные чтения: материалы всерос. конф. с междунар. участием, посвящ. памяти проф. Г.З. Гершуни, Е.М. Жуховицкого и Д.В. Любимова / отв. ред. М.А. Кашина; Перм. гос. нац. исслед. ун-т. Пермь, 2018. С. 268–270.
Dubov A.L., Nizkaya T.V., Asmolov E.S., and Vinogradova O.I. Boundary conditions at the gas sectors of superhydrophobic grooves // Phys. Rev. Fluids. 2018. V. 3. 014002. https://doi.org/10.1103/PhysRevFluids.3.014002
Аристов С.Н., Шварц К.Г. Вихревые течения адвективной природы во вращающемся слое жидкости. Пермь: Перм. ун-т, 2006. 155 с.
Тарунин Е.Л., Шварц К.Г. Исследование линейной устойчивости адвективного течения методом сеток // Вычисл. технологии. 2001. Т. 6. № 6. С. 108–117.
Тарунин Е.Л. Вычислительный эксперимент в задачах свободной конвекции. Иркутск: Изд-во Иркут. Ун-та, 1990. 225 с.
Самарский А.А. Теория разностных схем. М.: Наука, 1977. 656 с.
Демидович Б.П., Марон И.А., Шувалова Э.З. Численные методы анализа. Приближение функций, дифференциальные и интегральные уравнения. Спб.: Изд-во “Лань”, 2008. 400 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика жидкости и газа