Известия РАН. Механика жидкости и газа, 2020, № 2, стр. 123-137

1. ИДЕАЛЬНЫЕ ХАРАКТЕРИСТИКИ ВРД С МЕДЛЕННЫМ И ДЕТОНАЦИОННЫМ ГОРЕНИЕМ

В исследуемых далее ВРД горению обычно предшествует сжатие в воздухозаборнике воздуха, поступающего из атмосферы со скоростью V₀ и числом Маха М₀ и всегда – расширение в сопле продуктов сгорания. Вслед за [4] в идеальных моделях всех рассматриваемых двигателей предварительное сжатие воздуха и расширение продуктов сгорания (совершенных газов с постоянными теплоемкостями c_p и ${{c}_{v}}$ и показателем адиабаты γ = ${{c}_{p}}{\text{/}}{{c}_{v}}$) в сопле до давления р₀ набегающего потока принимаются стационарными и изэнтропическими. Параметрам заторможенного воздуха припишем индекс “1”, а параметрам продуктов сгорания (в частности, за ДВ) и на срезе сопла – индексы “2” и “е”. Тогда справедливые в силу этого условия сохранения полной энтальпии и энтропии запишутся в форме

Здесь а, ρ, Т и ψ – скорость звука, плотность, температура и введенное в [4] отношение температур. Из определения ψ и первого равенства (1.1) имеем

Для расходов ${{\dot {m}}_{0}}$ и ${{\dot {m}}_{f}}$ воздуха и добавляемого к нему в сечении “1” (после торможения) топлива у изучаемых далее типов ВРД ${{\dot {m}}_{f}} \ll {{\dot {m}}_{0}}$. Поэтому расходы горючей смеси и продуктов сгорания приравняем ${{\dot {m}}_{0}}$, учтя вклад топлива только в энтальпию горючей смеси. В соответствии с этим параметры смеси (в сечении “1”) и продуктов сгорания (без индексов) даются формулами

где q – удельная теплотворная способность горючей смеси, а h, ω = 1/ρ и R = c_p – ${{c}_{{v}}}$ – удельные энтальпия и объем и газовая постоянная.

Хотя величины R, c_p, ${{c}_{{v}}}$ и γ воздуха, смеси и продуктов сгорания отличаются и зависят от температуры, примем их постоянными и одинаковыми. При сравнении ВРД разных типов это непринципиально. Тогда, интегрируя с привлечением уравнений (1.4) равенство Tds = dh – ωdp, придем для разности удельных энтропий s_b – s_a при любом обратимом переходе (в том числе с отводом и подводом тепла) из состояния “a” в состояние “b” к выражениям

Определение идеальных термического кпд (η) и тяг начнем с идеального ПВРД, горение в котором происходит при постоянном давлении в смеси, заторможенной до $M_{1}^{2} \ll 2{\text{/}}(\gamma - 1)$, когда формула (1.3) сводится к

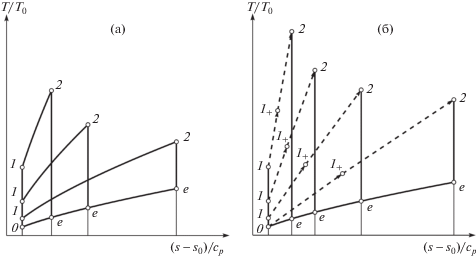
Отвечающий такому ПВРД термодинамический цикл Брайтона в плоскости sT представлен на рис. 1а, где кривые “1–2” подвода тепла (q_add) в камере сгорания и “е–0” отвода тепла (q_rej) от реактивной струи – изобары p = p₁ и p = p_е = p₀. Вертикали “0–1” и “2–е” – изэнтропы сжатия воздуха в воздухозаборнике и расширения продуктов сгорания в сопле. В силу (1.5) имеем

Количество подведенного тепла ${{q}_{{add}}} = q = {{c}_{p}}{{T}_{0}}q^\circ $ задано, а отведенного q_rej таково, что уменьшение энтропии s₀ – s_е равно ее росту s₂ – s₁. При постоянных давлениях р = р₁ и р = р_е = р₀ равенство s_е – s₀ = s₂ – s₁ дает

Следствия этого и (1.6) – формулы для термического кпд идеального цикла Брайтона

При стационарном изэнтропическом расширении продуктов сгорания в сопле ПВРД до р_е = р₀ в силу сохранения полной энтальпии и формул (1.4) и (1.6)–(1.7) придем к формуле для скорости V_e истекающих из сопла газов

Такая же формула получается при подстановке в выражение для V_e из [4]

η и $M_{0}^{2}$ из (1.8) и (1.6). По V_e/V₀, найденному по формуле (1.9) или (1.10), удельные тяга $F{\text{/}}{{\dot {m}}_{0}}$, расход топлива S и импульс I_sp определятся равенствами (g – ускорение свободного падения)

При замене изобары “1–2” на рис. 1а изохорой: ω ≡ ω₁ = ω₀/ψ^{1/(γ – 1)} получившийся идеальный цикл Хэмфри опишет процесс с горением при постоянном объеме с термическим кпд

Если теперь, как в [4], для определения скорости V_e на срезе сопла воспользоваться формулами (1.10) с η из (1.12) и $M_{0}^{2}$ из (1.6), то получим

По V_e/V₀ удельные тяга, расход топлива и импульс определятся формулами (1.11). Однако именно это выражение для V_e/V₀ – следствие справедливого лишь для стационарного истечения условия постоянства полной энтальпии от “сечения” начала зажигания горючей смеси с h₁ из (1.4) до среза сопла. Действительно, записав это условие, получим формулу (1.13). Но полная энтальпия в процессе нестационарного истечения из камеры сгорания не сохраняется, и использование формулы (1.13) и ее подстановка в (1.11) незаконны.

Идеальному пульсирующему ВРД с детонационным горением (PDE) в плоскости sT, как и в [4], отвечает термодинамический цикл рис. 1б. Его отличие от циклов рис. 1а лишь в ломанной “1–1₊–2” из стрелки “1–1₊”, которая представляет сжатие ударной волной “замороженной” по составу горючей смеси, и стрелки “1₊–2”, описывающей зону горения. В плоскости ωр зоне горения отвечает отрезок “прямой Рэлея–Михельсона” [21, 22]. Согласно ему при детонационном горении давление падает, а удельный объем растет. Как в [4], примем, что в идеальном PDE ДВ, самоподдерживающаяся (ДВ_CJ) и прямая, сжигает неподвижную горючую смесь. Параметры смеси перед ней метит индекс “1”, а продуктов сгорания за ней – индекс “2”.

Известная особенность прямой ДВ_CJ – звуковая скорость газа за ней в движущейся с ДВ системе координат. В силу этого свойства, справедливых на ДВ законов сохранения [21, 22] и уравнений состояния (1.4), найдем, что

со скоростью D_CJ движения ДВ по неподвижному газу перед ней. После подстановки в (1.5) отношений (1.14) для приращения энтропии получим

Как и в предыдущих случаях, на изобаре “е–0” с учетом (1.16)

Отсюда найдем q_rej и, вспомнив определение (1.8), – термический кпд

Если теперь по-прежнему для определения V_e вслед за [4] воспользоваться формулой (1.10), то после подстановки в нее η из (1.17) придем к выражению

Однако именно такое выражение для V_e/V₀ – следствие справедливого лишь для стационарного течения условия постоянства полной энтальпии от горючей смеси перед ДВ_CJ с h₁ из (1.4) до среза сопла. Действительно, учтя формулы (1.14) и изэнтропичность сжатия и расширения на отрезках на 0–1 и 2–е, найдем

Подставив найденное выражение для Т_е/Т₁ в указанное условие, получим формулу (1.18) при нестационарном переходе между состояниями “1” и “e”.

ВРД с горением в стационарной ДВ_CJ без предварительного сжатия воздуха (SDE_{ψ =1}) рассмотрел еще Я.Б. Зельдович [1]. Здесь ДВ_CJ стоит на входе в двигатель, точки “0” и “1” на рис. 1б совпадают, М₀ = М_CJ и в (1.15) ψ = 1. В результате для η и V_e/V₀ SDE_{ψ =1} придем к формулам

Течение во всем тракте SDE_ψ=1, как и в ПВРД, стационарно. Поэтому применение формулы для V_e/V₀ из (1.19) и следствий ее подстановки в выражения из (1.11) для определения тяговых характеристик законно.

Для чисел Маха полета М₀, превышающих для заданного q° величину, определяемую формулой (1.15) с ψ = 1, возможна модификация SDE_{ψ = 1} – SDE_{ψ > 1}, допускающая предварительное торможение набегающего потока. В идеальной модели SDE_{ψ > 1} поток стационарно-изэнтропически тормозится до М₁ = M_CJ < M₀. Проделав необходимые выкладки, найдем, что при этом

Течение в SDE_{ψ > 1}, как и в SDE_{ψ = 1}, стационарно. Поэтому последняя формула, вытекающая также из условия сохранения полной энтальпии в стационарных течениях, в отличие от ее аналога – формулы (1.18) для PDE обоснованна.

Еще один тип SDE – с косой ДВ_CJ (SDE_ODW). Вектор скорости V₀ перед ней имеет постоянную нормальную и переменную касательную к ДВ компоненты V_n0 и V_τ0, причем

Из-за отсутствия предварительного поджатия воздуха ψ = 1, определяемая постоянной величиной $M_{{n0}}^{2}$ интенсивность ДВ не зависит от М₀, а постоянный термический кпд η дается формулой (1.19) с заменой $M_{0}^{2}$ на $M_{{CJ}}^{2}$, найденный при ψ = 1. Для SDE_ODW отношение V_e/V₀ уменьшается с ростом М₀:

Типичные результаты расчета η и V_e/V₀ в зависимости от М₀ для рассмотренных ВРД при γ = 1.4 и q° = 4 и 8 представлены на рис. 2 и 3. Их обсуждение начнем с ВРД со стационарными ДВ. Это – ВРД с прямой ДВ_CJ без предварительного торможения сверхзвукового потока воздуха (SDE_ψ=1) и с его торможением (SDE_{ψ > 1}) и без предварительного торможения с косой ДВ_CJ (SDE_ODW). Для фиксированного q° SDE_ψ=1 возможен при единственном числе Маха полета М₀, чему отвечает одна точка каждого рисунка. Горизонтали, выходящие из этих точек на рис. 2а и 3а, дают независящие от М₀ значения кпд SDE_ODW, а идущие вправо-вниз кривые на рис. 2б и 3б – соответствующие отношения скоростей V_e/V₀. По η и по V_e/V₀, а следовательно, по тяговым характеристикам SDE_ODW и SDE_{ψ = 1}, много хуже всех рассмотренных ВРД. Кривые, идущие на рис. 2а и 3а из тех же точек вверх, а на рис. 2б и 3б сначала вверх, дают заметно лучшие характеристики SDE_ψ>1. Напомним, что определение V_e/V₀ через η по формуле (1.10) законно только для ВРД со стационарным горением, т.е. из рассмотренных двигателей – для SDE_{ψ ≥ 1}, SDE_ODW и ПВРД.

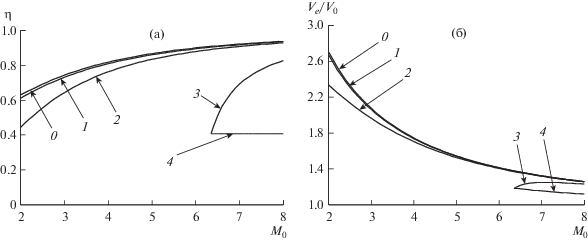
По η и определенным по η отношениям скоростей V_e/V₀ при дозвуковых и малых сверхзвуковых числах Маха М₀ ПВРД много хуже PDE. Однако для всех реальных значений q° с ростом М₀ даже по так определенным тяговым характеристикам превосходство PDE над ПВРД и SDE_{ψ > 1} быстро уменьшается. Как видно из дальнейшего, эффекты нестационарности приводят к тому, что по тяговым характеристикам PDE уступают ПВРД, начиная с небольших сверхзвуковых скоростей полета.

2. ВЛИЯНИЕ НЕСТАЦИОНАРНОСТИ ТЕЧЕНИЯ В КАМЕРЕ СГОРАНИЯ НА ТЯГОВЫЕ ХАРАКТЕРИСТИКИ PDE

Эффекты нестационарности, делающие незаконным определение через термические кпд отношения V_e/V₀, а по нему – тяговых характеристик PDE, рассчитывались в приближении невязкого и нетеплопроводного газа. PDE имел n ≥ 2 работающих синхронно пар идентичных цилиндрических детонационных камер с мгновенно открывающимися и закрывающимися входами на левых концах (при х = 0, течение слева направо). В любой момент времени часть камер открыта, обеспечивая расчетную работу воздухозаборника и постоянство (в одномерном приближении) параметров смеси перед связкой камер (в “ресивере” двигателя – с индексом r), включая отличное от нуля число Маха, такое, что $(\gamma - 1)M_{r}^{2} \ll 2$. Клапаны открываются, когда давления при х = 0 и среднее по камере становятся меньше давления смеси p_r в ресивере.

После мгновенного открытия клапана в камеру начинает поступать идеально перемешанная (гомогенная) горючая смесь, приносящая в сечение входа постоянные значения правого инварианта Римана (I⁺), энтропийной (S = p/ρ^γ) и “маркерной” (ζ) функций

Маркерная функция, равная единице в свежей смеси и нулю в продуктах сгорания, вводится для “сквозного” счета контактного разрыва (на рис. 4а – “КР”) между свежей смесью и продуктами сгорания. Для этого к интегрируемым численно уравнениям одномерного нестационарного течения добавляются уравнение “неразрывности” для ζ и такие формулы для e и h

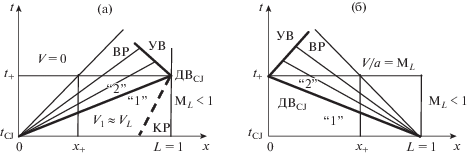
Перед выделяемой явно ДВ ζ = 1, а за ней ζ = 0. Траектория контактного разрыва отождествляется с линией уровня: ζ(x, t) = 0.5.

Правый конец камер (x = L) – сечение внезапно сужающейся части сопла с заданным отношением f < 1 площади критического сечения к площади камеры. Напомним, что при одинаковых полных длинах сопла с плавным входом хуже сопел с внезапным сужением [22, 25, 26]. Для выбранного f < 1 и предполагаемого всегда сверхкритического перепада давления p_L/p₀ число Маха М_L продуктов сгорания на правом конце камеры – функция f и γ. Уравнения, определяющие сначала λ (отношение скорости газа к критической скорости), а затем М_L, имеют вид

Эти уравнения – следствия равенства М = 1 в минимальном сечении сопла (справа от разрыва) и непрерывности на “стационарном разрыве” x = L расхода, полной энтальпии и энтропийной функции p/ρ^γ. В интервале 0 < λ < 1 решение первого уравнения (2.2) единственно. Определенное по нему число Маха М_L(f, γ) < 1. Найденная однажды величина М_L постоянна в течение полных циклов работы всех одинаковых детонационных камер связки.

Инициируемая мгновенно без дополнительных энергозатрат у одного из концов камеры ДВ_CJ отражается от частично открытого правого или закрытого левого ее конца как ударная волна (УВ). Она и УВ, возникающие при дальнейших отражениях, – не учитываемые при определении идеальных характеристик PDE источники роста энтропии. Однако и при отсутствии УВ в процессе истечения осредненная по камере полная энтальпия продуктов сгорания уменьшается в отличие от диаграммы sT рис. 1б, на которой продукты сгорания изэнтропически расширяются от определяемых формулами (1.14) и (1.15) параметров за ДВ_CJ.

При фиксированых M₀, q°, f и параметрах смеси в “ресивере” почти весь период работы камеры нестационарное течение в ней рассчитывается интегрированием уравнений одномерной газовой динамики и уравнения для маркерной функции явной монотонной “распадной” разностной схемой второго порядка (на гладких решениях) по координате х и времени t со сквозным счетом УВ и КР – границы холодной свежей горючей смеси и горячих продуктов сгорания. Эта схема – модификация схемы С.К. Годунова со вторым порядком аппроксимации по t, реализуемым процедурой Рунге–Кутты.

При открытом клапане параметры смеси в сечении х = 0 определяются уравнениями (2.1) с добавленным равенством

Здесь и ниже величины p, ρ, a и V находятся по известным к рассматриваемому моменту распределениям параметров на известном или промежуточном временном слое вблизи сечения x = 0 или x = L. Равенство (2.3) – следствие приближенного интегрирования условия совместности по малому отрезку С^–-характеристики. При закрытом клапане при х = 0 справедливо условие непротекания: V(0,t) = 0. Для его выполнения с экстраполированными в сечение х = +0 значениями p, ρ и V при х = –0 задаются те же p и ρ и скорость, направленная в другую сторону (–V). При так заданных параметрах решение задачи о распаде разрыва дает правильное давление p(0,t) – единственную величину, нужную для интегрирования выбранной разностной схемой.

Два уравнения для определения параметров на правом конце камеры подобно равенству (2.3) получаются приближенным интегрированием дифференциальных соотношений, справедливых на траекториях частиц и на С⁺-характеристиках. Добавление к ним выражения для квадрата найденного выше постоянного числа Маха M_L образует систему

Подстановка в третье уравнение ρ(1, t) и V(1, t) из первого и второго уравнений приводит к кубическому уравнению для р(1, t) и его следствию

Правильные, близкие к р, ρ, ... значения р(1,t), ρ(1,t), ... находятся итерациями.

В последних уравнениях и далее координата х отнесена к длине камеры L, время – к L/V₀, скорости – к V₀, плотности – к ρ₀ и давления – к ${{\rho }_{0}}V_{0}^{2}$. Индекс “0” здесь метит размерные, как и длина L, параметры набегающего потока.

Численным интегрированием исследуемые течения рассчитывались на двух временных отрезках: от открытия клапана до инициирования ДВ_CJ и после ее прихода на противоположный конец камеры – до открытия клапана. На разделяющем эти отрезки малом (по сравнению с периодом работы камеры) временном интервале быстрого пробега ДВ_CJ течения описывались автомодельными решениями. На рис. 4 даны xt-диаграммы двух вариантов таких течений с инициированием ДВ_CJ на левом (а) и на правом (б) концах камеры. Автомодельные решения с центрированными волнами разрежения (ВР) реализуются при замене близких к постоянным параметров смеси перед ДВ постоянными величинами, полученными осреднением распределений параметров свежей смеси. На ДВ_CJ по-прежнему справедливы формула (1.15) и три первых равенства (1.14) при замене четвертого равенства формулой

в которой по-прежнему индекс “1” метит параметры перед ДВ. При вычислении M_CJ в случае рис. 4а (б) корень из найденной по формуле (1.15) величины $M_{{CJ}}^{2}$ берется со знаком “плюс” (“минус”).

Не вдаваясь в детали построения волн разрежения, остановимся на расчете УВ, возникающей при приходе ДВ_CJ на частично закрытый конец камеры (рис. 4а). В момент возникновения УВ поток перед ней – известный поток сразу за ДВ_CJ, пришедшей на этот конец камеры. Согласно сказанному выше, в сечении x = 1 всегда постоянно и известно число Маха M_L < 1. Следовательно, на УВ при ее возникновении справедливы три закона сохранения, а за ней – еще равенство ${{\rho }_{L}}V_{L}^{2} = \gamma {{p}_{L}}M_{L}^{2}$. При известных параметрах перед УВ (с индексом “2”) это позволяет определить все параметры за УВ (с индексом “L”) и начальную скорость УВ D_SW. Если ввести обозначения

то решение задачи сведется к нахождению корня уравнения и к определению по нему остальных неизвестных формулами

Как ожидалось и подтвердилось расчетами, уравнение (2.4) имеет два действительных корня. Один корень отвечает скачку уплотнения (ρ_L/ρ₂ > 1), второй – скачку разрежения (ρ_L/ρ₂ < 1). Естественно, что в дальнейших расчетах используются корни, отвечающие скачкам уплотнения.

На рис. 4а момент инициирования ДВ_CJ выбирается так, что она и КР приходят в сечение x = 1 одновременно. В случае рис. 4б клапан закрывается в момент прихода ДВ_CJ на левый конец камеры. Столь тонкие “настройки”, как и мгновенные открытия и закрытия клапана, нулевые энергия и время инициирования ДВ_CJ, идеально перемешанная смесь на входе в камеру (при том, что между ней и продуктами сгорания нужна воздушная “прослойка”) и идеально регулируемые сопла, – нереализуемые “подарки” PDE. В модели ПВРД таких “подарков” нет.

Определенные автомодельными решениями распределения параметров при t = t₊ + τ в случае рис. 4а и при t = t₊ в случае рис. 4б служили начальными данными для расчета течения до следующего инициирования ДВ_CJ. Численное интегрирование велось с разбиением камеры на N ячеек длины Δx = 1/N. В случае рис. 4а τ = Δx/D_SW – время пробега одной ячейки УВ, возникшей при приходе ДВ_CJ в сечение x = 1. При t = t₊ + τ в крайне правой ячейке параметры определялись уравнениями (2.4) и (2.5), а в остальных – решением с ВР и покоем у левого конца камеры. В использованной разностной схеме, начиная с некоторого отличия параметров в соседних ячейках, распад разрыва считался точно. Это при принятом способе задания начальных данных обеспечивало требуемую “точность” счета размазанных УВ с момента их возникновения.

Параметры на срезе идеально регулируемых сопел (p_e = p₀ – изменением площади выхода при неизменном минимальном сечении) находились по параметрам при x = 1 (перед внезапным сужением поперечного сечения) рассчитываемого численно или аналитически потока (с известным постоянным М_L < 1) и М = 1 в минимальном сечении одномерными стационарными соотношениями. При выходе на периодический режим, фиксируемый по совпадению с заданной точностью продолжительности периода, расхода газа за период и средних значений отношения V_e/V₀, находились средние по периоду V_e/V₀, а по ним – тяговые характеристики с учетом нестационарности течения и ударных волн.

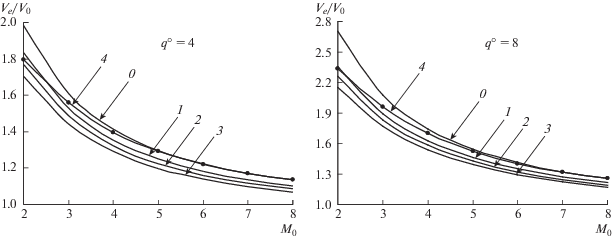
На рис. 5 для q° = 4 и 8 и f = 0.1, 0.2 и 0.3 даны кривые V_e/V₀ для PDE с ДВ_CJ, инициированной при х = 1, определенные по термическим кпд (кривые 0) и в рамках нестационарной модели (кривые 1, 2, 3 для f = 0.1, 0.2, 0.3), и для ПВРД (кривые 4). Видно, что эффекты нестационарности ограничивают преимущество PDE над ПВРД умеренными сверхзвуковыми числами Маха М₀ (для q° = 4–8 и f = 0.2–0.3 – при М₀ < 2). Правда, и для таких М₀ PDE уступают турбореактивным двигателям с медленным горением. Расчеты для PDE с ДВ_CJ, инициированной при х = 0, дали чуть меньшие значения V_e/V₀, а для ВРД с горением при постоянном объеме – чуть большие величины V_e/V₀. При 1 ≤ q° ≤ 10 взаимное расположение кривых такое же.

3. О ТЯГОВЫХ ХАРАКТЕРИСТИКАХ ВРД С ГОРЕНИЕМ ВО ВРАЩАЮЩИХСЯ ДЕТОНАЦИОННЫХ ВОЛНАХ

В интенсивно изучаемых в последнее время [12–20] ВРД с горением во вращающихся (“спиновых”) детонационных волнах (RDE) течение при переходе во вращающуюся систему координат становится стационарным. Исключая потери на нестационарность, это позволяет надеяться на высокие тяговые характеристики RDE. Такой надежде, правда, противоречат упомянутые выше результаты расчетов [17] и экспериментов [18–20], в связи с чем проанализируем результаты этих работ подробнее. Как и в [23], речь здесь пойдет не о качестве расчета течений и достоверности измерений тяг и сопротивлений моделей в импульсных аэродинамических трубах, а о “методологии обработки” результатов расчетов и измерений при представлении тяговых характеристик RDE.

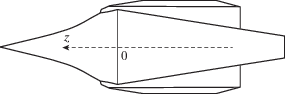
В табл. 1 собраны данные [17] по четырем RDE с горением идеально перемешанной стехиометрической водородно-воздушной смеси при полете с числом Маха М₀ = 5 на высоте 20 км. Давление и температура набегающего потока смеси были взяты для этой высоты по “стандартной атмосфере”. Рис. 6 дает меридиональные сечения тех поверхностей вращения одного из RDE [17], интегрированием по которым вычислялись (по терминологии [17]) “эффективная тяга” F_E и “сила внешнего сопротивления” R: F_E – проекция на ось z сил, действующих на все поверхности рис. 6, а R < 0 – такая же проекция сил, действующих на внешнюю часть мотогондолы и на центральное тело до входа в кольцевой канал. “Тяга двигателя” F = F_E – R > F_E в [17] проекция на ось z сил, действующих только на “внутренность” двигателя. Невключение в тягу сопротивления внешней поверхности мотогондолы общепринято. Исключение же сопротивления головной части центрального тела – новация, необоснованно увеличивающая тяги RDE, рассчитанных в [17]. Отрицательный “вклад” этой части сопротивления в тягу ПВРД при сравнениях с другими ВРД всегда учитывается.

Взятые из [17] 2–4-й и 6-й столбцы табл. 1 позволяют оценить вклад, который описанные манипуляции с сопротивлением вносят в “увеличение” тяги рассмотренных RDE. В действительности к F_E следует добавить только модуль сопротивления внешней поверхности мотогондолы. По нашей оценке для выбранных RDE и условий полета он не превышает 1.7 кН. Добавление к F_E 1.7 кН дает величины, представленные в 5-м и 7-м столбцах. Для водородно-воздушного стехиометрического ПВРД при тех же условиях полета I_sp ≈ 4100 с, т.е. в 2.2–2.9 раза больше правильно определенных I_sp RDE № 1–4 из [17].

Сопротивление головной части центрального тела – мелочь по сравнению с добавками, введенными в [18–20], к замеренной в импульсных аэродинамических трубах ИТПМ СО РАН “эффективной тяге” модели RDE. Читаем [18]: “Измеренная эффективная тяга … модели детонационного ПВРД оказалась либо близкой к нулевой, либо положительной (около 100 Н), несмотря на повышенное гидродинамическое сопротивление модели с присоединенными устройствами инициирования и дроссельными дисками, а также с системой измерения тяги …” и [19, 20]: “… зажигание водорода в огневом испытании приводит к уменьшению отрицательной составляющей мгновенной силы почти до нуля”. На самом же деле, “близкая к нулю” и “почти до нуля” означают (см. рис. 4 в [18] и [20] и рис. 8 в [19]) отрицательные значения до – 1200 Н (т.е. не тягу, а сопротивление) большую часть рабочего режима трубы. Итак, в [18–20] работающая (в “горячих испытаниях”) модель RDE тяги не создавала. Разумеется, в это внесли вклад внешние “устройство инициирования”, “система измерения тяги”, магистрали подачи топлива, провода зажигания и измерительной аппаратуры и др. Измеренное или рассчитанное сопротивление именно этих устройств следовало бы добавить (со знаком “минус”) к измеренной, близкой к нулю или отрицательной эффективной тяге. Этого, однако, слишком мало, ибо даже сопротивление головной части центрального тела [17] дало недостаточный (для конкуренции с ПВРД) “прирост” тяги.

Много больший эффект был достигнут продувкой неработающей модели и добавлением большого модуля сопротивления, замеренного в таком “холодном испытании”, к близкой к нулю или отрицательной измеренной в “горячем испытании” эффективной тяге. Именно так, якобы “экспериментально определенные” тяга (названная “внутренней”) и удельный импульс достигли 2200 Н и 3600 с. Приведенные величины, однако, неверны, как и противоречащая всему отечественному и мировому опыту принятая в [18–20], а теперь и пропагандируемая (см. [24]) методология их “экспериментального получения”. Ошибочность этой же методологии определения тяговых характеристик по результатам расчета течений в работающем и “продуваемом без горения” PDE показана в [23].

Для выяснения причин низких тяговых характеристик RDE обратимся к уравнениям, описывающим течение в их узких кольцевых детонационных камерах. Начнем с того, что вращающаяся система координат неинерциальная. Поэтому в течении, стационарном во вращающихся с угловой скоростью ω цилиндрических координатах x, y, φ', вдоль линий тока ydφ'/w' = = $dx{\text{/}}u = dy{\text{/}}v$ сохраняется не полная энтальпия $H = h + V{{{\text{'}}}^{2}}{\text{/}}2$, а разность $H{\text{'}} = H - {{y}^{2}}{{\omega }^{2}}{\text{/}}2$. Здесь $V{\text{'}}$ – вектор скорости во вращающихся координатах, $w{\text{'}} = w - y\omega $ – его окружная компонента, а u, $v$ и w – компоненты скорости V в неподвижных координатах x, y, φ = φ' + ωt.

При незакрученном потоке на входе в камеру определенный по Γ = yw полный массовый поток осевого момента количества движения равен нулю для любых поперечных сечений камеры и сопла. Полный нулевой поток не означает малости окружной скорости w, которая за ДВ – величина порядка скорости ДВ. Следовательно, компонента w знакопеременна, а максимумы |ywω| – величины порядка квадрата скорости ДВ при того же порядка неоднородности $H{\text{'}}$.

В силу условия непротекания на стенках узких цилиндрических каналов $v \approx 0$, и уравнения, описывающие течение в таких каналах, принимают вид

Часто вместо этой системы ограничиваются двумерной системой без третьего уравнения с линиями тока: $yd\varphi {\text{'/}}w{\text{'}} = dx{\text{/}}u$ на цилиндрических поверхностях y = const. Вдоль таких линий тока сохраняется $h + ({{V'}^{2}} - {{y}^{2}}{{\omega }^{2}}){\text{/}}2$ с $v = 0$, что эквивалентно сохранению полной энтальпии h + $V{{'}^{2}}{\text{/}}2$, определенной по скорости газа во вращающихся координатах.

Сказанное о системе из четырех уравнений (3.1) известно. Однако, вопреки этому, в силу третьего уравнения (3.1) в тех подобластях узких цилиндрических камер RDE, где модуль w порядка скорости ДВ, относительная радиальная неравномерность давления – величина порядка единицы. Итак, даже в таких камерах при почти нулевой радиальной скорости, течение пространственное с большими неравномерностями параметров по всем координатам, включая радиальную. Большим неравномерностям течения, как правило, сопутствуют большие потери тяги. Рост энтропии в ударных волнах, хотя и более слабых, чем в PDE, в RDE также имеет место. Из-за сохранения на отклоняющихся к оси симметрии линиях тока не полной энтальпии, а $H{\text{'}}$ возможны дополнительные потери в соплах RDE [17–20] с сужающимися центральными телами и цилиндрическим внешним контуром. Однако, увеличивая волновое сопротивление мотогондолы, переход к расширяющимся внешним контурам принципиально ситуацию не изменит.

ЗАКЛЮЧЕНИЕ

Выполнен термодинамический анализ разных типов ВРД с детонационным и дефлаграционным горением. Рассмотренные типы ВРД включают ПВРД с горением при постоянном давлении, пульсирующие детонационные двигатели (PDE) с горением в ДВ_CJ, ВРД с горением в стационарной прямой ДВ_CJ с предварительным торможением потока (SDE_{ψ > 1}) и в косой ДВ_CJ без такого торможения (SDE_ODW).

При одинаковых показателях адиабаты воздуха, горючей смеси и продуктов сгорания идеальные характеристики рассмотренных ВРД, предполагающие отсутствие потерь при торможении воздуха, его смешении с газообразным топливом и истечении продуктов сгорания из реактивного сопла, зависят от двух безразмерных параметров: числа Маха полета М₀ и безразмерной удельной теплотворной способности горючей смеси q°. Сравнение термических кпд, удельных тяг и импульсов рассмотренных двигателей выполнено для М₀ ≤ 8. Для всех реальных величин q° PDE по идеальной тяге намного лучше, чем ПВРД только при М₀ < 1.2. С ростом М₀ превосходство PDE по этой характеристике над остальными из рассмотренных ВРД за исключением SDE_ODW быстро уменьшается.

При сравнениях ВРД по их идеальным тяговым характеристикам не учитывались эффекты нестационарности, существенные для PDE с ДВ, сжигающими горючую смесь в их цилиндрических детонационных камерах. Учет этих эффектов выполнен в рамках математической модели с численным и аналитическим решением уравнений одномерной нестационарной газовой динамики. Согласно выполненным с ее помощью газодинамическим расчетам для всех реальных значений q° эффекты нестационарности делают тяговые характеристики PDE хуже характеристик ПВРД при М₀ > 2.

Интерес к ВРД с вращающимися ДВ (RDE) во многом “подогревают” сообщения о больших тягах, якобы, измеренных в экспериментах на модели RDE в импульсных аэродинамических трубах ИТПМ им. С.А. Христиановича СО РАН. На самом деле, однако, эти “большие тяги” – результат неверной методологии их определения по результатам весовых измерений в “горячих” и “холодных” испытаниях. Правильно же определенные и в расчетах, и в экспериментах тяги RDE малы из-за больших неравномерностей потоков продуктов сгорания.

Данная статья – итог исследований, которые велись в течение нескольких лет. По мере получения результаты докладывались на многих научных форумах [27–36] и частично опубликованы в материалах двух из них [37, 38].

Авторы признательны В.Г. Александрову, Х.Ф. Валиеву и К.С. Пьянкову за оказанную помощь. Работа выполнена при поддержке РФФИ (проекты 17-01-00126 и 18-31-20059).