Известия РАН. Механика жидкости и газа, 2020, № 2, стр. 61-69

КРИТИЧЕСКАЯ ЭВОЛЮЦИЯ КОНЕЧНЫХ ВОЗМУЩЕНИЙ ПОВЕРХНОСТИ ИСПАРЕНИЯ ВОДЫ В ПОРИСТЫХ СРЕДАХ

С. В. Горкунов^a, b, А. Т. Ильичев^c, d, *, В. А. Шаргатов^a, b, **

^a Институт прикладной механики им. А.Ю. Ишлинского
Москва, Россия

^b Национальный исследовательский ядерный университет МИФИ
Москва, Россия

^c Математический ин-т им. В.А. Стеклова РАН
Москва, Россия

^d Московский государственный технический университет им. Н.Э. Баумана
Москва, Россия

^* E-mail: ilichev@mi-ras.ru
^** E-mail: shargatov@mail.ru

Поступила в редакцию 30.09.2019
После доработки 08.10.2019
Принята к публикации 08.10.2019

DOI: 10.31857/S0568528120020048

Полный текст (PDF)

Аннотация

Показано, что приближенные стационарные решения, удовлетворяющие модельному диссипативному уравнению, описывающему процесс испарения воды вблизи порога неустойчивости поверхности фазового перехода, определяют затухающие локализованные возмущения конечной амплитуды при выполнении некоторого условия. Эти стационарные решения могут с хорошей точностью использоваться для предсказания того, по какому сценарию пойдет развитие возмущения, если это возмущение не имеет общих точек ни с одним стационарным решением. Если начальное положение фронта фазового перехода находится между спектрально устойчивым решением и любым из стационарных решений, то оно затухает. Если начальное положение фронта находится выше хотя бы одного спектрально неустойчивого стационарного решения, то происходит катастрофическая перестройка решения.

Ключевые слова: поверхность фазового перехода, локализованные возмущения, уединенная волна, устойчивость

Явление перехода к неустойчивости движения жидкостей с различными плотностями впервые обсуждалось в [1]. С тех пор подобная неустойчивость продолжает оставаться предметом исследований: ей подвержены границы жидкости и пара в ячейке Хеле–Шоу [2], она имеет место в пористой среде, например, при восстановлении почвы и в процессах сушки, а также в геотермальных системах, при испарении жидкости и т.д. (см., например, [3–6]).

В данной работе рассматривается устойчивость относительно конечных возмущений вертикальных течений в горизонтально протяженной двумерной области пористой среды при наличии фронта фазового перехода, когда более тяжелая жидкость (вода) располагается над более легкой (воздухом) в изотермической постановке. Порода в низкопроницаемом слое считается несмачиваемой. Подобная постановка задачи была сформулирована в ряде статей (см., например, [7]).

Если пористая среда несмачиваема, то могут существовать два стационарных решения с плоским фронтом фазового перехода. Спектральная устойчивость этих стационарных решений исследована в [6, 7]. Нижнее положение фронта фазового перехода всегда устойчиво по отношению к бесконечно малым длинноволновым возмущениям, но может быть неустойчиво по отношению к коротковолновым возмущениям.

Если это решение устойчиво по отношению к бесконечно малым возмущениям, то оно является аттрактором. Какое бы положение не занимал фронт фазового перехода в начальный момент, он либо асимптотически приближается к устойчивому стационарному решению, либо фронт за конечное время достигает верхней границы низкопроницаемого слоя, граничные условия перестают выполняться, и постановка задачи должна быть изменена. Последний сценарий рассматривается как катастрофическая перестройка течения [6]. Если в начальный момент фронт плоский, то его движение при определенном, но обычно выполняющемся допущении, можно описать аналитически [8]. Это допущение о том, что в каждый момент времени распределение влажности близко к стационарному распределению для данного положения фронта (“квазистационарное” приближение). Из полученного аналитического решения следует, что если горизонтальный плоский фронт находится ниже неустойчивого стационарного решения, то он асимптотически приближается к устойчивому фронту фазового перехода, если выше, то он за конечное время достигает верхней границы низкопроводящего слоя. Первый сценарий также реализуется, если поверхность фазового перехода имеет произвольную форму, но каждая ее точка лежит ниже неустойчивого стационарного положения плоского фронта. Если в начальный момент вся поверхность фазового перехода лежит выше этого положения, то реализуется второй сценарий. Если в начальный момент поверхность фазового перехода пересекает линию, соответствующую неустойчивому положению плоского фронта, то может реализоваться любой из двух сценариев (см. [9]). Все сказанное выше относительно фронта произвольной формы заведомо справедливо только в квазистационарном приближении. Как показано в [8, 9], спектрально устойчивое решение устойчиво также и по отношению к локализованным конечным возмущениям, если амплитуда этих возмущений меньше некоторого порогового значения, зависящего от ширины возмущения.

В данной работе c использованием слабонелинейного приближения получено достаточное условие отсутствия роста локализованных возмущений устойчивого фронта фазового перехода. Более того, каждое конечное локализованное возмущение устойчивого фронта, которое удовлетворяет этому условию, затухает.

1. ПОСТАНОВКА ЗАДАЧИ

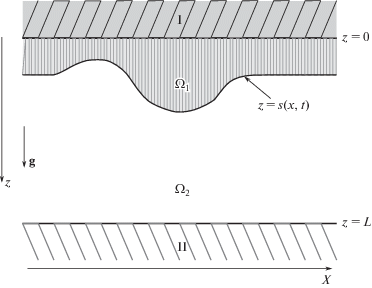
Низкопроницаемый слой делится на две области (см. рис. 1). Верхняя область заполнена жидкостью, а нижняя – смесью воздуха с парами жидкости. Эти области разделены поверхностью фазового перехода, которая считается бесконечно тонкой. Положение поверхности фазового перехода изменяется вследствие процессов фильтрации и испарения жидкости. Поскольку температура среды постоянна, то конденсация пара происходит при одном и том же постоянном значении влажности. То, что тяжелая жидкость находится над легкой, создает возможность для развития неустойчивости поверхности фазового перехода. Предполагается, что в нижнем горизонтальном высокопроницаемом слое поддерживается постоянное значение влажности воздуха. Очевидно, что указанные граничные условия выполняются, пока поверхность фазового перехода не достигла верхней или нижней границы малопроницаемого слоя.

Рис. 1.

Схема течения.

В декартовой системе координат $xyz$ c осью z, направленной вниз, верхняя граница малопроницаемого слоя пористой среды имеет координату z = 0, а нижняя граница – z = L. В рассматриваемом двумерном приближении задачи зависимостью решений от координаты y пренебрегается. Внутри низкопроницаемого слоя находится граница фазового перехода $z = s(x,t)$. Система уравнений, описывающих рассматриваемое течение, приведена в [7]. Доказательство существования и единственности решения такой системы получено в [10].

Предполагается, что в области $0 < z < s(x,t)$ жидкость несжимаема и подчиняется закону Дарси с учетом действия силы тяжести:

(1.1)

${\text{div}}{{{\mathbf{v}}}_{w}} = 0,\quad {{{\mathbf{v}}}_{w}} = - \frac{k}{{m{{\mu }_{w}}}}{\text{grad}}(P - {{\rho }_{w}}gz)$

Здесь ${{{\mathbf{v}}}_{w}}$ – скорость фильтрации воды, $m$ – пористость, $k$ – проницаемость, ${{\mu }_{w}}$ – вязкость воды, g – ускорение свободного падения, ${{\rho }_{w}}$ – плотность воды.

Если коэффициенты пористости и проницаемости постоянны, то система уравнений (1.1) эквивалентна уравнению Лапласа для давления

(1.2)

$\Delta P = 0,\quad {\text{при}}\quad 0 < z < s(x,t)$

Давление в жидкости на нижней границе слоя не зависит от времени:

(1.3)

$P = {{P}_{0}},\quad z = 0$

Диффузия пара в области $s(x,t) < z < L$ описывается уравнением

$\frac{{\partial {{\rho }_{v}}}}{{\partial t}} = {\text{div}}(D{\text{grad}}({{\rho }_{v}}))$

где ${{\rho }_{v}}$ – плотность пара, D – коэффициент диффузии.

Если парциальное давление пара мало по сравнению с атмосферным давлением и коэффициент диффузии постоянен, то для влажности воздуха $\nu = {{\rho }_{v}}{\text{/}}({{\rho }_{a}} + {{\rho }_{v}})$ справедливо уравнение

(1.4)

$\frac{{\partial \nu }}{{\partial t}} = D\Delta \nu $

Влажность при z = L не зависит от времени и равна влажности атмосферного воздуха:

(1.5)

$\nu = {{\nu }_{a}},\quad z = L$

Как показано в [9], для рассматриваемой задачи с хорошей степенью точности выполняется предположение о том, что в каждый момент времени распределение функции влажности близко к стационарному, поэтому вместо уравнения (1.4) можно использовать уравнение

(1.6)

$\Delta \nu = 0,\quad s(x,t) < z < L$

Давление в области $s(x,t) < z < L$ постоянно и равно атмосферному давлению ${{P}_{a}}$. На поверхности фазового перехода существует скачок давления, величина которого равна капиллярному давлению ${{P}_{c}}$:

(1.7)

$P = {{P}_{a}} + {{P}_{c}},\quad z = s(x,t)$

Предполагается, что на поверхности фазового перехода влажность воздуха равна влажности насыщенного пара

(1.8)

$\nu = {{\nu }_{ * }},\quad {\text{при}}\quad z = s(x,t)$

которая является известной функцией температуры T и давления ${{P}_{a}}$. В [9] показано, что температуру T можно считать постоянной, поэтому ${{\nu }_{*}}$ также является постоянной величиной.

Нормальная компонента скорости поверхности фазового перехода вычисляется по формуле

(1.9)

${{V}_{n}} = - \frac{k}{{m{{\mu }_{w}}}}{{[{\text{grad}}(P - {{\rho }_{w}}gz)]}_{n}} + D\frac{{{{\rho }_{a}}}}{{{{\rho }_{w}}}}{{({\text{grad}}\nu )}_{n}},\quad {\text{при}}\quad z = s(x,t)$

Соотношение (1.9) является следствием условия сохранения массы и уравнений (1.1) и (1.4). Индекс $n$ обозначает нормаль, направленную из области воды.

Система уравнений, описывающих изучаемый процесс, совместно с граничными условиями даются формулами (1.2)–(1.3), (1.5)–(1.9).

Введем безразмерные переменные

$x{\text{*}} = \frac{x}{L},\quad z{\text{*}} = \frac{z}{L},\quad s{\text{*}} = \frac{s}{L},\quad t{\text{*}} = \frac{{tk{{\rho }_{w}}g}}{{m{{\mu }_{w}}L}}$

$\nu {\text{*}}(x{\text{*}},z{\text{*}},t{\text{*}}) = \frac{{\nu (x,z,t) - {{\nu }_{a}}}}{{{{\nu }_{*}} - {{\nu }_{a}}}},\quad P{\text{*}}(x{\text{*}},z{\text{*}},t{\text{*}}) = \frac{{P(x,z,t) - {{P}_{0}}}}{{{{\rho }_{{_{{_{w}}}}}}gL}}$

В безразмерных переменных соотношения (1.2)–(1.3), (1.5)–(1.9) имеют вид:

$\Delta P{\text{*}} = 0,\quad 0 < z < s{\text{*}}(x{\text{*}},t{\text{*}})$

$P{\text{*}} = 0,\quad z{\text{*}} = 0$

$\nu {\text{*}} = 0,\quad z{\text{*}} = 1$

(1.10)

$\begin{gathered} \Delta \nu {\text{*}} = 0,\quad s{\text{*}}(x{\text{*}},t{\text{*}}) < z{\text{*}} < 1 \\ P{\text{*}} = \alpha ,\quad z = s{\text{*}}(x{\text{*}},t{\text{*}}) \\ \nu {\text{*}} = 1,\quad z = s{\text{*}}(x{\text{*}},t{\text{*}}) \\ \end{gathered} $

$V_{n}^{*} = - {{[{\text{grad*}}(P{\text{*}} - z{\text{*}})]}_{n}} + \beta ({\text{grad*}}\nu )_{n}^{{}},\quad z = s{\text{*}}(x{\text{*}},t{\text{*}})$

$\alpha = \frac{{{{P}_{c}} + {{P}_{a}} - {{P}_{0}}}}{{{{\rho }_{w}}gL}}$

$\beta = \frac{D}{k}\frac{{{{\rho }_{a}}}}{{{{\rho }_{w}}}}\frac{{m{{\mu }_{w}}}}{{{{\rho }_{w}}gL}}({{\nu }_{*}} - {{\nu }_{a}})$

Более сложные модели, учитывающие изменение капиллярного давления внутри слоя пористой среды, использовались в работах [11–15], а модели, принимающие во внимание перенос влажности за счет движения воздуха, изучались в [16, 17].

2. СТАЦИОНАРНЫЕ РЕШЕНИЯ ДЛЯ ПЛОСКОГО ФРОНТА

Рассмотрим решение задачи (1.10) в случае, когда капиллярное давление не зависит от вертикальной координаты z*, а поверхность фазового перехода является плоской и перпендикулярна оси Oz. Если поверхность фазового перехода покоится, то $V_{n}^{*} = 0$ или

(2.1)

$ - \frac{\alpha }{{z{\text{*}}}} + \frac{\beta }{{z{\text{*}} - 1}} + 1 = 0$

Корни уравнения (2.1) равны безразмерным координатам покоящейся поверхности фазового перехода $H_{{S,L}}^{*}$, которые задаются соотношением [7]:

(2.2)

$H_{{S,L}}^{*} = - \frac{{(\beta - \alpha - 1)}}{2} \pm \frac{{\sqrt {{{{(\beta - \alpha - 1)}}^{2}} - 4\alpha } }}{2}$

Если граничные условия фиксированы, а капиллярное давление ${{P}_{c}}$ постоянно и 0 < $\alpha < {{(1 - \sqrt \beta )}^{2}}$, то $H_{{S,L}}^{*} > 0$. В этом случае существуют два стационарных решения. Условие α > 0 выполняется, если

(2.3)

${{P}_{c}} > {{P}_{0}} - {{P}_{a}}$

Поскольку давление на нижней границе водоносного слоя всегда больше атмосферного, то неравенство (2.3) может быть справедливо только для несмачиваемых сред.

Таким образом, если пористая среда несмачиваема, то могут существовать два стационарных решения с плоским фронтом фазового перехода. В [7] показано, что для нижнего решения $H_{L}^{*}$ может иметь место неустойчивость по отношению бесконечно малым коротковолновым возмущениям, но это решение устойчиво по отношению к бесконечно малым длинноволновым возмущениям. Ниже мы будем рассматривать только случаи, когда нижнее решение спектрально устойчиво. При этом известно, что локализованные конечные возмущения могут приводить к катастрофической перестройке решения [8, 9]. Причины, по которым одни возмущения приводят к такой эволюции решения, а другие – нет, исследуются ниже в рамках слабонелинейного приближения.

3. УРАВНЕНИЯ ДЛЯ ЭВОЛЮЦИИ ФРОНТА ФАЗОВОГО ПЕРЕХОДА В СЛАБОНЕЛИНЕЙНОМ ПРИБЛИЖЕНИИ

В настоящей работе найдено приближенное аналитическое выражение для порогового значения амплитуды локализованного возмущения, которое приводит к катастрофической перестройке решения. Для этого получено приближенное уравнение для описания вторичных структур в окрестности перехода к неустойчивости. Это амплитудное уравнение, как показано ниже, может быть сведено к форме уравнения Колмогорова–Петровского–Пискунова. В параболическом случае (1.4) такое уравнение было получено в [6, 7], что позволило в [18] исследовать глобальную и конвективную устойчивость фронта фазового перехода, распространяющегося в виде бегущей волны. В случае эллиптического приближения для влажности (1.6), рассматриваемого здесь, можно получить аналогичное уравнение, коэффициенты которого будут мало отличаться от случая параболического уравнения для влажности. Ключевые предположения для получения этого уравнения следующие. Вводятся два малых параметра, характеризующих величину, обратную длине волны $\lambda $, и амплитуду волны ${{\eta }_{a}}$:

$\lambda \gg 1,\quad {{\eta }_{a}} = max(s{\text{*}}(x{\text{*}},0) - H),\quad {{\eta }_{a}} \ll 1$

где $H = H_{L}^{*}$ или $H = H_{S}^{*}$, в зависимости от того, на какое из стационарных решений для плоского фронта фазового перехода накладывается возмущение. Поскольку предполагается, что возмущение остается малым, но при этом сравнимо с $H_{L}^{*} - H_{S}^{*}$, то разность$H_{L}^{*} - H_{S}^{*}$ должна быть также мала. В результате применения асимптотической процедуры, где малыми параметрами считаются $\chi = 1{\text{/}}{{\lambda }^{2}}$ и ${{\eta }_{a}}$ можно получить уравнение

(3.1)

$\begin{gathered} \frac{{\partial s{\text{*}}(x{\text{*}},t{\text{*}})}}{{\partial t{\text{*}}}} = \frac{1}{3}\left( {\beta - \alpha } \right)\frac{{{{\partial }^{2}}s{\text{*}}(x{\text{*}},t{\text{*}})}}{{\partial x{{{\text{*}}}^{2}}}} + \left( {\frac{\alpha }{{{{H}^{2}}}} - \frac{\beta }{{{{{(1 - H)}}^{2}}}}} \right)s{\text{*}}(x{\text{*}},t{\text{*}}) - \\ \, - \left( {\frac{\alpha }{{{{H}^{3}}}} + \frac{\beta }{{{{{(1 - H)}}^{3}}}}} \right)s{\text{*}}{{(x{\text{*}},t{\text{*}})}^{2}} \\ \end{gathered} $

Коэффициенты уравнения (3.1) зависят только от безразмерных параметров $\alpha $ и $\beta $, поскольку H является функцией $\alpha $ и $\beta $ (см. (2.2)). Уравнение (3.1) позволяет исследовать решение задачи (1.10) в слабонелинейном приближении и сделать выводы о фундаментальных свойствах решения полной задачи.

При $H = H_{S}^{*}$ выполняется условие

$\frac{\alpha }{{{{H}^{2}}}} - \frac{\beta }{{{{{(1 - H)}}^{2}}}} > 0$

Тогда уравнение (3.1) сводится к уравнению Колмогорова–Петровского–Пискунова

$\frac{{\partial \vartheta (\xi ,\tau )}}{{\partial \tau }} = \frac{{{{\partial }^{2}}\vartheta (\xi ,\tau )}}{{\partial {{\xi }^{2}}}} + \vartheta (\xi ,\tau ) - \vartheta {{(\xi ,\tau )}^{2}}$

Действительно, это достигается заменой переменных

${{c}_{{xS}}} = \mathop {(\alpha - \beta )}\nolimits^{1/2} \mathop {\left( {3\left( {\frac{\alpha }{{{{H}^{2}}}} - \frac{\beta }{{\mathop {\left( {1 - H} \right)}\nolimits^2 }}} \right)} \right)}\nolimits^{ - 1/2} $

${{c}_{{tS}}} = \mathop {\left( {\frac{\alpha }{{{{H}^{2}}}} - \frac{\beta }{{\mathop {\left( {1 - H} \right)}\nolimits^2 }}} \right)}\nolimits^{ - 1} $

${{c}_{{sS}}} = \left( {\frac{\alpha }{{{{H}^{2}}}} - \frac{\beta }{{\mathop {\left( {1 - H} \right)}\nolimits^2 }}} \right)\mathop {\left( {\frac{\beta }{{\mathop {\left( {1 - H} \right)}\nolimits^3 }} + \frac{\alpha }{{{{H}^{3}}}}} \right)}\nolimits^{ - 1} \vartheta $

$x{\text{*}} = {{c}_{{xS}}}\xi ,\quad t{\text{*}} = {{c}_{{tS}}}\tau ,\quad s{\text{*}} = {{c}_{{sS}}}\vartheta $

Если $H = H_{L}^{*}$, то

$\frac{\alpha }{{{{H}^{2}}}} - \frac{\beta }{{{{{(1 - H)}}^{2}}}} < 0$

и, сделав замену переменных,

${{c}_{{xL}}} = \mathop {(\alpha - \beta )}\nolimits^{1/2} \mathop {\left( {3\left( {\frac{\beta }{{\mathop {\left( {1 - H} \right)}\nolimits^2 }} - \frac{\alpha }{{{{H}^{2}}}}} \right)} \right)}\nolimits^{ - 1/2} $

${{c}_{{tL}}} = \mathop {\left( {\frac{\beta }{{\mathop {\left( {1 - H} \right)}\nolimits^2 }} - \frac{\alpha }{{{{H}^{2}}}}} \right)}\nolimits^{ - 1} $

${{c}_{{sL}}} = \left( {\frac{\beta }{{\mathop {\left( {1 - H} \right)}\nolimits^2 }} - \frac{\alpha }{{{{H}^{2}}}}} \right)\mathop {\left( {\frac{\beta }{{\mathop {\left( {1 - H} \right)}\nolimits^3 }} + \frac{\alpha }{{{{H}^{3}}}}} \right)}\nolimits^{ - 1} \vartheta $

$x{\text{*}} = {{c}_{{xL}}}\xi ,\quad t{\text{*}} = {{c}_{{tL}}}\tau ,\quad s{\text{*}} = {{c}_{{sL}}}\vartheta $

получаем уравнение

(3.2)

$\frac{{\partial \vartheta (\xi ,\tau )}}{{\partial \tau }} = \frac{{{{\partial }^{2}}\vartheta (\xi ,\tau )}}{{\partial {{\xi }^{2}}}} - \vartheta (\xi ,\tau ) - \vartheta {{(\xi ,\tau )}^{2}}$

4. ДОСТАТОЧНОЕ УСЛОВИЕ УСТОЙЧИВОСТИ ПО ОТНОШЕНИЮ К ЛОКАЛИЗОВАННЫМ КОНЕЧНЫМ ВОЗМУЩЕНИЯМ

Рассмотрим возмущение спектрально устойчивого стационарного решения при $H = H_{L}^{*}$. Этому случаю соответствует уравнение (3.2). Оно имеет ограниченные стационарные решения, удовлетворяющие автономному дифференциальному уравнению второго порядка

$\frac{{{{\partial }^{2}}\vartheta (\xi )}}{{\partial {{\xi }^{2}}}} - \vartheta (\xi ) - \vartheta {{(\xi )}^{2}} = 0$

Это уравнение при определенных условиях имеет решение, устойчивое по отношению к бесконечномалым возмущениям (см. [7])

(4.1)

${{\vartheta }_{1}}(\xi )) = 0$

и спектрально неустойчивые решения

(4.2)

${{\vartheta }_{2}}(\xi ) = - 1$

(4.3)

${{\vartheta }_{3}}(\xi ) = - 1.5{\text{sec}}{{{\text{h}}}^{2}}(0.5(\xi + {{C}_{1}}))$

(4.4)

${{\vartheta }_{4}}(\xi ) = \frac{{\left( {6b - 3 - c} \right)}}{4}{\text{sn}}\mathop {\left( {\frac{{\sqrt 6 \sqrt {6b - 3 + c} ( - \sqrt b (\xi + {{C}_{1}}) + \sqrt 3 )}}{{12\sqrt b }},\frac{{\sqrt 3 \left( {6b - 3 - c} \right)}}{{12\sqrt {{{b}^{2}} - b} }}} \right)}\nolimits^2 - b$

где ${\text{sn}}$ – эллиптическая функция Якоби, $c = \sqrt { - 12{{b}^{2}} + 12b + 9} $, ${{C}_{1}}$ – произвольное число, b – параметр решения, такой что $0 < b < 1$. Максимальное значение $\vartheta (\xi )$ для решения (4.4) равно $ - b$. Эллиптическая функция Якоби sn является периодической функцией с периодом

$T = 4\frac{{\sqrt 6 }}{{\sqrt {6b - 3 + \sqrt { - 12{{b}^{2}} + 12b + 9} } }}K\left( {\frac{{\sqrt 3 (6b - 3 - \sqrt { - 12{{b}^{2}} + 12b + 9} )}}{{12\sqrt {{{b}^{2}} - b} }}} \right)$

и минимальным значением

${{\vartheta }_{{min}}} = - 3{\text{/}}4 + b{\text{/}}2 - 1{\text{/}}4\sqrt { - 12{{b}^{2}} + 12b + 9} $

Здесь $K(k)$ – полный эллиптический интеграл. При $b \to 0$ решение (4.4) стремится к решению (4.3) и ${{\vartheta }_{{min}}} \to - 3{\text{/}}2$, а период решения $T \to \infty $. При $b \to 1$ решение (4.4) стремится к решению (4.2), а период решения $T \to 2\pi $ (см. рис. 2). Таким образом, имеем $ - 3{\text{/}}2 < {{\vartheta }_{{min}}} < - 1$. Устойчивость решений (4.1)–(4.3) исследована в [6, 7]. Свойства оператора Штурма–Лиувилля для возмущения решения (4.4) аналогичны свойствам этого оператора с рассеивающим потенциалом, построенным по (4.3), которые использовались в [6, 7], т.е. неустойчивый спектр является не пустым. Отсюда следует, что решение (4.4), как и решение (4.3) неустойчиво, т.е. его линейные возмущения экспоненциально растут по времени.

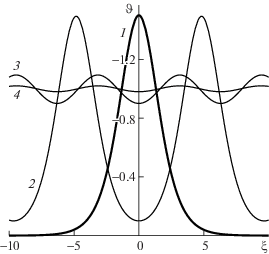
Рис. 2.

Ограниченные стационарные решения уравнения (3.2). 1 – солитоноподобное решение, 2, 3, 4 – периодические решения для $b = 0.1,0.9$ и 0.98 соответственно.

Несмотря на то что решения (4.3) и (4.4) не являются асимптотиками решений, описывающих эволюцию поверхности фазового перехода, их можно использовать для формулировки достаточного условия того, что с течением времени произойдет катастрофическая перестройка решения или что решение будет асимптотически приближаться к решению (4.1). Если существует такое b, что для любого $\xi $ в начальный момент выполняется неравенство

(4.5)

$\vartheta (\xi ,0) > {{\vartheta }_{4}}(\xi )$

то $\vartheta (\xi ,\tau ) \to 0$ при $\tau \to \infty $. Подобные возмущения изображены на рис. 3 и рис. 4 линиями 3 и 2 соответственно. Таким образом, стационарное решение ${{\vartheta }_{1}}$ (4.1) устойчиво по отношению к конечным возмущениям, удовлетворяющим неравенству (4.5). Неравенство (4.5) является достаточным условием затухания возмущения, которое наложено на устойчивое стационарное решение с плоским фронтом фазового перехода. Это условие заведомо выполняется в следующем случае. Пусть в начальный момент $\hat {\vartheta }$ есть минимальное значение возмущения $\vartheta (\xi ,0)$, которое достигается при $\xi = \hat {\xi }$. Тогда достаточно проверить выполнение условия (4.5) для $\hat {b}$ и C₁ = = $ - \hat {\xi } + \sqrt 3 {\text{/}}{{\hat {b}}^{{ - 1}}}$, где $\hat {b}$ – решение уравнения

$\hat {\vartheta } = - 3{\text{/}}4 + \hat {b}{\text{/}}2 - 1{\text{/}}4\sqrt { - 12{{{\hat {b}}}^{2}} + 12\hat {b} + 9} .$

Рис. 3.

Спектрально неустойчивое стационарное солитоноподобное решение (1), начальное возмущение, приводящее к катастрофической перестройке решения (2), затухающее начальное возмущение (3).

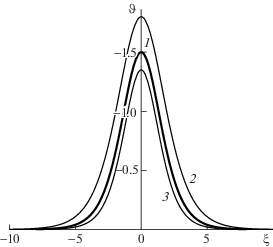
Рис. 4.

Спектрально неустойчивое периодическое стационарное решение (1), затухающее начальное возмущение (2).

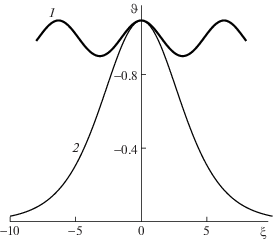
Условие (4.5) выполняется для возмущения, показанного на рис. 3 линией 3, и не выполняется для возмущения, показанного линией 2. Линия 1 соответствует солитоноподобному стационарному спектрально неустойчивому решению. Возмущение, которое показано линией 3, эволюционирует в плоский фронт с $\vartheta = 0$, а возмущение 2 приведет к катастрофической перестройке решения. Для неустойчивого периодического фронта 1 на рис. 4 возмущение 2 плоского устойчивого фронта затухает, поскольку, как уже упоминалось, оно удовлетворяет условию (4.5).

ЗАКЛЮЧЕНИЕ

В слабонелинейном приближении уравнение для эволюции фронта фазового перехода сводится к уравнению Колмогорова-Петровского-Пискунова (КПП). При выводе этого уравнения сделано предположение, что движение фронта является наиболее медленным процессом и в каждый момент времени распределение влажности воздуха близко к стационарному. Это позволяет для описания процесса диффузии использовать не параболическое, как в работах [6, 7], а эллиптическое уравнение для насыщенности. Для такого случая уравнение для поверхности фронта фазового перехода в слабонелинейном приближении получено впервые. Полученное приближенное уравнение предсказывает существование стационарных решений в основной задаче. Такими решениями являются два решения для плоского фронта, одно солитоноподбное решение и семейство периодических решений, описываемых эллиптическими функциями. На существование подобных в решений в слабонелинейном приближении для случая, когда диффузия пара описывается параболическим уравнением, ранее указывалось в [6]. Все найденные решения, кроме одного решения для плоского фронта, являются спектрально неустойчивыми и не могут возникнуть в результате асимптотического приближения решения, которое имело начальные условия, отличные от тех, которые совпадают с этим неустойчивым стационарным решением. Любое конечное начальное возмущение спектрально устойчивого решения либо асимптотически затухает, либо приводит к катастрофической перестройке течения, а именно: образованию пальца и прорыву воздуха к верхней границе малопроницаемого слоя пористой среды.

Показано, что приближенные стационарные решения (удовлетворяющие модельному уравнению КПП (4.1)) определяют затухающие локализованные возмущения конечной амплитуды условием (4.5). Эти стационарные решения могут с хорошей точностью использоваться для предсказания того, по какому сценарию пойдет развитие возмущения, если это возмущение не имеет общих точек ни с одним стационарным решением. Если начальное положение фронта фазового перехода находится между спектрально устойчивым решением и любым из стационарных решений, то оно затухает. Если начальное положение фронта находится выше хотя бы одного спектрально неустойчивого стационарного решения, то происходит катастрофическая перестройка решения. Отношение полученных результатов к эволюции локализованных конечных возмущений устойчивой плоской поверхности фазового перехода в случае полной задачи (1.10) является предметом следующей публикации на эту тему.

Данное исследование выполнено при финансовой поддержке гранта РНФ № 16-11-10195.

Список литературы

Rayleigh L. Investigation of the character of the equilibrium of an incompressible heavy fluid of variable density// Proc. London Math. Soc. 1883. V. 14. P. 170–177.
Saffman P.G. Exact solutons for the growth of fingers from a flat interface between two fluids in a porous medium or Hele-Shaw cell// Quart. Journ. Mech. and Applied Math. 1959. V. 12. P. 146–150.
Il’ichev A.T., Tsypkin G.G., Pritchard D., Richardson C.N. Instability of the salinity profile during the evaporation of saline groundwater// Journal of Fluid Mechanics. 2008. V. 614. P. 87–104.
Sahli A., Moyne C., Stemmelen D. Boiling stability in a porous medium heated from below //Int. J. Heat Mass Transfer. 2010. V. 82. P. 527–545.
Straus J.M., Schubert G. One-dimensional model of vapor-dominated geothermal systems// J. Geophys. Res. 1981. V. 86. P. 9433–9438.
Il’ichev A., Tsypkin G. Catastrophic transition to instability of evaporation front in a porous medium// Eur. J. Mech. B/Fluids. 2008.V. 27. P. 665–677.
Ильичев А.Т., Цыпкин Г.Г. Неустойчивости однородных фильтрационных течений с фазовым переходом// ЖЭТФ. 2008. Т. 134. С. 815–830, (пер. Il’ichev A.T., Tsypkin G.G. Instabilities of uniform filtration flows with phase transition // JETP. 2008. V. 107. I. 4. P. 699–711.
Ильичев А.Т., Шаргатов В.А. Динамика фронтов испарения воды// Ж. вычисл. матем. и матем. физ. 2013. Т. 53. № 9. С. 1531–1553, (пер. Il’ichev A.T., Shargatov V.A. Dynamics of Water Evaporation Fronts // Computational Mathematics and Mathematical Physics. 2013. V. 53. № 9. P. 1350–1370).
Shargatov V.A., Il’ichev A.T., Tsypkin G.G. Dynamics and stability of moving fronts of water evaporation in a porous medium //Int. J. Heat and Mass Transfer. 2015. V. 83. P. 552–561.
Lippoth F., Prokert G. Well-posedness for a moving boundary vodel of an evaporation front in a porous medium// Journal of Mathematical Fluid Mechanics. 2019. V. 21.
Шаргатов В.А. О неустойчивости фронта фазового перехода жидкость-пар в неоднородных пористых смачиваемых средах// Изв. РАН. МЖГ. 2017. № 1. С. 148–159, (пер. Shargatov V.A., Instability of a liquid-vapor phase transition front in inhomogeneous wettable porous media// Fluid Dynamics. 2017. V. 52. P. 146–157).
Tsypkin G.G., Shargatov V.A. Influence of capillary pressure gradient on connectivity of flow through a porous medium // Int. J. Heat Mass Transfer. 2018. V. 127. P. 1053–1063.
Шаргатов В.А., Цыпкин Г.Г., Богданова Ю.А. Фрагментация фильтрационного течения в среде с градиентом капиллярного давления // Доклады Академии наук. 2018. Т. 480. № 1. С. 40–44, (Shargatov V.A., Tsypkin G.G., Bogdanova Yu. A. Filtration-Flow Fragmentation in Medium with Capillary-Pressure Gradient // Doklady Physics. 2018. V. 63. № 5. P. 199–202.)
Цыпкин Г.Г. Неустойчивость фронта фазового перехода при инжекции воды в высокотемпературные породы // Труды Математического института им. В.А. Стеклова РАН. 2018. Т. 300. № 1. С. 197–204, (Tsypkin G.G. Instability of the Phase Transition Front during Water Injection into High-Temperature Rock Article//Proceedings of the Steklov Institute of Mathematics. V. 300. № 1. P. 189–195.)
Цыпкин Г.Г. Об устойчивости поверхностей испарения и конденсации в пористой среде// Изв. РАН. МЖГ. 2017. № 6. С. 70–78 (Tsypkin G.G. Stability of the evaporation and condensation surfaces in a porous medium//Fluid Dynamics. 2017. V. 52. № 6. P. 777–785.)
Khan Z.H., Pritchard D. Liquid vapour fronts in porous media: Multiplicity and stability of front positions // Int. J. Heat Mass Transfer. 2013. V. 61. P. 1–17.
Khan Z.H., Pritchard D. Anomaly of spontaneous transition to instability of liquid-vapour front in a porous medium //Int. J. Heat Mass Transfer. 2015. V. 84. P. 448–455.
Shargatov V.A., Gorkunov S.V., Il’ichev A.T. Dynamics of front-like water evaporation phase transition interfaces // Communications in Nonlinear Science and Numerical Simulation. 2019. V. 67. P. 223–236.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал