Известия РАН. Механика жидкости и газа, 2020, № 2, стр. 12-18

К ЗАДАЧЕ ОБ ОБТЕКАНИИ КРУГОВОЙ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ

А. Г. Хакимов^*

Институт механики им. Р.Р. Мавлютова УФИЦ РАН
Уфа, Россия

Поступила в редакцию 13.09.2019
После доработки 08.10.2019
Принята к публикации 08.10.2019

DOI: 10.31857/S0568528120020073

Аннотация

Представлены результаты моделирования струйного безотрывного обтекания упругой цилиндрической оболочки с нелинейными граничными условиями. Учитывается действие среднего давления на оболочку. Решение получено в виде рядов по степеням параметра аэрогидроупругости. Приводятся формы поперечного сечения оболочки, распределение давлений на деформированной и недеформированной оболочках, распределение безразмерного изгибающего момента, перерезывающей силы, усилия натяжения.

Ключевые слова: безотрывное обтекание, цилиндрическая оболочка, параметры аэрогидроупругости, среднее давление, форма оболочки, усилия, момент

Н.Е. Жуковский, первым исследовавший струйные течения с учетом капиллярных сил, построил точное решение задачи о симметричном обтекании газового пузыря в прямолинейном канале [1]. В работах [2, 3] исследованы задачи о струйном обтекании упругой пластины и цилиндрической оболочки малой кривизны. В линеаризованной постановке названная задача рассматривалась в [4]. Нелинейные граничные условия и некоторые численные результаты впервые получены в [5]. В [6] доказана теорема о существовании и единственности решения нелинейной задачи при заданных условиях на параметры и решение может быть найдено методом простых итераций при любом начальном приближении.

1. ПОСТАНОВКА ЗАДАЧИ

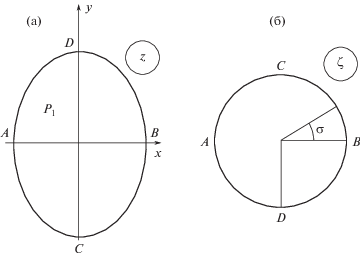
Рассматривается поперечное обтекание круговой цилиндрической оболочки плоским безграничным потоком идеальной несжимаемой невесомой жидкости плотностью ρ с учетом действия среднего давления (рис. 1a).

Рис. 1.

Плоскость течения z и вспомогательная плоскость ζ.

Ставится задача определения формы оболочки, поля скоростей течения жидкости, усилий и моментов в оболочке, если заданы давление внутри оболочки ${{P}_{1}}$, полное давление в потоке $P{\text{*}}$, скорость жидкости на бесконечности ${{V}_{\infty }}$.

Ось x направим по потоку, а начало координат совместим с точкой пересечения вертикальной оси симметрии с линией поперечного сечения оболочки (рис. 1a).

В качестве параметрической области примем круг единичного радиуса на плоскости вспомогательного переменного ζ, причем потребуем, чтобы линии поперечного сечения оболочки соответствовала дуга окружности ${{\zeta }^{{i\sigma }}}$, $0 \leqslant \sigma \leqslant 2\pi $, а бесконечно удаленной точке потока – точка $\zeta = 0$ (рис. 1б).

Комплексный потенциал W на плоскости единичного круга имеет вид

(1.1)

$W = N{{V}_{\infty }}\left( {\zeta + \frac{1}{\zeta }} \right)$

где N – характерный размер деформированной оболочки.

Когда жесткость оболочки стремится к бесконечности, функция, отображающая круг единичного радиуса в плоскости ζ на область течения в плоскости $z = x + iy$, записывается

(1.2)

$z = f\left( \zeta \right) = \frac{{{{R}_{0}}}}{\zeta }$

где ${{R}_{0}}$ – радиус круговой недеформированной оболочки, i – мнимая единица.

Безразмерная комплексно-сопряженная скорость при обтекании недеформированной оболочки также находится из выражений (1.1), (1.2)

$\frac{1}{{{{V}_{\infty }}}}\frac{{dW}}{{dz}} = \frac{N}{{{{R}_{0}}}}(1 - {{\zeta }^{2}})$

индекс 0 относится к величинам при недеформированной оболочке. В общем случае, когда цилиндрическая жесткость оболочки имеет конечную величину и деформированная оболочка остается гладкой, безразмерную комплексно-сопряженную скорость будем определять в виде [2]

(1.3)

$\frac{1}{{{{V}_{\infty }}}}\frac{{dW}}{{dz}} = \frac{N}{{{{R}_{0}}}}(1 - {{\zeta }^{2}})\exp \left( { - \omega (\zeta )} \right)$

Здесь $\omega (\zeta )$ – функция, аналитическая в круге $\zeta \leqslant 1$ и обращается в нуль при ζ = 0. Из условий на бесконечности (ζ = 0): V(ζ) = 0 и вычет функции dz/dζ = 0 следует, что аналитическая функция $\omega (\zeta )$ представима в виде ряда

(1.4)

$\omega (\zeta ) = \sum\limits_{n = 1}^\infty {{{c}_{n}}{{\zeta }^{n}}} $

с комплексными коэффициентами ${{c}_{n}} = {{a}_{n}} + i{{b}_{n}}$. Форма деформируемой поверхности находится из выражений (1.1), (1.3)

(1.5)

$\frac{{dz}}{{d\zeta }} = - \frac{N}{{{{\zeta }^{2}}}}\exp \left( {\omega (\zeta )} \right).$

Для элемента деформированной оболочки запишем уравнения равновесия [7] с учетом действия среднего давления [8, 9]

(1.6)

$\frac{{dT}}{{ds}} + \frac{Q}{R} = 0$

(1.7)

$\frac{{dQ}}{{ds}} - \frac{T}{R} + {{P}_{1}} - P - \frac{{\left( {{{P}_{1}} + P} \right)h}}{{2R}} = 0$

(1.8)

$\,\,Q = \frac{{dM}}{{ds}}$

где T, Q, M – усилие натяжения, перерезывающая сила и изгибающий момент, R, s – радиус кривизны и длина дуги поперечного сечения оболочки, P – давление в жидкости, которое определяется из уравнения Бернулли

$P = P{\text{*}} - \frac{{\rho {{V}^{2}}}}{2}$

где ρ, V – плотность и скорость жидкости на поверхности оболочки. Изгибающий момент определяется

(1.9)

$M = D\left( {\frac{1}{R} - \frac{1}{{{{R}_{u}}}}} \right),\quad D = \frac{{E{{h}^{3}}}}{{12(1 - {{\nu }^{2}})}}$

где E, ν, h – модуль упругости, коэффициент Пуассона и толщина оболочки, D – цилиндрическая изгибная жесткость оболочки, R_u – радиус кривизны в недеформированном начальном состоянии. Из (1.6) с учетом (1.8) и (1.9) следует

(1.10)

$T = {{T}_{1}} - \frac{D}{2}\left( {\frac{1}{{{{R}^{2}}}} - \frac{1}{{R_{1}^{2}}}} \right)$

где T₁, R₁ – усилие натяжения и радиус кривизны линии поперечного сечения деформированной оболочки в точке A. Уравнение (1.7) с учетом (1.8)–(1.10), R = ds/dθ и уравнения Бернулли запишется

(1.11)

$\begin{gathered} \frac{{{{d}^{3}}\theta }}{{d{{s}^{3}}}} + \frac{1}{2}{{\left( {\frac{{d\theta }}{{ds}}} \right)}^{3}} - \frac{\alpha }{{{{N}^{2}}}}\frac{{d\theta }}{{ds}} - \frac{{\left( {{{P}_{1}} + P{\text{*}}} \right)h}}{{2D}}\frac{{d\theta }}{{ds}} + \frac{{\rho {{V}^{2}}h}}{{4D}}\frac{{d\theta }}{{ds}} + \frac{{{{P}_{1}} - P{\text{*}}}}{D} + \frac{{\rho {{V}^{2}}}}{{2D}} = 0 \\ \alpha = {{N}^{2}}\left( {\frac{1}{{2R_{1}^{2}}} + \frac{{{{T}_{1}}}}{D}} \right) \\ \end{gathered} $

Здесь θ – угол между осью x и касательной к линии поперечного сечения оболочки. Угол θ, скорость на поверхности оболочки V, элемент длины дуги ds находятся из выражений (1.3)–(1.5). Полагая $\zeta = \exp \left( {i\sigma } \right)$, получим

(1.12)

$\begin{gathered} \theta = {{\theta }_{0}} + \mu ,\quad V = {{V}_{\infty }}g{{e}^{{ - \lambda }}}{\text{,}}\quad ds = - N{{e}^{\lambda }}d\sigma ,\quad {{\theta }_{0}} = \frac{\pi }{2} - \sigma ;\quad 0 < \sigma < \pi \\ {{\theta }_{0}} = \frac{{3\pi }}{2} - \sigma ,\quad 0 < \sigma < 2\pi ,\quad g = \left| {2\sin \sigma } \right| \\ \end{gathered} $

Здесь λ, μ – действительная и мнимая части функции $\omega \left( {\exp \left( {i\sigma } \right)} \right)$. Дифференциальное уравнение (1.11) с учетом соотношений (1.12) и h/R₀ = δ записывается

(1.13)

$\begin{gathered} \mu {\text{'''}} - 3\lambda {\text{'}}\mu {\text{''}} + \left[ { - \lambda {\text{''}} + 2\lambda {{{\text{'}}}^{2}} + \frac{1}{2}{{{\left( {\mu {\text{'}} - 1} \right)}}^{2}} - \alpha {{e}^{{2\lambda }}} - \left( {{{\beta }_{m}}{{e}^{{2\lambda }}} - \frac{{{{g}^{2}}}}{2}} \right){{e}^{\lambda }}\gamma \delta } \right]\left( {\mu {\text{'}} - 1} \right) - (\beta {{e}^{{2\lambda }}} + {{g}^{2}}){{e}^{\lambda }}\gamma = 0 \\ \beta = \frac{{2\left( {{{P}_{1}} - P{\text{*}}} \right)}}{{\rho V_{\infty }^{2}}},\quad {{\beta }_{m}} = \frac{{{{P}_{1}} + P{\text{*}}}}{{\rho V_{\infty }^{2}}},\quad \gamma = \frac{{\rho V_{\infty }^{2}{{N}^{3}}}}{{2D}} \\ \end{gathered} $

Здесь β, β_m γ – параметры аэрогидроупругости. Штрихи обозначают производную по переменной σ. Условия для дифференциального уравнения (1.13). На оси симметрии поперечного сечения оболочки в точках С и Д угол θ = 0, также равна нулю перерезывающая сила Q, поэтому при $\sigma = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$, $\sigma = {{3\pi } \mathord{\left/ {\vphantom {{3\pi } 2}} \right. \kern-0em} 2}$: $\mu = \mu {\text{''}} = 0$. Когда оболочка имеет две оси симметрии, то функция ω(ζ) представима в виде ряда

(1.14)

$\omega \left( \zeta \right) = \sum\limits_{n = 1}^\infty {{{a}_{{2n}}}{{\zeta }^{{2n}}}} $

поэтому на единичной окружности ζ = exp(iσ) справедливы выражения

$\begin{gathered} \lambda \left( \sigma \right) = \lambda \left( {\pi - \sigma } \right),\quad \mu \left( \sigma \right) = - \mu \left( {\pi - \sigma } \right) \\ \lambda {\text{'}}\left( \sigma \right) = - \lambda {\text{'}}\left( {\pi - \sigma } \right),\quad \mu {\text{'}}\left( \sigma \right) = \mu {\text{'}}\left( {\pi - \sigma } \right) \\ \lambda {\text{''}}\left( \sigma \right) = \lambda {\text{''}}\left( {\pi - \sigma } \right),\quad \mu {\text{''}}\left( \sigma \right) = - \mu {\text{''}}\left( {\pi - \sigma } \right) \\ \end{gathered} $

2. РЕШЕНИЕ В ВИДЕ РЯДОВ ПО СТЕПЕНЯМ ПАРАМЕТРА γ

Пусть γ = 0, тогда уравнение (1.13) удовлетворится, если положить ω(ζ) = 0 (λ = μ = 0), α = α₀, N = N₀ = R₀. В общем случае ω(ζ), λ, μ, α, N зависят от γ. Считая эти зависимости аналитическими в окрестности γ = 0, будем искать решение в виде рядов по степеням параметра аэрогидроупругости γ

(2.1)

$\omega \left( \zeta \right) = \sum\limits_{k = 1}^\infty {{{\gamma }^{k}}{{\omega }_{k}}\left( \zeta \right)} ,\,\,\,\alpha = {{\alpha }_{u}} + \sum\limits_{k = 1}^\infty {{{\gamma }^{k}}{{\alpha }_{k}}} $

На единичной окружности ζ = exp(iσ):

${{\omega }_{k}}\left( {\exp \left( {i\sigma } \right)} \right) = {{\lambda }_{k}}\left( \sigma \right) + i{{\mu }_{k}}\left( \sigma \right)$

Из (1.14) следует

(2.2)

${{\lambda }_{k}}\left( \sigma \right) = \sum\limits_{n = 1}^k {a_{{2n}}^{k}\cos 2n\sigma } ,\quad {{\mu }_{k}}\left( \sigma \right) = \sum\limits_{n = 1}^k {a_{{2n}}^{k}\sin 2n\sigma } $

Подставляя (2.1) в (1.14), далее в (1.13) и сравнивая коэффициенты при γ^k (k = 1, 2,…), получим бесконечную систему уравнений вида

$\begin{gathered} \mu _{k}^{{'''}} + \lambda _{k}^{{''}} + \left( {\frac{3}{2} - {{\alpha }_{u}}} \right)\mu _{k}^{'} + 2{{\alpha }_{u}}{{\lambda }_{k}} + {{\alpha }_{k}} = {{G}_{k}},\quad k = 1,2,3,... \\ {{G}_{1}} = 4\left( {1 + {{h{\text{*}}} \mathord{\left/ {\vphantom {{h{\text{*}}} 2}} \right. \kern-0em} 2}} \right){{\sin }^{2}}\sigma + \beta - {{\beta }_{m}}\delta \\ {{G}_{2}} = 3\lambda _{1}^{'}\mu _{1}^{{''}} + \lambda _{1}^{{''}}\mu _{1}^{'} + 2{{(\lambda _{1}^{'})}^{2}} + \frac{3}{2}{{(\mu _{1}^{'})}^{2}} - 2{{\alpha }_{u}}\lambda _{1}^{2} + 2{{\alpha }_{u}}{{\lambda }_{1}}\mu _{1}^{'} - 2{{\alpha }_{1}}{{\lambda }_{1}} + \\ \end{gathered} $

(2.3)

$\begin{gathered} \, + {{\alpha }_{1}}\mu _{1}^{'} + 3\left( {\beta - {{\beta }_{m}}\delta } \right){{\lambda }_{1}} + {{\beta }_{m}}\delta \mu _{1}^{'} + 4\left( {1 + {\delta \mathord{\left/ {\vphantom {\delta 2}} \right. \kern-0em} 2}} \right){{\lambda }_{1}}{{\sin }^{2}}\sigma - 2\delta \mu _{1}^{'}{{\sin }^{2}}\sigma \\ {{G}_{3}} = 2{{\alpha }_{u}}{{\lambda }_{2}}\mu _{1}^{'} + 2{{\alpha }_{1}}{{\lambda }_{1}}\mu _{1}^{'} + 2{{\alpha }_{u}}{{\lambda }_{1}}\mu _{2}^{'} - \frac{4}{3}{{\alpha }_{u}}\lambda _{1}^{3} + 2{{\alpha }_{u}}\lambda _{1}^{2}\mu _{1}^{'} - 4{{\alpha }_{u}}{{\lambda }_{1}}{{\lambda }_{2}} - \\ \, - 2{{(\lambda _{1}^{'})}^{2}}\mu _{1}^{'} + 4\lambda _{1}^{'}\lambda _{2}^{'} + 3\mu _{1}^{'}\mu _{2}^{'} + {{\alpha }_{2}}\mu _{1}^{'} + {{\alpha }_{1}}\mu _{2}^{'} - 2{{\alpha }_{1}}\lambda _{1}^{2} - 2{{\alpha }_{2}}{{\lambda }_{1}} - 2{{\alpha }_{1}}{{\lambda }_{2}} + \\ \end{gathered} $

$\begin{gathered} \, + \lambda _{2}^{{''}}\mu _{1}^{'} + \lambda _{1}^{{''}}\mu _{2}^{'} + 3\lambda _{2}^{'}\mu _{1}^{{''}} + 3\lambda _{1}^{'}\mu _{2}^{{''}} + 3\left( {\beta - {{\beta }_{m}}\delta } \right){{\lambda }_{2}} + \frac{9}{2}\left( {\beta - {{\beta }_{m}}\delta } \right)\lambda _{1}^{2} + \\ \, + {{\beta }_{m}}\delta (\mu _{2}^{'} + 3{{\lambda }_{1}}\mu _{1}^{'}) + 4{{\lambda }_{2}}\left( {1 + {\delta \mathord{\left/ {\vphantom {\delta 2}} \right. \kern-0em} 2}} \right){{\sin }^{2}}\sigma + 2\lambda _{1}^{2}\left( {1 + {\delta \mathord{\left/ {\vphantom {\delta 2}} \right. \kern-0em} 2}} \right){{\sin }^{2}}\sigma - \\ \, - 2\delta (\mu _{2}^{'} + {{\lambda }_{1}}\mu _{1}^{'}){{\sin }^{2}}\sigma - \frac{1}{2}{{(\mu _{1}^{'})}^{3}} \\ \end{gathered} $

Функция G_k разлагается в ряд Фурье по косинусам

(2.4)

${{G}_{k}} = \sum\limits_{n = 0}^k {G_{{2n}}^{k}\cos 2n\sigma } .$

В табл. 1 приводятся значения коэффициентов $G_{{2n}}^{k}$ для β = 0, β_m = 1, δ = 0.01.

Таблица 1

k	n = 0	2	4	6
1	–1.99	–2.01	0	0
2	–1.449111	2.452199	1.045200	0
3	–1.489232	–0.414129	2.486437	–0.293890

Подставляя в (2.3), (2.2), (2.4) и сравнивая коэффициенты при косинусах с одинаковыми аргументами, получим систему алгебраических уравнений, решение которой имеет вид

${{\alpha }_{k}} = G_{0}^{k},\quad a_{{2n}}^{k} = - \frac{{G_{{2n}}^{k}}}{{8{{n}^{3}} + 4{{n}^{2}} - \left( {3 - 2{{\alpha }_{u}}} \right)n - 2{{\alpha }_{u}}}}$

Значения коэффициентов ${{\alpha }_{k}},\,\,a_{{2n}}^{k}$ даются в табл. 2 для β = 0, β_m = 1, δ = 0.01.

Таблица 2

k	α_k	$a_{2}^{k}$	$a_{4}^{k}$	$a_{6}^{k}$
1	1.99	0.22333	0	0
2	–1.449111	–0.272466	0.013936	0
3	–1.489232	–0.046014	–0.033152	0.001199

Постоянная N находится из условия нерастяжимости срединной поверхности оболочки

$N = \frac{{\pi {{R}_{0}}}}{{2\int\limits_0^{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} {{{e}^{\lambda }}d\sigma } }}$

Функция ω(ζ) с точностью до γ³ включительно находится

$\omega \left( \zeta \right) = \gamma a_{2}^{1}{{\zeta }^{2}} + {{\gamma }^{2}}(a_{2}^{2}{{\zeta }^{2}} + a_{4}^{2}{{\zeta }^{4}}) + {{\gamma }^{3}}(a_{2}^{3}{{\zeta }^{2}} + a_{4}^{3}{{\zeta }^{4}} + a_{6}^{3}{{\zeta }^{6}})$

Разлагая в ряд exp(ω(ζ)), получим

$\begin{gathered} \exp \omega \left( \zeta \right) = 1 + \gamma a_{2}^{1}{{\zeta }^{2}} + {{\gamma }^{2}}[a_{2}^{2}{{\zeta }^{2}} + (a_{4}^{2} + {{{{{(a_{2}^{1})}}^{2}}} \mathord{\left/ {\vphantom {{{{{(a_{2}^{1})}}^{2}}} 2}} \right. \kern-0em} 2}){{\zeta }^{4}}] + \\ \, + {{\gamma }^{3}}[a_{2}^{3}{{\zeta }^{2}} + (a_{4}^{3} + a_{2}^{1}a_{2}^{2}){{\zeta }^{4}} + (a_{6}^{3} + a_{2}^{1}a_{4}^{2} + {{{{{(a_{2}^{1})}}^{3}}} \mathord{\left/ {\vphantom {{{{{(a_{2}^{1})}}^{3}}} 6}} \right. \kern-0em} 6}){{\zeta }^{6}}] \\ \end{gathered} $

Функция z(ζ) определяется, интегрируя (1.5), получим

(2.5)

$\begin{gathered} z\left( \zeta \right) = N\left[ {\frac{1}{\zeta } - \gamma a_{2}^{1}\zeta - {{\gamma }^{2}}\left( {a_{2}^{2}\zeta + \frac{{a_{4}^{2} + {{{{{(a_{2}^{1})}}^{2}}} \mathord{\left/ {\vphantom {{{{{(a_{2}^{1})}}^{2}}} 2}} \right. \kern-0em} 2}}}{3}{{\zeta }^{3}}} \right) - } \right. \\ \, - \left. {{{\gamma }^{3}}\left( {a_{2}^{3}\zeta + \frac{{a_{4}^{3} + a_{2}^{1}a_{2}^{2}}}{3}{{\zeta }^{3}} + \frac{{6a_{6}^{3} + 6a_{2}^{1}a_{4}^{2} + {{{(a_{2}^{1})}}^{3}}}}{{30}}{{\zeta }^{5}}} \right)} \right] \\ \end{gathered} $

3. ФОРМА ОБОЛОЧКИ

Форма деформированной оболочки находится из (2.5) при ζ = exp(iσ):

$\begin{gathered} x = N\left[ {\cos \sigma - \gamma a_{2}^{1}\cos \sigma - {{\gamma }^{2}}\left( {a_{2}^{2}\cos \sigma + \frac{{2a_{4}^{2} + {{{(a_{2}^{1})}}^{2}}}}{6}\cos 3\sigma } \right) - } \right. \hfill \\ - \left. {{{\gamma }^{3}}\left( {a_{2}^{3}\cos \sigma + \frac{{a_{4}^{3} + a_{2}^{1}a_{2}^{2}}}{3}\cos 3\sigma + \frac{{a_{6}^{3} + a_{2}^{1}a_{4}^{2} + {{{{{(a_{2}^{1})}}^{3}}} \mathord{\left/ {\vphantom {{{{{(a_{2}^{1})}}^{3}}} 6}} \right. \kern-0em} 6}}}{5}\cos 5\sigma } \right)} \right] \hfill \\ \end{gathered} $

(3.1)

$\begin{gathered} y = N\left[ {\sin \sigma + \gamma a_{2}^{1}\sin \sigma + {{\gamma }^{2}}\left( {a_{2}^{2}\sin \sigma + \frac{{2a_{4}^{2} + {{{(a_{2}^{1})}}^{2}}}}{6}\sin 3\sigma } \right) + } \right. \\ \, + \left. {{{\gamma }^{3}}\left( {a_{2}^{3}\sin \sigma + \frac{{a_{4}^{3} + a_{2}^{1}a_{2}^{2}}}{3}\sin 3\sigma + \frac{{6a_{6}^{3} + 6a_{2}^{1}a_{4}^{2} + {{{(a_{2}^{1})}}^{3}}}}{{30}}\sin 5\sigma } \right)} \right] \\ \end{gathered} $

На рис. 2 приводятся формы поперечного сечения оболочек для β = 0, β_m = 1, δ = 0.01, определенные по формулам (3.1) с учетом одного, двух, трех членов разложения решения в ряд по степеням γ (пунктирная, штриховая, сплошная линии соответственно). Форма оболочки, определенная с учетом одного члена разложения в ряд по степеням γ, незначительно отличается от формы, определенной с учетом двух и трех членов. Формы поперечного сечения оболочек, определенные с учетом двух и трех членов разложения в ряд по степеням γ, практически совпадают. Формы оболочек для β = 0, β_m = 1, δ = 0.01 при различных γ = 0.2; 0.1; 0 (пунктирная, штриховая, сплошная линии соответственно) приводятся на рис. 3. С увеличением параметра аэрогидроупругости γ оболочки вытягиваются в направлении, перпендикулярном скорости потока на бесконечности.

Рис. 2.

Формы поперечного сечения оболочек, определенные по формулам (3.1) с учетом одного, двух, трех членов разложения решения в ряд по степеням γ (пунктирная, штриховая, сплошная линии соответственно): β = 0, β_m = 1, δ = 0.01.

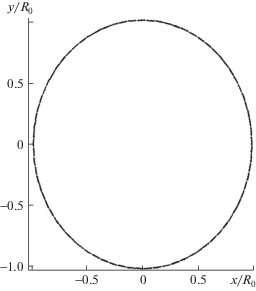
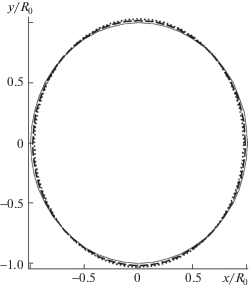
Рис. 3.

Формы поперечного сечения оболочек при различных γ = 0.2; 0.1; 0 (пунктирная, штриховая, сплошная линии соответственно): β = 0, β_m = 1, δ = 0.01.

Длина дуги линии поперечного сечения оболочки, отсчитываемая от точки C, находится интегрированием модуля dz:

$\begin{gathered} s = N\left[ {\sigma + \gamma \frac{{a_{2}^{1}}}{2}\sin \sigma + \frac{{{{\gamma }^{2}}}}{4}\left( {{{{(a_{2}^{1})}}^{2}}\sigma + 2a_{2}^{2}\sin 2\sigma + \frac{{4a_{4}^{2} + {{{(a_{2}^{1})}}^{2}}}}{4}\sin 4\sigma } \right) + {{\gamma }^{3}}} \right.\left( {a_{2}^{1}a_{2}^{2}\sigma {{ + }_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}}}}}}}} \right. \\ \,\left. {\left. { + \left( {a_{2}^{3} + \frac{{a_{2}^{1}a_{4}^{2}}}{2} + \frac{{{{{(a_{2}^{1})}}^{3}}}}{8}} \right)\sin 2\sigma + \frac{1}{4}\left( {a_{4}^{3} + \frac{{a_{2}^{1}a_{2}^{2}}}{2}} \right)\sin 4\sigma + \frac{1}{6}\left( {a_{6}^{3} + \frac{{a_{2}^{1}a_{4}^{2}}}{2} + \frac{{{{{(a_{2}^{1})}}^{3}}}}{{24}}} \right)\sin 6\sigma } \right)} \right] \\ \end{gathered} $

4. РАСПРЕДЕЛЕНИЕ ДАВЛЕНИЙ

Коэффициент давления ${{C}_{p}}$ в жидкости на поверхности оболочки определяется

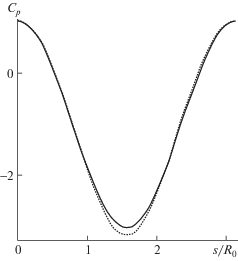
${{C}_{p}} = 2\frac{{P - {{P}_{\infty }}}}{{\rho V_{\infty }^{2}}} = 1 - 4\sin {{\sigma }^{2}}{\text{exp}}\left( { - 2\lambda } \right).$

Распределение давлений на оболочке дается рис. 4 для β = 0, β_m = 1, δ = 0.01, γ = 0.1; 0 (пунктирная, сплошная линии соответственно). Деформация оболочки вызывает уменьшение давления в точках, удаленных от оси x и увеличение давления в окрестности точек А и В.

Рис. 4.

Распределение давлений на оболочке: β = 0, β_m = 1, δ = 0.01, γ = 0.1, 0 (пунктирная, сплошная линии соответственно).

5. УСИЛИЯ И МОМЕНТЫ В ОБОЛОЧКЕ

Безразмерные изгибающий момент, перерезывающая сила, усилие натяжения определяются по формулам (1.8)–(1.10):

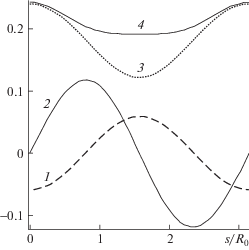
$\begin{gathered} \frac{{M{{R}_{0}}}}{D} = \frac{{1 - \mu {\text{'}}}}{{{{N}_{1}}{{e}^{\lambda }}}} - 1,\quad {{N}_{1}} = \frac{N}{{{{R}_{0}}}} \\ \frac{{QR_{0}^{2}}}{D} = \frac{{\mu {\text{''}} - \lambda {\text{'}}(\mu {\text{'}} - 1)}}{{N_{1}^{2}{{e}^{{2\lambda }}}}} \\ \frac{{TR_{0}^{2}}}{D} = \frac{1}{{N_{1}^{2}}}\left( {\alpha - \frac{{R_{0}^{2}}}{{{{R}^{2}}}}} \right) \\ \end{gathered} $

Распределение безразмерного изгибающего момента (кривая 1), перерезывающей силы (кривая 2), усилия (кривая 3 по формуле (1.7), кривая 4 по формуле (1.10) ) в оболочке для β = 0, β_m = 1, γ = 0.1, δ = 0.01 приводится на рис. 5. Видно, что усилия натяжения меньше в точках удаленных от оси x.

Рис. 5.

Распределение безразмерного изгибающего момента (кривая 1), перерезывающей силы (кривая 2), усилия в оболочке (кривая 3 по формуле (1.10), кривая 4 по формуле (1.7)): β = 0, β_m = 1, γ = 0.1, δ = 0.01.

ЗАКЛЮЧЕНИЕ

С увеличением параметра аэрогидроупругости оболочка вытягивается в направлении, перпендикулярном скорости потока на бесконечности. Деформация оболочки вызывает уменьшение давления в точках, удаленных от оси x. Усилия натяжения меньше в точках, удаленных от оси x. Решение получено с учетом действия среднего давления на оболочку.

Список литературы

Жуковский Н.Е. Определение движения жидкости при каком-нибудь условии, данном на линии тока. Собр. соч. Т. II. Гидродинамика. М.–Л.: ОГИЗ, 1949. 763 с.
Киселев О.М., Рапопорт Э.Ф. О струйном обтекании упругой пластины // Изв. АН СССР. МЖГ. 1976. № 4. С. 35–42.
Киселев О.М., Рапопорт Э.Ф. О струйном обтекании упругой оболочки // Изв. АН СССР. МЖГ. 1977. № 2. С. 24–32.
Ильгамов М.А. Изгиб и устойчивость цилиндрической оболочки при ее поперечном обтекании жидкостью // Прикл. мех. 1975.Т. 11. Вып. 3. С. 12–19.
Хакимов А.Г. Обтекание гибкой цилиндрической оболочки плоским потоком идеальной жидкости // Изв. АН СССР. МЖГ. 1975. № 6. С. 147–151. https://doi.org/10.1007/BF01023279
Киселев О.М. Безотрывное обтекание круговой цилиндрической оболочки // Тр. сем. по краев. задачам. 1982. Вып. 18. С. 104–115.
Огибалов П.М., Колтунов М.А. Оболочки и пластины. М.: Изд-во Моск. ун-та. 1969. 695 с.
Ильгамов М.А. Взаимодействие неустойчивостей в гидроупругой системе // ПММ. 2016. Т. 80. Вып. 5. С. 566–579. https://doi.org/10.1016/j.jappmathmech.2017.02.007
Ильгамов М.А. Влияние давления окружающей среды на изгиб тонкой пластины и плeнки // ДАН. 2017. Т. 476. № 4. С. 402–405. https://doi.org/10.1134/S1028335817100020

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал