Известия РАН. Механика жидкости и газа, 2020, № 4, стр. 96-104

Решение уравнений Фолкнер–Скэн для гиперзвуковых течений

И. И. Липатов^a, b, *, К. Т. Нго^a

^a Московский физико-технический институт (государственный университет),
Москва, Россия

^b Центральный аэрогидродинамический институт им. проф. Н.Е. Жуковского
Московская обл., Жуковский, Россия

^* E-mail: igor_lipatov@mail.ru

Поступила в редакцию 10.12.2019
После доработки 17.12.2019
Принята к публикации 17.12.2019

DOI: 10.31857/S0568528120040076

Полный текст (PDF)

Аннотация

Впервые получены результаты решения уравнения Фолкнера–Скэн для сжимаемых течений ${{f}^{{'''}}} + f{{f}^{{''}}} + \beta (g - f{{'}^{2}})$ = 0 в дополнение к тем, которые были найдены Хартри и Стюартсоном. Определены зависимости напряжения трения $f_{w}^{{''}}$ на стенке и градиента температуры $g_{w}^{'}$ от параметра $\beta $ при различных значениях температурного фактора g_w.

Ключевые слова: пограничный слой, сверхзвуковое течение, уравнения Фолкнера–Скэн

1. ПОСТАНОВКА ЗАДАЧИ

Рассматривается обтекание пластины потоком под нулевым углом атаки в предположении о том, что число Маха набегающего потока велико и что реализуется режим слабого гиперзвукового взаимодействия, для которого характерны следующие соотношения:

${{{\rm M}}_{\infty }} \to \infty $ ${{{\text{M}}}_{\infty }}{\tau } \ll 1$

где ${{{\rm M}}_{\infty }}$ – число Маха набегающего потока, $\tau $ – безразмерная толщина ламинарного пограничного слоя. Для декартовых координат, отсчитываемых вдоль поверхности пластины и по нормали к поверхности, времени, компонентов вектора скорости, плотности, давления, полной энтальпии, динамического коэффициента вязкости, введены следующие обозначения: lx, ly, $lt{\text{/}}{{u}_{\infty }}$, ${{u}_{\infty }}u$, ${{u}_{\infty }}{v}$, ${{\rho }_{\infty }}\rho $, ${{\rho }_{\infty }}u_{\infty }^{2}p$, $u_{\infty }^{2}H{\text{/}}2$, ${{\mu }_{0}}\mu $. Параметр l представляет собой характерную длину пластины; $\tau = {{\left( {{{\rho }_{\infty }}{{u}_{\infty }}l{\text{/}}{{\mu }_{0}}} \right)}^{{ - 1/2}}}$, где индексом “$\infty $” отличены размерные величины в набегающем потоке, μ₀ – размерная величина динамического коэффициента вязкости, вычисленного при температуре торможения. Предполагается, что газ является термодинамически совершенным и характеризуется постоянной величиной отношения удельных теплоемкостей γ. Хотя в гиперзвуковых потоках эффекты реального газа существенны, в данной работе они не рассматриваются, поскольку их учет в принципе не меняет соотношений, полученных ниже. Число Рейнольдса велико, но не превышает критической величины, при которой происходит ламинарно-турбулентный переход. Известно, что для сверх- и гиперзвуковых течений число Рейнольдса перехода достаточно велико. Предполагается также, что динамическая вязкость линейно зависит от температуры, так что ${\rho \mu } = {\text{const}}$.

2. УРАВНЕНИЯ ПОГРАНИЧНОГО СЛОЯ

Учитывая сделанные приближения, основные уравнения для ламинарного течения в двумерном пограничном слое имеют вид

Уравнение неразрывности

(2.1)

$\frac{{\partial \rho u}}{{\partial x}} + \frac{{\partial \rho {v}}}{{\partial y}} = 0$

Уравнение количества движения

(2.2)

$\rho u\frac{{\partial u}}{{\partial x}} + \rho {v}\frac{{\partial u}}{{\partial y}} = - \frac{{\partial p}}{{\partial x}} + \frac{\partial }{{\partial y}}\left( {\mu \frac{{\partial u}}{{\partial y}}} \right)$

Уравнение энергии

(2.3)

$\rho u\frac{{\partial H}}{{\partial x}} + \rho {v}\frac{{\partial H}}{{\partial y}} = \frac{\partial }{{\partial y}}\left( {\frac{\mu }{{\Pr }}\frac{{\partial H}}{{\partial y}}} \right) + \frac{\partial }{{\partial y}}\left[ {\mu \left( {1 - \frac{1}{{\Pr }}} \right)\frac{\partial }{{\partial y}}\left( {\frac{{{{u}^{2}}}}{2}} \right)} \right]$

Здесь u и ${v}$ – компоненты скорости соответственно вдоль осей x и y, x – расстояние вдоль поверхности тела, y – расстояние по нормали к поверхности тела, $h$ – удельная энтальпия, полная энтальпии $H = h + {{u}^{2}}{\text{/}}2$, Pr – число Прандтля, p – давление в пограничном слое.

Здесь индекс w использован для условий на поверхности тела и индекс e для обозначения условий на внешней границе пограничного слоя.

Граничные условия для рассматриваемой здесь задачи обтекания

$u\left( {x,0} \right) = 0,\quad {v}\left( {x,0} \right) = {{{v}}_{w}}\left( x \right),\quad H\left( {x,0} \right) = {{H}_{w}}\left( x \right)$

$\mathop {\lim }\limits_{y \to \infty } u\left( {x,y} \right) = {{u}_{e}}\left( x \right),\quad \mathop {\lim }\limits_{y \to \infty } H\left( {x,y} \right) = {{H}_{e}}\left( x \right)$

Используя преобразование Дородницына–Лиза, можно получить уравнения в новых переменных

(2.4)

$\xi \left( x \right) = \int\limits_0^x {{{\rho }_{w}}{{\mu }_{w}}{{u}_{e}}dx} ,\quad \eta \left( {x,y} \right) = \frac{{{{u}_{e}}}}{{\sqrt {2\xi } }}\int\limits_0^y {\rho dy} $

(2.5)

$f = \int\limits_0^\eta {\frac{u}{{{{u}_{e}}}}d\eta } ,\quad \frac{{\partial f}}{{\partial \eta }} = \frac{u}{{{{u}_{e}}}},\quad g = \frac{H}{{{{H}_{e}}}}$

(2.6)

$\frac{\partial }{{\partial \eta }}\left( {N\frac{{{{\partial }^{2}}f}}{{\partial {{\eta }^{2}}}}} \right) + f\frac{{{{\partial }^{2}}f}}{{\partial {{\eta }^{2}}}} + 2\frac{{d\ln {{u}_{e}}}}{{d\ln \xi }}\left[ {\frac{{{{\rho }_{e}}}}{\rho } - {{{\left( {\frac{{\partial f}}{{\partial \eta }}} \right)}}^{2}}} \right] = 2\xi \left( {\frac{{\partial f}}{{\partial \eta }}\frac{{{{\partial }^{2}}f}}{{\partial \eta \partial \xi }} - \frac{{\partial f}}{{\partial \xi }}\frac{{{{\partial }^{2}}f}}{{\partial {{\eta }^{2}}}}} \right)$

(2.7)

$\frac{\partial }{{\partial \eta }}\left( {\frac{N}{{\Pr }}\frac{{\partial g}}{{\partial \eta }}} \right) + f\frac{{\partial g}}{{\partial \eta }} + \frac{{u_{e}^{2}}}{{{{H}_{e}}}}\frac{\partial }{{\partial \eta }}\left[ {N\left( {1 - \frac{1}{{\Pr }}} \right)\frac{{\partial f}}{{\partial \eta }}\frac{{{{\partial }^{2}}f}}{{\partial {{\eta }^{2}}}}} \right] = 2\xi \left( {\frac{{\partial f}}{{\partial \eta }}\frac{{\partial g}}{{\partial \xi }} - \frac{{\partial f}}{{\partial \xi }}\frac{{\partial g}}{{\partial \eta }}} \right)$

$N = \frac{{{\rho \mu }}}{{{{{\rho }}_{w}}{{{\mu }}_{w}}}} = {{\left( {\frac{{g - f{\kern 1pt} {{'}^{2}}}}{{{{g}_{w}}}}} \right)}^{{{\omega } - 1}}}$, ω – показатель степени в соответствующем законе зависимости вязкости от температуры.

Для случая Pr = 1 можно получить автомодельные дифференциальные уравнения пограничного слоя

(2.8)

$\left( {Nf{\kern 1pt} {\text{''}}} \right){\kern 1pt} '\, + ff{\kern 1pt} {\text{''}} + 2\frac{{d\ln {{u}_{e}}}}{{d\ln \xi }}\left( {\frac{{{{\rho }_{e}}}}{\rho } - {{f}^{'}}^{2}} \right) = 0$

(2.9)

$\left( {\frac{N}{{\Pr }}g{\text{'}}} \right)'\, + fg{\text{'}} = 0$

Индекс “штрих” используется здесь для обозначения частной производной по η. Дальнейшие упрощения уравнения (2.8) вытекают из равенства H_e = const.

Тогда уравнение (2.8) приводится к виду

(2.10)

$\left( {Nf{\kern 1pt} {\text{''}}} \right){\kern 1pt} '\, + ff{\kern 1pt} {\text{''}} + 2\frac{{d\ln {{u}_{e}}}}{{d\ln \xi }}\frac{{{{H}_{e}}}}{{h{}_{e}}}[g - {{\left( {f{\kern 1pt} {\text{'}}} \right)}^{2}}] = 0$

$2\frac{{d\ln {{u}_{e}}}}{{d\ln \xi }}\frac{{{{H}_{e}}}}{{{{h}_{e}}}} = - \frac{{\left( {\gamma - 1} \right)}}{\gamma }\frac{{\int\limits_0^x {pdx} }}{{{{p}^{2}}}}\frac{{dp}}{{dx}}$

Далее для левой части соотношения введено обозначение

$\beta = 2\frac{{d\ln {{u}_{e}}}}{{d\ln \xi }}\frac{{{{H}_{e}}}}{{{{h}_{e}}}}$

Условие автомодельности может быть выполнено только в том случае, когда распределение давления описывается степенным законом, т.е. давление пропорционально xⁿ или $p = {{c}_{1}}{{x}^{n}}$. В результате следует

$\beta = - \frac{{\gamma - 1}}{\gamma }\frac{n}{{n + 1}}$

Величина β эквивалентна классической константе Фолкнера–Скэн. Для давления пропорционального xⁿ можно переписать систему уравнений пограничного слоя в следующем виде:

(2.11)

$\left( {Nf{\kern 1pt} {\text{''}}} \right){\kern 1pt} {\text{'}} + ff{\kern 1pt} {\text{''}} + \beta (g - {{f}^{'}}^{2}) = 0$

(2.12)

$\left( {Ng{\text{'}}} \right){\text{'}} + fg{\text{'}} = 0$

с граничными условиями

(2.13)

$f\left( 0 \right) = f{\kern 1pt} {\text{'}}\left( 0 \right) = 0;\quad f{\kern 1pt} {\text{'}}\left( \eta \right) \to 1,\quad \eta \to \infty $

(2.14)

$g\left( 0 \right) = {{g}_{w}};\quad g\left( \eta \right) \to 1,\quad \eta \to \infty $

Предполагается, что N = 1.

3. ОПИСАНИЕ ВЫЧИСЛИТЕЛЬНОЙ ПРОЦЕДУРЫ

Для численного интегрирования систему (2.11) и (2.12) с граничными условиями (2.13), (2.14) можно преобразовать в систему уравнений первого порядка посредством следующих замен

$f \to {{f}_{0}};\quad f{\kern 1pt} {\text{'}} \equiv f_{0}^{'} = {{f}_{1}}$

$f{\kern 1pt} {\text{''}} \equiv \left( {{{f}_{1}}} \right){\kern 1pt} {\text{'}} = {{f}_{2}}$

(3.1)

$f{\kern 1pt} {\text{'''}} \to f_{2}^{'}$

$g \to {{f}_{3}};\quad g{\text{'}} \equiv f_{3}^{'} = {{f}_{4}}$

$g{\text{''}} \to f_{4}^{'}$

Уравнения (2.11) и (2.12) сводятся к системе обыкновенных дифференциальных уравнений первого порядка

(3.2)

$f_{0}^{'} = {{f}_{1}}$

(3.3)

$f_{1}^{'} = {{f}_{2}}$

(3.4)

$f_{2}^{'} = - {{f}_{0}}{{f}_{2}} - \beta [{{f}_{3}} - {{\left( {{{f}_{1}}} \right)}^{2}}]$

(3.5)

$f_{3}^{'} = {{f}_{4}}$

(3.6)

$f_{4}^{'} = - {{f}_{0}}{{f}_{4}}$

В векторной записи система уравнений имеет вид

(3.7)

$\frac{\partial }{{\partial \eta }}f = D\left( {\eta ,f} \right)$

где зависимая переменная и правая часть определены как вектор-функции

(3.8)

$f = \left( \begin{gathered} {{f}_{0}} \\ {{f}_{1}} \\ {{f}_{2}} \\ {{f}_{3}} \\ {{f}_{4}} \\ \end{gathered} \right);\quad D\left( {\eta ,f} \right) = \left( \begin{gathered} f{}_{1} \\ {{f}_{2}} \\ - {{f}_{0}}{{f}_{2}} - \beta [{{f}_{3}} - {{\left( {{{f}_{1}}} \right)}^{2}}] \\ {{f}_{4}} \\ - {{f}_{0}}{{f}_{4}} \\ \end{gathered} \right)$

Для решения использован следующий алгоритм:

1. Задаются некоторые значения f₂(0) и f₄(0).

2. Используется метод Рунге–Кутты для интегрирования системы уравнений (1.11), (1.12).

3. Проверяются условия

$\begin{gathered} \xi _{1}^{i} = f_{1}^{i}\left( {{{\eta }_{{\inf }}}} \right) - 1 \\ \xi _{3}^{i} = f_{3}^{i}\left( {{{\eta }_{{\inf }}}} \right) - 1 \\ \end{gathered} $

Если $\left| {\xi _{1}^{i}} \right| < {{\xi }_{1}}$ и $\left| {\xi _{3}^{i}} \right| < {{\xi }_{3}}$, решения получены. В противном случае используется модифицированный метод Ньютона.

Система уравнений решалась при различных значениях параметров. Для положительных значений β > 0 процесс итераций достаточно быстро сходится. Вычисления производились таким образом, чтобы обеспечить точность в определении поверхностного трения f₂(0) и градиента температуры на поверхности f₄(0), соответствующую трем правильным значащим цифрам. Сходимость процесса итераций при интегрировании системы уравнений контролировалась по значениям f₂(0) и f₄(0). Значение правого предела интегрирования $\eta {}_{{\inf }}$ в вариантных расчетах увеличивалось до тех пор, пока не переставали изменяться первые три значащие цифры отыскиваемых величин f₂(0) и f₄(0).

4. ОПИСАНИЕ ПОЛУЧЕННЫХ ЗАВИСИМОСТЕЙ ОТ $\beta $ И ${{g}_{w}}$

Температурный фактор задается соотношением

${{g}_{w}} = {{T}_{w}}{\text{/}}{{T}_{0}}$

Здесь T_w – температура поверхности, T₀ – температура торможения внешнего потока.

Если g_w = 1, то это случай изолированной поверхности. Тогда температура торможения остается постоянной в поперечном сечении пограничного слоя, а температура поверхности равна температуре торможения внешнего потока. В том случае, когда нет теплопередачи на стенку, частным решением уравнения (2.9), которое удовлетворяет всем граничным условиям, будет $g(\eta )$ = 1.

В настоящем исследовании получены решения для параметра β, начиная от $\beta = 1$, соответствующего отрицательному градиенту давления до значения градиента, вызывающего отрыв. Все решения определены для различных значений температурного фактора, начиная с ${{g}_{w}} = 1$ и заканчивая значением ${{g}_{w}} = 0.1$ с шагом 0.1. Ранее расчеты проводились для несжимаемых течений при ${{g}_{w}} = 1$ в [2] и [3]. Решение получено для нескольких значений температурного фактора g_w. Результаты показывают, что отрыв течения происходит при $\beta = - 0.1988$. Для $\beta < 0$ решение уравнения неединственно, одно из них характеризуется отрицательным трением на поверхности.

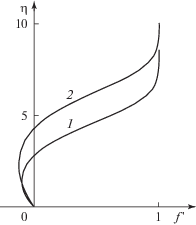
На рис. 1 приведены профили скорости в зависимости от η для случаев $\beta = - 0.1$; –0.05 с получением отрицательных значений поверхностного трения $f_{w}^{{''}}$. В обоих случаях область определения искомых функций разбивалась на две части. Одна из них соответствует скорости $f{\text{'}} < 0$ и другая $f{\text{'}} > 0$.

Рис. 1.

График распределения скорости течения при ${{g}_{w}} = 1$: 1, 2 – $\beta = - 0.1$; $ - 0.05$.

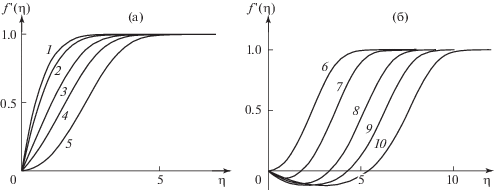
На рис. 2 приведены типичные профили скорости.

Рис. 2.

График распределения скоростей для течений с постоянной $\beta $ при ${{g}_{w}} = 1$: a – 1–5 – ${\beta } = 1$, 0.5, 0, –0.15, $ - 0.1988$; б – 6–10 – ${\beta } = - 0.1988$, –0.15, $ - 0.08$, –0.05, –0.03.

Полученная в результате расчетов зависимость поверхностного трения $f_{w}^{{''}}$ представлена как функция параметра $\beta $. Для сравнения приведенного результата с данными статей [2, 3] значения $f_{w}^{{''}}$ нанесены на один рис. 3.

Рис. 3.

Зависимость поверхностного трения от параметров β при ${{g}_{w}} = 1$: 1 – настоящие результаты, 2, 3 –данные [2, 3].

Сравнение результатов, полученных в данной работе, на рис. 3 с данными в [2] и [3] показывает совпадение значений поверхностного трения $f_{w}^{{''}}$.

Система уравнений решалась для различных значений температурного фактора, g_w, изменявшегося от значения 0.9 до 0.1. Для каждого значения g_w получена зависимость значения поверхностного трения $f_{w}^{{''}}$ от параметра $\beta $, характеризующего градиент давления (рис. 4).

Рис. 4.

Зависимость поверхностного трения от параметра β для каждого ${{g}_{w}}$: a–г – ${{g}_{w}} = 0.9$, 0.7, 0.5, 0.3.

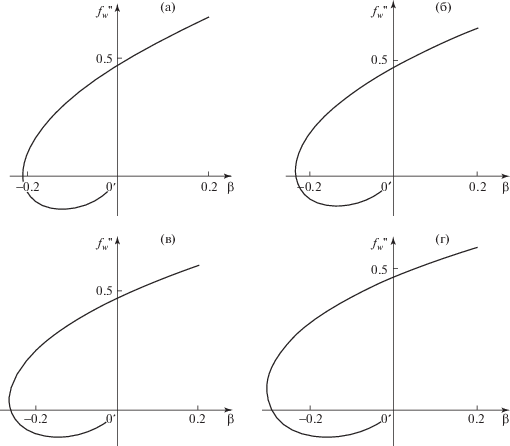
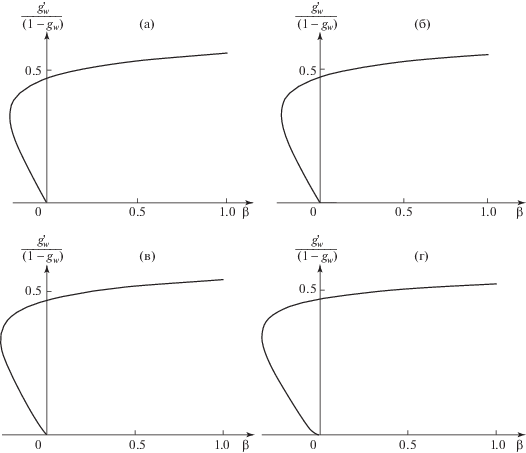
Зависимость параметра теплопередачи $g_{w}^{'}{\text{/}}\left( {1 - {{g}_{w}}} \right)$ от параметра $\beta $ представлена на рис. 5.

Рис. 5.

Зависимость параметра теплопередачи от параметра β для каждого ${{g}_{w}}$: а–г – ${{g}_{w}} = 0.9$, 0.7, 0.5, 0.2.

Профили скорости и температуры, полученные при решении, представлены как функции от $\eta $ на рис. 6 и 7 соответственно.

Рис. 6.

Профили скорости как функции переменной подобия η с постоянной $\beta $ при ${{g}_{w}} = 0.5$: а – 1–5 – ${\beta } = 1$, $0$, $ - 0.15$, $ - 0.25$, $ - 0.26$; б – 6–10 – ${\beta } = - 0.26$, $ - 0.2$, $ - 0.12$, $ - 0.08$, $ - 0.04$.

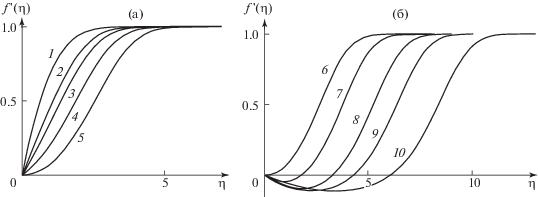
Рис. 7.

Профили энтальпии как функции переменной подобия η с постоянной $\beta $ при ${{g}_{w}} = 0.9$: а – 1–5 – ${\beta } = 1$, 0, –0.15, $ - 0.2$, $ - 0.21$; б – 6–10 – ${\beta } = - 0.21$, –0.15, $ - 0.1$, –0.05, $ - 0.03$; при ${{g}_{w}} = 0.2$: в – 1–5 – ${\beta } = 1$, 0, –0.3, $ - 0.329$, $ - 0.31$; г – 6–10 − ${\beta } = - 0.3$, –0.15, –0.1, $ - 0.06$, $ - 0.03$.

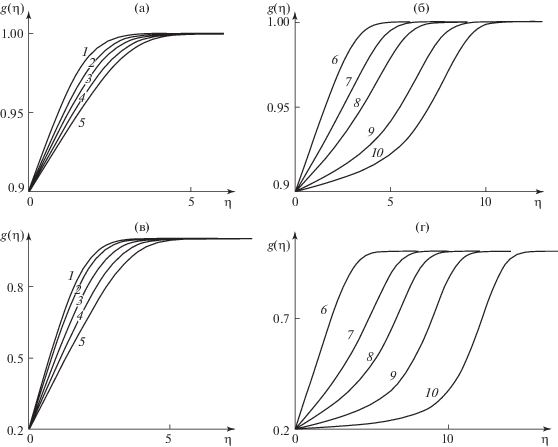
На рис. 7 показано, что при Pr = 1 температура монотонно меняется по всему пограничному слою от значения на стенке до значения в свободном потоке. Для благоприятных градиентов давления $\beta $ с холодной стенкой есть небольшое видоизменение этого распределения. Трансформация профиля температуры становится более выраженной с увеличением температуры стенки. Для неблагоприятных градиентов давления распределение более чувствительно к величине параметра $\beta $. Тепловой пограничный слой утолщается при приближении к отрыву и при уменьшении неблагоприятных градиентов давления после отрыва.

Для β > 0 максимальное $f{\kern 1pt} {\text{''}}$ находится у стенки, тогда как для β < 0 точка максимального $f{\kern 1pt} {\text{''}}$ все больше перемещается наружу.

Можно видеть, что снижение температурного фактора g_w уменьшает чувствительность поверхностного трения к градиенту давления, тогда как рост g_w имеет противоположный эффект. Предлагаемая физическая интерпретация этой тенденции связана с влиянием температуры стенки на среднюю плотность жидкости в пограничном слое. Когда происходит увеличение температурного фактора g_w, плотность пограничного слоя становится меньше плотности свободного потока, что делает жидкость пограничного слоя более восприимчивой к силам ускорения свободного потока, чем у холодной стенки.

Рис. 8.

Зависимость поверхностного трения от параметра $\beta $ при различных значениях температурного фактора${{g}_{w}}$: 1–10 – ${{g}_{w}} = 1$, $0.9$, 0.8, $0.7$, $0.6$, $0.5$, $0.4$, 0.3, 0.2, $0.1$.

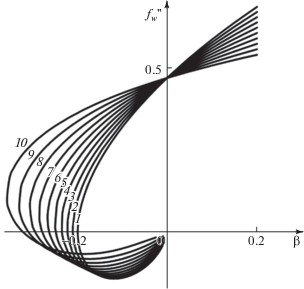
Из анализа данных на рис. 8 также следует, что для $\beta > 0$ существует только одно решение, два вязких решения, которые возникают при неблагоприятных градиентах давления для заданных $\beta $ и g_w, также нанесены на рисунок. Видно, что два решения существуют даже для изолированной поверхности (${{g}_{w}} = 1$), хотя в статье [2] представлено только одно. В этом случае решение нижней ветви соответствует отрицательному значению поверхностного трения $f_{w}^{{''}} < 0$, которое не рассматривалось в [2].

На рис. 8 видно, что наличие теплообмена затягивает появление отрыва ($f_{w}^{{''}} = 0$). При наличии сильного теплообмена существует сравнительно небольшой диапазон изменений $\beta $, характеризующего градиент давления, в котором каждому его значению соответствуют два решения с положительным значением $f_{w}^{{''}}$.

Полученные данные указывают на утолщение теплового слоя при приближении к отрыву. В этой зоне теплопередача происходит в основном за счет теплопроводности из-за близких к нулю скоростей в окрестности поверхности.

ЗАКЛЮЧЕНИЕ

Найдены решения уравнения Фолкнера–Скэн для сжимаемых течений, в дополнение к известным решениям для несжимаемых течений. Показано, что при отрицательных значениях параметра β < 0 решение задачи неединственно, причем одна из ветвей описывает течение с возвратными токами.

Наличие теплообмена затягивает появление профилей скорости $f{\kern 1pt} {\text{'}}$ отрывного типа на непрерывной ветви решения, кроме того, уменьшение температурного фактора приводит к снижению критического значения параметра $\beta $, при котором трение на поверхности обращается в ноль.

При наличии сильного теплообмена существует сравнительно небольшой диапазон изменений $\beta $, характеризующего градиент давления, в котором каждому его значению соответствуют два решения с положительным значением $f_{w}^{{''}}$.

Найденные в результате численного решения задачи профили скорости и полной энтальпии могут быть использованы для определения скорости распространения возмущений вверх по потоку.

Статья поддержана грантом Министерства образования и науки РФ (договор № 14.G39.31.0001 от 13.02.2017 г.) и грантом РФФИ (проект № 17-01-00129 а).

Список литературы

Falkner V.M., Skan S.W. Solutions of the boundary-layer equations // Phil. Mag. 1931. V. 7. № 12. P. 865.
Hartree D.R. // Proc. Camb. Phil. Soc. 1937. V. 33. P. 223.
Stewartson K. Further solution of the falkner-skan equation // Proc. Cambridge Philos. Soc. 1954. V. 50. P. 454–465.
Нейланд В.Я., Боголепов В.В., Дудин Г.Н., Липатов И.И. Асимптотическая теория сверхзвуковых течений вязкого газа. М.: Физматлит, 2003.
Хэйз У.Д., Пробстин Р.Ф. Теория гиперзвуковых течений. М.: Изд.-во иностр. лит., 1962.
Шевелев Ю.Д. Трехмерные задачи теории ламинарного пограничного слоя. М.: Наука, 1977. 222 с.
Шалаев В.И. Применение аналитических методов в современной аэромеханике. Часть 1. Теория пограничного слоя. М.: МФТИ, 2011. 300 с.
Солодов А.П. Электронный курс тепломассообмена // Открытое образование. 2013. Т. 1. № 96. С. 8–16.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал