1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 5, 2020

Известия РАН. Механика жидкости и газа, 2020, № 5, стр. 28-32

Моделирование динамики ударного воздействия на водные пены с учетом вязкоупругих свойств и явлений синерезиса

Р. Х. Болотнова a, *, Э. Ф. Гайнуллина a, **

a Институт механики им. Р.Р. Мавлютова УФИЦ РАН
Уфа, Россия

* E-mail: bolotnova@anrb.ru
** E-mail: elina.gef@yandex.ru

Поступила в редакцию 01.03.2020
После доработки 12.03.2020
Принята к публикации 12.03.2020

Полный текст (PDF)

Аннотация

Предложена двухфазная модель водной пены, основанная на законах сохранения массы, импульса и энергии фаз в соответствии с однодавленческим, двухскоростным, двухтемпературным приближениями в осесимметричной постановке с учетом сил межфазного сопротивления, контактного теплообмена, вязкоупругих свойств и синерезиса пены. Термодинамические свойства воды и воздуха описаны уравнениями состояния в форме Ми–Грюнайзена и Пенга–Робинсона соответственно. Численная реализация модели выполнена в пакете OpenFOAM. Полученные результаты удовлетворительно согласуются с данными эксперимента по сферическому взрыву в водной пене. Дан анализ эволюции сферической ударной волны при ее распространении в водной пене.

Ключевые слова: сферическая ударная волна, водная пена, пакет OpenFOAM, численное моделирование

Важность исследования демпфирующих свойств водных пен при динамическом нагружении связана с возможностью использования пенных барьеров в качестве эффективных противоударных защит от разрушительного воздействия ударных волн (УВ).

В [1–4] исследованы свойства водных пен, позволяющие снижать основные параметры УВ.

Взаимодействие сферического ударного импульса с пенным экраном изучено в [1, 2] с применением метода подвижных лагранжевых сеток [1] и пакета OpenFOAM [2, 5] в двумерной осесимметричной постановке. Численное моделирование эволюции УВ, инициированной взрывом ВВ, в водной пене для условий экспериментов [3] проведено в [4] в одномерном приближении методом сквозного счета с анализом влияния межфазного контактного теплообмена на степень диссипации энергии УВ.

В настоящей работе проведено математическое и численное моделирование динамики сферического взрыва в водной пене в соответствии с экспериментами [3] с более детальным по сравнению с [4] учетом сил межфазного сопротивления, контактного теплообмена, вязкоупругих свойств и синерезиса пены с реалистическими уравнениями состояния ее компонент. Предложенная модель водной пены численно реализована в новом решателе, разработанном авторами настоящего исследования в открытом пакете OpenFOAM.

1. ОСНОВНЫЕ УРАВНЕНИЯ

Система модельных уравнений включает законы сохранения [6] массы, импульса и энергии фаз

(1.1)
$\frac{{\partial ({{\alpha }_{i}}\rho _{i}^{{}})}}{{\partial t}} + {\text{div(}}{{\alpha }_{i}}\rho _{i}^{{}}{{{\vec {v}}}_{i}}{\text{)}} = 0$
(1.2)
$\frac{{\partial ({{\alpha }_{i}}\rho _{i}^{{}}{{{{\vec {v}}}}_{i}})}}{{\partial t}} + {\text{div(}}{{\alpha }_{i}}\rho _{i}^{{}}{{{\vec {v}}}_{i}}{{{\vec {v}}}_{i}}{\text{)}} = - {{\alpha }_{i}}\nabla p + {\text{div(}}{{\alpha }_{i}}{{\vec {\tau }}_{i}}{\text{)}} + {{\vec {F}}_{{i,drag}}} + {{\vec {F}}_{{i,vm}}}$
(1.3)
$\begin{gathered} \frac{{\partial ({{\alpha }_{i}}\rho _{i}^{{}}({{e}_{i}} + {{K}_{i}}))}}{{\partial t}} + {\text{div(}}{{\alpha }_{i}}\rho _{i}^{{}}({{e}_{i}} + {{K}_{i}}){{{{\vec {v}}}}_{i}}{\text{)}} = \\ = - p\frac{{\partial {{\alpha }_{i}}}}{{\partial t}} - {\text{div(}}{{\alpha }_{i}}{{{{\vec {v}}}}_{i}}p{\text{)}} + {\text{div}}\left( {{{\alpha }_{i}}\frac{{{{c}_{{p,i}}}}}{{{{c}_{{V,i}}}}}{{\lambda }_{i}}\nabla {{h}_{i}}} \right) + {{K}_{{ht}}}({{T}_{j}} - {{T}_{i}}) \\ \end{gathered} $

Здесь ${{\vec {\tau }}_{i}}$ – тензор вязкоупругих напряжений: ${{\vec {\tau }}_{i}} = {{\mu }_{{i,eff}}}(\nabla {{{\vec {v}}}_{i}} + \nabla {{{\vec {v}}}_{i}}^{T}) - \frac{2}{3}({{\mu }_{{i,eff}}}{\text{div}}{{{\vec {v}}}_{i}})I$, ${{\vec {F}}_{{i,drag}}}$ – сила межфазного сопротивления: ${{\vec {F}}_{{i,drag}}} = \frac{3}{4}{{\alpha }_{1}}{{C}_{D}}\frac{{{{\rho }_{2}}}}{{{{d}_{{10}}}}}({{{\vec {v}}}_{i}} - {{{\vec {v}}}_{j}})\left| {{{{{\vec {v}}}}_{i}} - {{{{\vec {v}}}}_{j}}} \right|$, ${{\vec {F}}_{{i,vm}}}$ – сила присоединенных масс: ${{\vec {F}}_{{i,vm}}} = 0.5{{\alpha }_{1}}{{\rho }_{2}}\left( {\frac{{{{d}_{j}}{{{{\vec {v}}}}_{j}}}}{{dt}} - \frac{{{{d}_{i}}{{{{\vec {v}}}}_{i}}}}{{dt}}} \right)$, ${{\mu }_{{i,eff}}}$ – эффективная вязкость Гершеля–Балкли [7], которая ниже предела текучести τ0 зависит от скорости сдвига $\dot {\gamma }$, коэффициента консистенции k' и показателя отклонения от ньютоновских свойств n: ${{\mu }_{{i,eff}}} = k{\text{'}}{{\dot {\gamma }}^{n}}$, а выше предела ${{\tau }_{0}}$ – соответствует динамической вязкости ${{\mu }_{{i{\kern 1pt} }}}$: ${{\mu }_{{i,eff}}} = {{\mu }_{i}}$.

Потеря водосодержания в верхних слоях пены за счет ее осаждения учтена при описании межфазного сопротивления Шиллера–Наумана [6] введением в коэффициент CD параметра ${{c}_{S}}({{\alpha }_{{10}}})$, зависящего от исходного водосодержания

(1.4)
${{C}_{D}} = \frac{{{{с}_{s}}({{\alpha }_{{10}}})(1 + 0.15{{{\operatorname{Re} }}^{{0.687}}})}}{{\operatorname{Re} }},\quad \operatorname{Re} \leqslant 1000$

Коэффициент теплообмена ${{K}_{{ht}}}$ определен моделью Ранца-Маршалла [6]

${{K}_{{ht}}} = \frac{{{{\kappa }_{2}}}}{{{{d}_{{10}}}}}{\text{Nu,}}\quad {\text{Nu}} = 2 + 0.6{{\operatorname{Re} }^{{1/2}}}{{\Pr }^{{1/3}}}$

В приведенных выше уравнениях используются следующие обозначения: p – давление; ρi – плотность; Ti – температура; αi – объемное содержание; ${{{\vec {v}}}_{i}}$ – вектор скорости; ei, Ki – внутренняя и кинетическая энергии; hi – энтальпия; κi – теплопроводность; ${{c}_{{p,i}}}$, ${{c}_{{V,i}}}$ – удельные теплоемкости при постоянном давлении и объеме; λi – температуропроводность; i, j = 1, 2 – обозначения жидкой и газовой фаз; I – единичный тензор.

Для уравнения состояния воздуха принята форма Пенга–Робинсона [8]

(1.5)
$p = \frac{{R{{T}_{2}}}}{{{{V}_{m}} - b}} - \frac{{a({{T}_{2}})}}{{{{V}_{m}}({{V}_{m}} + b) + b({{V}_{m}} - b)}}$

Для жидкой фазы использовано уравнение состояния воды Нигматулина, Болотновой [9] в форме Ми–Грюнайзена с упругим потенциалом типа Борна–Майера

(1.6)
$p = {{p}^{{(p)}}} + {{p}^{{(T)}}},\quad e = {{e}^{{(p)}}} + {{e}^{{(T)}}}$
${{p}^{{(p)}}}(\rho ) = A{{\left( {\frac{{\rho }}{{{{\rho }_{{\text{0}}}}}}} \right)}^{{ - {\beta } + {\text{1}}}}}exp\left[ {b\left( {1 - {{{\left( {\frac{{\rho }}{{{{\rho }_{{\text{0}}}}}}} \right)}}^{{ - {\beta }}}}} \right)} \right] - K{{\left( {\frac{{\rho }}{{{{\rho }_{{\text{0}}}}}}} \right)}^{{{\xi } + {\text{1}}}}},\quad \rho = \frac{1}{V}$
(1.7)
${{e}^{{(p)}}}(\rho ) = \int\limits_{{{\rho }^{ \circ }}}^\rho {\frac{{{{p}^{{{\text{(}}p{\text{)}}}}}\left( \rho \right)}}{{{{\rho }^{2}}}}} {\text{d}}\rho = \frac{A}{{{\beta }{{\rho }_{0}}b}}exp\left[ {b\left( {1 - {{{\left( {\frac{{\rho }}{{{{\rho }_{{\text{0}}}}}}} \right)}}^{{ - {\beta }}}}} \right)} \right] - \frac{K}{{{\xi }{{\rho }_{0}}}}{{\left( {\frac{{\rho }}{{{{\rho }_{{\text{0}}}}}}} \right)}^{{\xi }}} + {{e}^{ \circ }}$
(1.8)
$\begin{gathered} \frac{{{{\xi }_{V}}(\rho )}}{\rho } = \Gamma (\rho ){{c}_{V}} = \\ = \;\frac{R}{M}\left( {{{a}^{{(0)}}} + \left( {1 - {{a}^{{(0)}}}} \right)\exp \left( { - {{{\left( {\frac{{\rho }}{{{{{\rho }}^{{{\text{(}}0{\text{)}}}}}}}} \right)}}^{{1.7}}}} \right) + {{a}^{{(1)}}}\exp \left( { - {{{\left( {\frac{{\rho }}{{{{{\rho }}^{{{\text{(}}1{\text{)}}}}}}}} \right)}}^{{ - 3.5}}}} \right) + {{a}^{{(2)}}}\exp \left( { - {{{\left( {\frac{{\rho }}{{{{{\rho }}^{{{\text{(}}2{\text{)}}}}}}}} \right)}}^{{ - 5.0}}}} \right)} \right) \\ \end{gathered} $

Здесь $e^\circ $ – константа интегрирования при условии ${{e}^{{(p)}}}(\rho ^\circ ) = 0$, ${{p}^{{(p)}}}(\rho ^\circ ) = 0$.

В модели предполагается, что за фронтом сильной УВ пена разрушена на микрокапли диаметра ${{d}_{{10}}} = 8 \times {{10}^{{ - 4}}}$ м [10] в виде монодисперсной газокапельной смеси. Для слабых УВ, когда напряжения сдвига ниже предела упругости, при описании свойств водной пены используется вязкоупругая модель Гершеля–Балкли [7].

2. ПОСТАНОВКА ЗАДАЧИ И АНАЛИЗ РЕЗУЛЬТАТОВ

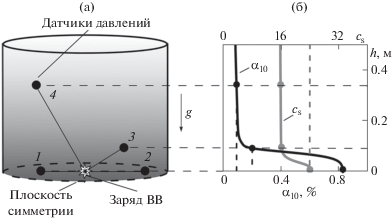
При численном исследовании моделировалась динамика распространения УВ для условий эксперимента [3] по сферическому взрыву в водной пене. На рис. 1а показана схема эксперимента. В центре сосуда, заполненного водной пеной, расположено ВВ. Датчики давления 1…4 помещены на расстояниях l1 = 0.41, l2 = 0.53, l3 = 0.67 и l4 = 0.93 м от центра взрыва. Степень насыщенности серого цвета в сосуде характеризует исходное распределение объемного водосодержания пены, формирующееся под влиянием синерезиса.

Рис. 1.

Схема эксперимента (а). Распределения начального водосодержания пены и коэффициента ${{c}_{s}}({{\alpha }_{{10}}})$ в зависимости от высоты от центра взрыва (б).

Граничные и начальные условия задачи соответствуют моделируемому эксперименту. Начальный импульс давления задавался в виде

(2.1)
$p(x,y,z) = {{p}_{0}} + \Delta p{{e}^{{ - {{({{x}^{2}} + {{y}^{2}} + {{z}^{2}})} \mathord{\left/ {\vphantom {{({{x}^{2}} + {{y}^{2}} + {{z}^{2}})} {{{a}^{2}}}}} \right. \kern-0em} {{{a}^{2}}}}}}}$
где Δp = 3000 МПа, ${{p}_{0}}$ = 0.1 МПа, $a$ = 0.035 м.

Система уравнений (1.1)–(1.8) численно решалась в разработанном авторами решателе в пакете OpenFOAM с применением алгоритма PIMPLE.

При анализе степени синерезиса для наилучшего согласования с данными эксперимента принято начальное распределение водосодержания пены ${{\alpha }_{{10}}}$ в виде функции, убывающей от максимального значения ${{\alpha }_{{10}}}$ = 0.0083 [3] для датчиков 1 и 2, закрепленных в одной горизонтальной плоскости с центром взрыва, до величин ${{\alpha }_{{10}}}$ = 0.002 и ${{\alpha }_{{10}}}$ = 0.001 в местоположениях датчиков 3 и 4 (см. черную линию на рис. 1б). На том же рисунке сплошной линией серого цвета показана зависимость параметра для силы межфазного сопротивления ${{c}_{s}}\left( {{{\alpha }_{{10}}}} \right)$ (1.4) от высоты столба пены.

На рис. 2 показаны расчетные (1) и экспериментальные (2–5) осциллограммы давления в пене в указанные моменты времени (мс) в зависимости от расстояния до центра взрыва: 2, 3 – обобщенные данные по взрывам в газе и пене [3]; 4, 5 – пиковые амплитуды давлений [3]. На рис. 3 представлены расчетные временные зависимости давления, полученные для местоположений датчиков 1–4 (черные линии) и соответствующие экспериментальные данные [3] (серые штриховые линии).

Рис. 2.

Эволюция давления в пене от расстояния до центра взрыва в моменты времени в мс; 1 – расчеты; 2–5 – экспериментальные данные [3] пиковых давлений УВ в воздухе (2) и водной пене (3–5); 2, 3 – обобщенные данные; l1–l4– расстояния до датчиков.

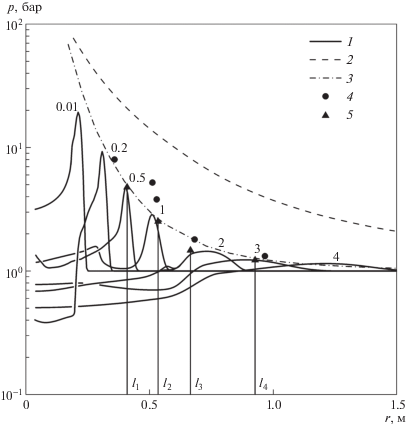
Рис. 3.

Эволюция давления в пене в точках расположения датчиков на расстояниях l1–l4 от центра взрыва: 1 – расчеты; 2 – экспериментальные данные [3].

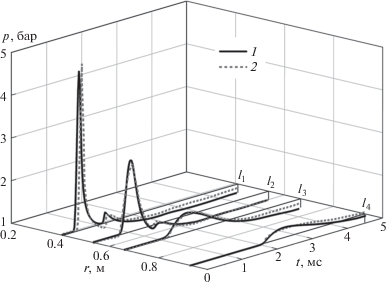
Установлено, что в процессе взаимодействия с водной пеной амплитуда сферической УВ, изначально равная p = 30 000 бар (2.1), ослабевает до 5 бар к моменту прихода УВ к датчику 1 (при $t$ = 0.5 мс). Двухволновая структура ударного импульса, образованная основным пиком и скачком давления, отраженным от центра симметрии, фиксируется на датчиках 1, 2 как в эксперименте, так и в расчетах. Исследования показали, что при распространении УВ в глубь водной пены с течением времени происходит значительное ослабление интенсивности фронта УВ и “размытие” его двухволновой структуры.

Отмеченные эффекты обусловлены диссипацией энергии сферической УВ по пространству, энергопоглощающими свойствами водной пены и влиянием ее вязкоупругих характеристик. Учет процессов синерезиса на удалении от центра взрыва приводит к некоторому увеличению скорости УВ и ослаблению влияния сил межфазного сопротивления.

Сравнительный анализ экспериментальных данных и полученных решений по предложенной 3D модели водной пены показал их наилучшее согласование по отношению к ранее полученным результатам для аналогичной задачи в более простом одномерном приближении [4].

ЗАКЛЮЧЕНИЕ

Разработана трехмерная двухфазная модель водной пены в однодавленческом, двухскоростном, двухтемпературном приближениях, учитывающая силы межфазного сопротивления, контактный теплообмен, вязкоупругие свойства пены и явление синерезиса. Термодинамические свойства пены описаны реалистичными уравнениями состояния. Рассматриваемая задача численно реализована в разработанном авторами новом решателе в среде открытого программного комплекса OpenFOAM.

Исследована динамика распространения в водной пене сферической УВ, вызванной взрывом ВВ, для условий экспериментов [3]. Выявлены причины значительного ослабления интенсивности фронта УВ, обусловленные диссипативными и вязкоупругими свойствами изучаемой среды. Показано влияние процесса синерезиса пены, приводящее к уменьшению водосодержания в ее верхних слоях, сопровождающееся увеличением скорости УВ и снижением межфазного сопротивления.

Работа выполнена при финансовой поддержке средствами государственного бюджета по госзаданию 0246-2019-0052.

Список литературы

  1. Агишева У.О., Болотнова Р.Х., Гайнуллина Э.Ф. и др. Особенности вихреобразования при воздействии импульса давления на газовую область, ограниченную пенным слоем // Изв. РАН. МЖГ. 2016. № 6. С. 47–55.

  2. Bolotnova R.Kh., Gainullina E.F. Wave dynamics and vortex formation under the impact of a spherical impulse on the boundary between gas and aqueous foam // J. Phys.: Conf. Ser. 2019. V. 1268. 012015.

  3. Del Prete E., Chinnayya A., Domergue L., et al. Blast Wave Mitigation by Dry Aqueous Foams // Shock Waves. 2013. V. 23. № 1. P. 39–53.

  4. Bolotnova R.Kh., Gainullina E.F. Influence of Heat-exchange Processes on Decreasing an Intensity of a Spherical Explosion in Aqueous Foam // Fluid Dynamics. 2019. V. 54. № 7. P. 970–977.

  5. OpenFOAM. The Open Source Computational Fluid Dynamics (CFD) Toolbox. URL: http://www.openfoam.com.

  6. Zeno Tacconi. Feasibility analysis of a two-fluid solver for cavitation and interface capturing as implemented in OpenFOAM // Tesi di Laurea Magistrale in Ingegneria Energetica, Politecnico di Milano. 2018. 134 p.

  7. Monloubou M., Le Clanche J., Kerampran S. New experimental and numerical methods to characterise the attenuation of a shock wave by a liquid foam // Actes 24ème Congrès Français de Mécanique. Brest: Association Française de Mécanique (AFM). 2019. 255125.

  8. Peng D.Y., Robinson D.B. A new two-constant equation of state // Industrial and Engineering Chemistry: Fundamentals. 1976. V. 15. P. 59–64.

  9. Нигматулин Р.И., Болотнова Р.Х. Широкодиапазонное уравнение состояния воды и пара. Упрощенная форма // ТВТ. 2011. Т. 49. № 2. С. 310–313.

  10. Ждан С.А. Численное моделирование взрыва заряда ВВ в пене // ФГВ. 1990. Т. 26. № 2. С. 103–110.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал