Известия РАН. Механика жидкости и газа, 2020, № 5, стр. 56-60

1. ПОСТАНОВКА ЗАДАЧИ

Рассматривается идеальная, несжимаемая вертикально стратифицированная среда конечной глубины H. Пусть $(U(z),V(z))$ – вектор фонового сдвигового течения на горизонте z. В приближении Буссинеска уравнение для малых возмущений вертикальной компоненты скорости $w$ имеет вид [1–3, 6, 8]

где ${{N}^{2}}(z)$ – квадрат частоты Брента-Вяйсяля (частоты плавучести), g – ускорение свободного падения, ${{\rho }_{0}}(z)$ – невозмущенная плотность среды. Граничные условия берутся в виде (вертикальная ось z направлена вверх)

В силу линейности рассматриваемой задачи вертикальная компонента скорости w и вектор горизонтальных скоростей u связаны соотношением: ${{\Delta }_{2}}{\mathbf{u}} + \nabla \partial w{\text{/}}\partial z$ [4, 7]. Далее используются следующие предположения. Частота Брента-Вяйсяля предполагается постоянной: $N(z) = N$ = = const, фоновое сдвиговое течение – одномерным: $V(z) \equiv 0$. Функция U(z) – линейная функция глубины: $U(z) = {{U}_{0}} + ({{U}_{0}} - {{U}_{H}})z{\text{/}}H$, ${{U}_{0}} = U(0)$, ${{U}_{H}} = U( - H)$. Также предполагается выполненным условие устойчивости Майлса–Ховарда для числа Ричардсона: $Ri = {{N}^{2}}{{(\partial U{\text{/}}\partial z)}^{{ - 2}}} > 1{\text{/}}4$ [1–3, 8, 9]. Характерные значения чисел Ричардсона в акваториях Мирового океана (Атлантический океан, моря Арктического бассейна) при отсутствии динамической неустойчивости сдвиговых течений могут находиться в интервалах от 2 до 20 [3, 5, 6, 8, 9]. В безразмерных координатах и переменных

$x* = \pi x{\text{/}}H,y* = \pi y{\text{/}}H,z* = \pi z{\text{/}}H,$ $\omega * = \omega {\text{/}}N,t* = tN,$ $M(z*) = U(z)\pi {\text{/}}NH = a + bz*,$ a = πU₀/NH, $b = ({{U}_{0}} - {{U}_{H}}){\text{/}}NH$ уравнения (1.1)–(1.2) можно представить в виде (звездочка “*” далее опускается)

Параметр b есть величина, обратная квадратному корню из числа Ричардсона: $b = 1{\text{/}}\sqrt {Ri} $, параметр a – отношение амплитуды приповерхностного течения U₀ к максимальной групповой скорости распространения ВГВ в океане, равной $NH{\text{/}}\pi $ [4, 6, 7]. Решение задачи (1.3) ищется в виде свободных гармонических волн: $w\left( {t,x,y,z} \right) = \varphi (z)exp(i(\omega t - \mu x - \nu y)$. Тогда для определения функции $\varphi (z)$ имеем

В качестве двух линейно независимых решений задачи (1.4) возьмем: $\mathop f\nolimits_ \pm (z)$ = = $\sqrt {2\beta r(z))} \mathop I\nolimits_{ \pm i\lambda } (\beta r(z))$, где $\mathop I\nolimits_{ \pm i\lambda } $ – модифицированная функция Бесселя мнимого индекса iλ, r(z) = = $\omega - \mu M(z)$, $\lambda = \sqrt {\mathop \beta \nolimits^2 - 1{\text{/}}4} $, $\beta = k{\text{/}}b\mu $ [10, 12]. Решение, удовлетворяющее граничному условию при z = 0, имеет вид: $\varphi (z) = i(\mathop f\nolimits_ + (0)\mathop f\nolimits_ - (z) - \mathop f\nolimits_ - (0)\mathop f\nolimits_ + (z))$. Функции $\mathop f\nolimits_ \pm (z)$ – комплексно сопряжены, поэтому решение $\varphi (z)$ является действительным. Так как предполагается, что выполнено условие устойчивости Майлса–Ховарда для числа Ричардсона, то ${{b}^{2}} < 4$. Отсюда, в частности, следует, что ${{\beta }^{2}} > 1{\text{/}}4$ и значения λ действительны. Требование удовлетворения граничному условию при z = –π определяет дисперсионное соотношение

2. СВОЙСТВА ДИСПЕРСИОННЫХ КРИВЫХ И ФАЗОВЫЕ КАРТИНЫ

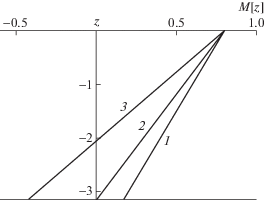
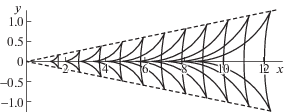
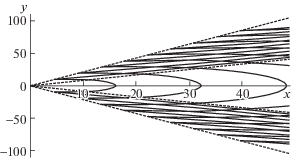
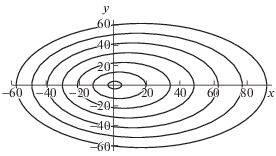
Решения дисперсионного уравнения (1.5) можно представить в виде ${{\omega }_{n}}(\mu ,\nu )$ или ${{\mu }_{n}}(\nu ,\omega )$. Ниже исследуется дисперсионная зависимость ${{\mu }_{n}}(\nu )$ при следующих значениях: $\omega = 0.54$, a = 0.8 ($\omega $ – фиксированный параметр). В использованных моделях сдвиговых течений – a < 1; это означает, что амплитуды фоновых сдвиговых течений не превышают максимальной групповой скорости распространения ВГВ, что наблюдаемо в условиях Мирового океана. Параметр ω < 1 определяет отношение частоты свободной волны к максимальному значению частоты плавучести, и описывает распространение ВГВ с частотой, почти в два раза меньше частоты плавучести, что также наблюдаемо в реальных океанических условиях [5, 6]. Исходя из многочисленных результатов океанологических наблюдений сдвиговых течений в различных акваториях Мирового океана, можно рассмотреть три модельных распределения фонового одномерного сдвигового течения по глубине [3, 5, 6]. Первая модель – однонаправленное течение, амплитуда течения уменьшается с глубиной, причем на дне амплитуда придонного течения отлична от нуля ${{U}_{H}} \ne 0$ (кривая 1 на рис. 1). Вторая модель – однонаправленное течение, амплитуда придонного течения на дне мала по сравнению с амплитудой приповерхностного течения U_H = 0 (кривая 2 на рис. 1). Третья модель – разнонаправленные течения, амплитуда придонного течения по порядку величины сравнима с амплитудой приповерхностного течения (кривая 3 на рис. 1). Используя для решения уравнения (1.5) дебаевские асимптотики модифицированной функции Бесселя мнимого индекса, можно изучить качественные картины поведения дисперсионных кривых для различных моделей распределения фоновой сдвиговой скорости [10, 12]. Дисперсионные кривые для первой модели представляют собой два семейства разомкнутых кривых, причем каждая дисперсионная кривая является ограниченной. Фазовая картина волнового поля ВГВ, отвечающая первой модели, приведена на рис. 2. Дисперсионные кривые для второй модели состоят только из одного семейства, каждая кривая заключена в соответствующем полубесконечном интервале. Фазовая картина волнового поля ВГВ, отвечающая второй модели, приведена на рис. 3. Дисперсионные кривые, отвечающие третьей модели, состоят из одного семейства замкнутых кривых. Фазовая картина волнового поля ВГВ, отвечающая третьей модели, представляет собой систему кольцевых волн и приведена на рис. 4. Качественная картина поведения дисперсионных кривых в виде замкнутых линий получается при изучении генерации ВГВ движущимся с постоянной скоростью осциллирующим источником возмущений. Однако необходимо отметить, что для данного случая (постоянное, не зависящее от глубины фоновое течение) волновая картина возбуждаемых полей ВГВ определяется частотой осцилляции $\omega $, и, например, кольцевые волны могут существовать только при малых частотах [13, 14]. Для линейных фоновых сдвиговых течений качественная волновая картина ВГВ определяется только характером течения (безразмерной амплитудой приповерхностного течения a и вертикальным градиентом $b$) и не зависит от частоты гармонической волны $\omega $. В частности, однонаправленное течение порождает как клиновидные (продольные), так и кольцевые (поперечные) волны (рис. 2, 3), а разнонаправленное течение генерирует только кольцевые волны (поперечные) (рис. 4). Для первой модели, в силу наличия двух различных семейств дисперсионных кривых, существует волновая система только клиновидных (продольных) волн (рис. 2). Для второй модели кольцевые (поперечные) волны занимают всю пространственную область внутри волнового клина с углом полураствора $\alpha $, длина поперечной волны n моды при y = 0 равна $2\pi {\text{/}}{{\mu }_{n}}(0)$. Клиновидные (продольные) волны каждой моды ограничены как волновым фронтом с углом полураствора α ($\alpha = arctg(\mu _{n}^{'}(\nu *))$, где $\nu *$ – корень уравнения $(\mu _{n}^{{''}}(\nu *)) = 0$), так и волновым фронтом, положение которого определяется асимптотикой ${{\mu }_{n}}(\nu )$ при больших значениях ν, с углом полураствора, меньшим α. Полученные результаты показывают значительную зависимость фазовой структуры возбуждаемых полей ВГВ от соотношения амплитуд придонного и приповерхностного сдвигового течения. В частности, для третьей модели, если амплитуды придонного и приповерхностного сдвигового течений равны, то соответствующая фазовая картина волнового поля – симметрична. Если амплитуды придонного и приповерхностного течений различны, то фазовая картина возбуждаемых полей ВГВ становится асимметричной. Поэтому асимметричность фазовых картин волновых полей ВГВ может являться одним из признаков заметной перестройки в распределении по глубине фоновых сдвиговых океанических течений.

ЗАКЛЮЧЕНИЕ

Решена задача о поле ВГВ в стратифицированной среде конечной глубины для модельных распределений фоновых сдвиговых течений. Для аналитического решения задачи использованы постоянное распределение частоты плавучести и различные линейные зависимости фонового сдвигового течения от глубины. Получены дисперсионные зависимости, которые выражаются через модифицированную функцию Бесселя мнимого индекса. При выполнении условия устойчивости Майлса–Ховарда и больших числах Ричардсона для построения аналитических решений были использованы дебаевские асимптотики модифицированной функции Бесселя мнимого индекса. Изучены качественные свойства дисперсионного уравнения и исследованы основные аналитические свойства дисперсионных кривых в зависимости от характеристик модельных фоновых сдвиговых течений. Качественная картина дисперсионных кривых и соответствующих им фазовых картин ВГВ определяется свойствами фоновых сдвиговых течений. При относительно малых вертикальных градиентах фоновых сдвиговых течений (течения на поверхности и дне различны по амплитуде, но однонаправлены) волновая картина ВГВ представляет собой систему как клиновидных (продольных), так и кольцевых (поперечных) волн. При больших вертикальных градиентах фоновых сдвиговых течений (сдвиговые течения на поверхности и дне разнонаправлены) волновая картина состоит только из кольцевых (поперечных) волн, при этом соотношение амплитуд придонного и приповерхностного течений определяет степень асимметрии генерируемых волновых картин.

Работа выполнена при финансовой поддержке РФФИ проект 20-01-00111А.