Известия РАН. Механика жидкости и газа, 2020, № 5, стр. 7-15
ТРЕХВОЛНОВЫЕ ВЗАИМОДЕЙСТВИЯ ВОЗМУЩЕНИЙ В СВЕРХЗВУКОВОМ ПОГРАНИЧНОМ СЛОЕ
С. А. Гапонов a, *, Н. М. Терехова a, **
a Институт теоретической и прикладной механики им. С.А. Христиановича СО РАН
Новосибирск, Россия
* E-mail: gaponov@itam.nsc.ru
** E-mail: terekh@itam.nsc.ru
Поступила в редакцию 05.12.2019
После доработки 05.03.2020
Принята к публикации 05.03.2020
Аннотация
В рамках слабонелинейной теории устойчивости рассмотрено взаимодействие вихревых возмущений (волн Толлмина–Шлихтинга) в сверхзвуковом пограничном слое на непроницаемой поверхности. Исследуется первый уровень нелинейного взаимодействия – в трехволновых резонансных системах. Рассмотрены основные закономерности взаимодействия в единичных триплетах, составленных из плоских и трехмерных компонент, после чего изучается групповое взаимовлияние (совместная реализация нескольких простых триплетов). Моделируется продольная динамика возмущения двух типов – контролируемых и естественных. Изучена возможность перераспределения энергии в таких волновых системах при реализации нелинейного взаимодействия составляющих пакетов волн. Показано, что резонансные взаимодействия адекватны реальным нелинейным процессам на ранних стадиях перехода.
Математический аппарат, разработанный в разделе механики, связанной с исследованиями ламинарно-турбулентного перехода в дозвуковых течениях [1], может быть применен к исследованию высокоскоростных потоков. В последние годы проводится углубленное изучение ряда методов эволюции возмущений в сверхзвуковых пограничных слоях сжимаемого газа. Работы по математическому моделированию делятся на две группы. В первой развиваются методы прямого численного интегрирования систем уравнений в частных производных [2–5]. Этому подходу присущи трудности, связанные с обработкой большого массива данных (достоверность которых не всегда очевидна) и физической интерпретацией полученных результатов. Поэтому, например, в [5] при обзоре публикаций по численному моделированию ламинарно-турбулентного перехода пограничных слоев при высоких числах Маха (М) не сделано обобщающих выводов по нелинейному взаимодействию возмущений. Несмотря на определенную модность этого подхода, гораздо более эффективными для моделирования нелинейных процессов оказались методы второй группы, проводимые в рамках теории возмущений (для средних характеристик и малых колебаний).
Исследования в нелинейной области проводятся на основе изучения взаимодействия в трехволновых системах (триадах или триплетах). Физическое обоснование такого моделирования заключается в изучении эволюции одной волны в силовом поле двух других волн, проходящее в условиях синхронизации фаз возмущений, что позволяет изучить составляющие, управляющие процессом. Амплитудные уравнения для трехволновых систем получены при использовании стандартной процедуры осреднения и условия разрешимости [6, 7]. Благодаря им удается построить модель начальной стадии развития неустойчивости течения (приближение слабой нелинейности), существенно упрощающую анализ и позволяющую дифференцировать управляющие процессом механизмы.
При теоретических исследованиях высокоскоростных потоков сжимаемого газа, кроме рассмотрения возмущений скорости, необходимо учитывать возмущения температуры и плотности. Связь теории и эксперимента обеспечивается сотрудничеством с коллективом сверхзвуковой аэродинамической трубы Т-325 ИТПМ им. С.А. Христиановича СО РАН. Экспериментально исследуются два типа возмущений – контролируемые и естественные. В [8] подробно исследован состав, и продольная динамика контролируемых возмущений на непроницаемых поверхностях при М = 2 и на основе изучения линейной стадий развития четко выявлены особенности, которые уже не могут быть отнесены к линейным.
При невысоком уровне контролируемых возмущений реализуется субгармоническая неустойчивость, в спектре возмущений преобладают трехмерные моды, а заполнение его представляет собой каскадный процесс выделения трехмерных субгармоник в параметрической области.
Раздел изучения динамики естественных возмущений значительно менее популярен и, соответственно, исследован. Для них фиксируется широкий спектр частот при полном отсутствии данных об азимутальном составе компонент спектра, а перераспределение энергии осуществляется не только в субгармоническую область, но и в область высоких частот (обертонов). В этих условиях наряду с рассмотрением синхронизованных частотных триплетов возникает необходимость удовлетворить условиям фазового синхронизма и по азимутальным волновым числам.
Работа проведена в два этапа. Предварительно была подробно изучена принципиальная возможность моделирования взаимодействия в триплетах возмущений произвольного азимутального состава. На втором этапе последовательно изучены взаимодействия в так называемых групповых триплетах, составленных из нескольких простых.
В окончательном варианте, который представлен в данной работе, для естественных возмущений задействовано 12 синхронизированных частот, а общее число простых триплетов, входящих в групповой, равнялось 36. Основными несущими компонентами выбирались трехмерные волны, имеющие максимальные инкременты внутри нейтральной кривой при начальных числах Рейнольдса (Re = 300 или 600). Для контролируемых возмущений число азимутальных мод было значительно большим (около 20), а число простых триплетов, входящих в групповой, было 48.
Параметры [8] являлись отправными при расчетах – рассмотрен пограничный слой на непроницаемой теплоизолированной пластине под нулевым углом атаки при М = 2, показателе адиабаты γ = 1.4, температуре торможения 310 K, числе Прандтля σ = 0.72 и единичном числе Рейнольдса Re1 = 12.5 × 106 м–1. Интервал продольных чисел Рейнольдса соответствовал экспериментальному, введено расчетное число Рейнольдса $\operatorname{Re} = \sqrt {{{R}_{X}}} $.
1. ОСНОВНЫЕ СООТНОШЕНИЯ И МЕТОДЫ РЕШЕНИЯ
Основные положения нелинейной модели взаимодействия возмущений в трехволновых резонансных системах в пограничных слоях сжимаемого газа подробно изложены в [7]. Через ε обозначается масштаб пульсационного поля (${\varepsilon }$ $ \ll $ 1). Рассматриваются возмущенные поля скоростей u, плотности ρ, давления p и температуры T сжимаемого газа $u = \left| {U(Y) + {\varepsilon }u{\text{'}},{\varepsilon }{v}{\text{'}},{\varepsilon }w{\text{'}}} \right|$, $\rho = \rho (Y) + {\varepsilon \varsigma '}$, p = $P(Y) + {\varepsilon }p{\text{'}}$, $T = T(Y) + {\varepsilon }\Theta '$, $p{\text{'/}}P(Y) = {\varsigma '/\rho (Y)} + \Theta {\text{'/}}T(Y)$ в безразмерной декартовой системе координат (X, Y, Z) = (x, y, z)/δ (δ = $\sqrt {{{{\nu }}_{e}}x{\text{/}}{{U}_{e}}} $ – характерный масштаб, индекс e соответствует параметрам на внешней границе; штрихами и без штрихов обозначены пульсационные и средние величины). Решение строится с помощью разложения по малому параметру ε и двухмасштабному разложению продольной координаты. Помимо “быстрого” масштаба $X$, вводится “медленный” масштаб ${\xi } = {\varepsilon }X$, что обусловлено существенным различием скоростей изменения фазы и амплитуды возмущений.
Решения для волн ищутся в виде
(1.1)
$H_{j}^{'} = {{A}_{j}}({\xi })H_{j}^{0}(Y)\exp (i{{{\theta }}_{j}}) + {\text{к}}{\text{.с}}{\text{.}} + {\varepsilon H}_{j}^{1} + \; \ldots ,\quad j = {\text{ }}1,2,3~$Из полной системы уравнений движения и законов сохранения для сжимаемого газа [9] в рамках слабонелинейной теории для вектора-функции H выписывается исходная рекуррентная система для возмущений [7]
(1.2)
$\begin{gathered} {\varepsilon }\left\{ {\sum\limits_{j = 1}^n {{\text{exp}}(i{{{\theta }}_{j}}} )} \right.\left[ {L(H_{j}^{0}) + \left( {\frac{{\partial L(H_{j}^{0})}}{{\partial {{{\alpha }}_{j}}}}} \right)\left( {\frac{\partial }{{\partial X}}} \right)} \right. + \left. {\left( {\frac{{\partial L(H_{j}^{0})}}{{\partial {{{\omega }}_{j}}}}} \right)\left( {\frac{\partial }{{\partial t}}} \right)} \right]{{A}_{j}} + \\ + \;{\varepsilon }\left. {\sum\limits_{k,l}^n {{\text{exp(}}i{\text{(}}{{{\theta }}_{{\text{k}}}} + {{{\theta }}_{l}}} ))[L(H_{{k + l}}^{1}) + {{A}_{k}}{{A}_{l}}Q_{{k,l}}^{j}(H_{j}^{0}H_{{lX}}^{0}, \ldots )]} \right\} = 0 \\ \end{gathered} $Выражения для линейного оператора L хорошо изучены, это так называемая система Дана–Линя [9].
Краевые условия для возмущений – {u, ${v}$, w, $\Theta $} = 0 при Y = 0, {u, ${v}$, w, $\Theta $} → 0 при Y →$\infty $. При М = 2 толщина ламинарного пограничного слоя соответствует Y ≈ 7–8, а интегрирование проводится в интервале $0 \leqslant Y \leqslant 15$. Все величины обезразмерены по параметрам на внешней границе пограничного слоя; нормировка собственных функций: |${v}$|$_{{{{Y}_{k}}}}$ = 1.
Для возмущений первого порядка по ${\varepsilon }$ на основе однородной системы Дана–Линя находятся собственные значения ${\alpha }$ при заданных ${\beta }$, ${\omega }$ и числах Рейнольдса Re = x/${\delta }$ ($\operatorname{Re} = \sqrt {{{R}_{X}}} $), а также собственные амплитудные функции линейных волн (1.1) при неопределенном амплитудном параметре A, после чего законы развития возмущений в линейной области считаются установленными. Согласно слабонелинейной теории при указанных искомых параметрах нелинейность оказывает влияние только на амплитуду волны A.
В основе резонансной модели лежит процесс попарного взаимодействия волн, влияющих на динамику третьей компоненты, в условиях синхронизации их фаз ${{{\theta }}_{j}} = {{{\theta }}_{k}} + {{{\theta }}_{l}}$. Во втором порядке по ${\varepsilon }$ из неоднородных уравнений, следующих из (1.2), можно найти возмущения более высокого порядка H1, а также (используя условия разрешимости) построить амплитудные уравнения для резонансных триад, аналогичные системе, полученной в [8, 10, 11]. Для простой трехволновой системы $j,k,l$ волн (как правило, $j \ne k \ne l$) эти уравнения имеют вид
(1.3)
$\begin{gathered} \frac{{d{{A}_{j}}}}{{d{\xi }}} = - {\alpha }_{j}^{i}{{A}_{j}} + S_{{k,l}}^{j}{{A}_{k}}{{A}_{l}}\exp (i\Delta ) \\ \frac{{d{{A}_{k}}}}{{d{\xi }}} = - {\alpha }_{k}^{i}{{A}_{k}} + S_{{j,l}}^{k}{{A}_{j}}A_{l}^{*}\exp (i\Delta ) \\ \frac{{d{{A}_{l}}}}{{d{\xi }}} = - {\alpha }_{l}^{i}{{A}_{l}} + S_{{j,k}}^{l}{{A}_{j}}A_{k}^{*}\exp (i\Delta ) \\ S_{{k,l}}^{j} = \int\limits_0^{{{Y}_{k}}} {{\text{H}}_{j}^{{0 + }}} Q_{{k,l}}^{j}dY{{\left( {\int\limits_0^{{{Y}_{k}}} {{\text{H}}_{j}^{{0 + }}\left( {\frac{{\partial L({\text{H}}_{j}^{0})}}{{\partial {{{\alpha }}_{j}}}}} \right)} dY} \right)}^{{ - 1}}},\quad \Delta = \int {({{{\alpha }}_{k}} + {{{\alpha }}_{l}}} - {{{\alpha }}_{j}}{{)}^{r}}dX \\ \end{gathered} $В работе полагалось, что для каждой волновой моды безразмерный частотный параметр F, связанный с частотой зависимостью ${\omega }$ = ReF, а также приведенное безразмерное волновое число b = 103β/Re являются постоянными. Рассматривались и плоские (двумерные 2D) волны с b = 0 и косые (трехмерные 3D) волны с $b \ne $ 0.
Для удобства физической интерпретации результатов в (1.3) вводилась тригонометрическая форма записи комплексных амплитуд А = аexp(iψ), где а = |А|, ψ = arctg(Ai/Ar). Амплитудные уравнения решались для модуля амплитуд а и взаимной фазы ψ = ψ3 – ψ1 – ψ2.
Принималось, что в Ym значение пульсации массовой скорости $m = {\rho (Y)}u + {\varsigma }U(Y)$ для преобладающей волновой компоненты (такая компонента определяется из амплитудно-частотного спектра возмущений) максимально. Численно рассчитывалось значение средней массовой скорости ${\rho }U$$({{Y}_{m}})$, и начальные амплитуды Aj выражались в долях ${\rho }U$. Начальные значения амплитуд волн варьировались в широком диапазоне.
2. РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЯ
2.1. Общие положения
Рассматриваются основные закономерности взаимодействия трех волн, связанных условиями фазового синхронизма [10]. Сами триплеты могут быть двух видов – симметричные и несимметричные, в них 2D- и 3D-волны входят в разнообразных комбинациях. Для контролируемых волн наиболее представительны амплитуды 3D-компонент на f2. Представленный ниже ряд рисунков носит демонстрационный характер, в нем не конкретизируются ни состав (2D или 3D), ни значения параметров и начальных амплитуд компонент триплетов.
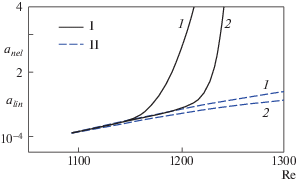
А. Существование волны накачки. Установлено, что нелинейное взаимодействие наиболее эффективно, если одна из составляющих триплета является волной накачки [7]. У такой волны максимальная начальная амплитуда, которая растет вниз по потоку в соответствии с линейным инкрементом. Такой эффективный триплет показан на рис. 1. Это несимметричный триплет, состоящий из трех 3D-волн, причем начальная амплитуда гармоники A3 (линия 3) на f2 на порядок превышает амплитуды трехмерных субгармоник A1 и A2 (линии 1, 2) на f1. Линии II показывают динамику линейных волн.
Рис. 1.
Эффективный триплет 3D-гармоники и 3D-субгармоник: I – нелинейные амплитуды гармоники (3) и субгармоник (1, 2); II – линейные амплитуды взаимодействующих волн.
Из рисунка видно, насколько эффективно и быстро нелинейный процесс приводит к выравниванию амплитуд взаимодействующих волн (линии I). Применимость слабонелинейного приближения ограничивается диапазоном A1, А2 ≤ A3. При сближении амплитуд волн могут меняться как интенсивность, так и направленность передачи энергии. Размеры сообщения не позволяют проследить за интересными особенностями динамики всех трех компонент при больших Re. Выбор такой волны накачки очень важен при рассмотрении динамики естественных возмущений.
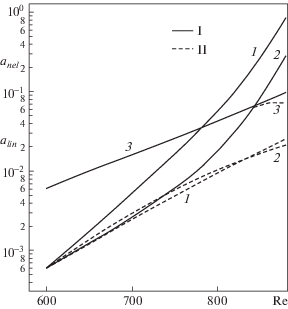
Б. Существование почти взрывного режима накачки субгармоник. Обнаружено существование так называемых каталитических режимов [1], при которых реализуется очень быстрая (близкая к взрывному) нелинейная интенсивность субгармоник. На рис. 2 показывается один из вариантов такого взаимодействия. При этом амплитуда субгармоники может превышать амплитуду вынуждающей волны, не оказывая обратного влияния. Конечно, сам пограничный слой, как естественный осциллятор, находит способы регулирования подобных всплесков, но то, что они могут выявиться при численном моделировании, необходимо знать.
В. Важная роль отводится соотношению фаз взаимодействующих колебаний. Так как амплитуды представлены в комплексной области, обнаружена важная роль соотношения фаз волн в триплете. Существует широкий диапазон параметров возмущений, в котором фаза ψ практически не влияет на нелинейную эволюцию компонент триплетов, но есть триплеты, где ее роль значительна. На рис. 3 показан такой вариант. Найдена фаза максимальной передачи энергии от гармоники к субгармонике (ψ ∼ 0), в противофазе к ней располагается фаза минимальной передачи. Характер развития субгармоники вниз по потоку зависит от интенсивности волны накачки. Если она значительна, то волны любых фаз скоро сблизятся по амплитуде, а если недостаточна, то будут наблюдаться два сценария развития субгармоники.
Рис. 3.
Зависимость степени усиления anel/alin субгармоники от начальной взаимной фазы ψ = 0, π/2, π, 3/2π (1–4).
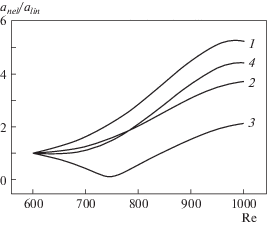
Г. Возможен режим “слабого” взаимодействия, когда невозможно определить, в какую сторону пойдет нелинейный процесс и что будет усиливаться. На рис. 4 показан один из возможных вариантов. Обычно он реализуется при малых интенсивностях гармоники (как правило, двумерной плоской или трехмерной малого азимутального ${\beta }$ компоненты).
Рис. 4.
Пример слабого взаимодействия; степени усиления anel/alin субгармоник (1, 2) и гармоники (3) при разных (I и II) начальных значениях амплитуд.
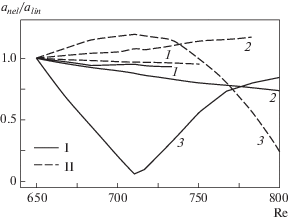
Это предварительное рассмотрение позволяет сделать вывод, что нет такого триплета, который в одиночку может представить реальную динамику нелинейного взаимодействия в сложных волновых системах, результат заведомо будет не адекватен процессу. Оказалось, что необходимо учитывать возможно большее число компонент волнового поезда, включая как самые интенсивно растущие в линейном приближении, так и самые незначительные, на первый взгляд выпадающие из числа потенциальных участников, могущие повлиять на реальную картину.
2.2. Контролируемые возмущения
В экспериментах [8] установлено, что в начальном спектре искусственно вводимых в пограничный слой возмущений фиксируются два волновых пакета на кратных частотах (основная частота гармоники f2 = 20 кГц, частота субгармоники f1 = 10 кГц), при этом доминирует пакет на f2, компоненты которого и считаются волнами накачки. Пакеты представляют собой волновые поезда широкого состава по азимутальному числу β, в которых присутствуют волны, распространяющиеся под углами –90° ≤ χ ≤ 90° к направлению основного потока (χ = arctg(β/αr). С ростом Re наблюдается значительный рост интенсивности компонент, имеющих низкие линейные инкременты (это плоские 2D- и 3D-волны высоких β). Интенсивности волновых поездов достаточно симметричны по β в исследованном интервале Re, хотя чаще в реалиях фиксируется нарушение этой симметрии, с более высокими амплитудами компонент с β < 0. Если предположить, что взаимодействие осуществляется в рамках слабонелинейной теории, то это может быть следствием разницы в нелинейных коэффициентах Q в (1.3) для положительных и отрицательных β. В данной работе моделирование осуществлялось только для β > 0, затем результаты были расширены на отрицательные β. Рассмотрен групповой триплет из 48 простых, учитывающий взаимодействие более 20 азимутальных компонент [10].
На рис. 5а приведена экспериментально измеренная сложная картина нестандартной нелинейной динамики волнового поезда на f1 вниз по потоку в разных продольных сечениях х [8]. Сечение х = 130 мм соответствует Re = 920 рис. 5б. Аномалия заключается в том, что обнаружен наибольший рост не трехмерных компонент с максимальными линейными инкрементами (размерные β ~ 0.15), как следует из линейной теории, а компоненты высоких азимутальных чисел (β ~ 0.3), так называемые “хвосты”, у которых очень низкие линейные инкременты. Такие компоненты обычно дают ничтожный вклад в энергетическую картину волнового поезда.
Рис. 5.
Моделирование динамики контролируемых возмущений: (а) – экспериментальная картина спектров; (б) – численный расчет – амплитуды субгармоник на f1 при Re = 920.
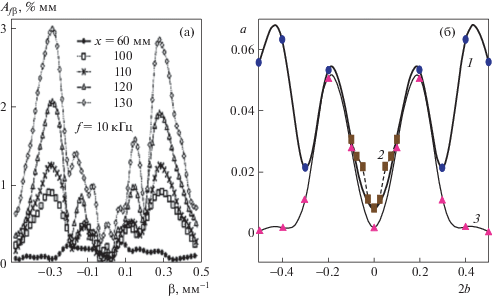
На рис. 5б приведены результаты моделирования и показана заключительная картина распределений нелинейной амплитуды субгармоники при Re = 920 (кривая 1) в сравнении с линейными значениями (3). Для сближения расчетных и экспериментальных данных были специально проработаны диапазоны, имеющие зафиксированные в [8] дополнительные нерегулярности и особенности (β ~ 0.08). На рис. 5б это показано кривой 2.
На возникающий вопрос – может ли моделирование взаимодействия в триплетах описать такую сложную аномальную динамику, дан положительный ответ, подтверждаемый сравнением экспериментальной и расчетной картин. При рассмотрении надо учесть, что на экспериментальной картине представлены размерные β.
2.3. Естественные возмущения
В основе данного моделирования лежат амплитудно-частотные спектры естественных возмущений, полученные в Т-325 экспериментальной группой А.Д. Косинова, Н.В. Семенова, Ю.Г. Ермолаева. Спектры измерены для разных диапазонов частот в широкой полосе Re. Они характеризуются отсутствием ярко выраженных преобладающих компонент, более высокими начальными амплитудами низкочастотных составляющих и преобладающим ростом высокочастотных компонент вниз по потоку. Диапазон применимости слабонелинейного приближения оценивается 600 < Re < 900. При моделировании динамики естественных возмущений [11] были рассмотрены два частотных диапазона. Узкий диапазон частот охватывал полосу (2.5 ≤ f ≤ 30) кГц с шагом Δf = 2.5 кГц. Это соответствовало безразмерным частотным параметрам (0.048 < F < < 0.576) × 10–4. Широкий диапазон (5 ≤ f ≤ 60) кГц (0.096 < F < 1.152) × 10–4 пройден с шагом Δf = 5 кГц.
Второй крайне важной особенностью являлась необходимость синхронизовать в триплетах не только частоты ω (или F), но и азимутальные волновые числа β, при полном отсутствии экспериментальных данных об их реальных значениях. Для синхронизации по β необходимо решать алгебраическую систему на совместность. При этом возникает один свободный азимутальный номер, через который определяются остальные.
Такой определяющей компонентой выбрана волна на частоте f = 20 кГц с азимутальным волновым числом 2b = 0.16. В процессе расчета моделировалось также несколько других вариантов [11]. В таблице приведены комбинации частот и волновых чисел, признанных оптимальными.
Таблица 1.
| 104F | b | f, кГц | 104F | b | f, кГц | 104F | b | f, кГц | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.048 | 0.02 | 2.5 | 2 | 0.096 | 0.04 | 5 | 3 | 0.144 | 0.06 | 7.5 |
| 4 | 0.192 | 0.08 | 10 | 5 | 0.240 | 0.10 | 12.5 | 6 | 0.288 | 0.12 | 15 |
| 7 | 0.336 | 0.14 | 17.5 | 8 | 0.384 | 0.16 | 20 | 9 | 0.432 | 0.18 | 22.5 |
| 10 | 0.480 | 0.20 | 25 | 11 | 0.528 | 0.22 | 27.5 | 12 | 0.576 | 0.24 | 30 |
На рис. 6 показано сравнение результатов моделирования и экспериментальных данных в слабонелинейной области для двух вариантов диапазона частот (рис. 6а, 6б) в сравнении с экспериментальными спектрами (рис. 6в). Результаты моделирования оказались в достаточной степени близки друг другу и экспериментальным данным, что свидетельствует об адекватности рассматриваемой модели истинному процессу эволюции естественных вихревых возмущений при умеренном сверхзвуковом числе М = 2. Интегрирование начиналось от Re = 620, амплитудные спектры в этом сечении на рисунках обозначены цифрой 1.
Рис. 6.
Результаты моделирования динамики естественных возмущений в узком (а) и широком (б) диапазонах частот в сравнении с экспериментом (в); Re = 620, 720, 820, 920 (1–4); линейные спектры в Re = 820 (5).
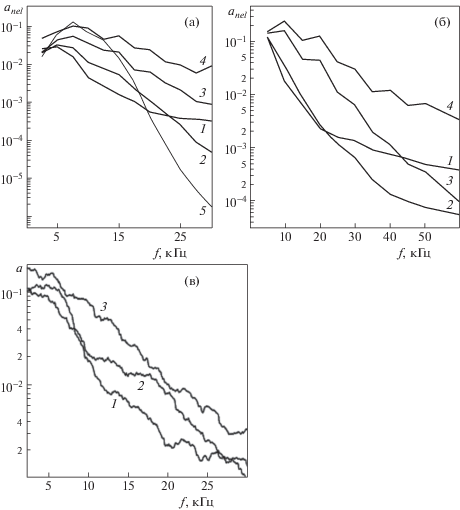
Сравнение расчетных спектров при другом выборе несущей частоты (не 20, а 15 кГц) показало, что такая перенормировка не слишком сказывается на характере продольной динамики спектральных компонент, по-прежнему сильнее растут высокочастотные компоненты и следует ожидать, что при больших Re картины станут адекватны.
Определенные усилия были предприняты для понимания того, каким образом формируется в эксперименте начальный спектр при Re ∼ 600. Для этого начало расчетов было перенесено в более устойчивую область при низком Re0 ∼ 300. Изучалась продольная динамика возмущений разных начальных интенсивностей в Re0. Тестировались разные варианты начальных комбинаций.
Поставленная цель не была достигнута и вопрос ждет последующих исследований. По-видимому, для определения уровня возмущений в пограничном слое вблизи нижней ветви нейтральной кривой при частотах из спектра возмущений в Т-325 нужно рассматривать взаимодействие акустических волн с пограничным слоем, как это сделано в [12].
В целом можно констатировать, что хотя рассмотренная модель взаимодействия возмущений в рамках трехволновых резонансных систем является первым шагом в описании динамики естественных волн в слабонелинейной области развития и сильным упрощением реальных нелинейных процессов, она отражает ряд важных особенностей и адекватна истинному процессу. Конечно, в дальнейшем эксперименты должны дать ряд более точных определяющих параметров, которые позволят приблизить моделирование к реальному процессу.
ЗАКЛЮЧЕНИЕ
Рассмотренные основные закономерности взаимодействия в единичных триплетах, составленных из плоских и трехмерных компонент, позволили перейти к реализации группового взаимовлияния, рассмотренного в работе для естественных и контролируемых возмущений. Изученная возможность перераспределения энергии в сложных волновых системах показала полную адекватность реальным нелинейным процессам на ранних стадиях перехода в сверхзвуковых пограничных слоях сжимаемого газа при М = 2.
Работа выполнена в рамках Программы фундаментальных научных исследований государственных академий наук на 2013–2020 годы (проект АААА-22.6.4.) и финансовой поддержке Российского научного фонда (проект № 17-19-01289).
Список литературы
Бойко А.В., Грек Г.Р., Довгаль А.В., Козлов В.В. Физические механизмы перехода к турбулентности в открытых течениях. М.–Ижевск: НИЦ “Регулярная и хаотическая динамика”, Ин-т компьютерных исслед., 2006. 304 с.
Balakumar P. Receptivity of a Supersonic Boundary Layer to Acoustic Disturbances// AAIA J. 2009. V. 47. № 5. P. 463–471.
Ma Y., Zhong X. Receptivity of a supersonic boundary layer over a flat plate. Part 1. Wave structures and interactions layers // J. Fluid Mech. 2003. V. 488. P. 31–78.
Mayer C., Wernz S., Fasel H.F. Numerical investigation of the nonlinear transition regime in Mach 2 boundary layer layers // J. Fluid Mech. 2011. V. 668. P. 113–149.
Zhong L.X., Wang X. Direct Numerical Simulation on the Receptivity, Instability, and Transition of Hypersonic Boundary // Annu. Rev. Fluid Mech. 2012. V. 44. P. 527–561.
Craik A.D.D. Non-linear resonant instability in boundary layers // J. Fluid Mech. 1971. V. 50. P. 393–413.
Гапонов С.А., Масленникова И.И. Субгармоническая неустойчивость сверхзвукового пограничного слоя // Теплофизика и аэромеханика. 1997. Т. 4. № 1. С. 3–12.
Ермолаев Ю.Г., Косинов А.Д., Семенов Н.В. Характерные особенности слабонелинейного взаимодействия волн неустойчивости в сверхзвуковом пограничном слое // Вест. НГУ. Сер. Физика. 2008. Т. 3. Вып. 3. С. 3–13.
Гапонов С.А., Маслов А.А. Развитие возмущений в сжимаемых потоках. Новосибирск: Наука, 1980. 134 с.
Гапонов С.А., Терехова Н.М. Трехволновые взаимодействия контролируемых возмущений в сверхзвуковом пограничном слое // Междунар. журн. прикладных и фундаментальных исслед. 2016. Т. 6. № 5. С. 833–838.
Терехова Н.М. Моделирование нелинейного развития естественных возмущений в сверхзвуковом пограничном слое в рамках слабонелинейной теории устойчивости // Междунар. журн. прикладных и фундаментальных исслед. 2017. Т. 10. № 1. С. 30–35.
Гапонов С.А. Ламинарно-турбулентный переход сверхзвукового пограничного слоя в присутствии внешних возмущений // Теплофизика и аэромеханика. 2019. Т. 26. № 3. С. 407–416.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика жидкости и газа