Известия РАН. Механика жидкости и газа, 2020, № 5, стр. 3-6

Осредненные виброконвективные течения жидкости в двухслойных системах разной проницаемости при нулевой гравитации

Е. А. Колчанова^*

Пермский государственный национальный исследовательский университет
Пермь, Россия

Поступила в редакцию 01.03.2020
После доработки 12.03.2020
Принята к публикации 12.03.2020

DOI: 10.31857/S0568528120050096

Аннотация

Исследуется осредненная валиковая конвекция, возникающая под действием вибрации в двухслойной жидкостной системе с однородной пористой зоной разной проницаемости. Система совершает высокочастотные осцилляции поперечно вертикальному градиенту температуры в невесомости. Моделирование конвективной задачи проводится на основе метода осреднения. Определяются диапазоны частот вибрации и проницаемостей пористой зоны, характерные для коротковолновых и длинноволновых валов. При нулевой гравитации обнаружена резкая смена вида валов с ростом проницаемости, типичная для свободной тепловой конвекции в слоистых системах в обычных земных условиях. Найдено минимальное значение числа Дарси, ниже которого резкий переход от коротковолновой к длинноволновой конвекции с ростом частоты вибрации не происходит.

Ключевые слова: двухслойная система, пористая зона, разная проницаемость, продольные вибрации, предельное число Дарси

Тепловая конвекция в слоистых жидкостных системах, содержащих пористую зону в гравитационном поле, может возникать двумя способами: 1 – в виде длинноволновых валов, проникающих во все слои, 2 – в виде коротковолновых валов, формирующихся, главным образом, внутри жидкостных слоев без пористой зоны [1, 2]. Такое различие в поведении жидкости проявляется при изменении отношения толщин слоев, проницаемости пористой зоны. Смена типа валов также возможна под действием вертикальной высокочастотной вибрации [3], вызывающей осредненное валиковое течение в слоях. Однако порог возбуждения этих валов оказывается несколько выше, чем его значение в отсутствие вибрации.

В невесомости гравитационной конвекции нет. Течение здесь можно создать с помощью осредненной вибрационной силы в случае, когда система совершает колебания поперечно градиенту температуры. Эта ситуация для однослойных жидкостной и пористой систем подробно изучена в работах [4, 5]. В настоящем исследовании уделяется внимание особенностям термовибрационной конвекции в двухслойной системе, включающей пористую зону при нулевой гравитации. Изучается смена типа валов с ростом частоты вибрации и проницаемости этой зоны.

ТЕОРИЯ

В работе исследуется возникновение осредненного виброконвективного течения в двухслойной жидкостной системе, содержащей пористую зону и участвующей в продольных высокочастотных осцилляциях в условиях нулевой гравитации. Поперек слоев создается градиент температуры таким образом, что подогрев системы осуществляется снизу (рис. 1). Период вибрации 2π/ω считается малым по сравнению с характерными временами распространения гидродинамических и тепловых возмущений в слоях, а ее амплитуда a – малой по сравнению с толщиной слоев [4, 5]. Пористая среда однородна и имеет пористость m, связанную с проницаемостью K формулой Кармана–Козени.

Рис. 1.

Двухслойная система с пористой зоной осциллирует в поперечном градиенту температуры направлении в невесомости.

Уравнения осредненной термовибрационной конвекции несжимаемой жидкости приводятся в неинерциальной системе отсчета и получаются на основе метода осреднения. Этот метод был впервые применен для однослойных жидкостной и пористой систем в работах [4, 5]. Выпишем аналогичные уравнения для двухслойной системы “жидкость–пористая зона” с учетом безразмерных параметров в жидкостном слое

(1)

$\frac{{{\text{Da}}}}{{{{{\Pr }}_{m}}}}\left\{ {\frac{{\partial {\mathbf{v}}}}{{\partial t}} + b\left( {{\mathbf{v}}\nabla } \right){\mathbf{v}}} \right\} = - \nabla {{p}_{f}} + {\text{Da}}\Delta {\mathbf{v}} + {{R}_{{\text{v}}}}\left( {{\mathbf{V}}\nabla } \right)\left( {T{\mathbf{n}} - {\mathbf{V}}} \right)$

(2)

$\frac{\kappa }{b}\frac{{\partial T}}{{\partial t}} + \kappa \left( {{\mathbf{v}}\nabla } \right)T = \Delta T,\quad {\text{div}}\,{\mathbf{v}} = 0$

(3)

${\text{rot}}\,{\mathbf{V}} = \nabla T \times {\mathbf{n}},\quad {\text{div}}\,{\mathbf{V}} = 0$

в пористом слое

(4)

$\frac{{{\text{Da}}}}{{{{{\Pr }}_{m}}}}\left( {\frac{1}{m}\frac{{\partial {\mathbf{u}}}}{{\partial t}} + \frac{1}{{{{m}^{2}}}}\left( {{\mathbf{u}}\nabla } \right){\mathbf{u}}} \right) = - \nabla {{p}_{m}} - {\mathbf{u}} + {{R}_{{\text{v}}}}\left( {{\mathbf{W}}\nabla } \right)\left( {\vartheta {\mathbf{n}} - \frac{b}{{m\delta }}{\mathbf{W}}} \right)$

(5)

$\frac{{\partial \vartheta }}{{\partial t}} + \left( {{\mathbf{u}}\nabla } \right)\vartheta = \Delta \vartheta ,\quad {\text{div}}\,{\mathbf{u}} = 0$

(6)

${\text{rot}}\,{\mathbf{W}} = \nabla \left( {\delta \vartheta } \right) \times {\mathbf{n}},\quad {\text{div}}\,{\mathbf{W}} = 0$

где введены переменные величины для осредненного течения в слое жидкости: v – скорость жидкости, p_f – конвективная добавка к давлению, T – отклонение температуры от некоторого среднего значения, V – соленоидальная часть вектора Tn, определяющая амплитуду пульсационной скорости жидкости. Аналогичным образом вводятся переменные величины в пористом слое u, p_m, ϑ и W, соответственно, только в уравнении движения (4) используется скорость фильтрации жидкости ${\mathbf{u}}$. Вектор ${\mathbf{n}} = (1,\,0,\,0)$ направлен по горизонтальной оси x, параллельной оси вибрации. Разницу в тепловых свойствах сред описывают такие параметры, как отношение теплопроводностей насыщенной пористой среды и жидкости κ и отношение теплоемкостей среды и жидкости b.

Верхняя и нижняя границы двухслойной системы являются твердыми и идеально теплопроводными. Граница раздела плоская и проницаемая для жидкости.

(7)

$z = d{\text{:}}\quad {\mathbf{v}} = 0,\quad T = {{T}_{f}}$

(8)

$\begin{gathered} z = 0{\text{:}}\quad T = \vartheta ,\quad \frac{{\partial T}}{{\partial z}} = \kappa \frac{{\partial \vartheta }}{{\partial z}},\quad {{{\mathbf{v}}}_{z}} = {{{\mathbf{u}}}_{z}},\quad {{{\mathbf{v}}}_{x}} = 0, \\ {{p}_{f}} + {{R}_{{v}}}\left\{ {{\mathbf{V}}_{z}^{2} - \frac{b}{{m\delta }}{\mathbf{W}}_{z}^{2}} \right\} = {{p}_{m}},\quad {{{\mathbf{V}}}_{z}} = {{{\mathbf{W}}}_{z}},\quad \delta {{{\mathbf{V}}}_{x}} = {{{\mathbf{W}}}_{x}} \\ \end{gathered} $

(9)

$z = - 1{\text{:}}\quad {{{\mathbf{u}}}_{z}} = 0,\quad T = {{T}_{m}}$

Безразмерные параметры в системе уравнений (1)–(6) и граничных условиях (7)–(9) – вибрационное число Рэлея–Дарси ${{R}_{{v}}} = {{\left( {{{\beta }_{T}}a\omega \Delta T} \right)}^{2}}K{\text{/}}2{{\nu }_{f}}{{\chi }_{{eff}}}$, число Прандтля ${{\Pr }_{m}} = b{{\nu }_{f}}{\text{/}}{{\chi }_{{eff}}}$, число Дарси ${\text{Da}} = K{\text{/}}h_{m}^{2}$, отношение толщин жидкостного и пористого слоев $d = {{h}_{f}}{\text{/}}{{h}_{m}}$. В уравнениях и граничных условиях также содержится дополнительный параметр $\delta = {{{{\Omega }^{2}}} \mathord{\left/ {\vphantom {{{{\Omega }^{2}}} {[mb(1 + {{\Omega }^{2}}{\text{/}}{{m}^{2}})]}}} \right. \kern-0em} {[mb(1 + {{\Omega }^{2}}{\text{/}}{{m}^{2}})]}}$, где Ω – безразмерная частота вибрации. Он определяет разницу в амплитудах касательных скоростей пульсаций жидкости в слоях и вблизи их границы раздела (см. формулу (8)).

Численное решение системы уравнений (1–6) с граничными условиями (7)–(9) получено на основе метода стрельбы. Выбраны параметры слоев, характерные для системы “вода–стеклянные сферы”. Находились пороговое число Рэлея–Дарси и длина волны осредненных конвективных валов, формирующихся непосредственно после потери устойчивости основного пульсационного течения. Основное течение представляло собой осциллирующее замкнутое плоскопараллельное течение с нулевой средней скоростью при вертикальном градиенте температуры. При превышении порогового числа Рэлея–Дарси на фоне высокочастотных пульсаций появлялись осредненные валы.

РЕЗУЛЬТАТЫ РАСЧЕТОВ

На рис. 2а и рис. 2б показаны графики зависимости порогового числа Рэлея–Дарси и длины волны осредненных конвективных валов от числа Дарси при разных фиксированных значениях безразмерной частоты вибрации и отношении толщин слоев d = 0.15. При параметрах системы из области A на рис. 2а жидкость в среднем остается неподвижной на фоне быстро осциллирующего течения. При параметрах из области B на рис. 2а в слоях генерируется осредненное валиковое течение. Длина волны валов растет с ростом числа Дарси (рис. 2б). Последнее задает характер фильтрации жидкости в порах и по определению является безразмерной проницаемостью пористого слоя. Поэтому рост этого параметра сопровождается переходом от коротковолновых валов, локализующихся в слое жидкости над порами, к длинноволновым валам, проникающим в пористую среду (рис. 2б). Этот переход происходит резко, скачком, что является характерной особенностью свободной тепловой конвекции в слоистых системах, включающих несколько чередующихся слоев жидкости и пористой среды в гравитационном поле (синяя и красная сплошные линии и черная штриховая линия на рис. 2б) [1, 2]. Описанная особенность впервые выявлена автором в двухслойной системе, осциллирующей при нулевой гравитации.

Рис. 2.

Зависимости порогового числа Рэлея–Дарси (а) и длины волны (б) осредненных конвективных валов, формирующихся сразу после потери устойчивости основного пульсационного течения, от числа Дарси при разных частотах вибрации: Ω = 0.1, 0.5, 0.8, 10 (1–4). Область A относится к основному пульсационному течению с нулевой средней скоростью, область B характеризует осредненное конвективное течение.

На рис. 3 показана граница скачкообразного перехода от осредненных коротковолновых валов к длинноволновым валам. Этот переход наблюдается при увеличении частоты вибрации и проницаемости среды. Из рис. 3 видно, что имеется минимальное асимптотическое значение числа Дарси ${\text{D}}{{{\text{a}}}_{*}} \approx 4 \cdot {{10}^{{ - 6}}}$, ниже которого переход от коротковолновой к длинноволновой конвекции вообще не происходит.

Рис. 3.

Зависимость частоты вибрации от числа Дарси, определяющая границу между длинноволновыми (область LW rolls) и коротковолновыми осредненными валами (область SW rolls), образующимися сразу после потери устойчивости основного пульсационного течения.

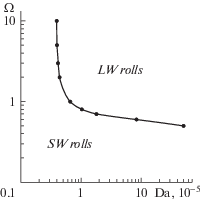
Отметим, что в сравнении со свободной конвекцией в земных условиях порог возбуждения осредненного виброконвективного течения в невесомости может не только понижаться с ростом проницаемости, но и повышаться в зависимости от выбора частоты вибрации. При безразмерных частотах, больших 0.8, рост проницаемости обычным образом усиливает конвекцию. В противоположном случае возможно подавление конвекции с ростом числа Дарси (рис. 2а). Такое различие, на наш взгляд, связано со сложной зависимостью параметра δ, характеризующего разницу амплитуд касательных скоростей пульсаций на границе раздела слоев системы.

ЗАКЛЮЧЕНИЕ

Рассмотрена задача о возбуждении осредненной термовибрационной конвекции при нулевой гравитации. Конвективные течения возникали на фоне высокочастотных осцилляций жидкости в двухслойной системе с пористой зоной различной проницаемости. Определены диапазоны частот продольной вибрации и проницаемостей пористой зоны, при которых происходит резкий переход от коротковолновых к длинноволновым конвективным валам. Найдено минимальное асимптотическое значение числа Дарси и показано, что ниже этого значения резкое изменение длины волны валов с ростом частоты осцилляций не наблюдается.

Список литературы

Hirata S.C., Goyeau B., Gobin D. Stability of thermosolutal natural convection in superposed fluid and porous layers // Transport in Porous Media. 2009. V. 78. P. 525–536.
Kolchanova E.A., Lyubimov D.V., Lyubimova T.P. The onset and nonlinear regimes of convection in a two-layer system of fluid and porous medium saturated by the fluid // Transport in Porous Media. 2013. V. 97. № 1. P. 25–42.
Любимов Д.В., Любимова Т.П., Муратов И.Д., Шишкина Е.А. Влияние вибраций на возникновение конвекции в системе горизонтального слоя чистой жидкости и слоя пористой среды, насыщенной жидкостью // Изв. РАН. МЖГ. 2008. № 5. С. 132–143.
Gershuni G.Z., Lyubimov D.V. Thermal Vibrational Convection. Wiley: N.Y. et al., 1998. 358 p.
Зеньковская С.М., Роговенко Т.Н. Фильтрационная конвекция в высокочастотном вибрационном поле // Прикладная механика и техническая физика. 1999. № 3. С. 22–29.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал