Известия РАН. Механика жидкости и газа, 2020, № 6, стр. 98-105

ВРАЩАТЕЛЬНЫЕ КОЛЕБАНИЯ ПОРИСТОЙ СФЕРИЧЕСКОЙ ОБОЛОЧКИ В ВЯЗКОЙ ЖИДКОСТИ

О. А. Базаркина^a, *, Н. Г. Тактаров^a, **

^a Мордовский государственный педагогический институт им. М.Е. Евсевьева
Саранск, Россия

^* E-mail: o.a.bazarkina@mail.ru
^** E-mail: n.g.taktarov@mail.ru

Поступила в редакцию 25.02.2020
После доработки 10.03.2020
Принята к публикации 12.03.2020

DOI: 10.31857/S0568528120060043

Аннотация

Определены течения вязкой жидкости, вызванные вращательными колебаниями погруженной в нее пористой сферической оболочки. В приближении Стокса получены аналитические решения нестационарного уравнения Бринкмана в области внутри пористой оболочки и уравнения Навье–Стокса – вне оболочки. Определен момент сил трения, действующих на контрольную сферическую поверхность вокруг пористого тела. Приведен анализ полученных решений. Рассмотрены различные частные случаи, в том числе случай равномерного вращения оболочки.

Ключевые слова: пористая сферическая оболочка, вращательно-колебательное движение, уравнение Бринкмана

В рамках модели фильтрации Бринкмана рассматриваются течения вязкой жидкости, вызванные вращательно-колебательным движением погруженной в нее пористой сферической оболочки. Подобные задачи могут представлять интерес для изучения некоторых технологических процессов, в которых используются пористые среды [1].

Задачи об обтекании пористых сферических оболочек стационарным потоком вязкой жидкости рассматривались ранее для закона фильтрации Дарси в работах [2, 3]. Поперечное обтекание стационарным потоком вязкой жидкости пористой цилиндрической оболочки и коаксиального с ней сплошного (непроницаемого) цилиндрического ядра исследовано в [4] с использованием уравнения Бринкмана и граничных условий, являющихся частным случаем граничных условий [5].

Целью настоящей работы является определение полей скоростей жидкости в областях внутри и вне пористой сферической оболочки в рамках модели фильтрации Бринкмана в приближении Стокса, а также оценка момента сил трения, действующих на контрольную сферическую поверхность, охватывающую пористую сферическую оболочку, совершающую вращательно-колебательное движение в вязкой жидкости вокруг фиксированной оси.

1. ПОСТАНОВКА ЗАДАЧИ

Рассматриваются течения вязкой жидкости, вызванные вращательно-колебательным движением погруженной в нее пористой сферической оболочки. Внутренний и внешний радиусы пористой сферической оболочки равны соответственно а и b (a < b). Предполагается, что пористая среда является однородной, изотропной, недеформируемой, имеет высокий коэффициент проницаемости K и достаточно большую пористость $\Gamma $. При таких свойствах пористой среды в ней могут возникать колебательные движения жидкости со скоростью, заметно отличающейся от скорости пористой среды.

Угловую скорость вращения пористой сферической оболочки с центром О вокруг фиксированной оси, проходящей через точку О, запишем как функцию от времени t* в виде Ω* = ${{\Omega }_{0}}{\text{exp}}( - i\omega t*)$, где Ω₀ – постоянный вещественный вектор, ω – частота колебаний. Скорость любой точки вращающегося твердого тела с радиусом-вектором r*, выходящим из точки О, имеет вид: ${\mathbf{v}}* = {\mathbf{\Omega }}{\text{*}} \times {\mathbf{r}}{\text{*}}$. Знаком “*” здесь и далее обозначены размерные переменные (но не размерные параметры), чтобы отличать их от безразмерных, обозначаемых теми же символами. В окончательных результатах везде подразумеваются действительные части комплексных выражений.

Течение вязкой жидкости внутри и вне пористой сферической оболочки, совершающей вращательно-колебательные движения, рассматривается в неподвижной декартовой системе координат Ох*у*z*, начало которой совпадает с центром О сферической оболочки. Ось Оz* этой системы координат направлена вдоль единичного вектора ${\mathbf{e}} = {{{\mathbf{\Omega }}}_{0}}{\text{/}}{{\Omega }_{0}}$.

Для решения задачи введем сферическую систему координат r*, θ, φ c ортонормированным базисом e_r, e_θ, e_φ, полярная ось которой совмещена с осью Оz*. Полярный угол θ отсчитывается от положительной полуоси Оz*.

Величины, относящиеся к областям, занятым свободной жидкостью внутри полости (0 < r* < a), в пористой оболочке (а < r* < b) и вне пористой среды (r* > b), обозначаются индексами 1, 2 и 3 соответственно.

Нестационарные уравнения движения свободной жидкости в областях 1, 3 запишем в приближении Стокса

(1.1)

$\frac{{\partial {\mathbf{u}}_{j}^{*}}}{{\partial t{\text{*}}}} = - \frac{1}{\rho }{\text{grad*}}p_{j}^{*} + \eta \nabla {{{\text{*}}}^{2}}{\mathbf{u}}_{j}^{*},\quad {\text{div*}}{\mathbf{u}}_{j}^{*} = 0\quad {\text{(}}j{\text{ }} = {\text{1,3)}}$

Здесь ${\mathbf{u}}_{j}^{*}$ – скорость свободной жидкости, $p_{j}^{*}$ – давление, ρ – плотность жидкости, η – вязкость свободной (вне пористой среды) жидкости, $\nabla {\text{*}}$ – набла оператор.

Уравнения нестационарного движения вязкой жидкости в пористой среде (область 2) в рамках модели Бринкмана запишем в виде [5–9, 13]

(1.2)

$\frac{\rho }{\Gamma }\frac{{\partial {\mathbf{u}}_{2}^{*}}}{{\partial t{\text{*}}}} = - {\text{grad*}}p_{2}^{*} + \eta {\text{'}}\nabla {{{\text{*}}}^{2}}{\mathbf{u}}_{2}^{*} - \frac{\eta }{K}({\mathbf{u}}_{2}^{*} - {\mathbf{u}}*),\quad {\text{div*}}{\mathbf{u}}_{2}^{*} = 0$

Здесь $\Gamma = {\text{const}}$ – пористость, ${\mathbf{u}}_{2}^{*}$ – скорость фильтрации, $p_{2}^{*}$ – среднее по объему пор давление, η' – величина с размерностью вязкости, ${\mathbf{u}}* = \Gamma {\mathbf{v}}{\text{*}}$.

Вследствие осевой симметрии относительно оси вращения давление выпадает из уравнений (1.1), (1.2). Предполагаем, что $u_{{j\varphi }}^{*} \ne 0$, $u_{{jr}}^{*} = 0$, $u_{{j\theta }}^{*} = 0$ (j = 1, 2, 3), и что от азимутального угла φ все величины не зависят вследствие осевой симметрии.

Уравнения (1.1), (1.2) в сферической системе координат примут вид

(1.3)

$\rho \frac{{\partial u_{{j\varphi }}^{*}}}{{\partial t{\text{*}}}} = \eta \left( {\Delta {\text{*}}u_{{j\varphi }}^{*} - \frac{{u_{{j\varphi }}^{*}}}{{r{{{\text{*}}}^{2}}{\text{si}}{{{\text{n}}}^{2}}\theta }}} \right)\quad (j = 1,3)$

$\frac{\rho }{\Gamma }\frac{{\partial u_{{2\varphi }}^{*}}}{{\partial t{\text{*}}}} = \eta {\text{'}}\left( {\Delta {\text{*}}u_{{2\varphi }}^{*} - \frac{{u_{{2\varphi }}^{*}}}{{r{{{\text{*}}}^{2}}{\text{si}}{{{\text{n}}}^{2}}\theta }}} \right) - \frac{\eta }{K}(u_{{2\varphi }}^{*} - u_{\varphi }^{*})$

Здесь $u_{\varphi }^{*} = \Gamma {v}_{\varphi }^{*}$, ${v}_{\varphi }^{*} = {{\Omega }_{0}}\exp ( - i\omega t*)r{\text{*sin}}\theta $.

Граничные условия к уравнениям (1.3) имеют следующий вид.

На внутренней поверхности пористой оболочки при r* = a

(1.4)

$u_{{1\varphi }}^{*} - {v}_{\varphi }^{*} = u_{{2\varphi }}^{*} - \Gamma {v}_{\varphi }^{*}$

$\Lambda \left[ {\eta {\text{'}}\left( {\frac{{\partial (u_{{2\varphi }}^{*} - \Gamma {v}_{\varphi }^{*})}}{{\partial r{\text{*}}}} - \frac{{u_{{2\varphi }}^{*} - \Gamma {v}_{\varphi }^{*}}}{a}} \right) - \eta \left( {\frac{{\partial (u_{{1\varphi }}^{*} - {v}_{\varphi }^{*})}}{{\partial r{\text{*}}}} - \frac{{u_{{1\varphi }}^{*} - {v}_{\varphi }^{*}}}{a}} \right)} \right] = - \eta (u_{{2\varphi }}^{*} - \Gamma {v}_{\varphi }^{*})$

На внешней поверхности пористой оболочки при r* = b

$u_{{2\varphi }}^{*} - \Gamma {v}_{\varphi }^{*} = u_{{3\varphi }}^{*} - {v}_{\varphi }^{*}$

$\Lambda \left[ {\eta {\text{'}}\left( {\frac{{\partial (u_{{2\varphi }}^{*} - \Gamma {v}_{\varphi }^{*})}}{{\partial r{\text{*}}}} - \frac{{u_{{2\varphi }}^{*} - \Gamma {v}_{\varphi }^{*}}}{b}} \right) - \eta \left( {\frac{{\partial (u_{{3\varphi }}^{*} - {v}_{\varphi }^{*})}}{{\partial r{\text{*}}}} - \frac{{u_{{3\varphi }}^{*} - {v}_{\varphi }^{*}}}{b}} \right)} \right] = \eta (u_{{2\varphi }}^{*} - \Gamma {v}_{\varphi }^{*})$

Здесь Λ – параметр с размерностью длины. Параметр Λ определяется равенством $\Lambda = \sqrt K {\text{/}}\tau $, где τ – безразмерный параметр, характеризующий свойства пористой среды [5–7]. Отметим, что граничные условия (1.4) являются обобщением граничных условий, приведенных в [5–7, 10, 11] для неподвижной плоской поверхности раздела пористой среды и жидкости, на случай движущейся сферической поверхности.

К граничным условиям (1.4) следует добавить также условие конечности решений всюду в областях их определения, в том числе при $r* \to 0$ и $r* \to \infty $.

2. РЕШЕНИЕ ЗАДАЧИ

Введем безразмерные переменные, принимая за единицу длины b, за единицу времени 1/ω, за единицу скорости ${{{v}}_{0}} = {{\Omega }_{0}}b$: ${\mathbf{r}} = {\mathbf{r}}{\text{*/}}b$, $t = \omega t{\text{*}}$, ${{{\mathbf{u}}}_{{1\varphi }}} = {\mathbf{u}}_{{1\varphi }}^{*}{\text{/}}{{{v}}_{0}}$, ${{{\mathbf{u}}}_{{2\varphi }}} = {\mathbf{u}}_{{2\varphi }}^{*}{\text{/}}{{{v}}_{0}}$, ${{{\mathbf{u}}}_{{3\varphi }}} = {\mathbf{u}}_{{3\varphi }}^{*}{\text{/}}{{{v}}_{0}}$, u = ${\mathbf{u}}{\text{*/}}{{{v}}_{0}} = \Gamma ({\mathbf{e}} \times {\mathbf{r}})$exp(–it).

Уравнения (1.3) движения жидкости в безразмерном виде в областях 1 ($0 < r < \alpha $), 2 ($\alpha < r$ < 1), 3 (r > 1) примут вид

(2.1)

$\frac{{\omega {{b}^{2}}}}{\nu }\frac{{\partial {{u}_{{j\varphi }}}}}{{\partial t}} = \Delta {{u}_{{j\varphi }}} - \frac{{{{u}_{{j\varphi }}}}}{{{{r}^{2}}{{{\sin }}^{2}}\theta }}\quad (j = 1,\;3)$

$\frac{{\omega {{b}^{2}}}}{{\Gamma \nu }}\frac{{\partial {{u}_{{2\varphi }}}}}{{\partial t}} = \frac{1}{{{{\gamma }^{2}}}}\left[ {\Delta {{u}_{{2\varphi }}} - \frac{{{{u}_{{2\varphi }}}}}{{{{r}^{2}}{{{\sin }}^{2}}\theta }}} \right] - \frac{{{{b}^{2}}}}{K}({{u}_{{2\varphi }}} - \Gamma r\sin \theta {{e}^{{ - it}}})$

Здесь $\alpha = a{\text{/}}b$ (α < 1), ${{\gamma }^{2}} = \eta {\text{/}}\eta {\text{'}}$, $\nu = \eta {\text{/}}\rho $,

$\Delta f = \frac{1}{{{{r}^{2}}}}\frac{\partial }{{\partial r}}\left( {{{r}^{2}}\frac{{\partial f}}{{\partial r}}} \right) + \frac{1}{{{{r}^{2}}\sin \theta }}\frac{\partial }{{\partial \theta }}\left( {\sin \theta \frac{{\partial f}}{{\partial \theta }}} \right)$

Безразмерные граничные условия

(2.2)

${\text{при}}\quad r = \alpha {\text{:}}\,\,{{u}_{{1\varphi }}} - {{{v}}_{\varphi }} = {{u}_{{2\varphi }}} - \Gamma {{{v}}_{\varphi }},\quad {{{v}}_{\varphi }} = \alpha {{e}^{{ - it}}}\sin \theta $

$\lambda \left[ {\frac{1}{{{{\gamma }^{2}}}}\left( {\frac{{\partial {{u}_{{2\varphi }}}}}{{\partial r}} - \frac{{{{u}_{{2\varphi }}}}}{\alpha }} \right) - \left( {\frac{{\partial {{u}_{{1\varphi }}}}}{{\partial r}} - \frac{{{{u}_{{1\varphi }}}}}{\alpha }} \right)} \right] = - ({{u}_{{2\varphi }}} - \Gamma \alpha \sin \theta {{e}^{{ - it}}})$

${\text{при}}\quad r = 1{\text{:}}\,\,{{u}_{{2\varphi }}} - \Gamma {{{v}}_{\varphi }} = {{u}_{{3\varphi }}} - {{{v}}_{\varphi }},\quad {{{v}}_{\varphi }} = {{e}^{{ - it}}}\sin \theta $

$\lambda \left[ {\frac{1}{{{{\gamma }^{2}}}}\left( {\frac{{\partial {{u}_{{2\varphi }}}}}{{\partial r}} - {{u}_{{2\varphi }}}} \right) - \left( {\frac{{\partial {{u}_{{3\varphi }}}}}{{\partial r}} - {{u}_{{3\varphi }}}} \right)} \right] = {{u}_{{2\varphi }}} - \Gamma \sin \theta {{e}^{{ - it}}}$

${\text{при}}\quad r \to \infty {\text{:}}\,\,{{u}_{{3\varphi }}} = 0$

Здесь $\lambda = \Lambda {\text{/}}b$.

Скорость жидкости в областях 1, 2, 3 будем искать в виде [12, §24]

${{u}_{{1\varphi }}} = {{e}^{{ - it}}}{{F}_{1}}(r)\sin \theta ,\quad {{u}_{{2\varphi }}} = {{e}^{{ - it}}}{{F}_{2}}(r)\sin \theta ,\quad {{u}_{{3\varphi }}} = {{e}^{{ - it}}}{{F}_{3}}(r)\sin \theta $

Подставляя в (2.1) выражения для ${{u}_{{1\varphi }}}$, ${{u}_{{2\varphi }}}$ и ${{u}_{{3\varphi }}}$, получим уравнения для определения функций F₁(r), F₂(r) и F₃(r). Граничные условия к этим уравнениям имеют вид

(2.3)

${\text{при}}\quad r = \alpha {\text{:}}\,\,{{F}_{1}}(r) - {{F}_{2}}(r) = \alpha (1 - \Gamma )$

$\lambda \left[ {\frac{1}{{{{\gamma }^{2}}}}\left( {F_{2}^{'}(r) - \frac{{{{F}_{2}}(r)}}{\alpha }} \right) - \left( {F_{1}^{'}(r) - \frac{{{{F}_{1}}(r)}}{\alpha }} \right)} \right] = - {{F}_{2}}(r) + \alpha \Gamma $

${\text{при}}\quad r = 1{\text{:}}\,\,{{F}_{2}}(r) - {{F}_{3}}(r) = \Gamma - 1$

$\lambda \left[ {\frac{1}{{{{\gamma }^{2}}}}(F_{2}^{'}(r) - {{F}_{2}}(r)) - (F_{3}^{'}(r) - {{F}_{3}}(r))} \right] = {{F}_{2}}(r) - \Gamma $

Сюда добавляется также условие конечности решений в областях их определения.

Уравнение для F₁(r) имеет вид

(2.4)

${{r}^{2}}F_{1}^{{''}}(r) + 2rF_{1}^{'}(r) + (m_{2}^{2}{{r}^{2}} - 2){{F}_{1}}(r) = 0$

где $m_{2}^{2} = 2i{{\left( {b{\text{/}}{{\delta }_{2}}} \right)}^{2}}$, ${{m}_{2}} = (b{\text{/}}{{\delta }_{2}})\left( {1 + i} \right)$.

Конечное при $r \to 0$ решение уравнения (2.4) имеет вид

(2.5)

${{F}_{1}}(r) = \frac{{{{A}_{1}}}}{{m_{2}^{2}{{r}^{2}}}}\left( {\sin {{m}_{2}}r - {{m}_{2}}r\cos {{m}_{2}}r} \right)$

Здесь А₁ – неопределенный коэффициент.

Уравнение для F₂(r)

(2.6)

${{r}^{2}}F_{2}^{{''}}(r) + 2rF_{2}^{'}(r) + (m_{1}^{2}{{r}^{2}} - 2){{F}_{2}}(r) + 2{{\gamma }^{2}}{{\left( {b{\text{/}}{{\delta }_{1}}} \right)}^{2}}{{r}^{3}} = 0$

Здесь $m_{1}^{2} = (2{\text{/}}\Gamma ){{\gamma }^{2}}[i{{\left( {b{\text{/}}{{\delta }_{2}}} \right)}^{2}} - {{\left( {b{\text{/}}{{\delta }_{1}}} \right)}^{2}}]$, ${{\delta }_{1}} = \sqrt {2K{\text{/}}\Gamma } $, ${{\delta }_{2}} = \sqrt {2\nu {\text{/}}\omega } $

${{m}_{1}} = (\gamma b{\text{/}}\sqrt \Gamma )(1{\text{/}}\delta + i\delta {\text{/}}\delta _{2}^{2}),\quad 1{\text{/}}{{\delta }^{2}} = - 1{\text{/}}\delta _{1}^{2} + \sqrt {1{\text{/}}\delta _{1}^{4} + 1{\text{/}}\delta _{2}^{4}} $

Решение уравнения (2.6) имеет вид

(2.7)

${{F}_{2}}(r) = \frac{{{{A}_{2}}}}{{m_{1}^{2}{{r}^{2}}}}\left( {\sin {{m}_{1}}r - {{m}_{1}}r\cos {{m}_{1}}r} \right) - \frac{{{{B}_{2}}}}{{m_{1}^{2}{{r}^{2}}}}\left( {\cos {{m}_{1}}r + {{m}_{1}}r\sin {{m}_{1}}r} \right) - Cr$

Здесь A₂, B₂ – неопределенные коэффициенты, $C = (2{{\gamma }^{2}}{\text{/}}m_{1}^{2}){{\left( {b{\text{/}}{{\delta }_{1}}} \right)}^{2}}$.

Уравнение для F₃(r)

(2.8)

${{r}^{2}}F_{3}^{{''}}(r) + 2rF_{3}^{'}(r) + (m_{2}^{2}{{r}^{2}} - 2){{F}_{3}}(r) = 0$

Решение уравнения (2.8), конечное при $r \to \infty $

(2.9)

${{F}_{3}}(r) = - \frac{{{{A}_{3}}}}{{m_{2}^{2}{{r}^{2}}}}\left( {i + {{m}_{2}}r} \right)\exp (i{{m}_{2}}r)$

Здесь A₃ – неопределенный коэффициент.

Подставляя выражения (2.5), (2.7) и (2.9) в граничные условия (2.3), получим систему четырех алгебраических уравнений для определения коэффициентов A₁, A₂, B₂, А₃, решая которую, находим

(2.10)

${{A}_{1}} = \frac{{{{\gamma }^{2}}m_{2}^{2}({{D}_{{11}}}{{D}_{{12}}} - {{\alpha }^{3}}{{D}_{{13}}}{{D}_{{14}}})({{D}_{2}}{{D}_{{15}}} - {{D}_{3}}{{D}_{{11}}})}}{{{{D}_{1}}{{D}_{{11}}}({{D}_{{14}}}{{D}_{{15}}} - {{D}_{{11}}}{{D}_{{16}}})}} + \frac{{{{\alpha }^{3}}{{\gamma }^{2}}m_{2}^{2}{{D}_{2}}{{D}_{{13}}}}}{{{{D}_{1}}{{D}_{{11}}}}} + \frac{{{{\alpha }^{3}}m_{2}^{2}(1 - \Gamma - C)}}{{{{D}_{1}}}}$

${{A}_{2}} = \frac{{{{\gamma }^{2}}m_{1}^{2}{{D}_{{15}}}({{D}_{{11}}}{{D}_{{12}}} - {{\alpha }^{3}}{{D}_{{13}}}{{D}_{{14}}})}}{{{{D}_{{11}}}({{D}_{{14}}}{{D}_{{15}}} - {{D}_{{11}}}{{D}_{{16}}})}} + \frac{{{{\alpha }^{3}}{{\gamma }^{2}}m_{1}^{2}{{D}_{{13}}}}}{{{{D}_{{11}}}}}$

${{B}_{2}} = \frac{{{{\gamma }^{2}}m_{1}^{2}({{D}_{{11}}}{{D}_{{12}}} - {{\alpha }^{3}}{{D}_{{13}}}{{D}_{{14}}})}}{{{{D}_{{14}}}{{D}_{{15}}} - {{D}_{{11}}}{{D}_{{16}}}}}$

${{A}_{3}} = \frac{{m_{2}^{2}{{e}^{{ - i{{m}_{2}}}}}}}{{i + {{m}_{2}}}}\left[ {\frac{{{{\gamma }^{2}}({{D}_{{11}}}{{D}_{{12}}} - {{\alpha }^{3}}{{D}_{{13}}}{{D}_{{14}}})({{D}_{8}}{{D}_{{11}}} - {{D}_{7}}{{D}_{{15}}})}}{{{{D}_{{11}}}({{D}_{{14}}}{{D}_{{15}}} - {{D}_{{11}}}{{D}_{{16}}})}} - \left. {\frac{{{{\alpha }^{3}}{{\gamma }^{2}}{{D}_{7}}{{D}_{{13}}}}}{{{{D}_{{11}}}}} + C + \Gamma - 1} \right]} \right.$

${{D}_{1}} = \sin {{m}_{2}}\alpha - {{m}_{2}}\alpha \cos {{m}_{2}}\alpha ,\quad {{D}_{2}} = \sin {{m}_{1}}\alpha - {{m}_{1}}\alpha \cos {{m}_{1}}\alpha $

${{D}_{3}} = \cos {{m}_{1}}\alpha + {{m}_{1}}\alpha \sin {{m}_{1}}\alpha $

${{D}_{4}} = (\alpha {{\gamma }^{2}} - 3\lambda )(\sin {{m}_{1}}\alpha - {{m}_{1}}\alpha \cos {{m}_{1}}\alpha ) + \lambda {{\alpha }^{2}}m_{1}^{2}\sin {{m}_{1}}\alpha $

${{D}_{5}} = (\alpha {{\gamma }^{2}} - 3\lambda )(\cos {{m}_{1}}\alpha + {{m}_{1}}\alpha \sin {{m}_{1}}\alpha ) + \lambda {{\alpha }^{2}}m_{1}^{2}\cos {{m}_{1}}\alpha $

${{D}_{6}} = 3\alpha {{m}_{2}}\cos {{m}_{2}}\alpha + ({{\alpha }^{2}}m_{2}^{2} - 3)\sin {{m}_{2}}\alpha $

${{D}_{7}} = \sin {{m}_{1}} - {{m}_{1}}{\text{cos}}{{m}_{1}},\quad {{D}_{8}} = {\text{cos}}{{m}_{1}} + {{m}_{1}}{\text{sin}}{{m}_{1}}$

${{D}_{9}} = (3\lambda + {{\gamma }^{2}}){{D}_{7}} - \lambda m_{1}^{2}\sin {{m}_{1}},\quad {{D}_{{10}}} = (3\lambda + {{\gamma }^{2}}){{D}_{8}} - \lambda m_{1}^{2}\cos {{m}_{1}}$

${{D}_{{11}}} = {{D}_{1}}{{D}_{4}} - \lambda {{\gamma }^{2}}{{D}_{2}}{{D}_{6}}$

${{D}_{{12}}} = (C + \Gamma )(i + {{m}_{2}}) + \lambda (3i + 3{{m}_{2}} - im_{2}^{2})(1 - C - \Gamma )$

${{D}_{{13}}} = \lambda {{D}_{6}} + (C + \Gamma )(\alpha {{D}_{1}} - \lambda {{D}_{6}})$

${{D}_{{14}}} = (i + {{m}_{2}}){{D}_{9}} - \lambda {{\gamma }^{2}}(3i + 3{{m}_{2}} - im_{2}^{2}){{D}_{7}}$

${{D}_{{15}}} = {{D}_{1}}{{D}_{5}} - \lambda {{\gamma }^{2}}{{D}_{3}}{{D}_{6}}$

${{D}_{{16}}} = (i + {{m}_{2}}){{D}_{{10}}} - \lambda {{\gamma }^{2}}(3i + 3{{m}_{2}} - im_{2}^{2}){{D}_{8}}$

На рис. 1, 2 показаны профили скоростей фильтрации и свободной жидкости. При построении профилей скоростей жидкости принято ${{\gamma }^{2}} = \Gamma $ [5, 6]. В связи с нестационарностью движения скорость фильтрации и скорость свободной жидкости на графиках приведены для момента времени t = 0. На всех графиках приведены зависимости действительной части $\operatorname{Re} ({{u}_{{1\varphi }}},{{u}_{{2\varphi }}}$, u_3φ) от r, т.е. $\operatorname{Re} {{u}_{{1\varphi }}}(r)$ ($0 < r < \alpha $), $\operatorname{Re} {{u}_{{2\varphi }}}(r)$ ($\alpha < r < 1$) и $\operatorname{Re} {{u}_{{3\varphi }}}(r)$ ($1 < r < \infty $).

Рис. 1.

Зависимость Re(u_1φ, u_2φ, u_3φ) от r при t = 0, α = 0.3, λ = 1, θ = π/2, Г = 0.95, b/δ₁ = 5: 1–5 – b/δ₂ = 1, 2, 3, 4, 5.

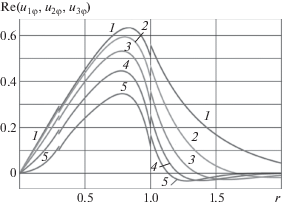
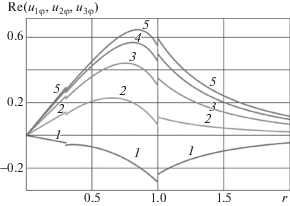
Рис. 2.

Зависимость Re(u_1φ, u_2φ, u_3φ) от r при t = 0; α = 0.3, λ = 1, θ = π/2, Г = 0.95, b/δ₂ = 0.5: 1–5 – b/δ₁ = 1, 2, 3, 4, 5.

На рис. 1 приведены графики зависимостей $\operatorname{Re} {{u}_{{1\varphi }}}(r)$, $\operatorname{Re} {{u}_{{2\varphi }}}(r)$ и $\operatorname{Re} {{u}_{{3\varphi }}}(r)$ для случая, когда величина b/δ₁ = 5 зафиксирована, а b/δ₂ принимает значения 1, 2, 3, 4, 5 при α = 0.3, λ = 1, θ = π/2, $\Gamma = 0.95$.

Из рис. 1 следует, что в области 3 имеются слои жидкости с противоположными направлениями скоростей. С увеличением значений b/δ₂ (а значит, с увеличением частоты ω) скорости $\operatorname{Re} {{u}_{{1\varphi }}}(r)$, $\operatorname{Re} {{u}_{{2\varphi }}}(r)$ и $\operatorname{Re} {{u}_{{3\varphi }}}(r)$ уменьшаются при каждом заданном значении r. Наличие разрывов графиков на границе пористой среды и свободной жидкости связано с тем, что скорость фильтрации не является скоростью частиц жидкости. При $\Gamma \to 1$ эти разрывы исчезают.

Профили скоростей на рис. 2 построены при фиксированных значениях b/δ₂ = 0.5, α = 0.3, λ = 1, θ = π/2, $\Gamma = 0.95$ для разных значений b/δ₁ = 1, 2, 3, 4, 5.

Из рис. 2 следует, что скорости жидкости внутри и вне пористой среды увеличиваются с возрастанием величины b/δ₁ при каждом значении r.

3. ЧАСТНЫЕ СЛУЧАИ

При переходе в полученном выше решении (2.5), (2.7), (2.9) к пределу ω → 0 (b/δ₂ → 0) находим поля скоростей жидкости внутри и вне пористой сферической оболочки при ее равномерном вращении вокруг оси Оz

${{u}_{{1\varphi }}} = {{V}_{1}}r\sin \theta ,\quad {{u}_{{3\varphi }}} = - \frac{{{{V}_{3}}}}{{{{r}^{2}}}}\sin \theta $

${{u}_{{2\varphi }}} = \sin \theta \left[ {\frac{{{{V}_{2}}}}{{m_{1}^{2}{{r}^{2}}}}\left( {\sin {{m}_{1}}r - {{m}_{1}}r\cos {{m}_{1}}r} \right) - } \right.\left. {\frac{{{{W}_{2}}}}{{m_{1}^{2}{{r}^{2}}}}\left( {\cos {{m}_{1}}r + {{m}_{1}}r\sin {{m}_{1}}r} \right) - Cr} \right]$

где

${{V}_{1}} = \frac{{{{\gamma }^{2}}{{N}_{4}}[{{\alpha }^{4}}{{N}_{1}}(C + \Gamma ) - {{N}_{3}}]}}{{{{\alpha }^{3}}{{D}_{4}}({{N}_{2}}{{D}_{4}} - {{N}_{1}}{{D}_{5}})}} + \frac{{\alpha {{\gamma }^{2}}{{D}_{2}}(C + \Gamma )}}{{{{D}_{4}}}} + 1 - \Gamma - C$

${{V}_{2}} = \frac{{{{\gamma }^{2}}m_{1}^{2}{{D}_{5}}[{{\alpha }^{4}}{{N}_{1}}(C + \Gamma ) - {{N}_{3}}]}}{{{{D}_{4}}({{N}_{2}}{{D}_{4}} - {{N}_{1}}{{D}_{5}})}} + \frac{{{{\alpha }^{4}}{{\gamma }^{2}}m_{1}^{2}(C + \Gamma )}}{{{{D}_{4}}}}$

${{W}_{2}} = \frac{{{{\gamma }^{2}}m_{1}^{2}[{{\alpha }^{4}}{{N}_{1}}(C + \Gamma ) - {{N}_{3}}]}}{{{{N}_{2}}{{D}_{4}} - {{N}_{1}}{{D}_{5}}}}$

${{V}_{3}} = \frac{{{{\gamma }^{2}}{{N}_{5}}[{{\alpha }^{4}}{{N}_{1}}(C + \Gamma ) - {{N}_{3}}]}}{{{{D}_{4}}({{N}_{2}}{{D}_{4}} - {{N}_{1}}{{D}_{5}})}} - \frac{{{{\alpha }^{4}}{{\gamma }^{2}}{{D}_{7}}(C + \Gamma )}}{{{{D}_{4}}}} + C + \Gamma - 1$

${{N}_{1}} = {{D}_{9}} - 3\lambda {{\gamma }^{2}}{{D}_{7}},\quad {{N}_{2}} = {{D}_{{10}}} - 3\lambda {{\gamma }^{2}}{{D}_{8}}$

${{N}_{3}} = {{D}_{4}}\left[ {C + \Gamma + 3\lambda (1 - \Gamma - C)} \right],\quad {{N}_{4}} = {{D}_{2}}{{D}_{5}} - {{D}_{3}}{{D}_{4}}$

${{N}_{5}} = {{D}_{4}}{{D}_{8}} - {{D}_{5}}{{D}_{7}},\quad m_{1}^{2} = - (2{\text{/}}\Gamma ){{\gamma }^{2}}{{\left( {b{\text{/}}{{\delta }_{1}}} \right)}^{2}}$

В пористой среде с высокой пористостью, близкой к единице, можно принять $\eta {\text{'}} \approx \eta $ [8]. При этом в частном случае при $\alpha \to 0$ из полученных результатов следует решение задачи о течении вязкой жидкости, вызванном вращательно-колебательным движением пористого шара [13]. Из этого решения, в свою очередь, следует (при $K \to 0$, $\lambda \to 0$) решение задачи о течении вязкой жидкости, вызванном вращательно-колебательным движением погруженного непроницаемого шара [12, §24].

4. МОМЕНТ СИЛ ТРЕНИЯ, ДЕЙСТВУЮЩИХ НА КОНТРОЛЬНУЮ ПОВЕРХНОСТЬ, ОХВАТЫВАЮЩУЮ ПОРИСТУЮ ОБОЛОЧКУ

Безразмерный момент относительно оси z сил трения, действующих со стороны свободной (внешней) жидкости на контрольную сферическую поверхность, охватывающую внешнюю поверхность насыщенной жидкостью пористой оболочки, совершающей вращательно-колебательное движение в вязкой жидкости, определяется равенством [12]

${{M}_{z}} = \iint {\sigma _{{3r\varphi }}^{'}\sin \theta }dS,\quad \sigma _{{3r\varphi }}^{'} = \frac{{\partial {{u}_{{3\varphi }}}}}{{\partial r}} - \frac{{{{u}_{{3\varphi }}}}}{r}$

Здесь $dS = 2\pi \sin \theta d\theta $ – элемент площади, интегрирование проводится по всей поверхности сферы r = 1, $\sigma _{{3r\varphi }}^{'}$ – безразмерный тензор вязких напряжений в области 3.

В результате находим

(4.1)

${{M}_{z}} = \frac{{8\pi }}{3}{{e}^{{ - it}}}(3i + 3{{m}_{2}} - im_{2}^{2})\frac{{{{A}_{3}}{{e}^{{i{{m}_{2}}}}}}}{{m_{2}^{2}}}$

Размерный момент сил трения равен $M_{z}^{*} = \eta {{\Omega }_{0}}{{b}^{3}}{{M}_{z}}$.

Момент сил трения (4.1) действует со стороны внешней жидкости на единую систему, состоящую из пористого тела и содержащейся в нем и в полости жидкости, которая в рассматриваемом здесь случае при движении не выходит из объема пористого тела. При этом моменты сил взаимодействия на поверхности контакта между жидкостью в полости и средой в пористом теле по третьему закону Ньютона при суммировании сокращаются. Вопрос об определении момента сил трения, действующих на одно только пористое тело, остается открытым.

В табл. 1 приведены действительные части выражения $\sigma _{{3r\varphi }}^{'}$ при r = 1 для следующих значений параметров: α = 0.3, λ = 1, $\Gamma = 0.95$, b/δ₁ = 5, b/δ₂ = 1, 2, 3, 4, 5.

Таблица 1

b/δ₂	$\operatorname{Re} \sigma ~{{_{{3r\varphi }}^{'}}_{{}}}$
1	1.98cos(t – 3.044)sinθ
2	2.28cos(t – 3.055)sinθ
3	2.46cos(t – 3.159)sinθ
4	2.47cos(t – 3.295)sinθ
5	2.34cos(t – 3.427)sinθ

Таким образом, между безразмерной силой трения, отнесенной к единице площади контрольной поверхности (r = 1), и безразмерной скоростью поверхности пористой оболочки $\operatorname{Re} {{{v}}_{\varphi }}$ = costsinθ при r = 1 имеется сдвиг фаз.

При α → 0 и $\eta {\text{'}} \approx \eta $ выражение (4.1) принимает вид момента сил трения, действующих на контрольную поверхность, окружающую пористый шар, совершающий вращательно-колебательное движение в вязкой жидкости [14]

(4.2)

${{M}_{z}} = \frac{8}{3}\pi {{e}^{{ - it}}}(m_{2}^{2} + 3i{{m}_{2}} - 3)\frac{{{{Q}_{1}}\sin {{m}_{1}} + {{m}_{1}}{{Q}_{2}}\cos {{m}_{1}}}}{{{{Q}_{3}}\sin {{m}_{1}} + {{m}_{1}}{{Q}_{4}}\cos {{m}_{1}}}}$

${{Q}_{1}} = - 1 + \lambda (m_{1}^{2} - 3)(1 - \Gamma - 2C);\quad {{Q}_{2}} = 1 + 3\lambda (1 - \Gamma - 2C)$

${{Q}_{3}} = - 1 + i{{m}_{2}} + \lambda (m_{1}^{2} - im_{1}^{2}{{m}_{2}} - m_{2}^{2});\quad {{Q}_{4}} = 1 - i{{m}_{2}} + \lambda m_{2}^{2}$

При λ → 0, ($K \to 0$) ($b{\text{/}}{{\delta }_{2}}$ – произвольное) выражение (4.2) принимает вид безразмерного момента сил трения, действующих на твердый непроницаемый шар, совершающий вращательно-колебательное движение в вязкой жидкости

${{M}_{z}} = - \frac{{8\pi }}{3}{{e}^{{ - it}}}\frac{{3 + 6(b{\text{/}}{{\delta }_{2}}) + 6{{{\left( {b{\text{/}}{{\delta }_{2}}} \right)}}^{2}} + 2{{{\left( {b{\text{/}}{{\delta }_{2}}} \right)}}^{3}} - 2{{i}_{{}}}{{{\left( {b{\text{/}}{{\delta }_{2}}} \right)}}^{2}}\left( {1 + b{\text{/}}{{\delta }_{2}}} \right)}}{{1 + 2(b{\text{/}}{{\delta }_{2}}) + 2{{{\left( {b{\text{/}}{{\delta }_{2}}} \right)}}^{2}}}}$.

В размерном виде $M_{z}^{*} = \eta {{\Omega }_{0}}{{b}^{3}}{{M}_{z}}$ этот момент сил совпадает с [12, §24].

При m₂ = 0 (ω = 0) формула (4.2) (без множителя ${{e}^{{ - it}}}$) дает выражение для момента сил трения, действующих на контрольной поверхности вокруг пористого шара, вращающегося с постоянной угловой скоростью в вязкой жидкости [14]

${{M}_{z}} = - 8\pi \frac{{(\lambda (m_{1}^{2} - 3)(1 - \Gamma - 2C) - 1)\sin {{m}_{1}} + {{m}_{1}}(1 + 3\lambda (1 - \Gamma - 2C))\cos {{m}_{1}}}}{{(\lambda m_{1}^{2} - 1)\sin {{m}_{1}} + {{m}_{1}}\cos {{m}_{1}}}}$

ЗАКЛЮЧЕНИЕ

Исследовано влияние вращательно-колебательного движения пористой сферической оболочки, погруженной в вязкую жидкость, на движение этой жидкости внутри и вне пористого тела. В сферической системе координат найдены в приближении Стокса аналитические решения нестационарного уравнения Бринкмана, описывающего движение жидкости в пористой среде, и уравнения Навье–Стокса, описывающего движение жидкости вне пористой среды.

Определены поля скорости фильтрации и скорости свободной жидкости внутри и вне пористого тела. Построены графики профилей скорости фильтрации и свободной жидкости при разных значениях параметров задачи.

Определен момент сил трения, действующих на контрольную сферическую поверхность, охватывающую внешнюю поверхность пористой сферической оболочки, совершающей вращательно-колебательное движение. Показано, что в частном случае из полученных результатов следуют известные ранее результаты для пористого шара, совершающего колебательные движения в вязкой жидкости, а также для сплошного (непроницаемого) шара.

Список литературы

Happel J., Brenner H. Low Reynolds number hydrodynamics. Englewood Cliffs, N. J.: Prentice-Hall, 1965. = Хаппель Дж., Бреннер Г. Гидродинамика при малых числах Рейнольдса. М.: Мир, 1976. 632 с.
Jones I.P. Low Reynolds number flow past a porous spherical shell // Math. Proc. Camb. Phis. Soc. 1973. V. 73. № 1. P. 231–238.
Rajvanshi S.C., Wasu S. Slow extensional flow past a non-homogeneous porous spherical shell // Int. J. Applied Mechanics and Engineering. 2013. V. 18. № 2. P. 491–502.
Deo S., Yadav P.K., Tiwari A. Slow viscous flow through a membrane built up from porous cylindrical particles with an impermeable core // Appl. Math. Modelling. 2010. V. 34. № 5. P. 1329–1343.
Ochoa-Tapia J.A., Whitaker S. Momentum transfer at the boundary between a porous medium and a homogeneous fluid. – I. Theoretical development // Int. J. Heat and Mass Transfer. 1995. V. 38. № 14. P. 2635–2646.
Ochoa-Tapia J.A., Whitaker S. Momentum transfer at the boundary between a porous medium and a homogeneous fluid. – II. Comparison with experiment // Int. J. Heat and Mass Transfer. 1995. V. 38. № 14. P. 2647–2655.
Tilton N., Cortelezzi L. Linear stability analysis of pressure-driven flows in channels with porous walls // J. Fluid Mech. 2008. V. 604. P. 411–445.
Brinkman H.C. A calculation of the viscous force exerted by a flowing fluid on a dense swarm of particles // Appl. Sci. Res. 1947. V. A1. № 1. P. 27–34.
Auriault J.-L. On the domain of validity of Brinkmah’s equation // Transp. Porous Med. 2009. V. 79. № 2. P. 215–223.
Alazmi B., Vafai K. Analysis of fluid flow and heat transfer interfacial conditions between a porous medium and a fluid layer // Int. J. Heat and Mass Transfer. 2001. V. 44. № 9. P. 1735–1749.
Goyeau B., Lhuillier D., Gobin D., Velarde M.G. Momentum transport at a fluid-porous interface // Int. J. of Heat and Mass Transfer. 2003. V. 46. № 21. P. 4071–1749.
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. 6. Гидродинамика. М.: Физматлит, 2006. 736 с. = Landau L.D., Lifshitz E.M. Theoretical Physics. V. 6. Fluid Mechanics. New York: Pergamon Press, 2013.
Тактаров Н.Г. Движение вязкой жидкости, вызванное вращательно-колебательным движением пористого шара // Изв. РАН. МЖГ. 2016. № 5. С. 133–138. = Taktarov N.G. Viscous fluid flow induced by rotational-oscillatory motion of a porous sphere // Fluid Dynamics. 2016. V. 51. № 5. Р. 703–708.
Тактаров Н.Г., Рунова О.А. Силы и момент сил сопротивления, действующие на пористое сферическое тело в вязкой жидкости в рамках модели Бринкмана // Изв. вузов. Поволжский регион. Физико-матем. науки. 2018. № 2 (46). С. 27–37.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал