Известия РАН. Механика жидкости и газа, 2020, № 6, стр. 33-41

ОБ ОДНОЙ МОДИФИКАЦИИ ДВУЧЛЕННОГО УРАВНЕНИЯ СОСТОЯНИЯ

Л. В. Шуршалов^*

Вычислительный центр им. А.А. Дородницына Федерального исследовательского центра “Информатика и управление” РАН
Москва, Россия

^* E-mail: shurshalov.lev@yandex.ru

Поступила в редакцию 05.02.2020
После доработки 16.03.2020
Принята к публикации 18.03.2020

DOI: 10.31857/S0568528120060109

Полный текст (PDF)

Аннотация

Предлагается простая модификация известного двучленного уравнения состояния, позволяющая существенно расширить диапазон применимости этого уравнения состояния и повысить точность получаемых с его помощью результатов расчета термодинамических величин, в частности, такой важной характеристики, как температура. Приведен пример построения модифицированного двучленного уравнения состояния воды.

Ключевые слова: модификация двучленного уравнения состояния, уравнение состояния воды

Двучленное уравнение состояния, являющееся несложным обобщением уравнения состояния идеального газа, хорошо известно (см., например, [1, 2]). Обычно оно приводится в виде

(1)

$e = \frac{{P + \gamma P{\text{*}}}}{{(\gamma - 1)\rho }} - \frac{{C_{0}^{2}}}{{\gamma - 1}},\quad P{\text{*}} = \frac{{\rho {\text{*}}C_{0}^{2}}}{\gamma }$

где e, P, ρ – удельная внутренняя энергия, давление и плотность, а γ, P*, ρ*, С₀ – постоянные величины. В некотором приближении это уравнение позволяет описывать свойства жидких или твердых материалов при высоких давлениях и плотностях, превышающих плотность при нормальных условиях. Такая важная характеристика, как температура Т при этом, как правило, опускается, хотя ее связь с давлением напрямую определяется с точностью до произвольной постоянной из термодинамических соотношений. Если произвольная постоянная выбирается из условия обращения в нуль упругой части давления при значении плотности ρ = ρ*, то эта связь имеет следующий вид

(2)

$P = (\gamma - 1){{c}_{{v}}}\rho T + P{\text{*}}\left[ {{{{\left( {\frac{\rho }{{\rho {\text{*}}}}} \right)}}^{\gamma }} - 1} \right]$

где ${{c}_{{v}}}$ – удельная теплоемкость при постоянном объеме, также считающаяся постоянной.

В работе [3] двучленное уравнение состояния в вышеприведенном виде со специальным образом подобранными константами использовалось для описания свойств графита, алмаза и их смеси с водой.

Как показывают расчеты с использованием уравнения состояния вида (1), (2), оно довольно неплохо (до определенного предела) определяет величину давления в различных быстро протекающих процессах с ударными волнами, но дает большую ошибку в определении температуры (см., например, [4]).

В этой связи, а также учитывая простоту и удобство использования двучленного уравнения состояния, возникает желание несколько модифицировать его, чтобы расширить диапазон его применимости и повысить точность получаемых с его помощью результатов, в частности, при определении температуры.

Основная цель данной работы – показать, как можно с помощью простого приема кардинально улучшить старое довольно грубое уравнение состояния. Ранее в работе [4] этот же прием позволил улучшить характеристики уравнения состояния другого, более общего вида.

1. МОДИФИКАЦИЯ ДВУЧЛЕННОГО УРАВНЕНИЯ СОСТОЯНИЯ

Уравнение состояния (1) принадлежит к классу уравнений состояния с линейной зависимостью давления от температуры вида

(1.1)

$P = f({v}) + F({v})T,\quad e = {{c}_{{v}}}T + E({v}) + {{e}_{0}},\quad E({v}) = - \int {f({v})d{v}} $

где ${v}$– удельный объем, f(${v}$), E(${v}$) – упругие части давления и внутренней энергии, F(${v}$) – температурный коэффициент давления, ${{e}_{0}}$ – произвольная постоянная, которая в данном случае может полагаться равной нулю.

Из сопоставления (1), (2) и (1.1) видно, что

(1.2)

$\begin{gathered} f({v}) = P{\text{*}}\left[ {{{{\left( {\frac{{{v}{\text{*}}}}{{v}}} \right)}}^{\gamma }} - 1} \right],\quad F({v}) = \frac{{\gamma - 1}}{{v}}{{c}_{{v}}} \\ E({v}) = \frac{{{v}f({v}) + \gamma P{\text{*}}({v} - {v}{\text{*}})}}{{\gamma - 1}},\quad {v}* = \frac{1}{{\rho {\text{*}}}} \\ \end{gathered} $

Теперь покажем, в чем причина ограниченности двучленного уравнения состояния в его обычной формулировке. Для этого рассмотрим выражение для ударной адиабаты вещества относительно его нормального состояния с давлением P = P₁ = 0.101325 МПа, температурой T = T₁ = 293 K, удельным объемом ${v}$ = ${{{v}}_{1}}$. Для воды ${{{v}}_{1}}$ = 1.0018${{{v}}_{{00}}}$

(1.3)

$\begin{gathered} {{{v}}_{{00}}} = {{10}^{{ - 3}}}\,\,{{{\text{м}}}^{3}}{\text{/кг}} \\ e({{{v}}_{2}},{{T}_{2}}) - e({{{v}}_{1}},{{T}_{1}}) = 0.5({{P}_{2}} + {{P}_{1}})({{{v}}_{1}} - {{{v}}_{2}}) \\ \end{gathered} $

Здесь ${{{v}}_{2}}$, T₂, P₂ – значения удельного объема, температуры и давления за фронтом ударной волны. Для уравнения состояния вида (1.1)

(1.4)

$\begin{gathered} {{P}_{2}}({{{v}}_{2}}) = f({{{v}}_{2}}) + F({{{v}}_{2}}){{T}_{2}} \\ e({{{v}}_{2}},{{T}_{2}}) = {{c}_{{v}}}{{T}_{2}} + E({{{v}}_{2}}) = {{c}_{{v}}}\frac{{{{P}_{2}}({{{v}}_{2}}) - f({{{v}}_{2}})}}{{F({{{v}}_{2}})}} + E({{{v}}_{2}}) \\ \end{gathered} $

Разрешая уравнение (1.3) относительно ${{P}_{2}}({{{v}}_{2}})$, получим

${{P}_{2}}({{{v}}_{2}}) = \left[ {0.5{{P}_{1}}({{{v}}_{1}} - {{{v}}_{2}}) + {{c}_{{v}}}\frac{{f({{{v}}_{2}})}}{{F({{{v}}_{2}})}} - E({{{v}}_{2}}) + E({{{v}}_{1}}) + {{c}_{{v}}}{{T}_{1}}} \right] \times {{\left[ {\frac{{{{c}_{{v}}}}}{{F({{{v}}_{2}})}} - 0.5({{{v}}_{1}} - {{{v}}_{2}})} \right]}^{{ - 1}}}$

Стоящее в знаменателе выражение, будучи положительным для самой слабой (звуковой) ударной волны с ${{{v}}_{1}} = {{{v}}_{2}}$, должно оставаться таковым и для ударных волн любой интенсивности. Отсюда следует ограничение сверху на величину функции $F({{{v}}_{2}})$:

(1.5)

$F({{{v}}_{2}}) < \frac{{2{{c}_{{v}}}}}{{{{{v}}_{1}} - {{{v}}_{2}}}}$

Если в соотношении (1.5) взять знак равенства, то получится уравнение ограничивающей кривой, при приближении к которой снизу ${{P}_{2}}({{{v}}_{2}})$ и ${{T}_{2}}({{{v}}_{2}})$ будут стремиться к бесконечности.

Для двучленного уравнения состояния в обычной форме (1), (2) это будет происходить при следующем значении удельного объема ${{{v}}_{2}}$

(1.6)

${{{v}}_{2}} = 0.5{{{v}}_{1}}\frac{{\gamma - 1}}{{1 + 0.5(\gamma - 1)}}$

Легко видеть, что для жидкостей, металлов и твердых тел, у которых показатель адиабаты γ может иметь значение порядка 3–7, значение удельного объема, при котором давление на фронте ударной волны обращается в бесконечность, оказывается существенно больше значения ${{{v}}_{2}}$, соответствующего точке предельного сжатия в ударной волне для конкретного вещества. Далее это будет видно на примере расчета для воды.

Для преодоления этого ограничения предлагается температурный коэффициент давления F(${v}$) вида (1.2) заменить на другое выражение, прямо следующее из аппроксимации экспериментальных данных на ударной адиабате для каждого конкретного вещества, для которого такие аппроксимации или хотя бы сами экспериментальные точки имеются. Для многих веществ в настоящее время построены широкодиапазонные ударные адиабаты [5], которые для этой цели можно использовать. Для воды такая аппроксимация приведена, например, в [6].

Допустим, что у нас имеется аппроксимация давления на ударной адиабате в виде некоторого аналитического выражения ${{P}_{2}}({{{v}}_{2}})$. Тогда, подставляя соотношения (1.4) в (1.3), разрешая полученное уравнение относительно $F({{{v}}_{2}})$ и заменяя ${{{v}}_{2}}$ на ${v}$, получим

(1.7)

$F({v}) = {{c}_{{v}}}\frac{{{{P}_{2}}({v}) - f({v})}}{{0.5[{{P}_{2}}({v}) + {{P}_{1}}]({{{v}}_{1}} - {v}) + {{c}_{{v}}}{{T}_{1}} + E({{{v}}_{1}}) - E({v})}}$

где f(${v}$), E(${v}$) определяются формулами (1.2), а ${{P}_{2}}({v})$ считается для каждого вещества заданным.

Обычно аппроксимации экспериментальных данных на ударной адиабате задаются в виде зависимостей D(U), где D – скорость ударного фронта, U – скорость вещества за ударным фронтом. В этих переменных аппроксимация экспериментальных данных представляется особенно просто: либо в виде линейной, либо в виде слабо квадратичной функций.

В линейном случае она имеет вид

(1.8)

$D = {{D}_{0}} + \lambda U$

где D₀ – скорость D при U = 0, λ – безразмерная константа.

Соответствующая (1.8) зависимость ${{P}_{2}}({v})$ получается из условий на ударном фронте и имеет очень простой вид

(1.9)

${{P}_{2}}({v}) = {{P}_{1}} + K\left( {1 - \frac{{v}}{{{{{v}}_{1}}}}} \right) \times {{\left[ {1 - \lambda \left( {1 - \frac{{v}}{{{{{v}}_{1}}}}} \right)} \right]}^{{ - 2}}},\quad K = D_{0}^{2}{\text{/}}{{{v}}_{1}}$

где K есть упругий модуль всестороннего сжатия вещества в начальной точке.

В квадратичном случае

(1.10)

$D = {{D}_{0}} + \lambda U - \varepsilon {{U}^{2}}$

Коэффициент ε обычно много меньше единицы, что оправдывает использованное выше название “слабо квадратичная” функция.

Соответствующая (1.10) зависимость для давления на ударном фронте имеет вид

(1.11)

${{P}_{2}}({v}) = {{P}_{1}} + D[U({v})]\frac{{U({v})}}{{{{{v}}_{1}}}}$

(1.12)

$U({v}) = \left[ {\lambda \left( {1 - \frac{{v}}{{{{{v}}_{1}}}}} \right) - 1 + {{{\left\{ {{{{\left[ {\lambda \left( {1 - \frac{{v}}{{{{{v}}_{1}}}}} \right) - 1} \right]}}^{2}} + 4\varepsilon {{{\left( {1 - \frac{{v}}{{{{{v}}_{1}}}}} \right)}}^{2}}{{D}_{0}}} \right\}}}^{{1/2}}}} \right] \times {{\left[ {2\varepsilon \left( {1 - \frac{{v}}{{{{{v}}_{1}}}}} \right)} \right]}^{{ - 1}}}$

Аппроксимация реальной ударной адиабаты часто представляется в виде двух или более линейных и квадратичных зависимостей [5, 6].

Окончательно, модифицированное двучленное уравнение состояния теперь будет иметь вид (1.1), (1.2), но с функцией F(${v}$), заданной формулой (1.7), и функцией ${{P}_{2}}({v})$, определяемой по формулам (1.8), (1.9) или (1.10), (1.11), (1.12). Как ясно из изложенного, данный подход пригоден для модификации уравнения состояния при значениях удельного объема v, меньшего начального ${{{v}}_{1}}$.

2. ПРИМЕР МОДИФИЦИРОВАННОГО УРАВНЕНИЯ СОСТОЯНИЯ

Перейдем теперь к рассмотрению конкретного примера уравнения состояния, построенного по вышеизложенной методике. Для построения возьмем уравнение состояния воды – наиболее распространенной и наиболее важной субстанции на нашей планете.

Для воды имеется большое количество уравнений состояния разной степени сложности и разной степени точности описания термодинамических функций (см. подробно об этом, например, в [7–9]). Однако общепринятого уравнения состояния воды пока еще нет.

Задача построения уравнения состояния по изложенной методике сводится к нахождению в литературе подходящей аппроксимации экспериментальных данных для ударной адиабаты и рациональному выбору значений констант, входящих в выше представленные формулы.

В работах [5, 6] имеются необходимые аппроксимации для многих веществ, в том числе и для воды.

Аппроксимация для воды имеет два участка: квадратичный в диапазоне $0 \leqslant U \leqslant {{U}_{{12}}}$, где D₀ = 1.483 км/с – скорость звука в начальной точке ударной адиабаты (при нормальных условиях), λ = 2, ε = 0.0001 c/м, и линейный – в диапазоне U₁₂ < U < 35 км/с, где D₀ = 2.61 км/с, λ = 1.27. Значение U₁₂ = 5.083 км/с. Это соответствует точке перехода по удельному объему ${{{v}}_{{12}}}$ = 0.4401${{{v}}_{{00}}}$.

Остается задать четыре константы: ${{c}_{{v}}}$, ${v}{\text{*}}$, P* и γ. Удельную теплоемкость при постоянном объеме зададим примерно равной ее значению при нормальных условиях, т.е. ${{c}_{{v}}}$ = 4.15 кДж/(кгK). Удельный объем ${v}{\text{*}}$, при котором упругое давление и упругая энергия воды равны нулю, достаточно хорошо определяется из изотермических данных Бриджмена [10, 11], что дает ${v}{\text{*}} = 0.81{{{v}}_{{00}}}$. Постоянную P* целесообразно определять при ${v}$ = ${v}{\text{*}}$. Для этого нужно линеаризовать квадратичную аппроксимационную зависимость (1.10) для D(U) в окрестности значения U = U*, отвечающего величине ${v}$ = ${v}{\text{*}}$. Тогда по формуле (1.9) определится значение упругого модуля всестороннего сжатия воды в этой точке K = 2.792 ГПа. Для зависимости упругого давления от объема вида (1.2) упругий модуль всестороннего сжатия связан с P* простым соотношением

(2.1)

$P* = \frac{K}{\gamma }$

Последнюю неизвестную постоянную γ определим по значению упругого давления f(${v}$) в начальной точке ударной адиабаты ${{{v}}_{1}} = 1.0018{{{v}}_{{00}}}$. Для этого воспользуемся данными Бриджмена [10, 11] для изотермы ${{T}_{{\exp }}} = 368$ K. Она хороша тем, что удельный объем одной из экспериментальных точек на этой изотерме почти совпадает с ${{{v}}_{1}}$. Это позволяет достаточно точно (квадратичной интерполяцией по трем экспериментальным точкам на изотерме) определить значение давления ${{P}_{{\exp }}}$ на изотерме ${{T}_{{\exp }}} = 368$ K в начальной точке, а затем по формуле

$f({{{v}}_{1}}) = \frac{{{{P}_{1}}{{T}_{{\exp }}} - {{P}_{{\exp }}}{{T}_{1}}}}{{{{T}_{{\exp }}} - {{T}_{1}}}}$

вычислить значение $f({{{v}}_{1}}) = - 0.3581$ ГПа, а по нему определить γ. Получилось, что γ = 5.23. По (2.1) вычисляется значение $P* = 0.5338$ ГПа.

Для конкретизации всех использованных данных и полученных констант представим их в виде табл. 1 для двух участков аппроксимационной зависимости D(U).

Таблица 1

Первый квадратичный участок: U (м/с), ${v}$/${{{v}}_{{00}}}$	D₀, м/с	λ	ε, с/м	${{c}_{{v}}}$, Дж/(кгК)	${v}{\text{*/}}{{{v}}_{{00}}}$	γ	P*, ГПа
$0 \leqslant U \leqslant 5083$,$0.4401 \leqslant {v}{\text{/}}{{{v}}_{{00}}} \leqslant 1.0018$	1483	2	10^–4	4150	0.81	5.23	0.5338
Второй линейный участок: U, м/с, ${v}$/${{{v}}_{{00}}}$	D₀, м/с	λ	ε, с/м	${{c}_{{v}}}$, Дж/(кг K)	${v}{\text{*/}}{{{v}}_{{00}}}$	γ	P*, ГПа
$5083 \leqslant U \leqslant 35{\kern 1pt} {\kern 1pt} 000$, $0.257 \leqslant {v}{\text{/}}{{{v}}_{{00}}} \leqslant 0.4401$	2610	1.27	0	4150	0.81	5.23	0.5338

Окончательно модифицированное двучленное уравнение состояния воды будет иметь вид:

$P = f({v}) + F({v}),\quad e = {{c}_{{v}}}T + E({v})$

$f({v}) = P{\text{*}}\left[ {{{{\left( {\frac{{{v}{\text{*}}}}{{v}}} \right)}}^{\gamma }} - 1} \right],\quad E({v}) = \frac{{{v}f({v}) + \gamma P{\text{*}}({v} - {v}{\text{*}})}}{{\gamma - 1}}$

$F({v}) = {{c}_{{v}}}\frac{{{{P}_{2}}({v}) - f({v})}}{{0.5\,[{{P}_{2}}({v}) + {{P}_{1}}]({{{v}}_{1}} - {v}) + {{c}_{{v}}}{{T}_{1}} + E({{{v}}_{1}}) - E({v})}}$

где

${{P}_{2}}({v}) = {{P}_{1}} + [{{D}_{0}} + \lambda U({v}) - \varepsilon {{U}^{2}}({v})]U({v}){\text{/}}{{{v}}_{1}}$

для первого квадратичного участка и

${{P}_{2}}({v}) = {{P}_{1}} + K\left( {1 - \frac{{v}}{{{{{v}}_{1}}}}} \right){{\left[ {1 - \lambda \left( {1 - \frac{{v}}{{{{{v}}_{1}}}}} \right)} \right]}^{{ - 2}}},\quad K = D_{0}^{2}{\text{/}}{{{v}}_{1}}$

для второго линейного участка.

Теперь представим некоторые графики, рассчитанные по получившемуся уравнению состояния.

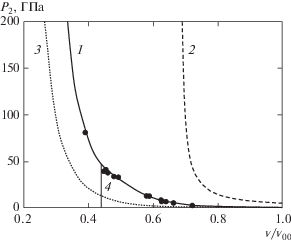
На рис. 1 показано давление P₂ на ударной адиабате. Сплошной линией – рассчитанное по модифицированному двучленному уравнению состояния, штриховой линией – по двучленному уравнению состояния без модификации при тех же значениях констант. Точки – экспериментальные данные из работ [12, 13]. Пунктирная линия – упругое давление f(${v}$), рассчитанное по формуле (1.2). Вертикальная линия 4 отмечает границу перехода в уравнении состояния от квадратичной к линейной аппроксимации D(U). Ударная адиабата в этой точке имеет едва заметный излом. Совпадение расчетных и экспериментальных данных для модифицированного уравнения состояния в данном случае есть прямое следствие способа построения температурного коэффициента давления по формуле (1.7). Согласие расчетных и экспериментальных данных здесь целиком определяется хорошей точностью используемой аппроксимации экспериментальных данных [6].

Рис. 1.

Давление на ударной адиабате в зависимости от удельного объема: 1 – расчет по модифицированному двучленному уравнению состояния; 2 – расчет по двучленному уравнению состояния без модификации; 3 – упругое давление; 4 – граница перехода от квадратичной к линейной аппроксимации D(U). Точки – эксперимент [12, 13].

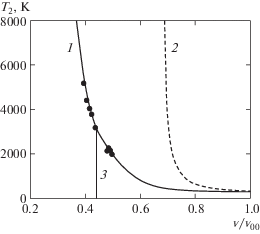
На рис. 2 представлены экспериментальные (из работ [14–16], жирные точки) и расчетные (сплошная линия – модифицированное двучленное уравнение состояния, штриховая – двучленное уравнение состояния без модификации) данные по температуре на ударной адиабате. Как и для давления, модифицированное уравнение состояния дает принципиально лучшие результаты по сравнению с обычным двучленным уравнением состояния. И это несмотря на то, что здесь используется довольно грубое предположение о постоянстве удельной теплоемкости при постоянном объеме c_v. Частично это связано с тем, что в экспериментальную зависимость D(U) для ударной адиабаты неявно вносит свой вклад реальная теплоемкость воды, а постоянная теплоемкость воды проявляется в тех соотношениях, где она входит явным образом. Как и на рис. 1, вертикальная линия 3 отмечает здесь границу перехода в уравнении состояния от квадратичной к линейной аппроксимации D(U).

Рис. 2.

Температура на ударной адиабате в зависимости от удельного объема: 1 – расчет по модифицированному двучленному уравнению состояния; 2 – расчет по двучленному уравнению состояния без модификации; 3 – граница перехода от квадратичной к линейной аппроксимации D(U). Точки – эксперимент [14–16].

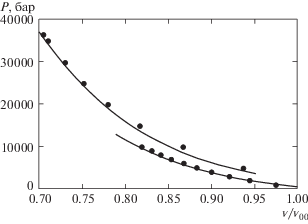
Интересно, что хорошее согласие с экспериментальными данными по температуре имеет место не только для температуры на ударной адиабате. На рис. 3 представлено сравнение двух рассчитанных изотерм T = 323, 448 K с соответствующими данными Бриджмена [10, 11], показанными жирными точками. Приведены только две изотермы, чтобы не “затенять” рисунок. Для других имеющихся изотерм согласие столь же хорошее. Обычное двучленное уравнение состояния при тех же начальных константах дает в этом случае совершенно неприемлемые результаты.

Рис. 3.

Изотермы T = 323, 448 K. Точки – эксперимент [10, 11].

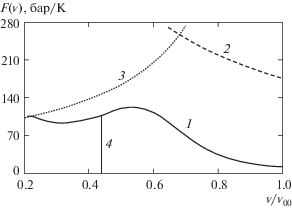
Наконец, любопытно посмотреть, как при изложенном подходе будет выглядеть температурный коэффициент давления F(${v}$) в сравнении с традиционным. Это сравнение показано на рис. 4. Здесь снова расчетная кривая по модифицированному уравнению состояния показана сплошной линией, а без модификации – штриховой. Пунктирная линия – ограничивающая кривая (1.5), при приближении к которой давление и температура на ударном фронте стремятся к бесконечности. Для модифицированного уравнения состояния это происходит в точке ${v} = {{{v}}_{{\min }}} = 0.213{{{v}}_{{00}}}$, соответствующей предельному сжатию воды в ударной волне. Причем сплошная линия подходит к этой точке по касательной к ограничивающей кривой. Для двучленного уравнения состояния без модификации обращение давления и температуры в бесконечность, как это было видно на рис. 1 и рис. 2, происходит гораздо раньше. Вертикальной линией 4 на рисунке отмечен переход в уравнении состояния от квадратичной к линейной аппроксимации D(U). В точке перехода у функции F(${v}$) имеет место едва заметный излом.

Рис. 4.

Температурный коэффициент давления F(${v}$) в зависимости от удельного объема: 1 – расчет по модифицированному двучленному уравнению состояния; 2 – расчет по двучленному уравнению состояния без модификации; 3 – ограничивающая кривая для функции F(${v}$); 4 – граница перехода от квадратичной к линейной аппроксимации D(U).

Предельное сжатие в ударной волне определяется из соотношения (1.9), являющегося прямым следствием линейной зависимости D(U) (1.8), при обращении в нуль его знаменателя, т.е. при

(2.2)

${{{v}}_{{\min }}} = {{{v}}_{1}}\left( {1 - \frac{1}{\lambda }} \right)$

Как отмечается в работе [6], линейная зависимость D(U) при больших U является паспортной характеристикой каждого структурно-однородного материала. Значение ${{{v}}_{{\min }}}$, определяемое по (2.2), предполагает, что линейная зависимость (1.8), подкрепленная экспериментальными данными вплоть до значения U = 35 км/c, остается таковой и для еще больших скоростей U вплоть до бесконечно больших значений. Хотя, строго говоря, предположение о линейной зависимости D(U) при еще больших скоростях может и нарушаться.

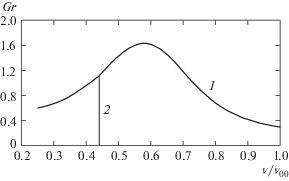
Далее на рис. 5 приведен график зависимости коэффициента Грюнайзена Gr, характеризующего отношение тепловой части давления к тепловой энергии [17]. Согласно [17] тепловая часть давления P_t выражается через коэффициент Грюнайзена по формуле ${{P}_{t}} = {\text{Gr}}({v}){{c}_{{v}}}T{\text{/}}{v}$. Для двучленного уравнения состояния традиционного вида (1), (2) ${{P}_{t}} = (\gamma - 1){{c}_{{v}}}T{\text{/}}{v}$ и Gr = γ – 1 = const, как и для идеального газа. Для модифицированного двучленного уравнения состояния этот коэффициент выражается формулой ${\text{Gr}}({v}) = {v}F({v}){\text{/}}{{c}_{{v}}}$, где F(${v}$) определена по (1.7) и коэффициент Грюнайзена уже далеко не постоянен. Его значение в начальной точке при ${v} = {{{v}}_{1}}$ равно ${\text{G}}{{{\text{r}}}_{1}} = {{{v}}_{1}}F({{{v}}_{1}}){\text{/}}{{c}_{{v}}} = {{{v}}_{1}}\left[ {{{P}_{1}} - f({{{v}}_{1}})} \right]{\text{/}}({{c}_{{v}}}{{T}_{1}})$. При выбранных значениях постоянных и вычисленного выше значения f(${{{v}}_{1}}$) оно составляет 0.295. Качественное поведение коэффициента Грюнайзена соответствует аналогичным данным из других работ (см., например, [18]). Как видно из рис. 5, в модифицированном двучленном уравнении состояния воды коэффициент Грюнайзена при уменьшении удельного объема после достижения своего максимального значения постепенно уменьшается, приближаясь к значению, соответствующему модели Томаса–Ферми Gr = 2/3 [17], что положительно характеризует проведенную модификацию уравнения состояния. Как и на предыдущих рисунках, вертикальной линией 2 на рисунке отмечена граница перехода в уравнении состояния от квадратичной к линейной аппроксимации D(U).

Рис. 5.

Коэффициент Грюнайзена в зависимости от удельного объема для модифицированного двучленного уравнения состояния воды: 1 – зависимость Gr(${v}$); 2 – граница перехода от квадратичной к линейной аппроксимации D(U).

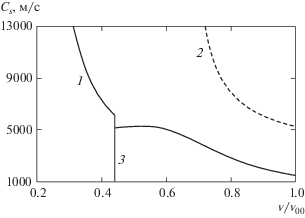
В заключение на рис. 6 приведен график зависимости скорости звука C_s на ударном фронте в воде от удельного объема. Сплошной кривой 1 приведен расчет скорости звука по модифицированному уравнению состояния, штриховой кривой 2 – по обычному двучленному уравнению состояния при тех же значениях констант. Вертикальная линия 3 отмечает границу перехода от квадратичного участка аппроксимации D(U) к ее линейному участку. Как для давления и температуры на рис. 1 и рис. 2, скорость звука для двучленного уравнения состояния без модификации устремляется в бесконечность при приближении к тому значению удельного объема, при котором происходит пересечение немодифицированной кривой F(${v}$) с ограничивающей линией (1.5). Что касается скорости звука с учетом модификации уравнения состояния, то, как видно, она в точке сшивки квадратичной и линейной аппроксимации D(U) изменяется скачком. По мнению авторов работы [6] (из которой взята аппроксимационная зависимость D(U) для ударной адиабаты) в этой точке имеет место фазовый переход от жидкой воды к ее новой твердой фазе, которую они назвали “лед CZ”. В этом случае возникновение разрыва в скорости звука в этом месте также свидетельствует в пользу образования новой фазы воды.

Рис. 6.

Скорость звука на ударном фронте в воде в зависимости от удельного объема: 1 – расчет по модифицированному двучленному уравнению состояния; 2 – расчет по двучленному уравнению состояния без модификации; 3 – граница перехода от квадратичной к линейной аппроксимации D(U).

В данной работе намеренно не проводилось сравнения со многими современными более сложными уравнениями состояния воды, ограничившись лишь сравнением с некоторыми экспериментами. Модифицированное двучленное уравнение состояния не претендует на то, чтобы конкурировать с ними. Возможно, оно лишь приближается к ним по своим характеристикам. Оценочно можно сказать, что построенное модифицированное двучленное уравнение состояния воды может давать неплохие результаты в диапазоне давлений до 100 ГПа, температур – до 6000 K, плотностей – до 2600 кг/м³.

ЗАКЛЮЧЕНИЕ

Главные задача и результат данной работы состоят в том, чтобы показать, как с помощью простого приема можно улучшить показатели даже очень грубого уравнения состояния. Пример, с уравнением состояния воды, на наш взгляд, это убедительно подтверждает. По всем параметрам оно дает гораздо лучшие результаты и в более широком диапазоне, чем традиционное двучленное уравнение состояния. Но, как отмечено выше, построенное здесь уравнение состояния воды не претендует на то, чтобы сравниться с лучшими современными более сложными уравнениями состояния воды. Оно может лишь приближаться к ним по своим характеристикам. При этом оно допускает дальнейшие улучшения, например, за счет учета зависимости теплоемкости от температуры, за счет лучшего выбора функции упругого давления. Изложенный в данной работе прием может быть применен для построения и улучшения характеристик простых уравнений состояния других сред, в частности, металлов.

Автор благодарит А.А. Чарахчьяна за ряд полезных обсуждений и предоставление некоторых материалов по уравнениям состояния воды.

Список литературы

Годунов С.К., Забродин А.В., Иванов М.Я., Крайко А.Н., Прокопов Г.П. Численное решение многомерных задач газовой динамики. М.: Наука, 1976. 400 с.
Куликовский А.Г., Погорелов Н.В., Семенов А.Ю. Математические вопросы численного решения гиперболических систем уравнений. М.: Физматлит, 2001. 608 с.
Шуршалов Л.В., Чарахчьян А.А., Хищенко К.В. Численный эксперимент по ударному сжатию смеси графита с водой // Физика горения и взрыва. 2017. Т. 53. № 4. С. 114–121.
Шуршалов Л.В. Численное моделирование ударного сжатия жидкой и парообразной воды для определения условий синтеза алмаза из графита // Физика горения и взрыва. 2020. Т. 56. № 1. С. 120–130.
Фортов В.Е., Альтшулер Л.В., Трунин Р.Ф., Фунтиков А.И. (редакторы) Ударные волны и экстремальные состояния вещества. М.: Наука, 2000. 425 с.
Черепанов Г.П., Закиров К.Р. Уравнение состояния при высоких давлениях: метод D-U диаграмм // Физическая мезомеханика. 2014. Т. 17. № 4. С. 13–28.
Нигматулин Р.И., Болотнова Р.Х. Широкодиапазонное уравнение состояния воды и пара. Метод построения // Теплофизика высоких температур. 2008. Т. 46. № 2. С. 206–218.
Нигматулин Р.И., Болотнова Р.Х. Широкодиапазонное уравнение состояния воды и пара. Результаты расчетов // Теплофизика высоких температур. 2008. Т. 46. № 3. С. 362–373.
Нигматулин Р.И., Болотнова Р.Х. Широкодиапазонное уравнение состояния воды и пара. Упрощенная форма // Теплофизика высоких температур. 2011. Т. 49. № 2. С. 310–313.
Bridgman P.W. Freezing Parameters and Compressions of Twenty One Substances to 50000 kg/cm² // Proc. Amer. Acad. Arts and Sci. 1942. V. 74. № 12. P. 399–424.
Bridgman P.W. Thermodynamic Properties of Liquid Water to 80° and 12000 kg/cm² // Proc. Amer. Acad. Arts and Sci. 1912. V. 48. P. 309–362.
Walsh J.M., Rice M.H. Dynamic compression of liquids from measurements of strong shock waves // J. Chem. Phys. 1957. V. 26. № 4. P. 815–823.
Альтшулер Л.В., Баканова А.А., Трунин Р.Ф. Фазовые превращения при сжатии воды сильными ударными волнами // Докл. АН СССР. 1958. Т. 121. № 1. С. 67–69.
Кормер С.Б. Оптические исследования свойств ударно-сжатых конденсированных диэлектриков // УФН. 1968. Т. 94. № 4. С. 641–687.
Lyzenga G.A., Ahrens T.J., Nellis W.J., Mitchell A.C. The Temperature of Shock-Compressed Water // J. Chem. Phys. 1982. V. 76. № 12. P. 6282–6286.
Бордзиловский С.А., Караханов С.М., Хищенко К.В. Тепловое излучение воды за фронтом отраженной ударной волны // Физика горения и взрыва. 2018. Т. 54. № 6. С. 95–103.
Зельдович Я.Б., Райзер Ю.П. Физика ударных волн и высокотемпературных гидродинамических явлений. М.: Наука, 1966. 688 с.
Gurtman G.A., Kirsch J.W., Hastings C.R. Analytical Equation of State for Water Compressed to 300 Kbar // J. Appl. Phys. 1971. V. 42. № 2. P. 851–857.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал