Известия РАН. Механика жидкости и газа, 2022, № 5, стр. 3-12

1. ПОСТАНОВКА ЗАДАЧИ И МЕТОД РЕШЕНИЯ

Рассматривается двумерное течение вязкой несжимаемой жидкости вокруг симметричного профиля, образованного дугой окружности и двумя касательными к ней – рис. 1. Отношение радиуса дуги R к длине отрезка L равно R/L = 0.078. Профиль закреплен в упругом вращательном шарнире, ось которого находится в центре кривизны головной части профиля. Шарнир совершает поперечные колебания вдоль оси Y по закону $y(t) = h\sin \left( {2\pi ft} \right)$, t > 0. При этом угловые перемещения профиля не заданы, а вырабатываются под действием гидродинамических сил со стороны жидкости и упругих сил в шарнире.

Течение жидкости подчиняется уравнениям Навье–Стокса, которые после применения оператора ротор записаны в форме [16]

где u – скорость жидкости, ${{{\mathbf{V}}}_{d}}$ – так называемая диффузионная скорость, ν – кинематический коэффициент вязкости. На поверхности профиля ставится условие прилипания. На бесконечности течение однородно u = U. В начальный момент (t = 0) реализуется мгновенный старт движения профиля из состояния покоя относительно жидкости, хорда профиля в начальный момент направлена вдоль потока, что соответствует равновесному положению шарнира в отсутствие внешних сил.

Изменение угла атаки α подчиняется уравнению динамики

Здесь I – погонный момент инерции профиля, r₀ – координата оси шарнира. M^hinge – крутящий момент шарнира

k – коэффициент жесткости шарнира. M^inertia – момент силы инерции, связанной с ускоренным движением оси m, r_m – масса и центр масс профиля. Момент гидродинамических сил M^hydro связан с потоком завихренности с поверхности ${{{\mathbf{\sigma }}}^{{{\text{new}}}}} = \left( {{\mathbf{n}} \cdot {{{\mathbf{V}}}_{d}}} \right){\mathbf{\omega }}$ соотношением [15] где ρ_f, m_f, I_f – плотность, масса и момент инерции вытесненной профилем жидкости соответственно, M_w – момент силы трения. Фигурирующие в приведенных выше соотношениях параметры I, m, r_m характеризуют инерционность профиля и в общем случае являются независимыми. Однако далее ограничимся вариантом, когда профиль инерционно симметричный и характеризуется однородной плотностью ρ = const. В этом случае параметры I, m, r_m перестают быть независимыми и вычисляются непосредственно через ρ, например $I = \rho \int\limits_s {{{{\left( {{\mathbf{r}} - {{{\mathbf{r}}}_{0}}} \right)}}^{2}}ds} $.

Численное моделирование выполнено с помощью программного комплекса Vvflow CFD¹¹, основанного на методе вязких вихревых доменов (ВВД) [15]. Метод ВВД представляет собой улучшенную версию метода диффузионной скорости (ДС) [16]. Вихревые области течения моделируются набором мелких вихревых частиц (доменов), которые движутся относительно жидкости с диффузионной скоростью и сохраняющейся циркуляцией. В отличие от метода ДС в методе ВВД для вычисления диффузионной скорости используются улучшенные дискретные выражения, позволяющие адекватно описывать поведение частиц вблизи поверхностей и вычислять напряжение трения с необходимой точностью. Метод протестирован в широком диапазоне значений числа Рейнольдса [17]. Он является робастным и обладает низкой схемной вязкостью [18].

На каждом шаге по времени в узлах контура профиля образуются новые частицы, циркуляции которых $\Gamma _{k}^{{new}}$ (k = 1, 2, …, N_k, где N_k – число узлов) должны обеспечивать граничные условия и выполнение уравнения движения профиля (1.1). С целью определения циркуляций новых доменов составляются уравнения на основе условия непротекания на контуре. Эти уравнения линейны относительно циркуляций $\Gamma _{k}^{{new}}$ и скорости движения профиля. Система уравнений замыкается уравнением (1.1), которое в дискретном виде также линейно относительно $\Gamma _{k}^{{new}}$, так как величина $\Gamma _{k}^{{new}}$ связана с потоком завихренности σ_k в k-й точке соотношением $\Gamma _{k}^{{new}} = {{\sigma }_{k}}\Delta {{l}_{k}}\Delta t$, где $\Delta {{l}_{k}}$ – длина отрезка контура. Соответственно интеграл в выражении (1.2) аппроксимируется суммой

В результате решения указанной системы уравнений все неизвестные значения циркуляций и угловой скорости вычисляются одновременно без расщепления шага по времени на части, описывающие движение жидкости и тела, и последующих итераций, как это обычно делается при решении сопряженных задач аэрогидроупругости.

2. РЕЗУЛЬТАТЫ РАСЧЕТОВ И ОБСУЖДЕНИЕ

Расчеты выполнены в безразмерных параметрах: $\bar {h} = h{\text{/}}L$, $\bar {t} = tU{\text{/}}L$, ${\mathbf{\bar {u}}} = {\mathbf{u}}{\text{/}}U$, ${\text{Sh}} = fL{\text{/}}U$, $\operatorname{Re} = UL{\text{/}}\nu $, $\bar {\rho } = \rho {\text{/}}{{\rho }_{f}}$, ${\mathbf{\bar {F}}} = {\mathbf{F}}{\text{/}}({{\rho }_{f}}{{U}^{2}}{{L}^{2}})$, ${\mathbf{\bar {M}}} = {{\mathbf{M}} \mathord{\left/ {\vphantom {{\mathbf{M}} {({{\rho }_{f}}{{U}^{2}}{{L}^{3}})}}} \right. \kern-0em} {({{\rho }_{f}}{{U}^{2}}{{L}^{3}})}}$, $\bar {k} = k{\text{/}}({{\rho }_{f}}U{{L}^{4}}),$ $\bar {m} = m{\text{/}}(\rho {{L}^{3}})$. Количество узлов на контуре равнялось 1200, безразмерный шаг по времени $\Delta \bar {t} = 0.001$. Дальнейшее измельчение отрезков контура и шага по времени не приводило к заметным изменениям результатов.

На рис. 2 показаны вихревые следы, полученные при Re = 200, Sh = 0.75, $\bar {h} = 0.5$ для различных значений жесткости пружины $\bar {k}$. Здесь и всюду далее $\bar {\rho } = 1$.

Следы асимметричны так же, как в численных и экспериментальных результатах [3, 4, 19], полученных для жестких профилей, совершающих поступательные или угловые колебания. Причины нарушения симметрии объяснены в [20] неустойчивостью реверсивной полубесконечной вихревой дорожки, образующейся за профилем, к изгибным деформациям при определенных соотношениях геометрических параметров и интенсивности вихрей. Отклонение следа может быть как в одну, так и в другую сторону. Это зависит от начальных условий, но не только. В [3] экспериментально наблюдалось, что направление следа может переключаться случайным образом. Это указывает на то, что относительно небольшого возмущения может быть достаточно, чтобы инициировать переключение. Бифуркационное поведение следа наблюдалось в [21] при медленном изменении частоты колебания профиля.

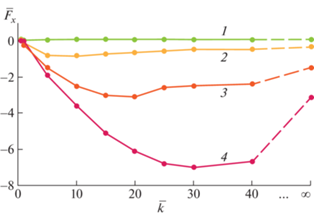
На рис. 3 представлены зависимости силы сопротивления от жесткости шарнира при $\bar {h}$ = 0.5, Re = 200, и различных значениях Sh. Отрицательная сила сопротивления представляет собой тягу (пропульсивную силу). Видно, что для фиксированной частоты существует значение $\bar {k}$, при котором тяга максимальна.

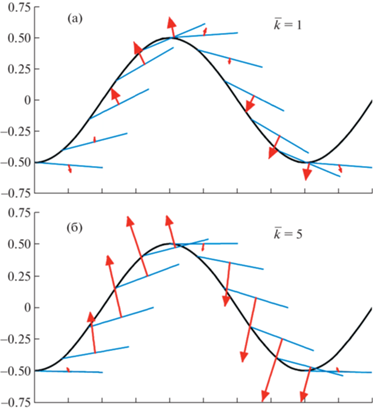
На рис. 4 показаны полученные в расчетах векторы гидродинамических сил и положение хорды профиля при Re = 500, $\bar {h}$ = 0.5, Sh = 0.5 и двух значениях жесткости шарнира в системе координат, связанной с набегающим потоком. В этой системе координат скорость жидкости в бесконечно удаленной точке равна нулю, а горизонтальная скорость оси шарнира равна –U. Из рисунка видно, что направление гидродинамической силы близко к перпендикуляру к хорде. Это объясняется малой толщиной профиля и преобладанием сил давления над силами трения. Поскольку горизонтальное положение хорды в отсутствие гидродинамических сил является для шарнира равновесным, то отклонение хорды вверх происходит, если гидродинамическая сила направлена вверх. Аналогично при отклонении хорды вниз сила направлена вниз. В обоих случаях горизонтальная составляющая гидродинамической силы направлена навстречу набегающему потоку, следовательно, сопротивление является отрицательным, т.е. имеет место тяга. При малой амплитуде и низкой частоте колебаний вклад силы давления по сравнению с силой трения уменьшается, поэтому сопротивление становится положительным, как это видно на рис. 3 при Sh = 0.25.

Из рис. 4 видно, что пропульсивная сила максимальна при движении профиля из крайних положений к средней линии траектории. Ниже показано, что это связано с влиянием силы присоединенных масс. В [22] строго доказано, что гидродинамическая сила, действующая на движущееся с ускорением тело, равна сумме двух сил ${{{\mathbf{F}}}^{{{\text{hydro}}}}} = {{{\mathbf{F}}}^{{ad}}} + {{{\mathbf{F}}}^{{st}}}$, где ${{{\mathbf{F}}}^{{st}}}$ – сила, действующая на тело, движущееся без ускорения при том же мгновенном распределении завихренности в пространстве, а ${{{\mathbf{F}}}^{{ad}}}$ – сила присоединенных масс, действующая на тело при движении с тем же ускорением в потенциальном потоке. Если известны значения коэффициентов присоединенных масс тела при потенциальном обтекании, эта сила может быть вычислена аналитически. В системе координат, показанной на рис. 1, справедливо выражение

где тензор присоединенных масс ${\mathbf{\Lambda }}$ выражается через с тензор ${\mathbf{\Lambda }}{\text{'}}$, вычисленный в связанной с профилем системе координат, как

Учитывая, что для симметричного профиля λ_x′y′ = λ_y′x′ = λ_x′α = λ_αx′ = 0, и λ_x′x′$ \ll $ λ _y′y′ λ_y′α = λ_αy′, подстановкой (2.2) в (2.1) получаем

Из (2.3) следует, что направление силы присоединенных масс близко к нормали к хорде.

Для профиля, рассматриваемого в данной работе, коэффициенты присоединенных масс имеют следующие значения

Подставляя эти значения в (2.3), получим

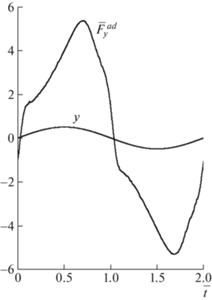
На рис. 5 показаны зависимости $F_{y}^{{ad}}$ и y от времени на одном периоде при Re = 500, $\bar {h}$ = 0.5, Sh = 0.5. Из рисунка видно, что вертикальная составляющая силы F^ad в верхней части траектории положительна, а в нижней – отрицательна. Сила F^st, зависящая от скорости в отсутствие ускорения, направлена вниз при движении вверх и вниз при обратном движении – рис. 6. В результате при движении из крайних точек траектории к средней линии эти силы сонаправленны и их модули складываются, а при движении от нее направлены в противоположные стороны, что приводит к уменьшению равнодействующей. Этим объясняется поведение пропульсивной силы в разных фазах движения. Отметим, что в отличие от результатов [14], полученных для детерминированных угловых колебаний профиля относительно неподвижной оси, вклад силы присоединенных масс в тягу при рассматриваемом в данной работе типе движения не является доминирующим.

Сравнение рис. 4а и 4б показывает, что с увеличением жесткости шарнира амплитуда изменения угла уменьшается, а модуль гидродинамической силы увеличивается. Уменьшение угла приводит к уменьшению проекции силы на ось X, а увеличение модуля силы –к ее увеличению. Эти два противоположно направленных процесса являются причиной существования оптимального значения жесткости шарнира.

Вертикальная сила в отличие от горизонтальной меняет знак во времени. Она положительна, когда ось профиля движется вниз, и отрицательна, когда ось поднимается. Если при движении вверх и вниз силы изменяются симметрично, то средняя подъемная сила равна нулю. При нарушении симметрии возникает положительная или отрицательная средняя подъемная сила.

В табл. 1 приведены значения вертикальной составляющей осредненной гидродинамической силы, соответствующие вихревым картинам на рис. 2. Как было сказано выше, направление осредненной вертикальной составляющей силы зависит от отклонения вихревого следа.

Представляется неожиданным, что средняя подъемная сила направлена в ту же сторону, что и отклонение вихревой дорожки. Однако аналогичный результат в рамках модели идеальной жидкости отмечался также в [3], где данное свойство объяснялось ненулевым значением средней циркуляции скорости вокруг профиля. При отклонении ближнего следа вверх среднее значение циркуляции, полученное в расчетах [3], отрицательно, а при отклонении вниз – положительно. Соответственно среднее значение силы Жуковского отрицательно в первом случае и положительно во втором.

На рис. 7 изображены линии тока осредненного поля скорости u' = 〈u〉 – U асимметричного вихревого следа, полученного при численном решении задачи, когда профиль совершает детерминированные угловые колебания около неподвижной оси с амплитудой α₀ = 10°, частотой Sh = 1.8 при Re = 1000. Осреднение выполнено по одному периоду колебания. Как видно из рисунка, циркуляция скорости вокруг профиля положительна (против часовой стрелки). При этом вихревая дорожка за профилем отклонена вниз, т.е. в ту же сторону, что и вертикальная составляющая гидродинамической силы. Таким образом, подтверждается вывод, сделанный в работе [3].

ЗАКЛЮЧЕНИЕ

В полной сопряженной постановке исследована задача о полудетерминированных колебаниях симметричного крылового профиля в неограниченном потоке вязкой несжимаемой жидкости в условиях, когда профиль установлен в упругом шарнире вращения, который совершает заданные поперечные по отношению к набегающему потоку гармонические колебания. Численные решения связанной задачи динамики и гидродинамики построены с помощью авторских кодов бессеточного безытерационного моделирования на основе метода вязких вихревых доменов (ВВД). Раскрыты механизмы возникновения пропульсивной силы (тяги) и подъемной силы колеблющегося профиля.

Тяга возникает благодаря корреляции направления гидродинамической силы и отклонения профиля от равновесного состояния шарнира. При этом проекция силы давления на направление набегающего потока оказывается отрицательной во всех фазах колебания. При прочих равных условиях влияние величины упругой жесткости шарнира на тягу, развиваемую колеблющимся профилем, не монотонное. Для всех сочетаний параметров задачи, при которых возникает пропульсивная сила, существует оптимальное значение жесткости пружины, доставляющее максимум тяги. Аналитически показано, что при движении шарнира от периферии к центру сила присоединенных масс вносит положительный вклад в тягу профиля, а при обратном движении ослабляет ее.

Причиной возникновения средней за период колебаний подъемной силы геометрически и инерционно симметричного профиля является нарушение симметрии реверсивной вихревой дорожки, неустойчивой к изгибным деформациям. При этом осредненная по времени подъемная сила направлена в ту же сторону, что и отклонение вихревой дорожки за профилем, что объясняется ненулевым значением осредненной циркуляции скорости вокруг профиля.

Работа выполнена в рамках темы № гос. рег. АААА-А16-116021110201-2.