1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 4, 2023

Известия РАН. Механика жидкости и газа, 2023, № 4, стр. 93-107

ЧИСЛЕННОЕ ИССЛЕДОВАНИЕ ВЛИЯНИЯ СТРУКТУРЫ СИСТЕМЫ ТРЕЩИН НА ФИЛЬТРАЦИЮ ЖИДКОСТИ В ПОРОУПРУГОЙ СРЕДЕ

Д. Ю. Легостаев a, *, С. П. Родионов a, **

a Тюменский филиал Института теоретической и прикладной механики им. С.А. Христиановича СО РАН
Тюмень, Россия

* E-mail: legostaevdy@yandex.ru
** E-mail: rodionovsp@bk.ru

Поступила в редакцию 05.08.2022
После доработки 12.11.2022
Принята к публикации 21.12.2022

Полный текст (PDF)

Аннотация

Рассматривается двумерная однофазная фильтрация слабосжимаемой жидкости в деформируемой трещиновато-пористой среде. Для совместного моделирования процессов фильтрации и связанного с ними изменения напряженно-деформированного состояния среды использована модель пороупругой среды, моделирование трещиноватости выполнено с помощью модели дискретных трещин. Трещины в рассматриваемой области имели случайное положение и ориентацию, распределение трещин по длинам подчинялось степенному закону. Исследовалась зависимость фильтрационных свойств трещиновато-пористой среды от ее напряженно-деформированного состояния и структуры системы трещин. Численное исследование выполнено для вариантов систем трещин, полученных путем множественной случайной генерации. Установлено, что фильтрационные свойства трещиновато-пористой среды определяются главным образом структурой системы трещин, характеризуемой параметром перколяции. Показано, что существенное влияние напряженно-деформированного состояния среды на ее фильтрационные свойства наблюдается для только связных систем трещин. Предложена формула для аппроксимации зависимости эквивалентной проницаемости трещиновато-пористой среды от параметров характеризующих связность системы трещин, напряженно-деформированное состояние среды, деформационные и фильтрационные свойства трещин.

Ключевые слова: трещиновато-пористая среда, абсолютная проницаемость, пороупругость, однофазная фильтрация, модель дискретных трещин, напряженно-деформированное состояние, перколяция

Исследование фильтрационных течений жидкостей и газов в горных породах и иных пористых средах имеет важное значение в различных приложениях [1–3]. Горные породы могут содержать трещины как естественного происхождения, так и искусственные, полученные, например, при проведении операции гидроразрыва пласта [4, 5]. При этом трещиноватость оказывает значительное влияние на процессы фильтрации пластовых флюидов [6, 7]. Трещины, обладая высокой проводимостью, могут выступать в качестве основных каналов при фильтрации жидкостей и газов. Так, при разработке нефтяных месторождений наличие трещиноватости может приводить к быстрым прорывам закачиваемой в пласт воды к добывающим скважинам и к существенной неравномерности вытеснения нефти. В связи с этим наличие трещин необходимо учитывать при планировании размещения скважин и выборе режима их работы [8].

Важным вопросом при моделировании фильтрационных процессов в трещиноватых средах является выбор подхода к моделированию трещин, который должен учитывать структуру и свойства системы трещин. Наиболее универсальной является модель дискретных трещин [9, 10], которая позволяет учесть положение, ориентацию, размер и физические свойства каждой трещины в системе. Данный подход не имеет ограничений на геометрическое строение системы трещин, однако его применимость ограничена высокой вычислительной сложностью. Кроме того, для сильнотрещиноватых сред не представляется возможным описать геометрические характеристики каждой отдельно взятой трещины. В этом случае для моделирования трещиноватости используется модель двойной пористости/двойной проницаемости [11, 12], в рамках которой матрица горной породы и система трещин представляются в виде сплошных сред с эффективными свойствами. Фильтрационные свойств трещиноватых горных пород сильно зависят от напряженно-деформированного состояния среды [13]. Для совместного описания фильтрационных процессов и связанного с ними изменения напряженно-деформированного состояния среды часто используют модель пороупругой среды [10, 14, 15].

Существенная степень неопределенности параметров системы трещин является ключевым фактором при моделировании трещиноватых сред. Так как истинное расположение всех трещин в пласте достоверно не известно, становится необходимым использование вероятностного описания системы трещин, которое предполагает задание законов распределения трещин по длинам, углу, пространству и раскрытию [16, 17]. Для описания распределения трещин по длинам наиболее широко используется степенной закон [18], который позволяет описать присущую системе трещин разномасштабность. Фильтрационные характеристики трещиноватых сред существенно зависят от параметров системы трещин [19, 20], наиболее значимыми из которых являются длина трещин и их концентрация в рассматриваемой области [21].

Для анализа влияния трещиноватости на фильтрационные свойства горных пород наряду с методами механики сплошной среды широкое распространение получили методы теории перколяции [22–25], использование которых позволяет оценить связность и проводимость системы трещин, опираясь на ее геометрические характеристики. При этом связность противоположных границ рассматриваемой области через систему трещин, характеризуемая параметром перколяции, существенным образом влияет на фильтрационные свойства среды.

Целью настоящей работы является исследование зависимости фильтрационных свойств трещиновато-пористых сред от их напряженно-деформированного состояния и структуры системы трещин. Фильтрационные свойства деформируемой трещиновато-пористой среды определены из результатов прямого численного моделирования процесса однофазной фильтрации в двумерной области. Исследование выполнено для вариантов систем трещин, полученных путем множественной случайной генерации. Рассмотрено влияние плотности системы трещин и параметра перколяции на величину эквивалентной проницаемости среды. Исследована зависимость эквивалентной проницаемости среды от ее напряженно-деформированного состояния, при различных давлениях закачки жидкости в исследуемую область. Предложен вид аппроксимирующей функции, учитывающий зависимость проницаемости трещиновато-пористой среды от основных параметров рассматриваемой задачи.

1. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

Рассматривается однофазная двумерная фильтрация слабосжимаемой жидкости в деформируемой трещиновато-пористой среде. Для описания фильтрационных процессов используется математическая модель пороупругой среды, которая включает в себя уравнения для давления жидкости в системе матрица-трещины и уравнения для перемещений скелета горной породы, учитывающие деформационные свойства трещин.

1.1. Фильтрация в трещиновато-пористой среде

Уравнение фильтрации жидкости в поровом пространстве деформируемого скелета горной породы записывается в виде [15]:

$\frac{1}{{{{M}_{m}}}}\frac{{\partial {{P}_{m}}}}{{\partial t}} + {{b}_{m}}\frac{\partial }{{\partial t}}(\nabla \cdot {\mathbf{u}}) = - \nabla \cdot {{{\mathbf{v}}}_{m}}$
${{P}_{m}}$ – давление жидкости в поровом пространстве, ${{M}_{m}} = {{C}_{l}}{{\phi }_{m}} + \frac{{{{b}_{m}} - {{\phi }_{m}}}}{{{{K}_{s}}}}$ – модуль Био пористой среды ${{C}_{l}}$ – сжимаемость жидкости, ${{\phi }_{m}}$ – пористость матрицы горной породы, ${{b}_{m}}$ – коэффициент Био матрицы, ${{K}_{s}}$ – объемный модуль зерен горной породы, u – вектор перемещений скелета горной породы, ${{{\mathbf{v}}}_{m}}$ – скорость фильтрации жидкости в поровом пространстве.

Скорость фильтрации жидкости в пористой среде определяется из уравнения Дарси:

${{{\mathbf{v}}}_{m}} = - \frac{{{{k}_{m}}}}{{{{\mu }_{l}}}}\nabla {{P}_{m}},$
где km – абсолютная проницаемость пористой среды, ${{\mu }_{l}}$ – вязкость жидкости.

Трещина представляет собой две поверхности ${{\Gamma }_{ + }}$ и ${{\Gamma }_{ - }}$, находящиеся в состоянии механического контакта, шероховатость которых не позволяет им полностью сомкнуться. Продольные размеры трещины существенно преобладают над ее поперечными размерами, что позволяет в двумерном случае рассматривать трещины как одномерные объекты. При рассмотрении процессов фильтрации трещина модельно представляется как узкая щель, окруженная матрицей горной породы. Уравнение для давления жидкости в трещине, учитывающее пороупругие эффекты, имеет вид [13]:

$\frac{\delta }{{{{M}_{f}}}}\frac{{\partial {{P}_{f}}}}{{\partial t}} + {{b}_{f}}\frac{{\partial {{u}_{n}}}}{{\partial t}} = - \frac{{\partial {{q}_{f}}}}{{\partial {{x}_{f}}}} - {{{v}}_{ + }} - {{{v}}_{ - }}$
где $\delta $ – раскрытие трещины, Pf – давление жидкости в трещине, ${{M}_{f}} = {{C}_{l}}{{\phi }_{f}} + \frac{{{{b}_{f}} - {{\phi }_{f}}}}{{{{K}_{s}}}}$ – модуль Био трещины, ${{\phi }_{f}}$ – пористость трещины, bf – коэффициент Био трещины, xf – координата, изменяющаяся вдоль трещины, qf – поток вдоль трещины, ${{{v}}_{ \pm }}$ – скорости фильтрации по нормали к границам трещины.

Течение жидкости в трещине рассматривается как движение между двумя параллельными плоскостями, находящимися на расстоянии δ друг от друга. Погонный расход через трещину в соответствии с кубическим законом [26] имеет вид:

${{q}_{f}} = - \frac{{{{\delta }^{3}}}}{{12{{\mu }_{l}}}}\frac{{\partial {{P}_{f}}}}{{\partial {{x}_{f}}}}.$

По аналогии с законом Дарси выражение для абсолютной проницаемости трещины может быть записано в виде:

${{k}_{f}} = \frac{{{{\delta }^{2}}}}{{12}} = \frac{{{{{\left( {{{\delta }_{0}} + \Delta \delta } \right)}}^{2}}}}{{12}},$
где ${{\delta }_{0}}$ – характерное раскрытие трещины, $\Delta \delta $ – изменение раскрытия.

На границах трещины ${{\Gamma }_{ \pm }}$ должны выполняться условия непрерывности давления и потоков. При этом скорость фильтрации ${{{v}}_{ \pm }}$ по нормали к границе матрица-трещина ${{\Gamma }_{ \pm }}$ пропорциональна градиенту давления и может быть определена как

${{{v}}_{ \pm }} = - \frac{{{{k}_{m}}}}{{{{\mu }_{l}}}}\frac{{\partial {{P}_{m}}}}{{\partial {{{\mathbf{n}}}_{ \pm }}}},$
где ${{{\mathbf{n}}}_{ \pm }}$ – вектор нормали к границам трещины.

При рассмотрении системы трещин две трещины либо не пересекаются, либо имеют одну общую точку. При этом в точке пересечения трещин также должны выполняться условия непрерывности давления и потоков.

1.2. Напряженно-деформированное состояние трещиновато-пористой среды

Трещиновато-пористая среда в каждый момент времени находится в состоянии механического равновесия. Закон сохранения импульса для пороупругой среды в квазистационарном приближении без учета объемных сил имеет вид [15]:

(1.1)
$\nabla \cdot \sigma = \nabla \cdot (\sigma {\kern 1pt} '\; - {{b}_{m}}\nabla {{P}_{m}}I) = 0$
где $\sigma $ – тензор полных напряжений, $\sigma {\kern 1pt} '$ – тензор эффективных напряжений, I – единичная матрица.

Для изотропной пороупругой среды в случае малых деформаций уравнение (1.1) с использованием закона Гука может быть записано относительно вектора перемещений скелета горной породы:

$\nabla \cdot [\mu \nabla {\mathbf{u}} + \mu {{(\nabla {\mathbf{u}})}^{T}} + \lambda I{\text{tr}}(\nabla {\mathbf{u}})] - {{b}_{m}}\nabla {{P}_{m}} = 0,$
где $\lambda $ и $\mu $ – коэффициенты Ляме.

При моделировании напряженно-деформированного состояния трещины рассматриваются как включения в скелет горной породы, обладающие собственными деформационными свойствами. Напряжения, действующие на границы трещины, в соответствии с условием механического равновесия (1.1) должны удовлетворять условию

${{\sigma }_{ + }} \cdot {{{\mathbf{n}}}_{ + }} = - {{\sigma }_{ - }} \cdot {{{\mathbf{n}}}_{ - }},$
где ${{\sigma }_{ + }}$, ${{\sigma }_{ - }}$ – полные напряжения, действующие на противоположные стороны трещины.

Выражение для эффективных напряжений, возникающих в трещине, может быть представлено в виде

(1.2)
$\sigma _{n}^{'} = {{\sigma }_{n}} + {{b}_{f}}{{P}_{f}},\quad \sigma _{s}^{'} = {{\sigma }_{s}},$
где ${{\sigma }_{n}}$, ${{\sigma }_{s}}$ – полные нормальное и сдвиговое напряжения, $\sigma _{n}^{'},$ $\sigma _{s}^{'}$ – эффективные нормальное и сдвиговое напряжения. Из (1.2) видно, что давление жидкости в трещине не влияет на сдвиговую компоненту напряжений.

Нормальные и сдвиговые напряжения, действующие на трещину, связаны с относительными перемещениями ее границ следующими линейными соотношениями:

(1.3)
$\sigma _{n}^{'} = {{k}_{n}}{{u}_{n}},\quad \sigma _{s}^{'} = {{k}_{s}}{{u}_{s}},$
где ${{u}_{n}}$ и ${{u}_{s}}$ – относительные нормальные и сдвиговые перемещения берегов трещины.

Раскрытие трещины $\delta $ может быть выражено через относительное нормальное перемещение ее берегов:

$\delta = {{\delta }_{0}} + \Delta \delta = {{\delta }_{0}} + {{u}_{n}}$

Таким образом, приведенные выше уравнения однофазной фильтрации в деформируемой трещиновато-пористой среде образуют замкнутую систему, которую необходимо дополнить начальными и граничными условиями.

2. ПОСТАНОВКА ЗАДАЧИ

Рассмотрим насыщенную жидкостью трещиновато-пористую среду, находящуюся в квадратной области $\Omega = \{ 0 \leqslant x \leqslant L;0 \leqslant y \leqslant L\} $ c левой ${{\Gamma }_{l}} = \{ x = 0;0 \leqslant y \leqslant L\} $, правой ${{\Gamma }_{r}} = \{ x = L;0 \leqslant y \leqslant L\} $, нижней ${{\Gamma }_{b}} = \left\{ {0 \leqslant x \leqslant L;y = 0} \right\}$ и верхней ${{\Gamma }_{t}} = \left\{ {0 \leqslant x \leqslant L;y = L} \right\}$ границами.

2.1. Граничные и начальные условия

Рассматриваются фильтрационные потоки в горизонтальном направлении, вызванные постоянным перепадом давления между левой и правой границами расчетной области Pin – ${{P}_{{out}}} = \Delta P$. На верхней и нижней границах расчетной области задано условие непротекания. Таким образом, граничные условия для давления имеют вид:

$P{{|}_{{{{\Gamma }_{r}}}}}\, = {{P}_{{out}}},\quad {{\left. {\frac{{\partial P}}{{\partial {\mathbf{n}}}}} \right|}_{{{{\Gamma }_{t}}}}} = 0,\quad P{{|}_{{{{\Gamma }_{l}}}}} = {{P}_{{in}}},\quad {{\left. {\frac{{\partial P}}{{\partial {\mathbf{n}}}}} \right|}_{{{{\Gamma }_{b}}}}} = 0$

Трещиновато-пористая среда находится под воздействием полных сжимающих напряжений, действующих перпендикулярно границам области. Для учета влияния прилегающих к расчетной области горных пород используются граничные условия “абсолютно жесткой пластины” [27], что приводит к граничным условиям следующего вида:

$\int\limits_{{{\Gamma }_{r}}} \sigma dy = {{\sigma }_{b}}L,\quad \int\limits_{{{\Gamma }_{t}}} \sigma dx = {{\sigma }_{b}}L,\quad {{u}_{n}}{\kern 1pt} |{{{\kern 1pt} }_{\Gamma }}_{{_{l}}} = 0,\;\,\;{{\left. {\frac{{\partial {{{\mathbf{u}}}_{\tau }}}}{{\partial {\mathbf{n}}}}} \right|}_{{{{\Gamma }_{l}}}}} = 0,\quad {{u}_{n}}{\kern 1pt} |{{{\kern 1pt} }_{\Gamma }}_{{_{b}}} = 0,\,\,\,\,{{\left. {\frac{{\partial {{{\mathbf{u}}}_{\tau }}}}{{\partial {\mathbf{n}}}}} \right|}_{{{{\Gamma }_{b}}}}} = 0,$

где un и uτ – нормальная и сдвиговая компоненты вектора перемещений.

В начальный момент времени давления жидкости в поровом пространстве и трещинах равны между собой ${{\left. {{{P}_{m}}} \right|}_{\Omega }} = {{\left. {{{P}_{f}}} \right|}_{\Omega }} = {{P}_{i}}$, а поле перемещений ui и раскрытие трещин ${{\delta }_{i}}$ определяются из решения поставленной задачи для невозмущенного поля давления при ${{P}_{{in}}} = {{P}_{{out}}} = {{P}_{i}}$. Все значения давлений и напряжений отсчитываются от величины начального давления ${{P}_{i}}$.

2.2. Трещиноватость

В рассматриваемой области расположена система трещин, состоящая из трещин со случайным положением и ориентацией. Распределение трещин по длинам подчиняется степенному закону [18]

(2.1)
$n(l) = A{{l}^{{ - a}}},$
где $l \in \left[ {{{l}_{{min}}},{{l}_{{max}}}} \right]$ – длина трещины, $n(l)dl$ – количество трещин с размером $l$ попадающих в интервал $\left[ {l,l + dl} \right]$, a – показатель степени, A – нормировочная константа.

Систему трещин можно охарактеризовать плотностью γ  и параметром перколяции p, выражения для которых имеют вид [22]:

$\gamma = \frac{1}{{{{L}^{2}}}}\int\limits_{{{l}_{{\min }}}}^{{{l}_{{\max }}}} n(l)l{\kern 1pt} 'dl,$
и
$p = \frac{1}{{{{L}^{2}}}}\int\limits_{{{l}_{{\min }}}}^{{{l}_{{\max }}}} n(l)l{\kern 1pt} {{'}^{2}}dl,$
где $l{\kern 1pt} '$ – длина трещины, включенной в рассматриваемую область. Параметр перколяции p характеризует степень связности системы трещин. При $p > {{p}_{c}}$, где pc – порог перколяции, трещины статистически связывают противоположные границы рассматриваемой области.

3. МЕТОДИКА ЧИСЛЕННОГО РЕШЕНИЯ

Для численного решения приведенной выше системы уравнений использовался метод контрольных объемов [28]. Совместное решение уравнений пороупругости для трещиноватой среды реализовано с помощью итерационного алгоритма “с фиксированными напряжениями” [29], который является безусловно устойчивым. Для учета положения трещин внутри расчетной области использованы неструктурированные расчетные сетки, построение которых проведено с помощью открытого пакета Gmsh [30]. Численные расчеты проведены с использованием разработанного программного модуля [31 ] .

Несмотря на то что модель дискретных трещин позволяет наиболее точно описать трещиноватость среды, ее использование осложняется высокими вычислительными затратами, связанными с необходимостью построения детальных расчетных сеток. Варианты системы трещин, полученные при случайной генерации, могут обладать геометрией, требующей чрезмерного измельчения расчетной сетки [32]. В связи с этим на процесс генерации системы трещин были наложены ограничения, позволяющие избежать подобного измельчения: заданы минимальное расстояние между непересекающимися трещинами dmin, минимальное расстояние между точками пересечения трещин dmin и минимальный угол пересечения трещин θmin.

4. РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Важным вопросом при изучении влияния трещиноватости на фильтрационные свойства горных пород является исследование зависимости эквивалентной проницаемости среды от структуры системы трещин. Эквивалентная абсолютная проницаемость трещиновато-пористой среды ${{k}_{{eq}}}$ может быть найдена из уравнения Дарси при заданном перепаде давления между границами расчетной области $\Delta P$ и известном расходе жидкости q при установившемся потоке:

$q = - \frac{{{{k}_{{eq}}}}}{{{{\mu }_{l}}}}\frac{{\Delta P}}{L}$
откуда

${{k}_{{eq}}} = - \frac{{q{{\mu }_{l}}L}}{{\Delta P}}$

В работе выполнено исследование зависимости эквивалентной проницаемости трещиновато-пористой среды от ее напряженно-деформированного состояния и параметров, характеризующих структуру системы трещин. Для этого проведена множественная случайная генерация систем трещин. Для каждого созданного варианта численно решалась задача о фильтрации однофазной жидкости в деформируемой трещиновато-пористой среде. Расчет эквивалентной проницаемости проведен на основе полученных из численного решения расходов жидкости на противоположных границах расчетной области. Решение для стационарного режима фильтрации было получено методом установления. Размер шага по времени и характерные размеры расчетных узлов выбраны таким образом, чтобы их дальнейшее уменьшение не оказывало существенного влияния на результаты расчетов.

Во всех расчетах использовались следующие значения параметров горной породы и насыщающей ее жидкости: пористость матрицы ${{\phi }_{m}} = 0.14$, пористость трещин ${{\phi }_{f}} = 1.0$, проницаемость матрицы ${{k}_{m}} = 1 \times {{10}^{{ - 15}}}$ м2, раскрытие трещин в недеформированном состоянии ${{\delta }_{0}} = 5 \times {{10}^{{ - 4}}}$ м, модуль Юнга $E = 2 \times {{10}^{4}}$ МПа, коэффициент Пуассона $\nu = 0.2$, объемный модуль материала зерен ${{K}_{s}} = 2.7 \times {{10}^{5}}$ МПа, нормальная жесткость трещин ${{k}_{n}} = 2 \times {{10}^{5}}$ МПа/м, сдвиговая жесткость трещин ${{k}_{s}} = 1 \times {{10}^{5}}$ МПа/м, коэффициент Био матрицы ${{b}_{m}} = 1.0$, коэффициент Био трещин ${{b}_{f}} = 1.0$, коэффициент сжимаемости жидкости ${{C}_{l}} = 3.7 \times {{10}^{{ - 4}}}$ МПа–1, вязкость жидкости ${{\mu }_{l}} = 1.0$ мПа ⋅ с.

Проницаемость трещин ${{k}_{f}}$ зависит от их раскрытия, определяемого напряженно-деформированным состоянием среды. Изменением проницаемости пористой среды, вызванным изменением напряженно-деформированного состояния, можно пренебречь по сравнению с изменением проницаемости трещин. Для трещин всех размеров использовано одинаковое значение раскрытия ${{\delta }_{0}}$. Отношение проницаемостей трещин и пористой матрицы при $\delta = {{\delta }_{0}}$ составляет ${{k}_{f}}{\text{/}}{{k}_{m}} \approx {{10}^{4}}$. Размер стороны расчетной области $L$ задавался равным 250 м, что соответствует характерному расстоянию между скважинами при разработке нефтяных пластов.

4.1. Варианты системы трещин

Для исследования влияния трещиноватости на фильтрационные свойства среды рассмотрены системы трещин с различными показателями степени a в степенном законе (2.1) и количеством трещин в системе ${{n}_{f}}$. Показатель степени в законе распределения принимал значения $a = 1.5,2.0,2.5,3.0,3.5$, количество трещин в системе ${{n}_{f}} = 50,100,150,200$. Для каждой пары значений параметров a и ${{n}_{f}}$ было создано 40 реализаций систем трещин. Таким образом, всего в работе рассмотрено $N = 5 \cdot 4 \cdot 40 = 800$ вариантов систем трещин. Для всех вариантов выбраны значения ${{l}_{{{\text{max}}}}} = 2L = 500$ м, ${{l}_{{{\text{min}}}}} = 0.06L = 15$ м. При генерации систем трещин использованы значения ${{d}_{{{\text{min}}}}} = 5$ м, ${{\theta }_{{{\text{min}}}}} = 20^\circ $. Плотность и параметр перколяции для всех созданных вариантов систем трещин принадлежали следующим интервалам: $\gamma \in \left[ {0.016;0.202} \right]$, $p \in \left[ {0.4;26.2} \right]$.

Некоторые примеры сгенерированных систем трещин для каждой из пар $({{n}_{f}},a)$ и соответствующие им значения $\gamma $ и $p$ приведены на рис. 1. Видно, что по мере уменьшения a увеличивается характерная длина трещин, возрастает их связность. Так, при $a = 3.5$ в области преобладают трещины малой длины, изолированные друг от друга. При $a = 1.5$ большинство трещин включено в один кластер, связывающий противоположные границы расчетной области.

Рис. 1.

Примеры вариантов сгенерированных систем трещин с различными значениями показателя a в законе распределения трещин по длинам (строки) и количеством трещин в системе ${{n}_{f}}$ (столбцы). Для каждой системы трещин приведены значения плотности системы трещин $\gamma $ и параметра перколяции p.

Под перколяцией будем понимать связь противоположных границ расчетной области системой трещин. В таком случае существует как минимум один путь по трещинам от одной границы до другой. Набор трещин, связывающий границы, образует перколяционный кластер. Для каждого варианта системы трещин исследовано наличие связи противоположных границ области в горизонтальном направлении. Для рассматриваемого набора систем трещин в 357 случаях имеет место перколяция расчетной области и в 443 случаях противоположные границы несвязны. На рис. 2 приведена зависимость вероятности перколяции расчетной области от параметра перколяции, которая аппроксимирована функцией следующего вида

(4.1)
$S(p) = \frac{1}{{1 + {{e}^{{ - \varepsilon (p - {{p}_{c}})}}}}},$
где ${{p}_{c}}$ – пороговое значение параметра перколяции, параметр $\varepsilon $ определяет ширину “переходной зоны”.

Рис. 2.

Зависимость вероятности связи противоположных границ расчетной области системой трещин от величины параметра перколяции p. Пороговое значение параметра перколяции ${{p}_{c}} = 4.8$.

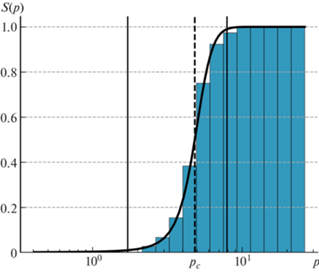
Для оценки качества аппроксимации использована средняя абсолютная ошибка mae = = $\frac{1}{n}\sum\limits_{i = 1}^n {\left| {{{{\hat {y}}}_{i}} - {{y}_{i}}} \right|} $, где ${{\hat {y}}_{i}}$ – результат аппроксимации, ${{y}_{i}}$ – истинное значение. Полученное значение $mae = 0.1$ свидетельствует об удовлетворительном качестве аппроксимации. За порог перколяции ${{p}_{c}}$ принимается значение, при котором вероятность перколяции расчетной области $S(p) = 0.5$. В результате аппроксимации из (4.1) получено значение ${{p}_{c}} = 4.8$. В зависимости от вероятности перколяции каждая система трещин может быть условно отнесена к одной из трех групп, разделенных на рис. 2 вертикальными линиями. К системам слабосвязных трещин отнесены варианты, для которых вероятность появления перколяционного кластера $S(p) \leqslant 0.01$, что соответствует параметру перколяции $p \leqslant 1.7$. Варианты систем трещин, для которых $S(p) \geqslant 0.99$ отнесены к сильно связным: $p \geqslant 7.9$. Системы трещин из интервала $1.7 < p < 7.9$ отнесены к “переходной зоне”, где появление перколяционного кластера имеет случайный характер.

4.2. Влияние параметров трещиноватой среды на эквивалентную проницаемость

Сперва рассмотрим влияние структуры трещиноватой среды на ее эквивалентную проницаемость при фиксированном раскрытии трещин ${{\delta }_{i}}$, которое соответствует начальному напряженно-деформированному среды при величине внешней нагрузки ${{\sigma }_{b}} = 15$ МПа. В этом случае для определения эквивалентной проницаемости среды может быть выбран произвольный перепад давления, для расчетов выбрано значение $\Delta P = 5$ МПа.

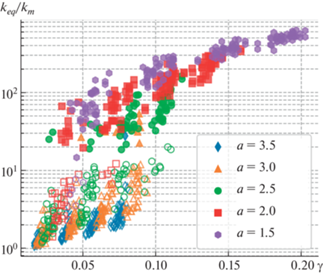
На рис. 3 приведена зависимость ${{k}_{{eq}}}{\text{/}}{{k}_{m}}$ от $\gamma $ в полулогарифмических координатах при различных значениях a. Закрашенные маркеры соответствуют высокопроницаемым средам с трещинами, образующими перколяционный кластер. При слабой связности трещин и отсутствии перколяционного кластера наблюдается низкая эквивалентная проницаемость среды, данные варианты обозначены полыми маркерами. Таким образом, при рассматриваемых значениях проницаемостей ${{k}_{f}} \gg {{k}_{m}}$ наличие перколяционного кластера оказывает определяющее влияние на эквивалентную проницаемость трещиноватой среды. Видно, что расчетные значения можно разделить на 2 “облака” точек. Область между “облаками”, в которой расчетные точки отсутствуют, соответствует порогу перколяции, а ее наличие объясняется использованием в алгоритме генерации системы трещин ограничения на минимальное расстояние между непересекающимися трещинами dmin.

Рис. 3.

Зависимость отношения ${{k}_{{eq}}}{\text{/}}{{k}_{m}}$ от плотности системы трещин $\gamma $ при различных показателях степени a. Закрашенные маркеры соответствуют случаю перколяции расчетной области, полые – отсутствию перколяционного кластера.

Для анализа поведения эквивалентной проницаемости трещиновато-пористой среды вблизи порога перколяции рассмотрим идеализированную трещиноватую среду, состоящую из набора параллельных трещин [33]. Трещины равной длины ${{l}_{\parallel }}$ расположены на одинаковом друг от друга расстоянии и ориентированы по направлению потока. При этом, если длина трещин больше размеров расчетной области ${{l}_{\parallel }} \geqslant L$, то проницаемость среды может быть определена как среднее арифметическое взвешенное проницаемостей пористой среды и трещин:

(4.2)
$k_{\parallel }^{I} = {{k}_{m}}\left( {1 - \frac{{\delta {{n}_{f}}}}{L}} \right) + {{k}_{f}}\frac{{\delta {{n}_{f}}}}{L}$

В противном случае, если длина трещин в системе меньше размеров расчетной области ${{l}_{\parallel }} < L$, то для оценки проницаемости используется среднее гармоническое взвешенное проницаемостей модельной трещиновато-пористой среды (4.2) и матрицы горной породы:

(4.3)
$k_{\parallel }^{{II}} = \frac{{L{{k}_{m}}k_{\parallel }^{I}}}{{{{l}_{\parallel }}{{k}_{m}} + (L - {{l}_{\parallel }})k_{\parallel }^{I}}}$

Отношение ${{l}_{\parallel }}{\text{/}}L$ имеет смысл доли расчетной области, занятой трещинами. Как следует из (4.3), при ${{k}_{m}} \ll {{k}_{f}}$ матрица горной породы ограничивает величину фильтрационных потоков. В то же время при ${{l}_{\parallel }} \to L$ проницаемость расчетной области быстро возрастает до величины $k_{\parallel }^{I}$, которая главным образом определяется величиной ${{k}_{f}}$. Таким образом, поведение эквивалентной проницаемости вблизи порога перколяции носит непрерывный характер.

Из рис. 3 также следует, что при близких значениях плотности системы трещин могут реализовываться существенно различные значения эквивалентной проницаемости. Для примера рассмотрим величины эквивалентной проницаемости для систем трещин, приведенных на рис. 1. Так, для вариантов ($a = 1.5,$ ${{n}_{f}} = 50$), ($a = 2.5,$ ${{n}_{f}} = 100$) и $(a = 3.5,{{n}_{f}} = 150)$ эквивалентная проницаемость составляет ${{k}_{{eq}}} = 70.5,$ 18.9 и $1.91 \times {{10}^{{ - 15}}}$ м2 соответственно. Отличие проницаемостей между вариантами при достаточно близких плотностях $\gamma \in \left[ {0.05,0.055} \right]$ может достигать 37 раз. Поэтому в данном случае не представляется возможным построение функциональной зависимости между плотностью системы трещин и эквивалентной проницаемостью среды. Таким образом, можно сделать вывод о том, что при выбранном законе распределения трещин по длинам плотность системы не может однозначно охарактеризовать фильтрационные параметры трещиновато-пористой среды.

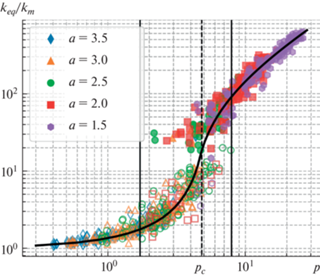
Далее рассмотрим приведенную на рис. 4 зависимость keq/km от параметра перколяции $p$. Видно, что на данной зависимости можно выделить два участка с разным характером функциональной зависимости ${{k}_{{eq}}}(p)$: до порогового значения параметра перколяции $(0 \leqslant p < {{p}_{c}})$ и после него $(p \geqslant {{p}_{c}})$. На первом участке, при малых значениях параметра перколяции ($p < 1.7$), величина эквивалентной проницаемости среды определяется матричной проницаемостью: в этой области трещины изолированы друг от друга матрицей горной породы. Затем, по мере увеличения p и приближению его к порогу перколяции, наблюдается рост проницаемости, вызванный увеличением степени связности системы трещин. На втором участке развитая система трещин образует перколяционный кластер, который оказывает определяющее влияние на поток жидкости. Трещины в таком случае выступают в роли “магистральных каналов” для фильтрационных потоков. При этом наибольшая неопределенность значений эквивалентных проницаемостей имеет место в “переходной зоне” $(1.7 < p < 7.9)$.

Рис. 4.

Зависимость отношения ${{k}_{{eq}}}{\text{/}}{{k}_{m}}$ от параметра перколяции p при различных показателях степени a и его аппроксимация. Закрашенные маркеры соответствуют случаю перколяции расчетной области, полые – отсутствию перколяционного кластера.

Учитывая вышеизложенное, аппроксимация эквивалентной проницаемости ${{k}_{{eq}}}(p)$ проведена с помощью непрерывной кусочно-заданной функции, учитывающей особенности структуры системы трещин. При $p \leqslant {{p}_{c}}$ для аппроксимации эквивалентной проницаемости используется среднее гармоническое взвешенное, определяемое формулой (4.3), где в качестве доли расчетной области, занятой трещинами, ${{l}_{\parallel }}{\text{/}}L$ использована величина $p{\text{/}}{{p}_{c}} \in [0;1]$. Также учитывался предложенный в [34] степенной характер зависимости эквивалентной проницаемости от параметра перколяции. Кроме того, аппроксимирующая функция должна удовлетворять следующим условиям: ${{k}_{{eq}}} = {{k}_{m}}$ при p = 0 и ${{k}_{{eq}}} = {{k}_{c}}$ при $p = {{p}_{c}}$, где ${{k}_{c}}$ – проницаемость трещиновато-пористой среды на пороге перколяции. Таким образом, для аппроксимации эквивалентной проницаемости трещиновато-пористой среды при $p \leqslant {{p}_{c}}$ выбрана функция в виде:

(4.4)
${{k}_{{eq}}} = {{\left( {\frac{{{{p}_{c}}{{{({{k}_{m}})}}^{{1/\alpha }}}{{{({{k}_{c}})}}^{{1/\alpha }}}}}{{p{{{({{k}_{m}})}}^{{1/\alpha }}} + ({{p}_{c}} - p)({{k}_{c}}{{)}^{{1/\alpha }}}}}} \right)}^{\alpha }}$

Известно, что поведение проницаемости системы трещин выше порога перколяции имеет степенной характер [35, 36]. Поэтому при $p \geqslant {{p}_{c}}$ использована степенная функция в виде:

(4.5)
${{k}_{{eq}}} = {{k}_{c}}{{\left( {p - {{p}_{c}} + 1} \right)}^{\beta }},$
где ${{k}_{{eq}}} = {{k}_{c}}$ при $p = {{p}_{c}}$.

Таким образом, выражения (4.4) и (4.5) определяют непрерывную кусочно-заданную функцию с настраиваемыми параметрами: $\alpha ,{{k}_{c}},\beta $. Результат аппроксимации результатов численного моделирования приведен на рис. 4. Для численной оценки аппроксимации использована средняя относительная ошибка mape = $\frac{1}{n}\sum\limits_{i = 1}^n {\frac{{\left| {{{{\hat {y}}}_{i}} - {{y}_{i}}} \right|}}{{\left| {{{y}_{i}}} \right|}}} = 0.2$. Полученное качество аппроксимации является удовлетворительным в условиях того, что в переходной зоне эквивалентные проницаемости сред при близких значениях параметра перколяции могут отличаться на порядок.

В результате аппроксимации для параметров α и $\beta $ получены значения 1.6 и 1.11 соответственно. При этом значение $\beta $ хорошо согласуется с данными, приведенными в литературе $\beta \approx 1.1$ [35]. Для оценки величины ${{k}_{c}}$ необходимо отметить, что вблизи порога перколяции существует единственный путь связи противоположных границ расчетной области трещинами, который при ${{k}_{m}} \ll {{k}_{f}}$ определяет фильтрационные свойства среды. Тогда эквивалентная проницаемость вблизи порога перколяции ${{k}_{c}}$ может быть оценена из выражения (4.2) $k_{\parallel }^{I} = 26.6 \times {{10}^{{ - 15}}}$ м2 при nf = 1. Полученное при аппроксимации результатов численного моделирования значение kc = $18.8 \times {{10}^{{ - 15}}}$ м2 несколько ниже аналитической оценки, что может быть объяснено извилистостью системы трещин, связывающей противоположные границы области. Например, на рис. 1 (a = 2.5 ${{n}_{f}} = 100$) красной линией выделен обладающий извилистостью кратчайший путь по системе трещин между левой и правой границами расчетной области.

В частном случае при ${{k}_{m}}{\text{/}}{{k}_{с}} \to 0$ формула (4.4) может быть сведена к виду [34]:

${{k}_{{eq}}} = {{k}_{m}}{{\left( {\frac{{{{p}_{c}}}}{{{{p}_{c}} - p}}} \right)}^{\alpha }}$

Также формула (4.4) учитывает предельный случай непроницаемой матрицы горной породы ${{k}_{m}} = 0$. В этом случае величина ${{k}_{{eq}}} = 0$ при $p < {{p}_{c}}$ и изменяется скачком до значения ${{k}_{c}}$ при $p = {{p}_{c}}$.

4.3. Влияние напряженно-деформированного состояния

В данном пункте исследовано изменение эквивалентной проницаемости трещиновато-пористой среды при изменении ее напряженно-деформированного состояния, вызванного закачкой жидкости в расчетную область. Исследование проведено при трех значениях давления закачки жидкости ${{P}_{{in}}} = 5,10,15$ МПа и постоянных величинах внешней нагрузки ${{\sigma }_{b}} = 15$ МПа и давления ${{P}_{{out}}} = 0$. Изменение эквивалентной проницаемости рассматривается относительно ее величины ${{k}_{{eq,i}}}$, соответствующей начальному состоянию среды, которая исследована в предыдущем пункте.

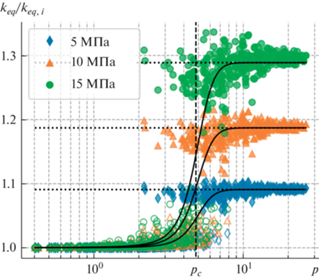
На рис. 5 представлена зависимость относительного изменения эквивалентной проницаемости среды ${{k}_{{eq}}}{\text{/}}{{k}_{{eq,i}}}$ от параметра перколяции p при различных давлениях ${{P}_{{in}}}$. Видно, что при увеличении параметра перколяции влияние напряженно-деформированного состояния на проницаемость среды возрастает. Так, при $p < {{p}_{c}}$ не наблюдается существенного влияния давления закачки на эквивалентную проницаемость среды. Напротив, при $p > {{p}_{c}}$ изменение проницаемости трещин начинает оказывать влияние на фильтрационные свойства среды: величина относительного изменения эквивалентной проницаемости достигает 30%.

Рис. 5.

Зависимость относительного изменения эквивалентной проницаемости ${{k}_{{eq}}}{\text{/}}{{k}_{{eq,i}}}$ от параметра перколяции p при различных давлениях закачки жидкости ${{P}_{{in}}}$. Закрашенные маркеры соответствуют случаю перколяции расчетной области, полые – отсутствию перколяционного кластера.

Для выбора аппроксимирующей функции рассмотрим влияние напряженно-деформированного состояния на проницаемость трещиноватой среды, состоящей из набора параллельных трещин при ${{l}_{\parallel }} \geqslant L$. Для простоты получаемых далее оценок пренебрежем в (4.2) проницаемостью матрицы горной породы по сравнению с проницаемостью трещин. Тогда выражение для проницаемости системы параллельных трещин с учетом зависимости их раскрытия от эффективных напряжений (1.3) можно записать в виде:

$k_{\parallel }^{I} = \frac{{{{{\left( {{{\delta }_{0}} + \frac{{\sigma _{n}^{'}}}{{{{k}_{n}}}}} \right)}}^{3}}}}{{12}}\frac{{{{n}_{f}}}}{L}$

В этом случае выражение для относительного изменения проницаемости набора параллельных трещин при изменении нормальных эффективных напряжений примет вид

(4.6)
$\begin{array}{*{20}{l}} {\frac{{k_{\parallel }^{I}}}{{k_{{\parallel i}}^{I}}} = {{{\left( {\frac{{{{\delta }_{0}}{{k}_{n}} + \sigma _{{ni}}^{'} + \Delta \sigma _{n}^{'}}}{{{{\delta }_{0}}{{k}_{n}} + \sigma _{{ni}}^{'}}}} \right)}}^{3}} = {{{\left( {1 + \frac{{\Delta \sigma {\kern 1pt} '}}{{{{\delta }_{0}}{{k}_{n}} + \sigma _{{ni}}^{'}}}} \right)}}^{3}} = {{{(1 + b\Delta \sigma _{n}^{'})}}^{3}},} \end{array}$
где ${{k}_{{\parallel i}}}$ – проницаемость упорядоченной системы трещин при начальных условиях, $\Delta \sigma _{n}^{'}$ – изменение эффективных нормальных напряжений относительно начального состояния, b = = $\frac{1}{{{{\delta }_{0}}{{k}_{n}} + \sigma _{{ni}}^{'}}}$ – параметр трещиноватой среды, зависящий от начального напряженно-деформированного состояния среды, фильтрационных и упругих свойств трещин, ${{\delta }_{0}}{{k}_{n}}$ – величина, соответствующая напряжению смыкания трещины при ее постоянной жесткости.

На рис. 5 в виде горизонтальных пунктирных линий приведены значения $k_{\parallel }^{I}{\text{/}}k_{{\parallel i}}^{I}$ для различных давлений закачки ${{P}_{{in}}}$. В качестве $\Delta \sigma _{n}^{'}$ в формуле (4.6) использовалась следующая оценка изменения среднего эффективного напряжения в расчетной области $\Delta \sigma _{n}^{'} = {{\sigma }_{b}} + {{b}_{f}}\left( {\frac{{{{P}_{{in}}} + {{P}_{{out}}}}}{2} - {{P}_{i}}} \right)$. Видно, что при $p > 7.9$ полученная оценка имеет удовлетворительное приближение к результатам прямого численного моделирования. Выражение (4.6) принято за величину максимального относительного изменения проницаемости ${{k}_{{eq}}}{\text{/}}{{k}_{{eq,i}}}$. С другой стороны, при p = 0 проницаемость среды ${{k}_{{eq}}} = {{k}_{{eq,i}}}$. Для построения зависимости эквивалентной проницаемости от p во всем диапазоне значений использована аппроксимация вероятности перколяции расчетной области $S(p)$, которая связывает области $p < 1.7$ и $p > 7.9$. Тогда аппроксимацию эквивалентной проницаемости среды с учетом изменения ее напряженно-деформированного состояния окончательно можно представить в виде:

(4.7)
${{k}_{{eq}}} = [({{(1 + b\Delta \sigma _{n}^{'})}^{3}} - 1)S(p) + 1]{{k}_{{eq,i}}}$

Результат аппроксимации изменения эквивалентной проницаемости функцией (4.7) приведен на рис. 5. Получено удовлетворительное качество аппроксимации, средняя относительная ошибка для различных давлений закачки жидкости принимала значения: $mape = 0.007$ при ${{P}_{{in}}} = 5$ МПа, $mape = 0.015$ при ${{P}_{{in}}} = 10$ МПа и $mape = 0.023$ при ${{P}_{{in}}} = 15$ МПа.

Таким образом, предложенная аппроксимация (4.7) учитывает зависимость эквивалентной проницаемости трещиновато-пористой среды от всех основных параметров задачи: структуры системы трещин (параметра перколяции p и его порогового значения ${{p}_{c}}$), напряженно-деформированного состояния системы (величины эффективных напряжений $\sigma _{n}^{'}$), упругих и фильтрационных свойств трещин (нормальной жесткости ${{k}_{n}}$ и раскрытия $\delta $ трещин).

5. ЗАКЛЮЧЕНИЕ

В работе выполнено исследование зависимости фильтрационных свойств трещиновато-пористых сред от их напряженно-деформированного состояния и структуры системы трещин. Для моделирования фильтрации в деформируемой трещиновато-пористой среде использована модель пороупругой среды, моделирование трещиноватости проведено с помощью модели дискретных трещин. Распределение трещин по длинам подчинялось степенному закону. Численное исследование выполнено для вариантов систем трещин, полученных путем множественной случайной генерации.

Полученные результаты показывают, что фильтрационные свойства трещиновато-пористой среды определяются главным образом структурой системы трещин, характеризуемой параметром перколяции. При этом вблизи порога перколяции наблюдаются изменение характера поведения эквивалентной проницаемости и ее резкий рост. В то же время плотность системы трещин для использованного степенного закона распределения трещин по длинам не позволяет с удовлетворительной точностью описать эквивалентную проницаемость среды.

Установлено, что для сильно связных систем трещин со значением параметра перколяции $p > 7.9$ напряженно-деформированное состояние существенно влияет на фильтрационные свойства среды: изменение эквивательной проницаемости для проведенных расчетов достигало 30%. Для слабосвязных систем трещин ($p < 1.7$) максимальное относительное изменение проницаемости составляет менее 1%.

Предложена формула для аппроксимации зависимости эквивалентной проницаемости трещиновато-пористой среды от параметров, характеризующих связность системы трещин, напряженно-деформированное состояние среды, деформационные и фильтрационные свойства трещин.

БЛАГОДАРНОСТИ

Работа выполнена в рамках государственного задания (№ госрегистрации 121030500156-6).

Список литературы

  1. Smirnov N.N., Nikitin V.F., Kolenkina (Skryleva) E.I., Gazizova. D. R. Evolution of a phase interface in the displacement of viscous fluids from a porous medium // Fluid Dynamics. 2021. V. 56. № 1. P. 79–92. https://doi.org/10.1134/S0015462821010122

  2. Nikitin V.F., Skryleva E.I., Weisman Yu. G. Control of capillary driven fluid flows for safe operation of spacecraft fluid supply systems using artificial porous media // Acta Astronautica. 2022. V. 194. P. 544–548. https://doi.org/10.1016/j.actaastro.2021.12.009

  3. Dushin V.R., Smirnov N.N., Nikitin V.F., Skryleva E. I., Weisman Yu.G. Multiple capillary-driven imbibition of a porous medium under microgravity conditions: Experimental investigation and mathematical modeling // Acta Astronautica. 2022. V. 193. P. 572–578. https://doi.org/10.1016/j.actaastro.2021.06.054

  4. Kiselev A.B., Kay-Zhui L., Smirnov N.N., Pestov D.A. Simulation of Fluid Flow through a Hydraulic Fracture of a Heterogeneous Fracture-Tough Reservoir in the Planar 3D Formulation // Fluid Dynamics. 2021. V. 56. № 2. P. 164–177. https://doi.org/10.1134/S0015462821020051

  5. Smirnov N., Li K., Skryleva E., Pestov D., Shamina A., Qi C., Kiselev A. Mathematical Modeling of Hydraulic Fracture Formation and Cleaning Processes // Energies. 2022. V. 15. № 6. https://doi.org/10.3390/en15061967

  6. Голф-Рахт Т.Д. Основы нефтепромысловой геологии и разработки трещиноватых коллекторов. M.: Недра, 1986. 608 с.

  7. Nelson R.A. Geologic Analysis of Naturally Fractured Reservoirs. Gulf Professional Publishing, 2001. 352 p.

  8. Пичугин О.Н., Родионов С.П., Соляной П.Н., Гаврись А.С., Косяков В.П., Кошеверов Г.Г. Принципы оптимизации систем заводнения месторождений, осложненных малоамплитудными тектоническими нарушениями // Российская нефтегазовая техническая конференции SPE, Москва, Россия. 2015.

  9. Karimi-Fard M., Durlofsky L.J., Aziz K. An Efficient Discrete-Fracture Model Applicable for General-Purpose Reservoir Simulators // SPE Journal. 2004. V. 9. № 2. P. 227–236. https://doi.org/10.2118/88812-PA

  10. Garipov T.T., Karimi-Fard M., Tchelepi H.A. Discrete fracture model for coupled flow and geomechanics // Computational Geosciences. 2016. V. 20. № 1. P. 149–160. https://doi.org/10.1007/s10596-015-9554-z

  11. Bai M. On equivalence of dual-porosity poroelastic parameters // Journal of Geophysical Research: Solid Earth. 1999. V. 104. № B5. P. 10461–10466. https://doi.org/10.1029/1999JB900072

  12. Chen H.-Y., Teufel L.W. Coupling Fluid-Flow and Geomechanics in Dual-Porosity Modeling of Naturally Fractured Reservoirs – Model Description and Comparison// SPE International Oil Conference and Exhibition in Mexico. 2000. https://doi.org/10.2118/59043-MS

  13. Rutqvist J., Stephansson O. The role of hydromechanical coupling in fractured rock engineering // Hydrogeology Journal. 2003. V. 11. № 1. P. 7–40. https://doi.org/10.1007/s10040-002-0241-5

  14. Biot M.A. General Theory of Three-Dimensional Consolidation // Journal of Applied Physics. 1941. V. 12. № 2. P. 155–164. https://doi.org/10.1063/1.1712886

  15. Coussy O. Poromechanics. John Wiley and Sons, Ltd, 2004. 315 p.

  16. Gutierrez M., Youn D.-J. Effects of fracture distribution and length scale on the equivalent continuum elastic compliance of fractured rock masses // Journal of Rock Mechanics and Geotechnical Engineering. 2015. V. 7. № 6. P. 626–637. https://doi.org/10.1016/j.jrmge.2015.07.006

  17. Liu R., Li B., Jiang Y., Huang N. Review: Mathematical expressions for estimating equivalent permeability of rock fracture networks // Hydrogeology Journal. 2016. V. 24. № 7. P. 1623–1649. https://doi.org/10.1007/s10040-016-1441-8

  18. Bonnet E., Bour O., Odling N.E., Davy P., Main I., Cowie P., Berkowitz B. Scaling of fracture systems in geological media // Reviews of Geophysics. 2001. V. 39. № 3. P. 347–383. https://doi.org/10.1029/1999RG000074

  19. Bogdanov I.I., Mourzenko V.V., Thovert J.-F., Adler P.M. Effective permeability of fractured porous media in steady state flow // Water Resources Research. 2003. V. 39. № 1. https://doi.org/10.1029/2001WR000756

  20. Hyman J.D., Karra S., Carey J.W., Gable C.W., Viswanathan H., Rougier E., Lei Z. Discontinuities in effective permeability due to fracture percolation // Mechanics of Materials. 2018. V. 119. P. 25–33. https://doi.org/10.1016/j.mechmat.2018.01.005

  21. Jafari A., Babadagli T. A Sensitivity Analysis for Effective Parameters on 2D Fracture-Network Permeability // SPE Reservoir Evaluation & Engineering. 2009. V. 12. № 3. P. 455–469. https://doi.org/10.2118/113618-PA

  22. Bour O., Davy P. Connectivity of random fault networks following a power law fault length distribution // Water Resources Research. 1997. V. 33. № 7. P. 1567–1583. https://doi.org/10.1029/96WR00433

  23. de Dreuzy J.-R., Davy P., Bour O. Hydraulic properties of two-dimensional random fracture networks following a power law length distribution: 1. Effective connectivity // Water Resources Research. 2001. V. 37. № 8. P. 2065–2078. https://doi.org/10.1029/2001WR900011

  24. de Dreuzy J.-R., Davy P., Bour O. Hydraulic properties of two-dimensional random fracture networks following a power law length distribution: 2. Permeability of networks based on lognormal distribution of apertures // Water Resources Research. 2001. V. 37. № 8. P. 2079–2095. https://doi.org/10.1029/2001WR900010

  25. Masihi M., King P.R. Connectivity Prediction in Fractured Reservoirs With Variable Fracture Size: Analysis and Validation // SPE Journal. 2008. V. 13. № 1. P. 88–98. https://doi.org/10.2118/100229-PA

  26. Witherspoon P.A., Wang J.S.Y., Iwai K., Gale J.E. Validity of Cubic Law for fluid flow in a deformable rock fracture // Water Resources Research. 1980. V. 16. № 6. P. 1016–1024. https://doi.org/10.1029/WR016i006p01016

  27. Gao K., Lei Q. Influence of boundary constraints on stress heterogeneity modelling //Computers and Geotechnics. 2018. V. 99. P. 130–136. https://doi.org/10.1016/j.compgeo.2018.03.003

  28. Tang T., Hededal O., Cardiff P. On finite volume method implementation of poro-elasto-plasticity soil model // International Journal for Numerical and Analytical Methods in Geomechanics. 2015. V. 39. № 13. P. 1410–1430. https://doi.org/10.1002/nag.2361

  29. Kim J., Tchelepi H.A., Juanes R. Stability and convergence of sequential methods for coupled flow and geomechanics: Fixed-stress and fixed-strain splits // Computer Methods in Applied Mechanics and Engineering. 2015. V. 200. № 13. P. 1591–1606. https://doi.org/10.1016/j.cma.2010.12.022

  30. Geuzaine C., Remacle J.-F. Gmsh: A 3-D finite element mesh generator with built-in pre- and post-processing facilities // International Journal for Numerical Methods in Engineering. 2009. V. 79. № 11. P. 1309–1331. https://doi.org/10.1002/nme.2579

  31. Легостаев Д.Ю., Родионов С.П. Численное исследование двухфазной фильтрации в трещиновато-пористой среде на основе моделей пороупругости и дискретных трещин // Прикладная механика и техническая физика. 2021. Т. 62. № 3. С. 126–136. https://doi.org/10.15372/PMTF20210312

  32. Berre I., Doster F., Keilegavlen E. Flow in Fractured Porous Media: A Review of Conceptual Models and Discretization Approaches // Transport in Porous Media. 2019. V. 130. № 1. P. 215–236. https://doi.org/10.1007/s11242-018-1171-6

  33. Басниев К.С., Кочина И.Н., Максимов В.М. Подземная гидромеханика. М.: Недра, 1993. 416 p.

  34. Lei Q., Wang X., Min K.-B., Rutqvist J. Interactive roles of geometrical distribution and geomechanical deformation of fracture networks in fluid flow through fractured geological media // Journal of Rock Mechanics and Geotechnical Engineering. 2020. V. 12. № 4. P. 780–792. https://doi.org/10.1016/j.jrmge.2019.12.014

  35. Hestir K., Long J.C.S. Analytical expressions for the permeability of random two-dimensional Poisson fracture networks based on regular lattice percolation and equivalent media theories // Journal of Geophysical Research: Solid Earth. 1990. V. 95. № B13. P. 21565–21581. https://doi.org/10.1029/JB095iB13p21565

  36. Berkowitz B., Balberg I. Percolation theory and its application to groundwater hydrology // Water Resources Research. 1993. V. 29. № 4. P. 775–7941. https://doi.org/10.1029/92WR02707

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал