Микроэлектроника, 2020, T. 49, № 4, стр. 262-270

Расчет электропроводности тонкой цилиндрической проводящей трубки с учетом анизотропии изоэнергетической поверхности

И. А. Кузнецова^a, *, Д. Н. Романов^a, **

^a Ярославский государственный университет им. П.Г. Демидова
150003 Ярославль, ул. Советская, 14, Россия

^* E-mail: kuz@uniyar.ac.ru
^** E-mail: romanov.yar357@mail.ru

Поступила в редакцию 24.01.2020
После доработки 24.01.2020
Принята к публикации 13.02.2020

DOI: 10.31857/S0544126920040043

Аннотация

В рамках кинетического подхода проведен расчет электропроводности тонкой проводящей трубки с использованием диффузных граничных условий для функции распределения. Рассмотрен случай анизотропной изоэнергетической поверхности проводника, имеющей форму трехосного эллипсоида, одна из осей которого параллельна оси трубки. Проведен анализ зависимостей модуля и аргумента электропроводности от эффективной массы носителей заряда.

ВВЕДЕНИЕ

В рамках кинетической теории показано, что электрические и оптические свойства малых проводящих объектов существенно отличаются от свойств “массивных” образцов [1]. Различие объясняется ограничением длины свободного пробега границей образца и, как следствие, увеличением влияния поверхностного рассеяния носителей заряда по сравнению с объемным рассеянием на процессы переноса, что ведет к существенному влиянию поверхностного рассеяния на кинетические коэффициенты (классический размерный эффект). В случае, когда характерный линейный размер образца много больше длины волны де Бройля, для количественного описания классического размерного эффекта применяется кинетическое уравнение Больцмана с использованием граничных условий, учитывающих механизм поверхностного рассеяния носителей заряда.

Закон дисперсии (зависимость энергии квазичастицы от импульса) оказывает существенное влияние на характер движения электронов (дырок) в полупроводнике. Изоэнергетическую поверхность ряда типичных полупроводников можно аппроксимировать эллипсоидом вращения (кремний, германий), что является естественным обобщением наиболее часто используемой модели сферической изоэнергетической поверхности.

Расчет статической проводимости тонкой металлической проволоки круглого сечения выполнен в работе [2], проволоки прямоугольного сечения – в работе [3]. Теоретическое исследование металлической пленки в квазиклассическом приближении при наличии постоянных магнитного и электрического полей проводилось Зондгеймером [4] с учетом диффузного механизма отражения электронов от верхней и нижней границы пленки. Расчет высокочастотной электропроводимости тонкой цилиндрической полупроводниковой проволоки проведен в работе [5]. В приведенных работах решается кинетическое уравнение Больцмана с учетом граничных условий Фукса [6]. Высокочастотная электропроводность тонкой цилиндрической проволоки с применением граничных условий Соффера [7] получена в работе [8]. В работах [2–6, 8] расчет электропроводности выполнен для проволок со сферической поверхностью Ферми. Влияние анизотропии поверхности Ферми на электропроводность тонкой неоднородной металлической проволоки исследовалось в работе [9].

В данной работе проводится расчет электропроводности тонкой проводящей трубки в случае эллипсоидальной изоэнергетической поверхности проводника с использованием модели диффузного отражения носителей заряда от границ трубки.

ПОСТАНОВКА ЗАДАЧИ

Рассматривается проводящая цилиндрическая трубка длиной $L$ с внутренним радиусом ${{R}_{1}}$ и с внешним радиусом ${{R}_{2}}.$ Предполагаем, что толщина стенки $\left( {{{R}_{2}} - {{R}_{1}}} \right)$ много меньше глубины скин-слоя, это позволяет пренебречь скин-эффектом.

Напряженность электрического поля направлена вдоль оси трубки (ось $Z$) и зависит от времени по следующему закону

(1)

${\mathbf{E}} = {{{\mathbf{E}}}_{0}}{\text{exp}}\left( { - i{\omega }t} \right).$

Неравновесную функцию распределения $f$ представим в виде двух составляющих: равновесной функции распределения Ферми-Дирака ${{f}_{0}}$ и неравновесной поправки ${{f}_{1}},$ возникающей под действием внешнего электрического поля

(2)

$f = {{f}_{0}} + {{f}_{1}}{\text{exp}}\left( { - i{\omega }t} \right),\,\,f = f\left( {{\mathbf{r}},{\mathbf{v}},t} \right),\,\,{{f}_{1}} = {{f}_{1}}\left( {{\mathbf{r}},{\mathbf{v}}} \right),$

(3)

${{f}_{0}} = {{\left( {1 + {\text{exp}}\left\{ {{{\left( {\varepsilon - \mu } \right)} \mathord{\left/ {\vphantom {{\left( {\varepsilon - \mu } \right)} {{{k}_{{\text{Б}}}}T}}} \right. \kern-0em} {{{k}_{{\text{Б}}}}T}}} \right\}} \right)}^{{ - 1}}},$

где ${\mathbf{r}}$, ${\mathbf{v}}~$ и $m$ – радиус-вектор, скорость и эффективная масса электрона (дырки).

В переменном электрическом поле ${\mathbf{E}}$ (1) уравнение Больцмана для квазисвободных электронов (дырок) в приближении времени релаксации ${\tau }$ принимает вид

(4)

$\frac{{\partial f}}{{\partial t}} + {\mathbf{v}}~\frac{{\partial f}}{{\partial {\mathbf{r}}}} + 2{\pi }\frac{{e{\mathbf{E}}}}{h}\frac{{\partial f}}{{\partial {\mathbf{\tilde {k}}}}} = - \frac{{f - {{f}_{0}}}}{{\tau }},$

где ${\mathbf{\tilde {k}}}$ – волновой вектор.

В данной работе предполагается, что время релаксации не зависит от скорости носителей заряда ${\tau }{\text{.}}$

В случае слабого внешнего электрического поля уравнение (4) преобразуется к виду:

(5)

$ - i{\omega }{{f}_{1}} + {\mathbf{v}}\frac{{\partial {{f}_{1}}}}{{\partial {\mathbf{r}}}} + e\left( {{\mathbf{vE}}} \right)\frac{{\partial {{f}_{0}}}}{{\partial {\varepsilon }}} = - \frac{{{{f}_{1}}}}{{\tau }}.$

Изоэнергетическая поверхность проводника – трехосный эллипсоид, главные оси которого совпадают с координатными осями $\left( {X,~Y,Z} \right),$ поэтому энергия электронов (дырок) проводимости определяется следующим образом:

(6)

${\varepsilon } = \frac{{{{m}_{1}}{v}_{x}^{2}}}{2} + \frac{{{{m}_{2}}{v}_{y}^{2}}}{2} + \frac{{{{m}_{3}}{v}_{z}^{2}}}{2},$

где ${{m}_{1}},$ ${{m}_{2}},$ ${{m}_{3}}$ – эффективные массы квазичастицы вдоль осей $X,$ $Y$ и $Z$ соответственно.

Электрическое поле (1), действуя на носители заряда, вызывает возникновение внутри проводящей трубки высокочастотного тока плотностью ${\mathbf{j}}{\text{:}}$

(7)

${\mathbf{j}} = en\left\langle {\mathbf{v}} \right\rangle = e\int {{\mathbf{v}}f\frac{{2{{d}^{3}}\left( {m{v}} \right)}}{{{{h}^{3}}}}} = 2e\frac{{{{m}_{1}}{{m}_{2}}{{m}_{3}}}}{{{{h}^{3}}}}\int {{\mathbf{v}}{{f}_{1}}{{d}^{3}}{v}} ,$

где концентрация $n$ определяется как

(8)

$n = 2\frac{{{{m}_{1}}{{m}_{2}}{{m}_{3}}}}{{{{h}^{3}}}}\int {{{f}_{0}}{{d}^{3}}{v}} .$

Функция распределения носителей заряда удовлетворяет уравнению (5). Отметим, что в случае эллипсоидальной изоэнергетической поверхности проводника решение кинетического уравнения для моделей диффузно-зеркального или зеркального отражения носителей заряда является сложной математической задачей. Это связано с тем, что модуль скорости для падающих на границу трубки электронов (дырок) не равен модулю скорости зеркально отраженных от границы носителей заряда. Во избежание громоздких вычислений будем использовать диффузные граничные условия для функции распределения:

(9)

${{f}_{1}}\left( {{\mathbf{v}},{{R}_{1}}} \right) = {{f}_{1}}\left( {{\mathbf{v}},{{R}_{2}}} \right) = 0.$

МЕТОД РЕШЕНИЯ И МАТЕМАТИЧЕСКИЙ РАСЧЕТ

Для решения кинетического уравнения (5) используется метод характеристик, подробно изложенный в [10]:

(10)

${{f}_{1}}\left( {\tilde {t}} \right) = \tilde {A}\left( {1 - {\text{exp}}\left( { - {\nu }\tilde {t}} \right)} \right),\,\,\tilde {A} = - \frac{{e\left( {{\mathbf{vE}}} \right)}}{{\nu }}\frac{{\partial {{f}_{0}}}}{{\partial {\varepsilon }}}.$

Параметр $\tilde {t}$ в формуле (10) принимает два значения; при отражении от поверхности трубки радиуса ${{R}_{1}}{\text{:}}$

(11)

$\tilde {t} = {{\tilde {t}}_{1}} = \frac{{{{{\mathbf{r}}}_{ \bot }}{{{\mathbf{v}}}_{ \bot }} - \sqrt {{{{\left( {{{{\mathbf{r}}}_{ \bot }}{{{\mathbf{v}}}_{ \bot }}} \right)}}^{2}} + \left( {R_{1}^{2} - r_{ \bot }^{2}} \right){v}_{ \bot }^{2}} }}{{{v}_{ \bot }^{2}}},$

при отражении от поверхности трубки радиуса ${{R}_{2}}{\text{:}}$

(12)

$\tilde {t} = {{\tilde {t}}_{2}} = \frac{{{{{\mathbf{r}}}_{ \bot }}{{{\mathbf{v}}}_{ \bot }} + \sqrt {{{{\left( {{{{\mathbf{r}}}_{ \bot }}{{{\mathbf{v}}}_{ \bot }}} \right)}}^{2}} + \left( {R_{2}^{2} - r_{ \bot }^{2}} \right){v}_{ \bot }^{2}} }}{{{v}_{ \bot }^{2}}}.$

Плотность тока (7) в цилиндрических координатах (в пространстве координат: ${{{\mathbf{r}}}_{ \bot }},$ ${\varphi },$ $z;$ полярная ось – ось $Z;$ в пространстве скоростей: ${{{v}}_{ \bot }},$ ${\alpha },$ ${{{v}}_{z}};$ ${{{v}}_{z}}$ – полярная ось) имеет проекцию только вдоль оси трубки (ось Z):

(13)

${{j}_{z}} = 2e\frac{{{{m}_{1}}{{m}_{2}}{{m}_{3}}}}{{{{h}^{3}}}}\int\limits_{ - \infty }^{ + \infty } {\int\limits_0^{ + \infty } {\int\limits_0^{2{\pi }} {{{{v}}_{z}}{{f}_{1}}{{{v}}_{ \bot }}d{{{v}}_{ \bot }}d{\alpha }d{{{v}}_{z}}} } } .$

Интеграл по углу 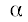в плотности тока (13) разбивается на три области интегрирования:

1. Траектория носителей заряда не пересекается с внутренней границей трубки радиуса $~{{R}_{1}}$ в случае ${{{\alpha }}_{0}} \leqslant {\alpha } \leqslant {\pi } - {{{\alpha }}_{0}},$ где

(14)

${{{\alpha }}_{0}} = {\text{arccos}}\left[ {{{{{{\left( {r_{ \bot }^{2} - R_{1}^{2}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \mathord{\left/ {\vphantom {{{{{\left( {r_{ \bot }^{2} - R_{1}^{2}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} {{{r}_{ \bot }}}}} \right. \kern-0em} {{{r}_{ \bot }}}}} \right],$

функция распределения квазичастиц – ${{f}_{1}}\left( {{{{\tilde {t}}}_{2}}} \right)$ (10, 12).

2. Свободные носители заряда движутся от внешней границы трубки радиуса ${{R}_{2}}$ к внутренней границе радиуса ${{R}_{1}},$ если ${\pi } - {{{\alpha }}_{0}} < {\alpha } \leqslant {\pi }{\text{.}}$ Функция распределения квазичастиц – ${{f}_{1}}\left( {{{{\tilde {t}}}_{2}}} \right)$ (10, 12).

3. Электроны (дырки) перемещаются от внутренней границы трубки радиуса ${{R}_{1}}$ к внешней границе радиуса ${{R}_{2}},$ если $0 < {\alpha } \leqslant {{{\alpha }}_{0}}.$ Функция распределения квазичастиц – ${{f}_{1}}\left( {{{{\tilde {t}}}_{1}}} \right)$ (10, 11) [10].

В формуле (13) подынтегральное выражение является четной функцией по переменной ${{{v}}_{z}},$ поэтому интегрирование по всему диапазону скоростей ${{{v}}_{z}}$ заменяется интегрированием по положительному диапазону, и результат удваивается. Кроме того, движение носителей заряда симметрично относительно любой диаметральной плоскости, в которой лежит точка их положения на траектории, поэтому можно считать, что угол ${\alpha }$ в пространстве скоростей меняется в пределах от 0 до ${\pi ,}$ и удваивать результат интегрирования по этой переменной.

Подставляя и в (6), получим выражение для энергии носителей заряда в цилиндрических координатах

(15)

${\varepsilon } = \frac{{{\beta }{v}_{ \bot }^{2}}}{2} + \frac{{{{m}_{3}}{v}_{z}^{2}}}{2},$

где ${\beta } = {{m}_{1}}{\text{co}}{{{\text{s}}}^{2}}{\alpha }$ + ${{m}_{2}}{\text{si}}{{{\text{n}}}^{2}}{\alpha }$ – параметр, который в случае ${{m}_{1}} = {{m}_{2}}$ переходит в поперечную массу ${{m}_{ \bot }}.$

Плотности тока (13) с у учетом (10) равна

(16)

$\begin{gathered} {{j}_{z}} = \frac{{8{{e}^{2}}{{E}_{z}}}}{{{\nu }{{k}_{Б}}T}}\frac{{{{m}_{1}}{{m}_{2}}{{m}_{3}}}}{{{{h}^{3}}}}\int\limits_0^{ + \infty } {\int\limits_0^{ + \infty } {\frac{{{{{v}}_{ \bot }}{v}_{z}^{2}{\text{exp}}\left( {{{\left( {{{{\beta }{v}_{ \bot }^{2}} \mathord{\left/ {\vphantom {{{\beta }{v}_{ \bot }^{2}} 2}} \right. \kern-0em} 2} + {{{{m}_{3}}{v}_{z}^{2}} \mathord{\left/ {\vphantom {{{{m}_{3}}{v}_{z}^{2}} 2}} \right. \kern-0em} 2} - {\mu }} \right)} \mathord{\left/ {\vphantom {{\left( {{{{\beta }{v}_{ \bot }^{2}} \mathord{\left/ {\vphantom {{{\beta }{v}_{ \bot }^{2}} 2}} \right. \kern-0em} 2} + {{{{m}_{3}}{v}_{z}^{2}} \mathord{\left/ {\vphantom {{{{m}_{3}}{v}_{z}^{2}} 2}} \right. \kern-0em} 2} - {\mu }} \right)} {{{k}_{{\text{Б}}}}T}}} \right. \kern-0em} {{{k}_{{\text{Б}}}}T}}} \right)}}{{{{{\left( {1 + {\text{exp}}\left( {{{\left( {{{{\beta }{v}_{ \bot }^{2}} \mathord{\left/ {\vphantom {{{\beta }{v}_{ \bot }^{2}} 2}} \right. \kern-0em} 2} + {{{{m}_{3}}{v}_{z}^{2}} \mathord{\left/ {\vphantom {{{{m}_{3}}{v}_{z}^{2}} 2}} \right. \kern-0em} 2} - {\mu }} \right)} \mathord{\left/ {\vphantom {{\left( {{{{\beta }{v}_{ \bot }^{2}} \mathord{\left/ {\vphantom {{{\beta }{v}_{ \bot }^{2}} 2}} \right. \kern-0em} 2} + {{{{m}_{3}}{v}_{z}^{2}} \mathord{\left/ {\vphantom {{{{m}_{3}}{v}_{z}^{2}} 2}} \right. \kern-0em} 2} - {\mu }} \right)} {{{k}_{{\text{Б}}}}T}}} \right. \kern-0em} {{{k}_{{\text{Б}}}}T}}} \right)} \right)}}^{2}}}}} } \times \\ \times \,\,\left\{ {\int\limits_0^{{{{\alpha }}_{0}}} {\left( {1 - {\text{exp}}\left( { - {\nu }{{{\tilde {t}}}_{1}}} \right)} \right)d{\alpha }} + \int\limits_{{{{\alpha }}_{0}}}^{\pi } {\left( {1 - {\text{exp}}\left( { - {\nu }{{{\tilde {t}}}_{2}}} \right)} \right)d{\alpha }} } \right\}d{{{v}}_{ \bot }}d{{{v}}_{z}}. \\ \end{gathered} $

Введем безразмерные параметры:

$\begin{gathered} {{m}_{0}} = \sqrt[3]{{{{m}_{1}}{{m}_{2}}{{m}_{3}}}},\,\,\,\,{{k}_{{m1}}} = \frac{{{{m}_{1}}}}{{{{m}_{0}}}},\,\,\,\,{{k}_{{m2}}} = \frac{{{{m}_{2}}}}{{{{m}_{0}}}},\,\,\,\,{{k}_{{m3}}} = \frac{{{{m}_{3}}}}{{{{m}_{0}}}},\,\,\,\,\,\,{{{\beta }}_{0}} = {{k}_{{m1}}}{\text{co}}{{{\text{s}}}^{2}}{\alpha } + {{k}_{{m2}}}{\text{si}}{{{\text{n}}}^{2}}{\alpha }, \\ {\xi } = \frac{{{{r}_{ \bot }}}}{{{{R}_{2}}}},\,\,\,\,K = \frac{{{{R}_{1}}}}{{{{R}_{2}}}},\,\,\,\,{{{\alpha }}_{0}} = {\text{arccos}}{{\left( {1 - \frac{{{{K}^{2}}}}{{{{{\xi }}^{2}}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},\,\,\,\,{{x}_{0}} = \frac{{{{R}_{2}}}}{{\lambda }},\,\,\,\,{{y}_{0}} = \frac{{{\omega }{{R}_{2}}}}{{{{v}_{1}}}},\,\,\,\,{{u}_{{\mu }}} = \frac{{\mu }}{{{{k}_{{\text{Б}}}}T}},\,\,\,\,u = \frac{{\varepsilon }}{{{{k}_{{\text{Б}}}}T}}, \\ \,\,\,\,\,{{z}_{0}} = \frac{{{\nu }{{R}_{2}}}}{{{{{v}}_{1}}}} = {{x}_{0}} - i{{y}_{0}},\,\,\,\,{\rho } = \frac{{{{{v}}_{ \bot }}}}{{{{{v}}_{1}}}},\,\,\,\,{\gamma } = \frac{{{{{v}}_{z}}}}{{{{{v}}_{1}}}},\,\,\,{\eta } = {\xi cos\alpha } - \sqrt {{{K}^{2}} - {{{\xi }}^{2}}{\text{si}}{{{\text{n}}}^{2}}{\alpha }} ,\,\,\,\,{\psi } = {\xi cos\alpha } + \sqrt {1 - {{{\xi }}^{2}}{\text{si}}{{{\text{n}}}^{2}}{\alpha }} . \\ \end{gathered} $

Здесь ${{k}_{{m1}}},$ ${{k}_{{m2}}},$ ${{k}_{{m3}}}$ – безразмерные эффективные массы вдоль осей $X,$ $Y,$ $Z$ соответственно; ${{x}_{0}}$ – безразмерный внешний радиус трубки; ${{y}_{0}}$ – безразмерная частота электрического поля; ${\lambda } = {{{v}}_{1}}{\tau }$ – длина свободного пробега электронов (дырок).

Отдельно стоит отметить взаимосвязь параметров эллиптичности, так как ${{m}_{0}} = \sqrt[3]{{{{m}_{1}}{{m}_{2}}{{m}_{3}}}},$ то ${{k}_{{m1}}}{{k}_{{m2}}}{{k}_{{m3}}} = 1,$ поэтому ${{k}_{{m3}}} = {1 \mathord{\left/ {\vphantom {1 {{{k}_{{m1}}}{{k}_{{m2}}}}}} \right. \kern-0em} {{{k}_{{m1}}}{{k}_{{m2}}}}}.$ Также при изменении параметров эллиптичности предполагается постоянство концентрации свободных носителей заряда (8), следовательно, ${{m}_{1}}{{m}_{2}}{{m}_{3}} = {\text{const}},$ ${{m}_{0}} = {\text{const}}{\text{.}}$

Параметры ${{x}_{0}},$ ${{y}_{0}}$ и ${{z}_{0}}$ обезразмерены на характеристическую скорость ${{{v}}_{1}}$ носителей заряда:

(17)

$n{v}_{1}^{2} = \frac{5}{3} \times 2\frac{{{{m}_{1}}{{m}_{2}}{{m}_{3}}}}{{{{h}^{3}}}}\int {{{{v}}^{2}}{{f}_{0}}{{d}^{3}}{v}} ,\,\,\,\,{{{\tilde {v}}}_{1}} = \sqrt {\frac{{{{m}_{0}}}}{{2{{k}_{{\text{Б}}}}T}}} {{{v}}_{1}},$

где $n$ – концентрация носителей заряда, определяемая выражением:

(18)

$n = 2\frac{{{{m}_{1}}{{m}_{2}}{{m}_{3}}}}{{{{h}^{3}}}}\int {{{f}_{0}}{{d}^{3}}{v}} = 4{\pi }{{\left( {\frac{{2{{m}_{0}}{{k}_{{\text{Б}}}}T}}{{{{h}^{2}}}}} \right)}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}{{I}_{0}},$

(19)

${{I}_{0}} = \int\limits_0^{ + \infty } {\frac{{\sqrt u du}}{{1 + {\text{exp}}\left( {u - {{u}_{{\mu }}}} \right)}}} .$

Отметим, что в случае вырожденного Ферми-газа $\left( {{{u}_{{\mu }}} \gg 1} \right){{{v}}_{1}} \to \sqrt {{{2{\mu }} \mathord{\left/ {\vphantom {{2{\mu }} {{{m}_{0}}}}} \right. \kern-0em} {{{m}_{0}}}}} ,$ т.е. имеет порядок скорости Ферми, а в случае невырожденного газа свободных носителей заряда $\left( {{{u}_{{\mu }}} \to - \infty } \right){{{v}}_{1}} \to $ $ \to \sqrt {{{5{{k}_{{\text{Б}}}}T} \mathord{\left/ {\vphantom {{5{{k}_{{\text{Б}}}}T} {{{m}_{0}}}}} \right. \kern-0em} {{{m}_{0}}}}} ,$ т.е. имеет порядок средней квадратичной скорости электронов (дырок) [5].

Используя выражения (11) и (12), выразим через безразмерные параметры величины ${\nu }{{\tilde {t}}_{1}}$ и ${\nu }{{\tilde {t}}_{2}}{\text{:}}$

(20)

$\begin{gathered} {\nu }{{{\tilde {t}}}_{1}} = \frac{{{{{v}}_{1}}{{z}_{0}}}}{{{{R}_{2}}}}\frac{{{{{\mathbf{r}}}_{ \bot }}{{{\mathbf{v}}}_{ \bot }} - \sqrt {{{{\left( {{{{\mathbf{r}}}_{ \bot }}{{{\mathbf{v}}}_{ \bot }}} \right)}}^{2}} + \left( {R_{1}^{2} - r_{ \bot }^{2}} \right){v}_{ \bot }^{2}} }}{{v_{ \bot }^{2}}} = \\ = {{z}_{0}}\frac{{{{r}_{ \bot }}}}{{{{R}_{2}}}}\frac{{{{{v}}_{1}}}}{{{{{v}}_{ \bot }}}}\left( {\frac{{\left( {{{{\mathbf{r}}}_{ \bot }}{{{\mathbf{v}}}_{ \bot }}} \right)}}{{{{r}_{ \bot }}{{{v}}_{ \bot }}}} - {{{\left( {\frac{{{{{\left( {{{{\mathbf{r}}}_{ \bot }}{{{\mathbf{v}}}_{ \bot }}} \right)}}^{2}}}}{{r_{ \bot }^{2}{v}_{ \bot }^{2}}} + \left( {\frac{{R_{1}^{2}}}{{r_{ \bot }^{2}}} - 1} \right)} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \right) = \\ = {{z}_{0}}\frac{{{{{v}}_{1}}}}{{{{{v}}_{ \bot }}}}\left( {{\xi cos\alpha } - \sqrt {{{K}^{2}} - {{{\xi }}^{2}}{\text{si}}{{{\text{n}}}^{2}}{\alpha }} } \right) = \frac{{{{z}_{0}}{{{v}}_{1}}{\eta }}}{{{{{v}}_{ \bot }}}} = \frac{{{{z}_{0}}{\eta }}}{{\rho }}, \\ \end{gathered} $

(21)

$\begin{gathered} {\nu }{{{\tilde {t}}}_{2}} = \frac{{{{{v}}_{1}}{{z}_{0}}}}{{{{R}_{2}}}}\frac{{{{{\mathbf{r}}}_{ \bot }}{{{\mathbf{v}}}_{ \bot }} + \sqrt {{{{\left( {{{{\mathbf{r}}}_{ \bot }}{{{\mathbf{v}}}_{ \bot }}} \right)}}^{2}} + \left( {R_{2}^{2} - r_{ \bot }^{2}} \right){v}_{ \bot }^{2}} }}{{v_{ \bot }^{2}}} = \\ = {{z}_{0}}\frac{{{{r}_{ \bot }}}}{{{{R}_{2}}}}\frac{{{{{v}}_{1}}}}{{{{{v}}_{ \bot }}}}\left( {\frac{{\left( {{{{\mathbf{r}}}_{ \bot }}{{{\mathbf{v}}}_{ \bot }}} \right)}}{{{{r}_{ \bot }}{{{v}}_{ \bot }}}} + {{{\left( {\frac{{{{{\left( {{{{\mathbf{r}}}_{ \bot }}{{{\mathbf{v}}}_{ \bot }}} \right)}}^{2}}}}{{r_{ \bot }^{2}{v}_{ \bot }^{2}}} + \left( {\frac{{R_{2}^{2}}}{{r_{ \bot }^{2}}} - 1} \right)} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \right) = \\ = {{z}_{0}}\frac{{{{{v}}_{1}}}}{{{{{v}}_{ \bot }}}}\left( {{\xi cos\alpha } + \sqrt {1 - {{{\xi }}^{2}}{\text{si}}{{{\text{n}}}^{2}}{\alpha }} } \right) = \frac{{{{z}_{0}}{{{v}}_{1}}{\psi }}}{{{{{v}}_{ \bot }}}} = \frac{{{{z}_{0}}{\psi }}}{{\rho }}. \\ \end{gathered} $

Тогда с учетом введенных безразмерных параметров, концентрации (19) и выражений (20), (21) плотность тока (16) преобразуется к следующему виду:

(22)

$\begin{gathered} {{j}_{z}} = \frac{{n{{e}^{2}}{\tau }}}{{{{m}_{0}}}}\frac{{4{{E}_{z}}{\tilde {v}}_{1}^{2}{{x}_{0}}}}{{{{z}_{0}}{\pi }{{I}_{0}}}}\int\limits_0^{ + \infty } {\int\limits_0^{ + \infty } {\frac{{{\rho }{{{\gamma }}^{2}}{\text{exp}}\left( {{\tilde {v}}_{1}^{2}\left( {{{{\beta }}_{0}}{{{\rho }}^{2}} + {{{{{\gamma }}^{2}}} \mathord{\left/ {\vphantom {{{{{\gamma }}^{2}}} {{{k}_{{m1}}}{{k}_{{m2}}}}}} \right. \kern-0em} {{{k}_{{m1}}}{{k}_{{m2}}}}}} \right) - {{u}_{{\mu }}}} \right)}}{{{{{\left( {1 + {\text{exp}}\left( {{\tilde {v}}_{1}^{2}\left( {{{{\beta }}_{0}}{{{\rho }}^{2}} + {{{{{\gamma }}^{2}}} \mathord{\left/ {\vphantom {{{{{\gamma }}^{2}}} {{{k}_{{m1}}}{{k}_{{m2}}}}}} \right. \kern-0em} {{{k}_{{m1}}}{{k}_{{m2}}}}}} \right) - {{u}_{{\mu }}}} \right)} \right)}}^{2}}}}} } \times \\ \times \,\,\left\{ {\int\limits_0^{{{{\alpha }}_{0}}} {\left( {1 - {\text{exp}}\left( {{{ - {{z}_{0}}{\eta }} \mathord{\left/ {\vphantom {{ - {{z}_{0}}{\eta }} {\rho }}} \right. \kern-0em} {\rho }}} \right)} \right)d{\alpha }} + \int\limits_{{{{\alpha }}_{0}}}^{\pi } {\left( {1 - {\text{exp}}\left( {{{ - {{z}_{0}}{\psi }} \mathord{\left/ {\vphantom {{ - {{z}_{0}}{\psi }} {\rho }}} \right. \kern-0em} {\rho }}} \right)} \right)d{\alpha }} } \right\}d{\rho }d{\gamma }. \\ \end{gathered} $

В экспериментальных условиях обычно находят усредненный по радиусу ток вдоль оси трубки (ось $Z$)

(23)

$\overline {{{j}_{z}}} = \frac{1}{{{\pi }\left( {R_{2}^{2} - R_{1}^{2}} \right)}}\int\limits_0^{2{\pi }} {\int\limits_{{{R}_{1}}}^{{{R}_{2}}} {{{j}_{z}}{{r}_{ \bot }}d{{r}_{ \bot }}d{\varphi }} } = \frac{2}{{\left( {1 - {{K}^{2}}} \right)}}\int\limits_K^1 {{{j}_{z}}{\xi }d{\xi }} .$

Подставив выражение (22) в (23), а также формально применив локальный закон Ома в виде $\overline {{{j}_{z}}} = {\sigma }{{E}_{z}},$ получим выражение для усредненной по радиусу удельной электропроводности:

(24)

${\sigma } = {{{\sigma }}_{0}}{\Sigma }\left( {{{x}_{0}},{{y}_{0}},{{k}_{{m1}}},{{k}_{{m2}}},{{u}_{{\mu }}},K} \right),\,\,\,\,{{{\sigma }}_{0}} = \frac{{n{{e}^{2}}{\tau }}}{{{{m}_{0}}}},$

(25)

$\begin{gathered} {\Sigma }\left( {{{x}_{0}},{{y}_{0}},{{k}_{{m1}}},{{k}_{{m2}}},{{u}_{{\mu }}},K} \right) = \frac{{{{x}_{0}}}}{{{{z}_{0}}}}{{k}_{{m1}}}{{k}_{{m2}}} - \frac{{8{{{\widetilde {{{{v}}_{1}}}}}^{5}}{{x}_{0}}}}{{{{z}_{0}}{\pi }{{I}_{0}}\left( {1 - {{K}^{2}}} \right)}}{\text{exp}}\left\{ { - {{u}_{{\mu }}}} \right\} \times \\ \times \,\,\int\limits_K^1 {\int\limits_0^{ + \infty } {\int\limits_0^{ + \infty } {{{A}_{1}}\left( {\int\limits_0^{{{{\alpha }}_{0}}} {{{A}_{0}}{\text{exp}}\left( {{{ - {{z}_{0}}{\eta }} \mathord{\left/ {\vphantom {{ - {{z}_{0}}{\eta }} {\rho }}} \right. \kern-0em} {\rho }}} \right)d{\alpha }} + \int\limits_{{{{\alpha }}_{0}}}^{\pi } {{{A}_{0}}{\text{exp}}\left( {{{ - {{z}_{0}}{\psi }} \mathord{\left/ {\vphantom {{ - {{z}_{0}}{\psi }} {\rho }}} \right. \kern-0em} {\rho }}} \right)d{\alpha }} } \right)} } } d{\rho }d{\gamma }d{\xi },~ \\ {{A}_{0}} = {\text{exp}}{{{{\left\{ {{{{\widetilde {{{{v}}_{1}}}}}^{2}}{{{\beta }}_{0}}{{{\rho }}^{2}}} \right\}} \mathord{\left/ {\vphantom {{\left\{ {{{{\widetilde {{{{v}}_{1}}}}}^{2}}{{{\beta }}_{0}}{{{\rho }}^{2}}} \right\}} {\left( {1 + {\text{exp}}\left\{ {{{{\widetilde {{{{v}}_{1}}}}}^{2}}\left( {{{{\beta }}_{0}}{{{\rho }}^{2}} + {{{{{\gamma }}^{2}}} \mathord{\left/ {\vphantom {{{{{\gamma }}^{2}}} {{{k}_{{m1}}}{{k}_{{m2}}}}}} \right. \kern-0em} {{{k}_{{m1}}}{{k}_{{m2}}}}}} \right) - {{u}_{{\mu }}}} \right\}} \right)}}} \right. \kern-0em} {\left( {1 + {\text{exp}}\left\{ {{{{\widetilde {{{{v}}_{1}}}}}^{2}}\left( {{{{\beta }}_{0}}{{{\rho }}^{2}} + {{{{{\gamma }}^{2}}} \mathord{\left/ {\vphantom {{{{{\gamma }}^{2}}} {{{k}_{{m1}}}{{k}_{{m2}}}}}} \right. \kern-0em} {{{k}_{{m1}}}{{k}_{{m2}}}}}} \right) - {{u}_{{\mu }}}} \right\}} \right)}}}^{2}}, \\ {{A}_{1}} = {\xi }{{{\gamma }}^{2}}{\rho exp}\left\{ {{{{{{\widetilde {{{{v}}_{1}}}}}^{2}}{{{\gamma }}^{2}}} \mathord{\left/ {\vphantom {{{{{\widetilde {{{{v}}_{1}}}}}^{2}}{{{\gamma }}^{2}}} {{{k}_{{m1}}}{{k}_{{m2}}}}}} \right. \kern-0em} {{{k}_{{m1}}}{{k}_{{m2}}}}}} \right\}. \\ \end{gathered} $

Здесь ${\Sigma }\left( {{{x}_{0}},{{y}_{0}},{{k}_{{m1}}},{{k}_{{m2}}},{{u}_{{\mu }}},K} \right)$ – безразмерная удельная электропроводность.

ПРЕДЕЛЬНЫЕ СЛУЧАИ

1. Случай вырожденного электронного (дырочного) газа $\left( {{{e}^{{{{u}_{{\mu }}}}}} \gg 1} \right).$

В случае вырожденного газа равновесная функция распределения Ферми-Дирака (3) переходит в ступенчатую аппроксимацию:

(26)

${{f}_{0}} = \left\{ {\begin{array}{*{20}{c}} {1,~\varepsilon < \mu ,} \\ {0,~\varepsilon > \mu .} \end{array}} \right.$

Интеграл ${{I}_{0}}$ (19) и безразмерная характеристическая скорость $\widetilde {{{{v}}_{1}}}$ (18) с учетом равновесной функции распределения Ферми-Дирака (26) преобразуются к виду:

(27)

${{I}_{0}} = \frac{2}{3}u_{{\mu }}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}},\,\,\,\,~\widetilde {{{{v}}_{1}}} = u_{{\mu }}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}.$

С учетом (26) и (27) выражение для безразмерной электропроводности (25) примет следующий вид:

(28)

$\begin{gathered} {\Sigma }\left( {{{x}_{0}},{{y}_{0}},{{k}_{{m1}}},{{k}_{{m2}}},K} \right) = \frac{{{{x}_{0}}}}{{{{z}_{0}}}}{{k}_{{m1}}}{{k}_{{m2}}}\left( {1 - \frac{{6{{{\left( {{{k}_{{m1}}}{{k}_{{m2}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}{{{\pi }\left( {1 - {{K}^{2}}} \right)}}\int\limits_K^1 {{\xi }d{\xi } \times } } \right. \\ \times \,\,\left\{ {\int\limits_0^{{{{\alpha }}_{0}}} {\int\limits_0^{{1 \mathord{\left/ {\vphantom {1 {\sqrt {{{{\beta }}_{0}}} }}} \right. \kern-0em} {\sqrt {{{{\beta }}_{0}}} }}} {{\rho exp}\left( {{{ - {{z}_{0}}{\eta }} \mathord{\left/ {\vphantom {{ - {{z}_{0}}{\eta }} {\rho }}} \right. \kern-0em} {\rho }}} \right)\sqrt {1 - {{{\rho }}^{2}}{{{\beta }}_{0}}} d{\rho }d{\alpha } + } } } \right. \\ \left. { + \,\,\left. {\int\limits_{{{{\alpha }}_{0}}}^\pi {\int\limits_0^{{1 \mathord{\left/ {\vphantom {1 {\sqrt {{{{\beta }}_{0}}} }}} \right. \kern-0em} {\sqrt {{{{\beta }}_{0}}} }}} {{\rho exp}\left( {{{ - {{z}_{0}}{\psi }} \mathord{\left/ {\vphantom {{ - {{z}_{0}}{\psi }} {\rho }}} \right. \kern-0em} {\rho }}} \right)\sqrt {1 - {{{\rho }}^{2}}{{{\beta }}_{0}}} d{\rho }d{\alpha }} } } \right\}} \right). \\ \end{gathered} $

Безразмерная электропроводность (28) совпадает с результатом работы [11] в случае диффузного рассеяния носителей заряда и ${{m}_{1}} = {{m}_{2}} = {{m}_{ \bot }},$ где ${{m}_{ \bot }}$ – поперечная эффективная масса.

Если частота внешнего поля ${\omega }$ и частота столкновений носителей заряда в объеме проводника малы по сравнению с частотой столкновения электронов (дырок) с поверхностями проводящей трубки $\left( {{\text{т}}{\text{.е}}{\text{.}}~~\left| {{{z}_{0}}} \right| \ll 1} \right),$ то экспоненты, входящие в выражение (28), можно разложить в ряд Тэйлора, ограничиваясь первыми двумя членами разложения. В результате для безразмерной проводимости получим следующее выражение

$\begin{gathered} {\Sigma }\left( {{{x}_{0}},{{y}_{0}},{{k}_{{m1}}},{{k}_{{m2}}},K} \right) = \frac{{6{{x}_{0}}{{{\left( {{{k}_{{m1}}}{{k}_{{m2}}}} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}{{{\pi }\left( {1 - {{K}^{2}}} \right)}}\int\limits_K^1 {{\xi }d{\xi } \times } \\ \times \,\,\left\{ {\int\limits_0^{{{{\alpha }}_{0}}} {\int\limits_0^{{1 \mathord{\left/ {\vphantom {1 {\sqrt {{{{\beta }}_{0}}} }}} \right. \kern-0em} {\sqrt {{{{\beta }}_{0}}} }}} {{\eta }\sqrt {1 - {{{\rho }}^{2}}{{{\beta }}_{0}}} d{\rho }d{\alpha }} } + \int\limits_{{{{\alpha }}_{0}}}^{\pi } {\int\limits_0^{{1 \mathord{\left/ {\vphantom {1 {\sqrt {{{{\beta }}_{0}}} }}} \right. \kern-0em} {\sqrt {{{{\beta }}_{0}}} }}} {{\psi }\sqrt {1 - {{{\rho }}^{2}}{{{\beta }}_{0}}} d{\rho }d{\alpha }} } } \right\}. \\ \end{gathered} $

Проинтегрировав по переменной ${\rho ,}$ имеем

${\Sigma }\left( {{{x}_{0}},{{k}_{{m1}}},{{k}_{{m2}}},K} \right) = \frac{{3{{x}_{0}}{{{\left( {{{k}_{{m1}}}{{k}_{{m2}}}} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}{{2\left( {1 - {{K}^{2}}} \right)}}\int\limits_K^1 {{\xi }d{\xi }} \left\{ {\int\limits_0^{{{{\alpha }}_{0}}} {\frac{{\eta }}{{\sqrt {{{{\beta }}_{0}}} }}d{\alpha }} + \int\limits_{{{{\alpha }}_{0}}}^{\pi } {\frac{{\psi }}{{\sqrt {{{{\beta }}_{0}}} }}d{\alpha }} } \right\}.$

2. Случай невырожденного электронного (дырочного) газа $\left( {{{e}^{{ - {{u}_{{\mu }}}}}} \gg 1} \right).$

Равновесная функция распределения Ферми-Дирака (3) невырожденного электронного газа описывается распределением Максвелла–Больцмана:

(29)

${{f}_{0}} = {\text{exp}}\left( {{{\left( {{\mu } - {\varepsilon }} \right)} \mathord{\left/ {\vphantom {{\left( {{\mu } - {\varepsilon }} \right)} {{{k}_{{\text{Б}}}}T}}} \right. \kern-0em} {{{k}_{{\text{Б}}}}T}}} \right).$

(30)

${{I}_{0}} = \frac{{\sqrt {\pi } }}{2}{{e}^{{{{u}_{{\mu }}}}}},\,\,\,\,~\widetilde {{{{v}}_{1}}} = \sqrt {5{\text{/}}2} .$

Подставляя (29) и (30) в выражение (25), получаем следующий вид для безразмерной удельной электропроводности

(31)

$\begin{gathered} {\Sigma }\left( {{{x}_{0}},{{y}_{0}},{{k}_{{m1}}},{{k}_{{m2}}},K} \right) = \frac{{{{x}_{0}}}}{{{{z}_{0}}}}{{k}_{{m1}}}{{k}_{{m2}}}\left( {1 - \frac{{10{{{\left( {{{k}_{{m1}}}{{k}_{{m2}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}{{{\pi }\left( {1 - {{K}^{2}}} \right)}}\int\limits_K^1 {{\xi }d{\xi }} \times } \right. \\ \times \,\,\left\{ {\int\limits_0^{{{{\alpha }}_{0}}} {\int\limits_0^{ + \infty } {{\rho exp}\left\{ {{{ - {{z}_{0}}{\eta }} \mathord{\left/ {\vphantom {{ - {{z}_{0}}{\eta }} {\rho }}} \right. \kern-0em} {\rho }}} \right\}{\text{exp}}\left\{ {{{ - 5{{{\beta }}_{0}}{{{\rho }}^{2}}} \mathord{\left/ {\vphantom {{ - 5{{{\beta }}_{0}}{{{\rho }}^{2}}} 2}} \right. \kern-0em} 2}} \right\}d{\rho }d{\alpha }} } + } \right. \\ \left. {\left. { + \,\,\int\limits_{{{{\alpha }}_{0}}}^{\pi } {\int\limits_0^{ + \infty } {{\rho exp}\left\{ {{{ - {{z}_{0}}{\psi }} \mathord{\left/ {\vphantom {{ - {{z}_{0}}{\psi }} {\rho }}} \right. \kern-0em} {\rho }}} \right\}{\text{exp}}\left\{ {{{ - 5{{{\beta }}_{0}}{{{\rho }}^{2}}} \mathord{\left/ {\vphantom {{ - 5{{{\beta }}_{0}}{{{\rho }}^{2}}} 2}} \right. \kern-0em} 2}} \right\}d{\rho }d{\alpha }} } } \right\}} \right). \\ \end{gathered} $

В низкочастотном случае $\left( {\left| {{{z}_{0}}} \right| \ll 1} \right)$ экспоненты в выражении (31), содержащие множитель ${{z}_{0}},$ можно разложить в ряд Тэйлора. В результате для безразмерной электропроводности получим выражение:

$\begin{gathered} {\Sigma }\left( {{{x}_{0}},{{y}_{0}},{{k}_{{m1}}},{{k}_{{m2}}},K} \right) = \frac{{10{{x}_{0}}{{{\left( {{{k}_{{m1}}}{{k}_{{m2}}}} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}{{{\pi }\left( {1 - {{K}^{2}}} \right)}}\int\limits_K^1 {{\xi }d{\xi }} \times \\ \left. { \times \,\,\left\{ {\int\limits_0^{{{{\alpha }}_{0}}} {\int\limits_0^{ + \infty } {{\eta exp}\left\{ {{{ - 5{{{\beta }}_{0}}{{{\rho }}^{2}}} \mathord{\left/ {\vphantom {{ - 5{{{\beta }}_{0}}{{{\rho }}^{2}}} 2}} \right. \kern-0em} 2}} \right\}d{\rho }d{\alpha }} } + \int\limits_{{{{\alpha }}_{0}}}^{\pi } {\int\limits_0^{ + \infty } {{\psi exp}\left\{ {{{ - 5{{{\beta }}_{0}}{{{\rho }}^{2}}} \mathord{\left/ {\vphantom {{ - 5{{{\beta }}_{0}}{{{\rho }}^{2}}} 2}} \right. \kern-0em} 2}} \right\}d{\rho }d{\alpha }} } } \right\}} \right). \\ \end{gathered} $

Проинтегрировав по переменной ${\rho ,}$ имеем

${\Sigma }\left( {{{x}_{0}},{{k}_{{m1}}},{{k}_{{m2}}},K} \right) = \frac{{\sqrt {10} {{x}_{0}}{{{\left( {{{k}_{{m1}}}{{k}_{{m2}}}} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}{{\sqrt {\pi } \left( {1 - {{K}^{2}}} \right)}}\int\limits_K^1 {{\xi }d{\xi }} \left\{ {\int\limits_0^{{{{\alpha }}_{0}}} {\frac{{\eta }}{{\sqrt {{{{\beta }}_{0}}} }}d{\alpha }} + \int\limits_{{{{\alpha }}_{0}}}^{\pi } {\frac{{\psi }}{{\sqrt {{{{\beta }}_{0}}} }}d{\alpha }} .} \right\}.$

3. Случай толстой трубки $\left( {\left| {{{R}_{2}} - {{R}_{1}}} \right| \gg {\lambda }} \right)$ или высоких частот $\left( {{{y}_{0}} \gg 1} \right).$

Если $\left| {{{z}_{0}}} \right| \gg 1,$ то в выражении (25) экспоненты ${\text{exp}}\left( {{{ - {{z}_{0}}{\eta }} \mathord{\left/ {\vphantom {{ - {{z}_{0}}{\eta }} {\rho }}} \right. \kern-0em} {\rho }}} \right)$ и ${\text{exp}}\left( {{{ - {{z}_{0}}{\psi }} \mathord{\left/ {\vphantom {{ - {{z}_{0}}{\psi }} {\rho }}} \right. \kern-0em} {\rho }}} \right)$ сильно затухают, в итоге получаем

${\Sigma }\left( {{{x}_{0}},{{y}_{0}},{{k}_{{m1}}},{{k}_{{m2}}}} \right) = \frac{{{{x}_{0}}}}{{{{z}_{0}}}}{{k}_{{m1}}}{{k}_{{m2}}}.$

Данный результат соответствует классической формуле Друде для “массивных” образцов.

4. Случай сферической изоэнергетической поверхности $\left( {{{k}_{{m1}}} = {{k}_{{m2}}} = {{{\beta }}_{0}} = 1} \right).$

Безразмерная электропроводность (25) в случае сферической изоэнергетической поверхности будет иметь вид

(32)

$\begin{gathered} {\Sigma }\left( {{{x}_{0}},{{y}_{0}},{{u}_{{\mu }}},K} \right) = \frac{{{{x}_{0}}}}{{{{z}_{0}}}} - \frac{{8{{{\widetilde {{{{v}}_{1}}}}}^{5}}{{x}_{0}}}}{{{{z}_{0}}{\pi }{{I}_{0}}\left( {1 - {{K}^{2}}} \right)}}{\text{exp}}\left\{ { - {{u}_{{\mu }}}} \right\} \times \\ \times \,\,\int\limits_K^1 {\int\limits_0^{ + \infty } {\int\limits_0^{ + \infty } {{{A}_{1}}{{A}_{0}}} } } \left( {\int\limits_0^{{{{\alpha }}_{0}}} {{\text{exp}}\left( {{{ - {{z}_{0}}{\eta }} \mathord{\left/ {\vphantom {{ - {{z}_{0}}{\eta }} {\rho }}} \right. \kern-0em} {\rho }}} \right)d{\alpha }} + \int\limits_{{{{\alpha }}_{0}}}^{\pi } {{\text{exp}}\left( {{{ - {{z}_{0}}{\psi }} \mathord{\left/ {\vphantom {{ - {{z}_{0}}{\psi }} {\rho }}} \right. \kern-0em} {\rho }}} \right)d{\alpha }} } \right)d{\rho }d{\gamma }d{\xi }, \\ {{A}_{0}} = {{{{{\text{exp}}\left\{ {{{{\widetilde {{{{v}}_{1}}}}}^{2}}{{{\rho }}^{2}}} \right\}} \mathord{\left/ {\vphantom {{{\text{exp}}\left\{ {{{{\widetilde {{{{v}}_{1}}}}}^{2}}{{{\rho }}^{2}}} \right\}} {\left( {1 + {\text{exp}}\left\{ {{{{\widetilde {{{{v}}_{1}}}}}^{2}}\left( {{{{\rho }}^{2}} + {{{\gamma }}^{2}}} \right) - {{u}_{{\mu }}}} \right\}} \right)}}} \right. \kern-0em} {\left( {1 + {\text{exp}}\left\{ {{{{\widetilde {{{{v}}_{1}}}}}^{2}}\left( {{{{\rho }}^{2}} + {{{\gamma }}^{2}}} \right) - {{u}_{{\mu }}}} \right\}} \right)}}}^{2}},\,\,\,\,~{{A}_{1}} = {\xi }{{{\gamma }}^{2}}{\rho exp}\left\{ {{{{\widetilde {{{{v}}_{1}}}}}^{2}}{{{\gamma }}^{2}}} \right\}. \\ \end{gathered} $

В предельном случае, когда радиус внутренней поверхности трубки стремится к нулю $\left( {{{R}_{1}} \to 0} \right),$ формула (32) переходит в выражение, соответствующее электропроводности тонкой проволоки [5].

$\begin{gathered} {\Sigma }\left( {{{x}_{0}},{{y}_{0}},{{u}_{{\mu }}}} \right) = \frac{{{{x}_{0}}}}{{{{z}_{0}}}}\left( {1 - \frac{{8{{{\widetilde {{{{v}}_{1}}}}}^{5}}}}{{{\pi }{{I}_{0}}}}{\text{exp}}\left\{ { - {{u}_{{\mu }}}} \right\} \times } \right. \\ \left. { \times \,\,\int\limits_0^1 {\int\limits_0^{ + \infty } {\int\limits_0^{ + \infty } {\frac{{{\xi }{{{\gamma }}^{2}}{\rho exp}\left\{ {{{{\widetilde {{{{v}}_{1}}}}}^{2}}\left( {{{{\rho }}^{2}} + {{{\gamma }}^{2}}} \right)} \right\}}}{{{{{\left( {1 + {\text{exp}}\left\{ {{{{\widetilde {{{{v}}_{1}}}}}^{2}}\left( {{{{\rho }}^{2}} + {{{\gamma }}^{2}}} \right) - {{u}_{{\mu }}}} \right\}} \right)}}^{2}}}}} } } \int\limits_0^{\pi } {{\text{exp}}\left( {{{ - {{z}_{0}}{\psi }} \mathord{\left/ {\vphantom {{ - {{z}_{0}}{\psi }} {\rho }}} \right. \kern-0em} {\rho }}} \right)d{\alpha }d{\rho }d{\gamma }d{\xi }} } \right). \\ \end{gathered} $

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

На рис. 1 и 2 изображены зависимости модуля и аргумента безразмерной проводимости от безразмерной эффективной массы вдоль оси $X.$ Из графиков видно, что с увеличением эффективной массы, модуль и аргумент проводимости возрастают. Это связано с тем, что рост эффективной массы вдоль направления, перпендикулярного оси трубки сопровождается уменьшением скорости носителей заряда в этом направлении и, следовательно, снижением относительного числа диффузно отраженных носителей заряда на границах трубки. Таким образом, поверхностное рассеяние носителей заряда оказывает меньшее влияние на функцию распределения, что приводит к увеличению модуля и аргумента электропроводности.

Рис. 1.

Зависимость модуля безразмерной проводимости Σ от безразмерной эффективной массы ${{k}_{{m1}}}$ вдоль оси $X$ при ${{x}_{0}} = {{y}_{0}} = 0.1,$ $K = 0.5.$ Сплошные кривые соответствуют случаю вырожденного полупроводника (металл) (28); пунктирные – случаю невырожденного полупроводника (31). Кривые 1 – ${{k}_{{m2}}} = 10;$ 2 – ${{k}_{{m2}}} = 1;$ 3 – ${{k}_{{m2}}} = 0.1.$

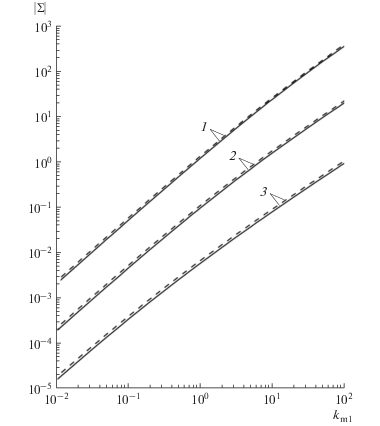
Рис. 2.

Зависимость аргумента безразмерной проводимости ${\Sigma }$ от безразмерной эффективной массы ${{k}_{{m1}}}$ вдоль оси $X$ при ${{x}_{0}} = {{y}_{0}} = 0.1,$ $K = 0.5.$ Сплошные кривые соответствуют случаю вырожденного полупроводника (металл) (28); пунктирные – случаю невырожденного полупроводника (31). Кривые 1 – ${{k}_{{m2}}} = 10;$ 2 – ${{k}_{{m2}}} = 1;$ 3 – ${{k}_{{m2}}} = 0.1.$

На рис. 3 и 4 показаны зависимости относительного различия $M$ модулей (рис. 3) и $A$ аргументов (рис. 4) проводимости между случаями вырожденного и невырожденного газа свободных носителей заряда от безразмерной эффективной массы вдоль оси $X.$ Относительное различие по модулю и по аргументу определяется по следующим формулам: $M = {{2\left| {\left| {{{{\Sigma }}_{1}}} \right| - \left| {{{{\Sigma }}_{2}}} \right|} \right|} \mathord{\left/ {\vphantom {{2\left| {\left| {{{{\Sigma }}_{1}}} \right| - \left| {{{{\Sigma }}_{2}}} \right|} \right|} {\left( {\left| {{{{\Sigma }}_{1}}} \right| + \left| {{{{\Sigma }}_{2}}} \right|} \right)}}} \right. \kern-0em} {\left( {\left| {{{{\Sigma }}_{1}}} \right| + \left| {{{{\Sigma }}_{2}}} \right|} \right)}},$ $A = 2{{\left| {{\text{arg}}\left( {{{{\Sigma }}_{1}}} \right) - {\text{arg}}\left( {{{{\Sigma }}_{2}}} \right)} \right|} \mathord{\left/ {\vphantom {{\left| {{\text{arg}}\left( {{{{\Sigma }}_{1}}} \right) - {\text{arg}}\left( {{{{\Sigma }}_{2}}} \right)} \right|} {\left( {\arg \left( {{{{\Sigma }}_{1}}} \right) + {\text{arg}}\left( {{{{\Sigma }}_{2}}} \right)} \right)}}} \right. \kern-0em} {\left( {\arg \left( {{{{\Sigma }}_{1}}} \right) + {\text{arg}}\left( {{{{\Sigma }}_{2}}} \right)} \right)}},$ где ${{{\Sigma }}_{1}}$ и ${{{\Sigma }}_{2}}$ – безразмерная электропроводность в вырожденном случае (28) и в невырожденном случае (31). Рост эффективной массы приводит к снижению относительного различая модулей иаргументов проводимости.

Рис. 3.

Зависимость относительного различия по модулю между вырожденным (28) и невырожденным (31) случаями от безразмерной эффективной массы ${{k}_{{m1}}}$ вдоль оси $X$ при ${{x}_{0}} = {{y}_{0}} = 0.1,$ $K = 0.5.$ Кривые 1 – ${{k}_{{m2}}} = 10;$ 2 – ${{k}_{{m2}}} = 1;$ 3 – ${{k}_{{m2}}} = 0.1.$

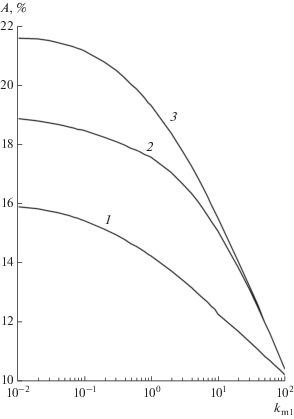
Рис. 4.

Зависимость относительного различия по аргументу между вырожденным (28) и невырожденным (31) случаями от безразмерной эффективной массы ${{k}_{{m1}}}$ вдоль оси $X$ при ${{x}_{0}} = {{y}_{0}} = 0.1,$ $K = 0.5.$ Кривые 1 – ${{k}_{{m2}}} = 10;$ 2 – ${{k}_{{m2}}} = 1;$ 3 – ${{k}_{{m2}}} = 0.1.$

ЗАКЛЮЧЕНИЕ

В рамках кинетической теории исследовано влияние анизотропии изоэнергетической поверхности на электропроводность тонкой проводящей цилиндрической трубки, рассчитанной длямодели диффузных граничных условий. Показано, что с ростом эффективной массы вдоль направления, перпендикулярного оси трубки, модуль и аргумент проводимости возрастают, а относительное различие модулей и аргументов проводимости в случаях металла (вырожденный электронный газ) и полупроводника (невырожденный электронный газ) уменьшается.

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 19-32-90008.

Список литературы

Морохов И.Д., Петинов В.И., Трусов Л.И. Структура и свойства малых металлических частиц // УФН. 1981. Т. 133. Вып. 1. С. 653–692.
Dingle R.B. Theelectricalconductivityofthinwires // Proc. Roy. Soc. A. 1950. V. 201. № 1067. P. 545–560.
Pierre F., Gougam A.B., Anthore A., Pothier H., Esteve D., Birge N.O. Dephasing of electrons in mesoscopic metal wires // Phys. Rev. B. 2003. V. 68. № 8. P. 085413.
Sondheimer E.H. The mean free path of electrons in metals // Adv. Phys. 2001. V. 50. № 6. P. 499–537.
Кузнецова И.А., Хадчукаева Р.Р., Юшканов А.А. Влияние поверхностного рассеяния носителей заряда на высокочастотную проводимость тонкой цилиндрической полупроводниковой проволоки // ФТТ. 2009. Т. 51. № 10. С. 2022–2027.
Fuchs K. The conductivity of thin metallic films according to the electron theory of metals // Proc. Camb. Phil. Soc. 1938. V. 34. P. 100–108.
Soffer S.B. Statistical Model for the Size Effect in Electrical Conduction // J. Appl. Phys. 1967. V. 38. № 4. P. 1710–1715.
Кузнецова И.А., Савенко О.В., Юшканов А.А. Влияние граничных условий на электропроводность тонкой цилиндрической проволоки // Микроэлектроника. 2016. Т. 45. № 2. С. 126–134.
Кузнецова И.А., Романов Д.Н., Юшканов А.А. Влияние анизотропии поверхности Ферми на электропроводность тонкой неоднородной металлической проволоки // Микроэлектроника. 2019. Т. 47. № 2. С. 1–14. https://doi.org/10.1134/S0544126919020066
Завитаев Э.В., Юшканов А.А. Поглощение электромагнитной волны неоднородной цилиндрической частицей // Квантовая электроника. 2005. Т. 35. № 6. С. 547–553.
Кузнецова И.А., Романов Д.Н., Юшканов А.А. Расчет высокочастотной электропроводности тонкого металлического слоя в случае эллипсоидальной поверхности Ферми // Микроэлектроника. 2018. Т. 47. № 3. С. 226–237.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Микроэлектроника

Архивы выпусков Информация о журнале Отправить рукопись в журнал