Микроэлектроника, 2022, T. 51, № 2, стр. 83-94
Преобразование Лоренца и его обобщения в задачах прецизионного контроля состояний многоуровневых квантовых систем
Ю. И. Богданов a, *, Н. А. Богданова a, Ю. А. Кузнецов a, В. Ф. Лукичев a
a Физико-технологический институт им. К.А. Валиева Российской академии наук
117218 Москва,
Нахимовский проспект, д. 36, корп. 1, Россия
* E-mail: bogdanov_yurii@inbox.ru
Поступила в редакцию 01.09.2021
После доработки 29.09.2021
Принята к публикации 30.09.2021
- EDN: MBOOSX
- DOI: 10.31857/S0544126922020041
Аннотация
Предложен метод прецизионных квантовых измерений, позволяющий с высокой точностью отслеживать состояния многоуровневых квантовых систем в гильбертовых пространствах различных размерностей. В основе разработанных алгоритмов квантового контроля лежит использование спинорного представления группы преобразований Лоренца, а также его обобщений на случай многоуровневых квантовых систем. Показано, что обратная связь посредством слабо возмущающих адаптивных квантовых измерений оказывается способной обеспечивать высокоточный контроль квантовой системы, внося при этом только слабые возмущения в исходное квантовое состояние
1. ВВЕДЕНИЕ
В настоящей работе представлен метод квантовой томографии, позволяющий с высокой точностью отслеживать эволюцию многоуровневых квантовых систем (кудитов) в гильбертовых пространствах различных размерностей. В основе разработанных алгоритмов квантового контроля лежит использование спинорного представления группы преобразований Лоренца [1, 2], а также его обобщений на случай многоуровневых квантовых систем [3].
В простейшем случае однокубитовых состояний оказывается, что помимо трехмерных вращений на сфере Блоха можно ввести четырехмерные псевдовращения Лоренца, подобные преобразованиям, характерным для специальной теории относительности.
Ниже мы показываем, что обратная связь посредством слабо возмущающих адаптивных квантовых измерений оказывается способной обеспечивать высокоточный контроль квантовой системы. Оказывается, что разработанные алгоритмы контроля эволюции состояния квантовой системы могут быть сверхэффективными, обеспечивая более высокую точность измерений, чем любые стандартные протоколы POVM (Positive-OperatorValuedMeasure).
В разделе 2 рассмотрены спинорныеи тензорные представления группы Лоренца. При этом однокубитовые матрицы плотности отвечают спинорному представлению, а вектор Минковского–Стокса – тензорному. Указанный формализм обобщен на многокубитовые состояния и поляризационные тензоры высших рангов. Наряду со стандартными спинорами введены “волнистые” спиноры и рассмотрено уравнение Дирака. Показано, что шум деполяризации приводит к появлению эффективной массы в уравнении Дирака. В разделе 3 изложены базовые представления о протоколах квантовых измерений и точности, которую они могут обеспечить с использованием процедур квантовой томографии. В разделе 4 на примере восьмиуровневого кудита рассмотрено адаптивное отслеживание эволюции квантового состояния. Здесь, в случае протоколов Лоренца, только небольшая часть от общего числа ионов оказывается сильно возмущена, высвечивает фотоны и несет информацию о текущем состоянии кудитов. Остальные же ионы не высвечивают фотоны, но при этом все же подвергаются некоторому слабому возмущению (такие кудиты обеспечивают ресурс для пошагового отслеживания эволюции квантового состояния). В разделе 5 представлены основные выводы проведенного исследования.
2. КВАНТОВЫЕ ИЗМЕРЕНИЯ НА ОСНОВЕ СПИНОРНЫХ ПРЕДСТАВЛЕНИЙ ГРУППЫ ЛОРЕНЦА И ИХ ОБОБЩЕНИЙ
Спинорное представление группы Лоренца имеет фундаментальное значение для теоретической и математической физики. Рассматриваемый подход основан на том, что комплексная матрица $L$ размерности $2 \times 2$ с определителем, равным единице ($\det \left( L \right) = 1$), порождает преобразование, сохраняющее релятивистский интервал (т.е. порождает преобразование Лоренца) [1, 2]. В работе [3] мы рассмотрели приложение указанного формализма к описанию преобразований и измерений двухуровневых квантовых систем (кубитов), а также систем более высокой размерности. Цель настоящего исследования заключается в том, чтобы применить результаты, полученные в [3], к задаче прецизионного контроля эволюции квантовых состояний многоуровневых систем (кудитов).
Суть спинорного представления группы Лоренца мы проиллюстрируем на примере смешанного состояния кубита. Заметим, что любое исходное смешанное состояние кубита можно рассматривать как смесь двух различных компонент. Тогда, смешанное состояние, дополненное до чистого состояния, можно задать в виде комплексной матрицы ${{\varphi }_{{in}}}$ размерности $2 \times 2$ (каждый столбец характеризует свою компоненту смеси). Исходная матрица плотности в этом случае есть:
Заметим, что процедура дополнения смеси до чистого состояния неоднозначна. В общем случае можно рассматривать различные комплексные матрицы ${{\varphi }_{{in}}}$ размерности $2 \times n$, $n \geqslant 2$ (смесь из $n$ компонент). Матрица ${{\varphi }_{{in}}}$ может быть умножена справа на произвольную унитарную матрицу $U$ размерности $n \times n$: ${{\varphi }_{{in}}} \to {{\varphi }_{{in}}}U$. Под действием такого преобразования матрица плотности ${{\varphi }_{{in}}}\varphi _{{in}}^{ + }$ очевидно остается инвариантом. Отметим, что матрица амплитуд ${{\varphi }_{{in}}}$ может быть вытянута в столбец амплитуд длины $2n$ (для этого второй столбец надо поместить по первым и т.д.). Однако, для наших целей удобнее представлять очищенное состояние в виде матрицы ${{\varphi }_{{in}}}$ размерности $2 \times n$. Заметим также, что процедура дополнения смешанного состояния до чистого играет фундаментальную роль в задачах квантовых измерений и томографии [4–6].
Спинорное преобразование задается посредством комплексной матрицы $L$ размерности $2 \times 2$ с определителем, равным единице:
Спинорное преобразование порождает на выходе матрицу плотности ${{\rho }_{{out}}} = {{\varphi }_{{out}}}\varphi _{{out}}^{ + }$, причем:
Рассматриваемое преобразование очевидно оставляет неизменным определитель матрицы плотности. Это, в свою очередь, обеспечивает инвариантность релятивистского квадрата интервала. Действительно, любую матрицу плотности кубита $\rho $ можно представить в базисе из четырех матриц ($I$, ${{\sigma }_{1}}$, ${{\sigma }_{2}}$, ${{\sigma }_{3}}$) [7]:
Здесь $I$ – единичная матрица $2 \times 2$; ${{\sigma }_{1}}$, ${{\sigma }_{2}}$, ${{\sigma }_{3}}$ – матрицы Паули. Будем интерпретировать данное соотношение в терминах квантовой оптики. В этом случае ${{P}_{0}} = Tr\left( \rho \right)$ – интенсивность излучения;
– компоненты вектора Стокса. Подчеркнем, что в настоящем рассмотрении след матрицы плотности равен не единице, как предполагается обычно, а интенсивности излучения ${{P}_{0}}$.
Используя стандартное представление для матриц Паули, получим:
(5)
$\rho = \frac{1}{2}\left( {\begin{array}{*{20}{c}} {{{P}_{0}} + {{P}_{3}}}&{{{P}_{1}} - i{{P}_{2}}} \\ {{{P}_{1}} + i{{P}_{2}}}&{{{P}_{0}} - {{P}_{3}}} \end{array}} \right).$Теперь становится очевидным, что инвариантность определителя матрицы плотности относительно спинорного преобразование приводит к инвариантности величины ${{s}^{2}} = P_{0}^{2} - {{\vec {P}}^{2}}$. Полученная величина играет роль квадрата релятивистского интервала, если интенсивность ${{P}_{0}}$ рассматривать в качестве нулевой компоненты, а компоненты вектора Стокса в качестве трех пространственных компонент четырех-вектора Минковского–Стокса $\left( {{{P}_{0}},\vec {P}} \right) = \left( {{{P}_{0}},{{P}_{1}},{{P}_{2}},{{P}_{3}}} \right)$. Считаем, что скорость света равна единице ($c = 1$). Четырех-вектор Минковского–Стокса можно интерпретировать как четырех-импульс некоторой эффективной частицы. Нетрудно видеть, что
Используя элементы комплексной матрицы преобразования кубита
Матрица $G$ лежит в основе тензорных преобразований Лоренца. В развернутой записи рассматриваемое преобразование можно представить в виде:
(6)
$\left( {\begin{array}{*{20}{c}} {P_{0}^{'}} \\ {P_{1}^{'}} \\ {P_{2}^{'}} \\ {P_{3}^{'}} \end{array}} \right) = \frac{1}{2} \times \left( {\begin{array}{*{20}{c}} {\alpha {\text{*}}\alpha + \beta {\text{*}}\beta + \gamma {\text{*}}\gamma + \delta {\text{*}}\delta }&{\alpha {\text{*}}\beta + \beta {\text{*}}\alpha + \gamma {\text{*}}\delta + \delta {\text{*}}\gamma }&{i(\alpha {\text{*}}\beta - \beta {\text{*}}\alpha + \gamma {\text{*}}\delta - \delta {\text{*}}\gamma )}&{\alpha {\text{*}}\alpha - \beta {\text{*}}\beta + \gamma {\text{*}}\gamma - \delta {\text{*}}\delta } \\ {\alpha {\text{*}}\gamma + \beta {\text{*}}\delta + \gamma {\text{*}}\alpha + \delta {\text{*}}\beta }&{\alpha {\text{*}}\delta + \beta {\text{*}}\gamma + \gamma {\text{*}}\beta + \delta {\text{*}}\alpha }&{i(\alpha {\text{*}}\delta - \beta {\text{*}}\gamma + \gamma {\text{*}}\beta - \delta {\text{*}}\alpha )}&{\alpha {\text{*}}\gamma - \beta {\text{*}}\delta + \gamma {\text{*}}\alpha - \delta {\text{*}}\beta } \\ { - i(\alpha {\text{*}}\gamma + \beta {\text{*}}\delta - \gamma {\text{*}}\alpha - \delta {\text{*}}\beta )}&{ - i(\alpha {\text{*}}\delta + \beta {\text{*}}\gamma - \gamma {\text{*}}\beta - \delta {\text{*}}\alpha )}&{\alpha {\text{*}}\delta - \beta {\text{*}}\gamma - \gamma {\text{*}}\beta + \delta {\text{*}}\alpha }&{ - i(\alpha {\text{*}}\gamma - \beta {\text{*}}\delta - \gamma {\text{*}}\alpha + \delta {\text{*}}\beta )} \\ {\alpha {\text{*}}\alpha + \beta {\text{*}}\beta - \gamma {\text{*}}\gamma - \delta {\text{*}}\delta }&{\alpha {\text{*}}\beta + \beta {\text{*}}\alpha - \gamma {\text{*}}\delta - \delta {\text{*}}\gamma }&{i(\alpha {\text{*}}\beta - \beta {\text{*}}\alpha - \gamma {\text{*}}\delta + \delta {\text{*}}\gamma )}&{\alpha {\text{*}}\alpha - \beta {\text{*}}\beta - \gamma {\text{*}}\gamma + \delta {\text{*}}\delta } \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{{P}_{0}}} \\ {{{P}_{1}}} \\ {{{P}_{2}}} \\ {{{P}_{3}}} \end{array}} \right)$Мы видим, что преобразование Лоренца описывается в простейшей форме в рамках спинорного представления и в более сложной форме в рамках тензорного представления. Можно предположить, что спиноры являются более фундаментальными объектами по сравнению с четырех-векторами координатного или импульсного пространств (в частности, на такого рода представлениях основывается так называемая твистерная программа Пенроуза [13, 14]). Для наших целей во всяком случае важно, что такое утверждение справедливо для кубитов и, в частности, для поляризационной степени свободы электромагнитного поля. В этом случае очевидно, что спинорное, в общем случае многокомпонентное, представление поляризации $\varphi $ более фундаментально по сравнению с вектором Минковского–Стокса $\left( {{{P}_{0}},\vec {P}} \right)$.
Рассмотрим простейшее преобразование Лоренца, задаваемое диагональной матрицей
(7)
$P_{0}^{'} = \cosh \left( \eta \right){{P}_{0}} - \sinh \left( \eta \right){{P}_{3}},\,\,\,\,P_{3}^{'} = - \sinh \left( \eta \right){{P}_{0}} + \cosh \left( \eta \right){{P}_{3}},\,\,\,\,P_{1}^{'} = {{P}_{1}},\,\,\,\,P_{2}^{'} = {{P}_{2}}.$Рассматриваемое преобразование описывает переход к новой системе отсчета, движущейся относительно старой вдоль оси $z$ со скоростью $v = \operatorname{th} \left( \eta \right)$. Заметим, что в рассматриваемом случае переход от гиперболического тангенса к гиперболическим косинусу и синусу приводит к следующим выражениям:
(8)
$\operatorname{ch} \left( \eta \right) = \frac{1}{{\sqrt {1 - {{v}^{2}}} }},\,\,\,\,\operatorname{sh} \left( \eta \right) = \frac{v}{{\sqrt {1 - {{v}^{2}}} }}.$Представленное преобразование можно рассматривать как псевдо-вращение в плоскости $\left( {t,z} \right)$. Аналогичным образом можно рассмотреть псевдо-вращения в плоскостях $\left( {t,x} \right)$ и $\left( {t,y} \right)$. Наряду с псевдо-вращениями, в группе Лоренца существуют, конечно, и обычные вращения (в плоскостях $\left( {x,y} \right)$, $\left( {x,z} \right)$ и $\left( {y,z} \right)$).
Заметим, что, в случае поляризационных оптических кубитов рассматриваемое преобразование L требует сжатия оптических состояний, когда одна из компонент поляризации (вертикальная или горизонтальная) ослабляется, а другая усиливается. В условиях обычного затухания, когда обе компоненты ослабляются, но в разной степени, возникает преобразование:
(9)
$\left( {\begin{array}{*{20}{c}} {\exp ( - {{\eta }_{1}}{\text{/}}2)}&0 \\ 0&{\exp ( - {{\eta }_{2}}{\text{/}}2)} \end{array}} \right) = \exp ( - {{\eta }_{0}}{\text{/}}2)\left( {\begin{array}{*{20}{c}} {\exp ( - \eta {\text{/}}2)}&0 \\ 0&{\exp (\eta {\text{/}}2)} \end{array}} \right),$Скорость эффективной частицы, отвечающей четырех-импульсу Минковского–Стокса $\left( {{{P}_{0}},\vec {P}} \right)$ с энергией ${{P}_{0}}$ и импульсом $\vec {P}$ равна $\vec {v} = {{\vec {P}} \mathord{\left/ {\vphantom {{\vec {P}} {{{P}_{0}}}}} \right. \kern-0em} {{{P}_{0}}}}$. Рассмотрим преобразование, обеспечивающее переход в систему отсчета, в которой для кубита обнуляется импульс эффективной частицы (пространственные компоненты четырех-вектора Минковского–Стокса). Такую систему отсчета можно назвать собственной системой отсчета эффективной частицы (а также системой центра инерции или системой центра масс). В этом случае кубит оказывается в центре сферы Блоха. Рассматриваемое преобразование описывается следующим псевдо-вращением:
(10)
${{L}_{{\vec {n}}}}\left( \theta \right) = \exp \left( { - \frac{\theta }{2}\vec {\sigma }\vec {n}} \right) = \operatorname{ch} \left( {\frac{\theta }{2}} \right)I - \operatorname{sh} \left( {\frac{\theta }{2}} \right)\vec {\sigma }\vec {n},$На примере поляризационного кубита рассмотрим процедуру измерения компонент четырех-вектора Минковского–Стокса. Пусть на пути светового пучка стоит поляризатор, плоскость пропускания которого ориентирована вертикально. Регистрируется число фотонов ${{N}_{V}}$, пропущенных поляризатором в заданный промежуток времени (который примем условно за единицу времени). В этом случае измеряется проекционный оператор $\left| V \right\rangle \left\langle V \right|$. После поворота поляризатора на 90°, аналогичные измерения проекционного оператора $\left| H \right\rangle \left\langle H \right|$ дадут число фотонов ${{N}_{H}}$. Суммарное число фотонов ${{N}_{V}} + {{N}_{H}}$ может служить оценкой компоненты ${{P}_{0}} = Tr\left( \rho \right)$ четырех-вектора Минковского–Стокса, а разностное число фотонов ${{N}_{V}} - {{N}_{H}}$ может служить оценкой компоненты ${{P}_{3}} = Tr\left( {\rho {{\sigma }_{3}}} \right)$. Пусть до прохождения через поляризатор фотон подвергается унитарному вращению $U$. Тогда преобразованные матрица плотности и третья компонента вектора Стокса есть:
Можно обобщить представленную процедуру квантовых измерений поляризационного кубита на случай, когда до унитарных вращений он подвергается буст-преобразованию Лоренца. Особенно важно рассмотреть буст-преобразование, соответствующее переходу в систему центра инерции для кубита, находящегося первоначально в произвольном смешанном состоянии. Оказывается, что в системе центра инерции, которая отвечает кубиту в центре сфера Блоха, точность квантовых измерений самая высокая (при заданном числе измеренных представителей [6, 15]).
Рассмотрим далее поляризационный тензор двухкубитового состояния. Пусть комплексная матрица L размерности 2 × 2 с определителем, равным единице (det(L) = 1), порождает преобразование Лоренца. Пусть G есть соответствующая этому преобразованию действительная матрица размерности 4 × 4, задающая преобразование Лоренца для четырех-векторов в пространстве Минковского. Рассмотрим начальное очищенное состояние двух кубитов ${{\varphi }_{{in}}}$, задаваемое комплексной матрицей размерности 4 × 4, и начальную матрицу плотности ${{\rho }_{{in}}} = {{\varphi }_{{in}}}\varphi _{{in}}^{ + }$. Тогда, конечное состояние есть ${{\varphi }_{{out}}} = (L \otimes L){{\varphi }_{{in}}}$, а конечная матрица плотности ${{\rho }_{{out}}} = {{\varphi }_{{out}}}\varphi _{{out}}^{ + }$ задается преобразованием:
Компоненты поляризационного тензора определяются формулой:
(12)
${{F}_{{\mu \nu }}} = Tr\left( {\rho \left( {{{\sigma }_{\mu }} \otimes {{\sigma }_{\nu }}} \right)} \right),$Здесь и далее по повторяющимся индексам предполагается суммирование.
В матричных обозначениях это преобразование можно записать в виде
Здесь эрмитово-сопряженная матрица ${{G}^{ + }}$ совпадает с транспонированной матрицей.
При этом оказывается, что величины $\det (F)$ и $Tr(FgFg)$ являются инвариантами преобразования Лоренца. Здесь g – метрический тензор (диагональная матрица, ненулевые элементы которой есть: ${{g}_{{00}}} = 1$, ${{g}_{{11}}} = {{g}_{{22}}} = {{g}_{{33}}} = - 1$).
Можно показать, что переход от тензора поляризации к матрице плотности задается формулой:
(15)
$\rho = \frac{1}{4}{{F}_{{\mu \nu }}}\left( {{{\sigma }_{\mu }} \otimes {{\sigma }_{\nu }}} \right).$По аналогии с одно- и двух-кубитовыми состояниями можно определить поляризационный тензор ранга n для общего случая n-кубитового состояния. При этом естественным образом обобщаются формулы для преобразования очищенного квантового состояния и соответствующей ему матрицы плотности, а также формулы для преобразований компонент поляризационного тензора и формулы, осуществляющие обратный переход от тензора поляризации к матрице плотности.
По аналогии с рассмотренной выше процедурой измерения компонент четырех-вектора Минковского–Стокса можно разработать процедуру измерения компонент поляризационного тензора второго ранга и обобщить эту процедуру на измерение поляризационного тензора произвольного ранга.
Важно существование в релятивистском случае спиноров двух различных типов. Пусть при переходе от одной системы отсчета к другой спинор $\left| \varphi \right\rangle $ преобразуется с помощью комплексной матрицы L размерности 2 × 2 с определителем, равным единице ($\det (L) = 1$): $\left| {\varphi {\kern 1pt} '} \right\rangle = L\left| \varphi \right\rangle $. Введем “волнистый” спинор $\left| {\tilde {\chi }} \right\rangle $ нового типа так, чтобы величина $\left\langle {\left. \varphi \right|\tilde {\chi }} \right\rangle $ оказалась релятивистски-инвариантным скаляром. Можно показать, что “волнистый” спинор $\left| {\tilde {\chi }} \right\rangle $ должен преобразовываться с использованием матрицы $\tilde {L} = {{({{L}^{ + }})}^{{ - 1}}}$, т.е. $\left| {\tilde {\chi }{\kern 1pt} '} \right\rangle = \tilde {L}\left| \chi \right\rangle $. Можно показать также, что $\tilde {L} = {{\sigma }_{2}}L{\text{*}}{{\sigma }_{2}}.$
В частном случае унитарных вращений $\tilde {L} = $ $ = {{({{L}^{ + }})}^{{ - 1}}} = L$. В этом случае “волнистые” спиноры совпадают (по своим трансформационным свойствам) с исходными спинорами.
Пусть при переходе от одной системы отсчета к другой спинор $\left| \varphi \right\rangle $ преобразуется с помощью комплексной матрицы L. Можно показать, что в этом случае “волнистый” спинор, если определить его как $\left| {\tilde {\varphi }} \right\rangle = {{\sigma }_{2}}\left| {\varphi {\text{*}}} \right\rangle $, преобразуется с помощью матрицы $\tilde {L} = {{\sigma }_{2}}L{\text{*}}{{\sigma }_{2}} = {{({{L}^{ + }})}^{{ - 1}}}$.
Мы видим, что переход от исходного к “волнистому” спинору сводится к двум последовательным действиям: комплексное сопряжение (которое приводит к так называемым “пунктирным” спинорам) и действие матрицы Паули σ2 (при этом матрица σ2 играет роль метрического тензора). Заметим, что наше изложение дополняет изложение, представленное в классической книге [16].
Пусть $\left| \varphi \right\rangle $ – очищенное состояние кубита. Согласно изложенному выше
Умножив представленную конструкцию справа на “волнистый” спинор $\left| {\tilde {\eta }} \right\rangle $, получим $2\left| \varphi \right\rangle \left\langle {\left. \varphi \right|\tilde {\eta }} \right\rangle $. Величина $\left\langle {\left. \varphi \right|\tilde {\eta }} \right\rangle $ есть релятивистский скаляр, поэтому $2\left| \varphi \right\rangle \left\langle {\left. \varphi \right|\tilde {\eta }} \right\rangle $ есть “обычный” спинор с размерностью массы. Обозначив его как $m\left| \xi \right\rangle $, получим:
(16)
$2\left| \varphi \right\rangle \left\langle \varphi \right|\left. {\tilde {\eta }} \right\rangle = m\left| \xi \right\rangle .$Можно показать, что представленное уравнение порождает следующее сопряженное уравнение:
(17)
$2\left| {\tilde {\varphi }} \right\rangle \left\langle {\tilde {\varphi }} \right|\left. \xi \right\rangle = m\left| {\tilde {\eta }} \right\rangle .$(18)
$\left( {\begin{array}{*{20}{c}} 0&{{{P}_{0}}I + \vec {P}\vec {\sigma }} \\ {{{P}_{0}}I - \vec {P}\vec {\sigma }}&0 \end{array}} \right)\left( {\begin{array}{*{20}{c}} \xi \\ {\tilde {\eta }} \end{array}} \right) = m\left( {\begin{array}{*{20}{c}} \xi \\ {\tilde {\eta }} \end{array}} \right).$Здесь ноль внутри матрицы означает нулевую матрицу размерности 2 × 2. Четырехкомпонентная величина $\left( {\begin{array}{*{20}{c}} \xi \\ {\tilde {\eta }} \end{array}} \right)$, представленная “обычным” и “волнистым” спинорами, есть биспинор. Уравнение Дирака может быть записано в следующем компактном виде:
Пусть ${{\varphi }_{1}} = \left( {\begin{array}{*{20}{c}} {{{\xi }_{1}}} \\ {{{{\tilde {\eta }}}_{1}}} \end{array}} \right)$ – биспинор, удовлетворяющий уравнению Дирака. Зададим “волнистый” спинор $\left| {{{{\tilde {\eta }}}_{2}}} \right\rangle $, ортогональный спинору $\left| {{{\xi }_{1}}} \right\rangle $: $\left\langle {\left. {{{\xi }_{1}}} \right|{{{\tilde {\eta }}}_{2}}} \right\rangle = \xi _{1}^{ + }{{\tilde {\eta }}_{2}} = 0$. Зная $\left| {{{{\tilde {\eta }}}_{2}}} \right\rangle $, можно найдите $\left| {{{\xi }_{2}}} \right\rangle $ и построить биспинор ${{\varphi }_{2}} = \left( {\begin{array}{*{20}{c}} {{{\xi }_{2}}} \\ {{{{\tilde {\eta }}}_{2}}} \end{array}} \right)$, также удовлетворяющий уравнению Дирака. Можно показать, что построенные биспиноры ортогональны: ${{\bar {\varphi }}_{1}}{{\varphi }_{2}} = 0$. Здесь ${{\bar {\varphi }}_{1}} = \varphi _{1}^{ + }{{\gamma }_{0}}$ – дираковски-сопряженный спинор. Важно, что ${{\bar {\varphi }}_{1}}{{\varphi }_{2}}$ – релятивистски-инвариантный скаляр. Пусть рассматриваемые биспиноры нормированы на единицу посредством следующих условий: ${{\bar {\varphi }}_{1}}{{\varphi }_{1}} = 1$, ${{\bar {\varphi }}_{2}}{{\varphi }_{2}} = 1$. Тогда разложение произвольного биспинора ψ в базисе из двух биспиноров φ1 и φ2 будет иметь вид: $\psi = ({{\bar {\varphi }}_{1}}\psi ){{\varphi }_{1}} + ({{\bar {\varphi }}_{2}}\psi ){{\varphi }_{2}}$. Пусть биспинор ψ также нормирован посредством аналогичного условия: $\bar {\psi }\psi = 1$. Тогда ${{\bar {\varphi }}_{1}}\psi $ и ${{\bar {\varphi }}_{2}}\psi $ есть амплитуды вероятностей получить при измерении базисные состояния φ1 и φ2 соответственно. Вероятности таких результатов есть соответственно ${{\Pr }_{1}} = {{\left| {{{{\bar {\varphi }}}_{1}}\psi } \right|}^{2}}$ и ${{\Pr }_{2}} = {{\left| {{{{\bar {\varphi }}}_{2}}\psi } \right|}^{2}}$ (причем ${{\Pr }_{1}}\,\, + {{\Pr }_{2}} = 1$). В случае статистической смеси величина ψ есть очищенное состояние, $\bar {\psi }\psi $ – матрица плотности поляризационного состояния дираковской частицы, ${{\varphi }_{1}}{{\bar {\varphi }}_{1}}$ и ${{\varphi }_{2}}{{\bar {\varphi }}_{2}}$ – операторы измерений. Тогда ${{\Pr }_{1}} = Tr{\text{(}}{{\varphi }_{1}}{{\bar {\varphi }}_{1}}\psi \bar {\psi })$, ${{\Pr }_{2}} = Tr{\text{(}}{{\varphi }_{2}}{{\bar {\varphi }}_{2}}\psi \bar {\psi })$.
Пусть имеется чистое состояние ${{\rho }_{{in}}} = \left| \psi \right\rangle \left\langle \psi \right|$, нормированное на единицу ($Tr({{\rho }_{{in}}}) = \left\langle {\left. \psi \right|\psi } \right\rangle = 1$). Проекционное измерение задается операторами чистых измерений $\Lambda _{ \pm }^{{pure}} = \frac{1}{2}({{P}_{0}}I \pm \vec {P}\vec {\sigma })$, где ${{P}_{0}}$ – интенсивность измерений (число измерений в единицу времени), $\left| {\vec {P}} \right| = {{P}_{0}},$ $\Lambda _{ + }^{{pure}} + \Lambda _{ - }^{{pure}} = {{P}_{0}}I$. Нетрудно показать, что квадраты операторовчистых измерений пропорциональны самим операторам, что характерно для чистых состояний: ${{\left( {\Lambda _{ + }^{{pure}}} \right)}^{2}} = {{P}_{0}}{{\Lambda }_{ + }}$. Интенсивности генераций событий в этом случае есть:
Пусть квантовое состояние подвергается процессу декогерентизации, который определяется операторной суммой:
где Ek– элементы преобразования, или операторы Крауса ($\sum\nolimits_k {E_{k}^{ + }{{E}_{k}} = I} $ – условие нормировки). Оказывается, что при интерпретации результатов измерений можно формально перенести действие процесса декогерентизации с квантового состояния на операторы измерения [17, 18], т.е.(20)
${{\lambda }_{ \pm }} = Tr\left( {\Lambda _{ \pm }^{{pure}}{{\rho }_{{out}}}} \right) = Tr\left( {\Lambda _{ \pm }^{{mixed}}{{\rho }_{{in}}}} \right),$Таким образом, операторы нечетких измерений позволяют восстановить квантовое состояние таким, каким оно было до того, как начало изменяться под действием окружения.
Пусть квантовое состояние подвергается процессу деполяризации, для которого
Введенные выше операторы нечетких измерений $\Lambda _{ \pm }^{{mixed}} = \frac{1}{2}({{P}_{0}}I \pm \vec {P}\vec {\sigma })$ позволяют определить биспинор $\psi = \left( {\begin{array}{*{20}{c}} \xi \\ {\tilde {\eta }} \end{array}} \right)$, удовлетворяющий уравнению Дирака (18), которое можно переписать также в следующем виде:
(21)
$\left( {\begin{array}{*{20}{c}} 0&{\Lambda _{ + }^{{mixed}}} \\ {\Lambda _{ - }^{{mixed}}}&0 \end{array}} \right)\left( {\begin{array}{*{20}{c}} \xi \\ {\tilde {\eta }} \end{array}} \right) = m\left( {\begin{array}{*{20}{c}} \xi \\ {\tilde {\eta }} \end{array}} \right).$Пусть исследуемое квантовое состояние $\left| \varphi \right\rangle $ нормировано на единицу ($\left\langle {\left. \varphi \right|\varphi } \right\rangle = 1$) и представлено “волнистым” спинором ($\left| \varphi \right\rangle = \left| {\tilde {\eta }} \right\rangle $). Можно показать, что в этом случае интенсивность генерации событий λ+ описывается формулой: ${{\lambda }_{ + }} = \frac{m}{2}\left\langle {\left. \xi \right|\tilde {\eta }} \right\rangle = \frac{m}{4}\bar {\psi }\psi $. Пусть теперь исследуемое квантовое состояние $\left| \varphi \right\rangle $, нормированное снова на единицу ($\left\langle {\left. \varphi \right|\varphi } \right\rangle = 1$), представлено “обычным” спинором ($\left| \varphi \right\rangle = \left| \xi \right\rangle $). Можно показать, что теперь посредством той же формулы, представленной выше, описывается сопряженная интенсивность генерации событий λ–, т.е.:
3. ПРОТОКОЛ КВАНТОВЫХ ИЗМЕРЕНИЙ И ПРОЦЕДУРА КВАНТОВОЙ ТОМОГРАФИИ
Протокол квантовой томографии будем описывать так называемой аппаратной матрицей X [4, 15]. В простейшем случае каждая строка Xj этой матрицы задает в гильбертовом пространстве бра-вектор, на который проецируется измеряемое состояние, j = 1, …, m, где m – число строк протокола (общее число измеряемых проекций). Амплитуда вероятности ${{M}_{j}}$, отвечающая вектору состояния $c$ и заданной строке протокола, есть: ${{M}_{j}} = {{X}_{j}}c$. Вероятность в единицу времени ${{\lambda }_{j}}$, задающая ожидаемое число регистрируемых событий, определяется квадратом модуля амплитуды: ${{\lambda }_{j}} = {{\left| {{{M}_{j}}} \right|}^{2}} = \left\langle c \right|{{\Lambda }_{j}}\left| c \right\rangle $, где ${{\Lambda }_{j}} = X_{j}^{ + }{{X}_{j}}$ – оператор измерения. Если состояние описывается матрицей плотности ρ, то ${{\lambda }_{j}} = Tr\left( {{{\Lambda }_{j}}\rho } \right)$.
Каждая строка аппаратной матрицы входит в протокол со своим весом. Пусть tj – вес j-ой строки (время экспозиции). Будем нормировать полную взвешенную вероятность на полный объем выборки (n – суммарный объем выборки по всем строкам протокола):
Для протоколов, которые сводятся к разложению единицы (так называемые POVM-протоколы), сумма всех матриц ${{t}_{j}}{{\Lambda }_{j}}$ протокола пропорциональна единичной матрице:
Здесь I – единичная матрица. Заметим, что условие (23) совместно с условием нормировки вектора состояния $\left\langle {c} \mathrel{\left | {\vphantom {c c}} \right. \kern-0em} {c} \right\rangle = 1$ непосредственно приводят к (22).
Как показано нами в [3], преобразование исходной аппаратной матрицы ${{X}^{{in}}}$ под действием преобразования Лоренца сводится к ее умножению справа на комплексную матрицу $L$:
Мы предполагаем, что все строки исходной аппаратной матрицы ${{X}^{{in}}}$ нормированы на единицу: $X_{j}^{{in}}{{(X_{j}^{{in}})}^{ + }} = 1$, $j = 1,2,...,m$. В результате преобразования Лоренца с не унитарной матрицей $L$ веса строк протокола изменяются. Пусть ${{t}_{j}} = X_{j}^{{out}}{{(X_{j}^{{out}})}^{ + }}$ – соответствующие веса. Их можно интерпретировать как времена экспозиции соответствующих проекционных измерений (времена экспозиции строк исходного протокола ${{X}^{{in}}}$ считаем равными единице).
Точность реконструкции квантового состояния (Fidelity) определяется следующей формулой [19, 20]:
где ${{\rho }_{0}}$ – теоретическая матрица плотности, а $\rho $ – реконструированная матрица плотности.Можно показать [6, 15], что для любого POVM- протокола средние потери точности $\left\langle {1 - F} \right\rangle $ не могут быть ниже следующей величины:
(26)
${{\left\langle {1 - F} \right\rangle }_{{\min }}} = \frac{{{{v}^{2}}}}{{4n\left( {s - 1} \right)}}.$Здесь $v = \left( {2s - r} \right)r - 1$ – число степеней свободы квантового состояния, $s$ – размерность гильбертова пространства, $r$ – ранг матрицы плотности, $n$ – суммарный объем выборки.
Эффективность протокола по отношению к любому рассматриваемому квантовому состоянию можно определить как отношение минимально возможных потерь точности к реально достижимым:
(27)
$eff = \frac{{{{{\left\langle {1 - F} \right\rangle }}_{{\min }}}}}{{\left\langle {1 - F} \right\rangle }}.$Принципиально важный момент нашего подхода к построению сверхэффективных квантовых измерений основан на том, что протокол Лоренца не сводится к разложению единицы (POVM), поэтому ограничение (26) на минимальные потери точности для него, вообще говоря, не является обязательным. Оказывается, что для такого рода измерений возможно возникновение сверхэффективности, когда формально $eff > 1$.
Рассмотренное выше преобразование Лоренца для отдельного кубита может быть обобщено на случай квантовых систем произвольной более высокой размерности. В этом случае, преобразование инструментальной матрицы в собственную систему координат также осуществляется с помощью формулы (24): ${{X}^{{out}}} = {{X}^{{in}}}L.$
Теперь матрица преобразования Лоренца строится по следующему правилу [3]:
(28)
$L = \frac{1}{{\sqrt s }}\psi _{{in}}^{{ - 1}},\,\,\,\,L \to \frac{L}{{{{{\left( {\det L} \right)}}^{{1/s}}}}}.$Заметим, что второе соотношение задает преобразование, обеспечивающее условие $\det L = 1$. Здесь $s$ – размерность гильбертова пространства; ${{\psi }_{{in}}}$ – очищенное состояние, которое задается матрицей размерности $s \times s$ и обеспечивает следующее представление для матрицы плотности: ${{\rho }_{{in}}} = {{\psi }_{{in}}}\psi _{{in}}^{ + }.$
Введенная нами матрица $L$ задает обобщенное преобразование Лоренца, которое действует на состояния, заданные в $s$ – мерном гильбертовом пространстве. Мы не сопоставляем этому преобразованию какое-либо тензорное преобразование в обычном четырехмерном пространстве-времени.
Можно видеть, что в новой системе координат матрица плотности пропорциональна единичной матрице: ${{\rho }_{{out}}} = {{\left( {\det {{\rho }_{{in}}}} \right)}^{{1/s}}}I$, где $I$ – единичная матрица размерности $s \times s$. Заметим, что из всех смешанных состояний наивысшая точность достигается именно для таких состояний, причем, не только для кубитов, как об этом уже было сказано выше, но и для состояний произвольной размерности [6, 15].
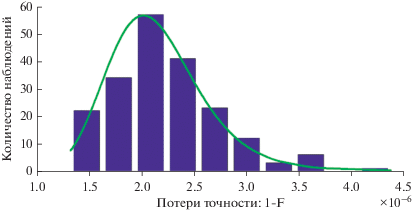
Пример, представленный на рис. 1, соответствует томографии квантового состояния восьмиуровневого кудита ($s = 8$). Исходный протокол измерений задает совокупность взаимно-несмещенных базисов (MUB-mutuallyunbiasedbases [21]). Рис. 1 иллюстрирует близкое соответствие между результатами численных экспериментов с протоколом Лоренца и теорией точности, развитой в наших работах [4–6, 15, 22]. Данный пример отвечает случайно сгенерированному смешанному состоянию полного ранга ($r = 8$), которое близко к чистому состоянию (главная компонента матрицы плотности имеет вес ${{\lambda }_{0}} = 0.9999$). Было выполнено 200 численных экспериментов, объем выборки (полное число зарегистрированных событий) в каждом из экспериментов составлял $n = {{10}^{4}}$, число степеней свободы квантового состояния равнялось $v = \left( {2s - r} \right)r - 1 = {{s}^{2}} - 1 = 63$. Средние потери точности в рассматриваемом случае составили чрезвычайно малую величину $\left\langle {1 - F} \right\rangle = 2.15997 \times {{10}^{{ - 6}}}$. В результате, в соответствии с формулой (27), эффективность составила очень высокую величину $eff = 6563$.
4. АДАПТИВНОЕ ОТСЛЕЖИВАНИЕ ЭВОЛЮЦИИ КВАНТОВОГО СОСТОЯНИЯ КУДИТА
Как отмечалось выше, свойство сверхэффективности протоколов Лоренца основано на том, что данные протоколы не сводятся к разложениям единицы (не образуют POVM). Фактически протоколы Лоренца описывают незаконченные измерения (unfinishedmeasurements). Это означает, что, пройдя через измерительную систему, отвечающую протоколу Лоренца, кудит (например, ионный) не обязательно будет зарегистрирован в одной из строк протокола измерений. Заметим, что в случае измерения ионных кудитов каждое элементарное измерение “прощупывает” населенность отдельного уровня. При этом, в случае протоколов Лоренца, только небольшая часть от общего числа ионов оказывается сильно возмущена (высвечивает фотоны). Остальные же ионы не высвечивают фотоны, но при этом все же подвергаются некоторому конечному, хотя и возможно слабому, возмущению (backaction). Оказывается, что всегда можно провести дополнение аппаратной матрицы Лоренца ${{X}_{L}} = {{X}^{{out}}}$ (см. формулу (24)) до разложения единицы (POVM). При этом, дополнительные операторы измерения можно подобрать так, чтобы они соответствовали слабому возмущению исходного состояния, в то время, как все операторы измерения исходного протокола Лоренца задавали бы сильные возмущения [3]. В случае протоколов Лоренца, дополненных до POVM, подавляющее большинство представителей квантового статистического ансамбля оказываются подверженными лишь весьма слабым возмущениям. Эти представители предоставляют нам ресурс для рассматриваемой ниже процедуры отслеживания эволюции квантового состояния.
Предполагая, что в ходе эволюции квантовое состояние системы изменяется медленно, можно считать, что в пределах одного шага эволюции квантовое состояние существенно не меняется (однако, за большое число шагов квантовое состояние меняется радикально).
Алгоритм обратной связи служит для адаптации протокола измерений под эволюцию квантового состояния для сохранения высокой точности реконструкции меняющегося состояния квантовой системы в течение всего времени наблюдения. Мы использовали в своих расчетах простейший алгоритм адаптации протокола квантовых измерений, когда матрица плотности, измеренная на $j$-ом шаге эволюции, служит для построения протокола Лоренца на $j + 1$ шаге. При этом на нулевом шаге эволюции использовался стандартный на основе взаимно-несмещенных базисов MUB-протокол, не подверженный действию преобразования Лоренца (24).
Эволюция квантового состояния на каждом отдельном шаге определялась инфинитезимальным унитарным оператором ${{U}_{0}}$:
(29)
$\rho = {{U}_{0}}{{\rho }_{0}}U_{0}^{\dag },\,\,\,\,{\text{где}}\,\,\,\,{{U}_{0}} = \exp \left( { - i\varepsilon H} \right).$Здесь $H$ – гамильтониан эволюции, $\varepsilon $ – малый временной шаг.
Мы предполагаем, что гамильтониан $H$ может медленно изменяться во времени. В процессе моделирования мы использовали простейшую периодическую зависимость гамильтониана от времени:
Здесь ${{H}_{0}}$ – невозмущенный гамильтониан (нами выбиралась случайная эрмитова матрица размерности $s \times s$), $g$ – параметр интенсивности периодического возмущения, $T$ – период колебаний, $j$ – номер шага эволюции.
В качестве примера мы рассмотрели адаптивную томографию эволюционирующего квантового состояния восьмиуровневого кудита ($s = 8$). Как и в примере на рис. 1, использовался протокол измерений на основе совокупности взаимно-несмещенных базисов, измененных с помощью преобразования Лоренца (24). Результаты моделирования представлены на рис. 2 и рис. 3. Были выбраны следующие параметры модели: временной шаг эволюции $\varepsilon = 3 \times {{10}^{{ - 5}}}$; параметр интенсивности периодического возмущения $g = 0.5$; период $T$ предполагался равным 1000 шагам эволюции ($T = 1000$).
Рис. 2.
Эволюция характеристики качества отслеживания квантового состояния кудита посредством слабых измерений и обратной связи. Вверху – точность реконструкции квантового состояния, внизу – эффективность (фактически сверхэффективность) протокола квантовых измерений.
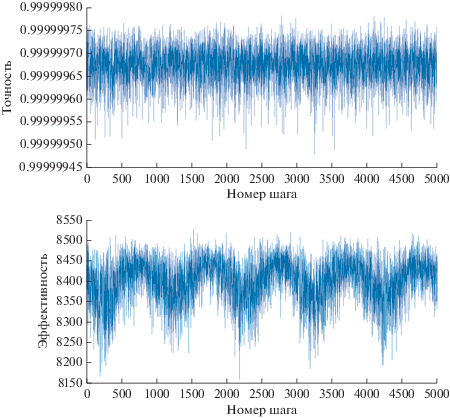
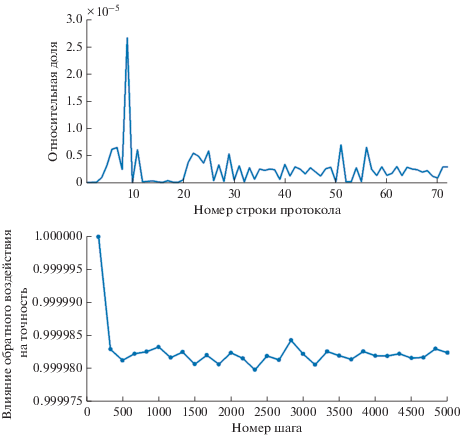
Рис. 3.
Оценка степени обратного воздействия квантовых измерений на измеряемое состояние. Вверху – доля сильно-возмущенных представителей; внизу – точность сохранения состояния (Fidelity) для слабовозмущенных представителей.
Исходное состояние было очень близко к чистому состоянию (главная компонента матрицы плотности имела вес ${{\lambda }_{0}} = 0.999999$). Нашей целью был контроль квантового состояния с точностью не ниже 4-х девяток (степень совпадения слабовозмущенного и невозмущенного состояний должна быть не ниже уровня $F = 0.9999$). Для этого, протокол измерений Лоренца настраивался на измерение матрицы плотности,главная компонента которой имела вес ${{\lambda }_{0}} = 0.9999$. Объем выборки, задающий число зарегистрированных в измерениях представителей, в каждом из экспериментов составлял $n = {{10}^{4}}$.
Протокол измерения восьмиуровневого кудитана основе совокупности взаимно-несмещенных базисов, измененных с помощью преобразования Лоренца, включает в себя проектирование на 72 различных квантовых состояния $\left| {{{\varphi }_{j}}} \right\rangle $, $j = 1,...,72$. Рассматриваемые нами протоколы Лоренца нацелены на измерения таких состояний $\left| \psi \right\rangle $, для которых вероятности регистраций событий ${{\left| {\left\langle {{{{\varphi }_{j}}}} \mathrel{\left | {\vphantom {{{{\varphi }_{j}}} \psi }} \right. \kern-0em} {\psi } \right\rangle } \right|}^{2}}$ малы для всех $j = 1,...,72$. При этом, проектор $\left| {{{\varphi }_{j}}} \right\rangle \left\langle {{{\varphi }_{j}}} \right|$ отвечает регистрации искомого события и, одновременно, сильному возмущению состояния. Напротив, проектор $I - \left| {{{\varphi }_{j}}} \right\rangle \left\langle {{{\varphi }_{j}}} \right|$, где $I$ – единичный оператор, отвечает кудиту, который претерпевает весьма слабое возмущение состояния и не регистрируется системой измерения. Такие кудиты обеспечивают нам ресурс для процедуры отслеживания непрерывного отслеживания эволюции квантового состояния. При этом, мы должны непрерывно оценивать обратное воздействие (backaction) проводимых измерений на квантовую систему (кудит). Для учета такого воздействия на отдельном шагеэволиции, вместо (29), имеем следующее преобразование:
(31)
$\rho = \left( {I - \left| {{{\varphi }_{j}}} \right\rangle \left\langle {{{\varphi }_{j}}} \right|} \right){{U}_{0}}{{\rho }_{0}}U_{0}^{\dag }\left( {I - \left| {{{\varphi }_{j}}} \right\rangle \left\langle {{{\varphi }_{j}}} \right|} \right).$Степень обратного влияния (backaction) на слабовозмущенных представителей мы описываем через степень совпадения (Fidelity $F$) квантовых состояний между результатами последовательного действия согласно (29) для невозмущенных представителей и результатами последовательного действия согласно (31) для слабовозмущенных представителей.
Согласно рис. 2 наш адаптивный метод обеспечивает реконструкцию эволюционирующего квантового состояния кудита с точностью более 6-ти девяток ($F > 0.999999$). Потери точности в рассматриваемом случае составили чрезвычайно малую случайную величину со средним значением $\left\langle {1 - F} \right\rangle = 3.2637 \times {{10}^{{ - 7}}}$ и стандартным отклонение ${{\sigma }_{F}} = 4.2026 \times {{10}^{{ - 8}}}$. Рисунок иллюстрирует высокую эффективность адаптивного метода отслеживания эволюции квантового состояния. Эффективность (фактически сверхэффективность) протокола в рассматриваемом случае была весьма высокой величиной со средним значением $\left\langle {eff} \right\rangle = 8403$ и стандартным отклонение ${{\sigma }_{{eff}}} = 54.36$. Также видно, что слабое периодическое возмущение эффективности квантовой томографии с периодом $T = 1000$, вызванное периодической модуляцией гамильтониана.
Рис. 3 (вверху) показывает относительную долю сильновозмущенных представителей для каждой из 72 строк протокола квантовых измерений. Относительная доля сильновозмущенных представителей не превышает $3 \times {{10}^{{ - 5}}}$ для всех строк протокола. Напротив, рис. 3 (внизу) иллюстрирует степень обратного влияния (backaction) на слабовозмущенных представителей (данные 5000 шагов представлены в 30 интервалах группирования). Оказывается, что под действием измерений степень совпадения квантовых состояний невозмущенных и слабовозмущенных представителей уже на первом шаге падает с 1 до уровня 0.99998 и далее остается стабильной во времени.
ЗАКЛЮЧЕНИЕ
На основе спинорных представлений группы Лоренца и их обобщений на случай многоуровневых квантовых систем (кудитов) предложен метод прецизионного контроля эволюции состояний квантовых систем посредством слабо возмущающих адаптивных квантовых измерений.
Показано, что в совокупности с обеспечением контроля квантовой системы посредством ее слабого возмущения, разработанные алгоритмы контроля эволюции состояния квантовой системы могут быть сверхэффективными, обеспечивая более высокую точность измерений, чем любые стандартные протоколы POVM.
Результаты исследования имеют важное значение для разработки оптимальных адаптивных методов управления квантовыми состояниями и операциями.
Работа выполнена в рамках Государственного задания ФТИАН им. К.А. Валиева РАН Минобрнауки РФ по теме № 0066-2019-0005 при поддержке РФФИ (грант № 19-37-90109) и Фонда развития теоретической физики и математики “БАЗИС” (грант № 20-1-1-34-1).
Список литературы
Wigner E. On unitary representations of the inhomogeneous Lorentz group // Ann. Math. 1939. V. 40. № 1. P. 149–204.
Naimark M.A. Linear representations of the Lorentz group // Russian Mathematical Surveys (Uspekhi Matematicheskikh Nauk), 1954. V. 9. Is. 4(62). Р. 19–93.
Bogdanov Yu.I., Bogdanova N.A., Bantysh B.I., Kuznetsov Yu.A. The concept of weak measurements and the super-efficiency of quantum tomography // Proc. SPIE 11022, International Conference on Micro- and Nano-Electronics 2018, 110222O (15 March 2019); https://doi.org/10.1117/12.2522078; arXiv:1906.06377 [quant-ph]
Bogdanov Yu.I. Unified Statistical Method for Reconstructing Quantum States by Purification // J. Experimental and Theoretical Physics. 2009. V. 108. № 6. P. 928–935.
Bogdanov Yu.I., Brida G, Genovese M., Kulik S.P., Moreva E.V., Shurupov A.P. Statistical Estimation of the Efficiency of Quantum State Tomography Protocols // Phys. Rev. Lett. 2010. V. 105. 010404.
Bogdanov Yu.I., Brida G., Bukeev I.D., Genovese M., Kravtsov KS., Kulik S.P., Moreva E.V., Soloviev A.A., Shurupov A.P. Statistical Estimation of Quantum Tomography Protocols Quality // Phys. Rev. A. 2011. V. 84. 042108.
Nielsen M.A., Chuang I.L. Quantum Computation and Quantum Information. Cambridge University Press, Cambridge, 2000; Mir, Moscow, 2006.
Han D., Kim Y.S., Noz M.E. Stokes parameters as a Minkowskian four-vector // Phys. Rev. Е. 1997. V. 56. P. 6065–6076.
Kim Y.S. Lorentz group in polarization optics // J. Optics B: Quantum and Semiclassical Optics. 2000. V. 2. № 2.
Teodorescu-Frumosu M., Jaeger G. Quantum Lorentz-group invariants of n-qubit systems // Phys. Rev. А. 2003. V. 67. 052305.
Baskal S., Georgieva E., Kim Y.S., Noz M. // Lorentz group in classical ray optics, J. Opt. B: Quantum Semiclass. Opt. 6 S455–S472. 2004.
Kim Y.S., Varró S., Ádám P., Biró T.S., Barnaföldi G.G., Lévai P. Poincaré Sphere and a Unified Picture of Wigner’ Little Groups // EPJ Web of Conferences 7801005. 2014.
Penrose R., Rindler W. Spinors and Space-Time. V. 1: Two-Spinor Calculus and Relativistic Fields // Cambridge University Press, 1984.
Penrose R., Rindler W. Spinors and Space-Time V. 2: Spinor and Twistor Methods in Space-Time Geometry // Cambridge University Press, 1986.
Bogdanov Yu.I., Bukeev I.D., Gavrichenko A.K. Studying Adequacy, Completeness, and Accuracy of Quantum Measurement Protocols // Optics and Spectroscopy. 2011. V. 111. № 4. P. 647–655.
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Курс в 10 томах. Т. 4. Берестецкий В.Б., Лифшиц Е.М., Питаевский Л.П. Квантовая электродинамика. М. Наука, 1989. 724 с.
Bogdanov Yu.I., Bantysh B.I., Bogdanova N.A., Kvasnyy A.B., Lukichev V.F. Quantum states tomography with noisy measurement channels // Proceedings of SPIE 10224, International Conference on Micro- and Nano-Electronics 2016, 102242O (December 30, 2016).
Bantysh B.I., Bogdanov Yu.I., Bogdanova N.A., Kuznetsov Yu.A. Precise tomography of optical polarization qubits under conditions of chromatic aberration of quantum transformations // Laser Phys. Lett. 2020. V. 17. 035205. 9 p.
Uhlmann A. The “transition probability” in the state space of a *-algebra // Rep. Math. Phys. 1976. V. 9. № 2. P. 273.
Uhlmann A. Fidelity and Concurrence of conjugated states // Phys. Rev. A. 2000. V. 62. 032307.
Durt T., Englert B., Bengtsson I., Życzkowski K. On mutually unbiased bases // International J. Quantum Information. 2010. V. 8. P. 535–640.
Bogdanov Yu.I., Chekhova M.V., Krivitsky L.A., Kulik S.P., Penin A.N., Zhukov A.A., Kwek L.C., Oh C.H., Tey M.K. Statistical Reconstruction of Qutrits // Physical Review A. 2004. V. 70. № 4. 042303.
Дополнительные материалы отсутствуют.
Инструменты
Микроэлектроника