Российские нанотехнологии, 2021, T. 16, № 3, стр. 339-347
МЕХАНИЗМЫ ТЕПЛОПЕРЕНОСА В ТЕРМОЭЛЕКТРИЧЕСКИХ МАТЕРИАЛАХ
М. С. Рогачев 1, М. Ю. Штерн 1, Ю. И. Штерн 1, *
1 Национальный исследовательский университет “МИЭТ”
Москва, Россия
* E-mail: hptt@miee.ru
Поступила в редакцию 25.11.2020
После доработки 04.12.2020
Принята к публикации 21.12.2020
Аннотация
Проведен анализ методов расчета составляющих теплопроводности твердых материалов. Определены проблемы использования этих методов и дана их оценка с точки зрения получения достоверных результатов. Приведены экспериментальные данные по температурным зависимостям термоэлектрических параметров основных термоэлектрических материалов (ТЭМ), используемых для изготовления термоэлементов Пельтье и Зеебека. С использованием полученных данных проведен расчет основных составляющих теплопроводности ТЭМ (фононной, электронной и биполярной) в интервале температур от 250 до 1200 К для твердых растворов на основе халькогенидов Bi, Sb, Pb, Ge, а также SiGe, полученных различными методами направленной кристаллизации. Установлена взаимосвязь механизмов теплопереноса в ТЭМ с температурными зависимостями электропроводности и термоэдс. Показана перспективность использования наноструктурированных ТЭМ для увеличения термоэлектрической добротности.
ВВЕДЕНИЕ
Термоэлектричество в последние годы является одним из наиболее активно развивающихся направлений в науке и технике [1–4]. Сдерживающим фактором широкого применения термоэлектрических устройств является их низкая эффективность, определяемая, в первую очередь, невысокой термоэлектрической добротностью (Z) полупроводниковых материалов, используемых для изготовления термоэлементов Пельтье и Зеебека. При этом отсутствуют какие-либо теоретические ограничения, препятствующие увеличению Z термоэлектрических материалов (ТЭМ), и работы в этом направлении интенсивно ведутся во многих лабораториях мира [4–9].
В последнее время с использованием нанотехнологий открылись новые возможности в создании перспективных ТЭМ и структур на их основе. В результате активных научных исследований в конце прошлого века сформировалось новое направление повышения эффективности ТЭМ, связанное с созданием низкоразмерных термоэлектрических структур. Многочисленные экспериментальные исследования подтверждают возможность значительного увеличения Z в структурах на основе сверхрешеток, квантовых проволок и квантовых точек по сравнению с объемными структурами на основе классических ТЭМ [10–15].
Однако с точки зрения практической реализации более актуальным является создание объемных наноструктурированных ТЭМ с низкой теплопроводностью. Повышение Z достигается за счет увеличения рассеяния фононов на границах потенциальных барьеров без существенного снижения подвижности носителей заряда. То есть фононы гораздо сильнее рассеиваются, чем носители заряда. Физическая причина этого эффекта связана с тем, что размеры неоднородностей в наноструктурированных ТЭМ меньше длины свободного пробега фононов, дающих основной вклад в теплопроводность. В то же время эти неоднородности остаются больше длины свободного пробега носителей заряда. Это приводит к уменьшению теплопроводности при сохранении высокой проводимости, что обеспечивает увеличение Z. Исследованию таких наноструктурированных материалов посвящено большинство научных работ в области термоэлектрического материаловедения, связанных с нанотехнологиями [16–25]. В связи с этим актуально внимание к экспериментальным исследованиям температурной зависимости теплопроводности, механизмам теплопереноса в ТЭМ.
Цель данной работы – используя опубликованные экспериментальные результаты по температурным зависимостям термоэлектрических параметров, провести расчет составляющих теплопроводности для основных ТЭМ, применяемых для изготовления термоэлементов Пельтье и Зеебека. Установить взаимосвязь механизмов теплопереноса с температурными зависимостями электропроводности и термоэдс.
АНАЛИЗ МЕТОДОВ РАСЧЕТА СОСТАВЛЯЮЩИХ ТЕПЛОПРОВОДНОСТИ
В интервалах рабочих температур механизмы теплопереноса в ТЭМ в основном определяются фононной (κф), электронной (κэ) и биполярной (κбп) составляющими теплопроводности [7, 25–27]:
(1)
${{\kappa }_{{{\text{общ}}}}} = {{\kappa }_{{\text{ф}}}} + {{\kappa }_{{\text{э}}}} + {{\kappa }_{{{\text{бп}}}}},$Описание расчета κэ наиболее широко представлено в [25, 28–32]. Электронная составляющая определяется согласно закону Видемана–Франца–Лоренца следующей формулой [7, 26–28, 30]:
где σ – электропроводность, T – температура, L – число Лоренца.Часто при расчетах используют постоянное значение числа Лоренца, равное 2.44 × 10–8 Вт Ом/К2. Однако в ряде случаев оно значительно отличается от этой константы и определяется по формуле для материалов с параболической зоной [29, 30]:
(3)
$L = \left( {\frac{{\left( {r + \frac{7}{2}} \right){{F}_{{r + {\text{5/2}}}}}({{\mu }}{\kern 1pt} *)}}{{\left( {r + \frac{3}{2}} \right){{F}_{{r + {\text{1/2}}}}}({{\mu }}{\kern 1pt} *)}} - \frac{{{{{\left( {r + \frac{5}{2}} \right)}}^{2}}F_{{r + {\text{3/2}}}}^{2}({{\mu }}{\kern 1pt} *)}}{{{{{\left( {r + \frac{3}{2}} \right)}}^{2}}F_{{r + {\text{1/2}}}}^{2}({{\mu }}{\kern 1pt} *)}}} \right){{\left( {\frac{{{{k}_{0}}}}{e}} \right)}^{2}},$Приведенный химический потенциал можно определить из экспериментальных значений термоэдс (s) по формуле [28, 29]:
(4)
$s = \left( {\frac{{\left( {r + \frac{5}{2}} \right){{F}_{{r + {\text{3/2}}}}}({{\mu }}{\kern 1pt} *)}}{{\left( {r + \frac{3}{2}} \right){{F}_{{r + {\text{1/2}}}}}({{\mu }}{\kern 1pt} *)}} - {{\mu }}{\kern 1pt} *} \right)\frac{{{{k}_{0}}}}{e}.$Для упрощения расчетов числа Лоренца в [30] предложена аппроксимация, исключающая приведенный химический потенциал:
(5)
$L = 1.49 - 0.49\exp \left( { - \frac{{{\text{|}}s{\text{|}}}}{{21}}} \right) + 1.40\exp \left( { - \frac{{{\text{|}}s{\text{|}}}}{{85}}} \right).$В случае непараболической зоны (например, у ТЭМ на основе PbTe) число Лоренца определяют по формуле [28–30, 32]:
(6)
$L = \left( {\frac{{{}^{2}F_{{ - 2}}^{1} \cdot {}^{0}F_{{ - 2}}^{1} - {{{({}^{1}F_{{ - 2}}^{1})}}^{2}}}}{{{{{({}^{0}F_{{ - 2}}^{1})}}^{2}}}}} \right){{\left( {\frac{{{{k}_{0}}}}{e}} \right)}^{2}},$(7)
${}^{n}F_{k}^{m}({{\beta ,\mu }}*) = \int\limits_0^\infty {\left( {\frac{{\partial {{f}_{0}}}}{{\partial x}}} \right){{x}^{n}}{{{(x + {{\beta }}{{x}^{2}})}}^{m}}{{{(1 + 2{{\beta }}x)}}^{k}}dx} ,$Приведенный химический потенциал в случае непараболической зоны определяется из формулы для термоэдс [28, 31, 32]:
(9)
$s = \left( {\frac{{{}^{1}F_{{ - 2}}^{1}}}{{{}^{0}F_{{ - 2}}^{1}}} - {{\mu }}{\kern 1pt} *} \right)\frac{{{{k}_{0}}}}{e}.$Данные, полученные при расчетах с использованием формул (6)–(9), при β = 0 (т.е. для параболической зоны) совпадают с результатом расчета по формулам (3)–(5). Это подтверждает корректность рассматриваемых методик расчета.
Расчет κф является самой сложной задачей. В [26, 27, 34] решеточную составляющую предлагается определять следующим образом:
(10)
${{\kappa }_{{\text{ф}}}} = 3.5{{\left( {\frac{{{{k}_{0}}}}{h}} \right)}^{3}}\frac{{M{{V}^{{{\text{1/3}}}}}\theta _{{\text{D}}}^{{\text{3}}}}}{{{{\gamma }^{2}}T}},$В [35] κф при температуре Дебая рассчитывали по формуле
(11)
${{\kappa }_{{\text{ф}}}} = \frac{{BM{{V}^{{{\text{1/3}}}}}{{\theta }}_{{\text{D}}}^{{\text{2}}}}}{{{{n}^{{{\text{2/3}}}}}{{\gamma }^{2}}}},$В [34, 36] κф рассчитывали по формуле
где Cν – удельная теплоемкость на единицу объема, v – скорость звука, lt – средняя длина свободного пробега фононов.Кроме того, κф может быть вычислена с использованием термического коэффициента объемного расширения α [34]:
где a – параметр решетки.Проведенный расчет κф при 300 К для твердых растворов на основе теллуридов висмута и сурьмы по указанным выше формулам дал корректные результаты. Различие полученных данных не превышало погрешностей определения физических параметров, используемых в данных формулах.
Однако провести расчет температурных зависимостей κф не представляется возможным. Это объясняется тем, что в литературе практически нет температурных зависимостей физических параметров, необходимых для расчета, тем более с учетом конкретного состава и кристаллической структуры ТЭМ. С учетом указанных выше проблем κф часто определяют следующим образом. При низких температурах, когда отсутствует биполярный теплоперенос, используя экспериментальные данные по электропроводности и термоэдс, проводят расчет κэ. Затем при этих температурах κф находят как разность общей теплопроводности, определенной экспериментально, и κэ:
Далее с учетом температурной зависимости (κф ~ T–1) проводят экстраполяцию κф в интервале температур, где проявляется биполярный теплоперенос. Главным образом такая методика определения κф использовалась в [34, 37–40].
Биполярная составляющая определяется по формуле
где Lбп – число Лоренца для биполярного теплопереноса.Число Лоренца для биполярного теплопереноса определяется следующим образом [25, 28]:
(16)
${{L}_{{{\text{бп}}}}} = {{\left( {\frac{{{{k}_{0}}}}{e}} \right)}^{2}}\frac{{{{\sigma }_{{\text{1}}}}{{\sigma }_{{\text{2}}}}}}{{{{{({{\sigma }_{{\text{1}}}} + {{\sigma }_{{\text{2}}}}{\text{)}}}}^{2}}}}{{\left( {4 + \frac{{{{E}_{g}}}}{{{{k}_{0}}T}}} \right)}^{2}},$В [41] вклад в электроперенос электронов и дырок определен через их подвижность:
(17)
${{L}_{{{\text{бп}}}}} = {{\left( {\frac{{{{k}_{0}}}}{e}} \right)}^{2}}\frac{b}{{{{{(1 + b)}}^{2}}}}{{\left( {4 + \frac{{{{E}_{g}}}}{{{{k}_{0}}T}}} \right)}^{2}},\quad b = \frac{{{{{{\mu }}}_{n}}}}{{{{{{\mu }}}_{p}}}},$В [34, 42, 43] биполярный теплоперенос определяли следующим образом:
(18)
${{\kappa }_{{{\text{бп}}}}} = \frac{{{{\sigma }_{{\text{1}}}}{{\sigma }_{{\text{2}}}}}}{{{{\sigma }_{{\text{1}}}} + {{\sigma }_{{\text{2}}}}}}{{({{s}_{1}} - {{s}_{2}})}^{2}}T,$Формула (18) может быть приблизительно описана в области собственной проводимости следующим образом [27, 41, 44]:
где A – константа, определяемая экспериментально.Биполярный теплоперенос начинается с ростом парциального вклада неосновных носителей заряда, т.е. когда наступает собственная проводимость. Составляющая κбп возникает при температуре, достаточной для переброса носителей через запрещенную зону. Сигналом этого явления служат рост электропроводности и падение термоэдс, что представлено ниже на графиках температурных зависимостей этих параметров.
Отметим, что с приемлемой погрешностью биполярная составляющая может быть определена по формуле
(20)
${{\kappa }_{{{\text{бп}}}}} = {{\kappa }_{{{\text{общ}}}}} - {{\kappa }_{{\text{ф}}}} - {{\kappa }_{{\text{э}}}}.$Таким образом, анализируя рассмотренные методы расчета составляющих теплопроводности, позволяющих судить о механизмах теплопереноса в ТЭМ, можно сделать следующие выводы. Для определения температурных зависимостей электронной и биполярной составляющих теплопроводности необходимы данные по электропроводности и термоэдс в исследуемом интервале температур. Это, как правило, не должно вызывать затруднений, так как при создании и исследовании ТЭМ необходимым условием являются данные по температурным зависимостям термоэлектрических параметров, которые определяют термоэлектрическую добротность ТЭМ.
С расчетом температурной зависимости κф сложнее. В литературе практически отсутствуют данные о физических параметрах, их температурных зависимостях, необходимых для расчета κф, тем более с учетом конкретного состава и кристаллической структуры ТЭМ. В этом случае предлагается использовать эмпирический метод определения κф.
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
Определение механизмов теплопереноса осуществляли для следующих ТЭМ:
– низкотемпературные ТЭМ n- и p-типов проводимости: Bi2Te2.8Se0.2 (0.14 мас. % CdCl2) и Bi0.5Sb1.5Те3 (2 мас. % Te и 0.14 мас. % TeI4) соответственно, полученные методом вертикальной зонной плавки;
– среднетемпературные ТЭМ: Bi2Te2.4Se0.6 (0.18 мас. % CuBr) и Bi0.4Sb1.6Te3 (0.12 мас. % PbCl2 и 1.50 мас. % Te), n- и p-типов соответственно, полученные методом экструзии;
– среднетемпературные наноструктурированные ТЭМ n- и p-типов: PbTe (0.2 мас. % PbI2 и 0.3 мас. % Ni) и GeTe (7.4 мас. % Bi) соответственно, полученные методом горячего прессования порошков размером 30–50 нм;
– высокотемпературные наноструктурированные материалы n- и p-типа: Si0.8Ge0.2 (1.7 мас. % P) и Si0.8Ge0.2 (0.5 мас. % B) соответственно, полученные методом искрового плазменного спекания порошков размером 30–50 нм.
Указанные ТЭМ разработаны для многосекционных термоэлементов с интервалом рабочих температур от 250 до 1200 К. При расчетах составляющих теплопроводности использовали экспериментальные данные по температурным зависимостям теплопроводности, электропроводности и термоэдс, полученные в [24]. Исследования проводили с помощью методик, представленных в [45, 46]. Измерения теплопроводности осуществляли абсолютным стационарным методом. Термоэлектрические параметры исследовали при температурах, соответствующих интервалам рабочих температур каждого из ТЭМ [24]. Расчет коэффициентов электропроводности, термоэдс и теплопроводности проводили согласно методикам [46].
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Температурные зависимости электропроводности и термоэдс ТЭМ представлены на рис. 1. Экспериментальные данные использовали не только для расчета составляющих теплопроводности, но и для объяснения механизма теплопереноса.
Рис. 1.
Температурная зависимость термоэдс и электропроводности для Bi2Te2.8Se0.2, Bi0.5Sb1.5Те3 (а), Bi2Te2.4Se0.6, Bi0.4Sb1.6Te3 (б), PbTе, GeTe (в), Si0.8Ge0.2 (1.7 мас. % P) и Si0.8Ge0.2 (0.5 мас. % B) (г).
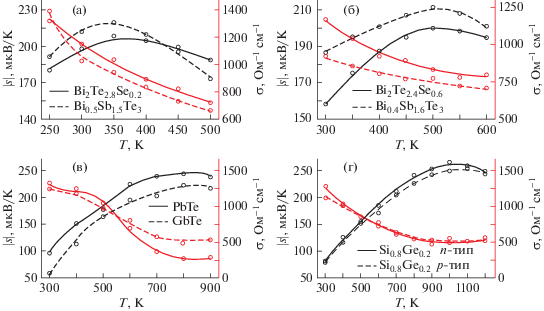
Расчет составляющих теплопроводности проводили следующим образом. Электронную составляющую рассчитывали по формуле (2), в которой число Лоренца определяли из формулы (6). Фононную теплопроводность рассчитывали по формуле (14) и экстраполировали с учетом температурной зависимости (κф ~ T–1) на весь температурный диапазон. Биполярную составляющую теплопроводности рассчитывали по формуле (20).
Экспериментальные данные по теплопроводности (κобщ) и результаты расчета ее составляющих для низкотемпературных материалов Bi2Te2.8Se0.2 и Bi0.5Sb1.5Те3 представлены на рис. 2.
Рис. 2.
Температурные зависимости теплопроводности и ее составляющих для Bi2Te2.8Se0.2 (а), Bi0.5Sb1.5Те3 (б).
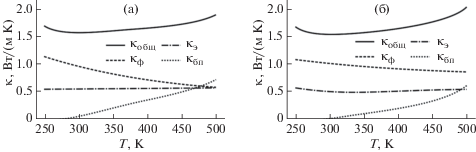
С ростом температуры теплопроводность падает с минимумом в области температур 290–320 К для Bi2Te2.8Se0.2 и 300–320 К для Bi0.5Sb1.5Те3 (рис. 2). Это определяется падением κф при незначительном изменении κэ и при отсутствии биполярного теплопереноса. Дальнейший рост теплопроводности определяется биполярным теплопереносом, появляющимся у ТЭМ n- и p-типа при температурах 300 и 310 К соответственно. После чего начинается значительный рост составляющей, которая достигает у Bi2Te2.8Se0.2 40% и у Bi0.5Sb1.5Те3 30% от общей теплопроводности в конце интервала рабочих температур. Электронная составляющая изменяется не существенно, с тенденцией на увеличение с ростом температуры, и вносит значительный вклад в теплоперенос во всем интервале температур (~30%).
Характер механизма теплопереноса и рост теплопроводности при увеличении температуры за счет κбп определяются увеличением вклада неосновных носителей заряда, что можно наблюдать на температурных зависимостях термоэдс и электропроводности (рис. 1а).
Полученные экспериментальные значения теплопроводности для рассмотренных ТЭМ согласуются с данными [47–49]. Данные [50, 51] по κбп несколько превосходят значения, полученные в настоящей работе. Результаты расчета κэ [52] коррелируют с полученными здесь данными.
Экспериментальные данные по теплопроводности (κобщ) и результаты расчета ее составляющих для среднетемпературных материалов Bi2Te2.4Se0.6 и Bi0.4Sb1.6Te3 в интервале 300–600 К представлены на рис. 3.
Рис. 3.
Температурные зависимости теплопроводности и ее составляющих для Bi2Te2.4Se0.6 (а), Bi0.4Sb1.6Te3 (б).
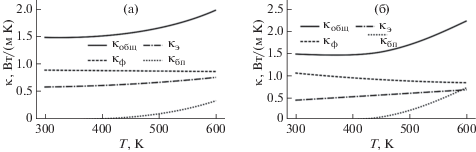
Для Bi2Te2.4Se0.6 теплопроводность от 300 до 450 К практически не изменяется (рис. 3а). Это связано с тем, что падение κф компенсируется ростом κэ. При дальнейшем увеличении температуры рост теплопроводности определяется электронным и биполярным механизмами теплопереноса. От 450 до 600 К теплопроводность увеличивается на 30%.
Незначительное снижение теплопроводности с минимумом при 380 К для Bi0.4Sb1.6Te3 определяется падением κф (рис. 3б). Однако после 450 К наблюдается резкое ее увеличение, что связано с ростом κэ и в большей степени κбп. К концу интервала рабочих температур (600 К) теплопроводность увеличивается в 1.5 раза.
Основным фактором, влияющим на характер изменения теплопроводности с ростом температуры у рассмотренных ТЭМ, также является рост парциального вклада в процесс электропереноса неосновных носителей заряда. Это подтверждается температурными изменениями термоэдс и электропроводности (рис. 1б). Что, соответственно, приводит к снижению Z ТЭМ и определяет максимальные температуры их использования.
Близкие значения общей теплопроводности для ТЭМ p-типа проводимости, изготовленных экструзией, получены в [40, 48, 53, 54].
Результаты измерения теплопроводности (κобщ) и расчета ее составляющих для ТЭМ на основе PbTe и GeTe представлены на рис. 4.
Резкое снижение теплопроводности с минимумом при 850 К у PbTe (рис. 4) определяется падением κф, которая уменьшается к этой температуре более чем в 3 раза. Электронная составляющая, вклад которой в теплоперенос не превышает 25%, также снижается в 2 раза. Затем κэ стабилизируется при 800 К с тенденцией на увеличение. В конце рабочего интервала температур наблюдается некоторое увеличение теплопроводности, определяемое κэ и κбп. Близкие значения общей теплопроводности для PbTe представлены в [55–57].
Теплопроводность GeTe с ростом температуры также снижается с минимумом при 750 К, но значительно меньше, чем для PbTe (на 30%). Характер изменения теплопроводности в качественном и количественном отношении согласуется с поведением фононной и электронной составляющих. Необходимо отметить значительный удельный вес κэ, которая при некоторых температурах достигает 40%. В области температур выше 780 К наблюдается увеличение теплопроводности, определяемое ростом κэ и κбп, что также связано с увеличением парциального вклада неосновных носителей. Это подтверждается данными по электропроводности и термоэдс (рис. 1в) при этих температурах. Начинаются рост электропроводности и падение термоэдс, вызванные неосновными носителями. Значения общей теплопроводности для GeTe коррелируют с данными [58–61].
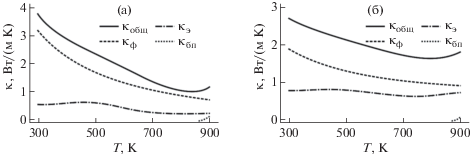
Экспериментальные данные по теплопроводности (κобщ) и расчета ее составляющих для ТЭМ на основе Si0.8Ge0.2 представлены на рис. 5. Как и следовало ожидать, характер температурных изменений и численные значения общей теплопроводности и ее составляющих у Si0.8Ge0.2n- и p-типа проводимости практически одинаковые. Различаются на уровне погрешностей определения этих параметров. Значение теплопроводности, определяемое в основном κф, с ростом температуры изменяется незначительно. Снижается на 13% с минимумом в области 1000 К. Тенденция к увеличению теплопроводности после этой температуры определяется ростом κэ, так как биполярный теплоперенос в области рассматриваемых температур практически не проявляется. Близкие значения общей теплопроводности для SiGe представлены [62–64].
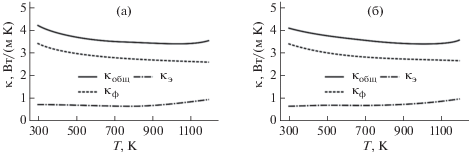
Рис. 5.
Температурные зависимости теплопроводности и ее составляющих для Si0.8Ge0.2 (1.7 мас. % P) (а), Si0.8Ge0.2 (0.5 мас. % B) (б).
Отметим, что экспериментальные данные по теплопроводности наноструктурированных материалов на основе PbTe, GeTe и SiGe при аналогичной температурной зависимости имеют значения на 5–8% ниже по отношению к теплопроводностям ТЭМ с обычной структурой.
Полученные результаты позволяют оценить механизмы теплопереноса в ТЭМ, которые являются основными, с некоторыми изменениями состава, для производства термоэлементов Пельтье и Зеебека. В настоящее время это является актуальным, так как основные попытки увеличения термоэлектрической добротности ТЭМ связаны со снижением их теплопроводности.
ЗАКЛЮЧЕНИЕ
Проведен анализ методов расчета составляющих теплопроводности и дана оценка достоверности результатов, полученных с помощью этих методов. Установлено, что для определения температурных зависимостей электронной и биполярной составляющих теплопроводности необходимы данные по электропроводности и термоэдс в исследуемом интервале температур. Это, как правило, не вызывает затруднений, поскольку при разработке и получении ТЭМ необходимым условием является исследование термоэлектрических параметров, определяющих термоэлектрическую добротность ТЭМ.
Механизмы теплопереноса определены в интервале температур от 250 до 1200 К для основных ТЭМ, используемых для изготовления термоэлементов Пельтье и Зеебека. Исследованы твердые растворы на основе халькогенидов: Bi, Sb, Pb, Ge, а также SiGe, полученные различными методами направленной кристаллизации.
С использованием полученных экспериментальных результатов по температурным зависимостям термоэлектрических параметров проведен расчет основных составляющих теплопроводности ТЭМ: фононной, электронной и биполярной. Установлена взаимосвязь механизмов теплопереноса с температурными зависимостями электропроводности и термоэдс. Для всех исследованных ТЭМ снижение теплопроводности с ростом температуры определяется фононной составляющей. Теплопроводность, достигая минимума с повышением температуры, увеличивается, как правило, в конце интервала рабочих температур. Рост теплопроводности ТЭМ в значительной степени определяется биполярным теплопереносом. Однако имеет место и некоторое повышение κэ с ростом температуры. Эти явления связаны с увеличением вклада в процессы тепло- и электропереноса неосновных носителей заряда. Повышение парциального вклада в процессы переноса неосновных носителей заряда можно наблюдать на температурных зависимостях термоэдс и электропроводности ТЭМ. Вклад неосновных носителей повышает теплопроводность и снижает термоэдс при некотором росте электропроводности, что снижает термоэлектрическую добротность ТЭМ. Это явление в основном определяет максимальные рабочие температуры ТЭМ.
Работа выполнена при поддержке Российского научного фонда (проект № 20-19-00494).
Список литературы
He R., Schierning G., Nielsch K. // Adv. Mater. Technol. 2018. V. 3. P. 1700256. https://doi.org/10.1002/admt.201700256
Dmitriev A.V., Zvyagin I.P. // Physics-Uspekhi. 2010. V. 53. P. 789. https://doi.org/10.3367/UFNe.0180.201008b.0821
He W., Zhang G., Zhang X. et al. // Appl. Energy. 2015. V. 143. P. 1. https://doi.org/10.1016/j.apenergy.2014.12.075
Sherchenkov A.A., Shtern Yu.I., Mironov R.E. et al. // Nanotechnologies in Russia. 2015. V. 10. № 11–12. P. 827. https://doi.org/10.1134/S1995078015060117
Shi X., Chen L., Uher C. // Int. Mater. Rev. 2016. V. 61. P. 379. https://doi.org/10.1080/09506608.2016.1183075
Tan G., Zhao L.-D., Kanatzidis M.G. // Chem. Rev. 2016. V. 116. P. 12123. https://doi.org/10.1021/acs.chemrev.6b00255
Aswal D.K., Basu R., Singh A. // Energy Convers. Manag. 2016. V. 114. P. 50. https://doi.org/10.1016/j.enconman.2016.01.065
Zhu T., Liu Y., Fu C. et al. // Adv. Mater. 2017. V. 29. P. 1605884. https://doi.org/10.1002/adma.201605884
Zhou Y., Zhao L.-D. // Adv. Mater. 2017. V. 29. P. 1702676. https://doi.org/10.1002/adma.201702676
Hicks L.D., Dresselhaus M.S. // Phys. Rev. B. 1993. V. 47. № 19. P. 12727. https://doi.org/10.1103/PhysRevB.47.12727
Hicks L.D., Harman T.C. // Phys. Rev. B: Condens. Matter Mater. Phys. 1996. V. 53. P. R10493. https://doi.org/10.1103/PhysRevB.53.R10493
Harman T.C., Walsh M.P., LaForge B.E., Turner G.W. // J. Electron. Mater. 2005. V. 34. P. L19. https://doi.org/10.1007/s11664-005-0083-8
Harman T.C., Taylor P.J., Walsh M.P., LaForge B.E. // Science. 2002. V. 297. P. 2229. https://doi.org/10.1126/science.1072886
Rabin O., Lin Y.-M., Dresselhaus M.S. // Appl. Phys. Lett. 2001. V. 79. P. 81. https://doi.org/10.1063/1.1379365
Hsu K.F., Loo S., Guo F. et al. // Science. 2004. V. 303. P. 818. https://doi.org/10.1126/science.1092963
Bux S.K., Blair R.G., Gogna P.K. et al. // Adv. Funct. Mater. 2009. V. 19. P. 2445. https://doi.org/10.1002/adfm.200900250
Bux S.K., Fleurial J.-P., Kaner R.B. // Chem. Commun. 2010. V. 46. P. 8311. https://doi.org/10.1039/c0cc02627a
Zhu G.H., Lee H., Lan Y.C. et al. // Phys. Rev. Lett. 2009. V. 102. P. 196803. https://doi.org/10.1103/PhysRevLett.102.196803
Lan Y., Minnich A.J., Chen G., Ren Z. // Adv. Funct. Mater. 2010. V. 20. P. 357. https://doi.org/10.1002/adfm.200901512
Wang X.W., Lee H., Lan Y.C. et al. // Appl. Phys. Lett. 2008. V. 93. P. 193121. https://doi.org/10.1063/1.3027060
Joshi G., Lee H., Lan Y. et al. // Nano Lett. 2008. V. 8. P. 4670. https://doi.org/10.1021/nl8026795
Sherchenkov A.A., Shtern Y.I., Shtern M.Y., Rogachev M.S. // Nanotechnologies in Russia. 2016. V. 11. P. 387. https://doi.org/10.1134/S1995078016040157
Булат Л.П., Освенский В.Б., Пшенай-Северин Д.А. // ФТТ. 2013. Т. 55. № 12. С. 2323.
Shtern M.Yu., Rogachev M.S., Sherchenkov A.A., Shtern Yu.I. // Materials Today: Proceedings. 2020. V. 20. P. 295. https://doi.org/10.1016/j.matpr.2019.10.066
Rowe D.M., Bhandari C.M. Modern thermoelectric. London: Holt, Rinehart and Winston, 1983. 157 p.
Nolas G.S., Sharp J., Goldsmid J. Thermoelectrics: Basic Principles and New Materials Developments. Berlin; Heidelberg: Springer-Verlag, 2001. 293 p. https://doi.org/10.1007/978-3-662-04569-5
Zhao L.D., Wu H.J., Hao S.Q. et al. // Energy Environ. Sci. 2013. V. 6. P. 3346. https://doi.org/10.1039/C3EE42187B
Смирнов И.А., Тамарченко В.И. Электронная теплопроводность в металлах и полупроводниках. Л.: Наука, 1977. 151 с.
Фистуль В.И. Сильно легированные полупроводники. М.: Наука, 1967. 416 с.
Kim H.-S., Gibbs Z.M., Tang Y. et al. // APL Mater. 2015. V. 3. P. 041506. https://doi.org/10.1063/1.4908244
Ravich Yu.I., Efimova B.A., Smirnov I.A. Semiconducting lead chalcogenides. Springer, 1970. 387 p. https://doi.org/10.1007/978-1-4684-8607-0
Аскеров Б.М. Электронные явления переноса в полупроводниках. М.: Наука, 1985. 320 с.
Аскеров Б.М. Кинетические эффекты в полупроводниках. М.: Наука, 1970. 303 с.
Tritt T.M. Thermal Conductivity Theory, Properties, and Applications. Springer US, 2004. 290 p. https://doi.org/10.1007/b136496
Slack G.A., Tsoukala V.G. // J. Appl. Phys. 1994. V. 76. P. 1665. https://doi.org/10.1063/1.357750
Goldsmid H.J. Introduction to Thermoelectricity. Springer, 2016. 291 p. https://doi.org/10.1007/978-3-662-49256-7
Kitagawaa H., Wakatsukia M., Nagaokaa H. et al. // J. Phys. Chem. Solids. 2005. V. 66. P. 1635. https://doi.org/10.1016/j.jpcs.2005.05.077
Liu W.-S., Zhang B.-P., Li J.-F. et al. // J. Appl. Phys. 2007. V. 102. P. 103717. https://doi.org/10.1063/1.2815671
Zhao L., Xiao Y., Wu H. et al. // Energy Environ. Sci. 2018. V. 11. P. 2486. https://doi.org/10.1039/C8EE01151F
Hu L.-P., Zhu T.-J., Wang Y.-G. et al. // NPG Asia Mater. 2014. V. 6. P. 86. https://doi.org/10.1038/am.2013.86
Yelgel O.C., Srivastava G.P. // Phys. Rev. B. 2012. V. 85. P. 125207. https://doi.org/10.1103/PhysRevB.85.125207
Wang H., Bahk J.-H., Kang C. et al. // J. Mater. Chem. A. 2013. V. 1. P. 11269. https://doi.org/10.1039/C3TA11825H
Pei Y., May A.F., Snyder G.J. // Adv. Energy Mater. 2011. V. 1. P. 291. https://doi.org/10.1002/aenm.201000072
Bahk J.-H., Shakouri A. // Appl. Phys. Lett. 2014. V. 105. P. 052106. https://doi.org/10.1063/1.4892653
Shtern Yu.I. // Inorgan. Mater. 2009. V. 45. № 14. P. 1631. https://doi.org/10.1134/S0020168509140234
Shtern M.Yu. // Proceedings of the 2019 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering / IEEE, 2019. P. 1920. https://doi.org/10.1109/EIConRus.2019.8657108
Ivanova L.D., Petrova L.I., Granatkina Yu.V. et al. // Inorgan. Mater. 2009. V. 45. № 2. P. 123. https://doi.org/10.1134/S0020168509020034
Ivanova L.D., Petrova L.I., Granatkina Yu.V. et al. // Inorgan. Mater. 2011. V. 47. № 5. P. 459. https://doi.org/10.1134/S0020168511050104
Korzhuev M.A., Ivanova L.D. // Inorgan. Mater. 2006. V. 42. № 7. P. 712. https://doi.org/10.1134/S0020168506070041
Zheng Y., Tan G., Luo Y. et al. // Materials. 2017. V. 10. P. 617. https://doi.org/10.3390/ma10060617
Zheng Y., Xie H., Shu S. et al. // J. Electron. Mater. 2014. V. 43. № 6. P. 2017. https://doi.org/10.1007/s11664-013-2938-8
Zheng Y., Zhang Q., Su X. et al. // Adv. Energy Mater. 2015. V. 5. P. 1401391. https://doi.org/10.1002/aenm.201401391
Wang X.-y., Yu J., Zhao R.-f. // J. Phys. Chem. Solids. 2019. V. 124. P. 281. https://doi.org/10.1016/j.jpcs.2018.09.003
Ivanova L.D., Petrova L.I., Granatkina Yu.V. et al. // Inorgan. Mater. 2008. V. 44. № 7. P. 687. https://doi.org/10.1134/S0020168508070030
Lee M.H., Park J.H., Park S.-D. et al. // J. Alloys Compd. V. 786. P. 515. https://doi.org/10.1016/j.jallcom.2019.01.387
Wang D., Qin Y., Wang S. et al. // Ann. Phys. 2019. P. 1900421. https://doi.org/10.1002/andp.201900421
Girard S.N., He J., Zhou X. et al. // J. Am. Chem. Soc. 2011. V. 133. P. 16588. https://doi.org/10.1021/ja206380h
Gelbstein Y., Davidow J., Girard S.N. et al. // Adv. Energy Mater. 2013. V. 3. P. 815. https://doi.org/10.1002/aenm.201200970
Qiu Y., Jin Y., Wang D. et al. // J. Mater. Chem. A. 2019. V. 7. P. 26393. https://doi.org/10.1039/c9ta10963c
Jin Y., Xiao Y., Wang D. et al. // ACS Appl. Energy Mater. 2019. V. 2. P. 7594. https://doi.org/10.1021/acsaem.9b01585
Perumal S., Samanta M., Ghosh T. et al. // Joule. 2019. V. 3. P. 2565. https://doi.org/10.1016/j.joule.2019.08.017
Basu R., Bhattacharya S., Bhatt R. et al. // J. Mater. Chem. A. 2014. V. 2. P. 6922. https://doi.org/10.1039/C3TA14259K
Li Y., Han J., Xiang Q. et al. // J. Mater. Sci.: Mater. Electron. 2019. V. 30. P. 9163. https://doi.org/10.1007/s10854-019-01245-9
Claudio T., Stein N., Petermann N. et al. // Phys. Status Solidi. A. 2016. V. 213. № 3. P. 515. https://doi.org/10.1002/pssa.201532500
Дополнительные материалы отсутствуют.
Инструменты
Российские нанотехнологии