1. На главную
  2. Электронные версии
  3. Неорганические материалы
  4. T. 55, № 1, 2019

Неорганические материалы, 2019, T. 55, № 1, стр. 16-20

Влияние исходного состава на переход жидкость–твердое тело в наночастицах сплава Cr–W
А. В. Шишулин, В. Б. Федосеев

А. В. Шишулин 1, *, В. Б. Федосеев 1

1 Институт металлорганической химии им. Г.А. Разуваева Российской академии наук
603137 Нижний, Новгород, ул. Тропинина, 49, Россия

* E-mail: Chichouline_Alex@live.ru

Поступила в редакцию 04.06.2018

Полный текст (PDF)

Аннотация

Фазовые превращения в системах нанометрового размера определяются множеством различных факторов. В работе методами равновесной химической термодинамики показано, что к числу таких факторов относится исходный состав наносистемы, и смоделирована зависимость от исходного состава фазовой диаграммы в двухфазной области между температурами ликвидуса и солидуса на примере наночастиц Cr–W. Показано, что равновесные составы жидкой и твердой фаз и температуры фазовых переходов зависят от исходного состава наночастицы. Температура ликвидуса наночастицы любого состава ниже температуры ликвидуса макросистемы, температура солидуса частицы нанометрового размера может быть в зависимости от состава как ниже, так и выше температуры солидуса макросистемы. При переходе в область нанометровых размеров температурный интервал области гетерогенности сужается.

Ключевые слова: фазовые превращения, наночастицы, размерный эффект, ликвидус, солидус

ВВЕДЕНИЕ

Стремительное развитие технологии наноматериалов и расширение области их применения требуют систематических исследований физических и химических свойств наночастиц, а также фазовых превращений в системах нанометрового размера. Для таких систем характерны иные температуры фазовых переходов [1, 2], иные положения характеристических точек, форма и положение характеристических линий на фазовых диаграммах по сравнению с диаграммами для систем макроскопического размера [3–17], а также иной набор стабильных и метастабильных фаз [14–17]. Величина и характер этих изменений зависят от объема системы [3–11, 14], формы всех межфазных границ [11, 12, 15, 16] и ряда других параметров [17].

Подобные эффекты в ряде систем наблюдались экспериментально [18, 19] и были смоделированы методами равновесной химической термодинамики, где состоянию фазового равновесия соответствует минимум функции Гиббса с учетом энергетического вклада всех межфазных границ [3–17]. Однако систематизация всех полученных результатов и переход от частных выводов для отдельных наносистем к общим закономерностям на данный момент затруднителен в силу малого перечня рассмотренных систем (включающего преимущественно бинарные металлические сплавы), ограниченного числа рассмотренных геометрических конфигураций и недостатков использованных термодинамических моделей. Существенное число термодинамических оценок получено для наночастиц размером 1–10 нм [3–6, 8, 10–12], применимость термодинамического подхода к которым требует отдельного обсуждения [20]. В большинстве работ не рассматривается возможность образования в наносистеме устойчивых метастабильных фаз. Дополнительный анализ экстремумов функции Гиббса для наночастиц бинарных сплавов с конфигурацией core–shell [14–17] позволил выявить состав, термодинамическую устойчивость и области существования стабильного и метастабильного гетерогенных состояний, фазовые диаграммы для которых различны. Учет формы наночастиц в [10–12] ограничивается перебором простых геометрических конфигураций, предложены также более общие подходы, использующие для задания формы фрактальную размерность [15] или параметр, численно равный отношению площади поверхности системы данной формы к площади поверхности сферы равного объема [15, 16]. Однако данные методы, позволяющие описывать широкий спектр реальных геометрических структур со сложной морфологией [21, 22], не являются единственными [23].

В настоящей работе рассматривается еще один характерный для систем малого объема эффект, связанный с зависимостью фазовой диаграммы наносистемы от ее исходного состава [24]. Диаграммы плавкости построены для наночастиц системы Cr–W, ранее рассматривавшейся нами в области расслаивания твердых растворов [14].

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

В качестве объекта моделирования рассматриваются наночастицы бинарного сплава разного состава при температуре выше солидуса. Предполагается, что при фазовом равновесии в такой частице образуется единичное твердое сферическое включение (core-фаза), окруженное шаровым слоем расплава (shell-фазой).

В закрытой двухкомпонентной системе условия сохранения вещества при фазовом превращении имеют следующий вид:

(1)
$\begin{gathered} {{n}_{2}} = xn,\,\,\,{{n}_{1}} = n - {{n}_{2}},\,\,\,x = \frac{{{{n}_{2}}}}{{{{n}_{1}} + {{n}_{2}}}}, \\ {{x}_{f}} = \frac{{{{n}_{{2f}}}}}{{{{n}_{{1f}}} + {{n}_{{2f}}}}},\,\,\,f = c,s,\,\,\,i = 1,2, \\ \end{gathered} $
где n – суммарное число молей, ni – число молей компонента i, x – мольная доля первого компонента в системе, xf – мольная доля первого компонента в фазе f, nif – число молей компонента i в фазе f, индексами c и s обозначены твердая core- и жидкая shell-фазы соответственно.

Условия сохранения вещества (1) позволяют вычислить объем системы V и сосуществующих фаз Vf.

(2)
$V = {{n}_{1}}{{V}_{1}} + {{n}_{2}}{{V}_{2}},\,\,\,{{V}_{f}} = {{n}_{{1f}}}{{V}_{1}} + {{n}_{{2f}}}{{V}_{2}},$
где Vi – мольные объемы компонентов.

Площади поверхности системы As и межфазной поверхности Ac вычисляются из (2) как

(3)
$\begin{gathered} {{A}_{s}} = 4\pi r_{s}^{2},\,\,\,\,{{r}_{s}} = \mathop {\left( {\frac{3}{{4\pi }}V} \right)}\nolimits^{\frac{1}{3}} ,\,\,\,\,{{A}_{c}} = 4\pi r_{c}^{2}, \\ {{r}_{c}} = \mathop {\left( {\frac{3}{{4\pi }}{{V}_{c}}} \right)}\nolimits^{\frac{1}{3}} , \\ \end{gathered} $
где rs и rc – радиусы core- и shell-фаз соответственно.

Критерием равновесного фазового состава системы является минимум функции Гиббса, записанной с учетом энергии всех границ раздела. Для рассматриваемой системы она имеет вид

(4)
$\begin{gathered} g = \left( {{{n}_{{1c}}} + {{n}_{{2c}}}} \right){{G}_{s}}\left( {{{x}_{c}},T} \right) + \\ + \,\,\left( {{{n}_{{1s}}} + {{n}_{{2s}}}} \right){{G}_{l}}\left( {{{x}_{s}},T} \right) + {{g}_{{surf}}}, \\ \end{gathered} $
где xc и xs – мольная доля компонента 2 в твердой core- и жидкой shell-фазах, ${{G}_{s}}\left( {x,T} \right),$ ${{G}_{l}}\left( {x,T} \right)$ – функция Гиббса твердого и жидкого растворов соответственно с концентрацией x при температуре T, ${{g}_{{surf}}}$ – поверхностная энергия, которая содержит вклады внешней и внутренней межфазных границ:
(5)
${{g}_{{surf}}} = {{\sigma }_{s}}{{A}_{s}} + {{\sigma }_{{cs}}}{{A}_{c}},$
где ${{\sigma }_{s}},$ ${{\sigma }_{{cs}}}$ – поверхностная энергия твердого раствора на внешней (shell-) границе расплав–внешняя среда и внутренней (core–shell) границе твердый раствор–расплав.

Необходимо заметить, что в системе с твердой фазой и расплавом, сосуществующими в равновесии, конфигурация твердая core-жидкая shell не является единственно возможной. Обзор возможных сферически симметричных конфигураций с сосуществующими жидкой и твердой фазами приведен в [25]. Впрочем, сферическая геометрия рассматриваемой системы также является приближением [16, 17].

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

В качестве объекта моделирования выбраны наночастицы сплава Cr–W, рассматривавшегося нами ранее в области расслаивания твердых растворов [14], содержащие разную долю Cr. Функции Гиббса данной системы имеют вид [26]

(6)
$\begin{gathered} {{G}_{l}}\left( {x,T} \right) = x\left( {{{{{24339.995 - 11.420225} \mathord{\left/ {\vphantom {{24339.995 - 11.420225} {T + 2.37615 \times {{{10}}^{{ - 24}}}}}} \right. \kern-0em} {T + 2.37615 \times {{{10}}^{{ - 24}}}}}} \mathord{\left/ {\vphantom {{{{24339.995 - 11.420225} \mathord{\left/ {\vphantom {{24339.995 - 11.420225} {T + 2.37615 \times {{{10}}^{{ - 24}}}}}} \right. \kern-0em} {T + 2.37615 \times {{{10}}^{{ - 24}}}}}} {{{T}^{7}}}}} \right. \kern-0em} {{{T}^{7}}}}} \right) + \\ + \,\,\left( {1 - x} \right)\left( {{{{{52160.584 - 14.10999} \mathord{\left/ {\vphantom {{52160.584 - 14.10999} {T + 2.713468 \times {{{10}}^{{ - 24}}}}}} \right. \kern-0em} {T + 2.713468 \times {{{10}}^{{ - 24}}}}}} \mathord{\left/ {\vphantom {{{{52160.584 - 14.10999} \mathord{\left/ {\vphantom {{52160.584 - 14.10999} {T + 2.713468 \times {{{10}}^{{ - 24}}}}}} \right. \kern-0em} {T + 2.713468 \times {{{10}}^{{ - 24}}}}}} {{{T}^{7}}}}} \right. \kern-0em} {{{T}^{7}}}}} \right) + \\ + \,\,RT\left( {xlnx + \left( {1 - x} \right)ln\left( {1 - x} \right)} \right) + x\left( {1 - x} \right)\left( {{{ - 7985.8 + 10.066} \mathord{\left/ {\vphantom {{ - 7985.8 + 10.066} {T - 18048.3\left( {1 - x} \right)}}} \right. \kern-0em} {T - 18048.3\left( {1 - x} \right)}}} \right), \\ \end{gathered} $
$\begin{gathered} {{G}_{s}}(x,T) = x(1 - x)(30202 + 2635.5x) + \\ + \,\,RT((1 - x)\ln (1 - x) + x\ln (x)), \\ \end{gathered} $
где x – мольная доля Cr, R – универсальная газовая постоянная.

Одной из проблем подобных вычислений является надежность теплофизических данных о поверхностной энергии чистых веществ в твердом и жидком состояниях и межфазной границы твердый раствор–расплав. Для вычисления σ(x) использована линейная аппроксимация $\sigma (x) = {{\sigma }_{{{\text{Cr}}}}}x + {{\sigma }_{{\text{W}}}}(1 - x).$ Поверхностные энергии чистых компонентов на границе раздела твердый раствор–расплав приведены в [27] и равны ${{\sigma }_{{\text{W}}}}$ = 700.57 мДж/м2, ${{\sigma }_{{{\text{Cr}}}}}$ = 428.58 мДж/м2. Поверхностные энергии расплавов чистых компонентов получены из уравнения Жирифалко и Гуда [27] по данным о поверхностных энергиях чистых компонентов в твердом состоянии вблизи температуры плавления [28] и составляют ${{\sigma }_{{\text{W}}}}$ = = 1799.43 мДж/м2, ${{\sigma }_{{{\text{Cr}}}}}$ = 1213.42 мДж/м2. Мольные объемы компонентов равны ${{V}_{{\text{W}}}}$ = 9.53 см3/моль, ${{V}_{{{\text{Cr}}}}}$ = 7.23 см3/моль [29]. Скачок объема при плавлении, для большинства металлов равный 1–5% [30–32], в первом приближении не учитывался.

Зависимость равновесного фазового состава системы нанометрового размера от исходного состава проиллюстрирована на рис. 1 серией фрагментов фазовых диаграмм системы Cr–W для частиц диаметром 40 нм, содержащих 30 (а), 50 (б) и 70 ат. % Cr (в). В системе макроскопического размера любому исходному составу соответствуют одни и те же фазовая диаграмма и составы жидкой и твердой фаз при заданной температуре, исходный состав определяет лишь объемные доли жидкой и твердой фаз, вычисляемые по правилу рычага.

Рис. 1.

Влияние размера и исходного состава частиц на положение ликвидуса и солидуса на фазовой диаграмме системы W–Cr; пунктиром показана диаграмма для системы макроскопического размера, сплошной линией – для наночастицы диаметром 40 нм; точкой на оси абсцисс показан исходный состав системы: a – 30 , б – 50, в – 70 ат. % Cr.

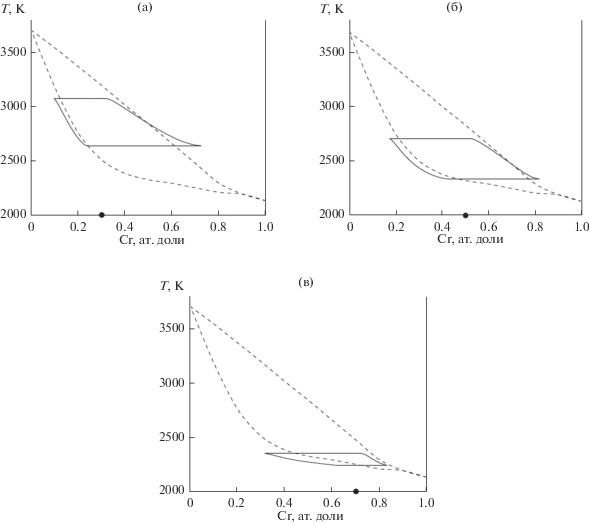
Как видно из рис. 1, фазовые диаграммы для частиц нанометрового размера разного исходного состава не совпадают. В частности, частица диаметром 40 нм, содержащая 30 ат. % Cr, находится полностью в твердом состоянии при температуре ниже ~2640 К, полностью в жидком – при температуре выше ~3070 K. Между данными точками находится область сосуществования твердой и жидкой фаз, составы которых отображены сплошными кривыми на рис. 1a. Точка солидуса, соответствующая данному исходному составу наносистемы, лежит выше аналогичной точки для макросистемы на ~140 К, а точка ликвидуса – ниже на ~120 К. Наночастицы того же диаметра эквимолярного состава находятся в твердом состоянии при температурах ниже ~2340 K, а в жидком – при температурах выше ~2710 K (рис. 1б). Точка солидуса частицы диаметром 40 нм с 50 ат. % Cr лежит выше макроскопического значения на ~20 K, а точка ликвидуса – ниже на ~120 К. Наконец, точка солидуса наночастицы диаметром 40 нм с 70 ат. % Cr соответствует температуре ~2240 К, что ниже значения для макросистемы на ~10 K, а точка ликвидуса – температуре ~2350 K, аналогичная точка в макросистеме лежит выше также на ~120 K.

Сужение температурных границ области гетерогенности связано со стремлением наносистемы понизить поверхностную энергию путем перехода в однофазное состояние без образования внутренней границы раздела. Еще одним эффектом, отображенным на рис. 1, является изменение равновесных составов твердой и жидкой фаз. Для всех рассмотренных исходных составов в области гетерогенности твердая фаза наночастицы содержит бóльшую долю W, чем твердая фаза в системе макроскопического размера. Для наночастицы с 30 ат. % Cr жидкая фаза вблизи температуры солидуса содержит больше Cr, чем макросистема, а вблизи температуры ликвидуса – меньшe. Для наночастицы эквимолярного состава тенденции аналогичны, но кривые, отображающие состав жидкой фазы в системах нанометрового и макроскопического размеров, пересекаются при более низкой температуре. Для наночастицы с 70 ат. % Cr жидкая фаза во всей области гетерогенности содержит меньше Cr, чем макросистема.

Подобные закономерности также можно объяснить понижением системой собственной поверхностной энергии, что в гетерогенном состоянии возможно посредством реализации двух механизмов: 1) путем межфазного перераспределения компонентов, сопровождающегося увеличением содержания в расплаве компонента с меньшей поверхностной энергией (Cr), а в твердой фазе – с большей (W) (т.к. поверхностные энергии компонентов на границе расплав–твердое тело ниже, чем на внешней границе); 2) путем увеличения объемной доли расплава, сопровождающегося уменьшением площади внутренней границы раздела. В наночастицах, содержащих 30 и 50 ат. % Cr, при температурах вблизи точки солидуса основным является механизм 1, при более высоких температурах, близких к температуре ликвидуса, – механизм 2. В наночастице с 70 ат. % Cr механизм 2 является основным во всем диапазоне температур области гетерогенности.

Следует отметить, что рассмотренные механизмы не противоречат полученным ранее закономерностям [10–12]. Авторы [10, 11] связывали изменение равновесной концентрации компонентов в приповерхностном слое наночастицы с реализацией одного из двух сформулированных ими “правил сегрегации” (“segregation rules”): в области нанометровых размеров приповерхностный слой преимущественно обогащается компонентом либо с бóльшей температурой плавления, либо с меньшей поверхностной энергией. Данные закономерности, подтвержденные экспериментально, на наш взгляд, могут быть более корректны, если принять во внимание, что все рассмотренные в [11] металлы, имеющие большую температуру плавления, имеют и больший мольный объем. Рассмотренные нами механизмы понижения поверхностной энергии могут реализовываться одновременно, поэтому для разных систем зависимости фазовых равновесий от размера, формы и т.д. могут существенно различаться [10–12, 16, 17].

Полученные результаты представляют интерес при моделировании фазовых превращений в многокомпонентных системах при высоких температурах, моделировании и оптимизации процессов получения наноматериалов, происходящих в присутствии жидкой фазы, например, спрей-пиролиза [33] или селективного лазерного сплавления [34].

ЗАКЛЮЧЕНИЕ

Методами равновесной химической термодинамики выполнено моделирование фазовых равновесий в наночастицах Cr–W различного состава в двухфазной области между температурами ликвидуса и солидуса. Показано, что изменение исходного состава наночастицы сопровождается существенной деформацией диаграммы плавкости: изменением равновесных составов сосуществующих твердой и жидкой фаз и сдвигом температур ликвидуса и солидуса. Для наночастиц любого состава точки ликвидуса сдвигается в область более низких температур. При этом температура солидуса наночастицы диаметром 40 нм с основным компонентом W превышает температуру солидуса для макросистемы, а для частицы с содержанием Cr выше 70 ат. % температура солидуса ниже макроскопического значения. Величина сдвига температур фазовых переходов зависит от исходного состава.

В общем случае и температуры фазовых переходов, и составы сосуществующих фаз зависят от объема системы [13, 14], ее формы [15, 16], исходного состава и некоторых других факторов [17]. Таким образом, без указания всех перечисленных характеристик оценки фазового состава наносистемы могут оказаться неточными или некорректными.

БЛАГОДАРНОСТЬ

Работа выполнена в рамках государственного задания 45.7 ИМХ РАН, а также при поддержке РФФИ (проект № 18-08-01356), РФФИ и Правительства Нижегородской области (проект № 18-43-520039).

Список литературы

  1. Андриевский Р.А., Рагуля А.В. Наноструктурные материалы. М.: Академия, 2005. 192 с.

  2. Алымов М.И., Шоршоров М.Х. Влияние размерных факторов на температуру плавления и поверхностное натяжение ультрадисперсных частиц // Металлы. 1999. № 2. С. 29–31.

  3. Park J., Lee J. Phase Diagram Reassessment of Ag–Au System Including Size Effect // CALPHAD. 2008. V. 32. № 1. P. 135–141.

  4. Sopoušek J., Vřešt’ál J., Pinkas J., Broz P., Buršík J., Styskalik A., Skoda D., Zobak A., Lee J. Cu–Ni Nanoalloy Phase Diagram – Prediction and Experiment // CALPHAD. 2014. № 45. P. 33–39.

  5. Monji F., Jabbareh M.A. Thermodynamic Model for Prediction of Binary Alloy Nanoparticle Phase Diagram Including Size-Dependent Surface Tension Effect // CALPHAD. 2017. V. 58. P. 1–5.

  6. Ivas T., Grundy A.N., Povoden-Karadeniz E., Gauckler L.J. Phase Diagram of CeO2–CoO for Nano-Sized Powders // CALPHAD. 2012. № 36. P. 57–64.

  7. Sim K., Lee J. Phase Stability of Ag–Sn Nanoparticles // J. Alloys Compd. 2014. V. 590. P. 140–146.

  8. Ghasemi M., Zanolli Z., Stankovski M., Johansson J. Size- and Shape-Dependent Phase Diagram of In–Sb Nano-Alloys // Nanoscale. 2015. V. 7. P. 17387–17396.

  9. Sopoušek J., Kryštofová A., Premović M., Zobač O., Polsterová S., Brož P., Buršík J. Au–Ni Nanoparticles: Phase Diagram Prediction, Synthesis, Characterization and Thermal Stability // CALPHAD. 2017. V. 58. P. 25–33.

  10. Guisbiers G., Mendoza-Cruz R., Bazán-Díaz L., Velázquez-Salazar J.J., Mendoza-Pérez R., Robledo-Torres J., Rodriguez-Lopez J.-L., Montejano-Carrizales J.M., Whetten R.L.,Yakamán M.J. Electrum, the Gold–Silver alloy, from the Bulk Scale to the Nanoscale: Synthesis, Properties, and Segregation Rules // ASC Nano. 2015. V. 10. № 1. P. 188–198.

  11. Guisbiers G., Mendoza-Pérez R., Bazán-Díaz L., Mendoza-Cruz R., Velázquez-Salazar J.J., Yakamán M.J. Size and Shape Effects on the Phase Diagrams of Nickel-Based Bimetallic Nanoalloys // J. Phys. Chem. 2017. V. 121. № 12. P. 6930–6939.

  12. Cui M., Lu H., Jiang H., Cao Z., Meng X. Phase Diagram of Continuous Binary Nanoalloys: Size, Shape and Segregation Effects // Sci. Rep. 2017. № 7. P. 1–10.

  13. Федосеев В.Б., Шишулин А.В., Титаева Е.К., Федосеева Е.Н. О возможности образования кристалла твердого раствора NaCl–KCl из водного раствора при нормальной температуре в системах малого объема // Физика твердого тела. 2016. Т. 58. № 10. С. 2020–2025.

  14. Шишулин А.В., Федосеев В.Б. Размерный эффект при расслаивании твердого раствора Cr–W // Неорган. материалы. 2018. Т. 54. № 6. С. 574–578.

  15. Fedoseev V.B., Potapov A.A., Shishulin A.V., Fedoseeva E.N. Size and Shape Effect on the Phase Transitions in a Small System with Fractal Interphase Boundaries // Eur. Phys. Tech. J. 2017. V. 14. № 1(27). P. 18–24.

  16. Федосеев В.Б., Шишулин А.В. Эффект формы при расслаивании твердых растворов в малом объеме на примере сплава Bi–Sb // Физика твердого тела. 2018. Т. 60. № 7. С. 1382–1388.

  17. Шишулин А.В., Федосеев В.Б., Шишулина А.В. О влиянии внешней среды на фазовые равновесия в системе малого объема на примере распада твердого раствора Bi–Sb // Бутлеровские сообщения. 2017. Т. 51. № 7. С. 31–37.

  18. Straumal B., Baretzky B., Mazilkin A., Protasova S., Myatiev A., Straumal P. Increase of Mn Solubility with Decreasing Grain Size in ZnO // J. Eur. Ceram. Soc. 2009. V. 10. № 29. P. 1963–1970.

  19. Sutter E.A., Sutter P.W. Size-Dependent Phase Diagram of Nanoscale Alloy Drops Used in Vapor−Liquid−Solid Growth of Semiconductor Nanowires // ACS Nano. 2010. V. 4. № 8. P. 4943–4947.

  20. Товбин Ю.К. Нижняя граница размеров применимости термодинамики // Журн. физ. химии. 2012. Т. 86. № 9. С. 1461–1476.

  21. Coelho D., Bekki S., Thovert J.-H. Uptake on Fractal Particles. 1. Theoretical Framework // J. Geophys. Res. 2000. V. 105. № 3. P. 3905–3916.

  22. Bose A., Schuh C.A., Tobia J.C. Tuncer N., Mykulowycz N.M., Preston A., Barbati A.C., Kernan B., Gibson M.A., Krause D., Brzezinski T. Schroers J., Fulop R., Myerberg J.S., Sowerbutts M., Chiang Y.-M., Hart A.J., Sachs E.M., Lomeli E.E., Lund A.C. Traditional and Additive Manufacturing of a New Tungsten Heavy Alloy Alternative // Int. J. Refract. Met. Hard Mater. 2018. V. 73. P. 22–28.

  23. Магомедов М.Н. О наноструктурировании и пластичности кристалла при сжатии // Журн. техн. физики. 2016. Т. 86. № 5. С. 86–91.

  24. Федосеев В.Б., Шишулин А.В. Влияние исходного состава на фазовые равновесия в системе Cr–W нанометрового размера // Сб. тез. докл. IX междунар. науч. конф. “Кинетика и механизм кристаллизации. Кристаллизация и материалы будущего”. Иваново. 2016. С. 28–29.

  25. Shirinyan A., Wilde J., Bilogorodskyy Y. Solidification Loops in the Phase Diagram of Nanoscale Alloy Particles: from a Specific Example towards a General Vision // J. Mater. Sci. 2018. V. 53. № 4. P. 2859–2879.

  26. Воронин Г.Ф., Белов Г.В. Раcчет фазовых равновесий с использованием термодинамических баз данных. М.: Изд-во МГУ, 2014. С. 19.

  27. Шебзухова М.А., Шебзухов З.А., Шебзухов А.А. Межфазное натяжение кристаллической наночастицы в жидкой материнской фазе в однокомпонентгой металлической системе // Физика твердого тела. 2012. Т. 54. № 1. С. 185–193.

  28. Keene B.J. Review of Data for the Surface Tension of Pure Metals // Int. Mater. Rev. 1993. V. 38. № 4. P. 157–192.

  29. Химическая энциклопедия. В 5 томах // Под ред. Зефирова Н.С. и др. М.: Сов. энциклопедия, 1988.

  30. Фортов В.Е. Уравнения состояния вещества: от идеального газа до кварк-глюонной плазмы. М.: Физматлит, 2013. 492 с.

  31. Зиновьев В.Е. Теплофизические свойства металлов при высоких температурах. М.: Металлургия, 1989. 383 с.

  32. Структура и свойства металлов и сплавов. Тепловые свойства металлов и сплавов / Под ред. Ларикова Л.Н., Юрченко Ю.Ф. Киев: Наук. думка, 1985. 437 с.

  33. Пенязьков О.Г., Саверченко В.И., Фисенко С.П., Ходыко Ю.А. Низкотемпературный синтез наночастиц оксидов металлов при испарительном охлаждении фемтолитровых капель водных растворов // Журн. техн. физики. 2014. Т. 84. № 8. С. 93–101.

  34. Харанжевский Е.В. Расслоение жидкости и формирование пересыщенных твердых растворов в системе Fe–Cu при высокоскоростном лазерном плавлении // Физика металлов и металловедение. 2016. Т. 117. № 9. С. 920–926.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Неорганические материалы

Архивы выпусков Информация о журнале Отправить рукопись в журнал