Неорганические материалы, 2020, T. 56, № 4, стр. 364-370
Новое понимание механизма роста нитевидных нанокристаллов пар → жидкая капля → кристалл
В. А. Небольсин 1, *, А. Ю. Воробьев 1, N. Swaikat 1
1 Воронежский государственный технический университет
394026 Воронеж, Московский пр., 14, Россия
* E-mail: vcmsao13@mail.ru
Поступила в редакцию 25.02.2019
После доработки 08.09.2019
Принята к публикации 24.10.2019
Аннотация
Рассмотрены измененные представления о механизме роста нитевидных нанокристаллов пар → жидкая капля → кристалл, которые обусловлены получением новых экспериментальных данных о смачиваемости кристаллической поверхности каплями металлов-катализаторов, предварительно насыщенных кристаллизуемым веществом.
ВВЕДЕНИЕ
Современные представления о механизме каталитического роста нитевидных нанокристаллов (ННК) по методу пар → жидкая капля → кристалл (ПЖК) основаны на воззрениях об облегчении двумерного зарождения под каплей катализатора при сильно пониженном активационном барьере (малой энергии образования двумерных зародышей), обусловленном малой величиной удельной свободной поверхностной энергии (УСПЭ) границы кристалл/жидкость (КЖ) [1–3].
Действительно, для большинства металлов (М), используемых в качестве катализаторов роста ННК, таких как Au, Ni, Pt, Cu, кристаллизуемый материал (Si, Ge, GaAs, GaP, InAs и др.) хорошо растворяется в их жидкой фазе, вследствие чего ПЖК-рост реализуется при температурах, более низких, чем температура плавления кристаллизуемого вещества [1, 3]. Поскольку переход вещества из твердой фазы в жидкую (растворение) является мощным источником снижения межфазной энергии, то на основании этого априори считается, что капля М-катализатора хорошо смачивает твердую фазу кристаллизуемого материала, а краевой угол смачиваемости кристалла каплей θ < 90° [1, 4]. Отсюда следует, что УСПЭ границы КЖ αSL также меньше УСПЭ жидкой αLV и твердой αSV фаз (αSL < αLV < αSV). И, поскольку энергия образования критических зародышей напрямую связана с αSL, а скорость роста ННК зависит от энергии зародышеобразования экспоненциально, делается вывод, что по причине малой величины αSL по ПЖК-механизму кристаллы растут с высокими скоростями [1, 3].
Однако если УСПЭ границы КЖ αSL меньше данной физической величины для границ жидкость/газ (ЖГ) αLV и кристалл/газ (КГ) αSV (αSL < αLV и αSL < αSV), то, во-первых, в процессе кристаллизации энергетически выгоднее увеличивать площадь раздела КЖ, чем формировать боковую поверхность ННК с большей энергией, а во-вторых, на основании принципа Кюри–Вульфа ($\sum\nolimits_{IJ} {{{\alpha }_{{IJ}}}} {{S}_{{IJ}}} = \min $, где αIJ и SIJ – УСПЭ и площадь отдельных частей поверхности тела I, контактирующих с фазами J при постоянном объеме фаз (V = const)) в статических условиях площадь участка поверхности капли SSL, граничащего с торцевой гранью ННК, должна быть больше площади фазовой границы ЖГ SLV. В действительности же при почти всегда наблюдаемых величинах угла контакта капли на вершине ННК β > 90°, наоборот, SSL < SLV и, следовательно, должно быть αSL > αLV, что не отвечает условию равновесия капли, хорошо смачивающей кристаллическую подложку (θ < 90°), и противоречит фундаментальным взглядам на ПЖК-механизм роста ННК.
Целью данной работы является пересмотр и корректировка существующих представлений о ПЖК-механизме роста ННК.
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
ННК Si, Ge, GaAs и др. выращивали методами молекулярно-лучевой эпитаксии и химического парофазного осаждения [1–3] при 600–800 и 1270–1370 K c участием частиц Au, Ni, Pt и Cu в качестве катализатора, диаметр которых составлял 30–200 нм. Изучалась смачиваемость Si-подложки каплями M-Si при температуре исследования. Величину краевого угла θ находили по ПЭМ-изображениям капель М-катализатора, предварительно насыщенных кристаллизуемым веществом и помещенных на Si-подложку. Угол θ измерялся между поверхностью подложки и касательной к кривой меридионального сечения капли. Сплавы М–Si приготовлялись длительным выдерживанием капель расплава в контакте с Si-подложкой в атмосфере Н2 и быстрой их закалкой. Содержание Si в полученных сплавах, по рентгеновскому микроанализу, составило ~38.4 ат. % в Au, ~58.1 ат. % в Ni, ~36.1 ат. % в Cu и ~59.0 ат. % в Pt. Таким образом, содержание Si в Ni и Pt соответствовало насыщению, а расплавы Au–Si и Cu–Si были несколько недонасыщены. Затем твердые растворы М–Si помещались на Si-подложку, производился нагрев до 1273–1373 K и длительное выдерживание капель на подложке. Частицы на Si-подложке выдерживали в печи в потоке очищенного водорода при T = 1173–1373 K для Au, Cu и при 1773 K для Ni, Pt в течение 10 мин, а затем резко охлаждали до комнатной температуры.
Закристаллизовавшиеся частицы исследовали методами РЭМ и ПЭМ. Погрешность измерения краевого угла, обусловленная изменением объема капли при ее затвердевании на подложке, не превышала ±5°. Аналогичные измерения θ проводили и для капель Au, Ni, Pt, Cu без их предварительного насыщения кремнием. Полученные капли М–Si затем были использованы для выращивания ННК и давали устойчивый рост.
РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ
Результаты измерений краевых углов представлены в табл. 1. Видно, что для чистых металлов, используемых для роста ННК, Si хорошо растворяется в жидкой фазе М-катализаторов и θ < 90° (рис. 1а). При этом образовавшаяся и растекшаяся капля с низким краевым углом устойчиво сохраняет свою форму. Такое поведение можно объяснить тем, что при растекании капли вследствие растворения Si изменяется геометрия поверхности раздела (образуется лунка). Таким образом, в неравновесной системе, когда с кремнием контактирует чистый металл и на границе протекает реакция растворения, угол смачивания Au, Ni, Pt, Cu мал (25°–55°), а работа адгезии велика (около 3.0 Дж/м2). Для тех же металлов, предварительно насыщенных Si, в условиях, близких к равновесным, краевой угол резко возрастает до (105°–130°), работа адгезии снижается почти в три раза (до 1.0 Дж/м2 и менее) (рис. 1б). Таким образом, эксперименты показывают, что капли Au, Ni, Pt и Cu, насыщенные Si, не смачивают Si-поверхность, образуя тупые краевые углы. Причем несмачиваемость (θ > 90°), наблюдаемая в наших экспериментах при контакте капли М-катализатора, насыщенной кремнием, и твердого Si не является следствием наличия промежуточных оксидных прослоек или загрязнений [5].
Таблица 1.
Краевые углы чистых металлов на поверхности {111} Si в водороде (1 атм) и результаты расчета работы адгезии в контактирующих фазах М–Si
| Контакти-рующие фазы | Т, K | θ, град | αL, Дж/м2 | Wa, Дж/м2 |
|---|---|---|---|---|
| Au–Si | 1273 | 25 ± 5 | 0.91 | 1.73 |
| Ni–Si | 1373 | 44 ± 5 | 1.75 | 3.01 |
| Pt–Si | 1373 | 45 ± 5 | 1.74 | 2.97 |
| Cu–Si | 1273 | 52 ± 5 | 1.30 | 2.10 |
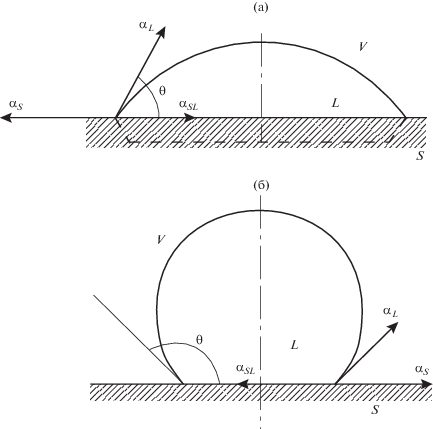
Рис. 1.
Измеренные краевые углы смачивания поверхности кремниевой подложки жидкофазными каплями М-катализатора: а – чистый металл (θ < 90°), б – сплав (насыщенный раствор) М–Si (θ > 90°).
Наблюдения за ростом ННК Si показывают, что капля М–Si не опускается на боковую поверхность ННК, а смачивает только вершинную грань {111} фронта кристаллизации (рис. 2). При этом капля ограничивает под собой размеры ростовой площадки периметром смачивания (ПС), а величина угла β на торцевой грани {111} ННК всегда превышает 90°.
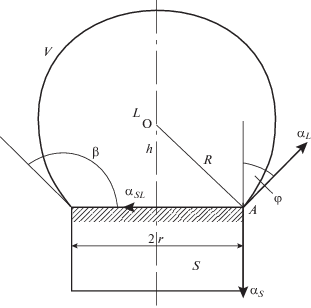
Рис. 2.
Схема сопряжения границ раздела трех фаз – твердой, жидкой и газообразной – для капли катализатора на вершине цилиндрического участка (β – угол наклона поверхности капли к грани фронта кристаллизации).
Полученные результаты по смачиванию каплей Si-подложки можно объяснить следующим образом. Работу адгезии между двумя фазами (твердой и жидкой) Wa можно представить как сумму работы адгезии для равновесного состояния системы Wa(eq), определяемой различием природы и свойств соприкасающихся фаз, и работы адгезии Wa(noneq), связанной с отклонением системы от равновесного состояния – разницы химических потенциалов компонентов [4]. Для условий равновесия (химические потенциалы жидкой и твердой фаз равны) в случае смачивания подложки каплями металлов, насыщенных кристаллизуемым веществом, вклад в суммарную работу адгезии составляющей Wa(noneq) исчезающе мал, поэтому силы когезии превышают силы адгезии и Si-поверхность не смачивается жидкофазными каплями М–Si, а угол смачивания θ > 90°. В случае насыщенной кристаллизуемым веществом капли катализатора краевые углы все же отличаются от 180°, поэтому силы сцепления жидкий сплав – твердый Si, по-видимому, определяются не химическим, а ван-дер-ваальсовым межфазным взаимодействием с заметными дисперсионными силами связи.
Для приближенных расчетов адгезии капли катализатора, насыщенной кристаллизуемым веществом, в качестве УСПЭ сплава (раствора) αLV можно принять величину УСПЭ чистого металла. Получающиеся при этом значения работы адгезии к Si для капель Au, Ni, Pt и Cu, насыщенных кремнием, приведены в табл. 2.
Таблица 2.
Краевые углы смачивания поверхности {111} Si каплями металлов, предварительно насыщенных кремнием (атмосфера – Н2)
| Cостав сплава, ат. % | Т, K | θ, град |
|---|---|---|
| Au + 38.4 Si | 1273 | 107 ± 5 |
| Ni + 58.1 Si | 1273 | 115 ± 5 |
| Pt + 59.0 Si | 1273 | 117 ± 5 |
| Cu + 36.1 Si | 1273 | 127 ± 5 |
Капля катализатора на вершине ННК представляет собой усеченный шаровой сегмент практически идеальной сферической формы (рис. 2). Фронт кристаллизации ННК, как правило, представлен плоской гранью семейства {111} [1, 3, 6]. Но первоначально капля формируется на ростовой подложке, насыщаясь кристаллизуемым веществом и образуя краевой угол θ > 90°. Проведем оценку эффективности влияния границы раздела фаз КЖ на устойчивость капли на вершине ННК для условий несмачивания кристаллической поверхности (θ > 90°). Запишем свободную поверхностную энергию равновесной капли на торцевой грани ННК в виде
(1)
$G* = 2\pi {{R}^{2}}\left( {1 + \frac{h}{R}} \right){{\alpha }_{{LV}}} + \pi {{r}^{2}}{{\alpha }_{{SL}}},$Перепишем выражение (1), учитывая, что h/R = = sin φ, а r/R = cos φ [7],
(2)
$G* = 2\pi {{R}^{2}}\left( {1 + \sin {\kern 1pt} \varphi } \right){{\alpha }_{{LV}}} + \pi {{R}^{2}}{{\cos }^{2}}{\kern 1pt} \varphi {{\alpha }_{{SL}}},$Продифференцируем G* по углу φ и приравняем к нулю производную уравнения (2). Тогда получим
Полученное выражение (3) описывает условие равновесия капли, насыщенной кристаллизуемым веществом, на вершинной грани ННК. Из уравнения (3) становится понятным, почему участки поверхности капли соотносятся как SSL/SLV < 1. Поскольку угол φ заключен в интервале 0° < φ < 90°, меньшая площадь границы контакта капли с кристаллом в сравнении с площадью поверхности, соприкасающейся с газовой фазой, объясняется тем, что у равновесной капли, насыщенной кристаллизуемым веществом, αSL > αLV. Поэтому еще на начальной стадии роста капля, уменьшая периметр смачивания, стремится сократить площадь контакта с кристаллической поверхностью и образует пьедестал ННК (рис. 3) [8].
Рис. 3.
ПЭМ-изображение начального сужающегося участка ННК Si (пьедестала), полученное в микроскопе высокого разрешения [8].

Обозначим отношение УСПЭ границ раздела фаз αLV/αSL в выражении (3) через m. Параметр m в данном случае может служить мерой несмачиваемости торцевой грани ННК. Если m ≥ 1, то в соответствии с (3) наблюдается полная несмачиваемость каплей кристаллической поверхности, контактный угол капли является неустойчивым (φ = 90°). Радиус кривизны трехфазной линии (ТЛ) равен нулю (r = 0). Для m ≤ –1 (полная смачиваемость торцевой грани) устойчивого угла также нет (φ = –90°), поскольку еще на ростовой подложке по мере увеличения периметра смачивания межфазная поверхностная энергия непрерывно уменьшается. Радиус линии трехфазного контакта капли на подложке будет стремиться к бесконечности. Если m = 0, то величина контактного угла капли φ = 0 и радиус ННК совпадает с радиусом капли (r = R), т.е. радиус кривизны ТЛ достигает наибольшего значения (безразличное смачивание). На торцевой грани ННК сферический сегмент капли катализатора с конечным радиусом кривизны 0 < r < R, для которой 0 < m < 1, будет устойчивым. Подставив (3) в (2), получим
(4)
$G* = 2\pi {{R}^{2}}\left[ {2\left( {1 + \sin {\kern 1pt} \varphi } \right) + \frac{{{{{\cos }}^{2}}{\kern 1pt} \varphi }}{{\sin {\kern 1pt} \varphi }}} \right]{{\alpha }_{{LV}}}.$При гомогенном образовании устойчивой сферической капли того же радиуса ее свободная поверхностная энергии равна
Тогда соотношение (4) и (5) выразится как
(6)
$\frac{{G{\kern 1pt} *}}{G} = \frac{1}{4}\left( {2(1 + \sin {\kern 1pt} \varphi ) + \frac{{{{{\cos }}^{2}}{\kern 1pt} \varphi }}{{\sin {\kern 1pt} \varphi }}} \right)\,.$Из уравнения (6) можно видеть, что соотношение свободной поверхностной энергии усеченного сегмента равновесной капли с контактным углом φ и капли в форме полной сферы зависит от величины этого угла.
Из уравнения (6) следуют два крайних и один промежуточный случаи.
1. φ = 90° (r = 0, h = R, полная несмачиваемость каплей кристаллической поверхности, т.е. отсутствие межатомного сцепления между атомами кристалла и капли), при котором G*/G = 1. В данном случае нет выигрыша в работе образования устойчивой капли катализатора (m ≥ 1). Это означает, что любое соприкосновение капли с кристаллом приводит к увеличению ее поверхностной энергии. Рост ННК в данных условиях невозможен (r = 0).
2. φ → 0 (r → R, h → 0, безразличное смачивание и максимальная длина ТЛ) и G*/G → ∞. В этом случае энергетические затраты возрастают (m → 0) и, следовательно, наличие границы КЖ не влияет на условия фазового превращения. Здесь устойчивого контактного угла у капли также нет и рост кристаллов невозможен.
3. 0° < φ < 90° (0 < m < 1) – наиболее распространенный случай. Он энергетически менее выгоден, чем состояние капли в отсутствие подложки, и тем выгоднее, чем меньше значение αSL, а следовательно, и больше φ.
Таким образом, энергетический барьер для нуклеации на площадке под каплей не снижен, как считалось ранее, а, наоборот, повышен. Поэтому нуклеация на торцевой грани ННК в центре под каплей энергетически невыгодна и практически неосуществима, поскольку появление зародыша увеличивает свободную поверхностную энергию капли. Появление зародышей или ступеней возможно только на границе раздела трех фаз.
В работе [8] показано, что при выращивании ННК изменение свободной поверхностной энергии dα трехфазной системы при испускании (поглощении) ступени (в расчете на единицу длины ТЛ и на одну ступень высотой dh) должно быть отрицательно
Величина dα в уравнении (7) складывается из члена αSL (исчезновение ступени) и некоторого члена α = $\alpha _{{SV}}^{'}$ − αLcosφ, связанного с изменением площадей трех смежных поверхностей при росте ННК. Здесь $\alpha _{{SL}}^{'}$ и $\alpha _{{SV}}^{'}$ – УСПЭ границы КЖ, имеющей ориентацию, совпадающую с ориентацией торцевой поверхности ступени, и границы КГ (боковой поверхности) соответственно. Если dα < 0, то ступени могут испускаться ТЛ. В условиях равновесия капли на боковой поверхности ННК в точке А, когда φ = θ', где θ' – угол смачивания боковой поверхности, и dα = 0, выражение (7) преобразуется к виду
Если контактный угол φ < θ', то возникает движущая сила (FG), приложенная к точкам на линии границы трех фаз. Тогда капля будет смещаться в направлении силы FG до тех пор, пока не достигнет состояния с краевым углом θ'. Величина этой силы на единицу длины ТЛ и краевого угла находится из совместного решения неравенства (7) и уравнения (8)
(9)
${{F}_{G}} = {{\alpha }_{{LV}}}(\cos {\kern 1pt} \varphi - \cos {\kern 1pt} \theta {\kern 1pt} ') > 0.$Неравенство (9) выполняется при φ < θ'. Поэтому смещение капли при росте ННК можно рассматривать как процесс, обратный растеканию жидкости по поверхности твердого тела, т.е. как процесс сфероидизации капли.
Выражение (9) показывает, что движущей силой процесса перемещения капли катализатора при росте ННК является избыток свободной энергии, источником которой служит наружная поверхность капли. При смещении капли происходит уменьшение ее свободной поверхностной энергии. При этом ступени роста формируются на ТЛ по ПС капли, поскольку α < $\alpha _{{SL}}^{'}$. Найдем область углов φ, в которой возможен рост ННК. Для этого, считая, что αSL = $\alpha _{{SL}}^{'}$ и αSV = $\alpha _{{SV}}^{'}$, подставим (3) в (7)
(10)
$\frac{{{{\alpha }_{S}}}}{{{{\alpha }_{L}}}} < \frac{1}{{\sin {\kern 1pt} \phi }} + \cos {\kern 1pt} \varphi .$На рис. 4 показана зависимость правой части неравенства (10) от величины угла φ. Для ННК Si, выращиваемых через жидкие капли Au–Si, и значений свободной поверхностной энергии αLV = = 0.91 Дж/м2 и αSV = 1.55 Дж/м2 [4, 9] пунктирной линией 1 обозначено отношение αS/αL ≈ 1.7. Пунктирными линиями 2–4 отмечено отношение αS/αL для ННК GaAs и InAs. Исходными данными для расчета были: для GaAs – αSV(ZB) = 1.50 Дж/м2, $\alpha _{{LV}}^{{{\text{Au}}}}$ = 1.0 Дж/м2; для InAs – αSV(ZB) = 1.19 Дж/м2, αSV(WZ) = 0.91 Дж/м2, $\alpha _{{LV}}^{{{\text{Au}}}}$ = 1.0 Дж/м2 [3]. В области I (рис. 4) неравенство (10) выполняется и реализуется устойчивый рост ННК. Здесь конфигурация капли такова, что энергетически выгодно образование новой поверхности КГ. В области II неравенство (10) не выполняется и в данных условиях не следует ожидать роста ННК по ПЖК-механизму. Здесь могут образовываться отрицательные ННК [10].
Рис. 4.
Зависимость ${1 \mathord{\left/ {\vphantom {1 {\sin {\kern 1pt} \varphi }}} \right. \kern-0em} {\sin {\kern 1pt} \varphi }} + \cos {\kern 1pt} \varphi $ от величины контактного угла φ насыщенных кристаллизуемым веществом капель катализатора на вершине бесконусных ННК (горизонтальными штриховыми линиями показано отношение αS/αL для ННК: 1 – кубического Si, 2 – кубического (ZB) GaAs, 3 – кубического (ZB) InAs, 4 – гексагонального (WZ) InAs; I и II – области стабильного роста ННК по ПЖК-механизму и травления кристаллов в КЖП-процессе соответственно).
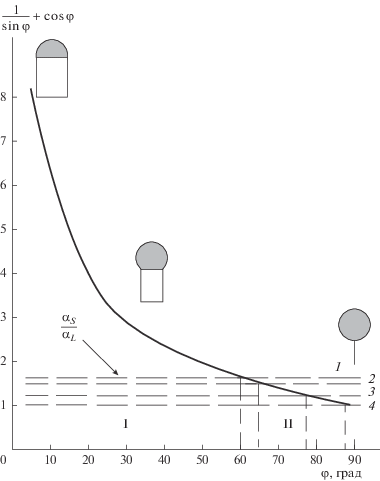
Итак, рис. 4 показывает, что существует некоторая область I углов φ, в пределах которой выполняется условие (10) и термодинамически возможен рост ННК. За пределами указанной области рост ННК невозможен.
Если для системы Au–Si пренебречь анизотропией свободной поверхностной энергии на границах КЖ и КГ и принять θ' = 107°, а φ = 30° [7], то для αLV = 0.91 Дж/м2 движущая сила FG = 1.06 Дж/м2, что по порядку величины сопоставимо с поверхностным натяжением жидкой фазы. Если свободная поверхностная энергия твердой фазы велика, т.е. $\alpha _{{SV}}^{'} > {{\alpha }_{{LV}}} + \alpha _{{SL}}^{'},$ и в предельном случае θ' = 0, то движущая сила
Поскольку 0° < φ < 90° и cos φ < 1, то в соответствии с (11) FG < 0, т.е. энергетически выгодно смачивание боковой поверхности ННК.
Если θ' > 90°, то в выражении (9) cos θ' < 0. Это означает, что в условиях несмачиваемости кристаллической поверхности каплей катализатора при любых величинах 0° < φ < 90° на линии границы контакта трех фаз всегда присутствует сила FG > 0, приводящая к смещению капли и росту ННК.
Таким образом, мы приходим к новому пониманию механизма ПЖК-роста ННК. Суть его состоит в следующем. Катализируемый каплей жидкости рост ННК обусловлен не облегчением двумерного зарождения по причине малой величины αSL, как считалось ранее, а снижением энергетического барьера нуклеации в области тройного стыка фаз за счет выделения сфероидизирующей каплей избыточной свободной энергии и понижения вследствие этого пересыщений, необходимых для роста вершинной грани ННК с заданной скоростью.
При V = const ПС подвижен, и капля катализатора способна за счет выделения кристаллизуемого вещества или, наоборот, его растворения, т.е. вследствие независимости изменений площади поверхности капли от изменений длины ТЛ, принять на вершине ННК равновесную форму. При механическом равновесии на протяженной подложке такая независимость отсутствует и форма капли не будет отвечать условию $\sum\nolimits_{IJ} {{{\alpha }_{{IJ}}}} {{S}_{{IJ}}} = \min ,$ поскольку приращение площади поверхности ЖГ зависит здесь от величины свободной энергии αSV, приводящей к растягиванию капли. Следовательно, в процессе роста ННК капля играет роль естественного формообразователя, определяющего округлую форму поперечного сечения кристалла.
Стремление к уменьшению αSL проявляется и в том, что кристаллизация при малых пересыщениях совершается таким образом, чтобы расположение атомов на торцевой грани ННК и на соприкасающейся с ней атомной плоскости новой фазы было максимально сходным. Соблюдение ориентационного соответствия атомных плоскостей особенно наглядно проявляется при гетероэпитаксии ННК материалов с некогерентными решетками (например, GaAs/InGaAs/InAs, InAs/InSb, GaP/Si и др.) [3].
ЗАКЛЮЧЕНИЕ
Установлено, что растворение Si в жидкофазных каплях М-катализаторов (Au, Ni, Pt и Cu) роста ННК ухудшает смачиваемость ими Si-поверхности, а краевой угол резко возрастает: от 25°–55° для чистых металлов до 105°–130° для М–Si в условиях, близких к равновесным.
Показано, что катализируемый жидкой фазой рост ННК обусловлен снижением энергетического барьера нуклеации за счет выделения сфероидизирующей каплей избыточной свободной энергии в области тройного стыка фаз. Движущей силой процесса перемещения капли в процессе роста ННК является избыток свободной энергии, источником которой служит наружная поверхность капли. При этом ступени роста формируются на границе раздела фаз по ПС капли.
На основании проведенных исследований можно сделать вывод о том, что в процессах роста ННК адгезионная и каталитическая активности жидкой фазы М-катализатора взаимосвязаны друг с другом. Чем хуже смачиваемость кристалла жидкофазным материалом катализатора, т.е. чем ниже адгезионная активность жидкости, тем он более каталитически активен.
Список литературы
Гиваргизов Е.И. Рост нитевидных и пластинчатых кристаллов из пара. М.: Наука, 1975. 304 с.
Небольсин В.А., Долгачев А.А., Дунаев А.И. Об общих закономерностях роста нитевидных микро- и нанокристаллов // Изв. РАН. Сер. физ. 2008. Т. 72. № 9. С. 1285–1288.
Dubrovskii V.G. Nucleation Theory and Growth Nanostructures. Berlin: Springer-Verlag, 2014. P. 601.
Найдич Ю.В. Контактные явления в металлических расплавах. К.: Наук. думка, 1972. 196 с.
Nebol’sin V.A., Dunaev A.I., Samofalova A.S., Korneeva V.V. Contact Interaction in an M–SiO2 (M = Metal Catalyst for Nanowhisker Growth) System // Inorg. Mater. 2018. V. 54. № 6. P. 558–563.
Nebol’sin V.A., Shchetinin A.A., Natarova E.I. Variation in Silicon Whisker Radius During Unsteady-State Growth // Inorg. Mater. 1998. V. 34. № 2. P. 87–89.
Nebol’sin V.A., Dunaev A.I., Tatarenkov A.F., Shmakova S.S. Scenarios of Stable NW VLS Growth //J. Cryst. Growth. 2016. V. 450. P. 207–214.
Schmidt V. et al. The Shape of Epitaxially Grown Silicon Nanowires and the Influence of Line Tension // J. Appl. Phys. 2005. V. 80. № 3. P. 445–450.
Shchetinin A.A., Darinskii B.M., Kozenkov O.D., Nebol’sin V.A. Mechanism for Early Stages of Si Whisker Growth // Inorg. Mater. 1990. V. 26. № 7. P. 1353–1357.
Nebol’sin V.A. et al. Formation of “Negative” Silicon Whiskers // Inorg. Mater. 2017. V. 53. № 8. P. 775–780.
Дополнительные материалы отсутствуют.
Инструменты
Неорганические материалы


