Неорганические материалы, 2020, T. 56, № 9, стр. 953-958

ВВЕДЕНИЕ

В 1921 г. Вегард, изучая параметры решеток (l) в твердых растворах изоструктурных веществ, обнаружил, что если температура постоянна, то изменение величины l с составом происходит в первом приближении линейно, т.е.

где l_A – параметр решетки растворителя, l_B – параметр решетки растворенного элемента, С – атомная концентрация растворенного элемента.

Выражение (1) получило название правила Вегарда. И хотя оно математически противоречит правилу аддитивности молекулярных объемов химически не реагирующих веществ, все же широко используется для изучения смесей различных веществ. Однако даже для сплавов замещения (например, для CuAu или SiGe) в большинстве случаев наблюдается отклонение от правила Вегарда (1) (так же, как и от правила аддитивности молекулярных объемов), характеризуемое величиной

Причем это отклонение может быть как положительным (например, для CuAu), так и отрицательным (например, для SiGe) [1–3]. Несмотря на то что было предложено много теоретических моделей для описания зависимости величины Δl от концентрации растворенного компонента (С), природа этой зависимости до конца не ясна даже для бинарных неупорядоченных сплавов замещения [3]. Кроме того, до сих пор не изучено изменение величины Δl с ростом давления (p) в твердом растворе.

В данной работе предложен один из возможных вариантов зависимости Δl(p) и показано, как эту зависимость можно использовать для оценки давления в сплаве замещения.

МЕТОДИКА РАСЧЕТА

Рассмотрим сплав двух изоструктурных веществ A и B, которые образуют при смешении твердый раствор замещения. Для изучения зависимости l(С) используем приближение “взаимодействия только ближайших соседей”, которое также называют “квазихимическим приближением”. Пусть P_A и P_B – вероятности нахождения в узле смешанной решетки атомов сорта A и B соответственно. Тогда для вероятности одновременного нахождения в соседних узлах решетки атомов одного сорта и атомов разных сортов можно принять: P_AA = $P_{{\text{A}}}^{{\text{2}}},$ P_BB = $P_{{\text{B}}}^{{\text{2}}}$ и P_AB = 2P_AP_B. Число парных связей для пар атомов одного сорта и для пар разных атомов равно:

где N = N_A + N_B – общее число атомов в сплаве, k_n – первое координационное число, т.е. число ближайших к данному атому узлов решетки.

Тогда, учитывая, что общее число всех парных связей в сплаве равно: NN = (k_n/2)N, для среднего значения параметра решетки сплава можно получить выражение

где l_AB – параметр решетки, в которой с равной вероятностью можно найти атом А или В из однородно распределенных по решетке атомов обеих сортов, с учетом релаксации такой решетки к минимуму энергии.

При внесении атомов одного сорта в решетку из атомов другого сорта объем общей решетки релаксирует так, чтобы достигался минимум свободной энергии. Поэтому разложим удельную (на атом своей подрешетки) свободную энергию для каждой из подрешеток в ряд по степеням отклонения удельного объема: ΔV_i = V_AB – V_i0 при постоянной температуре (T) и ограничимся квадратичными членами ряда:

Таким образом, добавочная удельная свободная энергия решетки, в которой с равной вероятностью можно обнаружить атом любого сорта (т.е. при P_A = P_A = 0.5) будет равна:

где p = –(∂F(A)/∂V)_T = –(∂F(B)/∂V)_T – давление, которое при термодинамическом равновесии одинаково для обеих решеток, B_i = V_i(∂²F(i)/∂V²)_T = = –V_i(∂P/∂V_i)_T – изотермический модуль упругости для i-й решетки.

Так как рассматриваемый твердый раствор замещения находится в термодинамическом равновесии, его термодинамический потенциал минимален. Поскольку твердый раствор Si_0.5Ge_0.5 не имеет полиморфных переходов, будем считать, так же как авторы работ [1–3], что в однородном состоянии он является упорядоченным.

Тогда из условия минимума функции (4) (∂ΔF_AB/∂V_AB)_T,p = 0 можно получить выражение для удельного объема смешанной решетки, где с равной вероятностью обнаруживаются атомы разных сортов, которая находится под давлением:

где введена функция, учитывающая разницу в сжимаемостях чистых компонентов:

Так как для твердого раствора замещения исходные и смешанная решетки имеют одинаковую структуру, то из (5) можно получить выражение для величины параметра решетки эквиатомного состава:

Заметим, что если изначально полагать p = 0, рассматривать одномерную модель и считать концентрацию атомов произвольной, то вместо формулы (7) аналогичным путем можно получить формулу, полученную G. Fournet [1], которая имеет вид:

Но здесь функция C_F будет отличаться от функции C_N из (6):

При p = 0 и C = 0.5 для одномерного случая формулы (7) и (8) совпадают, но значения C_F и C_N существенно различаются.

Входящие в уравнение (3) функции P_A и P_B = = 1 – P_A определим как геометрические вероятности того, что точка, случайно поставленная на линию длиной (1 – C)l_A + Cl_B, попадет на отрезки l_A или l_B соответственно:

Подставляя функции (7) и (10) в формулу (3), получаем выражение, с помощью которого можно рассчитать зависимость параметра решетки сплава исходя из характеристик чистых компонентов. Из (3) также можно получить выражение для расчета коэффициента теплового расширения бинарного сплава в виде:

Здесь α_i и α_AB – коэффициенты теплового расширения для i-го компонента и для решетки с равным числом атомов. В соответствии с (5), при p = 0 фукция α_AB имеет вид:

где введены обозначения:

Отметим, что в литературе отсутствуют какие-либо сведения о расчете (аналитическом либо численном) коэффициента теплового расширения твердого раствора, кроме формулы, которая следует из правила Вегарда (1).

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Для проверки предложенной методики была рассчитана зависимость параметра решетки для сплава SiGe, имеющего структуру алмаза (сфалерита). Входящие в формулы параметры чистых решеток при T = 300 K и p = 0 брали в виде:

Тогда из (6) и (7) получим: C_N = 0.678192 и l_SiGe = 5.52478 [10^–10 м].

На рис. 1 показано изменение параметра решетки сплава SiGe в зависимости от концентрации Ge. Точки – это экспериментальные данные из [2], которые были определены при T = 300 K с точностью ±0.0005 [10^–10 м]. Эти данные были аппроксимированы в [2] квадратичной зависимостью вида

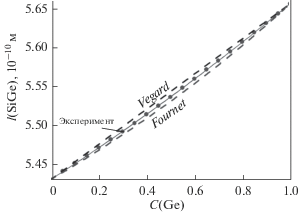
Наши расчеты при p = 0 практически совпадают с линией (13). Лежащая выше зависимости (13) пунктирная прямая – это расчет по правилу Вегарда:

Пунктирная кривая, которая лежит ниже экспериментальных данных и зависимости (11), рассчитана по формуле G. Fournet (8) с величиной C_F из формулы (9).

На рис. 2 показано изменение величины отклонения параметра решетки от зависимости, рассчитанной по правилу Вегарда (14): Δl = l – l_Vegard. Точки – это экспериментальные данные из [2]. Сплошная кривая 1 – это разница между зависимостями (13) и (14), точечная кривая 2 – отклонение расчетов от зависимости (14) при p = 0, пунктирная кривая 3 – разница между зависимостью (8) и правилом Вегарда (14), точечная кривая 4 – отклонение расчетов от зависимости, рассчитываемой по правилу Вегарда при p = 0.5 ГПa. Из рис. 1 и 2 видно, что расчеты при p = 0 хорошо согласуются с экспериментальными данными, полученными при этом же давлении. Отметим, что расчеты методом функционала плотности, проведенные в работе [3] при p = 0, показали плохое согласие с экспериментальными данными из [2]. Значение |Δl(C)| в точке максимума, т.е. при C(Ge) = 0.5, в [3] получилось очень большим: Δl(C = 0.5) = –0.09, в то время как в [2] было получено Δl(C = 0.5) = –0.0069 ± 0.0005, а в наших расчетах Δl(C = 0.5) = –0.0074 [10^–10 м].

Для изучения барической зависимости функции Δl = l – l_Vegard были использованы следующие выражения для изменения параметра решетки и модуля упругости чистых веществ при изотермическом изменении давления:

Здесь B'(p)_i = ∂B_i/∂p – производная модуля упругости по давлению для i-решетки. Значения этого параметра для чистых решеток брали из [4]:

Таким образом, с использованием (15) было рассчитано изменение функции Δl(C) при различных давлениях. Расчеты показали, что барическая зависимость функции Δl(C) = l – l_Vegard в точке максимума, т.е. при C(Ge) = 0.5, с коэффициентом корреляции R_cor = 0.99967 аппроксимируется линейной зависимостью следующего вида:

Из (16) видно, что при увеличении давления отрицательное отклонение от правила Вегарда для сплава SiGe уменьшается, и выше определенного давления (p₀ = 0.685 ГПa) величина Δl(C = 0.5) переходит в положительную область. Из (16) также следует, что наше значение Δl(C = 0.5) совпадет с экспериментальным, если допустить, что экспериментально созданный сплав SiGe находился под давлением p_s = 0.04 ГПa. Но если учесть точность измерения величин Δl, B_i и B'(p)_i, то значение p_s может быть значительно меньше.

Для непрерывного разупорядоченного твердого раствора CuAu с гранецентрированной кубической (ГЦК) структурой входящие в формулы параметры чистых решеток при T = 300 K и p = 0 брали в виде:

Тогда из (6) и (7) получим C_N = 0.874348, l_CuAu = = 3.84506 [10^–10 м].

На рис. 3 показано изменение параметра решетки ГЦК-сплава CuAu в зависимости от концентрации золота. Экспериментально данная зависимость изучалась многими авторами, ссылки на которых даны в обзоре [5]. Эти данные в [5] были аппроксимированы квадратичной зависимостью вида

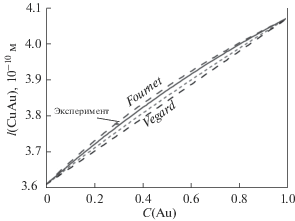
Зависимость (17) показана на рис. 3 сплошной выпуклой линией. Проходящая снизу пунктирная прямая – это результат расчета по правилу Вегарда:

Наши расчеты при p = 0 показаны точечной выпуклой кривой, лежащей между линиями из (17) и (18). Проходящая сверху пунктирная кривая рассчитана по формуле (8).

Из рис. 3 видно, что рассчитанная по предложенной методике зависимость l(C) при p = 0 лежит ниже экспериментальной кривой. При использовании выражения (15), а также значений из [6] B'(p)_Cu = 5.4 ± 0.2 и B'(p)_Au = 6.2 ± 0.2 было получено, что наша кривая совпадет с экспериментальной, если допустить, что изучаемый в экспериментах ГЦК-сплав Cu_{1– C}Au_C находился под давлением p_s = 5 ГПa. Реально ли это?

Экспериментально разупорядоченный твердый раствор CuAu получают путем быстрого охлаждения (т.е. закалки) закристаллизовавшегося сплава из высокотемпературной области 900–1100 K. Это позволяет как сохранить однородность состава, так и избежать фазового перехода (при температуре Курнакова) разупорядоченного твердого раствора в упорядоченное состояние, которое имеет другую структуру и свойства [5]. Легко понять, что такая технология может привести к заметным остаточным закалочным напряжениям в изучаемом при комнатных температурах сплаве. Поэтому значение p_s = 5 ГПa можно считать вполне реальным. Хотя, если учесть точность измерения входящих в формулы величин, эта оценка может быть значительно меньше.

Для расчета коэффициента теплового расширения сплава SiGe входящие в формулы (11) и (12) параметры чистых решеток при T = 300 K и p = 0 брали из работы [7] в виде: α_Si = 7.72 и α_Ge = 17.1 [10^–6 K^–1].

Тогда, полагая β_Si = β_Ge, из (12) получим α_SiGe = 11.5107 [10^–6 K^–1].

На рис. 4 представлено изменение коэффициента теплового расширения сплава SiGe в зависимости от концентрации Ge. Экспериментальные данные из [8] показаны точками и сплошной линией. Пунктирная прямая – расчет по формуле, которая следует из (1):

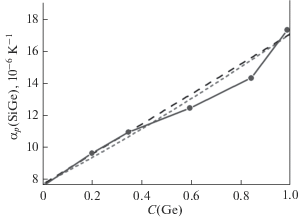
Лежащая ниже зависимости (19) вогнутая точечная линия – это результат расчета по формуле (11). Легко видеть, что наш расчет правильно передает отрицательное отклонение от зависимости (19). К сожалению, в литературе нет более свежих экспериментальных данных зависимости α(C) для разупорядоченного твердого раствора SiGe, чем оценки из [8], полученные в 1967 г., которые, однако, отклоняются от данных для чистых компонентов из [7].

Исследования последних лет [9–11] показали, что значения α(SiGe) даже при 300 K имеют большой разброс и зависят от многих факторов: от типа проводимости образца (n- или p-тип), от условий – при нагреве или при охлаждении проводились измерения, от состояния структуры: наноструктурирование образца увеличивает α. Поэтому известные из литературы экспериментальные данные для зависимости α(C) сильно различаются. Например:

Поэтому полученную зависимость α(C) можно также использовать для выделения вклада электронной подсистемы или вклада наноструктурирования в величину коэффициента теплового расширения. Отметим также, что предложенный метод изучения зависимости параметра решетки сплава SiGe от концентрации был успешно применен для расчета как температуры Дебая, так и фазовой диаграммы данного твердого раствора в [12]. Кроме этого, данный метод был применен при расчете термодинамических свойств твердого раствора Si_0.5Ge_0.5 как в макро-, так и в наноструктурном состоянии в [13].

ЗАКЛЮЧЕНИЕ

Получены выражения для расчета параметра решетки и коэффициента теплового расширения твердого раствора замещения, которые учитывают наличие давления в растворе.

Показано, что при p = 0 отклонение от правила Вегарда (Δl) обусловлено разностью в сжимаемостях и удельных объемах чистых кристаллов. При изотермическом росте давления Δl увеличивается для сплавов как с отрицательным, так и с положительным отклонением от зависимости, полученной по правилу Вегарда. Поэтому по величине Δl можно оценить напряжения в исследуемом разупорядоченном твердом растворе замещения.

Расчеты показали, что разупорядоченный твердый раствор CuAu имеет заметные остаточные напряжения после закалки из высокотемпературной области. Коэффициент теплового расширения твердого раствора замещения SiGe отклоняется в отрицательную сторону от зависимости, которая следует из правила Вегарда.