Журнал неорганической химии, 2019, T. 64, № 3, стр. 288-295

Теоретическое исследование изомеров допированных кластеров L₂Al₄₂ с допантами L переходных элементов внутри и на поверхности алюминиевого каркаса

О. П. Чаркин^1, *, Н. М. Клименко²

¹ Институт проблем химической физики РАН
Черноголовка, Московской обл., пр-т Академика Семенова, 1, Россия

² Московский государственный технологический университет им. М.В. Ломоносова
119571 Москва, пр-т Вернадского, 86, Россия

^* E-mail: charkin@icp ac.ru

Поступила в редакцию 25.06.2018
После доработки 15.08.2018
Принята к публикации 05.07.2018

DOI: 10.1134/S0044457X19030061

Полный текст (PDF)

Аннотация

В рамках метода функционала плотности выполнены расчеты структуры и стабильности внутренних и внешних изомеров у семейства наноразмерных кластеров L₂Al₄₂ с атомами допантов переходных элементов L внутри и на поверхности алюминиевого каркаса. Установлено, что для всех кластеров с L = Sc−Cu предпочтительны изомеры с допантами во внутренних (закрытых) позициях в ядре кластера. Переход допантов на поверхностные позиции и превращение их в открытые каталитические центры требуют затрат энергии ∼15−25 ккал/моль. Впервые предсказана высокая стабильность и возможность существования высокоспиновых кластеров типа L₅Al₃₉ с пятью допантами, расположенными в предпочтительных аксиальных и экваториальных внутренних позициях. Результаты могут быть полезными для теоретического прогнозирования и моделирования более крупных молекулярных алюминиевых сплавов c более высоким содержанием допантов L.

Ключевые слова: наноразмерные алюминиевые кластеры, допанты переходных металлов, внутренние и внешние изомеры, мультиплетность, магнетизм

В последние годы была опубликована серия работ, посвященных квантово-химическим расчетам электронной и геометрической структуры, стабильности, спектроскопических и других молекулярных характеристик алюминиевых кластеров, допированных атомами других элементов [1–8]. Авторы изучали зависимость структуры и свойств нейтральных и заряженных систем от размеров и формы алюминиевых кластеров [1], исследовали каталитические свойства микросплавов переходных 3d-металлов в поверхностной области алюминиевого каркаса [2], моделировали механизмы реакций взаимодействия анионов борзамещенных алюминидов с молекулярным кислородом [3], активации молекулярного азота с использованием Si- и P-допированных кластеров алюминия [4] и других процессов. В ряде работ рассчитаны поверхности потенциальной энергии и исследованы механизмы диссоциативного присоединения молекулярного водорода к алюминиевым кластерам, допированным атомом магния, 3d- и 4d-переходных металлов. Аналогичные расчеты были выполнены для реакций присоединения молекулы Н₂ к Mg-допированному кластеру MgAl₁₂ [6]. Структурные особенности алюминиевых сплавов с переходными металлами изучены в [7]. В [8] бинарные кластеры LAl₁₂ исследованы методами масс-спектрометрии и фотоэлектронной спектроскопии с интерпретацией результатов в рамках концепции “суператомов”.

Как правило, подобные расчеты выполняли с помощью методов теории функционала плотности (ТФП/DFT) и они посвящены небольшим кластерам типа LAl₁₂ с одним допантом L и икосаэдрической структурой каркаса, в которой все атомы занимают поверхностные позиции, за исключением одного – в центре икосаэдра. Недавно (см. работу [9] и библиографию в ней) DFT-подход был распространен на более сложные алюминиевые кластеры С₂Al₄₂, C₆Al₃₈, C₁₂Al₃₂, Si₆Al₃₈, N₆Al₃₈ и P₆Al₃₈ с пятиатомным внутренним ядром и несколькими допантами. В этих работах прослеживаются тенденции изменения структуры и относительной стабильности внутренних и внешних изомеров (c допантами в составе внутреннего ядра и на поверхности кластера соответственно) при изменении допантов L в ряду углерод–кремний–азот–фосфор. Этот вопрос связан с общей проблемой влияния примесей и легирующих добавок на структуру и свойства наноразмерных частиц. Важно также понять, в каких случаях предпочтительным сохраняется рассеянное распределение допантов по всему объему кластера в виде разделенных атомов (ионов) и в каких при увеличении числа допантов может появиться возможность микрокластеризации допантов с образованием их ковалентно-связанных двухатомных или более сложных частиц типа [L_m]. Этот вопрос связан с проблемой поиска пограничных областей в стехиометрическом соотношении допанта и основного металла, ниже которых атомы (ионы) допантов рассеиваются стохастически и выше которых становится существенной кластеризация допанта вплоть до сегрегации компонентов.

В нашей предыдущей работе [10] выполнены DFT-расчеты изомеров допированных кластеров L₂Al₄₂, полученных из алюминиевого кластера Al₄₄ при замещении двух его атомов Al атомами легких непереходных sp-элементов, Cu, Zn и H в различных позициях на поверхности и внутри алюминиевого каркаса. Нас интересовало, как меняется структура и относительная энергетическая стабильность внутренних и внешних изомеров при изменении допанта L вдоль второго и третьего непереходных периодов и при переходе от 2s2p-элементов к их 3s3p-аналогам. Расчеты [10] свидетельствовали, что для большинства допантов sp-элементов и атома Н предпочтительны позиции допантов либо на поверхности, либо в подповерхностном (промежуточном) пространстве, в котором допант L связан с атомами алюминия, расположенными как на поверхности, так и во внутреннем ядре каркаса. С другой стороны, для легких элементов второго периода (L = Ве и В) и элементов конца 3d-периода (L = Сu и Zn) самыми выгодными и более предпочтительными являются внутренние позиции допантов. Результаты сравнивали с данными предыдущих DFT-расчетов изомеров кластеров LAl₁₂ с теми же допантами L [11]. Рассмотрено влияние размера алюминиевого каркаса на относительную энергетическую стабильность поверхностных и внутренних позиций допантов.

В настоящем сообщении, являющемся продолжением [10], DFT-расчеты распространены на родственные кластеры L₂Al₄₂ с допантами элементов первого и второго переходных периодов (L = Sc−Ni, Zr, Mo и Pd), расположенными в позициях внутри и на поверхности каркаса. Основное внимание фокусируется на энергетических характеристиках внутренних и внешних изомеров и тенденциях их поведения при изменении допантов вдоль переходных периодов. Вопрос об относительной стабильности внутренних и внешних изомеров важен при рассмотрении каталитической активности допантов d- и f-переходных металлов, где максимальная активность соответствует открытым поверхностным позициям, в то время как во внутренних позициях допант пространственно закрыт атомами алюминия и не активен. Представляло также интерес оценить стабильность изомеров к распаду с отщеплением двух атомов допанта

(1)

${{{\text{L}}}_{{\text{2}}}}{\text{A}}{{{\text{l}}}_{{{\text{42}}}}} \to {\text{A}}{{{\text{l}}}_{{42}}} + 2{\text{L}} + {{Е }_{{{\text{д и с }}}}}$

и возможность существования структур, в которых атомы допанта ассоциированы в виде двухатомной молекулы L₂ или иона ${\text{L}}_{2}^{ - }$.

Экспериментальные исследования подобных проблем на уровне наноразмерных частиц сталкиваются с трудностями, и значительную помощь здесь могут оказать модельные квантово-химические подходы и расчеты, которые в некоторых случаях оказываются единственным источником полезной информации. Из-за приближенного характера метода DFT основное внимание уделяется не столько абсолютным значениям рассчитанных величин, сколько их относительным изменениям и тенденциям в родственных рядах кластеров L₂Al₄₂. Рассмотрение имеет модельный и предсказательный характер.

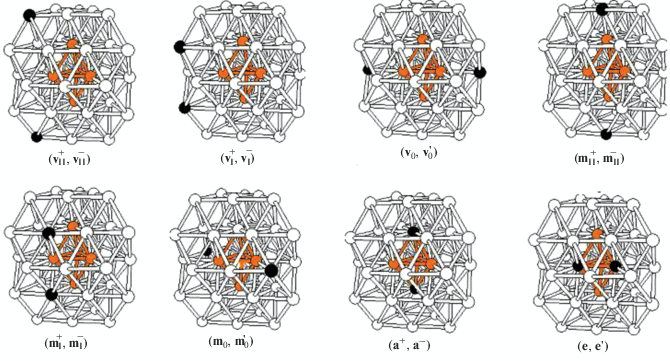
Работа состоит из нескольких частей. В первой части на примере тестовых кластеров Ti₂Al₄₂, Ni₂Al₄₂, Zn₂Al₄₂, Zr₂Al₄₂ и Pd₂Al₄₂ оптимизированы те же восемь базовых стартовых структур, которые подробно исследовались в [10] и изображены на рис. 1. Две из них – (${\mathbf{a}}_{{\mathbf{I}}}^{ + },{\mathbf{a}}_{{\mathbf{I}}}^{ - }$) и (${{{\mathbf{e}}}_{0}},{\mathbf{e}}_{0}^{{\text{'}}}$) – соответствуют внутренним, а остальные шесть – (${\mathbf{v}}_{{{\mathbf{II}}}}^{ + },{\mathbf{v}}_{{{\mathbf{II}}}}^{ - }$), (${\mathbf{v}}_{{\mathbf{I}}}^{ + },{\mathbf{v}}_{{\mathbf{I}}}^{ - }$), (${{{\mathbf{v}}}_{0}},{\mathbf{v}}_{0}^{{\text{'}}}$), (${\mathbf{m}}_{{{\mathbf{II}}}}^{ + },{\mathbf{m}}_{{{\mathbf{II}}}}^{ - }$), (${\mathbf{m}}_{{\mathbf{I}}}^{ + },{\mathbf{m}}_{{\mathbf{I}}}^{ - }$) и (${{{\mathbf{m}}}_{0}},{\mathbf{m}}_{0}^{{\text{'}}}$) − поверхностным изомерам. (Здесь используются обозначения позиций v, m, a, e и слоев 0, I^± и II^±, принятые в [10]). Относительные энергии равновесных структур, оптимизированных в настоящей работе, приведены в табл. 1. Расчеты ставили целью выявить в каждой из этих двух групп энергетически наиболее выгодные изомеры. Показано, что для большинства рассмотренных в первой группе кластеров наиболее выгодными являются близколежащие (аксиальный и экваториальный) внутренние изомеры (${\mathbf{a}}_{{\mathbf{I}}}^{ + },{\mathbf{a}}_{{\mathbf{I}}}^{ - }$) и (${{{\mathbf{e}}}_{0}},{\mathbf{e}}_{0}^{{\text{'}}}$), а во второй группе – изомер (${\mathbf{m}}_{{\mathbf{I}}}^{ + },{\mathbf{m}}_{{\mathbf{I}}}^{ - }$) с допантами в промежуточных слоях (см. ниже).

Рис. 1.

Базисные стартовые структуры кластеров М₂Al₄₂.

Таблица 1.

Относительные энергии Е_отн ключевых поверхностных и внутренних изомеров кластеров L(3d)₂Al₄₂, допированных атомами переходных металлов 3d-периода

Параметр	Относительная энергия, Е_отн, ккал/моль*
Параметр	Ti₂Al₄₂ (S = 1)	Mn₂Al₄₂ (S = 11)	Ni₂Al₄₂ (S = 1)	Zn₂Al₄₂ (S = 1)	Zr₂Al₄₂ (S = 1)	Pd₂Al₄₂ (S = 1)
(${\mathbf{v}}_{{{\mathbf{II}}}}^{ + },{\mathbf{v}}_{{{\mathbf{II}}}}^{ - }$)	47	34	35	29	40	9
(${\mathbf{v}}_{{\mathbf{I}}}^{ + },{\mathbf{v}}_{{\mathbf{I}}}^{ - }$)	30	36	46	24	29	18
(${{{\mathbf{v}}}_{0}},{\text{ }}{\mathbf{v}}_{0}^{{\text{'}}}$)	26	44	42	14	14	0
(${\mathbf{m}}_{{{\mathbf{II}}}}^{ + },{\mathbf{m}}_{{{\mathbf{II}}}}^{ - }$)	26	19	55	22	24	16
(${\mathbf{m}}_{{\mathbf{I}}}^{ + },{\mathbf{m}}_{{\mathbf{I}}}^{ - }$)	15	8	∼41	10	0
(${{{\mathbf{m}}}_{0}},{\text{ }}{\mathbf{m}}_{0}^{{\text{'}}}$)	23	10	47	11	20
(${\mathbf{a}}_{{\mathbf{I}}}^{ + },{\mathbf{a}}_{{\mathbf{I}}}^{ - }$)	2	0	0	0	9	0
(${{{\mathbf{e}}}_{0}},{\text{ }}{\mathbf{e}}_{0}^{{\text{'}}}$)	0	35	16	4	0

* Расчеты Е_отн выполнены в приближении B3LYP/6-31G* при геометрии, оптимизированной на уровне B3LYP/6-31G для наиболее выгодных высокоспинового состояния у изомеров Mn₂Al₄₂ (S = 11) и синглетных состояний у остальных кластеров. За начало отсчета выбраны энергии наиболее выгодных внутренних изомеров (${\mathbf{a}}_{{\mathbf{I}}}^{ + },{\mathbf{a}}_{{\mathbf{I}}}^{ - }$) и (${{{\mathbf{e}}}_{0}},{\text{ }}{\mathbf{e}}_{0}^{{\text{'}}}$).

Во второй части оба предпочтительных изомера – (${\mathbf{a}}_{{\mathbf{I}}}^{ + },{\mathbf{a}}_{{\mathbf{I}}}^{ - }$) и (${\mathbf{m}}_{{\mathbf{I}}}^{ + },{\mathbf{m}}_{{\mathbf{I}}}^{ - }$) – были оптимизированы для всей серии кластеров L₂Al₄₂ с допантами переходных металлов от Sc до Zn. Оптимизированные структуры изомеров (${\mathbf{a}}_{{\mathbf{I}}}^{ + },{\mathbf{a}}_{{\mathbf{I}}}^{ - }$) и (${\mathbf{m}}_{{\mathbf{I}}}^{ + },{\mathbf{m}}_{{\mathbf{I}}}^{ - }$) изображены на рис. 2. В табл. 2 рассмотрены тенденции поведения относительных энергий ΔE_отн изомеров при изменении L вдоль 3d-ряда. Как показали расчеты, для всех рассмотренных кластеров закрытые изомеры с допантами во внутренних позициях ${\mathbf{a}}_{{\mathbf{I}}}^{ + }$ и e₀ существенно более выгодны по сравнению с открытыми аналогами (см. ниже).

Рис. 2.

Оптимизированные структуры наиболее выгодных внутреннего (${\mathbf{a}}_{{\mathbf{I}}}^{ + },{\mathbf{a}}_{{\mathbf{I}}}^{ - }$) и поверхностного (${\mathbf{m}}_{{\mathbf{I}}}^{ + },{\mathbf{m}}_{{\mathbf{I}}}^{ - }$) изомеров кластеров L₂Al₄₂.

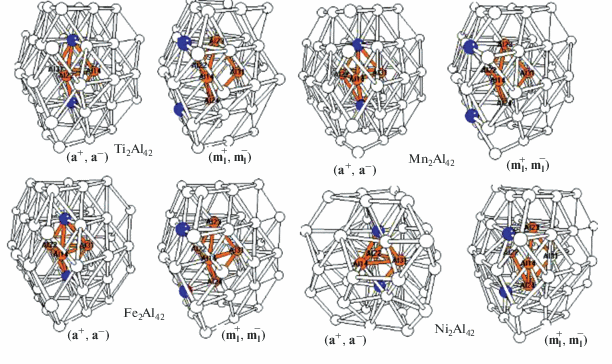
Таблица 2.

Рассчитанные характеристики низших внутреннего и поверхностного изомеров алюминиевых кластеров L₂Al₄₂, допированных атомами элементов 3d-периода, ккал/моль

Параметр*	Al₄₂Ti₂ (S = 5)		Al₄₂V₂ (S = 7)		Al₄₂Cr₂ (S = 9)		Al₄₂Mn₂ (S = 11)		Al₄₂Fe₂ (S = 9)		Al₄₂Co₂ (S = 7)		Al₄₂Ni₂ **
Параметр*	${\mathbf{a}}_{{\mathbf{I}}}^{ + },{\mathbf{a}}_{{\mathbf{I}}}^{ - }$	${\mathbf{m}}_{{\mathbf{I}}}^{ + },{\mathbf{m}}_{{\mathbf{I}}}^{ - }$	${\mathbf{a}}_{{\mathbf{I}}}^{ + },{\mathbf{a}}_{{\mathbf{I}}}^{ - }$	${\mathbf{m}}_{{\mathbf{I}}}^{ + },{\mathbf{m}}_{{\mathbf{I}}}^{ - }$	${\mathbf{a}}_{{\mathbf{I}}}^{ + },{\mathbf{a}}_{{\mathbf{I}}}^{ - }$	${\mathbf{m}}_{{\mathbf{I}}}^{ + },{\mathbf{m}}_{{\mathbf{I}}}^{ - }$	${\mathbf{a}}_{{\mathbf{I}}}^{ + },{\mathbf{a}}_{{\mathbf{I}}}^{ - }$	${\mathbf{m}}_{{\mathbf{I}}}^{ + },{\mathbf{m}}_{{\mathbf{I}}}^{ - }$	${\mathbf{a}}_{{\mathbf{I}}}^{ + },{\mathbf{a}}_{{\mathbf{I}}}^{ - }$	${\mathbf{m}}_{{\mathbf{I}}}^{ + },{\mathbf{m}}_{{\mathbf{I}}}^{ - }$	${\mathbf{a}}_{{\mathbf{I}}}^{ + },{\mathbf{a}}_{{\mathbf{I}}}^{ - }$	${\mathbf{m}}_{{\mathbf{I}}}^{ + },{\mathbf{m}}_{{\mathbf{I}}}^{ - }$	${\mathbf{a}}_{{\mathbf{I}}}^{ + },{\mathbf{a}}_{{\mathbf{I}}}^{ - }$	${\mathbf{m}}_{{\mathbf{I}}}^{ + },{\mathbf{m}}_{{\mathbf{I}}}^{ - }$
R(LL)	4.53	4.51	4.50	4.53	4.53	4.48	4.38	4.72	4.26	4.31	4.44	4.12	4.04	3.96
ν(LL)	353		360		378		385		387		403		390
ρ(2L)	2.6	3.4	5.8	6.2	7.6	9.0	9.0	9.6	6.4	7.2	2.6	4.2	0.2	2.0
ρ(Al₄₂)	1.4	0.6	0.5	–0.2	0.4	–1.1	1.1	0.3	1.5	0.7	3.5	1.7	3.8	2.0
Е_отн	0	12.5	0	22.0	0	14.0	0	3.8	0	23.2	0	20.7	0	41
E_дис(1)	64.6		62.7		80.9		–10		41.4		69.7		∼100

* Расстояние между допантами R(LL) и частота колебания ν(LL) выражены в Å и см^–1 соответственно. ρ(L) − спиновая плотность на атоме допанта, а ρ(Al₄₂) − суммарная спиновая плотность алюминиевого каркаса Al₄₂ (в долях е). Е_отн − относительные энергии изомеров ${\mathbf{a}}_{{\mathbf{I}}}^{ + },{\mathbf{a}}_{{\mathbf{I}}}^{ - }$ и ${\mathbf{m}}_{{\mathbf{I}}}^{ + },{\mathbf{m}}_{{\mathbf{I}}}^{ - }$; E_дис(1) – энергия распада допированного кластера по схеме L ₂Al₄₂ → Al₄₂ + 2L, приходящаяся на один атом L. Энергии Е_отн и E_дис(1) выражены в ккал/моль. ** У кластера Al₄₂Ni₂ предпочтительный синглет и соседние триплет и квинтет расположены тесной группой в пределах нескольких ккал/моль.

В третьем разделе рассчитана серия новых кластеров L₅Al₃₉ с пятью допантами (L = Sc−Ni). Их оптимизированные структуры, в которых допанты заполняют все пять самых выгодных внутренних позиций (2а + 3е) в форме искаженного бипирамидального ядра (сердечника), встроенного во внутреннюю полость каркаса Al₃₉, изображены на рис. 3. Согласно расчетам, этому изомеру отвечает самая низкая полная энергия Е_полн у всех кластеров L₅Al₃₉ с допантами переходных металлов. В табл. 3 приведены относительные энергии низколежащих мультиплетов и спиновые плотности на сердечнике ρ(L₅) и каркасе ρ(Al₃₉), рассчитанные для систем с разными допантами L.

Рис. 3.

Оптимизированные структуры кластеров L₅@Al₃₉ c бипирамидальным магнитным сердечником L₅ внутри алюминиевого каркаса Al₃₉.

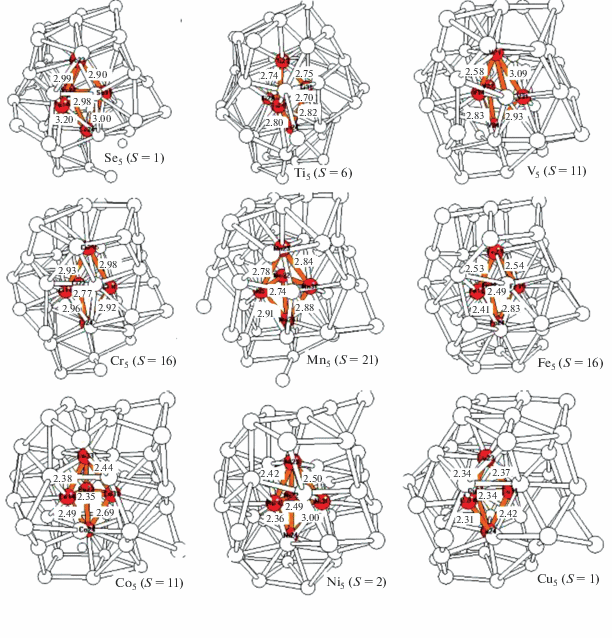
Таблица 3.

Относительные энергии ΔЕ_отн (в ккал/моль) и распределение спиновой плотности ρ между сердечником L₅ и каркасом Al₃₉ (в долях е) у низколежащих мультиплетов кластеров L₅@Al₃₉ (1)^*

Кластер L₅@Al₃₉	Спин, S	ΔЕ_отн, ккал/моль	ρ(L₅), е	ρ(Al₃₉), е	Кластер L₅@Al₃₉	Спин, S	ΔЕ_отн, ккал/моль	ρ(L₅), е	ρ(Al₃₉) е
Sc₅@Al₃₉	1 3 5	0 5.3 12.9	– 0.7 1.3	– 1.3 2.7	Fe₅@Al₃₉	16 12 8	0 14.9 38.0	14.3 13.8 13.6	0.7 –2.8 –6.6
Ti₅@Al₃₉	6 4 2	0 0.6 2.4	2.8 2.0 1.5	2.2 1.0 –1.5	Co₅@Al₃₉	11 7 3	0 17.7 26.4	8.5 7.4 2.1	1.5 –1.4 –0.1
V₅@Al₃₉	11 7 3	0 2.3 16.9	7.4 3.9 2.4	2.6 2.1 –0.4	Ni₅@Al₃₉	2 4 6	0 8.7 16.1	0.7 0.7 1.7	0.3 2.3 3.3
Cr₅@Al₃₉	16 12 8	0 18.8 51.8	17.7 17.0 16.1	–2.7 –6.0 –9.1	Cu₅@Al₃₉	1 3 5	0 11.7 30.0	– 0.3 0.5	– 1.7 3.5
Mn₅@Al₃₉	21 17 13	0 10.9 33.6	21.6 20.0 19.3	–1.6 –4.0 –7.3	Zn₅@All₃₉	2 4 6	0 10.1 27.1	0.1 0.4 0.5	0.9 2.6 4.5

* У систем с допантами L = Sc, Ni, Cu и Zn данные приведены для предпочтительных низкоспиновых, а у остальных кластеров − для предпочтительных высокоспиновых мультиплетов.

Все расчеты кластеров с допантами 3d-элементов выполнены с помощью программы GAUSSIAN-09 [12] в рамках приближения B3LYP [13, 14] с базисами 6-31G (оптимизация геометрии и расчеты частот колебаний) и 6-31G* (повторная оптимизация геометрии и расчет энергетических характеристик). В расчетах кластеров с допантами 4d-элементов использовали смешанный базис Gen = LANL2DZ(L) + 6-31G(Al).

Отметим, что расчеты кластеров с участием атомов d-металлов с открытыми оболочками могут представлять сложную задачу из-за высокой плотности и пересечений низколежащих термов с различной мультиплетностью, из-за присутствия термов с одинаковой мультиплетностью, но с разным распределением электронной и спиновой плотности, из-за многодетерминантного характера волновых функций и др. Здесь мы ограничились оптимизацией высокоспиновых мультиплетов c S = S_max и расчетом вертикальных состояний с мультплетностями S = S_max − 2, S_max − 4, S_max − 6 и т.д. при геометрии, оптимизированной для S = = S_max. В рамках приближения B3LYP высокоспиновые состояния (S = S_max) с однотерминантными функциями должны описываться точнее, чем низкоспиновые, и в настоящей работе основное внимание концентрировалось на относительных изменениях рассчитанных величин в рядах родственных систем.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Изомерия кластеров Ti₂Al₄₂, Mn₂Al₄₂, Ni₂Al₄₂, Zr₂Al₄₂ и Pd₂Al₄₂. Из табл. 1 следует, что в рамках приближения B3LYP/6-31G* кластерам Ti₂Al₄₂ и Mn₂Al₄₂ отвечают наиболее выгодные высокоспиновые состояния с мультиплетностями S_max = 5 и 11. Рядом с ними (в пределах 5−8 и 7−12 ккал/моль) располагаются состояния с более низкими значениями S = 3 и 1, 9 и 7 соответственно. У Ni₂Al₄₂ различия в энергиях синглета, триплета и квинтета не превышают ∼5 ккал/моль, причем синглет и триплет практически вырождены. У состояний кластеров Ti₂Al₄₂ и Mn₂Al₄₂ с S_max спиновые плотности на атомах 3d-металлов варьируют в пределах ∼1.3−1.6 и ∼4.5−4.8 e соответственно. На качественном уровне они ближе всего соответствуют двухвалентному состоянию атомов титана и марганца, где они сохраняют два и пять неспаренных электронов с параллельными спинами. С другой стороны, в триплетном состоянии Ni₂Al₄₂ спиновая плотность ρ(Ni) не превышает десятых долей е, так что состояние атомов никеля в этом кластере близко к нульвалентному.

При уменьшении суммарной мультиплетности кластера, например при переходе от S_max = 11 к S = 9, 7 и 5 у Mn₂Al₄₂ (табл. 2), спиновая плотность допанта ρ(Mn) уменьшается медленно и не опускается ниже 4.3−4.5 е. Этот результат свидетельствует о том, что уменьшение S связано в основном с перераспределением спиновой плотности каркаса ρ(Al₄₂). При этом спины допантов, с одной стороны, и спины каркаса Al₄₂ – с другой, могут иметь противоположное направление (антиферромагнитный эффект) и частично компенсировать друг друга. Похожая картина имеет место при возбуждении термов у внутреннего изомера Ni₂Al₄₂ (${\mathbf{а }}_{{\mathbf{I}}}^{ + },{\mathbf{а }}_{{\mathbf{I}}}^{ - }$). В этом случае спиновая плотность ρ(Ni) остается малой как в триплетном (0.07 е), так и в квинтетном (0.18 е) состоянии, так что увеличение мультиплетности S этого кластера почти целиком связано с увеличением спиновой плотности каркаса ρ(Al₄₂).

Из табл. 1 следует, что для всех тестовых кластеров явно предпочтительными являются внутренние изомеры с допантами в аксиальных (${\mathbf{а }}_{{\mathbf{I}}}^{ + },{\mathbf{а }}_{{\mathbf{I}}}^{ - }$) и экваториальных (e, e') позициях ядра. У Ti₂Al₄₂ эти изомеры близки друг к другу в пределах нескольких ккал/моль, а у Mn₂Al₄₂ и Ni₂Al₄₂ экваториальный изомер значительно менее выгоден, чем аксиальный. Среди поверхностных изомеров предпочтительна структура ${\mathbf{m}}_{{\mathbf{I}}}^{ + },{\mathbf{m}}_{{\mathbf{I}}}^{ - }$, но и она остается на ∼15 (Ti₂Al₄₂), ∼8 (Mn₂Al₄₂) и ∼41 (Ni₂Al₄₂) ккал/моль менее выгодной, чем ${\mathbf{а }}_{{\mathbf{I}}}^{ + },{\mathbf{а }}_{{\mathbf{I}}}^{ - }$. Аналогичный результат получен в расчетах кластеров Cu₂Al₄₂ и Zn₂Al₄₂, у которых внутренний изомер выгоднее поверхностного на ∼25 и ∼22 ккал/моль [10].

В отличие от систем L₂Al₄₂ с допантами 3d-элементов, для аналогов с допантами 4d-элементов (в табл. 1 приведены данные расчетов для кластеров Zr₂Al₄₂ и Pd₂Al₄₂) предпочтительны низкоспиновые (синглетные) состояния. Возбуждение ближайших триплетных и квинтетных состояний из основного синглетного связано с затратами энергии ∼4−6 и ∼10−12 ккал/моль соответственно.

Сравнение внутреннего (${\mathbf{а }}_{{\mathbf{I}}}^{ + },{\mathbf{а }}_{{\mathbf{I}}}^{ - }$) и поверхностного (${\mathbf{m}}_{{\mathbf{I}}}^{ + },{\mathbf{m}}_{{\mathbf{I}}}^{ - }$) изомеров кластеров L₂Al₄₂ (L = Ti−Ni). Рассмотрим тенденции поведения энергетических, структурных и электронных характеристик низших внутреннего и поверхностного изомеров у высокоспиновых кластеров L₂Al₄₂ при изменении допанта вдоль 3d-периода.

Анализ относительных энергий (Е_отн, табл. 2) показывает, что для всего семейства этих кластеров наиболее выгодны аксиальный и близко расположенный экваториальный внутренние изомеры ${\mathbf{а }}_{{\mathbf{I}}}^{ + },{\mathbf{а }}_{{\mathbf{I}}}^{ - }$ и e_O,e_O, в которых оба допанта полностью экранированы соседними поверхностными атомами алюминия. Ближайший изомер с допантами в открытых поверхностных позициях ${\mathbf{m}}_{{\mathbf{I}}}^{ + },{\mathbf{m}}_{{\mathbf{I}}}^{ - }$ лежит выше на ∼13−23 ккал/моль, а остальные поверхностные структуры еще менее выгодны. Во всех случаях перемещение (промотирование) допантов из закрытых внутренних на открытые (каталитически активные) поверхностные позиции должно быть связано с существенными затратами энергии.

Энергии Е_дис распада по схеме

(1)

${{{\text{L}}}_{{\text{2}}}}{\text{A}}{{{\text{l}}}_{{{\text{42}}}}}{\text{(}}{\mathbf{a}}_{{\mathbf{I}}}^{ + }{\text{,}}{\mathbf{a}}_{{\mathbf{I}}}^{ - }{\text{)}} \to {\text{A}}{{{\text{l}}}_{{{\text{42}}}}} + {\text{2L,}}$

приходящиеся на один атом допанта, в большинстве случаев значительны (∼60−80 кал/моль), что свидетельствует о высокой энергетической стабильности и о возможности существования в свободном состоянии кластеров L₂Al₄₂ с допантами Ti, V, Cr, Co и Ni. Исключение составляет кластер Mn₂Al₄₂, у которого энергия Е_дис отрицательна. Согласно расчетам, наиболее стабильными должны быть кластеры с допантами хрома и никеля, а наименее стабильным − кластер Fe₂Al₄₂.

Из табл. 2 видно, что расстояния R(LL) между допантами у обоих изомеров варьируют в пределах ∼4.0−4.5 Å и имеют тенденцию к уменьшению с увеличением порядкового номера атома М и его атомного радиуса. Из анализа спиновой плотности ρ следует, что допанты V, Cr и Mn в кластерах сохраняют ∼3, ∼4 и ∼5 неспаренных электронов с параллельными спинами, а плотность алюминиевого каркаса ρ(Al₄₂) при этом не превышает 0.5−1.1 е. В конце 3d-периода плотность ρ(Al₄₂) увеличивается до ∼3.8 е, свидетельствуя, в частности, о том, что у внутреннего изомера ${\mathbf{а }}_{{\mathbf{I}}}^{ + },{\mathbf{а }}_{{\mathbf{I}}}^{ - }$ кластера Ni₂Al₄₂ в квинтетном состоянии (S = 5) спиновая плотность практически полностью локализуется на алюминиевом каркасе, а атомы никеля остаются близкими к нульвалентным.

Помимо структур, изображенных на рис. 2, нами была рассчитана серия поверхностных изомеров с двумя соседними атомами L, которые располагаются на общих ребрах каркаса и могут играть роль двухцентровых каталитических центров. Их подробное рассмотрение будет дано позднее при изучении механизмов присоединения к ним молекул Н₂ и углеводородов к “активным” ребрам Ti−Ti, Ni−Ni и др. Здесь важен вывод, что все изомеры L₂Al₄₂ с допантами на общем ребре менее выгодны по сравнению с внутренним изомером ${\mathbf{а }}_{{\mathbf{I}}}^{ + },{\mathbf{а }}_{{\mathbf{I}}}^{ - }$ на 20−35 ккал/моль. Аксиальные и экваториальные позиции а и е внутреннего ядра остаются предпочтительными у всех рассмотренных выше соединений.

Кластеры L₅@Al₃₉. В заключение мы рассчитали структуру и свойства еще одного семейства кластеров типа L₅@Al₃₉ с пятью атомами переходных металлов, которые занимают самые выгодные позиции (2а + 3е) и образуют бипирамидальный сердечник L₅, встроенный во внутреннюю полость каркаса Al₃₉ (рис. 3). В табл. 3 сравниваются относительные энергии ΔE_отн низших мультиплетов кластеров L₅@Al₃₉, а также суммарные спиновые плотности на внутреннем сердечнике ρ(L₅) и алюминиевом каркасе ρ(Al₃₉). Из табл. 3 видно, что в зависимости от положения атома L в 3d-ряду сердечники L₅ претерпевают деформации со значительными изменениями валентных углов и расстояний R(LL) (по сравнению с параметрами свободных кластеров L₅, рассчитанных нами в том же приближении). В частности, при изменении L вдоль периода аксиальное расстояние R(L_a, L_a) удлиняется от ∼4.8 у Ti₅ до ∼5.2 Å у Cr₅ и далее монотонно укорачивается до ∼4.1 Å у Cu₅, вновь увеличиваясь до ∼4.4 Å у Zn₅.

Подобно L₂Al₄₂, для кластеров L₅@Al₃₉ с атомами L, стоящими в начале и в конце 3d-периода, предпочтительны низкоспиновые состояния (синглет для L₅ = Sc₅ и Cu₅ и дублет для L₅ = Ni₅). Для кластеров с атомами L в середине периода наиболее выгодны высокоспиновые состояния. У последних соединений (с L в середине периода) при последовательном уменьшении мультиплетности кластера от S_max к S_max −2, S_max −4 и т.д. спиновая плотность сердечников ρ(L₅) меняется сравнительно слабо. Так, при изменении мультиплетности кластера Cr₅@Al₃₉ в интервале S = = 12−16 плотность ρ(Cr₅) сохраняется на уровне 17.0−17.7 е. У кластера Fe₅@Al₃₉ при уменьшении S от16 до 8 плотность ρ(Fe₅) остается в интервале 13.6−14.3 е. Аналогичная картина наблюдается для ρ(Со₅), и в рамках приближенной модели можно полагать, что в этих мультиплетах у атомов Cr, Fe и Co в сердечниках L₅ сохраняется по 4, 3 и 2 неспаренных электрона с параллельными спинами, а атомы Ni находятся в нульвалентном состоянии. У кластеров с допантами Ti₅ и V₅ имеются группы из нескольких низколежаших и близких по энергии мультиплетов (табл. 3).

Особый интерес представляет самый высокоспиновый кластер Mn₅@Al₃₉, у которого в интервале S = 17−21 плотность ρ(Mn₅) сохраняется в пределах ∼20−21.6 е, что соответствует числу неспаренных электронов у каждого атома Mn, промежуточному между 4 и 5. Ступенчатое уменьшение суммарного спина кластера Mn₅@Al₃₉ в интервале S = 17−21 определяется соответствующим увеличением плотности на каркасе ρ(Al₃₉) с противоположным знаком (антиферромагнитный эффект). Кластер Mn₅@Al₃₉ может рассматриваться как простейший молекулярный магнит с высоким магнитным моментом и быть полезным при моделировании родственных наноразмерных частиц с более крупными магнитными сердечниками и более высокими магнитными моментами.

Отметим, что, согласно расчетам, у кластеров L₅@Al₃₉ с допантами атомов 4d-элементов наиболее выгодными оказываются низкоспиновые состояния и возбуждение уровней с более высокой мультиплетностью связано с затратами энергии. Аналогичная картина отмечалась выше для кластеров Zr₂Al₄₂ и Pd₂Al₄₄ (табл. 1), где энергии возбуждения триплета и квинтета из синглета лежат в умеренных границах ∼5−12 ккал/моль, а высокоспиновые термы явно невыгодны.

Можно полагать, что результаты расчетов и выводы, полученные для систем L₂Al₄₂ и L₅Al₃₉, могут быть полезными при распространении DFT-подходов на более крупные наноразмерные кластеры c более высоким содержанием допантов.

БЛАГОДАРНОСТЬ

Работа выполнена в рамках госзадания № 0089-2014-0030 при поддержке РФФИ (№ 18-03-01156а).

Список литературы

Jimmenes-Iszal E., Moreno D., Mercero J.M. et al. // J. Phys. Chem. A. 2014. V. 118. P. 4309.
Zheng M.M., Li S.J., Su Y., Kawazoe Y. // J. Phys. Chem. A. 2013. V. 117. P. 25077.
Costanzo E., van Hemert M.C., Kroes G-J. // J. Phys. Chem. C. 2014. V. 118. P. 513.
Smith J.C., Reber A.C., Khana S.N., Castleman J. // J. Phys. Chem. A. 2014. V. 118. P. 8485.
Das S., Pal S., Krishnamurty S. // J. Phys. Chem. C. 2014. V. 118. P. 19869.
Varano A., Henry D.J., Yarovsky I. // J. Phys. Chem. C. 2014. V. 118. P. 19865.
Brodova I.G., Shirinkina I.G., Petrova A.N. // Lett. Mat. 2011. V. 1. № 1. P. 32.
Akutsu M., Koyashi K., Atobe J. et al. // J. Phys. Chem. A. 2007. V. 110. № 7. P. 12073. doi 10.1021/jp065161p
Charkin O.P., Klimenko N.M. // Russ. J. Inorg. Chem. 2015. V. 60. № 5. P. 577. doi 10.1134/S0036023615050034 [Чаркин О.П., Клименко Н.М. // Журн. неорган. химии. 2015. Т. 60. С. 644.]
Charkin O.P., Klimenko N.M. // Russ. J. Inorg. Chem. 2018. V. 63. № 12. P. 1578. doi 10.1134/S00360-23618120069 [Чаркин О.П., Клименко Н.М. // Журн. неорган. химии. 2018. Т. 63. № 12. С. 1561.]
Charkin O.P., Klimenko N.M., Charkin D.O., Mebel A.M. // Faraday Discuss. Chem. Soc. 2003. V. 124. P. 215.
Frisch M.J. et al. GAUSSIAN-03. Revision B.03. Gaussian, Inc., Pittsburg, PA. 2003.
Becke A.D.J. // J. Chem. Phys. 1993. V. 98. P. 5648.
Lee C., Yang W., Parr R.G. // Phys. Rev. B. 1998. V. 37. P. 785.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал неорганической химии

Архивы выпусков Информация о журнале Отправить рукопись в журнал