1. На главную
  2. Электронные версии
  3. Журнал неорганической химии
  4. T. 64, № 7, 2019

Журнал неорганической химии, 2019, T. 64, № 7, стр. 746-753

Разбиение четырехкомпонентной взаимной системы Na,Rb||F,I,CrO4 и исследование стабильного тетраэдра NaF–RbI–RbF–Rb2CrO4

А. В. Бабенко 1, *, Е. М. Егорова 1, И. К. Гаркушин 1

1 Самарский государственный технический университет
443100 Самара, ул. Молодогвардейская, 244, Россия

* E-mail: anastasya.babenko2010@yandex.ru

Поступила в редакцию 06.12.2018
После доработки 07.01.2019
Принята к публикации 15.01.2019

Полный текст (PDF)

Аннотация

Исследована четырехкомпонентная взаимная система Na,Rb||F,I,CrO4, низкоплавкие смеси на основе которой перспективны в качестве расплавляемых электролитов для химических источников тока, теплоаккумулирующих материалов, сред для выращивания монокристаллов. С использованием теории графов проведено разбиение и построено древо фаз системы, которое является линейным и включает в себя четыре стабильных тетраэдра, связанных между собой стабильными секущими треугольниками. Методом дифференциального термического анализа исследован объединенный стабильный тетраэдр NaF–RbI–RbF–Rb2CrO4, поверхность кристаллизации которого представлена объемами фторида натрия, иодида рубидия, фторида рубидия, хромата рубидия и соединения Rb3CrO4F. Линии моновариантных равновесий сходятся в двух четырехкомпонентных нонвариантных точках: эвтектике Е◻491 и перитектике Р◻508.

Ключевые слова: фазовые равновесия, дифференциальный термический анализ, нонвариантное равновесие, эвтектика, перитектика

ВВЕДЕНИЕ

В настоящее время расширяется область практического использования функциональных материалов из солей s1-элементов [1, 2], которые в большинстве случаев представляют собой многокомпонентные системы. Системы из неорганических солей находят применение в качестве теплоаккумулирующих материалов [3], теплоносителей для отопительного оборудования жилых зданий [4]. Из-за относительно высокой теплопроводности и достаточно низкой вязкости расплавленные соли используются для теплообмена или охлаждения во многих системах, включая солнечные электростанции, а также при термообработке сталей [5].

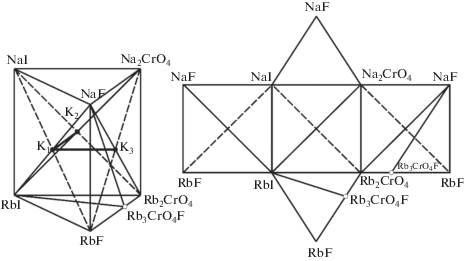
Объектом исследования является четырехкомпонентная взаимная система Na,Rb||F,I,CrO4, схема развертки и призма составов которой представлена на рис. 1. Треугольная призма системы Na,Rb||F,I,CrO4 включает две трехкомпонентные системы и три трехкомпонентные взаимные системы.

Рис. 1.

Cхема развертки и призма составов четырехкомпонентной взаимной системы Na,Rb||F,I,CrO4.

По данным [6], в системе NaF–NaI–Na2CrO4 кристаллизуется трехкомпонентная эвтектика. По данным [7], в системе RbF–RbI–Rb2CrO4 кристаллизуются тройная эвтектика и перитектика. Трехкомпонентные взаимные системы, ограняющие исследуемый объект, изучены ранее: в системе Na,Rb||F,I образуются две эвтектики [8], в системах Na,Rb||I,CrO4 [9] и Na,Rb||F,CrO4 [10] – две и три эвтектики соответственно. Данные по двухкомпонентным системам NaF–NaI, NaF–Na2CrO4, RbF–Rb2CrO4 и NaF–RbF представлены в [11], RbF–RbI – в [12], RbI–Rb2CrO4 – в [13], NaI–Na2CrO4 – в [14], по Na2CrO4–Rb2CrO4 и NaI–RbI – в [15].

С использованием теории графов [16] проведено разбиение системы Na,Rb||F,I,CrO4 на симплексы. Матрица смежности четырехкомпонентной взаимной системы Na,Rb||F,I,CrO4 приведена в табл. 1.

Таблица 1.

Матрица смежности четырехкомпонентной взаимной системы Na,Rb||F,I,CrO4

Соединение Индекс X1 X2 X3 X4 X5 X6 X46
NaF X1 1 1 1 1 1 1 1
NaI X2 1 1 0 1 0 0  
Na2CrO4 X3 1 0 1 1 0    
RbF X4 1 1 0 1      
RbI X5 1 1 1        
Rb2CrO4 X6 1 1          
Rb3CrO4F X46 1            

На основании данных таблицы составлено логическое выражение, представляющее собой произведение сумм индексов несмежных вершин:

$\begin{gathered} ({{{\text{X}}}_{{\text{2}}}} + {{{\text{X}}}_{{\text{4}}}})({{{\text{X}}}_{{\text{2}}}} + {{{\text{X}}}_{{\text{6}}}})({{{\text{X}}}_{{\text{2}}}} + {{{\text{X}}}_{{{\text{46}}}}}) \times \\ \times \,\,({{{\text{X}}}_{{\text{3}}}} + {{{\text{X}}}_{{\text{4}}}})({{{\text{X}}}_{{\text{3}}}} + {{{\text{X}}}_{{{\text{46}}}}})\left( {{{{\text{Х }}}_{{\text{4}}}} + {{{\text{Х }}}_{{\text{6}}}}} \right). \\ \end{gathered} $

После всех преобразований с учетом закона поглощения получен набор однородных несвязных графов:

$\{ {\text{1}}.{\text{ }}{{{\text{X}}}_{{\text{2}}}}{{{\text{X}}}_{{\text{3}}}}{{{\text{X}}}_{{\text{6}}}};\,\,{\text{2}}.{\text{ }}{{{\text{X}}}_{{\text{2}}}}{{{\text{X}}}_{{\text{3}}}}{{{\text{X}}}_{{\text{4}}}};\,\,{\text{3}}.{\text{ }}{{{\text{X}}}_{{\text{2}}}}{{{\text{X}}}_{{\text{4}}}}{{{\text{Х }}}_{{{\text{46}}}}};\,\,{\text{4}}.{\text{ }}{{{\text{Х }}}_{{\text{4}}}}{{{\text{Х }}}_{{\text{6}}}}{{{\text{Х }}}_{{{\text{46}}}}}\} .$

Путем выписывания недостающих вершин для несвязных графов получим набор стабильных ячеек и отвечающие им соли:

$\begin{gathered} {\text{I}})\,\,{{{\text{X}}}_{{\text{1}}}}{{{\text{X}}}_{{{\text{46}}}}}{{{\text{X}}}_{{\text{4}}}}{{{\text{X}}}_{{\text{5}}}}\quad\quad\quad\quad{\text{NaF}}{\kern 1pt} - {\kern 1pt} {{{\text{d}}}_{{\text{1}}}}{\kern 1pt} --{\kern 1pt} {\text{RbF}}{\kern 1pt} --{\kern 1pt} {\text{RbI}}, \hfill \\ {\text{II}})\,\,{{{\text{X}}}_{{\text{1}}}}{{{\text{X}}}_{{\text{6}}}}{{{\text{X}}}_{{{\text{46}}}}}{{{\text{X}}}_{{\text{5}}}}\quad\quad\quad{\text{NaF}}{\kern 1pt} --{\kern 1pt} {\text{R}}{{{\text{b}}}_{{\text{2}}}}{\text{Cr}}{{{\text{O}}}_{{\text{4}}}}{\kern 1pt} --{\kern 1pt} {{{\text{d}}}_{{\text{1}}}}{\kern 1pt} --{\kern 1pt} {\text{RbI}}, \hfill \\ {\text{III}})\,\,{{{\text{X}}}_{{\text{3}}}}{{{\text{X}}}_{{\text{1}}}}{{{\text{X}}}_{{\text{6}}}}{{{\text{X}}}_{{\text{5}}}}\quad\quad\quad{\text{N}}{{{\text{a}}}_{{\text{2}}}}{\text{Cr}}{{{\text{O}}}_{{\text{4}}}}{\kern 1pt} --{\kern 1pt} {\text{NaF}}{\kern 1pt} --{\kern 1pt} {\text{R}}{{{\text{b}}}_{{\text{2}}}}{\text{Cr}}{{{\text{O}}}_{{\text{4}}}}{\kern 1pt} --{\kern 1pt} {\text{RbI}}, \hfill \\ {\text{IV}})\,\,{{{\text{X}}}_{{\text{2}}}}{{{\text{X}}}_{{\text{1}}}}{{{\text{X}}}_{{\text{3}}}}{{{\text{X}}}_{{\text{5}}}}\quad\quad\quad{\text{NaI}}{\kern 1pt} --{\kern 1pt} {\text{NaF}}{\kern 1pt} --{\kern 1pt} {\text{N}}{{{\text{a}}}_{{\text{2}}}}{\text{Cr}}{{{\text{O}}}_{{\text{4}}}}{\kern 1pt} --{\kern 1pt} {\text{RbI}}{\text{.}} \hfill \\ \end{gathered} $

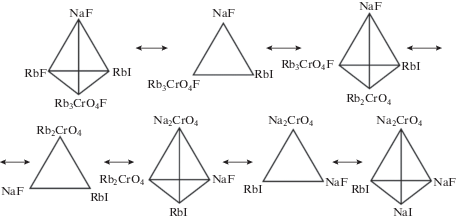
Общие элементы каждой пары смежных симплексов образуют секущие элементы (стабильные треугольники): NaF–d1–RbI, NaF–Rb2CrO4–RbI и NaF–Na2CrO4–RbI. Наличие соединения Rb3CrO4F (d1) в тетраэдрах NaF–d1–RbF–RbI и NaF–Rb2CrO4–d1–RbI и связывающем их секущем треугольнике NaF–d1–RbI приводит к тому, что эти элементы объединяются в один стабильный тетраэдр NaF–RbI–RbF–Rb2CrO4. Это происходит вследствие того, что в системе RbF–RbI–Rb2CrO4 соединение Rb3CrO4F с конгруэнтным типом плавления переходит в инконгруэнтное, поэтому один из симплексов, а именно NaF–Rb2CrO4–d1–RbI, не будет содержать четырехкомпонентных нонвариантных точек и его исследование нецелесообразно. В результате проведенного разбиения системы Na,Rb||F,I,CrO4 построено древо фаз (рис. 2).

Рис. 2.

Древо фаз четырехкомпонентной взаимной системы Na,Rb||F,I,CrO4.

Химическое взаимодействие в системе Na,Rb||F,I,CrO4 описывается двумя линиями конверсии: К2–К1 и К1–К3, которые сходятся в точке полной конверсии К1. Фигура конверсии системы Na,Rb||F,I,CrO4 представлена на рис. 1.

В трехкомпонентных взаимных системах протекают реакции обмена в точках полной конверсии (табл. 2). Суммируя реакции (2) и (1) для составов точек полной конверсии К2 и К1, получаем реакцию обмена, протекающую в составе, отвечающем центральной точке линии конверсии К2–К1:

$\begin{gathered} {\text{RbF}} + {\text{R}}{{{\text{b}}}_{{\text{2}}}}{\text{Cr}}{{{\text{O}}}_{{\text{4}}}} + {\text{3NaI}} \rightleftarrows \\ \rightleftarrows {\text{3RbI}} + {\text{NaF}} + {\text{N}}{{{\text{a}}}_{{\text{2}}}}{\text{Cr}}{{{\text{O}}}_{{\text{4}}}}. \\ \end{gathered} $
Таблица 2.

Реакции обмена в точках полной конверсии в трехкомпонентных взаимных системах

Система Реакция ${{\Delta }_{r}}H_{{298}}^{^\circ }$ ${{\Delta }_{r}}G_{{298}}^{^\circ }$
кДж
Na,Rb||F,I 2RbF + 2NaI ⇄ 2NaF + 2RbI (1) –121.9 –118.1
Na,Rb||I,CrO4 2NaI + Rb2CrO4 ⇄ 2RbI + Na2CrO4 (2) –19.9 –19.7
Na,Rb||F,CrO4 2RbF + Na2CrO4⇄ 2NaF + Rb2CrO4 (3) –102.1 –98.4

Выражая содержание компонентов в точке К2 через x, в точке К1 через (1 – x), получаем уравнение реакции обмена для любой точки линии конверсии К2–К1:

$\begin{gathered} ({\text{1}}--x){\text{RbF}} + x{\text{R}}{{{\text{b}}}_{{\text{2}}}}{\text{Cr}}{{{\text{O}}}_{{\text{4}}}} + {\text{NaI}} \rightleftarrows \\ \rightleftarrows {\text{RbI}} + \left( {{\text{1}}--x} \right){\text{NaF}} + x{\text{N}}{{{\text{a}}}_{{\text{2}}}}{\text{Cr}}{{{\text{O}}}_{{\text{4}}}}. \\ \end{gathered} $

Присутствующие фазы для линии конверсии К2–К1: NaF, RbI, Na2CrO4.

Суммируя уравнения (1) и (3) для составов точек полной конверсии К1 и К3, получаем реакцию обмена, протекающую в составе, отвечающем центральной точке линии конверсии К1–К3:

$\begin{gathered} {\text{NaI}} + {\text{N}}{{{\text{a}}}_{{\text{2}}}}{\text{Cr}}{{{\text{O}}}_{{\text{4}}}} + {\text{3RbF}} \rightleftarrows \\ \rightleftarrows \,\,{\text{3NaF}} + {\text{R}}{{{\text{b}}}_{{\text{2}}}}{\text{Cr}}{{{\text{O}}}_{{\text{4}}}} + {\text{RbI}}. \\ \end{gathered} $

Выражая содержание компонентов в точке К1 через y, в точке К3 через (1 – y), получаем уравнение реакции обмена для составов любой точки линии конверсии К1–К3:

$\begin{gathered} y{\text{NaI}} + \left( {{\text{1}}--y} \right){\text{N}}{{{\text{a}}}_{{\text{2}}}}{\text{Cr}}{{{\text{O}}}_{{\text{4}}}} + {\text{RbF}} \rightleftarrows \\ \rightleftarrows {\text{NaF}} + \left( {{\text{1}}--y} \right){\text{R}}{{{\text{b}}}_{{\text{2}}}}{\text{Cr}}{{{\text{O}}}_{{\text{4}}}} + y{\text{RbI}}. \\ \end{gathered} $

Таким образом, стабильными продуктами реакции для составов линии конверсии К1–К3 являются NaF, RbI и Rb2CrO4.

Образованная линиями конверсии К2–К1 и К1–К3 треугольная плоскость отражает взаимодействие трех пар солей в четверной взаимной системе Na,Rb||F,I,CrO4.

Некоторые стабильные элементы четырехкомпонентной взаимной системы Na,Rb||F,I,CrO4 были изучены авторами ранее: стабильный треугольник RbI–Na2CrO4–NaF, в котором образуется трехкомпонентная эвтектика при 502°С (состав: 37% RbI, 54% Na2CrO4, 9% NaF), стабильный треугольник NaF–Rb2CrO4–RbI, в котором выявлена трехкомпонентная эвтектика при 576°С (состав: 7.5% NaF, 30% Rb2CrO4, 62.5% RbI), стабильный тетраэдр Na2CrO4–NaF–Rb2CrO4–RbI, в котором кристаллизуются непрерывные ряды твердых растворов.

Экспериментальное исследование стабильного объединенного тетраэдра NaF–Rb2CrO4–RbI–RbF проведено методом дифференциального термического анализа. Исходные реактивы квалификации “ч. д. а.” (NaF), “ч.” (Rb2CrO4, RbF) и “х. ч.” (RbI) были предварительно обезвожены. Температуры плавления, полиморфного превращения (tα ⇄ β(Rb2CrO4) = 730°С) индивидуальных солей соответствовали справочным данным [17, 18]. Все составы выражены в экв. %.

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

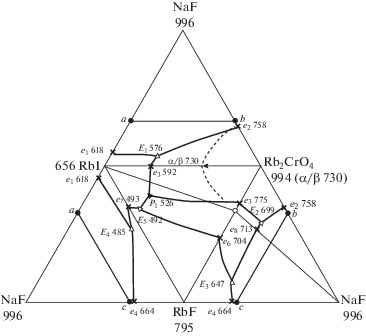
Развертка стабильного тетраэдра NaF–RbI–RbF–Rb2CrO4 представлена на рис. 3. Анализ элементов огранения позволил предположить образование четверных эвтектики и перитектики.

Рис. 3.

Развертка стабильного тетраэдра NaF–RbI–RbF–Rb2CrO4.

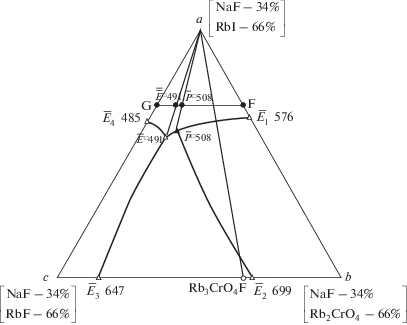
Для получения полной картины о фазовых взаимодействиях в системе рассмотрено политермическое сечение a[34% NaF + 66% RbI]–b[34% NaF + + 66% Rb2CrO4]–c[34% NaF + 66% RbF] в поле кристаллизации компонента фторида натрия (рис. 4). Из Т–х-диаграммы политермического разреза G[34.0% NaF + 46.2% RbI + 19.8% RbF]–F[34.0% NaF + 46.2% RbI + 19.8% Rb2CrO4] установлены направления на проекции четырехкомпонентных эвтектики и перитектики (рис. 5).

Рис. 4.

Политермическое сечение четырехкомпонентной взаимной системы Na,Rb||F,I,CrO4.

Рис. 5.

Т–х-диаграмма политермического разреза GF четырехкомпонентной взаимной системы Na,Rb||F,I,CrO4.

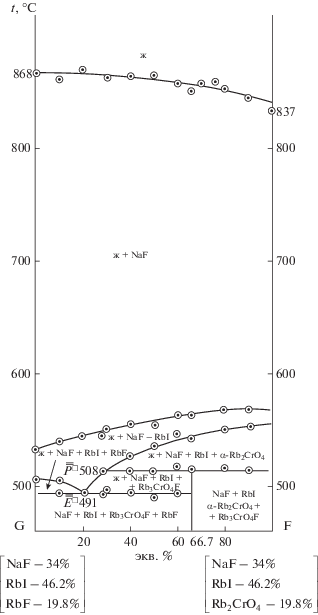
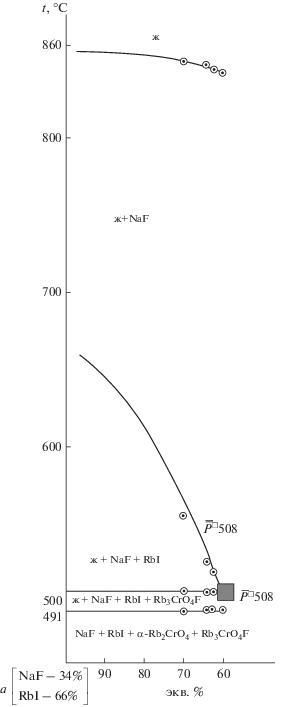
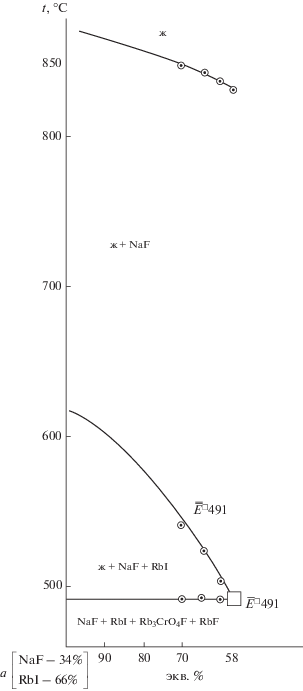
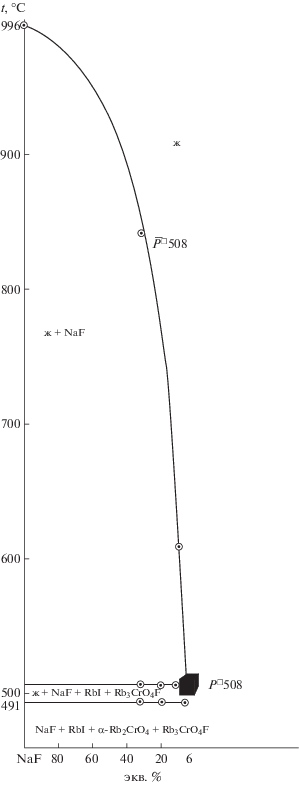
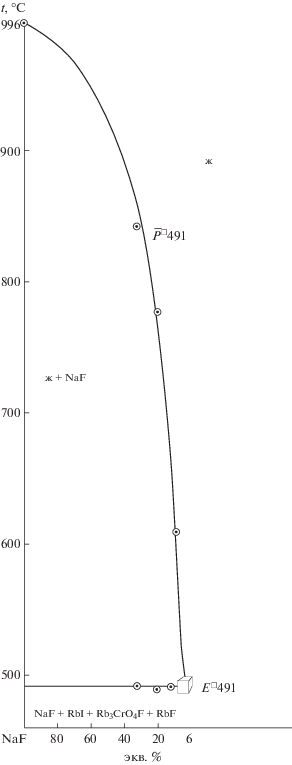
При исследовании разрезов, выходящих из вершины а[34% NaF + 66% RbI] и проходящих через направления ${{\bar {\bar {P}}}^{\square }}$508 (рис. 6) и ${{\bar {\bar {E}}}^{\square }}$491 (рис. 7), найдены проекции на четверные перитектику P□508 и эвтектику E□491. Содержание фторида натрия в четырехкомпонентных нонвариантных точках определено в ходе изучения разрезов NaF → Р□508 (рис. 8) и NaF → Е□491 (рис. 9).

Рис. 6.

Политермический разрез а[34% NaF + 66% RbI] → P□508.

Рис. 7.

Политермический разрез а[34% NaF + 66% RbI] →E□491.

Рис. 8.

Политермический разрез NaF → Р□508.

Рис. 9.

Политермический разрез NaF → Е□491.

ЗАКЛЮЧЕНИЕ

Проведено разбиение четырехкомпонентной взаимной системы Na,Rb||F,I,CrO4, которое представлено линейным древом фаз, включающим четыре стабильных тетраэдра, разделенных тремя стабильными секущими треугольниками. Аналогичный вариант разбиения приведен в работах [19, 20].

Исследован стабильный тетраэдр NaF–RbI–RbF–Rb2CrO4, поверхность кристаллизации которого представлена объемами фторида натрия, иодида рубидия, фторида рубидия, хромата рубидия и соединения Rb3CrO4F. Линии моновариантных равновесий сходятся в двух четырехкомпонентных нонвариантных точках: эвтектике Е□491 и перитектике Р□508.

Характеристики точек нонвариантного равновесия экспериментально исследованного тетраэдра NaF–RbI–RbF–Rb2CrO4 приведены в табл. 3.

Таблица 3.  

Характеристики точек нонвариантного равновесия в тетраэдре NaF–RbI–RbF–Rb2CrO4

Система Характер точки Содержание компонентов, экв. % tпл, °С
1 2 3 4
NaF–RbF–RbI–Rb2CrO4 Р□
Е□		 6
6 		26.79
31.02 		56.40
54.52 		10.81
8.46 		508
491

Фазовые равновесия элементов стабильного тетраэдра представлены в табл. 4.

Таблица 4.

Фазовые реакции, протекающие в тетраэдре NaF–RbI–RbF–Rb2CrO4

Элемент диаграммы Фазовая реакция
Точка E□ ж ⇄ NaF + RbI + RbF + Rb3CrO4F
Точка P□ ж + α-Rb2CrO4 ⇄ NaF + RbI + Rb3CrO4F
Монова- риантные линии:
E3–E□ ж ⇄ RbF + NaF + Rb3CrO4F
E4–E□ ж ⇄ RbF + RbI + NaF
E5–E□ ж ⇄ RbF + RbI + Rb3CrO4F
E□–P□ ж ⇄ NaF + RbI + Rb3CrO4F
E1–P□ ж ⇄ RbI + NaF + α-Rb2CrO4
E2–P□ ж ⇄ NaF + α-Rb2CrO4 + Rb3CrO4F
P1–P□ ж ⇄ RbI + α-Rb2CrO4 + Rb3CrO4F

ФИНАНСИРОВАНИЕ РАБОТЫ

Работа выполнена в рамках базовой части государственного задания ФГБОУ ВО СамГТУ, проект № 4.5534.2017/8.9.

Список литературы

  1. Mancini T. Advantages of Using Molten Salt. Sandia National Laboratories. Internet resources. http://www.webcitation.org/60AE7heEZ

  2. Uhlíř J. // J. Nucl. Mater. 2007. V. 360. № 1. P. 6. https://doi.org/10.1016/j.jnucmat.2006.08.008

  3. Dinker A., Agarwal M., Agarwal G.D. // J. Energy Institute. 2017. V. 90. № 1. P. 1. https://doi.org/10.1016/j.joei.2015.10.002

  4. Zhihang Zh., Mohammad T.A., Amanullah M.T.O. // Energy Procedia. 2017. V. 110. P. 243. https://doi.org/10.1016/j.egypro.2017.03.134

  5. Rapp B. // Materialstoday. 2015. V. 8. № 12. P. 6. https://doi.org/10.1016/S1369-7021(05)71195-0

  6. Garkushin I.K., Ignat’eva E.O., Dvoryanova E.M. // Russ. J. Inorg. Chem. 2012. V. 57. № 5. P. 732. [Гаркушин И.К., Игнатьева Е.О., Дворянова Е.М. // Журн. неорган. химии. 2012. Т. 57. № 5. С. 800.]https://doi.org/10.1134/S0036023612050063

  7. Burchakov A.V., Dvoryanova E.M., Kondratyuk I.M. // Russ. J. Inorg. Chem. 2015. V. 60. № 4. P. 511. [Бурчаков А.В., Дворянова Е.М., Кондратюк И.М. // Журн. неорган. химии. 2015. Т. 60. № 4. С. 572.]https://doi.org/10.1134/S0036023615040038

  8. Трунин А.С., Гаркушин И.К., Воронин К.Ю. и др. А.с. 1089100 СССР, МК 44 С09К 5106. Теплоаккумулирующий состав. СССР // Бюл. изобр. 1984. № 16. 2 с.

  9. Саламаткина А.А., Бехтерева Е.М. // VI Всерос. конф. молодых ученых, аспирантов и студентов с междунар. участием “Менделеев-2012”. СПб., 2012. С. 510.

  10. Саламаткина А.А. // Тез. докл. III Конф. молодых ученых по общей и неорган. химии. М., 2013. С. 107.

  11. Воскресенская Н.К., Евсеева Н.Н., Беруль С.И. и др. Справочник по плавкости систем из безводных неорганических солей. М.: Изд-во АН СССР. М., 1961. Т. 1. 845 с.

  12. Кондратюк И.М., Дворянова Е.М., Гаркушин И.К. // Изв. Самарск. научн. центра РАН. Химия и хим. технология. 2004. С. 12.

  13. Бурчаков А.В., Бехтерева Е.М., Кондратюк И.М. // Бутлеровские сообщения. 2014. Т. 39. № 8. С. 40.

  14. Игнатьева Е.О., Дворянова Е.М., Гаркушин И.К. // Вестн. Иркутск. гос. техн. ун-та. 2011. Т. 57. № 10. С. 153.

  15. Посыпайко В.И., Алексеева Е.А. Диаграммы плавкости солевых систем. Ч. II. Двойные системы с общим анионом. М.: Металлургия, 1977. 304 с.

  16. Оре О. Теория графов. М.: Наука, 1980.

  17. Термические константы веществ. Справочник / Под ред. Глушко В.П. М.: ВИНИТИ, 1981. Вып. X. Ч. 1. 300 с.

  18. Термические константы веществ. Справочник / Под ред. Глушко В.П. М.: ВИНИТИ, 1981. Вып. X. Ч. 2. 300 с.

  19. Гаркушин И.К., Губанова Т.В., Петров А.С. и др. Фазовые равновесия в системах с участием метаванадатов некоторых щелочных металлов. М.: Машиностроение-1, 2005. 118 с.

  20. Kosyakov V.I., Shestakov V.A., Grachev E.V. // Russ. J. Inorg. Chem. 2017. V. 63. № 3. P. 318. [Косяков В.И., Шестаков В.А., Грачев Е.В. // Журн. неорган. химии. 2017. Т. 63. № 3. С. 314.]https://doi.org/10.7868/S0044457X17030102

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал неорганической химии

Архивы выпусков Информация о журнале Отправить рукопись в журнал