Журнал неорганической химии, 2019, T. 64, № 7, стр. 741-745
Нонвариантные равновесия в многокомпонентных системах
1 Таджикский государственный педагогический университет им. С. Айни
734003 Душанбе, пр-т Рудаки, 121, Таджикистан
* E-mail: soliev.lutfullo@yandex.com
Поступила в редакцию 13.07.2018
После доработки 30.07.2018
Принята к публикации 11.11.2018
Аннотация
На основе принципа совместимости элементов строения диаграмм частных составляющих (n-компонентных) и общей ((n + 1)-компонентной) систем с учетом требования правила фаз Гиббса разработан метод трансляции для прогнозирования и построения диаграмм фазовых равновесий многокомпонентных систем. Исследовано состояние нонвариантных равновесий в пятикомпонентной системе NaCl–KCl–MgCl2–CaCl2–H2O при 25°C. Показано, что в исследованной многокомпонентной системе реализуются такие варианты нонвариантных равновесий, при которых один и тот же состав равновесных твердых фаз может находиться в равновесии с насыщенным раствором различной концентрации. Следовательно, такое нонвариантное равновесие на диаграмме должно отображаться не точкой, а геометрическим (нонвариантным) образом, имеющим размер (его условно можно назвать квазиточкой). Размер этого образа определяется пределами изменения концентрации компонентов в равновесном насыщенном растворе.
ВВЕДЕНИЕ
Основоположник теории и практики физико-химического анализа Н.С. Курнаков подразделял диаграммы состояния химических систем на две самостоятельные части: фазовый комплекс и координатный остов [1, 2]. Фазовый комплекс как самостоятельная часть химической диаграммы включает геометрические образы (поля, кривые, точки), расположенные на диаграмме согласно равновесной концентрации компонентов (составных частей) в жидкой фазе системы. В соответствии с правилом фаз Гиббса [3], положения нонвариантных точек на диаграмме должны отражать состояние системы, когда в равновесии с насыщенным раствором находится максимально допустимое число твердых фаз, исходя из компонентности системы.
ОБЪЕКТЫ И МЕТОДЫ
Варианты формирования нонвариантных точек тесно связаны с компонентностью системы. Чем больше компонентность системы, тем больше возможных путей (вариантов) формирования нонвариантных точек. Согласно теории физико-химического анализа [3], независимо от вариантов формирования нонвариантной точки, равновесная концентрация жидкой фазы для нее должна быть постоянной. Однако, согласно данным [4], во многих случаях для одного и того же фазового состава осадков, соответствующих нонвариантным точкам, установлены равновесные насыщенные растворы с разным содержанием составных частей (компонентов). Например, в пятикомпонентной системе NaCl–KCl–MgCl2–CaCl2–H2O при 25°С для одной из нонвариантных точек установлены два разных состава равновесной жидкой фазы (табл. 1, данные [4]).
Таблица 1.
Растворимость в системе NaCl–KCl–MgCl2–CaCl2–H2O при 25°С
| Стр. в [4] | Состав насыщенного раствора, мас. % | Фазовый состав осадков | ||||
|---|---|---|---|---|---|---|
| NaCl | KCl | MgCl2 | CaCl2 | H2O | ||
| 868 869 |
0.70 0.69 |
3.34 1.48 |
1.27 3.01 |
42.16 40.92 |
52.53 53.90 |
Га + Си + Кр + Са ⋅ 6 Га + Си + Кр + Са ⋅ 6 |
Как видно из табл. 1, для одного и того же состава равновесных твердых фаз характерна равновесная жидкая фаза с различным содержанием соответствующих солей. Следовательно, указанные четыре равновесные твердые фазы, отвечающие данной нонвариантной точке, могут совместно кристаллизоваться не при определенной (постоянной) концентрации равновесной для них жидкой фазы, а при определенном интервале концентраций содержащихся в ней солей. Это означает, что такая нонвариантная точка имеет определенный “размер” по концентрации солей в равновесной жидкой фазе. Если согласиться с таким утверждением, то, на наш взгляд, это может быть связанно с путями (вариантами) достижения данного равновесного состояния.
Обоснованность вышеприведенных суждений подтверждается результатами прогнозирования фазовых равновесий (фазовых комплексов) многокомпонентных систем методом трансляции [5], который базируется на совместимости элементов строения частных составляющих (например, n-компонентных) и общей (например, (n + 1)-компонентной) систем в одной диаграмме [6, 7] как один из наиболее универсальных методов исследования многокомпонентных систем [8].
Возможность осуществления такого метода прогнозирования строения многокомпонентных систем вытекает из высказывания Н.С. Курнакова, что “…всякую диаграмму многокомпонентной системы можно рассматривать как образованную из диаграммы системы с меньшим числом компонентов, усложненной введением новых компонентов или иных условий равновесия, причем характерные элементы более простой диаграммы не исчезают, а только принимают иной геометрический образ” [1, 2].
Согласно методу трансляции, трансформированные при переходе из n-компонентного в (n + 1)-компонентное состояние геометрические образы, в соответствии со своими топологическими свойствами и соблюдением правила фаз Гиббса, взаимно пересекаясь, образуют геометрические образы (поля, кривые, точки) системы на (n + 1)-компонентном уровне. Опыт применения метода трансляции для прогнозирования и построения диаграмм фазовых равновесий многокомпонентных систем (пяти- и шестикомпонентных) указывает на различные варианты формирования их геометрических образов [9–16]. Авторами [17–24] была предпринята попытка прогнозировать возможные сочетания твердых фаз в нонвариантных точках системы Na,K,Mg,Ca||SO4,Cl–H2O при 25°C методом минимизации энергии Гиббса. Однако получаемые результаты не позволяли строить соответствующие диаграммы фазовых равновесий. Кроме того, по признанию самих авторов, с увеличением компонентности системы они становились все менее надежными. В настоящей статье рассмотрены варианты формирования нонвариантных точек пятикомпонентной системы NaCl–KCl–MgCl2–CaCl2–H2O при 25°C, установленные методом трансляции.
Методом растворимости [4] для пятикомпонентной системы NaCl–KCl–MgCl2–CaCl2–H2O при 25°С установлены три нонвариантные точки с равновесными твердыми фазами: 1) Га + Си + + Кр + Са · 6, 2) Га + Кр + Тх + Би и 3) Га + Кр + + Тх + Са · 6 (расшифровка обозначений равновесных твердых фаз приведена в примечании к табл. 1). Для нонвариантной точки 1 экспериментально найдены два состава насыщенного раствора, для двух других – по одному составу. Данные, полученные методом трансляции, подтверждают наличие в указанной системе трех нонвариантных точек и одновременно объясняют разный состав насыщенного раствора для одной и тот же нонвариантной точки. Этот факт можно подтвердить, анализируя пути формирования нонвариантных точек системы NaCl–KCl–MgCl2–CaCl2‒H2O при 25°C.
РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ
Пятикомпонентная система NaCl–KCl–MgCl2–CaCl2–H2O включает четыре четырехкомпонентные системы, для которых при 25°C характерны указанные в табл. 2 нонвариантные точки с соответствующими для них равновесными твердыми фазами. Схематическая [25] диаграмма фазового комплекса системы NaCl–KCl–MgCl2–CaCl2–H2O при 25°C на уровне четырехкомпонентного состава, построенная по данным табл. 2, приведена на рис. 1.
Таблица 2.
Равновесные твердые фазы, соответствующие нонвариантным точкам системы NaCl–KCl–MgCl2–CaCl2–H2O при 25°С на уровне четырехкомпонентных составов
| Нонвариантные точки | Равновесные твердые фазы | Нонвариантные точки | Равновесные твердые фазы |
|---|---|---|---|
| Система NaCl–KCl–MgCl2–H2O | Система NaCl–MgCl2–CaCl2–H2O | ||
| $E_{1}^{4}$ | Би + Га + Кр | $E_{4}^{4}$ | Би + Га + Тх |
| $E_{2}^{4}$ | Га + Кр + Си | $E_{5}^{4}$ | Га + Тх + Са · 6 |
| Система NaCl–KCl–CaCl2–H2O | Система KCl–MgCl2–CaCl2–H2O | ||
| $E_{3}^{4}$ | Га + Си + Са · 6 | $E_{6}^{4}$ | Кр + Си + Са · 6 |
| $E_{7}^{4}$ | Кр + Тх + Са · 6 | ||
| $E_{8}^{4}$ | Би + Кр + Тх | ||
Примечание. Би – бишофит MgCl2 ⋅ 6H2O, Тх – тахгидрид 2MgCl2 ⋅ CaCl2 ⋅ 12H2O. См. также примечание к табл. 1.
Рис. 1.
Схематическая диаграмма фазового комплекса системы NaCl–KCl–MgCl2–CaCl2–H2O при 25°C на уровне четырехкомпонентного состава, построенная методом трансляции.
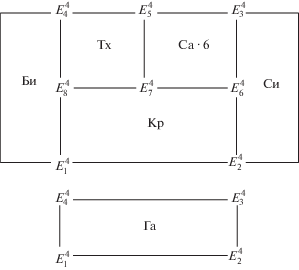
Трансляция четверных нонвариантных точек на уровень пятикомпонентного состава в виде моновариантных кривых и их взаимное пересечение с соблюдением правила фаз Гиббса сопровождается образованием следующих пятерных нонвариантных точек:
| $E_{1}^{4}$+ $E_{4}^{4}$ | 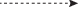 |
$E_{1}^{5}$= Би + Га + Кр + Тх; |
| $E_{1}^{4}$+ $E_{8}^{4}$ | 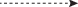 |
$E_{2}^{5}$= Би + Га + Кр + Тх; |
| $E_{4}^{4}$+ $E_{8}^{4}$ | 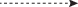 |
$E_{3}^{5}$ = Би + Га + Кр + Тх; |
| $E_{2}^{4}$+ $E_{3}^{4}$ |  |
$E_{4}^{5}$= Га + Кр + Си + Са · 6; |
| $E_{2}^{4}$+ $E_{6}^{4}$ |  |
$E_{5}^{5}$= Га + Кр + Си + Са · 6; |
| $E_{3}^{4}$+ $E_{6}^{4}$ |  |
$E_{6}^{5}$= Га + Кр + Си + Са · 6; |
| $E_{5}^{4}$+ $E_{7}^{4}$ |  |
$E_{7}^{5}$= Га + Кр + Тх + Са · 6. |
Из семи образовавшихся пятерных нонвариантных точек точки $E_{1}^{5},$ $E_{2}^{5}$ и $E_{3}^{5},$ а также $E_{4}^{5},$ $E_{5}^{5}$ и $E_{6}^{5}$ характеризуются идентичными равновесными твердыми фазами. Это означает, что они формируются в результате трехстороннего пересечения моновариантных кривых, образованных при трансляции четверных нонвариантных точек. Следовательно, для пятикомпонентной системы NaCl–KCl–MgCl2–CaCl2–H2O при 25°C характерно наличие не семи, а трех пятерных нонвариантных точек, сформированных следующим образом:
| $E_{1}^{4}$+ $E_{4}^{4}$ + $E_{8}^{4}$ |  |
$E_{1}^{5}$= Би + Га + Кр + Тх; |
| $E_{2}^{4}$+ $E_{3}^{4}$ + $E_{6}^{4}$ |  |
$E_{2}^{5}$ = Га + Кр + Си + Са · 6; |
| $E_{5}^{4}$+ $E_{7}^{4}$ |  |
$E_{3}^{5}$ = Га + Кр + Тх + Са · 6. |
Схематическая [25] диаграмма фазового комплекса системы NaCl–KCl–MgCl2–CaCl2–H2O при 25°С, построенная по этим данным методом трансляции, приведена на рис. 2.
Рис. 2.
Совмещенная схематическая диаграмма фазового комплекса системы NaCl–KCl–MgCl2–CaCl2–H2O при 25°C на уровнях четырех-, пятикомпонентного составов, построенная методом трансляции.
В обнаруженных методом трансляции нонвариантных точках данное равновесие экспериментально можно реализовать несколькими путями. Например, равновесие в нонвариантной точке $E_{3}^{5}$ может быть достигнуто при добавлении галита (NaCl) в раствор, насыщенный твердыми фазами Кр + Тх + Са ⋅ 6 ($E_{7}^{4}$), либо при добавлении карналлита (KCl ⋅ MgCl2 ⋅ 6H2O) в раствор, насыщенный твердыми фазами Га + Тх + Са · 6 ($E_{5}^{4}$), т.е. методом донасыщения [26]. Метод трансляции указывает также на третий способ достижения равновесия – смешивание насыщенного раствора с твердыми фазами, отвечающими точке $E_{5}^{4},$ с таковым для точки $E_{7}^{4}$ и последующее приведение полученной смеси в равновесие при 25°С. Этот способ требует меньше временных и материальных затрат.
Путей реализации равновесий в двух других пятерных нонвариантных точках, сформированных тройным пересечением моновариантных кривых, значительно больше: по три варианта донасыщения исходных смесей четверных нонвариантных точек следующей твердой фазой и один вариант, связанный со смешиванием исходных насыщенных растворов всех трех четверных нонвариантных точек с характерными для них равновесными твердыми фазами и приведением полученной смеси в равновесие.
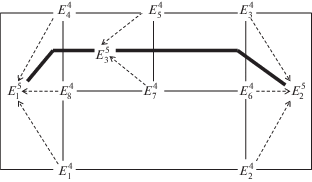
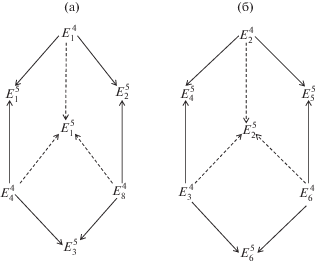
На основании вышеизложенного можно предположить, что различный состав насыщенного раствора нонвариантной точки многокомпонентной системы при одном и том же составе равновесных твердых фаз (табл. 1), связан с разными путями достижения равновесия. Формирование пятерных нонвариантных точек $E_{1}^{5}$ и $E_{2}^{5}$ системы NaCl–KCl–MgCl2–CaCl2–H2O при 25°С показано на рис. 3, где сплошными линиями со стрелками обозначено двухстороннее пересечение, а пунктирными линиями со стрелками – трехстороннее пересечение моновариантных кривых при формировании нонвариантных точек $E_{1}^{5}$ и $E_{2}^{5}.$ Равновесные твердые фазы, характерные для нонвариантных точек, обозначенных на рис. 3, приведены в тексте выше.
Рис. 3.
Схема вариантов формирования пятерных нонвариантных точек системы NaCl–KCl–MgCl2–CaCl2–H2O при 25°C при трансляции четверных нонвариантных точек на уровень пятикомпонентного состава с фазовым составом осадков: а – Би + Га + + Кр + Тх, б – Га + Кр + Си + Са · 6.
Вышеизложенное позволяет предположить, что на диаграмме многокомпонентных систем нонвариантные равновесия могут отображаться не только в виде точек, которые лишены размера, но и в виде геометрических (нонвариантных) образов, имеющих определенный размер, который определяется разными составами равновесной жидкой фазы, характерными для одного и того же состава равновесных твердых фаз. При этом изменение состава равновесной жидкой фазы может быть связано с разными путями (вариантами) формирования данного геометрического (нонвариантного) образа. Такое предположение подтверждается не только рассмотренным выше примером растворимости пятикомпонентной системы NaCl–KCl–MgCl2–CaCl2–H2O при 25°С, но и исследованием других многокомпонентных систем. Например, для пятикомпонентной системы Na,K,Mg||SO4,Cl–H2O при 0 и 50°С экспериментально установлено [4], что для одного и того же состава равновесных твердых фаз возможен разный состав равновесной жидкой фазы (табл. 3). Разный химический состав насыщенного раствора в системе Na,K,Mg||SO4,Cl–H2O при 0 и 50°C (табл. 3) для одного и того же состава равновесных твердых фаз, соответствующих нонвариантным точкам, очевидно, можно объяснить порядком последовательного добавления определенных солей к исходной смеси, что согласуется с разными вариантами трансляции четверных нонвариантных точек на уровень пятикомпонентного состава.
Таблица 3.
Растворимость в системе Na,K,Mg||SO4,Cl–H2O
| Стр. в [4] | Состав насыщенного раствора, мас. % | Фазовый состав осадков | ||||||
|---|---|---|---|---|---|---|---|---|
| NaCl | Na2SO4 | KCl | K2SO4 | MgCl2 | MgSO4 | H2O | ||
| Изотерма 50°С | ||||||||
| 1000–1001 | – 3.72 |
12.63 – |
– 10.51 |
6.22 8.19 |
– 10.38 |
19.80 – |
61.35 67.2 |
Ар + Гз + Лео + Си Ар + Гз + Лео + Си |
| Изотерма 0°С | ||||||||
| 1014–1015 | 8.38 1.77 |
– – |
4.87 2.31 | – – |
12.62 23.96 |
4.94 23.96 |
Га + Кр + Си + Эпс Га + Кр + Си + Эпс |
|
Примечание. Ар – арканит K2SO4, Гз – глазерит 3K2SO4 · Na2SO4, Лео – леонит K2SO4 · MgSO4 · 4H2O, Эпс – эпсомит MgSO4 · 7H2O. См. также примечание к табл. 1.
ЗАКЛЮЧЕНИЕ
Показана принципиальная возможность соответствия одному и тому же составу равновесных твердых фаз нонвариантных точек равновесных жидких фаз, разных по химическому составу, если исследуемая система многокомпонентная. Это может быть обосновано многообразием путей достижения нонвариантного равновесия. Как показывает метод трансляции при прогнозировании и построении диаграмм фазовых комплексов пяти- и шестикомпонентных систем, такой вывод не противоречит основным принципам физико-химического анализа и правилу фаз Гиббса. Следовательно, нонвариантное равновесие на диаграммах многокомпонентных систем может быть отражено не только в виде точки (когда существует один вариант его формирования), но и в виде геометрического (нонвариантного) образа (его условно можно назвать квазиточкой), имеющего определенный размер (когда существует несколько вариантов достижения равновесия).
Список литературы
Курнаков Н.С. // Докл. АН СССР. 1939. Т. 25. № 5. 384 с.
Курнаков Н.С. Введение в физико-химической анализ. М.–Л.: Изд-во АН СССР, 1940. 562 с.
Аносов В.Я., Озерова М.И., Фиалков Ю.Я. Основы физико-химического анализа. М.: Наука, 1976. 504 с.
Справочник экспериментальных данных по растворимости многокомпонентных водно-солевых систем. Т. 2. Кн. 1–2. СПб.: Химиздат, 2004. 1248 с.
Солиев Л. Деп. ВИНИТИ АН СССР 20.12.87 г. № 8990-В87.
Горощенко Я.Г. Физико-химической анализ гомогенных и гетерогенных систем. Киев: Наук. думка, 1978. 490 с.
Горощенко Я.Г. Массцентрический метод изображения многокомпонентных систем. Киев: Наук. думка, 1982. 264 с.
Горощенко Я.Г., Солиев Л. // Журн. неорган. химии. 1987. Т. 32. № 7. С. 1676.
Soliev L., Usmonov M. // Russ. J. Inorg. Chem. 2012. V. 57. № 3. Р. 452. [Солиев Л., Усмонов М.Б. // Журн. неорган. химии. 2012. Т. 57. № 3. С. 510.]
Soliev L. // Russ. J. Inorg. Chem. 2013. V. 58. № 5. P. 585. [Солиев Л. // Журн. неорган. химии. 2013. Т. 58. № 5. С. 663.]
Soliev L. // Russ. J. Phys. Chem. 2013. V. 87. № 9. P. 1442. [Солиев Л. // Журн. физ. химии. 2013. Т. 87. № 9. С. 1455.]
Soliev L. // Russ. J. Inorg. Chem. 2014. V. 59. № 9. P. 1030. [Солиев Л. // Журн. неорган. химии. 2014. Т. 59. № 9. С. 1263.]
Soliev L. // Russ. J. Inorg. Chem. 2015. V. 60. № 8. P. 1008. [Солиев Л. // Журн. неорган. химии. 2015. Т. 60. № 8. С. 1110.]
Солиев Л. // Докл. АН Респ. Таджикистан. 2015. Т. 58. № 1. С. 57.
Солиев Л., Низомов И.М., Джумаев М.Т., Гулом И. // Вестн. Тадж. нац. ун-та. Сер. естествен. наук. 2015. № 1/1 (156). С. 131.
Tursunbadalov Sh., Soliev L. // J. Solution Chem. 2015. V. 44. Iss. 8. P. 1626.
Pitser K.S. // J. Phys. Chem. 1973. V. 77. № 2. P. 268.
Pitser K.S., Mayarga G. // J. Phys. Chem. 1973. V. 77. № 19. P. 2300.
Pitser K.S., Mayarga G. // J. Solution Chem. 1974. V. 3. № 7. P. 359.
Pitser K.S., Kim J. // J. Am. Chem. Soc. 1974. V. 96. № 18. P. 5701.
Harviec C.F., Weare J.H. // Geochem. Cosmochim. Acta. 1980. V. 44. № 7. P. 981.
Wood J.R. // Geochem. Cosmochim. Acta. 1975. V. 39. № 8. P. 1147.
Eugster H.P., Harvie C.F., Weare J.H. // Geochem. Cosmochim. Acta. 1980. V. 44. № 9. P. 1335.
Harvie C.F., Eugster H.P., Weare J.H. // Geochem. Cosmochim. Acta. 1982. V. 46. № 9. P. 1603.
Солиев Л. // Журн. неорган. химии. 1988. Т. 33. № 5. С. 1305.
Горощенко Я.Г., Солиев Л., Горников Ю.И. // Укр. хим. журн. 1977. Т. 43. № 12. С. 1277.
Дополнительные материалы отсутствуют.
Инструменты
Журнал неорганической химии


