1. На главную
  2. Электронные версии
  3. Журнал неорганической химии
  4. T. 65, № 2, 2020

Журнал неорганической химии, 2020, T. 65, № 2, стр. 188-196

Теоретическое моделирование реакций ступенчатого присоединения молекул H2 к магниевым кластерам Mg18 и Mg17Ni

А. П. Мальцев a, b, *, О. П. Чаркин a, **

a Институт проблем химической физики РАН
142432 Московская обл., Черноголовка, пр-т Академика Семенова, 1, Россия

b Московский государственный университет имени М.В. Ломоносова
111991 Москва, Ленинские горы, 1, Россия

* E-mail: maltsevaleksej@gmail.com
** E-mail: charkin@icp.ac.ru

Поступила в редакцию 01.07.2019
После доработки 24.08.2019
Принята к публикации 03.10.2019

Полный текст (PDF)

Аннотация

В рамках метода функционала плотности рассчитана поверхность потенциальной энергии (ППЭ) вдоль минимальных энергетических путей элементарных реакций гидрирования Mg18 + H2 → Mg18H2 и Mg17Ni + H2 → Mg17NiH2 + H2 → Mg17NiH4 + H2 → Mg17NiH6. Определены локальные минимумы ППЭ в окрестностях низколежащих изомеров, интермедиатов и переходных состояний, рассчитаны их геометрические, энергетические и спектроскопические параметры. Проанализировано влияние допанта Ni на энергии и активационные барьеры этих реакций в зависимости от положения допанта на поверхности и во внутренней полости каркаса Mg17.

Ключевые слова: метод функционала плотности, допированные магниевые кластеры, гидрирование, влияние допанта

ВВЕДЕНИЕ

Магний является перспективным материалом для хранения водорода в связанном состоянии благодаря высокому содержанию водорода в гидриде, доступности, дешевизне и экологической чистоте, однако он уступает альтернативным материалам по своим кинетическим характеристикам [1] из-за высокого активационного барьера диссоциации молекулы водорода на поверхности частиц магния [2] и медленной диффузии водорода через гидридную фазу MgH2 [3]. Улучшение кинетических свойств достигается при введении катализирующих добавок переходных d-металлов и изменении микроструктуры магниевых зерен за счет их измельчения до субмикронных или нанометровых размеров и увеличения межфазной границы [1]. К сожалению, достигнутые результаты еще не полностью соответствуют практическим требованиям, предъявляемым к накопителям водорода. В области нано- и субнаноструктурированных материалов, где можно ожидать наилучшей кинетики [1], экспериментальные исследования сталкиваются с техническими трудностями и позволяют получить ограниченную информацию. В связи с этим в последние годы быстро растет интерес к исследованиям механизмов элементарных процессов сорбции-десорбции и диссоциативного присоединения молекул водорода на поверхности допированных магниевых кластеров, выполненным на молекулярном уровне. Благодаря развитию методов масс-спектрометрии, фотоэлектронной спектроскопии, ИК-спектроскопии в низкотемпературных инертных матрицах и интенсивному использованию квантово-химических расчетов быстро накапливается банк данных о составе и структуре небольших магниевых кластеров и их гидридов в изолированном состоянии. Так, при импульсном лазерном облучении металлического магния в атмосфере аргона и водорода обнаружена серия гидридов MgmHn c m = = 1–4 и n = 1–8, которые идентифицированы методами спектроскопии комбинационного и неупругого нейтронного рассеяния и ИК-спектроскопии, а их равновесная структура и частоты нормальных колебаний рассчитаны в рамках теории функционала плотности (ТФП/DFT) [4]. В работе [5] с использованием низкотемпературной спектроскопии КР в газовой фазе обнаружены гомоядерные магниевые кластеры Mgn (n = 2–5) и выполнены DFT-расчеты их структуры и колебательных частот. В работах [6–8] с помощью методов фотоэлектронной и масс-спектроскопии обнаружено семейство смешанных магний-алюминиевых кластеров и их отрицательных ионов Aln${\text{Mg}}_{m}^{ - }$ (m ≤ 3, n + m ≤ 15), выполнены DFT-расчеты их структуры и показано, что наиболее стабильными являются “магические” кластеры ${\text{A}}{{{\text{l}}}_{5}}{\text{Mg}}_{2}^{ - },$ ${\text{A}}{{{\text{l}}}_{{11}}}{\text{Mg}}_{3}^{ - },$ ${\text{A}}{{{\text{l}}}_{7}}{\text{Mg}}_{3}^{ - }$ и ${\text{A}}{{{\text{l}}}_{{11}}}{\text{Mg}}_{2}^{ - }.$ Аналогичные DFT-расчеты изомеров семейства магний-алюминиевых кластеров Mg28 –nAln свидетельствуют о том [9], что энтальпии смешения Mg и Al отрицательны для всех компонентов и что для атомов Al энергетически предпочтительными оказываются эндоэдральные, а для атомов Mg − поверхностные позиции кластера. Наиболее стабильными являются системы Mg24Al4, Mg21Al7, Mg14Al14, Mg26Al2 и Mg27Al1. В работах [10–13] с помощью DFT-расчетов определены равновесные структуры изомеров кластеров Mgn в интервале n = 2−56 и проанализирована зависимость относительной стабильности кластеров от числа атомов n, а наиболее стабильными являются кластеры Mg10 и Mg17 с “магическим” числом валентных электронов, равным 20 и 34.

Особый интерес представляют квантово-химические исследования механизмов элементарных реакций гидрирования. Ранее эта проблема была подробно исследована на примере реакций гидрирования алюминиевых кластеров

(1)
${\text{A}}{{{\text{l}}}_{m}}{\text{M}} + {{{\text{H}}}_{2}} \to {\text{A}}{{{\text{l}}}_{m}}{\text{M}}{{{\text{H}}}_{2}},$
для которых были выполнены DFT-расчеты поверхности потенциальной энергии (ППЭ) вдоль каталитического цикла диссоциативного присоединения молекулы Н2 c участием допантов Mg, Si [14, 15], B, C, P, Ca [15] и атомов переходных металлов 3d- и 4d-периодов [16–20]. В работах [21–23] с помощью методов масс-спектрометрии, ИК-многофотонной диссоциативной ионизации и DFT-расчетов исследовано взаимодействие молекулы Н2 с семействами кластеров AlnRh (n = = 1–12), AlnV (n = 1–18) и AlnCrН2 (n = 1–12) и проанализирована зависимость реакционной способности этих кластеров от их размера. В частности, согласно [17], допированные хромом кластеры Al2Cr и Al7Cr могут служить в качестве высокоэффективных и недорогих катализаторов диссоциации молекулярного водорода.

Родственные реакции гидрирования магниевых кластеров:

(2)
${\text{M}}{{{\text{g}}}_{m}}{\text{M}} + {{{\text{H}}}_{2}} \to {\text{M}}{{{\text{g}}}_{m}}{\text{M}}{{{\text{H}}}_{2}}$
на молекулярном уровне исследованы в меньшей степени. В работе [24] выполнены DFT-расчеты ППЭ вдоль минимальных энергетических путей (МЭП) реакции Mg5Al7Ni + Н2 → Mg5Al7NiН2 и показано, что на стадии физической сорбции образуется слабосвязанный молекулярный комплекс Mg5Al7Ni(H2), который трансформируется в “первичный” дигидрид Mg5Al7NiH2 с выигрышем энергии ∼15 ккал/моль. Гидрирование кластера Mg5Al7Ni должно идти легко (с барьером ∼3.5 ккал/моль), в то время как барьер обратного процесса дегидрирования Mg5Al7NiH2 составляет ∼18.5 ккал/моль и является серьезным препятствием на пути отрыва Н2 от дигидрида. В результате DFT-расчетов ППЭ реакций (2) с допантами M = Rh, Co и n = 2−10 [25, 26] установлено, что барьеры отрыва Н2 от дигидрида тоже составляют 20.6 и 15.8 ккал/моль, и сделан вывод о том, что кластеры Mg9Rh и Mg5Co могут быть “наиболее благоприятными для хранения связанного водорода”.

Настоящая работа посвящена DFT-расчетам поверхности потенциальной энергии вдоль МЭП реакции диссоциативного присоединения молекулы водорода к гомоядерному кластеру Mg18:

(3)
${\text{M}}{{{\text{g}}}_{{18}}} + {{{\text{H}}}_{2}} \to {\text{M}}{{{\text{g}}}_{{18}}}{{{\text{H}}}_{2}},$
к эндоэдральному допированному кластеру Ni@Mg17 с допантом внутри магниевого каркаса:
(4)
${\text{Ni@M}}{{{\text{g}}}_{{17}}} + {{{\text{H}}}_{2}} \to {\text{Ni@M}}{{{\text{g}}}_{{17}}}{{{\text{H}}}_{2}},$
а также трех последовательных циклов:
(5а)
${\text{M}}{{{\text{g}}}_{{{\text{17}}}}}{\text{Ni}} + {{{\text{H}}}_{2}} \to {\text{M}}{{{\text{g}}}_{{17}}}{\text{Ni}}{{{\text{H}}}_{2}},$
(5b)
${\text{M}}{{{\text{g}}}_{{17}}}{\text{Ni}}{{{\text{H}}}_{2}} + {{{\text{H}}}_{2}} \to {\text{M}}{{{\text{g}}}_{{{\text{17}}}}}{\text{Ni}}{{{\text{H}}}_{4}},$
(5c)
${\text{M}}{{{\text{g}}}_{{{\text{17}}}}}{\text{Ni}}{{{\text{H}}}_{{\text{4}}}} + {{{\text{H}}}_{2}} \to {\text{M}}{{{\text{g}}}_{{{\text{17}}}}}{\text{Ni}}{{{\text{H}}}_{6}}$
присоединения первой, второй и третьей молекул водорода к экзоэдральному кластеру Mg17Ni с допантом на поверхности каркаса.

Цель работы – расчет геометрических, энергетических, колебательных характеристик “ключевых” интермедиатов и переходных состояний, соответствующих МЭП этих реакций; анализ каталитического влияния допанта Ni, тенденций в изменении энергий и активационных барьеров, а также структурных изменений активного центра и магниевого каркаса с увеличением числа каталитических циклов и в зависимости от положения допанта в кластере.

РАСЧЕТНАЯ ЧАСТЬ

Все расчеты выполнены с помощью программы GAUSSIAN-09 [27] в приближениях BP86 [28] с базисом 6-31G*. Согласно расчетам [13], выполненным в разных вариантах DFT, приближение ВР86 лучше остальных описывает структурные и энергетические свойства магниевых кластеров, измеренные экспериментально или рассчитанные в рамках метода связанных кластеров (СCSDT). Проведенные нами BP86/6-31G*-расчеты олигомеров гидридов (MgH2)n c n = 1−4 лучше описывают экспериментальные значения частот колебаний по сравнению с B3LYP/6-31+G**-расчетами [4]. Характер переходных состояний и локальных минимумов ППЭ контролировали по наличию мнимой частоты у первых и отсутствию мнимых частот у последних, а также расчетами вдоль внутренней координаты реакции с помощью процедуры irc.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

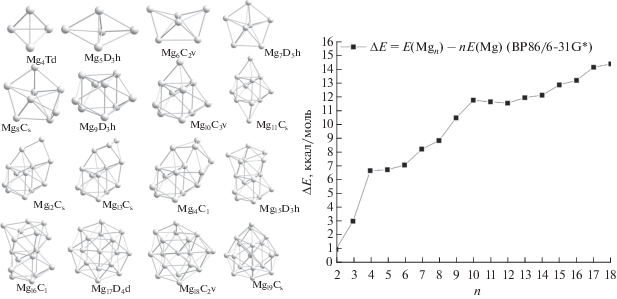
На первой стадии выполнены расчеты изомеров серии гомоядерных кластеров Mgn с величиной n, варьируемой в интервале 2−19. Стартовые структуры изомеров Mgn выбирали последовательным добавлением нового атома Mg в различные позиции оптимизированной структуры предыдущего кластера Mgn− 1. Структуры наиболее выгодных изомеров Mgn и энергии их когезии приведены на рис. 1.

Рис. 1.

Наиболее стабильные изомеры гомоядерных магниевых кластеров Mgn (n = 4–19) и энергии их когезии En (n = = 2–19).

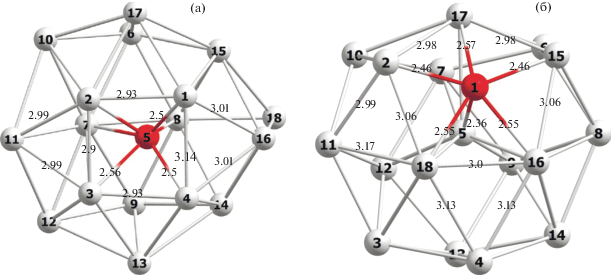
На основании их анализа кластер Mg18, характеризующийся высокой энергетической стабильностью и обладающий центрированной сфероидной структурой, был использован нами в качестве “стартового” объекта для допирования Mg18 → Mg17Ni. Далее была оптимизирована серия изомеров допированного кластера Mg17Ni c различными позициями допанта на поверхности и внутри каркаса Mg17. Для расчетов ППЭ реакций (4) и (5а)−(5с) были выбраны эндоэдральный и наиболее выгодный экзоэдральный кластеры Mg17Ni в синглетном состоянии со структурами 2A и 2B (рис. 2) с атомом Ni в центре и на поверхности каркаса Mg17.

Рис. 2.

Наиболее выгодные эндоэдральные (2А) и экзоэдральные (2В) структуры кластера Mg17Ni.

В основной части работы были выполнены расчеты ППЭ вдоль МЭП реакций (3), (4) и (5a)−(5c) с использованием каталитического цикла, предложенного в [16], который в нашем случае включает следующие стадии и особые точки ППЭ.

А − бесконечно удаленные реагенты Mg17Ni + + H2 (∞), энергия которых принимается за начало отсчета на энергетической шкале. B − переходное состояние TS-1 на пути образования физико-сорбированного комплекса. С − физико-сорбированный комплекс (ниже μ-комплекс) LM-1. D – переходное состояние TS-2 на пути трансформации физико-сорбированного комплекса в хемосорбированный. Е − хемосорбированный комплекс LM-2 (первичный дигидрид) с атомами Н в мостиковых позициях над ребрами или гранями с общим атомом допанта Ni. G − интермедиат LM-3, в котором один из атомов Н(1) смещен на ребро Mg−Mg, удаленное от допанта. Н − вторичный дигидрид LM-4, в котором оба атома H смещены на удаленные ребра Mg−Mg, а допант Ni полностью очищен и готов к присоединению новой молекулы Н2. F и I − переходные состояния TS-3 и TS-4 на пути очистки допанта и трансформации первичного дигидрида во вторичный.

Реакция гидрирования (3) гомоядерного кластера Mg18

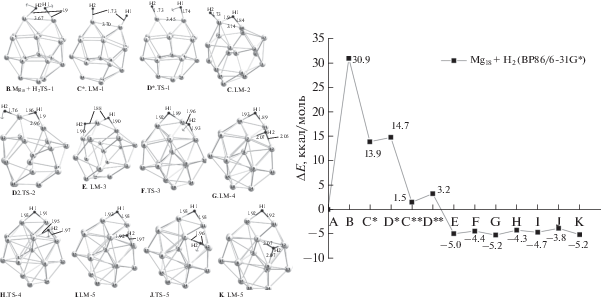
Равновесные структуры локальных минимумов и переходных состояний реакции (3) вместе с энергетической диаграммой вдоль МЭП синглетного терма приведены на рис. 3. Из диаграммы видно, что барьер хемосорбции D, которому отвечает мнимая частота ν(НН) ∼1315i и удлиненная связь H−H, составляет ∼31 ккал/моль и является труднопреодолимым препятствием на пути реакции (3). У хемосорбированного дигидрида Mg18H2 (Е) энергия образования оценивается в ∼5 ккал/моль, молекула Н2 диссоциирована на атомы, занимающие мостиковые позиции над смежными ребрами с длинами фрагментов R(MgH) ∼1.85−1.90 Å и частотами колебаний ∼1000–1100 см–1. Вклад малостабильных интермедиатов и переходных состояний между барьером B и дигидридом Е (на рисунках обозначены звездочками) малоощутим. Попытки локализовать особые точки ППЭ на стадиях физической сорбции А−Е оказались безрезультатными, и можно думать, что молекулярный комплекс Mg18−H2 также малоощутим или нестабилен. Для полноты картины мы локализовали серию локальных минимумов ППЭ, отвечающих мостиковым изомерам G−M дигидрида Mg18H2 c позициями атомов Н над различными ребрами и гранями каркаса Mg18. Согласно расчетам, все эти изомеры лежат в узком интервале порядка 1–2 ккал/моль и разделены низкими барьерами того же порядка. На этом основании можно полагать, что поверхностная миграция атомов водорода вокруг гомоядерных кластеров может протекать в условиях обычных или умеренно повышенных температур.

Рис. 3.

Структуры интермедиатов и переходных состояний реакции Mg18 + H2 → Mg18H2 и ее энергетическая диаграмма.

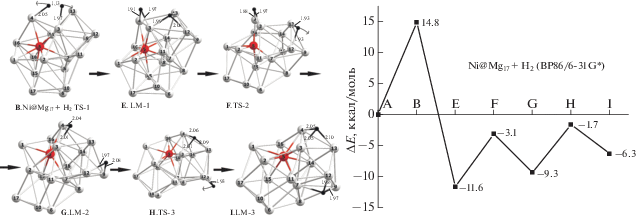
Реакция (4) гидрирования кластера Ni@Mg17 с допантом внутри каркаса

В изомере Ni@Mg17 (структура 2А на рис. 2) допант смещен из центра и координирован изнутри к одной из граней каркаса (ниже мы будем называть ее “активной”) тремя связями Ni−Mg с длинами ∼2.60−2.70 Å. Эндоэдральный изомер Ni@Mg17 лежит выше экзоэдрального Mg17Ni на ∼12 ккал/моль. Структуры интермедиатов и переходных состояний, а также молекулярная диаграмма, отвечающие стадиям сорбции молекулы Н2 и поверхностной миграции атомов Н, изображены на рис. 4. При сравнении диаграмм реакций (3) и (4) видно, что в самом начале обеих реакций образование физико-сорбционного комплекса нехарактерно, но на остальных участках влияние допанта оказывается значительным. Барьер В сорбции реакции (4) уменьшается до ~15 ккал/моль, т.е. почти вдвое по сравнению с аналогичным барьером реакции (3), но все же остается значительным. Напротив, энергия сорбции, оцениваемая по разности полных энергий структур Е и А, у реакции (4) увеличивается до –11.5 ккал/моль, т.е. почти вдвое по сравнению с –5.0 ккал/моль у реакции (3), что существенно повышает экзотермичность (4) по сравнению с (3). Помимо начальных участков ППЭ на стадии сорбции Н2 нами оптимизированы структуры переходных состояний F, H и интермедиатов дигидрида Ni@Mg17Н2, соответствующих стадии очистки “активного” ребра, к которому присоединилась молекула Н2, за счет смещений и удалений от него атомов Н. Оба интермедиата G и I лежат ниже диссоциационного предела в интервале ∼3 ккал/моль и разделены весьма ощутимыми барьерами ~7.5−8.5 ккал/моль, которые в несколько раз выше барьеров миграции атомов Н по поверхности гомоядерного кластера Mg18 в реакции (3). Иными словами, допирование кластера Mg18 эндоэдральным атомом Ni сопровождается двукратным понижением барьера и двукратным выигрышем энергии на стадии сорбции Н2 с одновременным увеличением барьеров на стадии очистки активного ребра, которые ограничивают смещения атомов Н по поверхности каркаса. Стадия сорбции остается лимитирующей у реакции (3) по аналогии с (4).

Рис. 4.

Ключевые структуры и энергетическая диаграмма реакции Ni@Mg17 + H2 → Ni@Mg17H2 c допантом внутри каркаса Mg17.

Реакции гидрирования (5) кластера Mg17Ni с допантом на поверхности каркаса

Равновесные структуры локальных минимумов и переходных состояний, отвечающих стадиям А−I трех последовательных циклов (5a), (5b), (5c), изображены на рис. 5. Их энергетические диаграммы вдоль МЭП приведены на рис. 6.

Рис. 5.

Ключевые структуры первых трех циклов гидрирования кластера NiMg17 c допантом на поверхности каркаса Mg17.

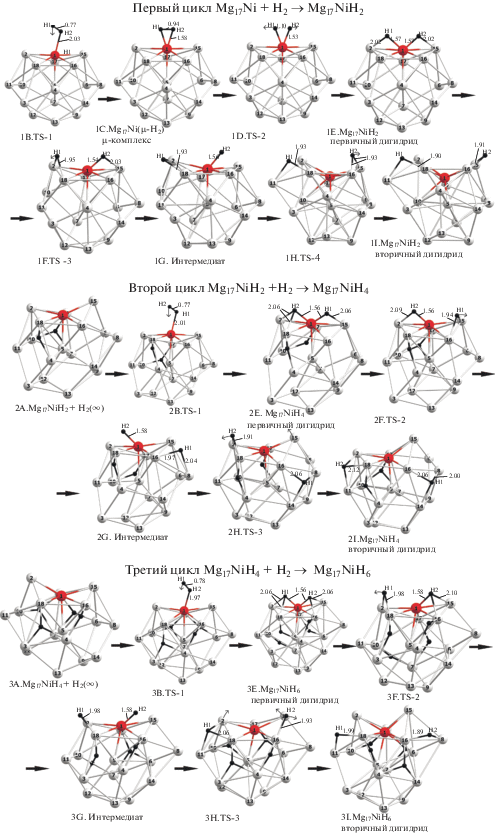
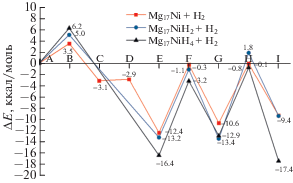
Рис. 6.

Энергетические диаграммы первых трех циклов гидрирования кластера Mg17Ni c допантом на поверхности каркаса Mg17 (ключевые структуры изображены на рис. 5).

Первый цикл Mg17Ni + H2 → Mg17NiH2 (5а). Из рис. 5 следует, что физико-сорбированный интермедиат 1С Ni(μ-Н2) лежит ниже диссоциационного предела на ∼3.1 ккал/моль и характеризуется расстояниями R(NiH) ∼1.58 и R(HH) ∼ 0.93 Å и частотой ν(НН) ∼ 2100 см–1. Перенос заряда между Н2 и кластером малоощутим. Комплекс 1С отделен от удаленных реагентов 1А переходным состоянием 1B (TS-1) с барьером ~3.5 ккал/моль, расстояниями R(HH) ∼ 0.76 и R(NiH2) ∼ 2.03 Å и мнимой частотой 370i.

В переходном состоянии 1D (TS-2) с мнимой частотой 685i расстояние R(HH) удлиняется до ~1.10 Å с последующей диссоциацией Н2 и трансформацией физико-сорбированного комплекса 1С в хемосорбированный 1Е. В последнем оба атома водорода имеют небольшой отрицательный заряд Z(H) ~ 0.1e, занимают асимметричные мостиковые позиции Hb над верхними гранями Ni−Mg2 и характеризуются параметрами R(NiH) ~ 1.58 Å, R(MgH) ~ 2.02−2.14 Å, φ(HNiH) ~ 95°, φ(NiHMg) ~ 85°−87° и частотами колебаний νвал(NiH) ~ 1480 см–1 и νдеф(NiH2) ~ 817 cм–1. Барьер 1D, разделяющий 1C и 1E, малоощутим, и трансформация 1C → 1E может легко проходить уже в обычных условиях. Хемосорбированному изомеру 1Е отвечает самый глубокий минимум ППЭ с энергией образования ~12.4 ккал/моль. Стадии 1А−1Е образуют сорбционную часть цикла.

В изомере 1Е допант экранирован связями Ni−H, затрудняющими присоединение новых молекул Н2. Для восстановления его каталитической активности за сорбционной стадией должна следовать стадия очистки допанта от связей Ni−H за счет перемещения атомов Н в более удаленные позиции и трансформации 1Е в локальные минимумы 1G и 1I, в которых один атом и оба атома Н соответственно смещены в позиции над соседними ребрами каркаса Mg17. Эти мостики характеризуются расстояниями R(MgH) ~ 1.90–1.95 Å, углами φ(MgHMg) ~ 100°−105° и отрицательным эффективным зарядом Z(Hb) ~ 0.15e. Переходным состояниям 1F (TS-3) и 1H (TS-4), которые связывают локальные минимумы 1E, 1G, 1I и имеют мнимую частоту ~450i, отвечают самые высокие барьеры ~12.1 и ~10.5 ккал/моль (отсчитаны от E и G соответственно), так что для реакций типа (5а) стадия очистки допанта от атомов Н оказывается лимитирующей. В расчетах родственных реакций гидрирования допированных алюминиевых кластеров типа Al12M + H2 → Al12MH2 с допантами первой половины 3d- и 4d-периодов (М = Ti, V, Сr и др. [16–23]) эта стадия является завершающей, поскольку очищенный атом допанта в них остается открытым на поверхности и готовым к присоединению следующей молекулы Н2 без существенных барьеров.

В случае Ni-допированных реакций типа (5а)–(5с) картина осложняется тем, что, согласно расчетам в рамках метода irc, параллельно с переносом атомов Н(1) и Н(2) в перегруппировках E → G и G → I атом допанта опускается c поверхностной позиции во внутреннюю полость каркаса почти на 1.5 Å и в изомере I оказывается экранированным поверхностными атомами магния. Барьер наикратчайшего пути присоединения второй молекулы Н2 к I (∼10 ккал/моль) соизмерим с барьерами F и H и является дополнительным препятствием перед началом второго цикла (5b). Аналогичное “ныряние” атома Ni внутрь магний-алюминиевого каркаса отмечалась ранее [24] для реакции Al7Mg5Ni + H2 → Al7Mg5NiH2. Мы пытались найти альтернативный путь с более низким барьером, связанный с предварительной трансформацией (“промотированием”) эндоэдрального изомера I в экзоэдральный аналог I* со стерически “открытым” допантом на поверхности. Нами локализовано несколько структур типа I*, которые лежат выше I на ~4−5 ккал/моль. Поиск МЭП трансформации I → I* связан с проведением более сложных расчетов из-за появления связанных (кооперативных) смещений нескольких атомов одновременно и может быть предметом отдельного рассмотрения.

Как показывает сравнение диаграмм реакций (4) и (5a), при переходе допанта из эндоэдральной позиции в экзоэдральную (Ni@Mg17 → NiMg17) барьер сорбции резко уменьшается с ∼15 до ∼3.5 ккал/моль, в результате чего лимитирующая стадия реакции гидрирования меняется с сорбционной на миграционную. На стадии очистки допанта изменения менее драматичны, но тоже вполне ощутимы. Энергия образования первичного дигидрида Е остается практически неизменной. У реакции (5а) энергии интермедиатов G и I на ∼1−3 ккал/моль больше, а барьеры F и H, отсчитанные от Е и G, на ∼3−3.5 ккал/моль выше, чем у реакции (4). Иными словами, перемещение Ni@Mg17 → NiMg17 сопровождается кратным уменьшением барьера на начальном участке сорбции с одновременным ощутимым увеличением барьеров на заключительной стадии Е − I.

Второй и третий циклы Mg17NiH2 + H2 → → Mg17NiH4 (5b) и Mg17NiH4 + H2 → Mg17NiH6 (5с). Из рис. 5 и 6 следует, что присоединение второй и третьей молекул Н2 начинается с разделенных реагентов 2А (Mg17NiH2 (1I*) + Н2) и 3А (Mg17NiH2 (2I*) + Н2), энергии которых приняты за начало отсчета, и протекает по аналогичному механизму. Отличия в относительных энергиях особых точек ППЭ у всех трех реакций (5а)−(5с) не выходят за пределы ∼3−3.5 ккал/моль. Первый барьер В на пути сближения из бесконечности и диссоциации Н2 монотонно возрастает от ∼3.5 ккал/моль у первого цикла до 5.0 и 6.2 ккал/моль у второго и третьего циклов. Энергия образования хемосорбционного комплекса Е увеличивается в том же ряду от 12.4 до 13.2 и 16.4 ккал/моль. На стадиях очистки допанта барьеры F и Н, отсчитанные от интермедиатов Е и G, варьируют в сравнительно узких пределах (12−13 и 9−12 ккал/моль соответственно) и лежат в области диссоциационного барьера. Как и у 1I первого цикла, у структур 2I и 3I следующих циклов атом Ni опускается на ~1.2 Å ниже уровня поверхности кластера. Можно отметить немонотонное поведение энергии образования очищенного дигидрида, которая близка (∼9.4 ккал/моль) у структур 1I и 2I первых двух циклов, но удваивается до ∼17.4 ккал/моль у структуры 3I третьего цикла.

Расчеты реакций (3)–(5) выполняли для основного синглетного терма. Ближайший триплетный терм лежит выше синглетного на 7–15 ккал/моль, причем его спиновая плотность почти полностью (на 90%) распределена по магниевому каркасу, а состояние допанта Ni остается близким к нульвалентному как у локальных минимумов, так и у переходных состояний МЭП.

ЗАКЛЮЧЕНИЕ

Выполнены квантово-химические расчеты поверхности потенциальной энергии реакции Mg18 + + H2 → Mg18H2 (3) и серии реакций Mg17Ni + H2 → → Mg17NiH2 + H2 → Mg17NiH4 + H2 → Mg17NiH6 (5) для исследования механизма начальных циклов сорбции молекулярного водорода на допированных субнаноразмерных кластерах. Показано, что гидрирование гомоядерного кластера Mg18 (3) затруднено из-за высокого барьера сорбции (>30 ккал/моль). Замещение поверхностного атома Mg атомом Ni резко снижает этот барьер до 4–5 ккал/моль. Энергия сорбции молекулы Н2 оценивается в ∼12 ккал/моль у первого цикла и возрастает до 16 и более ккал/моль при увеличении числа циклов. Критической стадией реакций (5) является смещение (миграция) связанных атомов Н от допанта на соседние ребра или грани каркаса Mg17 (стадия очистки допанта) с восстановлением каталитической активности допанта к началу каждого следующего цикла. У субнаноразмерных кластеров эти барьеры оцениваются в ∼10–12 ккал/моль и остаются ощутимым препятствием на пути реакций (5), преодолимым лишь при повышенных температурах.

Насколько нам известно, экспериментальные исследования реакций (3)–(5) на молекулярном уровне пока отсутствуют, и наши выводы имеют предсказательный характер.

Как отмечалось в [29, 30], реакции (3) и (5) являются лишь начальной стадией сложных процессов гидрирования. По мере нарастания числа диссоциированных молекул Н2 за реакциями типа (3) и (5) должны следовать стадии насыщения поверхности водородными мостиками, нарастания деформаций и образования дефектов каркаса в форме “надповерхностных” фрагментов MgHx и Mg2Hx и поверхностных “окон”, миграции атомов Н во внутреннюю полость, разрушения металлического каркаса и др. Каждая их этих стадий является предметом самостоятельных исследований и моделирования на молекулярном уровне. В связи с трудностями экспериментальных подходов в наноразмерной области информация, полученная с помощью квантово-химических расчетов, здесь может быть особенно полезной.

Настоящее сообщение ограничивается реакциями с участием атома Ni в качестве допанта. В следующей нашей работе будет рассмотрено влияние природы допанта на энергии и барьеры реакций (5) с участием кластеров Mg17M c атомами М других элементов 3d-периода.

Список литературы

  1. Tarasov B.P., Arbuzov A.A., Mozhzhuhin S.A. et al. // Int. J. Hydrogen Energy. https://doi.org/10.1016/j.ijhydene.2019.02.033

  2. Jensen T.R., Andreasen A., Vegge T. et al. // Int. J. Hydrogen Energy. 2006. V. 31. P. 2052.

  3. Sholl D.S. // J. Alloys Compd. 2007. V. 462. P. 446.

  4. Wang X., Andrews L. // J. Phys. Chem. A. 2004. V. 108. P. 11511. https://doi.org/10.1021/jp046410h

  5. Kaufmann A., Kornath A., Zoermer et al. // Inorg. Chem. 2010. V. 4. P. 3851. https://doi.org/10.1021/ic902485z

  6. Wang H. et al. // J. Chem. Phys. 2014. V. 140. P. 124  309. https://doi.org/10.1063/1.4869104

  7. Luo Z., Grover C.J., Reber A.C. et al. // J. Am. Chem. Soc. 2013. V. 135. P. 4307. https://doi.org/10.1021/ja310467n

  8. Grover C.J., Reber A.C., Khanna S.N. // J. Chem. Phys. 2017. V. 146. Art. 2243301. https://doi.org/10.1063/1.4985093

  9. Bao-Juan Lu, Xiao-Tian Li1, Yu-Jun Zhao et al. // Aip Advances. 2017. V. 7. Art. 095 023. https://doi.org/10.1063/1.5000792

  10. Janecek S., Krotscheck E., Liebrecht M., Wahl R. // Eur. Phys. J. 2011. V. 63. P. 377. https://doi.org/10.1140/epjd/e2011-10694-2

  11. Heidari I., De S., Ghazi S.M. et al. // J. Phys. Chem. A. 2011. V. 115. P. 12 307. https://doi.org/10.1021/jp204442e

  12. Xia X., Kuang X., Lu C. et al. // J. Phys. Chem. A. 2016. V. 120. P. 7947. https://doi.org/10.1021/acs.jpca.6b07322

  13. Duanmu K., Roberto-Neto O., Machado F.B.C. et al. // J. Phys. Chem. C. 2016. V. 120. P. 13 275. https://doi.org/10.1021/acs.jpcc.6b03080

  14. Henry D.J., Yarovsky I. // J. Phys. Chem. A. 2009. V. 113. P. 2565. https://doi.org/10.1021/jp809619q

  15. Wang L., Zhao J., Zhou Z. et al. // J. Comput. Chem. 2009. V. 30. P. 2514. https://doi.org/10.1002/jcc.21239

  16. Kochnev V.K., Charkin O.P., Klimenko N.M. // Russ. J. Inorg. Chem. 2010. V. 55. P. 65.

  17. Guo L. // J. Phys. Chem. 2013. V. 117. P. 3458. https://doi.org/10.1021/jp310833y

  18. Mikhailin A.A., Charkin O.P., Klimenko N.M. // Russ. J. Inorg. Chem. 2012. V. 57. P. 528.

  19. Mikhailin A.A., Charkin O P., Klimenko N.M. // Russ. J. Inorg. Chem. 2013. V. 58. P. 1439. https://doi.org/10.1134/S0036023613120073

  20. Varano A., Henry D.J., Yarovsky I. // J. Phys. Chem. C. 2014. V. 118. P. 19 865.

  21. Vanbuel J., Fernandes E.M., Ferrary P. et al. // Chem. Eur. J. 2017. V. 23. P. 15 638. https://doi.org/10.1002/chem.201704361

  22. Vanbuel J., Jia M.-Y., Ferrary P. et al. // Topics in Catalysis. 2018. V. 61. P. 62. https://doi.org/10.1007/s11244-017-0878-x

  23. Jia M.-Y., Vanbuel J., Ferrary V. et al. // J. Phys. Chem. C. 2018. V. 122. P. 18 247. https://doi.org/10.1021/acs.jpcc.8b04332

  24. Mikhailin A.A., Charkin O.P., Klimenko N.M. // Russ. J. Inorg. Chem. 2015. V. 60. № 10. P.1238. https://doi.org/10.1134/S0036023615100137

  25. Trivedi R., Bandyopadhyay D. // Int. J. Hydrogen Energy. 2015. V. 40. P. 12727e35.

  26. Trivedi R., Bandyopadhyay D. // Int. J. Hydrogen Energy. 2016. V. 41. P. 20113. https://doi.org/10.1016/j.ijhydene.2016.09.007

  27. Frisch M.J. et al. Gaussian 09, Revision A.02 Gaussian, Inc., Wallingford CT, 2013.

  28. Becke A.D. // J. Phys. Chem. 1993. V. 98. P. 5648.

  29. Charkin O.P., Klimenko N.M., Charkin D.O. // Chem. Phys. 2019. V. 522. P. 112. https://doi.org/10.10167/champhys.2019.02.007

  30. Charkin O.P., Klimenko N.M. // Russ. J. Inorg. Chem. 2018. V. 63. P. 479. https://doi.org/10.1134/S0036023618040058

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал неорганической химии

Архивы выпусков Информация о журнале Отправить рукопись в журнал