Журнал неорганической химии, 2020, T. 65, № 5, стр. 643-650
Теплоемкость и термодинамические функции ортониобата диспрозия в интервале 2–1300 K
Г. Е. Никифорова a, *, А. В. Тюрин a, М. А. Рюмин a, К. И. Брюханова a, А. В. Хорошилов a, К. С. Гавричев a
a Институт общей и неорганической химии им. Н.С. Курнакова РАН
119991 Москва, Ленинский пр-т, 31, Россия
* E-mail: gen@igic.ras.ru
Поступила в редакцию 19.11.2019
После доработки 20.12.2019
Принята к публикации 24.12.2019
Аннотация
Теплоемкость поликристаллического ортониобата диспрозия изучена в широком температурном интервале тремя калориметрическими методами: релаксационной (2–50 K), адиабатической (9–350 K) и дифференциальной сканирующей калориметрии (308–1300 K). Ниже 9 K зафиксирована нисходящая ветвь низкотемпературной аномалии, максимум которой находится за пределами измерений. При температуре 1086 K происходит обратимый фазовый переход. Поведение теплоемкости $C_{p}^{^\circ }(T)$ в области фазового перехода позволяет отнести его к фазовым переходам второго рода. На основании полученных данных рассчитаны температурные зависимости стандартных термодинамических функций DyNbO4 во всем изученном интервале.
ВВЕДЕНИЕ
Ортониобаты редкоземельных элементов (РЗЭ) являются перспективными соединениями для создания композиционных материалов, используемых в качестве люминофоров [1, 2], электролитов топливных элементов [3, 4], датчиков влажности [5, 6] и микроволновых устройств [7, 8]. Для прогнозирования поведения этих материалов в условиях эксплуатации необходимы надежные термодинамические данные в широком температурном интервале. Настоящая работа является продолжением исследований теплоемкости и термодинамических функций ортониобатов РЗЭ [9–12].
Подобно другим ортониобатам лантаноидов, DyNbO4 при комнатной температуре имеет моноклинную структуру типа фергусонита (пр. гр. I2/a). При повышении температуры происходит обратимое фазовое превращение в тетрагональную структуру типа шеелита (пр. гр. I41/a). Данный фазовый переход в ортониобатах LnNbO4 достаточно хорошо изучен методом высокотемпературной рентгеновской дифракции [12–16]. Большинство авторов отмечают монотонное изменение угла моноклинности при повышении температуры, что говорит в пользу фазового перехода второго рода. В то же время синхротронные исследования порошка DyNbO4 выявили наличие двухфазной области в районе фазового перехода [14]. Рентгеновские исследования показали, что чистая тетрагональная фаза существует лишь при температуре >1126 K, однако на кривой дифференциальной сканирующей калориметрии (ДСК) того же образца замечен скачок теплоемкости при 1099 K. Структурный переход фергусонит–шеелит сопровождается изменением диэлектрических свойств и переходом из антисегнетоэлектрического в диэлектрическое состояние. Температура фазового перехода, определенная из диэлектрических измерений DyNbO4, составила 1143 K [16]. Аналогичный разброс значений температуры фазового перехода в зависимости от метода исследования наблюдался и для LaNbO4, для которого значение Ttr варьировалось от 753 до 814 K [7, 14–16].
Информация о теплоемкости DyNbO4 в литературе отсутствует. Результаты изучения ортониобата диспрозия методом дифференциальной сканирующей калориметрии в работе [14] представлены лишь в графическом виде в качестве подтверждения наличия фазового перехода в образце.
Цель данного исследования – экспериментальное изучение теплоемкости DyNbO4 и расчет термодинамических функций в широком интервале температур, а также исследование фазового превращения фергусонит–шеелит калориметрическими методами.
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
Синтез ортониобата диспрозия проводили твердофазным способом – отжигом стехиометрической смеси оксидов при температуре 1400°С в течение 24 ч с промежуточными перетираниями. В качестве исходных реагентов использовали пентаоксид ниобия Nb2O5 (99.95%, Alfa Aesar) и оксид диспрозия Dy2O3 (99.9%, Химмед). Для удаления сорбированной влаги оксид диспрозия предварительно отжигали при температуре 1000°С в течение 3 ч.
Фазовую чистоту полученного образца контролировали методом рентгеновской дифракции на дифрактометре Bruker D8 Advance (CuKα-излучение, Ni-фильтр, LYNXEYE-детектор, геометрия на отражение) в интервале углов 10° < 2θ < 70° с шагом 0.0133° и выдержкой 0.3 с. Интерпретацию полученных данных и расчет кристаллографических параметров проводили с помощью программного обеспечения TOPAS R. Все наблюдаемые рефлексы были успешно проиндексированы в пр. гр. I2/a (15). Рассчитанные параметры кристаллической решетки хорошо согласуются с данными работ [14, 16, 17]:
Низкотемпературную теплоемкость DyNbO4 в интервале 2–50 K измеряли методом релаксационной калориметрии на установке PPMS-9 (Quantum Design). Образец, предварительно спрессованный в таблетку диаметром 3 мм, закрепляли на датчике с помощью криогенной высоковакуумной смазки Apiezon N. Погрешность измерений теплоемкости в изучаемом диапазоне составляет 2%.
Измерение теплоемкости в интервале 9–350 K проводили в автоматическом адиабатическом калориметре БКТ-3 с использованием гелия и азота в качестве криогенных жидкостей. Калибровку калориметра осуществляли путем измерения теплоемкости бензойной кислоты марки К-2 и меди “ос. ч.”. По результатам калибровки и поверки калориметра установлено, что погрешность измерений теплоемкости веществ составляет 2% при температуре <15 K, 0.5% в интервале 15 < Т < 40 K и 0.2% в области 40−350 K.
Теплоемкость DyNbO4 в области высоких температур была изучена в режиме нагревания и охлаждения с использованием дифференциального сканирующего калориметра STA 449 F1 Jupiter® (Netzsch). Измерения проводили в платиновых тиглях с крышкой в атмосфере аргона (чистотой 99.9999%) со скоростью нагрева 20 град/мин. В качестве стандарта использовали синтетический сапфир 720 (α-Al2O3).
Поскольку фазовые переходы второго рода характеризуются незначительным изменением теплоемкости, их не всегда удается зафиксировать калориметрическими методами. Стандартная методика определения теплоемкости методом ДСК состоит из трех последовательных измерений: теплового потока базовой линии, стандарта и изучаемого образца. Особое внимание было уделено максимальному повышению чувствительности этих сигналов. В связи с этим для всех измерений контролировали постоянство температуры, положения и ориентации тигля с крышкой на держателе образца.
РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ
Теплоемкость ортониобата диспрозия в интервале 0–400 K представлена на рис. 1. На графике можно отметить два участка, где экспериментальные значения теплоемкости получены двумя независимыми калориметрическими методами на разных приборах. Это релаксационная и адиабатическая калориметрия в температурном диапазоне 9–50 K и адиабатическая калориметрия и ДСК в интервале 308–350 K. В обоих случаях экспериментальные значения теплоемкости совпадают в пределах ошибки эксперимента, что свидетельствует о высокой достоверности полученных данных.
Рис. 1.
Низкотемпературная теплоемкость DyNbO4. Символами обозначены экспериментальные значения, полученные методами релаксационной (квадраты), адиабатической (ромбы) и дифференциальной сканирующей калориметрии (круги), линией – сглаженные значения $C_{p}^{^\circ }(T),$ рассчитанные по уравнению (1). На вставке выделена область низкотемпературной аномалии, пунктиром показана сглаживающая полиномиальная функция.
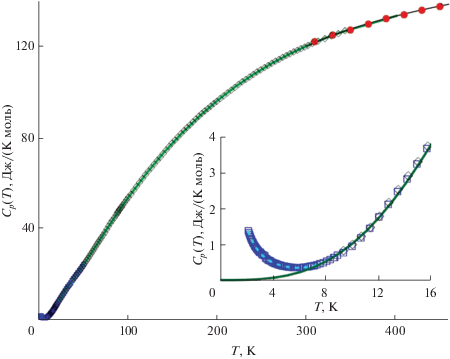
В области ниже 9 K наблюдается нисходящая ветвь низкотемпературной аномалии, максимум которой лежит за пределами наших измерений (вставка на рис. 1). Данная аномалия связана с переходом DyNbO4 из пара- в антиферромагнитное состояние и характерна для соединений, содержащих ион Dy3+ [18, 19]. К сожалению, в литературе не удалось найти каких-либо сведений о калориметрических или магнитных измерениях ортониобата диспрозия при температурах ниже 2 K. Поскольку характеристики данного перехода неизвестны, в дальнейших расчетах теплоемкость DyNbO4 в интервале температур 0–9 K принимали равной решеточной теплоемкости, описание которой будет дано ниже. Отметим лишь, что экспериментальные значения теплоемкости в области низкотемпературной аномалии удовлетворительно описываются полиномиальной функцией, коэффициенты которой представлены в табл. 1.
Таблица 1.
Параметры уравнения Cp(T) = a0 + a1T + + a2T2 + a3T3 + a4T4 + a5T5 + a6T6 для расчета теплоемкости DyNbO4 в температурном интервале 2–9 K
| Параметр | Значение |
|---|---|
| a0, Дж/(K моль) | 7.016285 |
| a1, Дж/(K2 моль) | –5.66160 |
| a2, Дж/(K3 моль) | 2.12222 |
| a3, Дж/(K4 моль) | –0.43809 |
| a4, Дж/(K5 моль) | 0.051014 |
| a5, Дж/(K6 моль) | –0.003114 |
| a6, Дж/(K7 моль) | 0.0000777 |
| R2 | 0.998 |
На участке 9–350 K экспериментальные значения теплоемкости монотонно возрастают без видимых аномалий и могут быть сглажены единым уравнением. В качестве аппроксимирующей функции было выбрано уравнение, представляющее собой комбинацию функций Дебая (D) и Эйнштейна (E):
(1)
$C_{p}^{^\circ }\left( T \right) = n\left[ {\left( {\frac{1}{3}} \right)\sum\limits_{j = 1}^3 {{{a}_{j}}{{D}_{j}}\left( {\frac{{{{\theta }_{j}}}}{T}} \right) + {{a}_{4}}E\left( {\frac{{{{\theta }_{E}}}}{T}} \right)} } \right],$Таблица 2.
Параметры уравнения (1) для расчета теплоемкости DyNbO4 в температурном интервале 9–350 K
| Параметр | Значение |
|---|---|
| a1, 1/моль | 0.51667 |
| a2, 1/моль | 0.85883 |
| a3, 1/моль | 0.84383 |
| a4, 1/моль | 0.30683 |
| Θ1, K | 125 |
| Θ2, K | 804 |
| Θ3, K | 1180 |
| ΘE, K | 312 |
| σ2, Дж2/(K2 моль2) | 0.012569 |
Уравнение (1) учитывает вклад акустических и оптических мод в теплоемкость вещества и может рассматриваться как суммарная теплоемкость кристаллической решетки, поэтому данное уравнение было использовано для экстраполяции температурной зависимости теплоемкости к 0 K.
На рис. 2 представлена теплоемкость DyNbO4, измеренная методом ДСК в интервале 308–1298 K, а также экспериментальные данные, полученные ранее [14] в интервале 500–1300 K. Поскольку в работе [14] значения теплоемкости были представлены только в графическом виде, предварительно они были оцифрованы и приведены к размерности Дж/(K моль). На графике видно, что значения теплоемкости, полученные в двух исследованиях, демонстрируют удовлетворительное совпадение в интервале температур 500–700 K. Но при более высоких температурах наблюдается расхождение между экспериментальными данными. В то же время следует отметить, что температуры фазового превращения очень близки.
Рис. 2.
Высокотемпературная теплоемкость DyNbO4. Символами обозначены экспериментальные значения, полученные методом ДСК в режиме нагревания (круги) и охлаждения (ромбы), линиями – сглаженные значения, рассчитанные по уравнению (2), пунктиром – экспериментальные значения из [14]. На вставке показана область фазового перехода.
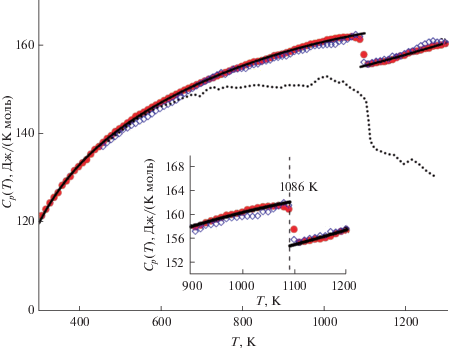
На вставке к рис. 2 видно, что значения теплоемкости, полученные в режимах нагревания и охлаждения, полностью совпадают. И в обоих случаях на температурной зависимости теплоемкости наблюдается четко выраженная ступенька. Такое поведение теплоемкости является характерной особенностью переходов второго рода. Отсутствие гистерезиса на температурной зависимости теплоемкости при Ttr подтверждает вывод о том, что термодинамически данный фазовый переход относится к классическим переходам второго рода.
Экспериментальные значения теплоемкости были разделены на два температурных интервала: 308.15–1078.15 и 1108.15–1298.15 K и сглажены по отдельности с помощью уравнения:
Экспериментальные точки при 1088.15 и 1098.15 K были исключены из расчетов, поскольку они находятся в диапазоне фазового перехода. Коэффициенты уравнения (2) представлены в табл. 3 для обоих температурных интервалов. Следует отметить, что в интервале перекрывания экспериментальных значений 308–350 K сглаженные значения теплоемкости, рассчитанные по уравнениям (1) и (2), совпадают в пределах 0.02%.
Таблица 3.
Параметры уравнения (2) для расчета теплоемкости DyNbO4 в интервале 308–1300 K
| Параметр | 308–1086 K | 1086–1300 K |
|---|---|---|
| a, Дж/(K моль) | 123.7709 | 112.3526 |
| b, Дж/(K2 моль) | 0.059172 | 0.033748 |
| c, Дж/(K моль) | –1792975 | 6823861 |
| d, Дж/моль | –2.06 × 10–5 | 0 |
| R2 | 0.9997 | 0.9908 |
Температуру фазового перехода определили как 1086 K. Это значение оказалось ниже значений, полученных при изучении изменения диэлектрических свойств и кристаллической структуры ортониобата диспрозия в процессе фазового превращения [14, 16]. Однако исследования in situ методом рентгеновской дифракции высокого разрешения показали, что тетрагональная фаза может сохраняться вплоть до 940 K [14]. Вероятно, большую роль здесь также играет предыстория изучаемого образца, дефектность, размерность и унимодальность частиц. Величину ступенчатого изменения теплоемкости при температуре фазового перехода оценили исходя из расчетов температурной зависимости теплоемкости $C_{p}^{^\circ }(T).$ Полученное значение 7.4 ± 0.3 Дж/(K моль) сопоставимо с величинами $\Delta C_{p}^{^\circ }(T),$ опубликованными ранее для других ортониобатов РЗЭ [9, 10, 12].
На основе сглаженных значений теплоемкости были рассчитаны температурные зависимости стандартных термодинамических функций (энтропии S°(T), изменения энтальпии H°(T) – H°(0) и приведенной энергии Гиббса Ф°(T)) во всем изучаемом температурном диапазоне (табл. 4). При 298.15 K эти функции имеют следующие значения: $C_{p}^{^\circ }$ (298.15 K) = 119.52 ± 0.18 Дж/(K моль), S°(298.15 K) = 135.52 ± 0.25 Дж/(K моль), H°(298.15 K) – H°(0) = 20 773 ± 37 Дж/моль, Ф°(298 K) = 65.85 ± 0.11 Дж/(K моль).
Таблица 4.
Теплоемкость и термодинамические функции DyNbO4 в интервале 2–1300 K
| T, K | C°p(T), Дж/(K моль) | S°(T), Дж/(K моль) | H°(T) – H°(0), Дж/моль | Ф°(T)a, Дж/(K моль) |
|---|---|---|---|---|
| 2 | 0.008294б | 0.002938 | 0.004925 | 0.0004752 |
| 4 | 0.06636 | 0.02264 | 0.07024 | 0.005076 |
| 6 | 0.2246 | 0.0755 | 0.3452 | 0.01801 |
| 8 | 0.5306 | 0.1784 | 1.079 | 0.04344 |
| 10 | 1.032 | 0.3470 | 2.615 | 0.08544 |
| 15 | 3.237 | 1.139 | 12.77 | 0.2876 |
| 20 | 6.373 | 2.486 | 36.58 | 0.6572 |
| 25 | 9.662 | 4.264 | 76.72 | 1.195 |
| 30 | 12.72 | 6.299 | 132.8 | 1.873 |
| 35 | 15.53 | 8.472 | 203.5 | 2.659 |
| 40 | 18.23 | 10.72 | 287.9 | 3.526 |
| 45 | 20.96 | 13.03 | 385.8 | 4.453 |
| 50 | 23.78 | 15.38 | 497.7 | 5.428 |
| 55 | 26.70 | 17.78 | 623.8 | 6.441 |
| 60 | 29.69 | 20.24 | 764.8 | 7.488 |
| 65 | 32.74 | 22.73 | 920.8 | 8.565 |
| 70 | 35.80 | 25.27 | 1092 | 9.667 |
| 75 | 38.84 | 27.84 | 1279 | 10.79 |
| 80 | 41.84 | 30.45 | 1480 | 11.94 |
| 85 | 44.81 | 33.07 | 1697 | 13.11 |
| 90 | 47.71 | 35.72 | 1928 | 14.29 |
| 95 | 50.54 | 38.37 | 2174 | 15.49 |
| 100 | 53.31 | 41.03 | 2434 | 16.70 |
| 110 | 58.65 | 46.37 | 2994 | 19.15 |
| 120 | 63.72 | 51.69 | 3606 | 21.64 |
| 130 | 68.53 | 56.98 | 4267 | 24.16 |
| 140 | 73.11 | 62.23 | 4976 | 26.69 |
| 150 | 77.45 | 67.42 | 5729 | 29.23 |
| 160 | 81.57 | 72.55 | 6524 | 31.78 |
| 170 | 85.47 | 77.62 | 7359 | 34.33 |
| 180 | 89.15 | 82.61 | 8232 | 36.87 |
| 190 | 92.63 | 87.52 | 9142 | 39.41 |
| 200 | 95.92 | 92.36 | 10085 | 41.93 |
| 210 | 99.02 | 97.11 | 11059 | 44.45 |
| 220 | 101.9 | 101.8 | 12064 | 46.95 |
| 230 | 104.7 | 106.4 | 13098 | 49.43 |
| 240 | 107.3 | 110.9 | 14157 | 51.90 |
| 250 | 109.7 | 115.3 | 15242 | 54.35 |
| 260 | 112.0 | 119.7 | 16351 | 56.78 |
| 270 | 114.1 | 123.9 | 17482 | 59.19 |
| 280 | 116.2 | 128.1 | 18633 | 61.57 |
| 290 | 118.1 | 132.2 | 19804 | 63.94 |
| 300 | 119.8 | 136.3 | 20994 | 66.28 |
| 310 | 121.5 | 140.2 | 22201 | 68.61 |
| 320 | 123.1 | 144.1 | 23424 | 70.90 |
| 330 | 124.6 | 147.9 | 24663 | 73.18 |
| 340 | 126.0 | 151.7 | 25916 | 75.43 |
| 350 | 127.3 | 155.3 | 27182 | 77.67 |
| 400 | 132.9 | 172.7 | 33693 | 88.47 |
| 450 | 137.4 | 188.6 | 40455 | 98.73 |
| 500 | 141.0 | 203.3 | 47417 | 108.5 |
| 550 | 144.1 | 216.9 | 54548 | 117.7 |
| 600 | 146.9 | 229.5 | 61824 | 126.5 |
| 650 | 149.3 | 241.4 | 69229 | 134.9 |
| 700 | 151.4 | 252.5 | 76747 | 142.9 |
| 750 | 153.3 | 263.1 | 84367 | 150.6 |
| 800 | 155.1 | 273.0 | 92078 | 157.9 |
| 850 | 156.7 | 282.5 | 99873 | 165.0 |
| 900 | 158.1 | 291.5 | 107743 | 171.7 |
| 950 | 159.4 | 300.0 | 115679 | 178.3 |
| 1000 | 160.5 | 308.2 | 123677 | 184.6 |
| 1050 | 161.5 | 316.1 | 131728 | 190.6 |
| 1086 | 162.2 | 321.5 | 137554 | 194.9 |
| 1086 | 154.8 | 321.5 | 137554 | 194.9 |
| 1100 | 155.1 | 323.5 | 139723 | 196.5 |
| 1150 | 156.3 | 330.5 | 147509 | 202.2 |
| 1200 | 157.6 | 337.1 | 155356 | 207.7 |
| 1250 | 158.9 | 343.6 | 163269 | 213.0 |
| 1300 | 160.3 | 349.9 | 171248 | 218.1 |
| 1350 | 161.7 | 355.9 | 179295 | 223.1 |
| 1400 | 163.1 | 361.8 | 187414 | 228.0 |
| 1450 | 164.5 | 367.6 | 195604 | 232.7 |
Расчет термодинамических функций после фазового перехода проводили с учетом того, что данный переход является непрерывным и изменение энтальпии и энтропии происходит в точке.
ЗАКЛЮЧЕНИЕ
Теплоемкость ортониобата диспрозия измерена методами релаксационной, адиабатической и дифференциальной сканирующей калориметрии в интервале 2–1300 K. В области фазового перехода фергусонит–шеелит выявлен скачок температурной зависимости теплоемкости $C_{p}^{^\circ }(T).$ Отсутствие латентного тепла и гистерезиса на температурной зависимости теплоемкости при температуре фазового перехода позволяет утверждать, что переход фергусонит–шеелит относится к фазовым переходам второго рода. На основании полученной температурной зависимости теплоемкости $C_{p}^{^\circ }(T)$ рассчитаны стандартные термодинамические функции DyNbO4 во всем изученном температурном диапазоне.
Список литературы
Li K., Zhang Y., Li X. et al. // Phys. Chem. Chem. Phys. 2015. V. 17. P. 4283. https://doi.org/10.1039/c4cp03894k
Hirano M., Dozono H. // J. Am. Ceram. Soc. 2013. V. 96. P. 3389. https://doi.org/10.1111/jace.12595
Cao Y., Duan N., Yan D. et al. // Int. J. Hydrogen Energy. 2016. V. 41. P. 20633. https://doi.org/10.1016/j.ijhydene.2016.08.056
Norby T., Magrasó A. et al. // J. Power Sources. 2015. V. 282. P. 28. https://doi.org/10.1016/j.jpowsour.2015.02.027
Haugsrud R., Norby T. et al. // Nat. Mater. 2006. V. 5. P. 193. https://doi.org/10.1038/nmat1591
Balamurugan C., Lee D.-W., Subramania A. et al. // Appl. Surf. Sci. 2013. V. 283. P. 58.
Kim D.-W., Kwon D.-K., Yoon S.H. et al. // J. Am. Ceram. Soc. 2006. V. 89. P. 3861. https://doi.org/10.1111/j.1551-2916.2006.01302.x
Lee H.W., Park J.H., Nahm S. et al. // Mater. Res. Bull. 2010. V. 45. P. 21. https://doi.org/10.1016/j.materresbull.2009.09.008
Nikiforova G., Khoroshilov A., Tyurin A. et al. // J. Chem. Thermodyn. 2019. V. 132. P. 44. https://doi.org/10.1016/j.jct.2018.12.041
Kondrat’eva O.N., Nikiforova G.E., Tyurin A.V. et al. // J. Alloys Compd. 2019. V. 779. P. 660. https://doi.org/10.1016/j.jallcom.2018.11.272
Nikiforova G.E., Khoroshilov A.V., Gavrichev K.S. et al. // Appl. Solid State Chem. 2018. V. 2. P. 159. https://doi.org/10.18572/2619-0141-2018-4-5-159-162
Никифорова Г.Е., Хорошилов А.В., Гавричев К.С. и др. // Неорган. материалы. 2019. Т. 55. № 9. С. 1019. [Nikiforova G.E., Khoroshilov A.V., Gavrichev K.S. et al. // Inorg. Mater. 2019. V. 55. P. 964. https://doi.org/10.1134/S0020168519090085]https://doi.org/10.1134/S0002337X19090082
Arulnesan S.W., Kayser P., Kimpton J.A. et al. // J. Solid State Chem. 2019. V. 277. P. 229. https://doi.org/10.1016/j.jssc.2019.06.014
Sarin P., Hughes R.W., Lowry D.R. et al. // J. Am. Ceram. Soc. 2014. V. 97. P. 3307. https://doi.org/10.1111/jace.13095
Jian L., Wayman C. // J. Am. Ceram. Soc. 1997. V. 80. P. 803. https://doi.org/10.1111/j.1151-2916.1997.tb02905.x
Kukueva L.L., Ivanova L.A., Venevtsev Yu.N. // Ferroelectrics. 1984. V. 55. P. 129. https://doi.org/10.1080/00150198408015351
Keller C. // Z. Anorg. Allg. Chem. 1962. V. 318. P. 89. https://doi.org/10.1002/zaac.19623180108
Гавричев К.С., Рюмин М.А., Гуревич В.М. и др. // Неорган. материалы. 2014. Т. 50. С. 993. [Gavrichev K.S., Ryumin M.A., Gurevich V.M. et al. // Inorg. Mater. 2014. V. 50. P. 917. https://doi.org/10.1134/S0020168514090039]https://doi.org/10.7868/S0002337X14090036
Filippi J., Lasjaunias J.C., Ravex A. et al. // Solid State Commun. 1977. V. 23. P. 613. https://doi.org/10.1016/0038-1098(77)90531-2
Гуревич В.М., Горбунов В.Е., Гавричев К.С. и др. // Геохимия. 1999. № 4. С. 423. [Gurevich V.M., Gorbunov V.E., Gavrichev K.S. et al. // Geochem. Int. 1999. V. 37. P. 367.]
Дополнительные материалы отсутствуют.
Инструменты
Журнал неорганической химии


