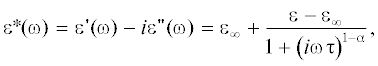Журнал неорганической химии, 2020, T. 65, № 8, стр. 1114-1118
Связь диэлектрической проницаемости с коэффициентами активности воды и ионов в водных растворах сульфатов лития и натрия
И. Ю. Шилов a, *, А. К. Лященко b
a Московский государственный университет им. М.В. Ломоносова, Химический факультет
119991 Москва, Ленинские горы, 1, Россия
b Институт общей и неорганической химии им. Н.С. Курнакова РАН
119991 Москва, Ленинский пр-т, 31, Россия
* E-mail: ignatshilov@mail.ru
Поступила в редакцию 25.02.2020
После доработки 12.03.2020
Принята к публикации 27.03.2020
Аннотация
Рассчитаны коэффициенты активности в водных растворах сульфатов лития и натрия при 298 K по обобщенной теории Дебая–Хюккеля с использованием экспериментальных значений статической диэлектрической проницаемости растворов. Рассмотрено влияние гидратации и ионной ассоциации на диэлектрические и термодинамические свойства растворов электролитов.
ВВЕДЕНИЕ
Обобщенная теория Дебая–Хюккеля (ОТДХ), развитая в 2015 г. [1], учитывает зависимость статической диэлектрической проницаемости (ДП) растворов электролитов от концентрации и тем самым позволяет проанализировать взаимосвязь их диэлектрических и термодинамических свойств. Поскольку статическая ДП экспериментально определяется методами диэлектрической спектроскопии [2, 3], ОТДХ может применяться для прогнозирования коэффициентов активности в концентрированных растворах и изучения закономерностей, которым подчиняются термодинамические свойства растворов электролитов [4–6]. Расчеты для водных растворов 1,1-валентных электролитов показали, что в отдельных случаях наблюдается количественное согласие с экспериментальными данными до концентрации 6–7 моль/кг [1, 4, 5]. Во многих случаях отклонение от экспериментальных значений коррелирует с образованием ионных пар в исследуемых растворах [4, 5], что позволяет анализировать не только вклады дальнодействующих кулоновских и сольватационных взаимодействий, но и проявление ионной ассоциации в коэффициентах активности.
Цель настоящей работы – изучение взаимосвязи ДП и коэффициентов активности в водных растворах сульфата лития и натрия при 298 K, в которых различными физико-химическими методами установлено образование ионных пар, разделенных молекулами воды.
КОНЦЕНТРАЦИОННАЯ ЗАВИСИМОСТЬ ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ
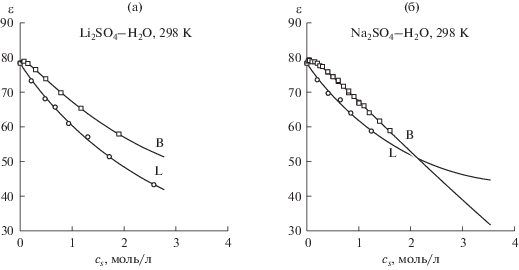
Диэлектрические свойства растворов сульфата лития изучались в работах [7–11], а сульфата натрия – в работах [7–10, 12]. Для использования в расчетах коэффициентов активности диэлектрическая проницаемость растворов была аппроксимирована аналитическими выражениями, приведенными в табл. 1. Для ДП чистой воды везде использовано значение из [13]. Концентрационные зависимости ДП из разных источников приведены для сравнения на рис. 1. Их различие связано с разными условиями проведения эксперимента и методами обработки результатов. Комплексную диэлектрическую проницаемость ε*(ω) растворов сульфатов лития и натрия в работе [7] определяли в интервале частот Δν = 7–25 ГГц и аппроксимировали уравнением Коула–Коула:
где ω – круговая частота, τ – время релаксации, α – параметр распределения времен релаксации, ε – статическая ДП, ε∞ – высокочастотный предел ДП, который принимали равным 5 для всех концентраций. Таким образом, был установлен только один релаксационный процесс, связанный с молекулами воды. Другой вариант расчета по уравнению (1) с включением данных на частотах 80–110 ГГц привел к близким результатам [10].Таблица 1.
Концентрационная зависимость статической диэлектрической проницаемости ε водных растворов сульфатов лития и натрия при 298 K, cs – молярная концентрация соли (моль/л), cs, max, ms, max – максимальные молярная концентрация и моляльность соли в экспериментальных данных по ε
| Соль | Зависимость ε(cS) | cs,max, моль/л | ms,max, моль/кг | Литература |
|---|---|---|---|---|
| Li2SO4 | $\varepsilon = 78.36{\text{ }} - 25.2{{с}_{s}} + 7.23с_{s}^{{3/2}}$ | 2.6 | 2.8 | [7] |
| Li2SO4 | $\varepsilon = 78.36{\text{ }} + {\text{9}}{\text{.70}}\sqrt {{{с}_{s}}} - 28.6{{с}_{s}} + 7.82с_{s}^{{3/2}}$ | 1.9 | 2.0 | [11] |
| Na2SO4 | $\varepsilon = 78.36{\text{ }} - 24.5{{с}_{s}} + 7.96с_{s}^{{3/2}}$ | 1.2 | 1.3 | [7] |
| Na2SO4 | $\varepsilon = 78.36{\text{ }} + 9.75\sqrt {{{с}_{s}}} - 23.5{{с}_{s}} + 2.72с_{s}^{{3/2}}$ | 1.6 | 1.7 | [12] |
В работе [11] измерения ДП растворов сульфата лития проводили в интервале 0.2–89 ГГц и результаты аппроксимировали уравнением с 4 дебаевскими выражениями (модель 4D), включающими соответственно 4 времени релаксации. Время релаксации τ1, составляющее 142–222 пс в зависимости от концентрации, было отнесено к движению сольватно-разделенных ионных пар (2SIP), а время τ2 (26–45 пс) – к сольватно-связанным ионным парам (SIP). Времена релаксации τ3 (7.36–8.4 пс) и τ4 (0.5 пс) были отнесены к молекулам воды.
Растворы сульфата натрия были изучены ранее той же научной группой [12] с аналогичными результатами. Отличие методики заключалось в том, что для описания комплексной ДП использовали более простую 3D-модель, в которой к молекулам воды относилось только одно время релаксации.
С молекулярной точки зрения ДП растворов из работы [7] определяется главным образом водной подсистемой, тогда как результаты [11, 12] дополнительно учитывают вклады ионных пар в поляризацию среды.
Как следует из результатов работ [11, 12], контактные ионные пары не выявляются методом диэлектрической спектроскопии в указанных растворах при концентрациях <2 моль/л, что согласуется с данными рентгеновской дифракции [14]. По данным нейтронографии [15], в 1.5-моляльном растворе Li2SO4 ион лития обладает четко выраженной гидратной оболочкой из пяти молекул, практически совпадающей с гидратной сферой в растворах LiCl в интервале концентраций 1–6 моль/кг, что также интерпретируется как отсутствие прямых контактов между ионами.
Концентрационные изменения спектров КР растворов сульфата лития также связывают с процессами ионной ассоциации, и хотя детальная структурная интерпретация наблюдаемых эффектов затруднена [16–19], образование контактных ионных пар представляется маловероятным. Влияние взаимодействий между противоионами на спектры КР растворов Na2SO4 выражено еще слабее, чем у Li2SO4 [17, 20–22], что приводит к выводу о наличии в растворах хотя бы одной молекулы растворителя между противоположно заряженными ионами.
В связи с этим следует отметить, что моделирование растворов Li2SO4 и Na2SO4 методом классической молекулярной динамики с обычными силовыми полями без учета поляризации частиц давало искаженное описание структуры с сильно преувеличенной концентрацией контактных ионных пар [23–27]. Для более реалистического моделирования структуры разрабатываются новые методы учета межчастичных взаимодействий [25–27].
РАСЧЕТ КОЭФФИЦИЕНТОВ АКТИВНОСТИ И ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ
Расчет коэффициентов активности компонентов исследуемых растворов проводили с помощью уравнений ОТДХ, которые подробно обсуждались в работах [1, 4–6]. Следует отметить, что в этой модели логарифмы коэффициентов активности рассчитываются как сумма вклада кулоновских ион-ионных взаимодействий и сольватационного вклада, характеризующего взаимодействие ионов с окружающей средой, содержащей как растворитель, так и ионы.
Параметрами модели служат расстояние наибольшего сближения ионов a и средний ионный радиус R±, рассчитываемые по формулам:
где R+ и R– – радиусы катиона и аниона. Размеры ионов Li+ (R+ = 0.6 Å) и Na+ (R+ = 0.95 Å) оценивали по Полингу [28], а радиус иона $SO_{4}^{{2 - }}$ (R– = 2.3 Å) – по Маркусу [29]. Плотности растворов были взяты из справочника [30].Результаты расчета коэффициента активности воды γw и среднеионного коэффициента активности γ± при 298 K изображены на рис. 2 и 3 в сравнении с экспериментальными данными [31]. Расчеты проводили, используя значения ДП из работ: [7] и [11, 12], так что линии L и B на рис. 2 и 3 соответствуют линиям L и B для данных по ДП на рис. 1.
Рис. 2.
Коэффициент активности воды (a) и среднеионный коэффициент активности (б) в водных растворах сульфата лития при 298 K. Линии – расчет по обобщенной теории Дебая–Хюккеля: кривая L рассчитана с использованием данных по диэлектрической проницаемости [7], кривая B – с использованием данных по диэлектрической проницаемости [11], кружки – экспериментальные данные [31], ms – моляльность соли.
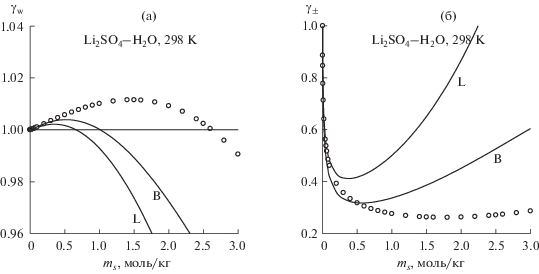
Рис. 3.
Коэффициент активности воды (a) и среднеионный коэффициент активности (б) в водных растворах сульфата натрия при 298 K. Линии – расчет по обобщенной теории Дебая–Хюккеля: кривая L рассчитана с использованием данных по диэлектрической проницаемости [7], кривая B – с использованием данных по диэлектрической проницаемости [12], кружки – экспериментальные данные [31], ms – моляльность соли.
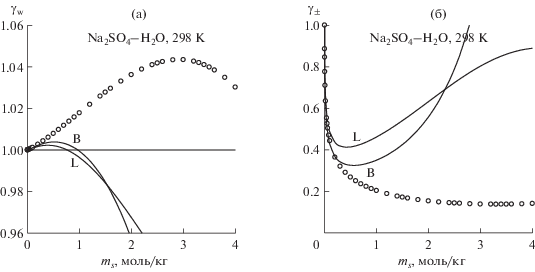
Линии L и B на рис. 2 и 3 демонстрируют немонотонную концентрационную зависимость коэффициентов активности, которая также свойственна и экспериментальным данным (для растворов Na2SO4 минимум γ± находится в области пересыщенных растворов). Линии B дают меньшие значения γ±, чем линии L, и в целом лучше соответствуют экспериментальным данным, хотя количественное согласие наблюдается только для разбавленных растворов. Таким образом, учет влияния ионной ассоциации через экспериментальную ДП приводит в рамках данного подхода к улучшению описания коэффициентов активности.
Из опыта описания термодинамических свойств растворов хлоридов и иодидов щелочных металлов [1, 4] следует, что расхождение между результатами расчета по ОТДХ и экспериментом усиливается при увеличении степени ионной ассоциации раствора электролита. Общая картина описания растворов сульфатов лития и натрия в целом соответствует таковой для хлорида и иодида цезия [1, 4], которые, по данным разных методов, являются наиболее ассоциированными в соответствующих рядах систем. По склонности к ионной ассоциации растворы сульфатов щелочных металлов занимают промежуточное положение между галогенидами щелочных металлов и сульфатами двухвалентных катионов, что в первом приближении объясняется электростатическим фактором. Сравнение с недавно исследованными методом диэлектрической спектроскопии растворами MgCl2 и CaCl2 [32] показывает, что сульфаты щелочных металлов более ассоциированы, чем хлориды щелочноземельных металлов.
В соответствии с результатами работ [4, 5], лучшее согласие с экспериментом могло бы быть достигнуто путем явного учета образования ионных пар в рамках расширения ОТДХ. Однако это потребовало бы эмпирической оптимизации значений констант равновесия ионной ассоциации, что не является целью данной работы.
Список литературы
Shilov I.Yu., Lyashchenko A.K. // J. Phys. Chem. B. 2015. V. 119. № 31. P. 10087. https://doi.org/10.1021/acs.jpcb.5b04555
Buchner R., Hefter G. // Phys. Chem. Chem. Phys. 2009. V. 11. № 40. P. 8984. https://doi.org/10.1039/B906555P
Lyashchenko A., Lileev A. // J. Chem. Eng. Data. 2010. V. 55. № 5. P. 2008. https://doi.org/10.1021/je900961m
Shilov I.Yu., Lyashchenko A.K. // J. Mol. Liq. 2017. V. 240. P. 172. https://doi.org/10.1016/j.molliq.2017.05.010
Shilov I.Yu., Lyashchenko A.K. // J. Solution Chem. 2019. V. 48. № 2. P. 234. https://doi.org/10.1007/s10953-019-00860-8
Shilov I.Yu., Lyashchenko A.K. // Russ. J. Inorg. Chem. 2019. V. 64. № 9. P. 1186. [Шилов И.Ю., Лященко А.К. // Журн. неорган. химии. 2019. Т. 64. № 9. С. 1006.] https://doi.org/10.1134/S0036023619090213
Лилеев А.С., Лященко А.К., Борина А.Ф. Диэлектрические свойства в сантиметровом диапазоне длин волн и электропроводность водных растворов сульфатов щелочных металлов и аммония. Деп. в ВИНИТИ РАН. 06.07.1999. № 2180-В1999. 40 с.
Засецкий А.Ю., Лященко А.К. Квазиоптический метод измерения комплексной диэлектрической проницаемости водных растворов электролитов в миллиметровом диапазоне волн и релаксационные характеристики растворов. Деп. в ВИНИТИ РАН. 06.07.1999. № 2181-В1999. 62 с.
Lileev A.S., Filimonova Z.A., Lyashchenko A.K. // J. Mol. Liq. 2003. V. 103–104. P. 299. https://doi.org/10.1016/S0167-7322(02)00148-4
Lyashchenko A.K., Dunyashev V.S. // Russ. J. Inorg. Chem. 2018. V. 63. № 12. P. 1656. [Лященко А.К., Дуняшев В.С. // Журн. неорган. химии. 2018. Т. 63. № 12. С. 1635.] https://doi.org/10.1134/S0036023618120136
Wachter W., Fernandez Š., Buchner R., Hefter G. // J. Phys. Chem. B. 2007. V. 111. № 30. P. 9010. https://doi.org/10.1021/jp072425e
Buchner R., Capewell S.G., Hefter G., May P.M. // J. Phys. Chem. B. 1999. V. 103. № 7. P. 1185. https://doi.org/10.1021/jp983706c
Kaatze U. // J. Chem. Eng. Data. 1989. V. 34. № 4. P. 371. https://doi.org/10.1021/je00058a001
Смирнов П.Р., Тростин В.Н., Крестов Г.А. // Докл. АН СССР. 1988. Т. 299. № 4. С. 925.
Mason P.E., Ansell S., Neilson G.W., Rempe S.B. // J. Phys. Chem. B. 2015. V. 119. № 5. P. 2003. https://doi.org/10.1021/jp511508n
Rull F. // Z. Naturforsch. A. 1995. V. 50. № 2–3. P. 292. https://doi.org/10.1515/zna-1995-2-322
Rull F., Sobrón F., Nielsen O.F. // J. Raman Spectrosc. 1995. V. 26. № 8–9. P. 663. https://doi.org/10.1002/jrs.1250260812
Tomišić V., Simeon V. // Phys. Chem. Chem. Phys. 2000. V. 2. № 9. P. 1943. https://doi.org/10.1039/B001506G
Watanabe D., Hamaguchi H. // J. Chem. Phys. 2005. V. 123. P. 034 508. https://doi.org/10.1063/1.1931660
Hester R.E., Plane R.A. // Inorg. Chem. 1964. V. 3. № 5. P. 769. https://doi.org/10.1021/ic50015a037
Daly F.P., Brown C.W., Kester D.R. // J. Phys. Chem. 1972. V. 76. № 24. P. 3664. https://doi.org/10.1021/j100668a027
Kratsis S., Hefter G., May P.M., Sipos P. // Aust. J. Chem. 2000. V. 53. № 5. P. 363. https://doi.org/10.1071/CH00011
Chialvo A.A., Simonson J.M. // Collect. Czech. Chem. Commun. 2010. V. 75. № 4. P. 405. https://doi.org/10.1135/cccc2009535
Zasetsky A.Y., Lyashchenko A.K., Lileev A.S. // Mol. Phys. 2011. V. 109. № 6. P. 813. https://doi.org/10.1080/00268976.2011.554329
Pluhařová E., Mason P.E., Jungwirth P. // J. Phys. Chem. A. 2013. V. 117. № 46. P. 11766. https://doi.org/10.1021/jp402532e
Wernersson E., Jungwirth P. // J. Chem. Theory Comput. 2010. V. 6. № 10. P. 3233. https://doi.org/10.1021/ct100465g
Pegado L., Marsalek O., Jungwirth P., Wernersson E. // Phys. Chem. Chem. Phys. 2012. V. 14. № 29. P. 10248. https://doi.org/10.1039/c2cp40711f
Pauling L. // J. Am. Chem. Soc. 1927. V. 49. № 3. P. 765. https://doi.org/10.1021/ja01402a019
Marcus Y. Ions in Solution and their Solvation. New Jersey: Wiley, Hoboken, 2015.
Зайцев И.Д., Асеев Г.Г. Физико-химические свойства бинарных и многокомпонентных растворов неорганических веществ. М.: Химия, 1988. 416 с.
Holmes H.F., Mesmer R.E. // J. Solution Chem. 1986. V. 15. № 6. P. 495. https://doi.org/10.1007/BF00644892
Friesen S., Hefter G., Buchner R. // J. Phys. Chem. B. 2019. V. 123. № 4. P. 891. https://doi.org/10.1021/acs.jpcb.8b11131
Дополнительные материалы отсутствуют.
Инструменты
Журнал неорганической химии