Журнал неорганической химии, 2021, T. 66, № 7, стр. 885-889

Концентрационные зависимости параметров решетки и плотности монокристаллов трехкомпонентного твердого раствора Sr_0.8La_{0.2 –} _xLu_xF_2.2 (0 ≤ x ≤ 0.2)

Н. И. Сорокин^a, *

^a Институт кристаллографии им. А.В. Шубникова ФНИЦ “Кристаллография и фотоника” РАН
119333 Москва, Ленинский пр-т, 59, Россия

^* E-mail: nsorokin1@yandex.ru

Поступила в редакцию 18.11.2020
После доработки 22.01.2021
Принята к публикации 25.01.2021

DOI: 10.31857/S0044457X21060180

Полный текст (PDF)

Аннотация

Изучены концентрационные зависимости параметра решетки a = f(x) и плотности ρ = f(x) для монокристаллов трехкомпонентного твердого раствора Sr_0.8La_{0.2 –}_xLu_xF_2.2 (тип флюорита − CaF₂, 0 ≤ ≤ x ≤ 0.2, x – мольная доля LuF₃), полученных из расплава по методу Бриджмена. Экспериментальные зависимости a(x) и ρ(x) подчиняются закону аддитивности. Денситометрические данные подтверждают схему гетеровалентного изоморфизма в твердом растворе Sr_0.8La_{0.2 –}_xLu_xF_2.2: Sr²⁺ → → (1−5x)La³⁺ + 5xLu³⁺ + ${\text{F}}_{i}^{ - }$. Избыток положительного заряда в катионной подрешетке кристаллов компенсируется образованием междоузельных ионов F_i^–. Эти закономерности позволяют рассчитать параметры кристаллической решетки и плотность большого числа новых функциональных фторидных материалов − флюоритовых твердых растворов 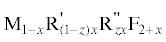в тройных системах MF₂–R'F₃–R"F₃ (M = Ca, Sr, Ba; R', R" = La–Lu, Y).

Ключевые слова: фториды, редкоземельные элементы, твердые растворы, структура флюорита, параметры решетки

ВВЕДЕНИЕ

Монокристаллические фторидные материалы представляют большой интерес для фундаментальной и прикладной науки. Они используются в качестве конструкционных оптических элементов, химических сенсоров, твердых электролитов для источников тока, детекторов для ионизирующих излучений и др. До сих пор поиск и активные исследования фторидных материалов проводились главным образом в бинарных системах MF₂–RF₃, где M – щелочноземельные элементы Ca, Sr, Ba и R – редкоземельные элементы (РЗЭ) La–Lu, Y. В этих системах наиболее многочисленными продуктами высокотемпературных химических взаимодействий являются двухкомпонентные твердые растворы M_{1 −}_xR_xF_{2 +}_x со структурой типа флюорита (CaF₂) [1]. Поэтому росту и физико-химическим свойствам кристаллов M_{1 −}_xR_xF_{2 +}_x уделяется повышенное внимание [1–3].

Изоморфные двойные замещения катионов РЗЭ в матрицах MF₂ многократно увеличивают число флюоритовых трехкомпонентных твердых растворов 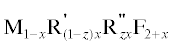в тройных системах MF₂–R'F₃–R"F₃. Однако свойства кристаллов практически не исследованы. Изучение большого числа трех- и более компонентных фторидных систем потребует значительных временных затрат, поэтому необходимо развивать прогнозирующие подходы в исследованиях многокомпонентных фторидов.

Для поиска таких подходов в качестве модельной системы нами выбрана тройная система SrF₂–LaF₃–LuF₃ [3, 4], в которой реализуется максимальное различие в ионных радиусах катионов РЗЭ (радиус Lu³⁺ по отношению к La³⁺ меньше на 15.1% [5]). В структурных исследованиях обнаружено, что флюоритовые кристаллы Sr_{1 –}_xLa_xF_{2 +}_x [6, 7] и Sr_{1 –}_xLu_xF_{2 +}_x [8–10] имеют разный тип дефектной (кластерной) структуры, в них образуются тетраэдрические [La₄F₂₆] и октаэдро-кубические [Sr₈Lu₆F₆₉] кластеры соответственно.

Согласно физико-химическим данным [11], в бинарных системах SrF₂–RF₃ (R = La и Lu) предельные области гомогенности флюоритовых твердых растворов простираются до 49 мол. % LaF₃ и 37 мол. % LuF₃ при нормальном давлении. Это позволяет получить непрерывный ряд трехкомпонентных твердых растворов Sr_0.8La_{0.2 –}_xLu_xF_2.2 при полном замещении катионов La³⁺ на Lu³⁺. Ранее [3, 4] нами обнаружено, что для кристаллов Sr_0.8La_{0.2 –}_xLu_xF_2.2 зависимость ионной проводимости является сложной функцией состава, в то время как экспериментальные зависимости параметров элементарных ячеек и плотности являются линейными функциями. В этих работах не исследовали влияние гетеровалентного изоморфизма на концентрационные зависимости параметров решетки и плотности трехкомпонентного твердого раствора и не проводили расчет величины их параметра элементарной ячейки и плотности с привлечением экспериментальных данных для двухкомпонентных фаз Sr_{1 –}_xLa_xF_{2 +}_x и Sr_{1 –}_xLu_xF_{2 +}_x.

Цель настоящей работы – определение расчетной величины параметра элементарной ячейки и плотности трехкомпонентных твердых растворов Sr_0.8La_{0.2 –}_xLu_xF_2.2 в предположении закона аддитивности и механизма компенсации разницы в зарядах замещающихся катионов за счет образования междоузельных ионов фтора.

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

Для выращивания кристаллов трехкомпонентного твердого раствора использовали коммерческие реактивы SrF₂ марки “ос. ч.”, LaF₃ и LuF₃ марки “ч”. Очистку реактивов от примеси кислорода осуществляли предварительным фторированием расплава продуктами пиролиза политетрафторэтилена. Кристаллы Sr_0.8La_{0.2 –}_xLu_xF_2.2 (x – мольная доля LuF₃) с x = 0, 0.03, 0.06, 0.1, 0.14, 0.17 и 0.2 были получены из расплава по методу Бриджмена в двухзонной установке КРФ-1 с графитовыми нагревателями сопротивления (конструкция и изготовление СКБ ИК РАН). Температуры плавления компонентов SrF₂, LaF₃ и LuF₃ равны 1464 ± 5, 1500 ± 10 и 1182 ± 10°С [1] соответственно. Рост кристаллов проводили в графитовом тигле, содержащем семь отдельных ячеек без затравочных каналов.

Осевой температурный градиент между горячей и холодной зонами печи равен ∼30°С/см, радиальный градиент в ростовой зоне не превышал 5°С/см. Для подавления характерной для фторидов реакции пирогидролиза выращивание кристаллов проводили в атмосфере He с добавлением в шихту дифторида PbF₂ с низкой температурой плавления (825 ± 5°С) марки “ос. ч.” в количестве 5 мас. %. Скорость опускания тигля составляла 5.3 ± 0.2 мм/ч.

Выращенные монокристаллические були представляли собой цилиндры диаметром 10 мм и длиной ∼30 мм. Потери массы шихты при кристаллизации составили 0.7% для твердых растворов с x = 0.1, 0.14, 0.17, 0.2; 2.5% для твердых растворов с x = 0.03, 0.06 и 4% для кристалла SrF₂ (x = 0).

Образцы вырезали из средней части выращенных монокристаллов, вид образца показан на рис. 1. По данным рентгенофлуоресцентного анализа [12], содержание трифторидов РЗЭ RF₃ в средних частях выращенных монокристаллов Sr_{1 −}_xR_xF_{2 +}_x соответствует составу шихты с точностью ±1 мол. % RF₃.

Рис. 1.

Вид монокристаллического образца Sr_0.8La_0.03Lu_0.17F_2.2.

Однофазность образцов подтверждена рентгенографически на порошковом дифрактометре Filips PW1710 (CuK_α-излучение, внутренний стандарт Si). Регистрацию дифрактограмм проводили в диапазоне углов 2θ 20°–110°. Рентгенограммы образцов относятся к кубической фазе со структурой типа CaF₂ (пр. гр. Fm$\bar {3}$m, Z = 4). Полученные рентгеноструктурные данные для кубической сингонии обработаны с использованием программы DECO1877 (E. Halwax, TU Wien). Погрешность определения параметров элементарных ячеек твердых растворов равна ±6 × 10^–4 Å. Параметры элементарной ячейки a(x) кристаллов Sr_0.8La_{0.2 –}_xLu_xF_2.2 приведены в табл. 1. Зависимость параметров решетки от состава показана на рис. 2.

Таблица 1.

Характеристики кристаллов SrF₂ и Sr_0.8La_{0.2 –}_xLu_xF_2.2

Кристалл	Масса, г/моль	Параметр решетки a, Å	Плотность, г/см³		Молярный объем, см³/моль
Кристалл	Масса, г/моль	Параметр решетки a, Å	ρ	ρ_cal	V	V_cal
SrF₂	125.616	5.800	−	4.277	−	29.37
Sr_0.8La_0.2–xLu_xF_2.2:
x = 0	139.679	5.8314(5)	4.688	4.679	29.80	29.85
x = 0.03	140.755	5.8195(4)	4.768	4.744	29.52	29.67
x = 0.06	141.837	5.8021(6)	4.823	4.823	29.41	29.41
x = 0.1	143.279	5.7831(3)	4.922	4.921	29.11	29.11
x = 0.14	144.722	5.7633(4)	5.018	5.021	28.84	28.82
x = 0.17	145.804	5.7466(4)	5.117	5.103	28.49	28.57
x = 0.2	146.885	5.7327(3)	5.180	5.178	28.36	28.37

Рис. 2.

Зависимость параметра решетки кристаллов Sr_0.8La_{0.2 –}_xLu_xF_2.2 от состава: кружки – эксперимент, прямая – аппроксимация экспериментальных данных линейным уравнением.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Концентрационная зависимость экспериментальных значений параметров решетки a = f(x) удовлетворяет линейному уравнению (правилу Вегарда) с коэффициентом корреляции 0.999 [3]:

(1)

$a(x) = 5.832 - 0.5x,$

где концентрация x выражается в мольных долях LuF₃, величина a – в Å. Параметр решетки двухкомпонентного кристалла Sr_0.8Lu_0.2F_2.2 по сравнению с параметром решетки Sr_0.8La_0.2F_2.2 меньше на 1.7%, это существенно меньше соотношения между ионными радиусами Lu³⁺ и La³⁺ с учетом концентрации последних. Параметр решетки трехкомпонентного твердого раствора Sr_0.8La_{0.2 –}_xLu_xF_2.2 с x = 0.064 соответствует параметру решетки матрицы SrF₂ (a₀ = 5.800 Å).

Расчет параметра решетки трехкомпонентного твердого раствора Sr_0.8La_{0.2 –}_xLu_xF_2.2 проведен из данных для двухкомпонентных растворов в предположении выполнения закона аддитивности:

(2)

${{a}_{{{\text{cal}}}}}\left( x \right) = {{a}_{0}} + 0.{\text{2}}{{k}_{{{\text{Sr}},{\text{La}}}}}--\left[ {{{k}_{{{\text{Sr}},{\text{La}}}}}--{{k}_{{{\text{Sr}},{\text{Lu}}}}}} \right]x,$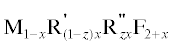

где a₀ – параметр решетки матрицы SrF₂, k_Sr,La – и k_Sr,Lu – линейные коэффициенты в концентрационных зависимостях параметров для твердых растворов Sr_{1 –}_xLa_xF_{2 +}_x и Sr_{1 –}_xLu_xF_{2 +}_x соответственно. Значения коэффициентов k_Sr,La = 0.1357 Å и k_Sr,Lu = − 0.3442 Å взяты из [13]. Сравнение экспериментальных и рассчитанных значений параметров решетки для кристаллов Sr_0.8La_{0.2 –}_xLu_xF_2.2 приведено на рис. 3. Из рисунка видно, что значения экспериментальных (a) и теоретических (a_cal) параметров решетки хорошо совпадают между собой. Таким образом, с учетом приведенных в литературе характеристик двухкомпонентных твердых растворов M_{1 −}_xR_xF_{2 +}_x (M = Ca, Sr, Ba; R = La–Lu, Y) [13] можно аналогичным способом рассчитать параметры кристаллической решетки большого семейства флюоритовых твердых растворов

в тройных системах MF₂–R'F₃–R"F₃.

Рис. 3.

Сравнение рассчитанных (a_cal) и экспериментальных (a) параметров элементарной ячейки для кристаллов Sr_0.8La_{0.2 –}_xLu_xF_2.2.

Денситометрические измерения проводили на образцах в виде дисков диаметром 10 мм и толщиной 1–2 мм. Плотность ρ измеряли методом гидростатического взвешивания в дистиллированной воде на приборе Mettler ME-33360 с точностью ±10^–3 г/см³. Экспериментальные значения плотности ρ и молярного объема V = μ/ρ (μ − молярная масса) приведены в табл. 1. По мере увеличения содержания LuF₃ плотность кристаллов Sr_0.8La_{0.2 –}_xLu_xF_2.2 растет от 4.69 г/см³ для Sr_0.8La_0.2F_2.2 до 5.18 г/см³ для Sr_0.8Lu_0.2F_2.2, что составляет 10.4% по отношению к меньшему значению плотности. Увеличение плотности в ряду кристаллов Sr_0.8La_{0.2 –}_xLu_xF_2.2 значительно превышает соответствующее изменение параметра решетки.

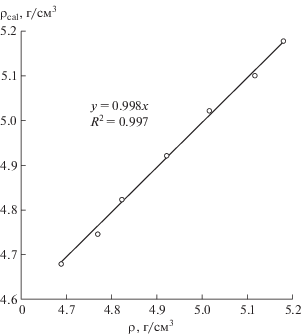
Концентрационная зависимость экспериментальной плотности ρ = f(x) также удовлетворяет правилу аддитивности (рис. 4) и может быть аппроксимирована линейным уравнением (коэффициент корреляции 0.997) [3]:

(3)

$\rho = {\text{4}}.{\text{68}} + {\text{2}}.{\text{47}}x,$

где плотность ρ задана в г/см³. Теоретическую рентгенографическую плотность кубических кристаллов Sr_0.8La_{0.2 –}_xLu_xF_2.2 рассчитывали по формуле:

(4)

${{\rho }_{{{\text{cal}}}}} = {\text{4}}\mu {\text{/}}({{a}^{{\text{3}}}}{{N}_{A}}),$

где μ – молярная масса и N_A – постоянная Авогадро. Расчет молярной массы μ выполнен в предположении, что компенсация разницы в зарядах замещающихся катионов происходит за счет образования междоузельных ионов F_i^–. При этом с увеличением x от 0 до 0.2 в структуре твердых растворов происходит замена тетраэдрических кластеров [La₄F₂₆] на октаэдро-кубические кластеры [Sr₈Lu₆F₆₉] [6–10].

Рис. 4.

Зависимость плотности кристаллов Sr_0.8La_0.2 ‒ _xLu_xF_2.2 от состава: кружки – эксперимент, прямая – аппроксимация экспериментальных данных линейным уравнением.

Схема изоморфных замещений для компенсации избыточного заряда в структуре трехкомпонентного твердого раствора Sr_0.8La_{0.2 –}_xLu_xF_2.2 (0 ≤ x ≤ 0.2) имеет вид:

(5)

${\text{S}}{{{\text{r}}}^{{{\text{2}} + }}} \to ({\text{1}} - {\text{5}}x){\text{L}}{{{\text{a}}}^{{{\text{3}} + }}} + {\text{5}}x{\text{L}}{{{\text{u}}}^{{{\text{3}} + }}} + {{{\text{F}}}_{i}}^{--}.$

Расчетные значения плотности ρ_cal и молярного объема V_cal = μ/ρ_cal приведены в табл. 1, из которой видно, что значения экспериментальной (ρ) и теоретической (ρ_cal) плотности хорошо совпадают между собой (рис. 5). Это подтверждает справедливость использования междоузельной модели гетеровалентного изоморфизма для трехкомпонентных кристаллов .

Рис. 5.

Сравнение рентгенографической (ρ_cal) и экспериментальной (ρ) плотности для кристаллов Sr_0.8La_{0.2 –}_xLu_xF_2.2.

ЗАКЛЮЧЕНИЕ

Из расплава методом направленной кристаллизации Бриджмена выращена концентрационная серия (0 ≤ x ≤ 0.2) флюоритовых кристаллов трехкомпонентного твердого раствора Sr_0.8La_{0.2 –}_xLu_xF_2.2. Особенности используемого метода получения кристаллов Sr_0.8La_{0.2 –}_xLu_xF_2.2: 1) очистка коммерческих реактивов SrF₂, LaF₃ и LuF₃ от примеси кислорода предварительным фторированием расплава этих соединений продуктами пиролиза политетрафторэтилена, 2) подавление пирогидролиза фторидных кристаллов при их росте путем добавления в шихту фторида PbF₂, 3) одновременное выращивание семи кристаллов твердого раствора разного состава, 4) низкие потери массы шихты при кристаллизации твердых растворов.

Экспериментальные зависимости параметра решетки a = f(x) и плотности ρ = f(x) трехкомпонентного твердого раствора от состава подчиняются закону аддитивности. Этот факт позволяет на основании характеристик двухкомпонентных твердых растворов M_{1 −}_xR_xF_{2 +}_x (M = Ca, Sr, Ba; R = La–Lu, Y) рассчитать параметры кристаллической решетки и плотность большого числа флюоритовых трехкомпонентных твердых растворов 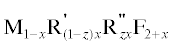в тройных системах MF₂–R'F₃–R"F₃. Такие расчеты необходимы для конструирования новых функциональных фторидных материалов с характеристиками, максимально отвечающими требованиям научных и технических решений, использующих такие материалы.

Монокристаллы Sr_0.8La_{0.2 –}_xLu_xF_2.2, содержащие в кристаллической структуре тетраэдрические [La₄F₂₆] и октаэдро-кубические [Sr₈Lu₆F₆₉] кластеры, можно использовать в качестве модельной системы для изучения связи дефектной (кластерной) структуры и физических свойств многокомпонентных флюоритовых фаз.

Список литературы

Sobolev B.P. The Rare Earth Trifluorides. Barcelona: Moscow Institute of Crystallography and Institut d’Estudis Catalans, 2000–2001. 980 p.
Sobolev B.P., Sorokin N.I., Bolotina N.B. // Photonic & Electronic Properties of Fluoride Materials / Eds. Tressaud A., Poeppelmeier K. Amsterdam: Elsevier, 2016. P. 465.
Сорокин Н.И., Кривандина Е.А., Жмурова З.И. // Кристаллография. 2013. Т. 58. № 6. С. 952. [Sorokin N.I., Krivandina E.A., Zhmurova Z.I. // Crystallogr. Rep. 2013. V. 58. № 6. P. 948.] https://doi.org/10.1134/S1063774513060217
Sorokin N.I., Breiter M.W. // Solid State Ionics. 1997. V. 104. P. 325.
Shannon R.D. // Acta Crystallogr., Sect. A. 1976. V. 32. P. 751.
Сульянова Е.А., Болотина Н.Б., Калюканов А.И. и др. // Кристаллография. 2019. Т. 64. № 1. С. 47. [Sulyanova E.A., Bolotina N.B., Kalukanov A.I. et al. // Crystallogr. Rep. 2019. V. 64. № 1. P. 41.] https://doi.org/10.1134/S1063774519010279
Мурадян Л.А., Максимов Б.А., Мамин Б.Ф. и др. // Кристаллография. 1986. Т. 31. № 2. С. 248.
Сульянова Е.А., Верин И.А., Соболев Б.П. // Кристаллография. 2012. Т. 57. № 1. С. 79. [Sulyanova E.A., Verin I.A., Sobolev B.P. // Crystallogr. Rep. 2012. V. 57. № 1. P. 73]. https://doi.org/10.1134/S1063774512010130
Сульянова Е.А., Молчанов В.Н., Верин И.А. и др. // Кристаллография. 2009. Т. 54. № 3. С. 554. [Sulyanova E.A., Molchanov V.N., Verin I.A. et al. // Crystallogr. Rep. 2009. V. 54. № 3. P. 516.] https://doi.org/10.1134/S1063774509030249
Лошманов А.А., Максимов Б.А., Мурадян Л.А. и др. // Коорд. химия. 1989. Т. 15. № 8. С. 1133.
Sobolev B.P., Seiranian K.B. // J. Solid State Chem. 1981. V. 39. № 2. P. 17.
Туркина Т.М., Федоров П.П., Соболев Б.П. // Кристаллография. 1986. Т. 31. № 1. С. 146.
Федоров П.П., Соболев Б.П. // Кристаллография. 1992. Т. 37. № 5. С. 1210.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал неорганической химии

Архивы выпусков Информация о журнале Отправить рукопись в журнал

Журнал неорганической химии, 2021, T. 66, № 7, стр. 885-889

Концентрационные зависимости параметров решетки и плотности монокристаллов трехкомпонентного твердого раствора Sr_0.8La_{0.2 –} _xLu_xF_2.2 (0 ≤ x ≤ 0.2)

ВВЕДЕНИЕ