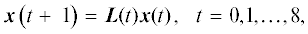Журнал общей биологии, 2019, T. 80, № 3, стр. 200-213
Неутешительный прогноз выживания ценопопуляции Androsace albana в случайно меняющейся среде
Д. О. Логофет 1, *, Е. С. Казанцева 2, **, И. Н. Белова 1, ***, В. Г. Онипченко 3, ****
1 Институт физики атмосферы им. А.М. Обухова РАН
119017 Москва, Пыжевский пер., 3, Россия
2 Институт биологии Чэнду Китайской Академии наук
610041 Чэнду, Ренмин Нань Роуд, 9, Секция 4, Китай
3 Московский государственный университет им. М.В. Ломоносова, биологический факультет,
кафедра геоботаники
119234 Москва, Ленинские горы, 1, Россия
* E-mail: danilal@postman.ru
** E-mail: biolenok@mail.ru
*** E-mail: iya@ifaran.ru
**** E-mail: vonipchenko@mail.ru
Поступила в редакцию 30.10.2018
После доработки 12.11.2018
Принята к публикации 29.11.2018
Аннотация
Итоги 10-летних наблюдений состояния ценопопуляции проломника Androsace albana на постоянных пробных площадках, заложенных на альпийской лишайниковой пустоши в 2009 г., мы подводим в форме неавтономной матричной модели динамики популяции со стадийной структурой. Модель соответствует построенному ранее графу жизненного цикла по стадиям онтогенеза и представляет собой 9 годичных “проекционных” матриц, откалиброванных однозначно по данным наблюдений. Пять из 9 матриц имеют доминантное собственное число больше 1, т.е. дают благоприятный прогноз выживания ценопопуляции, а у остальных четырех это число меньше 1, т.е. прогноз отрицательный. Получить итоговый прогноз позволяет оригинальная концепция структурно-геометрического осреднения заданных неотрицательных матриц, и доминантное собственное число, λ1(G9), средней матрицы G9 оказалось заметно меньше 1, указывая на убыль ценопопуляции в долговременной перспективе. Традиционный метод прогноза выживания ценопопуляции по λS – стохастической скорости роста популяции в случайной среде, формируемой случайным и равновероятным выбором из тех же 9 годичных матриц, – также дает негативный результат, хотя и с более высокими количественными значениями λS. Последнее обстоятельство мы связываем с искусственным допущением равной вероятности выбора при формировании случайной последовательности годичных матриц, каждая из которых опосредованно отражает условия среды, повлиявшие на рост и развитие растений в течение года до момента калибровки. Это мотивирует задачу построения более адекватной модели выбора годичных матриц, в которой вероятность выбора была бы связана с динамикой реальных факторов местообитания данной ценопопуляции.
Прогноз выживания ценопопуляции делается на основе оценки ее текущего состояния, и в отечественной литературе предлагались такие частные количественные показатели для сравнения ценопопуляций, как Δ – индекс возрастности, ω – индекс эффективности, Iв – индекс возобновления, Iст – индекс старения (Жукова, 1995; Глотов, 1998; Животовский, 2001), вычисляемые по данным о стадийной структуре ценопопуляции. При этом семантика термина “возрастной” не предполагает знание возраста в хронологических единицах (годах) и соответствующий индекс определяется по соотношению молодых и стареющих стадий в структуре ценопопуляции. Ботаники, ответственные за включение видов в региональные Красные книги, пытаются разработать обобщающие показатели на основе известных частных индексов, по фактическим значениям которых можно было бы судить о состоянии ценопопуляции и формулировать рекомендации к принятию решений о включении видов в Красные книги (см. Клинкова и др., 2011). Например, виталитет – показатель жизненности (степень процветания или угнетения), основанный на строгой количественной оценке одного параметра в строении особи (Злобин, 1989а, б, 1998), входит составной частью в индекс виталитета по нескольким параметрам (Ишбирдин, Ишмуратова, 2004, 2009; Злобин, 2009), и здесь возникает произвол исследователя в способе разбиения на классы виталитета и в придании конкретных весов разным параметрам особи, когда составляется суммарный индекс. Аналогичные элементы произвольных экспертных решений в ходе разработки количественных показателей характерны и для других индексов (ibid.). Такие бесспорные положения, как смещение в сторону молодых стадий онтогенеза в структуре растущей популяции, учитываются в индексах экспертным способом. Выбор конкретных показателей из весьма разнообразного набора существующих индексов также остается на усмотрение эксперта. Вопрос о том, способны ли такие индексы отразить смену тенденции в динамике ценопопуляции при резкой смене условий обитания и дать прогноз состояния на долгую перспективу, остается за рамками предложенных подходов к подсчету индексов.
В мировой практике для оценки состояния локальных популяций и их сравнения давно и плодотворно используются матричные модели популяций с дискретной структурой, сформированной на основании какого-либо (наблюдаемого и/или измеримого) признака особей: возраста, размера, стадии развития и т.п. (Caswell, 2001, и ссылки там же). Теоретическим фундаментом таких моделей служит классическая теорема Перрона–Фробениуса для неотрицательных матриц (Гантмахер, 1967; Horn, Johnson, 1990), и на ее основе разработан впечатляющий набор характеристик локальной популяции и методов их вычисления из проекционной матрицы популяции (ПМП) L – сердцевины матричной модели (см. пособие: Логофет, Уланова, 2017), которая преобразует (“проецирует” в неудачной, но устоявшейся терминологии) вектор x(t) стадийной структуры года наблюдения t в аналогичный вектор года t + 1 по правилу линейной алгебры: x(t + 1) = Lx(t).
В частности, доминантное собственное число λ1(L) матрицы L служит количественной мерой адаптации ценопопуляции к условиям среды, причем значение этой меры специфично в пространстве и времени, а именно, отражает состояние популяции там и тогда, где и когда собраны данные для калибровки матрицы L (На земле и …, 2013; Logofet et al., 2014; Логофет и др., 2015, 2016а, б). Поэтому, с одной стороны, ПМП является эффективным инструментом сравнительной демографии видов, а с другой, повышаются требования к надежности калибровки ПМП по эмпирическим данным (ibid.).
Популярность матричных моделей в научных и практических сферах неуклонно растет: мировые базы данных COMPADRE/COMADRE для видов растений и животных содержат уже более 7000 и около 2000 опубликованных моделей соответственно (COMPADRE, 2018; COMADRE, 2018).
Мониторинг состояния ценопопуляции длителен во времени, и если мы получаем не одну ПМП, а их временнóй ряд (например, ряд “годичных” ПМП, как в наших проектах), то прогноз жизнеспособности ценопопуляции через доминантное собственное число λ1(L) может меняться и количественно, и качественно – с роста популяции на ее убыль (Логофет и др., 2016а, 2017а, б, 2018). Идеология долгосрочного прогноза в этом случае связана с концепцией “динамики популяции в случайно меняющейся среде” (Tuljapurkar, 1990; Caswell, 2001). Суть концепции в том, что каждая ПМП рассматривается как обобщенная характеристика среды и тогда среда, “меняющаяся” в долгой череде лет, эквивалентна смене матриц в столь же длинной последовательности, а “случайно меняющаяся среда” эквивалентна случайному выбору матрицы из доступного набора на каждом шаге этой последовательности.
Давно установлено математически (Оселедец, 1968; Cohen, 1976), что (при определенных ограничениях на характер случайности) такая последовательность с вероятностью 1 сходится к пределу при t → ∞, т.е. при бесконечно большом числе шагов, и этот предел определяет величину, которую и назвали впоследствии λS – стохастической скоростью роста популяции (Tuljapurkar, 1986) – по аналогии, но и с отличием от асимптотической скорости λ1(L). Если λS > 1, то с вероятностью 1 общая численность популяции возрастает экспоненциально, а если λS < 1, то стремится к нулю (ibid.).
Изящная идея и удачный термин способствовали дальнейшему развитию теории в направлениях, замотивированных потребностями практики: никто не собирался выполнять бесконечное число шагов, и в математической теории предложены оценки величины λS, основанные на определенных допущениях о стохастическом характере выбираемых матриц (Tuljapurkar, 1990; Caswell, 2001; современный обзор у Sanz, 2019). В частности, если набор годичных ПМП рассматривать как малый случайный шум, аддитивно меняющий некоторую среднюю матрицу A, то оценку λS можно получить через λ1(A) (доминантное собственное число средней матрицы) и дисперсию случайного распределения вариаций (Caswell, 2001), а в качестве средней матрицы может тогда выступать среднее арифметическое заданного набора. Но столь значительные изменения годичных матриц, какие наблюдаются у альпийских малолетников (Логофет и др., 2016а, 2017а, б, 2018), заставляют усомниться в верности парадигмы малого шума и искать иную парадигму осреднения годичных ПМП, полученных в результате длительного мониторинга (ibid.; Logofet, 2018).
Оригинальная концепция структурно-геометрического среднего заданных ПМП (ibid.) исходит из логики преобразования вектора структуры популяции за весь период наблюдений – от начального до последнего момента – и выдвигает естественное требование к строению средней матрицы: оно должно совпадать со строением усредняемых матриц, т.е. соответствовать графу жизненного цикла – графическому выражению знаний о биологии вида и способе мониторинга (Caswell, 2001; Логофет, Уланова, 2017). Такая логика приводит к постановке математической задачи структурно-геометрического осреднения заданных неотрицательных матриц, которая допускает решение современными средствами вычислительной техники (например, в системе MatLab), когда размер матриц невелик, например 4 × 4 или 5 × 5, как для альпийских малолетников (Логофет и др., 2016а, 2017а, б). Найденная таким образом матрица G подводит итог всего периода мониторинга – своим доминантным собственным числом λ1(G) и прочими характеристиками.
Ежегодные наблюдения за ценопопуляцией проломника A. albana на постоянных площадках продолжаются с 2009 г. (Логофет и др., 2017б), и каждый очередной год добавляет новую матрицу в набор ПМП как исходный пункт в оценке стохастической скорости роста и в задаче структурно-геометрического осреднения. В настоящей работе представлены прогнозы выживания ценопопуляции, полученные двумя вышеназванными методами. Обе оценки оказались заметно меньше 1, что указывает на убыль популяции в долговременной перспективе.
ОБЪЕКТЫ И МЕТОДЫ
Объект. Androsace albana Stev. в ботанической литературе часто рассматривается как травянистый двулетний розеточный стержнекорневой монокарпик (Шишкин, Бобров, 1952; Шхагапсоев, 1999). По нашим данным A. albana в условиях альпийских лишайниковых пустошей проявляет себя как травянистый хамефит, летнезеленый стержнекорневой многолетний монокарпик (Казанцева, 2016; Логофет и др., 2017б). Вид включен в “Красную книгу Краснодарского края” (2007) и “Красную книгу Республики Адыгея” (2012) как редкий категории 3. Биология, экология и онтогенез вида описаны ранее (Казанцева, 2016; Логофет и др., 2017б), и построен граф жизненного цикла (ГЖЦ, рис. 1).
Рис. 1.
Граф жизненного цикла проломника Androsace albana: pl – проростки, j – ювенильные растения, im – имматурные, v – взрослые вегетативные, g – генеративные; штриховые стрелки – пополнение популяции, обнаруженное в соответствующих стадиях (Логофет и др., 2017б).
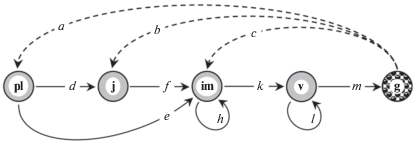
Наряду с последовательными переходами из стадии в стадию за 1 год, наблюдались также:
− задержки 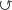 в стадиях im и v, объяснимые тем, что суровые условия высокогорий вынуждают растения прибегать к стратегии
“удержания места” (“space-holder strategy”, Körner, 2003), что означает оставаться
или расти на одном месте так долго, как это возможно. Бедность почвы приводит к тому,
что отдельные виргинильные растения накапливают ресурсы для плодоношения дольше одного
года (Работнов, 1950, 1978; Bender et al., 2000; Körner, 2003; Keller, Vittoz, 2014);
в стадиях im и v, объяснимые тем, что суровые условия высокогорий вынуждают растения прибегать к стратегии
“удержания места” (“space-holder strategy”, Körner, 2003), что означает оставаться
или расти на одном месте так долго, как это возможно. Бедность почвы приводит к тому,
что отдельные виргинильные растения накапливают ресурсы для плодоношения дольше одного
года (Работнов, 1950, 1978; Bender et al., 2000; Körner, 2003; Keller, Vittoz, 2014);
− ускоренные переходы pl 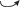 im как проявление поливариантности онтогенеза A. albana в условиях альпийского пояса С.-З. Кавказа.
im как проявление поливариантности онтогенеза A. albana в условиях альпийского пояса С.-З. Кавказа.
В жизненном цикле монокарпных растений только одно репродуктивное событие, но пополнение популяции может оказаться к моменту следующей переписи в каждой из трех стадий pl, j или im. Соответственно параметры a, b и c имеют смысл среднего (на одно генеративное растение) числа особей пополнения, найденных при очередной переписи в соответствующей стадии.
Изучаемая ценопопуляция A. albana нормальная полночленная, т.е. содержит особи всех стадий. В отдельные годы ее “возрастной спектр” по терминологии А.А. Уранова (1975) можно признать левосторонним, в иные – максимальные доли приходятся на стадии взрослых растений. В (арифметическом) среднем за 10 лет наблюдений: 48% популяции приходится на проростки и ювенильные особи, 50% – на имматурные и взрослые виргинильные и лишь 2% – на генеративные.
Методы исследования. Исследования проводили в Карачаево-Черкесской Республике, на территории Тебердинского государственного природного биосферного заповедника, на постоянных площадках, заложенных в 2009 г. на лишайниковой пустоши, на горе Малая Хатипара, 2800 м над ур. м. (Логофет и др., 2017б). Были заложены две трансекты размером 1.25 × 0.25 м, по 5 площадок размером 0.25 × 0.25 м в каждой. Все особи A. albana наносили на планы площадок со своими порядковыми номерами и метками их онтогенетических состояний (стадий). На следующий год особям, отмеченным в прошлом году, давали их прошлогодние номера, а новым особям присваивали новые; у всех особей определяли их онтогенетическое состояние на момент текущего наблюдения. Мониторинг проводили каждый год в конце августа в течение 10 лет с 2009 по 2018 год; опубликованный ранее ряд данных (ibid.) расширили еще 2 годами.
Собранные данные относятся к типу “идентифицированные особи” (‘identified individuals’, Caswell, 2001, p. 134), т.е. содержат сведения о стадии каждого растения A. albana с момента его появления на площадке и до момента цветения с шагом в 1 год. Поэтому, наряду со структурой ценопопуляции в каждый год наблюдения (табл. 1), известны и события переходов между стадиями (табл. 2). К настоящему моменту временнóй ряд данных расширен до 2018 г. включительно.
Таблица 1.
Структура ценопопуляции A. albana по годам согласно данным наблюдений (расширение табл. 1 из Логофет и др., 2017б)
| Стадия | Численность стадийных групп в год наблюдения | Средняя, % | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | ||
| pl | 37 | 30 | 19 | 49 | 19 | 16 | 4 | 10 | 3 | 12 | 12 |
| j | 110 | 48 | 45 | 86 | 137 | 98 | 19 | 29 | 8 | 23 | 36 |
| im | 99 | 55 | 43 | 87 | 95 | 34 | 10 | 13 | 12 | 13 | 27 |
| v | 35 | 26 | 57 | 58 | 73 | 50 | 20 | 22 | 28 | 23 | 23 |
| g | 13 | 1 | 1 | 4 | 6 | 3 | 4 | 2 | 1 | 2 | 2 |
Таблица 2.
Число особей пополнения и переходов по дугам ГЖЦ (рис. 1) согласно данным переписей (расширение табл. 2 из Логофет и др., 2017б)
| Переход t → t + 1 |
Год переписи (момент t + 1) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | |
a: pl g g |
30 | 19 | 49 | 19 | 16 | 4 | 10 | 3 | 12 |
b: j g g |
40 | 31 | 85 | 136 | 98 | 19 | 29 | 8 | 23 |
c: im  g g |
3 | 0 | 25 | 1 | 2 | 0 | 7 | 0 | 0 |
| d: pl → j | 8 | 14 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
e: pl 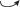 im im |
2 | 4 | 6 | 10 | 2 | 2 | 0 | 2 | 3 |
| f: j → im | 22 | 22 | 35 | 45 | 16 | 2 | 10 | 5 | 2 |
h: im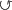 im im |
28 | 17 | 21 | 39 | 14 | 6 | 3 | 5 | 8 |
| k: im → v | 7 | 34 | 10 | 28 | 6 | 4 | 5 | 8 | 2 |
l: v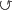 v v |
19 | 23 | 48 | 45 | 44 | 16 | 17 | 20 | 21 |
| m: v → g | 1 | 1 | 4 | 6 | 3 | 4 | 2 | 1 | 2 |
Матричная модель и калибровка матриц. В матричной модели структура популяции описывается вектором(-столбцом) x(t) = [pl(t), j(t), im(t), v(t), g(t)]T, компоненты которого суть числа особей, обнаруженных в соответствующих стадиях онтогенеза в год наблюдения t. Наблюдаемые изменения вектора x(t) по годам (табл. 1) описываются основным уравнением модели в векторно-матричной форме:
где L(t) – проекционная матрица популяции (ПМП, Caswell, 2001), ассоциированная с ГЖЦ (Логофет, Белова, 2007), который представлен на рис. 1. Все девять ПМП L(t) имеют размер 5 × 5 и общее строение:(2)
$L = \left[ {\begin{array}{*{20}{c}} 0&0&0&0&a \\ d&0&0&0&b \\ e&f&h&0&c \\ 0&0&k&l&0 \\ 0&0&0&m&0 \end{array}} \right];\,\,\,\,a,b, \ldots ,l,\,\,\,\,m \geqslant 0,$Прогноз дается величиной λ1(L) – доминантным собственным числом калиброванной ПМП L, которое показывает асимптотическую скорость роста популяции: если L(t) = L остается постоянной во времени, то при t → ∞ структура популяции x(t) сходится к равновесию – собственному вектору x*, отвечающему λ1(L), – а ее динамика x(t) ~ λ1(L)tx*, т.е. стремится к геометрическому росту (или убыли) с показателем λ1(L) > 0 (Logofet, 1993; Caswell, 2001; Логофет, Уланова, 2017). Поэтому прогноз выживания ценопопуляции положительный, если λ1(L) > 1, и отрицательный, если λ1(L) < 1. В неавтономной модели вместе с изменением матрицы L меняется и величина λ1(L), оставляя результирующий прогноз неопределенным.
Прогноз выживания через осреднение годичных ПМП. Чтобы зафиксировать онтогенетические переходы и пополнение популяции, необходимы данные двух последовательных переписей (в моменты t и t + 1), и потому число калиброванных ПМП всегда на единицу меньше числа лет наблюдений (10 лет наблюдений обеспечивают калибровку 9 матриц L(t)). Нет оснований полагать, что они окажутся одинаковыми, а практика калибровки показывает различия не только количественные, но и качественные: в отдельные годы прогноз выживания меняется на противоположный (Логофет и др., 2017а, б, 2018). Итог всего периода мониторинга способна отразить матрица G, найденная методом структурно-геометрического (pattern-geometric) осреднения неотрицательных матриц (Logofet, 2018).
Логика структурно-геометрического осреднения такова: согласно калиброванной модели (1) вектор x(0) структуры популяции в начальный момент наблюдений t = 0 преобразуется в x(9), вектор структуры в последний момент t = 9, путем последовательного умножения на 9 годичных ПМП L(t), т.е. (после переобозначения L(t) = Lt)
(3)
$x(9) = {{L}_{8}} \cdot {{L}_{7}} \cdot {{L}_{6}} \cdot {{L}_{5}} \cdot {{L}_{4}} \cdot {{L}_{3}} \cdot {{L}_{2}} \cdot {{L}_{1}} \cdot {{L}_{0}} \cdot x(0);$(4)
${{G}^{9}} = {{L}_{8}} \cdot {{L}_{7}} \cdot {{L}_{6}} \cdot {{L}_{5}} \cdot {{L}_{4}} \cdot {{L}_{3}} \cdot {{L}_{2}} \cdot {{L}_{1}} \cdot {{L}_{0}}.$Уравнение (4) заявляет геометрический характер осреднения, а общее для всех усредняемых матриц строение (2) требует того же и от средней матрицы G. Логично кроме того, что все элементы средней матрицы не выходят за границы соответствующих элементов усредняемых матриц.
Данная логика приводит к математической задаче минимизации ошибки приближения в решении матричного уравнения (4) (Приложение А). Положение доминантного собственного числа λ1(G) средней матрицы G относительно 1 позволяет сделать вывод о судьбе ценопопуляции в долговременной перспективе на основании десяти лет наблюдений: рост, если λ1(G) >1, убыль, если λ1(G) < 1, стабилизация, если λ1(G) = 1.
Интересно проследить, как меняется этот показатель с добавлением к усредняемым ПМП матрицы L(t), полученной в очередной год мониторинга, t + 1, когда число лет меняется от 2 до 9. Сам метод остается прежним, но изменяется только число сомножителей в произведении годичных ПМП в уравнении (4) и соответственно степень, в которую возводим матрицу G.
Прогноз выживания через стохастическую скорость роста. Стохастической скоростью роста популяции в случайно меняющейся среде называют величину λS, определенную пределом (Tuljapurkar, 1986, 1990; Caswell, 2001):
где Lτ –1 – годичная матрица, выбранная на шаге τ = 1, 2, … случайным образом из доступного набора годичных ПМП; N(τ) обозначает суммарный размер популяции, а ||…||1 – норму вектора как сумму его компонент по абсолютной величине. В простейшем случае случайный выбор имеет тип i.i.d. (independent, identically distributed; ibid.), т.е. выбор не зависит от результата на предыдущем шаге и распределение матриц неизменно. Значение λS относительно 1 указывает на экспоненциальный рост или убывание суммарного размера и дает таким образом прогноз выживания ценопопуляции в долгосрочной перспективе. Оценку λS мы получаем прямым методом, т.е. приближая значение предела (5) достаточно далеким (от начала), но конечным членом бесконечной последовательности; конечные реализации случайной последовательности (5) получаем методом Монте-Карло. Каждая из них дает в силу случайности свою отличную от иных оценку λS и потому результатом применения метода служит диапазон полученных оценок (от минимальной до максимальной) на конечном множестве реализаций.РЕЗУЛЬТАТЫ
Ретроспективная коррекция данных. Наряду с онтогенетическими переходами на шаге 2017 → 2018 и пополнением популяции, наблюдения последнего года зафиксировали выход из вторичного покоя в онтогенезе A. albana: особи, которых считали умершими из-за сильной засухи 2 года подряд (2016–2017), ожили и продолжили рост. Тем самым ранее зафиксированная структура ценопопуляции изменилась: по сравнению с прежними данными (Логофет и др., 2017б, табл. 1) новые значения получили компоненты v(2016), im(2017), v(2017) (табл. 1). Соответствующим образом изменилась и картина переходов (табл. 2) по сравнению с прежней (ibid., табл. 2), а вслед за нею – и соответствующие годичные матрицы L(t).
Калиброванные матрицы L(t). Вычисление элементов ПМП обеспечивается табл. 2, в которой подсчитаны все особи пополнения и все переходы между стадиями, зафиксированные в данных наблюдений. Элементы годичных матриц L(t) (табл. 3, 1- и 2-я колонки) получаем из соответствующих ячеек табл. 2 путем деления на численность нужной группы.
Таблица 3.
Результаты калибровки ПМП для A. albana по данным 2009–2018 гг. и структурно-геометрическое среднее Gm возрастающего числа m = t + 1 матриц L(0), L(1), …, L(t), t = 1, …, 8
| Год переписи | Матрица L(t) | λ1 (L(t)) | Вектор x*, % | $\Delta \left( {\frac{{100x(t + 1)}}{{{{{\left\| {x(t + 1)} \right\|}}_{1}}}} - x{\text{*}}} \right)$ | Gm | Погрешность осреднения† | λ1(Gm) | Вектор y*††, % | $\Delta \left( {\frac{{100x(t + 1)}}{{{{{\left\| {x(t + 1)} \right\|}}_{1}}}} - y{\text{*}}} \right)$ |
|---|---|---|---|---|---|---|---|---|---|
| 2009 t = 0 | $\left[ {\begin{array}{*{20}{c}} 0&0&0&0&{{\raise0.7ex\hbox{${30}$} \!\mathord{\left/ {\vphantom {{30} {13}}}\right.\kern-0em}\!\lower0.7ex\hbox{${13}$}}} \\ {{\raise0.7ex\hbox{$8$} \!\mathord{\left/ {\vphantom {8 {37}}}\right.\kern-0em}\!\lower0.7ex\hbox{${37}$}}}&0&0&0&{{\raise0.7ex\hbox{${40}$} \!\mathord{\left/ {\vphantom {{40} {13}}}\right.\kern-0em}\!\lower0.7ex\hbox{${13}$}}} \\ {{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 {37}}}\right.\kern-0em}\!\lower0.7ex\hbox{${37}$}}}&{{\raise0.7ex\hbox{${22}$} \!\mathord{\left/ {\vphantom {{22} {110}}}\right.\kern-0em}\!\lower0.7ex\hbox{${110}$}}}&{{\raise0.7ex\hbox{${28}$} \!\mathord{\left/ {\vphantom {{28} {99}}}\right.\kern-0em}\!\lower0.7ex\hbox{${99}$}}}&0&{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 {13}}}\right.\kern-0em}\!\lower0.7ex\hbox{${13}$}}} \\ 0&0&{{\raise0.7ex\hbox{$7$} \!\mathord{\left/ {\vphantom {7 {99}}}\right.\kern-0em}\!\lower0.7ex\hbox{${99}$}}}&{{\raise0.7ex\hbox{${19}$} \!\mathord{\left/ {\vphantom {{19} {35}}}\right.\kern-0em}\!\lower0.7ex\hbox{${35}$}}}&0 \\ 0&0&0&{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {35}}}\right.\kern-0em}\!\lower0.7ex\hbox{${35}$}}}&0 \end{array}} \right]$ | 0.5661 | $\left[ {\begin{array}{*{20}{c}} {10.61} \\ {18.20} \\ {16.99} \\ {51.59} \\ {2.60} \end{array}} \right]$ | 37.32 | G1 = L(0) | 0 | См. 3-ю колонку | См. 4-ю колонку | См. 5-ю колонку |
| 2010 t = 1 | $\left[ {\begin{array}{*{20}{c}} 0&0&0&0&{{\raise0.7ex\hbox{${19}$} \!\mathord{\left/ {\vphantom {{19} 1}}\right.\kern-0em}\!\lower0.7ex\hbox{$1$}}} \\ {{\raise0.7ex\hbox{${14}$} \!\mathord{\left/ {\vphantom {{14} {30}}}\right.\kern-0em}\!\lower0.7ex\hbox{${30}$}}}&0&0&0&{{\raise0.7ex\hbox{${31}$} \!\mathord{\left/ {\vphantom {{31} 1}}\right.\kern-0em}\!\lower0.7ex\hbox{$1$}}} \\ {{\raise0.7ex\hbox{$4$} \!\mathord{\left/ {\vphantom {4 {30}}}\right.\kern-0em}\!\lower0.7ex\hbox{${30}$}}}&{{\raise0.7ex\hbox{${22}$} \!\mathord{\left/ {\vphantom {{22} {48}}}\right.\kern-0em}\!\lower0.7ex\hbox{${48}$}}}&{{\raise0.7ex\hbox{${17}$} \!\mathord{\left/ {\vphantom {{17} {55}}}\right.\kern-0em}\!\lower0.7ex\hbox{${55}$}}}&0&{{\raise0.7ex\hbox{$0$} \!\mathord{\left/ {\vphantom {0 1}}\right.\kern-0em}\!\lower0.7ex\hbox{$1$}}} \\ 0&0&{{\raise0.7ex\hbox{${34}$} \!\mathord{\left/ {\vphantom {{34} {55}}}\right.\kern-0em}\!\lower0.7ex\hbox{${55}$}}}&{{\raise0.7ex\hbox{${23}$} \!\mathord{\left/ {\vphantom {{23} {26}}}\right.\kern-0em}\!\lower0.7ex\hbox{${26}$}}}&0 \\ 0&0&0&{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {26}}}\right.\kern-0em}\!\lower0.7ex\hbox{${26}$}}}&0 \end{array}} \right]$ | 1.2283 | $\left[ {\begin{array}{*{20}{c}} {15.90} \\ {31.99} \\ {18.25} \\ {32.83} \\ {1.03} \end{array}} \right]$ | 9.52 | $\left[ {\begin{array}{*{20}{c}} 0&0&0&0&{4.9964} \\ {0.2162}&0&0&0&{10.4811} \\ {0.0541}&{0.2000}&{0.2931}&0&0 \\ 0&0&{0.2383}&{0.6847}&0 \\ 0&0&0&{0.0385}&0 \end{array}} \right]$ | 5.96695 × 10–1 | 0.77037 | $\left[ {\begin{array}{*{20}{c}} {12.94} \\ {30.76} \\ {14.36} \\ {39.85} \\ {1.99} \end{array}} \right]$ | 11.70 |
| 2011 t = 2 | $\left[ {\begin{array}{*{20}{c}} 0&0&0&0&{{\raise0.7ex\hbox{${49}$} \!\mathord{\left/ {\vphantom {{49} 1}}\right.\kern-0em}\!\lower0.7ex\hbox{$1$}}} \\ {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {19}}}\right.\kern-0em}\!\lower0.7ex\hbox{${19}$}}}&0&0&0&{{\raise0.7ex\hbox{${85}$} \!\mathord{\left/ {\vphantom {{85} 1}}\right.\kern-0em}\!\lower0.7ex\hbox{$1$}}} \\ {{\raise0.7ex\hbox{$6$} \!\mathord{\left/ {\vphantom {6 {19}}}\right.\kern-0em}\!\lower0.7ex\hbox{${19}$}}}&{{\raise0.7ex\hbox{${35}$} \!\mathord{\left/ {\vphantom {{35} {45}}}\right.\kern-0em}\!\lower0.7ex\hbox{${45}$}}}&{{\raise0.7ex\hbox{${21}$} \!\mathord{\left/ {\vphantom {{21} {43}}}\right.\kern-0em}\!\lower0.7ex\hbox{${43}$}}}&0&{{\raise0.7ex\hbox{${25}$} \!\mathord{\left/ {\vphantom {{25} 1}}\right.\kern-0em}\!\lower0.7ex\hbox{$1$}}} \\ 0&0&{{\raise0.7ex\hbox{${10}$} \!\mathord{\left/ {\vphantom {{10} {43}}}\right.\kern-0em}\!\lower0.7ex\hbox{${43}$}}}&{{\raise0.7ex\hbox{${48}$} \!\mathord{\left/ {\vphantom {{48} {57}}}\right.\kern-0em}\!\lower0.7ex\hbox{${57}$}}}&0 \\ 0&0&0&{{\raise0.7ex\hbox{$4$} \!\mathord{\left/ {\vphantom {4 {57}}}\right.\kern-0em}\!\lower0.7ex\hbox{${57}$}}}&0 \end{array}} \right]$ | 1.5779 | $\left[ {\begin{array}{*{20}{c}} {17.20} \\ {30.40} \\ {39.39} \\ {12.45} \\ {0.55} \end{array}} \right]$ | 8.88 | $\left[ {\begin{array}{*{20}{c}} 0&0&0&0&{13.2202} \\ {0.0526}&0&0&0&{21.0070} \\ {0.0541}&{0.2000}&{0.2828}&0&{8.1642} \\ 0&0&{0.0707}&{0.8846}&0 \\ 0&0&0&{0.0702}&0 \end{array}} \right]$ | 7.13887 × 10–1 | 0.98109 | $\left[ {\begin{array}{*{20}{c}} {19.34} \\ {31.77} \\ {27.38} \\ {20.07} \\ {1.44} \end{array}} \right]$ | 3.61 |
| 2012 t = 3 | $\left[ {\begin{array}{*{20}{c}} 0&0&0&0&{{\raise0.7ex\hbox{${19}$} \!\mathord{\left/ {\vphantom {{19} 4}}\right.\kern-0em}\!\lower0.7ex\hbox{$4$}}} \\ {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {49}}}\right.\kern-0em}\!\lower0.7ex\hbox{${49}$}}}&0&0&0&{{\raise0.7ex\hbox{${136}$} \!\mathord{\left/ {\vphantom {{136} 4}}\right.\kern-0em}\!\lower0.7ex\hbox{$4$}}} \\ {{\raise0.7ex\hbox{${10}$} \!\mathord{\left/ {\vphantom {{10} {49}}}\right.\kern-0em}\!\lower0.7ex\hbox{${49}$}}}&{{\raise0.7ex\hbox{${45}$} \!\mathord{\left/ {\vphantom {{45} {86}}}\right.\kern-0em}\!\lower0.7ex\hbox{${86}$}}}&{{\raise0.7ex\hbox{${39}$} \!\mathord{\left/ {\vphantom {{39} {87}}}\right.\kern-0em}\!\lower0.7ex\hbox{${87}$}}}&0&{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 4}}\right.\kern-0em}\!\lower0.7ex\hbox{$4$}}} \\ 0&0&{{\raise0.7ex\hbox{${28}$} \!\mathord{\left/ {\vphantom {{28} {87}}}\right.\kern-0em}\!\lower0.7ex\hbox{${87}$}}}&{{\raise0.7ex\hbox{${45}$} \!\mathord{\left/ {\vphantom {{45} {58}}}\right.\kern-0em}\!\lower0.7ex\hbox{${58}$}}}&0 \\ 0&0&0&{{\raise0.7ex\hbox{$6$} \!\mathord{\left/ {\vphantom {6 {58}}}\right.\kern-0em}\!\lower0.7ex\hbox{${58}$}}}&0 \end{array}} \right]$ | 1.2641 | $\left[ {\begin{array}{*{20}{c}} {6.01} \\ {43.15} \\ {29.67} \\ {19.56} \\ {1.60} \end{array}} \right]$ | 2.78 | $\left[ {\begin{array}{*{20}{c}} 0&0&0&0&{2.3077} \\ {0.0204}&0&0&0&{15.1859} \\ {0.3158}&{0.6001}&{0.2828}&0&{1.5922} \\ 0&0&{0.1003}&{0.8846}&0 \\ 0&0&0&{0.1034}&0 \end{array}} \right]$ | 4.57088 × 10–1 | 1.03362 | $\left[ {\begin{array}{*{20}{c}} {5.22} \\ {34.43} \\ {34.67} \\ {23.34} \\ {2.34} \end{array}} \right]$ | 7.62 |
| 2013 t = 4 | $\left[ {\begin{array}{*{20}{c}} 0&0&0&0&{{\raise0.7ex\hbox{${16}$} \!\mathord{\left/ {\vphantom {{16} 6}}\right.\kern-0em}\!\lower0.7ex\hbox{$6$}}} \\ 0&0&0&0&{{\raise0.7ex\hbox{${98}$} \!\mathord{\left/ {\vphantom {{98} 6}}\right.\kern-0em}\!\lower0.7ex\hbox{$6$}}} \\ {{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 {19}}}\right.\kern-0em}\!\lower0.7ex\hbox{${19}$}}}&{{\raise0.7ex\hbox{${16}$} \!\mathord{\left/ {\vphantom {{16} {137}}}\right.\kern-0em}\!\lower0.7ex\hbox{${137}$}}}&{{\raise0.7ex\hbox{${14}$} \!\mathord{\left/ {\vphantom {{14} {95}}}\right.\kern-0em}\!\lower0.7ex\hbox{${95}$}}}&0&{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 6}}\right.\kern-0em}\!\lower0.7ex\hbox{$6$}}} \\ 0&0&{{\raise0.7ex\hbox{$6$} \!\mathord{\left/ {\vphantom {6 {95}}}\right.\kern-0em}\!\lower0.7ex\hbox{${95}$}}}&{{\raise0.7ex\hbox{${44}$} \!\mathord{\left/ {\vphantom {{44} {73}}}\right.\kern-0em}\!\lower0.7ex\hbox{${73}$}}}&0 \\ 0&0&0&{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 {73}}}\right.\kern-0em}\!\lower0.7ex\hbox{${73}$}}}&0 \end{array}} \right]$ | 0.6345 | $\left[ {\begin{array}{*{20}{c}} {7.76} \\ {47.54} \\ {14.34} \\ {28.51} \\ {1.85} \end{array}} \right]$ | 3.99 | $\left[ {\begin{array}{*{20}{c}} 0&0&0&0&{2.3077} \\ {0.00 \ldots }&0&0&0&{12.6185} \\ {0.1905}&{0.1966}&{0.3345}&0&{0.00 \ldots } \\ 0&0&{0.2405}&{0.8141}&0 \\ 0&0&0&{0.1034}&0 \end{array}} \right]$ | 1.42499 × 10–1 | 0.94661 | $\left[ {\begin{array}{*{20}{c}} {7.87} \\ {43.06} \\ {16.28} \\ {29.56} \\ {3.23} \end{array}} \right]$ | 6.42 |
| 2014 t = 5 | $\left[ {\begin{array}{*{20}{c}} 0&0&0&0&{{\raise0.7ex\hbox{$4$} \!\mathord{\left/ {\vphantom {4 3}}\right.\kern-0em}\!\lower0.7ex\hbox{$3$}}} \\ 0&0&0&0&{{\raise0.7ex\hbox{${19}$} \!\mathord{\left/ {\vphantom {{19} 3}}\right.\kern-0em}\!\lower0.7ex\hbox{$3$}}} \\ {{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 {16}}}\right.\kern-0em}\!\lower0.7ex\hbox{${16}$}}}&{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 {98}}}\right.\kern-0em}\!\lower0.7ex\hbox{${98}$}}}&{{\raise0.7ex\hbox{$6$} \!\mathord{\left/ {\vphantom {6 {34}}}\right.\kern-0em}\!\lower0.7ex\hbox{${34}$}}}&0&{{\raise0.7ex\hbox{$0$} \!\mathord{\left/ {\vphantom {0 3}}\right.\kern-0em}\!\lower0.7ex\hbox{$3$}}} \\ 0&0&{{\raise0.7ex\hbox{$4$} \!\mathord{\left/ {\vphantom {4 {34}}}\right.\kern-0em}\!\lower0.7ex\hbox{${34}$}}}&{{\raise0.7ex\hbox{${16}$} \!\mathord{\left/ {\vphantom {{16} {50}}}\right.\kern-0em}\!\lower0.7ex\hbox{${50}$}}}&0 \\ 0&0&0&{{\raise0.7ex\hbox{$4$} \!\mathord{\left/ {\vphantom {4 {50}}}\right.\kern-0em}\!\lower0.7ex\hbox{${50}$}}}&0 \end{array}} \right]$ | 0.3988 | $\left[ {\begin{array}{*{20}{c}} {11.71} \\ {56.64} \\ {11.69} \\ {17.46} \\ {3.50} \end{array}} \right]$ | 12.64 | $\left[ {\begin{array}{*{20}{c}} 0&0&0&0&{1.3333} \\ {0.2231}&0&0&0&{5.3702} \\ {0.0541}&{0.3196}&{0.1474}&0&{0.00 \ldots } \\ 0&0&{0.2249}&{0.7267}&0 \\ 0&0&0&{0.1034}&0 \end{array}} \right]$ | 2.66369 × 10–2 | 0.82772 | $\left[ {\begin{array}{*{20}{c}} {7.46} \\ {34.18} \\ {16.65} \\ {37.08} \\ {4.63} \end{array}} \right]$ | 3.28 |
| 2015 t = 6 | $\left[ {\begin{array}{*{20}{c}} 0&0&0&0&{{\raise0.7ex\hbox{${10}$} \!\mathord{\left/ {\vphantom {{10} 4}}\right.\kern-0em}\!\lower0.7ex\hbox{$4$}}} \\ 0&0&0&0&{{\raise0.7ex\hbox{${29}$} \!\mathord{\left/ {\vphantom {{29} 4}}\right.\kern-0em}\!\lower0.7ex\hbox{$4$}}} \\ 0&{{\raise0.7ex\hbox{${10}$} \!\mathord{\left/ {\vphantom {{10} {19}}}\right.\kern-0em}\!\lower0.7ex\hbox{${19}$}}}&{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 {10}}}\right.\kern-0em}\!\lower0.7ex\hbox{${10}$}}}&0&{{\raise0.7ex\hbox{$0$} \!\mathord{\left/ {\vphantom {0 4}}\right.\kern-0em}\!\lower0.7ex\hbox{$4$}}} \\ 0&0&{{\raise0.7ex\hbox{$5$} \!\mathord{\left/ {\vphantom {5 {10}}}\right.\kern-0em}\!\lower0.7ex\hbox{${10}$}}}&{{\raise0.7ex\hbox{${17}$} \!\mathord{\left/ {\vphantom {{17} {20}}}\right.\kern-0em}\!\lower0.7ex\hbox{${20}$}}}&0 \\ 0&0&0&{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {10}}}\right.\kern-0em}\!\lower0.7ex\hbox{${10}$}}}&0 \end{array}} \right]$ | 1.0679 | $\left[ {\begin{array}{*{20}{c}} {9.19} \\ {26.66} \\ {18.28} \\ {41.94} \\ {3.93} \end{array}} \right]$ | 15.46 | $\left[ {\begin{array}{*{20}{c}} 0&0&0&0&{3.3058} \\ {0.4667}&0&0&0&{7.7164} \\ {0.0178}&{0.2958}&{0.1787}&0&{0.00 \ldots } \\ 0&0&{0.1676}&{0.7608}&0 \\ 0&0&0&{0.1034}&0 \end{array}} \right]$ | 1.43747 × 10–2 | 0.85973 | $\left[ {\begin{array}{*{20}{c}} {13.20} \\ {37.98} \\ {16.85} \\ {28.54} \\ {3.43} \end{array}} \right]$ | 0.85 |
| 2016 t = 7 | $\left[ {\begin{array}{*{20}{c}} 0&0&0&0&{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 2}}\right.\kern-0em}\!\lower0.7ex\hbox{$2$}}} \\ 0&0&0&0&{{\raise0.7ex\hbox{$8$} \!\mathord{\left/ {\vphantom {8 2}}\right.\kern-0em}\!\lower0.7ex\hbox{$2$}}} \\ {{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 3}}\right.\kern-0em}\!\lower0.7ex\hbox{$3$}}}&{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 8}}\right.\kern-0em}\!\lower0.7ex\hbox{$8$}}}&{{\raise0.7ex\hbox{$8$} \!\mathord{\left/ {\vphantom {8 {12}}}\right.\kern-0em}\!\lower0.7ex\hbox{${12}$}}}&0&0 \\ 0&0&{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 {12}}}\right.\kern-0em}\!\lower0.7ex\hbox{${12}$}}}&{{\raise0.7ex\hbox{${21}$} \!\mathord{\left/ {\vphantom {{21} {28}}}\right.\kern-0em}\!\lower0.7ex\hbox{${28}$}}}&0 \\ 0&0&0&{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {22}}}\right.\kern-0em}\!\lower0.7ex\hbox{${22}$}}}&0 \end{array}} \right]$ | 0.9611 | $\left[ {\begin{array}{*{20}{c}} {5.26} \\ {14.04} \\ {6.02} \\ {71.30} \\ {3.37} \end{array}} \right]$ | 18.91 | $\left[ {\begin{array}{*{20}{c}} 0&0&0&0&{1.7620} \\ {0.00 \ldots }&0&0&0&{4.9696} \\ {0.2172}&{0.3872}&{0.4884}&0&{0.9473} \\ 0&0&{0.0945}&{0.8406}&0 \\ 0&0&0&{0.0443}&0 \end{array}} \right]$ | 1.16582 × 10–2 | 0.88336 | $\left[ {\begin{array}{*{20}{c}} {5.39} \\ {14.95} \\ {24.00} \\ {53.00} \\ {2.66} \end{array}} \right]$ | 1.66 |
| 2017 t = 8 | $\left[ {\begin{array}{*{20}{c}} 0&0&0&0&{{\raise0.7ex\hbox{${12}$} \!\mathord{\left/ {\vphantom {{12} 1}}\right.\kern-0em}\!\lower0.7ex\hbox{$1$}}} \\ 0&0&0&0&{{\raise0.7ex\hbox{${23}$} \!\mathord{\left/ {\vphantom {{23} 1}}\right.\kern-0em}\!\lower0.7ex\hbox{$1$}}} \\ {{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 3}}\right.\kern-0em}\!\lower0.7ex\hbox{$3$}}}&{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 8}}\right.\kern-0em}\!\lower0.7ex\hbox{$8$}}}&{{\raise0.7ex\hbox{$8$} \!\mathord{\left/ {\vphantom {8 {12}}}\right.\kern-0em}\!\lower0.7ex\hbox{${12}$}}}&0&0 \\ 0&0&{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 {12}}}\right.\kern-0em}\!\lower0.7ex\hbox{${12}$}}}&{{\raise0.7ex\hbox{${21}$} \!\mathord{\left/ {\vphantom {{21} {28}}}\right.\kern-0em}\!\lower0.7ex\hbox{${28}$}}}&0 \\ 0&0&0&{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 {28}}}\right.\kern-0em}\!\lower0.7ex\hbox{${28}$}}}&0 \end{array}} \right]$ | 1.1206 | $\left[ {\begin{array}{*{20}{c}} {12.93} \\ {24.78} \\ {42.13} \\ {18.95} \\ {1.21} \end{array}} \right]$ | 24.32 | $\left[ {\begin{array}{*{20}{c}} 0&0&0&0&{3.9690} \\ {0.3427}&0&0&0&{6.0519} \\ {0.0472}&{0.3728}&{0.2053}&0&{0.00 \ldots } \\ 0&0&{0.1708}&{0.7955}&0 \\ 0&0&0&{0.1034}&0 \end{array}} \right]$ | 1.11024 × 10–2 | 0.89262 | $\left[ {\begin{array}{*{20}{c}} {16.19} \\ {30.89} \\ {17.87} \\ {31.41} \\ {3.64} \end{array}} \right]$ | 0.96 |
Годичные ПМП L(t) (табл. 3), калиброванные по данным наблюдений, дают, хотя и опосредованную, но объективную картину вариаций условий среды, к которым чувствительна ценопопуляция, и эта картина убеждает, что условия были весьма критичны: мера приспособленности λ1(L(t)) падала в отдельные годы до крайне низких значений, например, ниже 0.4 в интервале между переписями 2014–2015 гг., а численность пополнения в 2015, 2017 гг. во всех трех стадиях была наименьшей за весь период наблюдений (табл. 2). По-видимому, в том интервале условия приживаемости молодых растений A. albana (проростков, ювенильных, имматурных), перезимовки и роста взрослых особей (вегетативных и генеративных) были наиболее суровыми за весь период наблюдений. Если бы они повторились хотя бы 2 года подряд, то ценопопуляция сократилась бы более чем до 0.42 × 100% = 16% численности, если 3 года подряд, то – до 0.43 × 100% ≈ 6%.
Однако на следующий год, т.е. в интервале 2015–2016, условия улучшились, и в результате ретроспективной коррекции данных 2016 г. прежний прогноз на убыль, т.е. λ1(2015) = 0.8382 (Логофет и др., 2017б, табл. 3), сменился на более благоприятный λ1(2015) = 1.0679.
Наряду с мерой приспособленности λ1 годичные ПМП предлагают и соответствующий собственный вектор x* (4-я колонка табл. 3) – равновесную структуру, которую имела бы ценопопуляция, если бы данные условия оставались неизменными достаточно долго. Среди равновесных структур разных лет нет отчетливой тенденции к левостороннему “возрастному спектру” – даже у растущих популяций он скорее двугорбый, причем “горбы” сливаются иногда в “плато” над ювенильной и имматурной стадиями.
Далека ли наблюдаемая (относительная) структура x(t + 1) от равновесия, показывает мера разности этих векторов по Кейфицу (Keyfitz, 1968), значения которой представлены в соседней колонке. В основном они не превышают 10–20% (при максимальном теоретическом расстоянии в 100% между двумя структурами).
В целом различия среди годичных ПМП весьма существенны, причем 4 из 9 матриц дают меру адаптации λ1(L), заметно меньшую 1, остальные 5 – заметно бóльшую 1. Позволяет ли такое преобладание дать благоприятный прогноз выживания ценопопуляции в итоге 10-летнего мониторинга? Простые “арифметические” рассуждения оставляют этот вопрос открытым.
Структурно-геометрическое среднее годичных ПМП. Приближенное решение для 9 матриц из табл. 3 с приемлемой точностью приближения дает матрица, представленная в последней строке табл. 3. Ее строение, очевидно, соответствует ГЖЦ (рис. 1), а значения коэффициентов переходов и репродукции не выходят из границ, заданных соответствующими элементами усредняемых матриц (табл. 3). В переходной части T матрицы G отчетливо проявилась тенденция, имевшая место лишь у некоторых годичных матриц T(t): в каждом столбце положительные элементы убывают с ростом номера строки. В однонаправленном (т.е. без возвратов) процессе (рис. 1) это значит, что растения чаще задерживаются в развитии, нежели переходят в следующую стадию, а ускоренные переходы (через стадию) менее вероятны, чем последовательные.
Несмотря на значения λ1(t) > 1 для 2010–2012, 2015, 2017 гг., тенденция к убыли ценопопуляции преобладает на 10-летнем отрезке наблюдений, что выражено значением λ1(G(8)) < 1. Характер равновесной структуры популяции (нормированного доминантного собственного вектора y*) скорее двугорбый, нежели левосторонний, с максимумами в ювенильной и взрослой вегетативной стадиях. Таким образом, он принципиально отличается от структуры, полученной арифметическим осреднением (табл. 1), добавляя еще один аргумент против арифметического среднего в матричных моделях.
Когда число m усредняемых ПМП (равное t + 1) последовательно возрастает от 2 до 9, в результатах осреднения наблюдаются определенные закономерности. Так, с ростом m уменьшается погрешность осреднения; если у очередной L(t) величина λ1(L(t)) меньше 1, то происходит снижение λ1 и у средней матрицы Gm, а если у очередной L(t), добавленной к набору усредняемых ПМП, величина λ1(L(t)) больше, чем у предыдущей, то и у средней Gm значение λ1(Gm) возрастает. Тем самым выявляется логически верная чувствительность структурно-геометрического среднего к изменениям в наборе усредняемых матриц, т.е. состоятельность данного метода прогноза выживания. Характер равновесных структур, отвечающих средним матрицам, двугорбый (как и после осреднения 9 матриц) с максимумами в ювенильной и взрослой вегетативной стадиях. Их отличие от структуры ценопопуляции, наблюдаемой в текущий момент t + 1, менее 8%, а для 7 и 9 годичных матриц разница крайне мала, менее 1% (табл. 3, крайняя правая колонка).
Оценка стохастической скорости роста. Результаты вычисления λS представлены в табл. 4 для четырех значений длины конечной последовательности случайных ПМП и трех вариантов по числу случайных реализаций этой последовательности. Чем больше это число, тем логично шире диапазон оценок λS, а с ростом “длины произведения” матриц диапазон закономерно сужается, иллюстрируя фундаментальное свойство сходящихся последовательностей; ширина диапазона меняется от 20 до 96 тысячных долей, оставляя сотые доли надежной значащей цифрой. Наиболее надежным следует признать диапазон [0.956316, 0.958686], полученный при наибольшем числе реализаций наиболее длинной последовательности.
Таблица 4.
Оценки стохастической скорости роста λS ценопопуляции A. albana прямым методом Монте-Карло с равновероятным выбором из 9 годичных ПМП (табл. 3)
| “Длина” произведения1 | Число случайных реализаций | Диапазон вариаций в оценке λS; размах вариаций2 |
|---|---|---|
| 1 × 105 | 13 | [0.954950, 0.960372]; 0.005422 |
| 33 | [0.954403, 0.963571]; 0.009168 | |
| 100 | [0.953962, 0.963571]; 0.009609 | |
| 2 × 105 | 13 | [0. 955718, 0.959426]; 0.003708 |
| 33 | [0. 955718, 0.960943]; 0.005225 | |
| 100 | [0.955435, 0.960943]; 0.005508 | |
| 3 × 105 | 13 | [0.956263, 0.958967]; 0.002704 |
| 33 | [0.956263, 0.959267]; 0.003004 | |
| 100 | [0.955935, 0.959531]; 0.003596 | |
| 5 × 105 | 13 | [0.956607, 0.958686]; 0.002079 |
| 33 | [0.956533, 0.958686]; 0.002153 | |
| 100 | [0.956316, 0.958686]; 0.002370 |
Примечание. 1 Конечный номер члена последовательности (5), которым аппроксимируется ее предел при τ → ∞ совпадает с числом сомножителей в произведении случайно выбранных матриц Lτ– 1Lτ– 2 … L1 ⋅ L0, которое не превращает вектор x(τ) в машинный нуль благодаря нормированию на каждом шаге числом coef = 0.957542… – специально подобранным “масштабирующим коэффициентом”. 2 Жирным шрифтом набраны значащие цифры, по которым следующее табличное значение отличается от предыдущего.
Все диапазоны оценок λS располагаются слева от 1, давая, как и метод структурно-геометрического осреднения (табл. 3), отрицательный прогноз выживания ценопопуляции. Но количественное различие в результатах обоих методов наблюдается уже во втором десятичном знаке, что заставляет искать причины такого расхождения.
ОБСУЖДЕНИЕ
Одну из возможных причин столь заметного количественного различия между λS и λ1(G9) = 0.89264 можно было бы усмотреть в ошибке осреднения, которая возникает объективно в результате отсутствия точного решения уравнения (4). Известны, правда, редкие случаи, где точное решение уравнения осреднения существует благодаря полноте орграфа переходов между возможными состояниями сообщества из двух видов в марковской модели (Логофет, Маслов, 2018), т.е. когда в графе есть переходы из каждой вершины в любую другую и в себя. Но такая полнота в принципе невозможна в графе жизненного цикла, отражающем ход онтогенеза, так что ненулевая ошибка осреднения объективно неизбежна. Но она составила величину порядка всего лишь 0.01 (табл. 3) при минимальной разнице в оценках λS и λ1(G9) около 0.06 (табл. 4). Причины такого расхождения, по-видимому, более глубокие, и концепция структурно-геометрического среднего неотрицательных матриц нуждается в математическом исследовании (Logofet, 2018).
Явление перехода во вторичный покой в жизненном цикле альпийских растений в принципе известно (Shefferson, 2009), однако в изучаемой ценопопуляции A. albana обнаружено впервые за 10 лет мониторинга. Соответствующая коррекция данных 2016–2017 гг. вызвала изменения и в годичных ПМП, причем у матрицы L(2015) – даже качественную смену прогноза: от значения λ1(L(2015) < 1 (Логофет и др., 2017б, табл. 3) к λ1(L(2015) > 1 после коррекции данных. Однако, несмотря на это обстоятельство и некоторый оптимизм, вызванный благоприятным состоянием ценопопуляции A. albana в 2018 г., результаты, обобщающие 10-летний период мониторинга, предсказывают убыль популяции по каждому из рассмотренных методов. При этом каждый метод открыт для критики – если не в идейном, то в методическом плане.
Структурно-геометрическое осреднение замотивировано логикой мониторинга, но соответствующая математическая задача поиска приближенного решения уравнения осреднения трудна в вычислительном плане, а погрешность приближения пока не поддается теоретическим оценкам. При осреднении от 2 до 9 ПМП для A. albana эта погрешность варьирует в пределах от примерно 0.7 до 0.01, уменьшаясь с ростом числа усредняемых матриц (табл. 3), что, по-видимому, приемлемо для качественного прогноза выживания.
Несмотря на существующее разнообразие теоретических приближений и оценок λS – стохастической скорости роста (Caswell, 2001; Sanz, 2019), – прямой метод оценки следовало бы признать самым надежным из всех существующих (ибо он обоснован фундаментальной леммой математического анализа о последовательностях, имеющих предел), если бы не одно слабое место: в отсутствие надежных сведений о законе чередования годичных матриц в последовательности (5), их случайный выбор принимали равновероятным на каждом шаге и не зависящим от выбора на шаге предыдущем (i.i.d.).
Разумеется, i.i.d. – это карикатура реальности, поскольку в смене условий местообитания, критических для роста и развития растений, действуют свои закономерности. Их действие в течение года с момента предыдущего учета отражено опосредованно набором демографических параметров, откалиброванных по данными учета в настоящий момент, т.е. соответствующей годичной ПМП. Поэтому первый шаг на пути к реальности был сделан в теоретических трудах (Cohen, 1976, 1977a, b) теоремами об эргодичности (иными словами, пригодности для моделирования динамики) возрастной структуры популяции, если случайная последовательность операторов Лесли управляется эргодической цепью Маркова. Позднее класс операторов был расширен до ПМП с обобщенной стадийной структурой (Tuljapurkar, 1986, 1990; Caswell, 2001), но марковская цепь оставалась по-прежнему однородной (во времени). Практические иллюстрации “управляющей” марковской цепи до сих пор не выходят за рамки искусственных конструкций – от переключения между “хорошей” и “плохой” ПМП в самом простом случае (Sanz, 2019) до весьма изобретательных (но по-прежнему искусственных, навязанных волей автора) схем, претендующих на моделирование эффектов глобальных изменений климата на случайный выбор годичной матрицы для локальной популяции (Rees, Ellner, 2009; Ozgul et al., 2010; Williams et al., 2015). Попытки связать управляющую цепь с изменениями реальных факторов среды, определяющих прорастание семян и рост/развитие растений, нам не известны.
Между тем сами факторы заведомо существуют и отмечались исследователями биологии A. albana и иных альпийских видов (Работнов, 1950, 1978; Grime, 1979, 2001; Динамика ценопопуляций…, 1985; Жукова, 1986, 1995; Chambers, 1993; Bowers et al., 1995; Bender et al., 2000; Körner, 2003; Onipchenko, 2004; Аджиев, Онипченко, 2011; Онипченко, 2013; Keller, Vittoz, 2014). Представить ход изменений этих факторов по годам в виде марковской цепи, управляющей сменой ПМП в случайной последовательности (5), – вот задача, решение которой сделает прямой метод оценки λS по-настоящему самым надежным.
ЗАКЛЮЧЕНИЕ
Итоги продолжительного мониторинга стадийной структуры популяции малолетнего вида на постоянных площадях отражены в прогнозе выживания ценопопуляции, который следует из соответствующей неавтономной матричной модели. Данные 10 лет наблюдений позволяют однозначно калибровать 9 годичных ПМП, а оригинальная концепция структурно-геометрического среднего (G9) приводит к прогнозу выживания ценопопуляции в виде доминантного собственного числа λ1(G9) средней матрицы. Полученное значение λ1(G9) = 0.89264 заметно меньше 1 и означает убыль популяции в долговременной перспективе.
Менее пессимистичным, но тоже на убыль оказался прогноз выживания по диапазону [0.956316, 0.958686] оценок λS – стохастической скорости роста популяции в случайной среде (сформированной случайным выбором из тех же 9 матриц). Однако весьма искусственное допущение равной вероятности выбора каждой из 9 матриц при формировании случайной среды подрывает веру в количественное значение этого прогноза. Поэтому на повестку дня выходит задача построения модели случайного выбора, адекватной динамике смен условий местообитания, влияющих на рост и развитие ценопопуляции данного вида.
Сбор и обработка полевого материала осуществлены при финансовой поддержке РФФИ (грант 14-04-00214). Модельная часть исследований поддержана РФФИ, гранты № 16-04-00832 и № 19-04-01227. Вычисления проделаны в среде Matlab, версия R2018b.
Список литературы
Аджиев Р.К., Онипченко В.Г., 2011. Экспериментальное изучение всхожести погребенных семян альпийских растений // Юг России: экология, развитие. № 2. С. 17–23.
Гантмахер Ф.Р., 1967. Теория матриц. М.: Наука. 576 с.
Глотов Н.В., 1998. Об оценке параметров возрастной структуры популяций растений // Жизнь популяций в гетерогенной среде. Ч. 1. Йошкар-Ола: Периодика Марий Эл. С. 146–149.
Динамика ценопопуляций растений, 1985 / Под ред. Серебряковой Т.И. М.: Наука. 207 с.
Животовский Л.А., 2001. Онтогенетическое состояние, эффективная плотность и классификация популяций // Экология. № 1. С. 3–7.
Жукова Л.А., 1986. Поливариантность онтогенеза луговых растений // Жизненные формы в экологии и систематике растений. Межвузовский сборник научных трудов / Под ред. Серебряковой Т.И., Соколовой Т.Г. М.: МГПИ. С. 104–114.
Жукова Л.А., 1995. Популяционная жизнь луговых растений. Йошкар-Ола: Ланар. 223 с.
Злобин Ю.А., 1989а. Принципы и методы изучения ценотических популяций растений. Учебно-методич. пособие. Казань: Изд-во Казан. ун-та. 147 с.
Злобин Ю.А., 1989б. Теория и практика оценки виталитетного состава ценопопуляций растений // Бот. журн. Т. 74. № 6. С. 769–781.
Злобин Ю.А., 1998. Популяции растений в гетерогенной среде // Жизнь популяций в гетерогенной среде. Ч. 1. Йошкар-Ола: Периодика Марий Эл. С. 64–66.
Злобин Ю.А., 2009. Популяционная экология растений; современное состояние, точки роста. Сумы: Университетская книга. 263 с.
Ишбирдин А.Р., Ишмуратова М.М, 2004. Адаптивный морфогенез и эколого-ценотические стратегии выживания травянистых растений // Методы популяционной биологии. Сб. материалов докл. VII Всерос. популяционного семинара, 16–21 февр. 2004 г. Сыктывкар: Коми науч. центр Ур. отд. РАН. С. 113–120.
Ишбирдин А.Р., Ишмуратова М.М., 2009. Некоторые направления и итоги исследований редких видов флоры республики Башкортостан // Вестн. Удмуртского ун-та. Вып. 1. С. 59–71.
Казанцева Е.С., 2016. Популяционная динамика и семенная продуктивность малолетних альпийских растений северо-западного Кавказа. Дис. … канд. биол. наук. М.: МГУ. 165 с.
Клинкова Г.Ю., Супрун Н.А., Луконина А.В., 2011. Мониторинг и оценка состояния ценных ботанических объектов. Ч. 1. Популяции редких видов растений. Волгоград: Волгоград. гос. пед. ун-т. 62 с.
Красная книга Краснодарского края, 2007. (Растения и грибы). Издание второе / Отв. ред. Литвинская С.А. Краснодар: ООО “Дизайн Бюро № 1”. 640 с.
Красная книга Республики Адыгея, 2012. Редкие и находящиеся под угрозой исчезновения объекты животного и растительного мира: в 2 ч. Изд. 2. Майкоп: Качество. 340 с.
Логофет Д.О., Белова И.Н., 2007. Неотрицательные матрицы как инструмент моделирования динамики популяций: классические модели и современные обобщения // Фундаментальная и прикладная математика. Т. 13. № 4. С. 145–164.
Логофет Д.О., Уланова Н.Г., 2017. Матричные модели в популяционной биологии. Уч. пособие. M.: МАКС Пресс. 128 с. https://istina.msu.ru/publications/book/84452436/
Логофет Д.О., Маслов А.А., 2018. Анализ мелкомасштабной динамики двух видов-доминантов в сосняке чернично-бруснично-долгомошном. II. Неоднородная марковская цепь и осредненные показатели // Журн. общ. биологии. Т. 79. № 2. С. 135–147.
Логофет Д.О., Уланова Н.Г., Белова И.Н., 2015. Поливариантный онтогенез у вейников: новые модели и новые открытия // Журн. общ. биологии. Т. 76. № 6. С. 438–460.
Логофет Д.О., Белова И.Н., Казанцева Е.С., Онипченко В.Г., 2016а. Ценопопуляция незабудочника кавказского (Eritrichium caucasicum) как объект математического моделирования. I. Граф жизненного цикла и неавтономная матричная модель // Журн. общ. биологии. Т. 77. № 2. С. 106–121.
Логофет Д.О., Уланова Н.Г., Белова И.Н., 2016б. От неопределенности к числу: развитие метода оценки приспособленности клонального вида с поливариантным онтогенезом // Журн. общ. биологии. Т. 77. № 5. С. 379–396.
Логофет Д.О., Казанцева Е.С., Белова И.Н., Онипченко В.Г., 2017а. Ценопопуляция незабудочника кавказского (Eritrichium caucasicum) как объект математического моделирования. II. Сколько лет живет малолетник? // Журн. общ. биологии. Т. 78. № 1. С. 56–66.
Логофет Д.О., Казанцева Е.С., Белова И.Н., Онипченко В.Г., 2017б. Сколько лет живет альпийский малолетник? Модельный подход // Журн. общ. биологии. Т. 78. № 5. С. 63–80.
Логофет Д.О., Казанцева Е.С., Белова И.Н., Онипченко В.Г., 2018. Ценопопуляция незабудочника кавказского (Eritrichium caucasicum) как объект математического моделирования. III. Рост популяции в случайной среде // Журн. общ. биологии. Т. 79. № 4. С. 1–13.
На земле и под землей: границы приспособленности для ценопопуляции клонального растения с поливариантным онтогенезом, 2013. Проект РФФИ № 13-04-01836. https://istina.msu.ru/projects/8473479/
Онипченко В.Г., 2013. Функциональная фитоценология: синэкология растений. М.: Красанд. 576 с. http://urss.ru/cgi-bin/db.pl?lang=Ru&blang=ru&page =Book&id=167497
Оселедец В.И., 1968. Мультипликативная эргодическая теорема. Характеристические показатели Ляпунова динамических систем // Тр. ММО (Изд. МГУ). Т. 19. С. 179–210.
Работнов Т.А., 1950. Жизненный цикл многолетних травянистых растений в луговых ценозах // Тр. БИН АН СССР. Сер. 3. Вып. 6. С. 7–204.
Работнов Т.А., 1978. Фитоценология. М.: Изд-во МГУ. 383 с.
Уранов А.А., 1975. Возрастной спектр фитоценопопуляций как функция времени и энергетических волновых процессов // Биол. науки. № 2. С. 7–34.
Шишкин Б.К., Бобров Е.Г., 1952. Род Androsace // Флора СССР / Под ред. Шишкина Б.К., Боброва Е.Г. Т. 18. М.; Л.: Изд-во АН СССР. С. 221–243.
Шхагапсоев С.Х., 1999. Морфоструктура подземных органов растений первичнообнаженных склонов Кабардино-Балкарии. Нальчик: Кабардино-Балкарский гос. ун-т им. Х.М. Бербекова. 72 с.
Bender M.H., Baskin J.M., Baskin C.C., 2000. Age of maturity and life span in herbaceous, polycarpic perennials // Botanical Review. V. 66. № 3. P. 311–349.
Bowers J.E., Webb R.H., Rondeau R.J., 1995. Longevity, recruitment and mortality of desert plants in Grand Canyon, Arizona, USA // J. Vegetation Science. V. 6. P. 551–564.
Caswell H., 2001. Matrix Population Models: Construction, Analysis, and Interpretation, 2nd ed. Sunderland, MA: Sinauer. 722 p.
Chambers J.C., 1993. Seed and vegetation dynamics in an alpine herb field: Effects of disturbance type // Canadian J. Botany. V. 71. № 3. P. 471–485.
Cohen J.E., 1976. Ergodicity of age structure in populations with Markovian vital rates, I. Countable states // J. Amer. Statistical Ass. V. 71. № 354. P. 335–339.
Cohen J.E., 1977a. Ergodicity of age structure in populations with Markovian vital rates, II. General states // Advances in Applied Probability. V. 9. P. 18–37.
Cohen J.E., 1977b. Ergodicity of age structure in populations with Markovian vital rates, III. Finite-state moments and growth rate; an illustration // Advances Applied Probability. V. 9. P. 462–475.
COMADRE, 2018. https://www.compadre-db.org/Data/Comadre
COMPADRE, 2018. https://www.compadre-db.org/Data/Compadre
Grime J.P., 1979. Plant Strategies, Vegetation Processes, and Ecosystem Properties. Chichester: John Wiley. 222 p.
Grime J.P., 2001. Plant Strategies, Vegetation Processes, and Ecosystem Properties. 2nd ed. Chichester: John Wiley. 417 p.
Horn R.A., Johnson C.R., 1990. Matrix Analysis. Cambridge: Cambridge University Press. 561 p.
Keller R., Vittoz P., 2014. Clonal growth and demography of a hemicryptophyte alpine plant: Leontopodium alpinum Cassini // Alpine Botany. V. 125. № 1. P. 31–40.
Keyfitz N., 1968. Introduction to the Mathematics of Population. Reading, MA: Addison-Wesley. 450 p.
Körner C., 2003. Alpine Plant Life: Functional Plant Ecology of High Mountain Ecosystems. 2nd ed. B.: Springer. 350 p.
Logofet D.O., 1993. Matrices and Graphs: Stability Problems in Mathematical Ecology. Boca Rato, FL: CRC Press. 308 p.
Logofet D.O., 2018. Averaging the population projection matrices: heuristics against uncertainty and nonexistence // Ecol. Complexity. V. 33. № 1. P. 66–74.
Logofet D.O., Ulanova N.G., Belova I.N., 2014. Adaptation on the ground and beneath: does the local population maximize its λ1? // Ecol. Complexity. V. 20. P. 176–184.
MathWorks, 2018a. http://www.mathworks.com/help/optim/ug/fmincon.html?s_tid=srchtitle.
MathWorks, 2018b. https://www.mathworks.com/help/search.html?qdoc=optimtool&s_tid=doc_ta.
MathWorks, 2018c. https://www.mathworks.com/help/gads/globalsearch.html.
Onipchenko V.G. (ed.), 2004. Alpine Ecosystems in the Northwest Caucasus. Dordrecht: Kluwer Acad. Publ. 407 p.
Ozgul A., Childs D.Z., Oli M.K., Armitage K.B., Blumstein D.T., Olson L.E., Tuljapurkar S., Coulson T., 2010. Coupled dynamics of body mass and population growth in response to environmental change // Nature. V. 466. P. 482–485.
Rees M., Ellner S.P., 2009. Integral projection models for populations in temporally varying environments // Ecol. Monographs. V. 79. P. 575–594.
Sanz L., 2019. Conditions for growth and extinction in matrix models with environmental stochasticity // Advances in Theory and Practice of Matrix Population Models / Eds Logofet D.O., Salguero-Gomes R. (in press).
Shefferson R.P., 2009. The evolutionary ecology of vegetation dormancy in mature herbaceous perennial plants // J. Ecology. V. 97. № 5. P. 1000–1009.
Tuljapurkar S.D., 1986. Demography in stochastic environments. II. Growth and convergence rates // J. Math. Biology. V. 24. P. 569–581.
Tuljapurkar S.D., 1990. Population Dynamics in Variable Environments. N.Y.: Springer. 154 p.
Williams H.J., Jacquemyn H., Ochocki B.M., Brys R., Miller T.E.X., 2015. Life history evolution under climate change and its influence on the population dynamics of a long-lived plant // J. Ecology. V. 103. P. 798–808.
Дополнительные материалы отсутствуют.
Инструменты
Журнал общей биологии