1. На главную
  2. Электронные версии
  3. Журнал общей биологии
  4. T. 80, № 6, 2019

Журнал общей биологии, 2019, T. 80, № 6, стр. 418-426

Возвращаясь к вопросу о популяционной регуляции: обобщенная модель формирования пополнения промысловых популяций рыб

А. И. Михайлов 1, *, А. Е. Бобырев 1, 2, **, Т. И. Булгакова 1, А. Д. Шереметьев 1

1 Всероссийский НИИ рыбного хозяйства и океанографии
107140 Москва, Верхняя Красносельская ул., 17, Россия

2 Институт проблем экологии и эволюции им. А.Н. Северцова РАН
119071 Москва, Ленинский просп., 33, Россия

* E-mail: mikhailov1984@gmail.com
** E-mail: abobyrev@mail.ru

Поступила в редакцию 10.04.2019
После доработки 07.08.2019
Принята к публикации 27.08.2019

Полный текст (PDF)

Аннотация

Предложена обобщенная модель формирования пополнения промысловых популяций рыб, дающая полное описание класса зависимостей “запас–пополнение”, основанных на плотностной регуляции динамики популяций. Представлены результаты анализа свойств детерминированной версии модели, включающей в себя пять управляющих параметров. Предлагаемая унифицированная модель, выведенная из первых принципов популяционной динамики, обеспечивает возможность количественных сопоставлений (на уровне значений параметров) качественно различных описаний процессов пополнения, основанных на альтернативных гипотезах о механизмах и факторах этих процессов. Общность формулировок модели допускает переход от ее детерминированного варианта к стохастическому, включающему в том числе и действие факторов внешней среды.

Проблема популяционной динамики является одной из ключевых фундаментальных проблем экологической теории. Интерпретация процессов популяционных изменений зачастую наталкивается на трудности, обусловленные огромным многообразием и непостоянством факторов и механизмов, их контролирующих. Крайние точки зрения на проблему механизмов динамики численности природных популяций могут быть обозначены как “регуляционизм” и “стохастизм” (Викторов, 1965). Согласно концепции регуляционизма, каждая популяция обладает равновесным уровнем плотности, поддерживаемым выработавшимися в ходе эволюции внутрипопуляционными (или внутриэкосистемными) механизмами. Стохастизм уделяет основное внимание факторам, случайно распределенным во времени и пространстве. С позиции стохастизма “равновесный” уровень численности есть просто артефакт усреднения за длительный срок: чем длиннее имеющийся ряд наблюдений за популяцией, тем больше шансов утверждать, что средняя плотность за ряд лет это и есть “равновесная” плотность, активно поддерживаемая специальными механизмами (Гиляров, 1990).

Несмотря на различия между регуляционизмом и стохастизмом, оба подхода сходятся на том, что ведущая роль в ограничении роста численности популяций принадлежит факторам внешней среды, таким как нехватка пищи или неблагоприятные условия среды. Однако в начале 1960-х годов была предложена завоевавшая вскоре большую популярность концепция саморегуляции популяций, согласно которой в процессе роста плотности популяции изменяется не только и не столько качество среды, в которой существует популяция, сколько качество самих составляющих ее особей. Это изменение свойств особей, направленное на торможение дальнейшего роста популяции, выражается в конечном счете в снижении плодовитости, удлинении сроков полового созревания, возрастании смертности и миграционной активности (Никольский, 1965; Шварц, 1969).

Вполне естественно, что, будучи интегрированным результатом множества биологических процессов и событий, феномен популяционной динамики практически не оставляет места для средств качественного анализа в изучении колебаний численности популяций животных. Наиболее распространенным, результативным, а в некоторых случаях и единственным методом изучения сложных динамических систем, каковыми являются популяции и сообщества животных, является моделирование (Меншуткин, 1971).

Излишне говорить, что моделей, описывающих плотностные эффекты в динамике популяций различных групп растений и животных, к настоящему времени разработано множество. Однако с практической точки зрения особое значение имеют модели пополнения промысловых популяций рыб, поскольку являются важнейшим инструментом анализа состояния рыбных запасов и управления их промыслом.

МОДЕЛИ “ЗАПАС–ПОПОЛНЕНИЕ”

Современная система управления биоресурсами водоемов опирается на теорию динамики промыслового запаса рыб, сложившуюся к середине прошлого века. Одной из общепризнанных в настоящее время частных теорий, интерпретирующих процессы популяционных изменений под действием промысла, является теория пополнения, впервые разработанная и примененная Рикером (Ricker, 1954). Подход Рикера исходит из наличия связи между темпом отмирания рыб и плотностью популяции, приводящей к торможению роста численности популяции при переуплотнении. Рикер рассматривал в качестве основного механизма образования подобной связи хищничество или каннибализм.

Подход, использованный Рикером, в дальнейшем получил развитие во множестве работ, посвященных анализу зависимости между величиной родительского стада и величиной продуцируемого им потомства. Одной из первых подобных работ было исследование Бивертона и Холта (Beverton, Holt, 1957), объектом которого послужила популяция североморской сельди. В модели Бивертона–Холта предполагается зависимость смертности молоди от текущей численности генерации, т.е. процесс пополнения лимитируется факторами внешней среды.

Наиболее широкое применение теория получила при анализе динамики запасов тихоокеанских лососей, добываемых на западном побережье Северной Америки. Положение о существовании определенных количественных соотношений между численностью родительского запаса и величиной продуцируемого им пополнения привело к возникновению концепции “управления пропуском производителей” на нерестилища. Тем не менее теорию пополнения вряд ли можно считать окончательно сформировавшейся, и ее развитие до сего времени остается одной из наиболее актуальных проблем популяционной динамики (Hilborn, Walters, 1992; Cushing, 1996; Needle, 2002).

В решении практических задач регулирования рыболовства наиболее употребительными до сих пор остаются модели “запас–пополнение”, предложенные Рикером, Бивертоном и Холтом. Зависимость Бивертона–Холта (Beverton, Holt, 1957) имеет вид

(1)
$R\left( S \right) = pS{{(1 + {S \mathord{\left/ {\vphantom {S {{{S}_{0}}}}} \right. \kern-0em} {{{S}_{0}}}})}^{{ - 1}}},$
где R(S) – величина пополнения; S – величина родительского стада; S0 – параметр, отражающий лимитирующее действие факторов среды; p – значение производной функции “запас–пополнение” в нуле. Максимальное значение пополнения (Rmax = pS0) достигается при бесконечно большом числе производителей.

Модель Рикера (Ricker, 1954), учитывающая эффекты хищничества или каннибализма, формализуется следующей зависимостью:

(2)
$R\left( S \right) = pS~{\text{exp}}\left( { - \frac{S}{{S{\text{*}}}}} \right),$
где S* – численность нерестового стада, при котором пополнение максимально. Для модели Рикера Rmax = pS*/e.

Следует отметить, что к настоящему времени, помимо оригинальных версий этих моделей, используется (особенно для прогнозирования подходов лососей к нерестовым рекам) множество модификаций, направленных на вовлечение в анализ дополнительной информации или на улучшение статистических свойств оценок параметров (Haeseker et al., 2005, 2008). В простейшем случае используется линеаризованная версия оригинальной модели Рикера:

$\ln ({{{{R}_{t}}} \mathord{\left/ {\vphantom {{{{R}_{t}}} {{{S}_{t}}) = a - b{{S}_{t}}}}} \right. \kern-0em} {{{S}_{t}}) = a - b{{S}_{t}}}} + {{\varepsilon }_{t}},$
где a и b – параметры, подлежащие оценке; St – численность производителей в год нереста t; Rt – численность рекрутов от производителей, отнерестившихся в год t; εt – случайная переменная, распределенная по нормальному закону, εt ~ N(0, $\sigma _{\varepsilon }^{2}$). Другие модификации включают (список не является исчерпывающим):

– модель, учитывающую авторегрессионные свойства остатков. В этом случае представление случайной переменной приобретает вид εt = φ εt– 1 + νt, где φ – оценка коэффициента автокорреляции, νt– случайная переменная, νt ~ N(0, $\sigma _{\nu }^{2}$);

– модель, предполагающую наличие межгодовых изменений продуктивности запаса,

$\ln \left( {{{{{R}_{t}}} \mathord{\left/ {\vphantom {{{{R}_{t}}} {{{S}_{t}}}}} \right. \kern-0em} {{{S}_{t}}}}} \right) = {{a}_{t}}--b{{S}_{t}} + {{\varepsilon }_{t}},$
где at = at – 1 + νt, νt ~ N(0, $\sigma _{\nu }^{2}$) (оценка параметров модели осуществляется с применением фильтра Калмана);

– модель, в простейшей форме учитывающую влияние температуры на выживание молоди,

$\ln \left( {{{{{R}_{t}}} \mathord{\left/ {\vphantom {{{{R}_{t}}} {{{S}_{t}}}}} \right. \kern-0em} {{{S}_{t}}}}} \right) = a--b{{S}_{t}} + \gamma {\text{SS}}{{{\text{T}}}_{t}}_{{\, + \,k}} + {{\varepsilon }_{t}},$
где γ – параметр влияния поверхностной температуры морской воды SSTt+k на момент ската молоди в море;

– модель, обобщающую данные по нескольким локальным популяциям,

$\begin{gathered} \ln \left( {{{{{R}_{{it}}}} \mathord{\left/ {\vphantom {{{{R}_{{it}}}} {{{S}_{{it}}}}}} \right. \kern-0em} {{{S}_{{it}}}}}} \right) = \alpha + {{a}_{i}}--{{b}_{i}}{{S}_{{it}}} + \\ + \,\,\gamma {\text{SS}}{{{\text{T}}}_{{i,t\, + \,k}}} + {{g}_{i}}{\text{SS}}{{{\text{T}}}_{{i,t\, + \,k}}} + {{\varepsilon }_{{it}}}, \\ \end{gathered} $
где α – фиксированный параметр, отражающий общую для всех запасов компоненту темпа воспроизводства; ai и bi – запас-специфичные параметры уравнения Рикера; γ и gi – постоянная и случайная компоненты температурных эффектов; εit – случайная переменная, учитывающая автокорреляцию остатков, εit = φ εit – 1 + νt, где φ – оценка коэффициента автокорреляции, νt – случайная переменная, νt ~ N(0, $\sigma _{\nu }^{2}$);

– модель Ларкина (Larkin, 1971), являющуюся расширением модели Рикера для полицикличных видов (используется в различных модификациях при оценивании состояния запаса нерки р. Фрейзер),

$\begin{gathered} \ln \left( {{{{{R}_{t}}} \mathord{\left/ {\vphantom {{{{R}_{t}}} {{{S}_{{t\,--\,4}}}}}} \right. \kern-0em} {{{S}_{{t\,--\,4}}}}}} \right) = a--{{b}_{0}}{{S}_{{t\,--\,4}}}--{{b}_{1}}{{S}_{{t\,--\,5}}}-- \\ - \,\,{{b}_{2}}{{S}_{{t\,--\,6}}}--{{b}_{3}}{{S}_{{t\,--\,7}}} + {{\varepsilon }_{t}}, \\ \end{gathered} $
где Rt – численность пополнения в год t, St –k (k = 4, …, 7) – численность нерестового стада k лет назад.

Из числа отечественных разработок заслуживает упоминания резонансная модель, предложенная М.Г. Фельдманом и Е.А. Шевляковым (2015), предполагающая наличие оптимального для выживаемости пополнения количества производителей. Модель имеет вид

$R = {{a{{S}^{2}}} \mathord{\left/ {\vphantom {{a{{S}^{2}}} {\sqrt {\left( {S_{0}^{2} - {{S}^{2}}} \right) + {{b}^{2}}{{S}^{2}}} }}} \right. \kern-0em} {\sqrt {\left( {S_{0}^{2} - {{S}^{2}}} \right) + {{b}^{2}}{{S}^{2}}} }}$
с параметрами а (предел численности пополнения при неограниченном нерестовом запасе), b (нерестовый запас, необходимый для продуцирования пополнения a при максимальной выживаемости) и S0 (нерестовый запас, обеспечивающий максимальную выживаемость потомков).

Поскольку зависимость пополнения от запаса в большинстве случаев довольно сильно зашумлена (Myers et al., 1995), существует естественное стремление сделать ее более гибкой с целью лучшей аппроксимации результатов наблюдений. Деризо (Deriso, 1980) и Шнютэ (Schnute, 1985) предложили обобщенную модель, частными случаями которой являются модели Рикера и Бивертона–Холта:

(3)
$R\left( S \right) = pS{{(1 - \beta ({S \mathord{\left/ {\vphantom {S {{{S}_{0}}}}} \right. \kern-0em} {{{S}_{0}}}}))}^{{{1 \mathord{\left/ {\vphantom {1 \beta }} \right. \kern-0em} \beta }}}},$
где β – коэффициент формы. При β = –1 модель Деризо–Шнютэ переходит в модель Бивертона–Холта, при β = 0 – в модель Рикера.

Шепард (Shepherd, 1982) предложил другое семейство кривых “запас–пополнение”:

(4)
$R\left( S \right) = {{pS} \mathord{\left/ {\vphantom {{pS} {\left( {1 + {{{({S \mathord{\left/ {\vphantom {S {{{S}_{0}}}}} \right. \kern-0em} {{{S}_{0}}}})}}^{\beta }}} \right)}}} \right. \kern-0em} {\left( {1 + {{{({S \mathord{\left/ {\vphantom {S {{{S}_{0}}}}} \right. \kern-0em} {{{S}_{0}}}})}}^{\beta }}} \right)}}.$

В этом семействе при любых β пополнение остается положительным, однако асимптотика при больших значениях величины запаса становится степенной. Семейство кривых Шепарда можно модифицировать таким образом, чтобы в асимптотике больших величин нерестового запаса величина пополнения выходила на константу, как в модели Бивертона–Холта:

(5)
$R\left( S \right) = {{pS} \mathord{\left/ {\vphantom {{pS} {{{{\left( {1 + {{{({S \mathord{\left/ {\vphantom {S {{{S}_{0}}}}} \right. \kern-0em} {{{S}_{0}}}})}}^{\beta }}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 \beta }} \right. \kern-0em} \beta }}}}}}} \right. \kern-0em} {{{{\left( {1 + {{{({S \mathord{\left/ {\vphantom {S {{{S}_{0}}}}} \right. \kern-0em} {{{S}_{0}}}})}}^{\beta }}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 \beta }} \right. \kern-0em} \beta }}}}}}.$

Это семейство примечательно тем, что при β → +∞ оно сходится к так называемой модели “хоккейной клюшки” (Barrowman, Myers, 2000):

(6)
$R\left( S \right) = p~\,min\left( {S,~{{S}_{0}}} \right).$

Пополнение прямо пропорционально величине родительского запаса, если она меньше S0, и постоянно, если больше. Заметим, что семейство зависимостей “запас–пополнение” вида (5) при β ≥ 1 ограничено снизу зависимостью Бивертона–Холта и сверху зависимостью вида (6):

(7)
$\begin{gathered} pS{{(1 + {S \mathord{\left/ {\vphantom {S {{{S}_{0}}}}} \right. \kern-0em} {{{S}_{0}}}})}^{{ - 1}}} \leqslant \\ \leqslant {{pS} \mathord{\left/ {\vphantom {{pS} {{{{\left( {1 + {{{({S \mathord{\left/ {\vphantom {S {{{S}_{0}}}}} \right. \kern-0em} {{{S}_{0}}}})}}^{\beta }}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 \beta }} \right. \kern-0em} \beta }}}}}}} \right. \kern-0em} {{{{\left( {1 + {{{({S \mathord{\left/ {\vphantom {S {{{S}_{0}}}}} \right. \kern-0em} {{{S}_{0}}}})}}^{\beta }}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 \beta }} \right. \kern-0em} \beta }}}}}} \leqslant ~p~\,min\left( {S,~{{S}_{0}}} \right). \\ \end{gathered} $

При этом верхняя и нижняя оценки пополнения отличаются не более чем в 2 раза, поэтому при высокой зашумленности связи “запас–пополнение” зависимость (6) оказывается простой и удобной аппроксимацией.

Исходя только из требований асимптотического поведения при малых и больших значениях родительского запаса, можно сформулировать достаточно много способов интерполяции между зависимостями Бивертона–Холта и Рикера, например такой:

(8)
$R\left( S \right) = pS{{(1 + {S \mathord{\left/ {\vphantom {S {{{S}_{0}}}}} \right. \kern-0em} {{{S}_{0}}}})}^{{ - 1}}}{\text{exp}}\left( { - \frac{S}{{S{\text{*}}}}} \right).$

Однако в данной работе мы рассмотрим вывод зависимости “запас–пополнение” общего вида, исходя из первых принципов популяционной динамики, как это сделано в работах Т.И. Булгаковой (1978) и Гомеса Муньоса (Gomez Muñoz, 1986).

ОБОБЩЕННАЯ МОДЕЛЬ ПОПОЛНЕНИЯ

Исходные предположения модели заключаются в следующем. Во-первых, предполагается, что численность молоди убывает согласно экспоненциальному закону:

(9)
$\dot {N} = - Z\left( {t,N,S} \right)N,$
где Z – смертность, зависящая от различных факторов, как эндогенных, так и экзогенных. Пока эта зависимость не указана в явном виде, это положение почти тривиально. Во-вторых, предполагается, что начальная численность пополнения, т.е. количество выметанной икры, есть функция величины запаса:

(10)
$N\left( 0 \right) = P\left( S \right).$

Сама же численность пополнения есть не что иное, как численность особей, выживших к определенному моменту времени T,

(11)
$R \equiv N\left( T \right).$

Будем решать следующее стохастическое дифференциальное уравнение динамики численности молоди:

(12)
$dN = - \left( {M\left( {t,S} \right) + a{{N}^{\gamma }}} \right)Ndt + \sigma NdB,$
где M – смертность молоди, определяемая всеми факторами, кроме ее численности (плотности); a – фактор конкуренции, причем конкуренция может быть нелинейной11 (степень нелинейности задается коэффициентом формы γ); σ – дисперсия флуктуаций смертности; dB – дифференциал стандартного броуновского движения, т.е. случайного процесса с независимыми приращениями, подчиняющегося нормальному закону распределения с нулевым средним и дисперсией t, причем 〈B(t)B(t')〉 = min(t, t'). Иными словами, смертность молоди определяется тремя независимыми факторами: фактором плотности, фактором, не зависящим от плотности, включающим в себя как воздействие среды, так и каннибализм, и случайным фактором.

Для того чтобы решить уравнение (12), обезразмерим численность и сделаем замену переменных, используемую при решении уравнений Бернулли (Зайцев, Полянин, 2001):

(13)
$W = \frac{1}{\gamma }{{N}^{{ - \gamma }}} - \frac{1}{\gamma }.$

Тогда по правилам К. Ито (1960, 1963), в соответствии с которыми dt2 = 0 = –dtdB, как в классическом дифференциальном исчислении, а dB2 = dt, что связано с автокоррелированностью броуновского движения, после замены переменной уравнение (12) приобретает вид

(14)
$dW = - {{N}^{{ - \gamma \, - \,1}}}dN + \frac{1}{2}\left( {1 + \gamma } \right){{N}^{{ - \gamma \, - \,2}}}{{\left( {dN} \right)}^{2}}.$

Подставляя (12) в (14), получаем

(15)
$\begin{gathered} dW = {{N}^{{ - \gamma \, - \,1}}}\left( {\left( {M\left( {t,S} \right) + a{{N}^{\gamma }}} \right)Ndt + \sigma NdB} \right) + \\ + \,\,\frac{{{{\sigma }^{2}}}}{2}\left( {1 + \gamma } \right){{N}^{{ - \gamma \, - \,2}}}{{N}^{2}}dt. \\ \end{gathered} $

В новых переменных уравнение принимает вид

(16)
$\begin{gathered} dW = \left( {\gamma \left( {M\left( {t,S} \right) + \frac{{{{\sigma }^{2}}}}{2}\left( {1 + \gamma } \right)} \right)W} \right. + a + \\ + \,\,\left. {\left( {M\left( {t,S} \right) + \frac{{{{\sigma }^{2}}}}{2}\left( {1 + \gamma } \right)} \right)} \right)dt + \sigma \left( {\gamma W + 1} \right)dB. \\ \end{gathered} $

Будем искать решение в виде

(17)
$W = {{\left( {A{{e}^{{\gamma \omega }}} - 1} \right)} \mathord{\left/ {\vphantom {{\left( {A{{e}^{{\gamma \omega }}} - 1} \right)} \gamma }} \right. \kern-0em} \gamma },$
где $dA = \gamma a{{e}^{{ - \gamma \omega }}}dt$ и ω подчиняется уравнению $d\omega = \left( {M\left( {t,S} \right) + \frac{{{{\sigma }^{2}}}}{2}} \right)dt + \sigma dB.$ Используя правила К. Ито, получаем, что dW совпадает с (16):

(18)
$\begin{gathered} dW = \frac{1}{\gamma }{{e}^{{\gamma \omega }}}dA + A{{e}^{{\gamma \omega }}}d\omega + \\ + \,\,\frac{\gamma }{2}A{{e}^{\omega }}{{\left( {d\omega } \right)}^{2}} + {{e}^{\omega }}dAd\omega = \\ = \left( {\left( {M\left( {t,S} \right) + \frac{{{{\sigma }^{2}}}}{2}\left( {1 + \gamma } \right)} \right)A{{e}^{{\gamma \omega }}} + a} \right)dt + \sigma A{{e}^{{\gamma \omega }}}dB. \\ \end{gathered} $

В итоге имеем следующее решение:

(19)
$\begin{gathered} W(T) = \frac{1}{\gamma }{{\left( {P(S)} \right)}^{{ - \gamma }}} \times \\ \times \,\,\exp \left( {\gamma \left( {\int\limits_0^T {\left( {M(\tau ,S) + \frac{{{{\sigma }^{2}}}}{2}} \right)d\tau } + \sigma B\left( T \right)} \right)} \right) + \\ + \,\,\int\limits_0^T {a(t)\exp \left( {\gamma \left( {\int\limits_t^T {\left( {M(\tau ,S) + \frac{{{{\sigma }^{2}}}}{2}} \right)d\tau } } \right.} \right.} + \\ \left. {\left. {\frac{{^{{^{{}}}}}}{{_{{_{{_{{}}}}}}}} + \,\,\sigma \left( {B\left( T \right) - B\left( t \right)} \right)} \right)} \right)dt - \frac{1}{\gamma }. \\ \end{gathered} $

Окончательно общая зависимость пополнения от численности родительского стада и зависящих от времени экзогенных факторов, как случайных, так и детерминированных, приобретает следующий вид:

(20)
$\begin{gathered} N(T) = \left[ {{{{\left( {P(S)} \right)}}^{{ - \gamma }}} \times \frac{{^{{^{{}}}}}}{{_{{_{{_{{}}}}}}}}} \right. \\ \times \,\,\exp \left( {\gamma \left( {\int\limits_0^T {\left( {M(\tau ,S) + \frac{{{{\sigma }^{2}}}}{2}} \right)d\tau } + \sigma B\left( T \right)} \right)} \right) + \\ + \,\,\gamma \int\limits_0^T {a(t)\exp \left( {\gamma \left( {\int\limits_t^T {\left( {M(\tau ,S) + \frac{{{{\sigma }^{2}}}}{2}} \right)d\tau } } \right.} \right.} + \\ {{\left. {\left. {\left. {\frac{{^{{^{{^{{}}}}}}}}{{_{{_{{}}}}}} + \,\,\sigma \left( {B\left( T \right) - B\left( t \right)} \right)} \right)} \right)dt} \right]}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} \gamma }} \right. \kern-0em} \gamma }}}}. \\ \end{gathered} $

СВОЙСТВА МОДЕЛИ

Рассмотрим важный частный случай, когда смертность молоди в течение периода формирования пополнения (T) остается постоянной. Тогда интегралы в формуле (20) поддаются расчету, и соотношение “запас–пополнение” общего положения при наличии факторов конкуренции и каннибализма/хищничества принимает вид

(21)
$R\left( S \right) = \frac{{P\left( S \right){\text{exp}}\left( { - M} \right)}}{{{{{\left[ {1 + {{{\left( {\frac{{P\left( S \right)}}{{{{S}_{0}}}}} \right)}}^{\gamma }}\frac{1}{M}\left( {1 - \exp \left( { - \gamma M} \right)} \right)} \right]}}^{{{1 \mathord{\left/ {\vphantom {1 \gamma }} \right. \kern-0em} \gamma }}}}}},$
где P(S) – функция, связывающая годовой прирост численности запаса за счет пополнения с численностью родительского стада, в простейшем случае – линейная (N(0) = pS, где коэффициент пропорциональности p имеет смысл средней индивидуальной плодовитости); M – безразмерный показатель смертности молоди от всех факторов за исключением конкуренции; S0 – фактор конкуренции, имеющий смысл численности нерестового стада, при которой эффекты конкуренции начинают оказывать существенное влияние на величину пополнения; γ – коэффициент формы. Ранее формула (21) была приведена без вывода в работе А.И. Михайлова (2019).

Смертность молоди, в свою очередь, также является функцией величины запаса и иных факторов22:

(22)
$M = \left( {1 + \frac{S}{{S{\text{*}}}} + f + \varepsilon } \right){{M}_{0}},$
где S* – фактор каннибализма/хищничества, интерпретируемый аналогично фактору конкуренции (S0) в предыдущей формуле; M0 – безразмерный коэффициент смертности молоди от иных факторов (физиологическая смертность); f – переменная, отражающая влияние внешних факторов; ε – ошибка процесса. Если имеется информация о воздействии факторов окружающей среды на смертность/выживаемость молоди, переменная f может быть конкретизирована, например, в виде f = c1X1 + … + ckXk, где X1, …, Xk – влияющие факторы. Попытки учесть влияние внешних факторов на процессы формирования пополнения неоднократно предпринимались ранее применительно к известным моделям пополнения. Так, например, модель Рикера в этом случае принимает вид R = αSexp(–βS + γ1X1 + … + γkXk) (Tang, 1985; Caputi, 1988; Quinn, Niebauer, 1995). Тем не менее корреляционные связи между конкретными факторами среды и смертностью/выживаемостью молоди тех или иных видов рыб не всегда оказываются достаточно сильными, чтобы существенно улучшить прогностические свойства модели (Bradford, 1992). По этой причине существуют лишь немногие примеры их использования в практике управления промысловыми запасами рыб (Myers, 1998).

В общей сложности детерминированный вариант модели (21)–(22) при отсутствии влияния внешних факторов содержит пять параметров, что обеспечивает ей достаточную гибкость при описании разнообразных форм кривой пополнения.

При S0 → ∞, т.е. в отсутствие конкуренции, соотношение (21) переходит в модель Рикера, причем график зависимости Рикера (рис. 1, крупный пунктир) всегда лежит выше графика общего положения:

(23)
$\begin{gathered} \mathop {\lim }\limits_{{{S}_{0}} \to \infty } \frac{{P\left( S \right){\text{exp}}\left( { - M} \right)}}{{{{{\left[ {1 + {{{\left( {\frac{{P\left( S \right)}}{{{{S}_{0}}}}} \right)}}^{\gamma }}\frac{1}{M}\left( {1 - \exp \left( { - \gamma M} \right)} \right)} \right]}}^{{{1 \mathord{\left/ {\vphantom {1 \gamma }} \right. \kern-0em} \gamma }}}}}} = \\ = P\left( S \right)\exp \left( { - M\left( S \right)} \right), \\ \end{gathered} $
(24)
$\begin{gathered} R\left( S \right) = \frac{{P\left( S \right){\text{exp}}\left( { - M} \right)}}{{{{{\left[ {1 + {{{\left( {\frac{{P\left( S \right)}}{{{{S}_{0}}}}} \right)}}^{\gamma }}\frac{1}{M}\left( {1 - \exp \left( { - \gamma M} \right)} \right)} \right]}}^{{{1 \mathord{\left/ {\vphantom {1 \gamma }} \right. \kern-0em} \gamma }}}}}} \leqslant \\ \leqslant P\left( S \right)\exp \left( { - M\left( S \right)} \right). \\ \end{gathered} $
Рис. 1.

Вид зависимости “запас–пополнение” при различных значениях параметра S0 (S0 = 1.36, 3.26, 27.18 млн экз.). Точечными пунктирными линиями обозначены положения асимптот. Крупный пунктир соответствует функции Рикера.

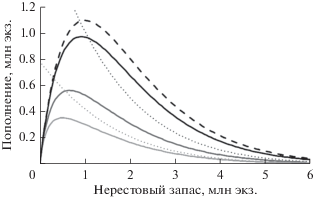
Асимптотика при больших значениях S задается выражением

(25)
$\begin{gathered} \frac{{P(S)\exp \left( { - M} \right)}}{{{{{\left[ {1 + {{{\left( {\frac{{P(S)}}{{{{S}_{0}}}}} \right)}}^{\gamma }}\frac{1}{M}\left( {1 - \exp \left( { - \gamma M} \right)} \right)} \right]}}^{{{1 \mathord{\left/ {\vphantom {1 \gamma }} \right. \kern-0em} \gamma }}}}}}\xrightarrow{{S \to \infty }} \\ \to \frac{{{{S}_{0}}{{M}^{{{1 \mathord{\left/ {\vphantom {1 \gamma }} \right. \kern-0em} \gamma }}}}\exp \left( { - M} \right)}}{{{{{\left[ {1 - \exp \left( { - \gamma M} \right)} \right]}}^{{{1 \mathord{\left/ {\vphantom {1 \gamma }} \right. \kern-0em} \gamma }}}}}}, \\ \end{gathered} $
причем пополнение ограничено сверху своим асимптотическим значением в соответствии с неравенством

(26)
$\begin{gathered} R(S) = \frac{{P(S)\exp \left( { - M} \right)}}{{{{{\left[ {1 + {{{\left( {\frac{{P(S)}}{{{{S}_{0}}}}} \right)}}^{\gamma }}\frac{1}{M}\left( {1 - \exp \left( { - \gamma M} \right)} \right)} \right]}}^{{{1 \mathord{\left/ {\vphantom {1 \gamma }} \right. \kern-0em} \gamma }}}}}} \leqslant \\ \leqslant \frac{{{{S}_{0}}{{M}^{{{1 \mathord{\left/ {\vphantom {1 \gamma }} \right. \kern-0em} \gamma }}}}\exp \left( { - M} \right)}}{{{{{\left[ {1 - \exp \left( { - \gamma M} \right)} \right]}}^{{{1 \mathord{\left/ {\vphantom {1 \gamma }} \right. \kern-0em} \gamma }}}}}}. \\ \end{gathered} $

Неравенства (24) и (26) являются следствиями замены знаменателя в формуле (21) меньшим значением, путем исключения первого или второго неотрицательного слагаемого соответственно.

Поскольку неравенства (24) и (26) верны при всех S, верно и неравенство

(27)
$\begin{gathered} R(S) = \frac{{P(S)\exp \left( { - M} \right)}}{{{{{\left[ {1 + {{{\left( {\frac{{P(S)}}{{{{S}_{0}}}}} \right)}}^{\gamma }}\frac{1}{M}\left( {1 - \exp \left( { - \gamma M} \right)} \right)} \right]}}^{{{1 \mathord{\left/ {\vphantom {1 \gamma }} \right. \kern-0em} \gamma }}}}}} \leqslant \\ \leqslant min\left( {\frac{{{{S}_{0}}{{M}^{{{1 \mathord{\left/ {\vphantom {1 \gamma }} \right. \kern-0em} \gamma }}}}\exp \left( { - M} \right)}}{{{{{\left[ {1 - \exp \left( { - \gamma M} \right)} \right]}}^{{{1 \mathord{\left/ {\vphantom {1 \gamma }} \right. \kern-0em} \gamma }}}}}},P(S)\exp \left( { - M\left( S \right)} \right)} \right). \\ \end{gathered} $

Кривая, ограничивающая величину пополнения в соответствии с неравенством (27), образуется из сегментов двух асимптот (рис. 1, 2, пунктирные линии).

Рис. 2.

Вид зависимости “запас–пополнение” общего положения при различных значениях параметра γ (γ = = 1, 2, 5) при S* = 1 млн экз. На рис. 2–3 пунктирными линиями обозначены положения асимптот.

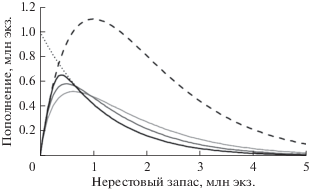
Более того, асимптотика при больших γ приводит к модификации зависимости “запас–пополнение” типа “хоккейной клюшки”:

(28)
$\begin{gathered} \frac{{P(S)\exp \left( { - M} \right)}}{{{{{\left[ {1 + {{{\left( {\frac{{P(S)}}{{{{S}_{0}}}}} \right)}}^{\gamma }}\frac{1}{M}\left( {1 - \exp \left( { - \gamma M} \right)} \right)} \right]}}^{{{1 \mathord{\left/ {\vphantom {1 \gamma }} \right. \kern-0em} \gamma }}}}}}\xrightarrow{{\gamma \to \infty }} \\ \to min\left( {P(S),{{S}_{0}}} \right)\exp \left( { - M\left( S \right)} \right). \\ \end{gathered} $

При этом положение точки излома (пересечение асимптот) зависит от соотношения величин pS* и S0 (рис. 1–3).

Рис. 3.

Вид зависимости “запас–пополнение” общего положения при различных значениях параметра γ (γ = = 1, 2, 5) при отсутствии каннибализма/хищничества.

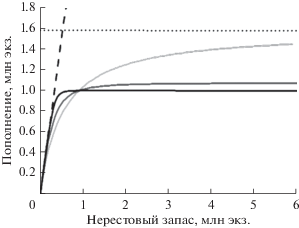
Изменения формы кривой в зависимости от величины параметра γ иллюстрируются сплошными линиями на рис. 2, 3. На рис. 2 отображено семейство кривых, возникающих при фиксированном значении параметра каннибализма/хищничества (S*) и варьировании параметра нелинейности конкуренции (γ). Как видно из рисунка, при одновременном действии обоих факторов тип конкуренции влияет и на проявление эффектов каннибализма. Семейство кривых, возникающих при варьировании параметра нелинейности конкуренции (γ) в отсутствие каннибализма, изображено на рис. 3. Видно, что при увеличении параметра γ форма кривой, исходно имевшей вид функции Бивертона–Холта, стремится к форме, характерной для модели “хоккейной клюшки”. Отсюда следует, что модель “хоккейной клюшки” обусловлена сильно нелинейными эффектами конкуренции.

По мере того, как влияние эффектов конкуренции становится все более выраженным, наблюдается переход от кривой типа Бивертона–Холта к кривой общего положения (рис. 4).

Рис. 4.

Вид зависимости “запас–пополнение” при различных значениях параметра S* (S* = 2, 10, 1000 млн экз.). Пунктирными линиями обозначены положения асимптот кривой Бивертона–Холта.

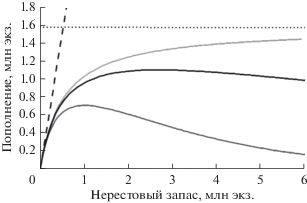
В настоящей работе мы ограничились анализом свойств детерминированной версии модели при ряде упрощающих допущений. Так, мы заменили зависимость смертности молоди от времени ее средней величиной, а для построения графиков, иллюстрирующих форму зависимости “запас–пополнение”, были использованы дополнительные предположения о линейности функции p(S) и отсутствии внешних воздействий. В то же время общая формулировка модели (уравнение 20) позволяет учитывать самые разнообразные эффекты, обусловленные изменениями принятых допущений. В частности, при введении степенной зависимости p(S) модель способна воспроизводить функцию пополнения Кушинга (Cushing, 1973). Помимо всего прочего, задавая формальные характеристики внешних факторов и случайных процессов, влияющих на динамику естественной смертности (ε в уравнении 22), от детерминированного варианта модели нетрудно перейти к стохастическому, учитывающему одновременно и действие факторов среды.

ЗАКЛЮЧЕНИЕ

Со времени опубликования пионерской работы Рикера (Ricker, 1954) прошло без малого 65 лет. За истекший период усилиями специалистов в области количественной экологии и представителей рыбохозяйственной науки теория пополнения значительно продвинулась вперед (Максименко, Антонов, 2003). Среди наиболее интересных и нетривиальных разработок можно отметить модели, вовлекающие в рассмотрение в качестве одного из главных факторов динамики пополнения процессы весового роста молоди (Chapman, 1973; Shepherd, Cushing, 1980; Криксунов, Снетков, 1985; Переварюха, 2008); модели, интерпретирующие процессы формирования пополнения с позиций индивидуальных взаимодействий молоди рыб с кормовыми объектами и позволяющие учитывать пространственные эффекты в их распределении (Bobyrev, Kriksunov, 1998; Pitchford, Brindley, 2001); модели, разбивающие период формирования пополнения на отдельные стадии/фазы, в течение которых реализуются различные регуляторные механизмы (Домбровский и др., 1992; Touzeau, Gouzé, 1998). Помимо собственно конструирования моделей, развиваются и процедуры их параметризации, среди которых все большую популярность в последнее время приобретает байесовский подход (Peterman et al., 2000; Michielsens, McAllister, 2004; Jiao et al., 2009).

Тем не менее, несмотря на объяснительную ценность существующих теоретических построений, их предсказательная способность все еще остается недостаточной. В практике управления системами “запас–промысел” прогнозирование численности рекрутов осуществляется, как правило, на основе статистических свойств временных рядов пополнения, восстановленных в ходе ретроспективного анализа динамики промысловой популяции (Бабаян, 2000; Бабаян и др., 2018). Идентификация конкретных моделей затрудняется крайне высокой вариабельностью величины пополнения и многообразием факторов, ее контролирующих (Garrod, 1983). Выбор той или иной модели, таким образом, оказывается сопряженным с неопределенностями, игнорирование которых может серьезно искажать результаты анализа (Draper, 1995). В этом отношении задача унификации имеющихся моделей пополнения представляется весьма актуальной. Определенным шагом на этом пути является и обобщенная модель, предлагаемая в настоящей статье, поскольку она объединяет в себе возможности целого класса традиционных описаний процессов формирования пополнения в популяциях рыб.

Поскольку модель выведена из первых принципов, в рамках используемого подхода не остается места для феноменологии – все ее свойства, связанные с проявлением эффектов плотностной регуляции, находят должное биологическое обоснование. В этом смысле представляют отдельный интерес предельные формы зависимости “запас–пополнение” типа “хоккейной клюшки”, которые позволяют существенно облегчить процедуру оценивания параметров модели. Модель “хоккейной клюшки” ранее рассматривалась как упрощенный вариант функции пополнения Бивертона–Холта, однако результаты настоящего исследования указывают на существование ее аналога (28), соответствующего функции Рикера. Интересно отметить, что зависимость подобного типа ранее была описана Хорвудом (Horwood, 1995) при анализе данных о пополнении пикши Джорджес-банки. В модели Хорвуда предполагается, что смертность личинок в период формирования пополнения (до метаморфоза и перехода на донный тип питания) не зависит от плотности и остается постоянной, однако продолжительность этого периода определяется темпом роста молоди, который, в свою очередь, зависит от обилия кормовых организмов (копепод). По мере роста численности нерестового стада величина пополнения сначала линейно возрастает, а затем сменяется экспоненциальной убылью (рис. 2 в Horwood, 1995), поскольку при определенной плотности личинок вступают в силу эффекты пищевой конкуренции, и их рост замедляется. Положение точки излома на кривой пополнения определяется концентрацией кормовых организмов. Таким образом, выведенная теоретически зависимость (28) позволяет более точно описать наблюдаемые наборы эмпирических данных в области значений численности нерестового стада, при которых эффекты конкуренции становятся существенными в динамике пополнения.

В целом одно из главных преимуществ разработанной обобщенной модели состоит в том, что она позволяет проводить количественные сопоставления (на уровне значений параметров) качественно различных описаний процессов пополнения, основанных на альтернативных гипотезах о механизмах и факторах этих процессов. Таким образом, представлено полное описание класса зависимостей “запас–пополнение”, основанных на плотностной регуляции динамики популяций.

Работа выполнена при частичной финансовой поддержке РФФИ (грант № 17-04-00892).

Список литературы

  1. Бабаян В.К., 2000. Предосторожный подход к оценке общего допустимого улова. М.: Изд-во ВНИРО. 192 с.

  2. Бабаян В.К., Бобырев А.Е., Булгакова Т.И., Васильев Д.А., Ильин О.И. и др., 2018. Методические рекомендации по оценке запасов приоритетных видов водных биологических ресурсов. М.: Изд-во ВНИРО. 312 с.

  3. Булгакова Т.И., 1978. Модель популяции типа “запас–пополнение”, учитывающая влияние кормовой базы производителей на выживание молоди // Тр. ВНИРО. Т. 128. С. 16–32.

  4. Викторов Г.А., 1965. Колебания численности насекомых как регулируемый процесс // Журн. общ. биологии. Т. 26. № 1. С. 43–55.

  5. Гиляров А.М., 1990. Популяционная экология. М.: Изд-во МГУ. 191 с.

  6. Домбровский Ю.А., Обущенко Н.И., Сурков Ф.А., 1992. Изучение динамики популяции хамсы и тюльки на основе математической модели с учетом конкуренции, факторов среды и промыслового воздействия // Гидробиол. журн. Т. 28. № 1. С. 70–77.

  7. Зайцев В.Ф., Полянин А.Д., 2001. Справочник по обыкновенным дифференциальным уравнениям. М.: Физматлит. 576 с.

  8. Ито К., 1960. Вероятностные процессы. Вып. 1. М.: Изд-во иностранной литературы. 133 с.

  9. Ито К., 1963. Вероятностные процессы. Вып. 2. М.: Изд-во иностранной литературы. 135 с.

  10. Криксунов Е.А., Снетков М.А., 1985. Расширенная модель формирования пополнения нерестового стада рыб // Теория формирования численности и рационального использования стад промысловых рыб. М.: Наука. С. 46–55.

  11. Максименко В.П., Антонов Н.П., 2003. Количественные методы оценки рыбных запасов. Петропавловск-Камчатский: КамчатНИРО. 256 с.

  12. Меншуткин В.В., 1971. Математическое моделирование популяций и сообществ водных животных. Л.: Наука. 196 с.

  13. Михайлов А.И., 2019. Вопросы диагностики моделей динамики численности промысловых гидробионтов // Вопр. рыболовства. Т. 20. № 2. С. 183–191.

  14. Никольский Г.В., 1965. Теория динамики стада рыб. М.: Наука. 379 с.

  15. Переварюха А.Ю., 2008. Нелинейная динамическая модель системы запас–пополнение // Информационно-управляющие системы. № 2. С. 9–14.

  16. Фельдман М.Г., Шевляков Е.А., 2015. Выживаемость камчатской горбуши как результат совокупного воздействия плотностной регуляции и факторов внешней среды // Изв. ТИНРО. Т. 185. С. 88–114.

  17. Шварц С.С., 1969. Эволюционная экология животных // Тр. ин-та экологии растений и животных. Вып. 69. М.: Изд-во МГУ. 199 с.

  18. Agmour I., Achtaich N., Foutayeni Y.E., 2018. Stability analysis of a competing fish populations model with the presence of a predator // Int. J. Nonlinear Sci. V. 26. № 2. P. 108–121.

  19. Barrowman N. J., Myers R.A., 2000. Still more spawner-recruitment curves: The hockey stick and its generalizations // Can. J. Fish. Aquat. Sci. V. 57. P. 665–676.

  20. Beverton R.J.H., Holt S.J., 1957. On the Dynamics of Exploited Fish Populations // U.K. Min. Agr. Fish. Food Fish. Invest. Ser. 2. V. 19. 533 p.

  21. Bobyrev A.E., Kriksunov E.A., 1998. A spatially explicit individual-based model of larval fish feeding, growth and mortality // Russ. J. Aquat. Ecol. V. 7. P. 29–39.

  22. Bradford M.J., 1992. Precision of recruitment estimates from early life stages of marine fishes // Fish. Bull. V. 90. P. 439–453.

  23. Caputi N., 1988. Factors affecting the time series bias in stock recruitment relationships and the interaction between time series and measurement error bias // Can. J. Fish. Aquat. Sci. V. 45. P. 178–184.

  24. Chapman D.G., 1973. Spawner-recruit models and estimation of the level of maximum sustainable catch // Rapp. Proc.-Verb. Reun. Cons. Intern. Explor. Mer. V. 164. P. 325–332.

  25. Cushing D.H., 1973. Dependence of recruitment on parent stock // J. Fish. Res. Board Can. V. 30. P. 1965–1976.

  26. Cushing D.H., 1996. Towards a Science of Recruitment in Fish Populations // Excellence in Ecology. № 7. Nordbünte, Germany: Ecology Institute. 175 p.

  27. Deriso R.B., 1980. Harvesting strategies and parameter estimation for an age-structured model // Can. J. Fish Aquat. Sci. V. 37. P. 268–282.

  28. Draper D., 1995. Assessment and propagation of model uncertainty (with discussion) // J. Roy. Statist. Soc. Ser. B. V. 57. P. 45–97.

  29. Garrod D.J., 1983. On the variability of year-class strength // J. Cons. Perm. Int. Explor. Mer. V. 41. P. 63–66.

  30. Gomez Muñoz V.M., 1986. A general model of stock and recruitment // Inv. Pesq. V. 50. № 3. P. 421–435.

  31. Haeseker S.L., Peterman R.L., Su Z., Wood C.C., 2005. Retrospective evaluation of preseason forecasting models for sockeye and chum salmon // N. Am. J. Fish. Manag. V. 25. P. 897–918.

  32. Haeseker S.L., Peterman R.L., Su Z., Wood C.C., 2008. Retrospective evaluation of preseason forecasting models for pink salmon // N. Am. J. Fish. Manag. V. 28. P. 12–29.

  33. Hilborn R., Walters C.J., 1992. Quantitative Fisheries Stock Assessment: Choice, Dynamics and Uncertainty. N.Y.; L.: Chapman and Hall. 570 p.

  34. Horwood J., 1995. Plankton-generated chaos in the modeled dynamics of haddock // Phil. Trans. R. Soc. Lond. B. V. 350. № 1332. P. 109–118.

  35. Jiao Y., Reid K., Smith E., 2009. Model selection uncertainty and Bayesian model averaging in fisheries recruitment modeling // The Future of Fisheries Science in North America. Fish & Fisheries Series / Eds Beamish R.J., Rothschild B.J. Springer Science + Business Media B.V. P. 505–524.

  36. Larkin P.A., 1971. Simulation studies of the Adams River sockeye salmon, Oncorhynchus nerka // J. Fish. Res. Board Can. V. 28. P. 1493–1502.

  37. Michielsens C.G.J., McAllister M.K., 2004. A Bayesian hierarchical analysis of stock–recruit data: Quantifying structural and parameter uncertainties // Can. J. Fish. Aquat. Sci. V. 61. P. 1032–1047.

  38. Myers R.A., 1998. When do environment–recruitment correlations work? // Rev. Fish Biol. Fisher. V. 8. P. 285–305.

  39. Myers R.A., Bridson J., Barrowman N.J., 1995. Summary of worldwide spawner and recruitment data // Can. Tech. Rep. Fish. Aquat. Sci. V. 2024. 327 p.

  40. Needle C.L., 2002. Recruitment models: Diagnosis and prognosis // Rev. Fish Biol. Fisher. V. 11. P. 95–111.

  41. Peterman R.M., Pyper B.J., Grout J.A., 2000. Comparison of parameter estimation methods for detecting climate-induced changes in productivity of Pacific salmon (Onchorhynchus spp.) // Can. J. Fish. Aquat. Sci. V. 57. P. 181–191.

  42. Pitchford J.W., Brindley J., 2001. Prey patchiness, predator survival and fish recruitment // Bull. Math. Biol. V. 63. P. 527–546.

  43. Quinn T.J., II, Niebauer H.J., 1995. Relation of eastern Bering Sea walleye pollock recruitment to environmental and oceanographic variables // Can. Sp. Pub. Fish. Aquat. Sci. V. 121. P. 497–507.

  44. Ricker W.E., 1954. Stock and recruitment // J. Fish. Res. Board Can. V. 11. № 5. P. 559–623.

  45. Scheuring I., 2006. Nonlinear phenomena in ecology. Competition in mixing water and discrete state population dynamics. Budapest. 132 p.

  46. Schnute J., 1985. A general theory for analysis of catch and effort data // Can. J. Fish Aquat. Sci. V. 42. P. 414–429.

  47. Shepherd J.G., 1982. A versatile new stock-recruitment relationship for fisheries, and the construction of sustainable yield curves // J. Cons. Int. Explor. Mer. V. 40. № 1. P. 67–75.

  48. Shepherd J.G., Cushing D.H., 1980. A mechanism for density-dependent survival of larval fish as the basis of a stock-recruitment relationship // J. Cons. Int. Explor. Mer. V. 39. № 2. P. 160–167.

  49. Shirakihara K., Tanaka S., 1978. Two fish species competition model with nonlinear interactions and equilibrium catches // Res. Popul. Ecol. V. 20. P. 123–140.

  50. Tang Q., 1985. Modification of the Ricker stock recruitment model to account for environmentally induced variation in recruitment with particular reference to the blue crab fishery in Chesapeake Bay // Fish. Res. № 3. P. 13–21.

  51. Touzeau S., Gouzé J.-L., 1998. On the stock–recruitment relationships in fish population models // Environ. Model. Assess. V. 3. P. 87–93.

  52. Ward A.J.W., Webster M.M., Hart P.J.B., 2006. Intraspecific food competition in fishes // Fish Fish. V. 7. P. 231–261.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал общей биологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал