Журнал общей биологии, 2020, T. 81, № 3, стр. 174-193

ЗНАЧИМОСТЬ ПОРОГОВЫХ ЭФФЕКТОВ

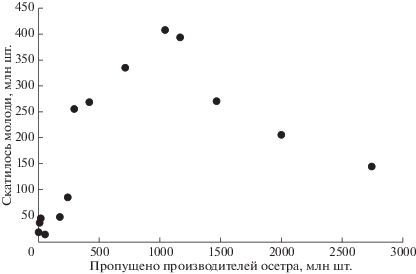
К пороговым эффектам относится резкое увеличение эффективности воспроизводства (величины пополнения относительно численности половозрелой части популяции) – часто наблюдаемое явление у инвазионных видов при эволюционной адаптации или ослаблении подавляющего их биотического фактора. Стремительное падение объемов восполнения рыбных запасов, которое в процентном отношении может быть непропорционально больше, чем сокращение общей численности популяции после периода действия на популяцию чрезмерной промысловой нагрузки, – альтернативный пороговый эффект. Влияние таких пороговых эффектов в настоящее время обсуждается для различных истощенных промыслом сообществ водных организмов (Hutchings, 2015). Подобный пороговый эффект можно увидеть на построенном нами графике “запас–пополнение” (рис. 1). На рисунке представлены обработанные нами методом скользящего среднего данные из публикаций (Иванов, Мажник, 1997; Иванов, 2000, 2001; Журавлева, Иванова, 2001, 2006, 2010) по изменению численности молоди русского осетра Acipenser gueldenstaedtii в Волге в зависимости от численности производителей, пропущенных из Каспийского моря для нереста в реку выше зоны промысла. На графике видно, как резко падает эффективность воспроизводства из-за сокращения родительского поголовья ниже 350 тыс. особей. Отметим, что коэффициент корреляции для анализируемых данных будет незначительный. Зависимость для воспроизводства осетра описывается куполообразной кривой с высокой горизонтальной асимптотой, тогда как обычно применяемый расчет корреляции может показать только близость к линейной зависимости. Популяции трех осетровых видов рыб Каспия поддерживались за счет выпуска заводской молоди, но при этом не учитывалась сложная внутрипопуляционная структура этих анадромных рыб с сезонными расами – обособленными нерестовыми группировками (Соловьева, Переварюха, 2016). Интересно, что качественные свойства зависимости запаса и пополнения для нерестящихся в Волге популяций всех трех осетровых видов рыб существенно различаются (Дубровская и др., 2017).

У многих совместно обитающих организмов отмечено действие положительного фактора агрегированной группы особей (Kanarek, Webb, 2013), который часто отождествляют с демографическим эффектом Олли (Stephens et al., 1999). В некоторых современных работах обсуждается эффект, называемый “selfish herd” – “эффект эгоистического стада” (Viscido et al., 2002). Сообща легче защищать потомство и избегать хищников. Социальным насекомым жизненно необходимо поддерживать большую численность коллектива. В современной работе Ньюфельда с соавт. (Neufeld et al., 2017) показана роль эффекта Олли на таком неожиданном примере, как прогнозирование скорости рецидива опухоли после ее резекции. Эффект Олли связывают с критической численностью, необходимой для продолжительного существования вида (Dennis, 1989). Пороговую численность L, такую, что при $N(t) < L$ популяция не выживает (Базыкин, Березовская, 1979), в явной форме включает следующее известное уравнение динамики популяции:

Существуют модели со сценарием вымирания популяции из-за проявления эффекта Олли без явного включения минимальной пороговой численности (Тютюнов и др., 2013). В современной работе (Дубровская, 2019) рассмотрена модификация данного уравнения для циклической активности насекомых с переменной амплитудой. В работе Гасконь и Липшас (Gascoigne, Lipcius, 2004) изучалось, как этот эффект проявляется в морских экосистемах, и указаны методологические проблемы при расчете уровня эксплуатации запасов для случая сильного действия пороговых эффектов. Бушар (Bouchard, 2018) на примере популяции лососевых рыб отмечал важность агрегации кладок икры, снижающей действие стохастических факторов на величину пополнения. В работе Морелла и Джеймса (Morrella, James, 2008) отмечалось, что успешность агрегации особей для воспроизводства находится в зависимости от экологической обстановки. Аналогично отмечалось, что эффект от агрегирования репродуктивной группы может поменять знак – превратиться в негативный фактор (Odum, Allee, 1954). Защищенность на ранних стадиях онтогенеза в группе повышается, но обеспеченность пищей не всегда. Конкуренция особей возрастает при ограниченности ресурсов, которые истощаются предыдущими многочисленными поколениями. Высокая выживаемость наблюдается только при наличии достаточных ресурсов и снижении внутривидового противоборства, включая каннибализм среди хищных рыб как важный фактор регуляции (Fromentin et al., 2001).

Метод описания пороговых явлений в эффективности воспроизводства, которые следуют из действия демографического эффекта Олли, будем строить на основе математического описания выживаемости поколений у популяций в раннем онтогенезе, что актуально и для рыб, и для насекомых. Эти эффекты обычно связаны с некоторыми критическими стадиями развития, специфическими для того или иного вида. У видов с большой плодовитостью колебания выживаемости на самых ранних стадиях на 3–4% значимы (Houde, 1987). Применительно к меняющимся факторам в эколого-физиологическом развитии наши вычислительные модели логично формализовать в форме логико-событийных структур, но основанных на решениях дифференциальных уравнений.

ИДЕЯ КОМБИНИРОВАННОГО ВРЕМЕНИ В БИОЛОГИЧЕСКИХ МОДЕЛЯХ

Если мы хотим достичь целенаправленного математического описания пороговых эффектов, которые связаны с переходами в критические состояния, то прежде необходимо обозначить их место на оси модельного времени. Такие моменты определят качественную смену внутреннего характера развития биологического процесса. Процессы убыли численности идут непрерывно, но объемы уловов или размеры пораженного вредителями леса фиксируются по окончании сезона. Временны́е шкалы индивидуального развития и смены стадий в раннем онтогенезе и отчетов промысловой статистики имеют разный порядок. Для построения модели, где будет важна стадийность развития, используем форму времени и с дискретной, и с непрерывной составляющей. Применим упорядоченное кадрирование непрерывных отрезков времени. Комбинированное время формализуем в виде мультимножества кортежей из упорядоченных элементов:

где n – число кадров непрерывного времени в модельном эксперименте, i – порядковый номер для внутрикадровых событий при объединении субинтервалов. В сценариях удобно рассматривать дискретные изменения траектории. В кадрированном формате вводим компоненту событийности для реализации изменений непрерывного процесса. Форма времени с непрерывной и дискретной компонентой оставляет “щели” вне кадров для перехода к расчету развития следующего смежного поколения – границы $\partial L$ слева и $\partial R$ справа от непрерывного кадра, разбитого внутри на три субинтервала: $[0,{{t}_{1}}),[{{t}_{1}},{{t}_{2}}),[{{t}_{2}},T]$. Такое разделение кадра $[0,\;T]$ актуально для видов с тремя стадиями и двумя вычисляемыми модельными метаморфозами в моменты $\{ {{t}_{1}},{{t}_{2}}\} $. Максимальное число событий ${{i}_{{\max }}}$ можно увеличить, например, если нужно рассмотреть искусственное вмешательство в процесс воспроизводства рыб (выпуск молоди), но делить кадр на слишком большое количество субинтервалов не имеет смысла. Только дискретные перемены в моменты смены кадров будут видны внешнему наблюдателю.

Первая идея нашего метода состоит в том, что модель популяционного процесса формируется с помощью динамического переопределения системы. Осуществим перестроения в выделенных условиями точках системных событий ${{t}_{i}}$. В задачах о сложной динамике рыб или насекомых биологический аспект позволяет рассматривать последствия изменений в их жизненном цикле как фактор проявления пороговой нелинейной зависимости в эффективности воспроизводства. Пороговые эффекты при формировании нового поколения отражаются на кривой “запас–пополнение”, которая приобретает дополнительные экстремумы. Наличие дополнительного локального экстремума меняет поведение траектории модели при итерациях функций с несколькими экстремумами.

Вторая идея метода построения модели – по предикатам, не обязательно связанным с модельным временем, устанавливать события (например, смены стадий онтогенеза), за которыми следуют изменения формы правой части уравнений, описывающих текущую численность поколения. N(0) – максимальная численность поколения.

ПЕРЕОПРЕДЕЛЯЕМАЯ ВЫЧИСЛИТЕЛЬНАЯ СТРУКТУРА

Для построения вычислительной модели с переходами в раннем онтогенезе мы предлагаем предикативно переопределяемую вычислительную структуру. Определим три последовательных режима изменения состояния для поколения от N(0) до N(T). Оптимально рассмотрение в вычислительных моделях трех эколого-физиологических стадий. Столько их существует у насекомых с неполным циклом развития. Физиологи выделяют у рыб больше стадий в личиночном развитии, но дальнейшее усложнение не прибавит модели новых возможностей, только трудности при согласовании параметров уравнений и условий завершения расчетной активности для всех форм правых частей.

Система описывается дифференциальным уравнением с набором из трех возможных форм темпов убыли и дополнительно множеством предикатов для моментов смены режима расчетов правой части. Представим гибридную модель с неспецифичными обобщенными тремя стадиями онтогенеза на объединенном интервале:

с включением запаздывания $\eta < \tau $ для старшей стадии, которое предназначено для распространенной ситуации регуляции с последействием, когда на текущую смертность влияет исчерпание жизненных ресурсов особями в некоторый момент $t - \eta $ в прошлом:

В системе (1) различно трактуемые мгновенные коэффициенты ювенильной смертности введены в зависимость от плотности исходной генерации; параметры ${{\alpha }_{1}},{{\alpha }_{2}},{{\alpha }_{3}}$ учитывают компенсационную смертность, убывающую по мере прохождения стадий; $\beta $ – депенсационный коэффициент смертности (depensatory mortality), важный для многих популяций рыб (Irwin et al., 2009). Разделение факторов смертности поколения рыб по отношению к его плотности на три типа: компенсационную, депенсационную, независимую (в оригинале экстрапенсационную, “extrapensatory mortality”) – введено в работе Нива (Neave, 1951). Параметр $\bar {w}$ – пороговый уровень показателя размерного развития для перехода из стадии в стадию. В работе А.В. Русакова с соавт. (2016) значения пороговых w для возрастных стадий определены на примере плотвы. Согласно работе Рикера о связи исходного запаса и величины пополнения (Ricker, 1964), время $[0,\;T]$ – интервал уязвимости у формирующегося поколения до выхода из-под действия факторов ювенильной смертности – одно из основных понятий разработанной Рикером теории пополнения. Количество половозрелых особей – “запаса” – традиционно в моделях пополнения обозначают через S (Криксунов, 1995). Соответственно, начальное условие $N(0) = \lambda S$ для расчета задачи Коши для первой стадии развития определяется средней индивидуальной плодовитостью λ. Соотношение полов примем 1 : 1.

Формой реализации модели в вычислительной среде служит особый ориентированный граф – автомат со смешанным временем “hybrid time structure” (Perevaryukha, 2011). Алгоритм автомата выполняет трансформации правой части от входного состояния. Для каждой смежной формы правой части рассчитываются сопряженные начальные условия $N{{(0)}_{i}}$ внутренним функционалом программного средства расчетов. В нашем методе перестройки будут между режимами изменения состояния. Алгоритм с непрерывными кадрами времени и выделенными по расчетам уравнений событиями отличается от методики организации дискретно-событийных моделей (Skobelev V.V., Skobelev V.G., 2018), где переходы происходят только между заданным набором заранее фиксированных состояний. Автоматная структура подразумевает использование логики для переходов.

Перестроения правой части уравнения (1) происходят предикативно. Либо по отсчетам кадров времени – назовем такие переходы таймированными (“time-forced”), – либо будут вызваны реляционными (“relation-forced”) переходами. Во втором случае смена формы уравнения происходит по вычислению определенных соотношений среди внутренних модельных переменных, которые связаны с расчетами вспомогательных уравнений модели. Дополнительное условие предиката с $\tau + 7\eta $ указано тут как предельное время пребывания особей данного поколения на второй стадии развития. Длительность первой стадии $\tau $ примем строго фиксированной и независимой от иных условий.

Расчет сокращения численности необходимо дополнить и совместить с вычислением других биологических показателей. Расширение нужно, чтобы иметь возможность проводить сравнения в наборе предикатов. Важнейшим фактором является скорость роста для средней размерно-весовой группы особей поколения. От нее зависят пищевые потребности и способность рыб избегать хищников. Использовать скорость роста в моделях пополнения как отдельный показатель развития молоди рыб, но взаимосвязанный с динамикой численности $w{\kern 1pt} '(t) = v({{N}^{{ - 1}}}(t))$, предложено Е.А. Криксуновым и М.А. Снетковым (Kriksunov, Snetkov, 1980) и именно в форме дифференциального уравнения убыли. На старших стадиях показатель развития замедляет темпы убыли поколения. Показатель скорости роста может выступать и в роли предиката завершения периода уязвимости.

Базовую гибридную структуру модели (1) рассчитываем численно во взаимосвязи со вспомогательным показателем размерного развития, $w(t)$, поколения. Второе уравнение запишем так:

где ρ отражает доступность пищевых ресурсов. Фиксированный показатель ρ можно применять в большинстве случаев, когда скорость восполнения кормовых объектов велика по сравнению с изменениями N(t); δ – поправочный коэффициент. Скорость роста у многих рыб связана с плотностью (Irwin et al., 2009) и конкуренцией, поэтому в уравнении (2) выбрана обратная дробно-степенная зависимость $w{\kern 1pt} '(t) = v({{N}^{{ - 2/3}}}(t))$. Можно моделировать скорость роста организмов при большой роли плотности поколения с использованием стандартного весового показателя и расчета отклонений от этой весовой нормы.

Мультистадийный подход к описанию кривых “запас–пополнение” предлагался Поликом (Paulik, 1973) как функциональная композиция $R = {{f}_{1}}({{f}_{2}}({{f}_{3}}(S)))$ унимодальных зависимостей – функций Рикера с разными значениями параметров. В таком случае анализировать приходится функциональные итерации уже со многими экстремумами, и данный способ становится некорректным из-за их математических свойств. Циклические точки итераций ${{x}_{{n + 1}}} = f({{x}_{n}}),$ ${{x}_{0}} > 0$ – это стационарные точки у старших итераций, например $x_{2}^{*} = f(f(x_{2}^{*}))$, поэтому у таких сложных композиций будут возникать сосуществующие альтернативные циклы различных периодов. Притяжение траектории к разным циклическим аттракторам будет изменяться от незначительного сдвига начальной точки, ${{x}_{0}} \pm \varepsilon $, поэтому целесообразно развивать метод Е.А. Криксунова и М.А. Снеткова с непрерывным описанием убыли рыб от исходного количества икры $N(0)$.

Биологическое обоснование для вычисления пополнения в форме “оператора эволюции” для анализа итераций ${{R}_{{n + 1}}} = \varphi ({{R}_{n}})$ основано на известной теории Рикера для пополнения промысловых запасов рыб и ее современном развитии (Subbey et al., 2014; Perevaryukha, 2017 в том числе), с использованием стохастической компоненты, как у А.И. Михайлова с соавт. (2019).

Для многих видов насекомых и рыб актуально рассчитывать численно именно колебания ювенильной выживаемости. В результате численного решения задачи Коши для всех значимых $N(0)$ из ограниченного подмножества натуральных чисел получим функциональную зависимость $\varphi (N(0))$ для расчета выживаемости $N(0) \to N(T)$ от размера, $N(0) = \lambda S$, начальной группы (яиц или икры).

Представление модели с предикатами и последовательно сменяемыми формами правой части обладает значительной вариативностью при выборе формы и количества вспомогательных уравнений. В дополнительных уравнениях описываются факторы опосредованной регуляции численности итогового половозрелого поколения, тогда как в базовой модели – непосредственные коэффициенты смертности.

СПОСОБ РАСШИРЕНИЯ БАЗОВОЙ МОДЕЛИ

Хорошую биологическую модель можно совершенствовать, дополняя перечень ее факторов. В расширении модели (1)–(2) показатель в числителе (2) можно задать динамически как $\rho (t)$ – третьим уравнением. Если полагать, что кормовая база пребывает в стационарном состоянии, $\rho (t) \to K$, то в зависимости от удобства настройки уравнения кибернетической саморегуляции на интервале $[0,T]$, можно применить уравнение для $\rho (t)$ c самой популярной квадратичной формой регуляции, выбрав начальные условия $\rho (0) = {K \mathord{\left/ {\vphantom {K 2}} \right. \kern-0em} 2}$, где K достаточно велико:

Здесь r – репродуктивный параметр, сравнимый с коэффициентом потребления корма $\varsigma $; K – равновесное значение численности, означающее емкость экологической ниши для данного вида.

Если в моделируемой ситуации наблюдаются колебания в обилии кормовых ресурсов, вызванные климатическими или сезонными изменениями, то для моделирования можно использовать уравнение с запаздыванием: $\dot {\rho } = rf(N(t - \xi ))$, где при увеличении $r\xi $ наблюдаем обычную бифуркацию Андронова–Хопфа с возникновением орбитально устойчивого цикла $\rho {\text{*}}(t;r\xi )$, амплитуда которого зависит от $r\xi $. Можно ввести запаздывание непосредственно в уравнение (3а):

– или использовать вместо квадратичной более сложную функцию саморегуляции, такую как

Запаздывание $\xi $ в регуляции даст возможность описать невынужденные колебания обилия ресурсов $\rho (t)$. Тогда зависимость $\varphi (S)$ для системы запаса и пополнения перестанет быть гладкой кривой. Очевидные варианты уравнений с запаздыванием при численном моделировании демонстрируют существенный недостаток. При необходимости увеличить период между максимумами колебаний с ростом $r\xi $ происходит быстрое увеличение амплитуды цикла $\rho {\text{*}}(t;r\xi )$. Минимумы становятся чрезвычайно малыми: $\mathop {\lim }\limits_{\xi r \to \infty } \min \rho {\text{*}}(t) = 0$. Околонулевые значения $\rho $ не соотносятся с реальностью и недопустимы для расчетов по уравнению (2): возникнет программная ошибка расчетов.

Предложим специальное уравнение для колебательного варианта модели с учетом истощения пищевых ресурсов:

После бифуркации рождения цикла получим релаксационные колебания – пики значительной амплитуды негармонической формы, начинающиеся от ненулевого порогового значения $N(t) \approx K$ около потерявшего устойчивость равновесия. Вариант (3b) без неприемлемых глубоких минимумов флуктуаций будет актуален и для ряда задач с сезонной изменчивостью, когда несколько поколений появляются в разных условиях.

УЧЕТ ЭКОЛОГИЧЕСКОЙ СПЕЦИФИЧНОСТИ В МЕТОДЕ МОДЕЛИРОВАНИЯ

Метод, который позволяет легко расширять базовую модель как блочный конструктор, делает идею описания выживаемости поколений значимой для многих видов с большой плодовитостью $\lambda $, особенно для насекомых-вредителей, известных стремительными переходами к экстремальной динамике. Влияние на выживаемость фактора плотности скопления личинок и темпов их роста установлено экспериментально для некоторых насекомых, например для опасного короеда Dendroctonus micans (Storer et al., 1997). Ранее явные закономерности в регуляции численности на преимагинальных стадиях в зависимости от плотности поколения установлены для жука Ips typographus (Огибин, 1974).

Для анализа нашим методом подходят локальные вспышки малоподвижных насекомых с неполным циклом превращений, таких как тли и псиллиды. Численность многих вредных насекомых фитофагов регулируют мелкие осы-паразитоиды. Паразитоиды могут использоваться для целенаправленного активного подавления фитофагов (Morozov et al., 2003). Уровень воздействия врагов мелких насекомых обусловлен скученностью самых доступных для атаки жертв. Наездники атакуют обычно одну из стадий развития, чаще всего яйца (Frolov, 2015). Несколько видов наездников-яйцеедов из сем. Trichogrammatidae успешно разводят в лабораториях и выпускают для борьбы с яйцами вредителей посевов (Smith, 1996). Реакция паразитов обусловлена наличием скопления доступных жертв, а именно величиной N(0). Давление наездников на начальную численность бабочек обусловит специфическую модификацию первой формы уравнения в базовой модели (1):

Паразитоиды не атакуют другие стадии, потому выживаемость старших стадий немного увеличится: ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\alpha } }_{2}} < {{\alpha }_{2}},$${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\alpha } }_{3}} < {{\alpha }_{3}}$. Так мы учтем на первой модельной стадии особенности регуляции выживаемости для насекомых-фитофагов в агроценозах под специально созданным биогенным воздействием, где вызывающие смертность яиц факторы отличаются от трофического давления на личинок рыб или лесных насекомых.

ОБЩАЯ ИДЕЯ ПРИМЕНЕНИЯ ФУНКЦИЙ-ТРИГГЕРОВ

В зависимости, полученные из решения систем уравнений на интервале уязвимости, следует добавить возможности для описания резких изменений в поведении траектории, избегая скачкообразных изменений во внутренних параметрах системы. Другая методическая новизна нашего подхода – внедрение функций-триггеров в базовую, предикативно переопределяемую динамическую систему – фактически динамических коэффициентов для итераций, ${{\varphi }^{t}}({{x}_{0}};\Psi ),$ $\Psi \ne const$, но только с ограниченной областью воздействия на допустимом множестве значений аргумента. Функции будут сохранять свое значение на всем объединенном интервале непрерывного модельного времени. Менять значения функции будем при смене кадра. Функции необходимо подбирать отдельно из условий каждой обсуждаемой экологической проблемы, общим полагается только метод внедрения функций в уравнения для стадий развития.

В нашем уравнении убыли численности поколения два члена, которые описывают смертность: зависящий от внутривидового взаимодействия квадратично, $\alpha {{N}^{2}},$ и линейный, $\beta N$. Сомножитель $\alpha w$ учитывает быстрейшее исчерпание необходимых для развития ресурсов по мере повышения биомассы поколения. Актуально в некоторых случаях учитывать потери воспроизводства до оплодотворения. У рыб при низкой плотности зашедших на нерест половозрелых особей будет увеличиваться количество неоплодотворенной икры. Эффект потерь репродуктивной активности рыб реализован в модели функцией $\Psi $, зависящей от величины родительской популяции S, которая влияет на расчет модели (1)–(2) через начальные условия N(0). Значения ${\rm E}(\Psi )$, которые может принимать функция, ограничены диапазоном: ${\rm E}(\Psi ) = [2,1)$. Биологическая причина проявления эффекта, описываемого функцией $\Psi (S)$, – это снижение вероятности образования нерестовых пар на большом пространстве нерестовой акватории при чрезмерном изъятии. Именно данный пороговый эффект мы учтем, дополняя расчеты членом $\Psi \beta N$, куда включен триггерный сомножитель. Область значений функции ${\rm E}(\Psi )$ справа (или слева) должна иметь единичный предел:

где параметр $\sigma < 1$ отражает степень выраженности порогового эффекта. Когда численность запаса велика, значение функции-триггера не должно отличаться от единичного. При добавлении $\Psi $ у итераций возникнет критическое значение численности запаса, но в форме плавающего порогового равновесия $R_{1}^{*} = \varphi (R_{1}^{*})$ у кривой зависимости $\varphi (S)$. В модификации (3) мы опишем действие эффекта Олли на первой стадии развития более гибко, чем в дифференциальном уравнении А.Д. Базыкина (1985).

ОБЩНОСТЬ И РАЗНООБРАЗИЕ ДИНАМИКИ ИТЕРАЦИЙ

Достаточная сложность и вычислительные затраты метода моделирования окупаются интересными описательными возможностями и вариативностью поведения модели даже без перенастройки параметров. Мы можем получить как классическую куполообразную форму зависимости “запас–пополнение” с ненулевой горизонтальной асимптотой, так и $\varphi (S)$ c нужным количеством экстремумов. По сравнению с применявшимися ранее для расчетов нелинейными итерационными моделями возникают оригинальные свойства динамики, актуальные непосредственно для рассматриваемых проблем.

В разных моделях на основе функциональных итераций часто наблюдается хаотическое поведение. Хаотизацию траектории через бифуркации удвоения периода можно получить в итерациях известных в биологии зависимостей, таких как ${{x}_{{n + 1}}} = {\mathbf{a}}{{x}_{n}}{{e}^{{ - b{{x}_{n}}}}},$ ${{e}^{2}} < {\mathbf{a}} < \pi {{e}^{2}}$ – модель Рикера (Ricker, 1954), или ${{x}_{{n + 1}}} = {{{{a{{x}_{n}}} \mathord{\left/ {\vphantom {{a{{x}_{n}}} {1 + \left( {{{{{x}_{n}}} \mathord{\left/ {\vphantom {{{{x}_{n}}} B}} \right. \kern-0em} B}} \right)}}} \right. \kern-0em} {1 + \left( {{{{{x}_{n}}} \mathord{\left/ {\vphantom {{{{x}_{n}}} B}} \right. \kern-0em} B}} \right)}}}^{{\mathbf{u}}}},$ ${\mathbf{u}} > 2,\,\,a > 0$ – модель Шепарда (Shepherd, 1982). Изменение поведения происходит при увеличении параметров, набранных жирным шрифтом. Бифуркационные параметры в этих двух моделях имеют противоположный смысл: репродуктивный потенциал a и фактор сопротивления среды u. Метаморфозы у этих итераций, где возможен бесконечный каскад удвоения периода цикла, $p = {{2}^{{i + 1}}},$ $i \to \infty $, происходят одинаково, что, вероятно, сделает эти модели взаимно противоречивыми при интерпретации результатов их применения. Путь к хаосу универсален вплоть до констант сходимости (Вул и др., 1984) для класса таких функций с экстремумом, где главным критерием бесконечного числа бифуркаций удвоения выступает отрицательное значение производной Шварца – исключительно математический показатель. Если пользоваться моделью Рикера только до $\max \varphi (S)$, а после максимума заменять постоянной величиной $S > {{S}_{{\max }}},$ $f(R) = {\text{const}}$, как предлагал еще В.В. Меншуткин (1971), то никаких перестроений фазового портрета и изменений поведения траектории наблюдаться не будет.

Из критерия устойчивости циклов итераций следует, что в модели Рикера с эксплуатацией ${{x}_{{n + 1}}} = {\mathbf{a}}{{x}_{n}}{{e}^{{ - b{{x}_{n}}}}} - q{{x}_{n}}$ доля изъятия q – тоже бифуркационный параметр, но увеличение q вызывает образование цикла периода$p = {{2}^{{i - 1}}}$, бифуркацию “ополовинивания” периода (period-halving bifurcation). Универсальность поведения итераций означает, что интервалы между соседними бифуркационными значениями у параметров сокращаются для разных моделей с одинаковой скоростью (Ланда, 2013).

Один бифуркационный параметр в модели – это тривиальный случай. Если нелинейная модель многокомпонентная и воспроизводит колебания составляющих трофических цепей, как в работе А.Е. Бобыpева c соавт. (2013), то в таких сложных системах, как правило, будет несколько конкурирующих бифуркационных величин, которые составят n-мерное пространство факторов изменений поведения траектории.

Следствием является тот факт, что если локальная биосистема наблюдается нами только в асимптотически устойчивом состоянии, то мы не можем установить вид функциональной зависимости, которой подчиняется ее эволюция. Аттракторы нельзя различить по графикам данных. В различных функциональных итерациях притягивающие множества эквивалентны. Поэтому нам интересны данные о популяциях вне равновесия, прошедших через критические значения и перешедших в состояние деградации.

Когда стационарная точка $x* = \varphi (x*)$ унимодальной функции теряет устойчивость, возникает цикл из двух стационарных точек $x_{1}^{*},x_{2}^{*}$. Это стационарные точки второй итерации $x_{2}^{*} = \varphi (\varphi (x_{2}^{*}))$. К этому циклу притягиваются точки, кроме самой неустойчивой стационарной $x{\text{*}}$ и тех точек, которые под действием итерации отображаются именно в $x{\text{*}}$. Попадание ${{x}_{0}}$ слева или справа относительно $x{\text{*}}$ изменяет порядок обхода цикла. Циклы дискретных итераций отличаются не только длиной периода, но и порядком обхода циклических точек. Точки циклов периодов 2ⁱ возникают симметрично относительно $x{\text{*}}$. Отрицательность производной Шварца означает, что возникновение новых циклов возможно до бесконечности. У многих мелких млекопитающих известны циклические изменения численности с периодом 3–5 сезонов, но это последовательные циклические перестановки $x_{1}^{*} < x_{2}^{*} < x_{3}^{*}...$ c явным пиком в конце периода. Порядок сосуществования четных и нечетных циклов в ходе итераций определяет теорема А.Н. Шарковского (1965).

Потеря устойчивости и удвоение циклов ${{2}^{{i + 1}}},\;i \to \infty $ в сценарии Фейгенбаума происходит бесконечное количество раз при конечном увеличении параметра. В результате в точке накопления каскада бифуркаций существует бесконечное количество циклических траекторий всех периодов, которые все неустойчивы. Эти неустойчивые точки циклов разделяют всю область притяжения на все уменьшающиеся интервалы вплоть до формирования нигде не плотного канторовского множества, не имеющего ни внутренних, ни изолированных точек. Так как в любой ε-окрестности точки аттрактора есть точки, не принадлежащие его области притяжения, это вызывает наблюдаемое экспоненциальное разбегание траекторий. Теорема Огнева–Мисюревича дает нам в явном виде условия, при которых в итерациях возникает хаотизация (Синай, 1995). Введение дискретных единиц измерения в модель исключило бы хаотизацию поведения через фрактализацию аттрактора. Хаотический режим в узких параметрических интервалах значения a или u моделей Рикера и Шепарда прерывается периодическим. Мы не считаем свойство хаотизации, связанное с аттрактором в форме дисконтинуума (фрактального объекта), интересным для наших задач. Существуют альтернативные типы апериодического нерегулярного движения, как и различные определения самого понятия динамического хаоса.

ОГРАНИЧЕНИЯ И ВОЗМОЖНОСТИ НОВОЙ МОДЕЛИ

Рассмотрим одну из областей применения модели с триггерным дополнением. Для всех рассматриваемых нами вариантов зависимости мы получим разделение фазового портрета неустойчивой точкой-репеллером $R_{1}^{*}$. Численное решение $R = N(T)$ итоговой модели (1)–(3) мы используем как оператор эволюции функциональных итераций ${{R}_{{n + 1}}} = \varphi ({{R}_{n}}) - {{q}_{n}}{{R}_{n}}$, ${{R}_{0}} > R_{1}^{*}$, где $q \in [0,1)$ – доля промыслового изъятия. При регулируемом промысле доля q_n рассчитывается на каждый сезон n. Изменения внешнего воздействия будем варьировать по заложенному в вычислительную среду алгоритму. Правила алгоритма изменения q_n составят сценарий стратегии эксплуатации запаса с начальным состоянием ${{R}_{0}}$.

В интересующем нас варианте зависимость $\varphi (R)$ будет обладать более чем одним максимумом, а итерации получат две области притяжения альтернативных аттракторов. Таким образом, у нашей неунимодальной функции уже не выполняются критерии теоремы Зингера (Singer, 1978) для реализации упомянутого выше сценария перехода к хаосу через каскад удвоения периода цикла по теории Фейгенбаума (Feigenbaum, 1980).

Модель обладает возможностью образования хаотического репеллера при изменении положения экстремумов зависимости $\varphi (\lambda S)$, но это иной тип переходного хаотического движения, нежели в аттракторе канторовской формы. Для функциональных итераций аттракторов возможно только три топологических типа: равновесие (цикл конечного периода), аттрактор в форме совершенного канторовского множества, интервальный аттрактор. В последнем случае аттрактор образуется из объединения бесконечного количества отрезков, которые останутся, если исключить из ограниченного интервала множество прообразов точек-репеллеров или неустойчивых циклических траекторий.

Для итераций возможны три типа бифуркаций – метаморфозов стационарных точек, число $\Theta $ которых (включая точку $\varphi (0) = 0$) есть важная характеристика. Бифуркации бывают прямыми, такими как появление цикла ${{2}^{{i + 1}}}$, возникновение пары стационарных точек. Возникают и обратные метаморфозы, такие как образование цикла периода $p = {{2}^{{i - 1}}}$ или редукция двух точек $x_{1}^{*},x_{2}^{*}$ в одну неустойчивую $x* = \varphi (x*)$ и ее исчезновение. Таковы ограниченные возможности из арсенала дискретной динамики, которыми мы можем воспользоваться для описания изменений в различных популяционных сценариях.

ЯВЛЕНИЕ СТРЕМИТЕЛЬНОЙ ДЕГРАДАЦИИ БИОРЕСУРСОВ

Коллапс запасов атлантической трески Gadus morhua в Северо-Западной Атлантике в 1992 г. считается самым масштабным по экономическим последствиям неожиданным крахом рыболовства (Ruitenbeek, 1996). Резкий коллапс отличается от постепенного и монотонного истощения запасов – распространенного явления перелова.

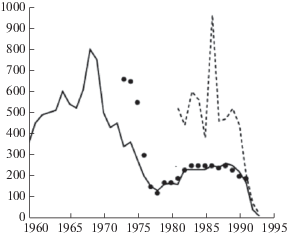
На графике коллапса (рис. 2) сплошной линией показана динамика уловов, а точками размеры квоты, предназначенной для вылова, в тысячах тонн (Roughgarden, Smith, 1996). Пунктиром обозначена рассчитанная предполагаемая величина запасов трески. Оценка численности, как выяснилось только после коллапса 1992 г., была излишне оптимистична, иначе столь внезапное исчезновение популяции объяснить невозможно. Оценка запасов по когортным моделям была завышена (Myers, Cadigan, 1995). Влияние негативных климатических факторов среды на выживаемость молоди трески опровергнуто в работе Хатчингса и Майерса (Hutchings, Myers, 1994). Отметим явную флуктуационную форму динамики. Резких падений уловов трески у берегов Канады без их восстановления было два. Коллапсом считается только второй, хотя логика подсказывает нам, что первое падение уловов было важнее. Первый кризис запустил деструктивные внутрипопуляционные процессы, которые не могли быть вовремя замечены. Потому в вычислительном сценарии коллапса у траектории тоже должно быть две трансформации.

После первого падения уловов в 1970-х годах рыбаки не могли несколько лет освоить выделенную им квоту. Потом уловы пришли к консенсусу с оценками квоты. Все 1980-е годы квота успешно осваивалась, почти не менялась, так как не было видимых причин для упреждающего регулирования и более жесткого квотирования. В это время вылавливали не затронутые первым переловом поколения трески. Доля изъятия превышала 0.45. Внезапно все обрушилось. До какой степени глубоким является кризис осознали не сразу. Изначальный мораторий был введен на 18 месяцев. Рафгарден и Смит (Roughgarden, Smith, 1996) с оптимизмом прогнозировали в 1996 г. восстановление промысла трески у берегов Ньюфаундленда через 9 лет, но возобновления промысла не произошло. Никто из авторитетных экспертов не смог предсказать четвертьвековую деградацию ценной локальной популяции. Треска Gadus morhua – крупный хищник-каннибал с длинным жизненным циклом, и промысел использовал несколько поколений. Каннибализм у трески – фактор, определяющий плотностно-зависимую смертность и большую продолжительность периода уязвимости (Anderson, Gregory, 2000). Коллапсы ранее случались с тихоокеанской сельдью и анчоусом Engraulis ringens у берегов Перу – короткоцикловыми рыбами, и эти популяции восстанавливались после снятия давления промысла (Bailey, 2011). Отличие ситуации с переловом трески от состояния осетровых рыб Волги в том, что треска Северной Атлантики постепенно восстановит свою численность, а трем видам осетровых рыб грозит вымирание (Вилкова, Глубоковский, 2018).

Как отмечают другие авторы, помимо сокращения численности произошли изменения в размерно-возрастной структуре популяции трески. Увеличился темп полового созревания, сократился жизненный цикл, рыбы стали тугорослыми, но увеличилась их естественная смертность (Olsen et al., 2004). Подобные сдвиги характеристик описываются именно в коэффициентах вспомогательных уравнений нашей вычислительной структуры.

МОДЕЛЬНЫЙ СЦЕНАРИЙ КОЛЛАПСА БИОРЕСУРСОВ

Устойчивость стационарного состояния на модельной кривой “запас–пополнение” определяет угол наклона касательной в этой точке. Если выполняется условие $\left| {\varphi {\kern 1pt} '(R_{i}^{*})} \right| > 1$, то точка будет неустойчивой – репеллером. При $\varphi {\kern 1pt} '(R_{i}^{*}) = - 1$ произойдет бифуркация появления цикла периода ${{2}^{{i + 1}}}$, при выполнении $\varphi {\kern 1pt} '(R_{i}^{*}) = 1$ – касательная бифуркация с появлением одной точки-равновесия. За данным простым критерием устойчивости равновесия – превышение угла наклона касательной ${\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$ в точке пересечения кривой с биссектрисой координатного угла – стоит сложная математика, теорема о топологической эквивалентности линейных гиперболических систем и теорема Лагранжа.

Для математической реализации подобного сценария коллапса из двух резких сокращений численности и режима флуктуаций между ними мы предлагаем сценарий с двумя метаморфозами в динамике итераций зависимости c четырьмя нетривиальными стационарными состояниями $R_{i}^{*} = \varphi (R_{i}^{*})$: $R_{1}^{*} < R_{2}^{*} < R_{3}^{*} < R_{4}^{*}$. Устойчиво $R_{4}^{*}$, и в циклы ${{2}^{i}}$ это равновесие не переходит. Тривиальная точка начала координат $\varphi (0) = 0$ тоже устойчива.

Первый метаморфоз, который реализуем, – обратная касательная бифуркация с редукцией притягивающего состояния равновесия вместе с $R_{3}^{*}$. Второе качественное перестроение – граничный кризис интервального аттрактора, который станет притягивающим после редукции устойчивой точки. Для такого перестроения фазового портрета необходимо помимо трех неустойчивых стационарных точек, разделенных экстремумами, еще сохранение устойчивости нулевого равновесия. Система уравнений дает возможность масштабировать зависимость по оси S и целенаправленно изменять положения экстремумов $\varphi (\lambda S)$. Трансформации зависимости показаны на рис. 3. Четыре пересечения кривой с биссектрисой координатного угла, показанной нами как график 2 на рис. 3, сохраняются только в отсутствие внешнего воздействия. Функция $\Psi $ не меняет относительное положение устойчивого равновесия большой численности $R_{4}^{*}$, но может действовать на положение $\min \varphi (\lambda S)$ относительно неустойчивого репеллера $R_{2}^{*}$ (рис. 3б), изъятие оказывает масштабирующее воздействие на функцию по оси ординат.

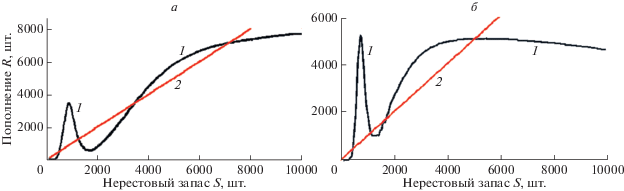
Пусть в базовом варианте зависимости модельная кривая в окрестности максимума немного превосходит третье равновесие (рис. 3а), $\varphi (max\varphi (N(0)) \pm \varepsilon ) > R_{3}^{*}$, и если исходное состояние популяции ${{R}_{0}}$ соответствует диапазону ${{R}_{0}} \in (R_{1}^{*},R_{3}^{*}) \cap \{ {{\varphi }^{{ - n}}}(R_{2}^{*})\} $, то через ряд апериодических флуктуаций достигается состояние $R_{4}^{*}$ высокой стабильной численности. Здесь $\{ {{\varphi }^{{ - n}}}(R_{2}^{*})\} $ – множество прообразов точек репеллера. Все точки интервала, которые отображаются в неустойчивые стационарные точки или неустойчивые циклы, никогда не притягиваются к аттракторам. Неустойчивая точка-репеллер $R_{1}^{*}$ может не иметь ни одного прямого прообраза, но может получить два прообраза справа. Соответственно, область притяжения $\Omega $ для точечного аттрактора $R_{4}^{*}$, ${{R}_{0}} \ne R_{4}^{*},$ ${{R}_{0}} \in \Omega ,$ $\mathop {\lim }\limits_{n \to \infty } {{\varphi }^{n}}({{R}_{0}}) = R_{4}^{*}$, не включает все прообразы неустойчивых точек: $\Omega \cap \left\{ {\{ {{\varphi }^{{ - n}}}(R_{2}^{*})\} \cup \{ {{\varphi }^{{ - n}}}(R_{3}^{*})\} \cup } \right.$ $\left. { \cup \,\{ {{\varphi }^{{ - n}}}(R_{1}^{*})\} } \right\} = \emptyset $.

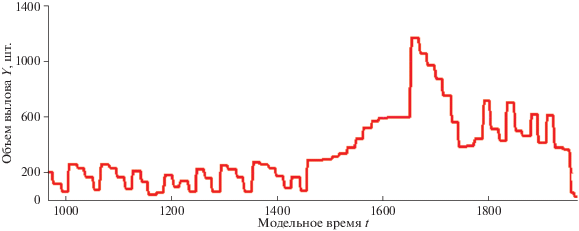
Допустим, в вычислительном эксперименте промысловая популяция восстановилась после нестабильного режима до устойчивого равновесия и экологического оптимума. Уловы $Y = {{R}_{n}}{{q}_{n}}$ пошли вверх, после чего принимается решение об увеличении годовой квоты до ${{\bar {q}}_{n}}$. Уловы на первом этапе демонстрируют исторические максимумы, но затем довольно очевидно снижаются, успешно проходят локальный минимум, не попадая сразу в окрестность критического состояния $R_{1}^{*}$. Теперь $R_{3}^{*}$ слилось с $R_{4}^{*}$, и оба они исчезли.

Промысловые прогнозы гарантированно учли в расчетах высокую эффективность воспроизводства в предыдущие годы, когда ослабло давление каннибализма. Уловы после спада, как кажется, начинают возвращать былые объемы, траектория выходит к максимуму между точками $R_{2}^{*}$ и $R_{1}^{*}$. Нет видимых статистикам причин радикально пересмотреть долю изъятия q. Тренд восстановления обманчив, и продолжительность колебаний связана со случайными факторами, а в модели – с интервальным аттрактором. В реальности величина запаса после интенсификации промысла возвращается в апериодический малочисленный режим со сжимающейся амплитудой колебаний. Эти колебания при их статистическом усреднении в оценках вполне будут выглядеть как стабилизация, так как в прогнозах учитывают средние показатели за предшествующие годы. В случае запоздалого установления прежней доли изъятия после кратких колебаний следует второе безвозвратное падение уловов (рис. 4), которое называют собственно коллапсом. На графиках вычислительных экспериментов в инструментальной среде по оси времени указывается шкала непрерывной компоненты гибридного модельного времени.

Модель показала, что коллапс – это процесс закономерный, растянутый и состоящий из этапов. В вычислительном эксперименте сценарий коллапса промысловых запасов развивается из двух фаз, продолжительность которых зависит от повышения ${{\bar {q}}_{n}}$.

Наблюдаемый в вычислительных экспериментах апериодический режим вызван локально-несвязным характером границы области притяжения аттрактора $R_{4}^{*}$. Область не включает множество не притягивающихся к аттрактору прообразов двух неустойчивых точек: $\Delta = \{ {{\varphi }^{{ - n}}}(R_{2}^{*})\} \cup \{ {{\varphi }^{{ - n}}}(R_{3}^{*})\} $. В случае негативного внешнего воздействия на выживаемость изменится конфигурация стационарных точек у масштабируемой по оси ординат кривой “запас–пополнение”. В полученной модели возможна обратная касательная бифуркация: при слиянии $R_{3}^{*},R_{4}^{*}$ с исчезновением устойчивой стационарной точки $R_{4}^{*}$, при сохранении оставшихся $R_{1}^{*},R_{2}^{*}$. Изменения означают пребывание популяции в режиме флуктуаций значительной амплитуды при существенно меньшей среднемноголетней численности, чему отвечает интервальный аттрактор третьего топологического типа в перечне теоремы Гукейнхэймера (Guckenheimer, 1979). Продолжительность колебаний зависит от положения кривой в точке ее минимума ${{R}_{{\min }}}$. Когда происходит сдвиг $\varphi ({{R}_{{\min }}}) < R_{1}^{*}$, реализуется граничный кризис (“boundary crisis”) у интервального аттрактора. Точка $R_{1}^{*}$ – неустойчивое критическое равновесие. Если ${{R}_{0}} < R_{1}^{*} - \varepsilon $, то реализуется необратимая деградация $\forall {{R}_{0}} \notin \Delta ,$ ${{\psi }^{n}}({{R}_{0}}) \to 0$, так как никаких альтернативных притягивающих множеств у итераций уже не остается вне зависимости от выбора ${{R}_{0}}$.

При граничном кризисе аттрактор – инвариантное множество $\Lambda $ – соприкасается с границей своей области притяжения и теряет свойство инвариантности $\varphi (\Lambda ) \in \Lambda $. На его месте появляется уже непритягивающее хаотическое множество, где траектория пребывает недолго. Поведение хаотических систем, в том числе продолжительность нахождения в переходных апериодических режимах, отличается непредсказуемым характером из-за чувствительной зависимости от выбора начальной точки ${{R}_{0}}$.

Коллапс трески был спровоцирован представлениями о слишком благополучном состоянии и сохранении эффективности воспроизводства при любом состоянии нерестового запаса. Перед критическим порогом эффективность воспроизводства популяции согласно нашей модели достаточно высока, что вносит обманчивые ожидания, но далее пополнение падает катастрофическим образом. Мораторий на вылов трески ввели в расчете на вступление в репродуктивный возраст “резервных” поколений, но они не дали результата.

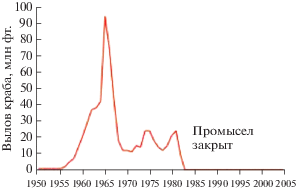
Аналогичным образом произошел коллапс камчатского краба Paralithodes camtschaticus (крупного и долгоживущего хищника-каннибала) в Тихом океане у берегов Аляски (рис. 5) (Dew, McСonnaughey, 2005).

МОДИФИКАЦИЯ МОДЕЛИ ДЛЯ СЦЕНАРИЯ ВСПЫШКИ ВРЕДИТЕЛЯ

Вспышки численности вредителей – глобальная проблема. Вспышки у насекомых различаются по фазам: запуска, перехода к так называемой эруптивной динамике, выходу на пик и стадии завершения опасного явления (Лямцев, Исаев, 2005). Вспышки насекомых – это ярко выраженный переходный режим изменения численности. Локальная вспышка должна завершаться самостоятельно. Изначально идея метода с раздельными расчетами по стадиям развития возникла при моделировании частной экстремальной ситуации у насекомых (Переварюха, 2016), которую автор анализировал на известном примере динамики размножения псиллид на востоке Австралии.

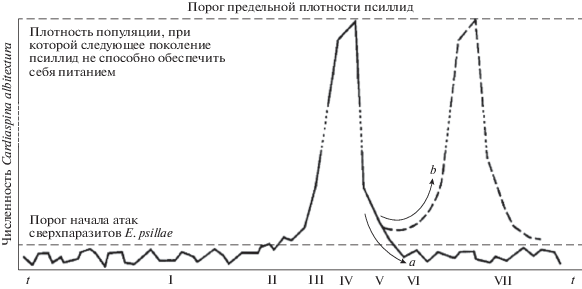
Один из распространенных сценариев перехода к вспышке численности – пороговый. Хрестоматийная ситуация преодоления порога описана в работе Кларка (Clark, 1964) на примере размножения мелких листоблошек из большого сем. Psyllidae (рис. 6). Сценарий a на этом рисунке показывает вариант одиночной вспышки, сценарий b – повторное развитие вспышки в седьмой фазе. Опасный вредитель псиллида Cardiaspina albitextura поражает эвкалиптовые деревья в вечнозеленом лесу Австралии в штатах Новый Южный Уэльс и Виктория. Пороговый эффект и взрывообразный рост численности псиллид возникает, так как паразиты-наездники, которые регулируют численность фитофагов, сами имеют своих врагов и паразитов. Порог представим математически как неустойчивое равновесие у итераций сложной функциональной зависимости. На первый взгляд, получение репеллерных точек итераций в нужной последовательности – не самая сложная математическая проблема, но есть несколько трудных аспектов.

Корень проблемы в том, что порог должен быть превышен спонтанно. Экстремальная фаза вспышки должна запускаться без внешнего воздействия (как случайный занос насекомых ветром из других ареалов или неординарные погодные факторы). Вспышка с гибелью леса – явление нечастое для регионов влажных лесов, у мелких насекомых хватает врагов. Полученный нами хаотический фрактальный репеллер из-за локально-несвязной границы областей притяжения двух альтернативных точечных аттракторов замечательно разрешает данную проблему вычислительного моделирования сценария вспышки.

В предложенной выше модели с (1a) и функцией $\Psi $ есть тип решения, когда спонтанное преодоление неустойчивого равновесия запускает вспышку вредителя с выходом к устойчивому равновесию большой численности популяции. Мы решили только первую часть проблемы моделирования вспышки. Такие явления скоро завершаются. Экосистема не выдержит подобное состояние долго. Популяция вредителя будет уничтожать необходимые ей ресурсы и вечное равновесие $R_{4}^{*}$ невозможно. Предельный случай вспышки – летальное завершение инфекционного заболевания. Следовательно, само количество стационарных точек $\Theta = 5$ не может оставаться в модельном сценарии фиксированным числом.

В новой модели необходимо рассчитать момент спонтанного завершения вспышки локальной популяции насекомых без внешнего независимого изъятия, что отличает данную ситуацию от примера промысла трески. Для этой цели мы иным образом модифицируем модель (1) универсальным методом функций-триггеров:

где параметр ${{с}_{2}} > 1$ характеризует темп исчерпания ресурсов, а коэффициент $\mu $ варьирует уровень численности, при котором эффект начнет заметно проявляться, ${{с}_{1}} < 1$ – масштабирующий коэффициент. Проведем имплементацию $\Xi $ для второй стадии развития. У насекомых-вредителей вторая стадия наиболее требовательна к обилию пищевых ресурсов. Плотностно-зависимая регуляция для личинок насекомых описана в работе Резника с соавт. (Reznik et al., 2017) в экспериментах с личинками азиатской божьей коровки Harmonia axyridis. Хищный жук был привезен из Китая целенаправленно для разведения и искусственно выпускался во многих странах для подавления массовых размножений тлей и кокцид, но успешно акклиматизировался в новом ареале. В настоящее время H. axyridis считается опасным инвазивным видом (Орлова-Беньковская, 2013).

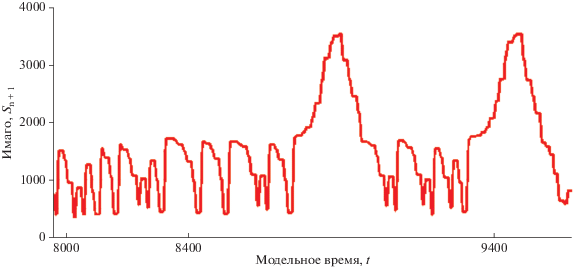
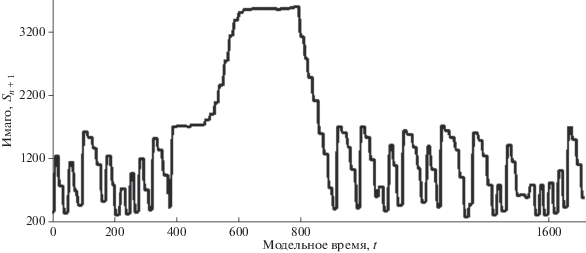
Ранее нам удалось описать в вычислительном эксперименте спонтанный непрогнозируемый переход от переходной хаотической динамики к устойчивому равновесию из-за быстрой фрактализации границы $\Omega $ (Переварюха, 2013). Мы получили сценарий фазы развития единичной вспышки после промежуточной стабилизации у $R_{3}^{*}$ (рис. 7). В таком модельном сценарии вспышка – единичное редкое событие, но ее пик длится достаточно долго. В данной модели сложно прогнозировать сам момент перехода к фазе запуска вспышки, но можно оценить продолжительность экстремального явления и предсказать скорость завершения вспышки.

В сценарии из работы Кларка мы видим вариант скорой повторной вспышки – два следующих друг за другом пика численности. Моделировать повторный сценарий запуска вспышки удобно, не изменяя базовую модель. Проще корректировать те характеристики, которые включены в состав триггерных функций, чем перенастраивать весь большой набор параметров модели заново. Имеется возможность несколько сдвинуть во времени значение переменной в функции $\Xi (N(\tau - u))$ и отрегулировать воздействие. Так мы получим очень краткий режим максимальной численности, но появится возможность скорой повторной вспышки.

Поведение траектории между пиками хаотично. Вероятность преодоления порога в хаотических флуктуациях зависит от ширины интервала $[R_{1}^{*},R_{3}^{*}],$ $\varphi (I) > R_{3}^{*}$, из которого траектория может при следующей итерации покинуть диапазон $[R_{1}^{*},R_{3}^{*}]$. Чем уже промежуток I, тем реже случается спонтанное преодоление порога для запуска вспышки насекомых.

Равновесие при большой численности может показаться устойчивым. Однако в новом модельном сценарии любое верхнее равновесие будет исчезать из-за действия $\Xi $. Траектория вернется к апериодическому движению в интервальном аттракторе, который представляет собой объединение множества интервалов, оставшихся после исключения всех множеств тех точек, которые не могут притягиваться к аттракторам: $\Phi = \{ {{\varphi }^{{ - n}}}(R_{2}^{*})\} \cup \{ {{\varphi }^{{ - n}}}(R_{3}^{*})\} \cup \{ {{\varphi }^{{ - n}}}(R_{1}^{*})\} $. Таким образом, $\omega $-предельное множество траектории составит разность двух множеств точек из отрезка между ограничивающими точками-репеллерами: $\Lambda = {{\left[ {R_{1}^{*},R_{3}^{*}} \right]} \mathord{\left/ {\vphantom {{\left[ {R_{1}^{*},R_{3}^{*}} \right]} \Phi }} \right. \kern-0em} \Phi }$. В современных работах используется термин “multiply-connected attractor” для таких составных притягивающих множеств (Gardini‎ et al., 2019).

В полученном сценарии (рис. 8) мы, исходя из реальных условий, можем варьировать и продолжительность пиковой фазы, и повторяемость событий вспышки. Модель (1) изначально строилась именно для особенностей поливольтинных полужесткокрылых (Переварюха, 2016), дающих несколько поколений в сезоне без долгих пауз. В настоящей модификации мы, сохранив структуру, перераспределили убыль между стадиями, и ввели согласованное запаздывание в показатель темпа индивидуального развития. Запаздывание можно включать и в регуляционную составляющую непрерывной модели.

Оказалось, что пороговый характер перехода к вспышкам описан в литературе также для бабочек-вредителей, например, для непарного шелкопряда Lymantria dispar –инвазивного в США вредителя – в штате Висконсин (McFadden, McManus, 1991). У чешуекрылых полный цикл превращений и четыре стадии онтогенеза, но эта трудность для применения гибридной модели в практических задачах разрешима. Дополнительная стадия (куколка) отличается отсутствием питания и весового роста, соответственно, отсутствуют конкурентные факторы, поэтому можно включить дополнительное уравнение для самой короткой стадии с простой линейной убылью: ${{dN} \mathord{\left/ {\vphantom {{dN} {dt}}} \right. \kern-0em} {dt}} = - \chi ,$ $\chi < {{\alpha }_{1}}$.

Более актуальная методическая задача для модификаций связана не с количеством стадий, а с разным временем развития у смежных поколений чешуекрылых с бивольтинным жизненным циклом, зимующих в умеренных широтах (Фролов, Грушевая, 2019), и фактором половой изоляции, описанным на примере мотылька Ostrinia nubilalis (Фролов, 1994). Принципиальная дальнейшая модификация организации итераций потребуется для учета фактора зимовки (Perevaryukha, 2016), соответственно, интервалы уязвимости поколений там не будут равномерными. Разные насекомые впадают в диапаузу на разных стадиях. У моновольтинного непарного шелкопряда в Северной Америке диапауза протекает на стадии яйца, которая, таким образом, становится самой длительной у зимующего поколения. В очагах вспышек при высокой плотности у непарного шелкопряда отмечается супердипауза (Марков, 1997), когда яйца могут зимовать дважды – интересный пример запаздывающей реализации репродуктивного потенциала. Климатические поправки в расчет выживаемости будут значимы для популяций насекомых в бореальных лесах, в усложненной задаче можно использовать известные методы. В работе В.Г. Суховольского с соавт. (2015) в рекурсивную статистическую модель динамики непарного шелкопряда на Урале, построенную из представлений о ведущей роли плотностно-зависимых факторов, добавлена функция влияния погоды на популяцию.

ЗАКЛЮЧЕНИЕ

Представлен метод построения вычислительных структур, которые правильно называть “динамическая система с логически переопределяемым оператором эволюции”. Способ расширения модели позволяет конкретизировать популяционную задачу и уйти от таких абстрактных типов взаимодействий, как интегро-дифференциальные уравнения “хищник–жертва” (Anisiu, 2014). Модель отличается сложностью согласования уравнений, но схематическое представление в модели стадий онтогенеза с регулируемой убылью наглядно. Обоснован оригинальный в математической биологии метод включения триггерных функций с единичным пределом. Метод вычислительного моделирования практически важных сценариев в живых системах применен для двух хорошо изученных специалистами реальных ситуаций, которые относятся к экстремальной и переходной динамике развития популяционных процессов.

С использованием возможности бифуркаций и образования разных типов аттракторов у функциональных итераций описан сценарий коллапса, который наблюдался для трески и камчатского краба. Длительный процесс, завершающийся резкой деградацией, в модели логически разделен на фазы. Математически они представлены с двумя метаморфозами аттракторов. Выводы сценария заключаются в том, что регулирование квоты недостаточно для предотвращения коллапса. Ошибки в определении величины запаса и ожидаемого от него пополнения будут быстро нарастать. Пороговое падение эффективности пополнения заранее предугадать практически невозможно. Промысловая смертность будет больше ожидаемой запланированной доли. Более осторожным видится подход с регуляцией технических возможностей промысла, ограничениями на число судов и параметры орудий лова. Резкое падение уловов должно быть поводом для введения краткосрочного моратория, даже если остаточная численность оценивается в текущий момент высоко.

Появление области хаотического режима в пространстве параметров накладывает ограничения на количественные предсказания из-за чувствительной зависимости итогового положения точки траектории от выбора начальной точки (Gorodetskyi, Osadchuk, 2012). Это явление есть следствие фундаментальных свойств континуума неустойчивых точек-прообразов. Появление апериодических колебаний после стабильного периода эксплуатации запаса и прохождение резкого пика уловов само должно сигнализировать об угрожающей ситуации, которая развивается согласно сценарию коллапса через 7–8 сезонов. Применение модели для прогнозирования перспектив промысла запаса с пороговыми эффектами основано на выявлении набора типовых ситуаций – характерных резких изменений популяционных процессов. Существует метод ситуационного прогнозирования по принципу наибольшего сходства значимых факторов (Petchey et al., 2015). При ситуационном анализе можно выделять типы переходных состояний на примере разных запасов, обладающих динамическим сходством согласно отмеченным фазам в вычислительных сценариях, но с разной логикой управления (Переварюха, 2020).

К сожалению, мы не можем сравнить сценарии и рассмотреть особенности важных отечественных примеров краха промысла из-за отсутствия надежных данных и достоверной информации, как в случае деградации четырех популяций осетровых рыб Каспийского моря. Имеются частные данные по естественному воспроизводству осетра и севрюги в Волге (Гутенева, Фомин, 2015), коррелированные с гидрологической обстановкой (Вещев, Гутенева, 2012). Интенсивный нелегальный промысел в море и недостоверность оценок общей численности по методу контрольных тралений не позволяет нам использовать официальную статистику для оценки естественной и промысловой смертности. Нами показано наличие порогового эффекта в воспроизводстве русского осетра в результате обработки данных о количестве мигрирующей из Волги в море молоди методом скользящего среднего.

Динамически описано явление развития и окончания вспышки вредителей из семи фаз. Регулируя момент действия триггерной функции, можно получить сценарий с редкой единичной, но масштабной вспышкой либо с серией кратких пиков. Сценарии различаются длительностью пребывания траектории в окрестности неустойчивых точек равновесия, что интересно для прогнозирования типа вспышки. Базовый сценарий вспышки у псиллид наблюдался в вечнозеленом лесу. В реальности для бореальной зоны старт и завершение вспышек у разных видов весьма разнообразны (Базыкин и др., 1995). Интересную задачу представляет классификация форм вспышек с точки зрения теории динамических систем. Может происходить серия колебаний (Frolov, 2015) пиков численности с нарастающей амплитудой, но затухающие флуктуации – наиболее распространенный сценарий. Интересный сценарий представляет образование популяционной волны насекомых вредителей, встречающийся, оказывается, более часто, чем считалось (Ермолаев, 2019).

Полученная вычислительная структура с предикатами и кадрами гибридного времени может использоваться и как отдельный блок расчетов в составе многокомпонентной модели, например, для озерного ихтиоценоза. Перспективной областью для применения предикативной модельной структуры расчетов видится задача анализа разнообразных активных инвазионных процессов, происходящих при вселении чужеродных видов с высоким репродуктивным потенциалом в ранее изолированную биосистему, как это происходило в Каспийском море (Гераскин и др., 2007). Для дальнейшего развития метода триггерных функций интересно рассмотреть в моделях для стадий развития рыб влияние фактора нарастающей сезонной эвтрофикации водоемов (Никитина, Семенов, 2013) на выживаемость молоди и действия сельскохозяйственных работ на личинок насекомых.

Работа выполнена при финансовой поддержке РФФИ (грант № 17-07-00125) и проекта научных работ СПИИРАН (№ AAAA-A16-116051250009-8).