Журнал общей биологии, 2020, T. 81, № 4, стр. 257-271
Обратный прогноз подтверждает вывод о жизнеспособности ценопопуляции растений
Д. О. Логофет 1, *, Е. С. Казанцева 2, **, И. Н. Белова 1, ***, В. Г. Онипченко 2, ****
1 Институт физики атмосферы им. А.М. Обухова РАН, лаборатория математической экологии
119017 Москва, Пыжевский пер., 3, Россия
2 Московский государственный университет им. М.В. Ломоносова, биологический факультет,
кафедра экологии и географии растений
Ленинские горы, 1
119234 Москва, Россия
* E-mail: danilal@postman.ru
** E-mail: biolenok@mail.ru
*** E-mail: iya@ifaran.ru
**** E-mail: vonipchenko@mail.ru
Поступила в редакцию 10.03.2020
После доработки 08.04.2020
Принята к публикации 26.04.2020
Аннотация
Очередной год наблюдений за структурой ценопопуляции проломника Androsace albana на постоянных пробных площадках, заложенных в альпийской лишайниковой пустоши в 2009 г., добавил 10-ю калиброванную матрицу к прежнему набору из 9 годичных проекционных матриц популяции как итогу 10-летних наблюдений, полученному с помощью матричной модели год назад. В настоящем исследовании оригинальная концепция структурно-мультипликативного осреднения неотрицательных матриц приводит к средней 10 матриц, которая сохраняет прежний “неутешительный прогноз выживания ценопопуляции”, мотивировав его подтверждение/опровержение методом обратного прогноза. Обоснована методика и представлен соответствующий вычислительный аппарат обратного прогноза в матричных моделях популяций с дискретной структурой через обращение вспять направления времени в данных наблюдений. В приложении к данным по A. albana методика дает 10 годичных матриц обратного прогноза, каждая из которых прогнозирует рост ценопопуляции, если ее прообраз в прямой модели предписывает убыль, и наоборот. Аналогично, результат осреднения дает итоговый обратный прогноз на рост ценопопуляции, в противоположность прогнозу прямому, подтверждая его адекватность.
В научных исследованиях, экспериментах или наблюдениях за ценопопуляциями возникает потребность сравнивать состояние (в том числе и разновидовых) популяций в разных точках по времени и/или пространству. В таких условиях особенно важно иметь показатель, который выражен числом и вычисляется по общей методике для разных объектов. Такой методикой служит матричное моделирование динамики популяций с дискретной структурой, и эта методика позволяет получить нужный показатель – меру приспособленности локальной популяции (На земле…, 2015). Матричная модель популяции описывает динамику во времени ее дискретной структуры, сформированной на основании какого-либо наблюдаемого и/или измеримого признака особей: возраста, размера, стадии развития и т.п. (Caswell, 1989, 2001; Логофет, Уланова, 2018). Теоретическим фундаментом таких моделей служит классическая теорема Перрона–Фробениуса для неотрицательных матриц (Гантмахер, 1967; Horn, Johnson, 1990). На ее основе разработан впечатляющий набор характеристик локальной популяции и методов их вычисления из проекционной матрицы популяции (ПМП) L – сердцевины матричной модели (Логофет, Уланова, 2018), которая преобразует (“проецирует” в неудачной, но устоявшейся терминологии) вектор x(t) стадийной структуры года наблюдения t в аналогичный вектор года t + 1 по правилу линейной алгебры: x(t + 1) = L x(t).
В частности, доминантное собственное число λ1(L) матрицы L служит количественной мерой адаптации ценопопуляции к условиям среды, причем значение этой меры специфично в пространстве и времени, а именно, отражает состояние популяции там и тогда, где и когда собраны данные для калибровки матрицы L (Logofet et al., 2014; На земле…, 2015; Логофет и др., 2015, 2016а, б, 2017а, б). Поэтому, с одной стороны, ПМП является эффективным инструментом сравнительной демографии видов, а с другой – повышаются требования к надежности калибровки ПМП по эмпирическим данным.
Данные о структуре ценопопуляции собирают в ходе мониторинга, который продолжается несколько (не менее трех) лет, и если мы получаем не одну ПМП, а их временнóй ряд (например, ряд годичных ПМП, как в наших проектах), то прогноз жизнеспособности ценопопуляции через доминантное собственное число λ1(L) может меняться год от года не только количественно, но и качественно – с роста популяции на ее убыль (Логофет и др., 2016б, 2017а, б, 2018). Итог всего периода наблюдений позволяет подвести матрица, полученная методом структурно-геометрического осреднения заданных ПМП (Logofet, 2018; Логофет и др., 2018). Она исходит из логики преобразования вектора структуры популяции за весь период наблюдений – от начального до последнего момента – через произведение годичных матриц (в хронологическом порядке) и выдвигает естественное требование к строению средней матрицы: оно должно совпадать со строением усредняемых матриц, т.е. соответствовать графу жизненного цикла (ГЖЦ; Логофет, Белова, 2007) – графическому выражению знаний о биологии вида и способе мониторинга (Caswell, 2001; Логофет, Уланова, 2018). Такая логика приводит к постановке математической задачи структурно-геометрического (точнее, структурно-мультипликативного) осреднения (СМО) заданных неотрицательных матриц, которая допускает решение современными средствами вычислительной техники (например, в системе MATLAB), когда размер матриц невелик, например, 4 × 4 или 5 × 5, как для альпийских малолетников (Логофет и др., 2016б, 2017а, б). Найденная таким образом матрица G подводит итог всего периода мониторинга – своим доминантным собственным числом λ1(G) и прочими характеристиками – и дает прогноз состояния ценопопуляции (скорости роста или убыли) в долговременной перспективе.
По фундаментальной математической причине (Сколько лет…, 2018), задача СМО имеет точное решение лишь в редких специальных случаях (Логофет, Маслов, 2018; Logofet, Maslov, 2019), а в ботанических проектах приходится довольствоваться решением приближенным, с некоторой ошибкой приближения (Логофет и др., 2017а, б, 2018, 2019). Поэтому возникает потребность в альтернативных методах прогноза, к которым относится и обратный прогноз, понимаемый как использование существующих данных для восстановления прошлых состояний системы. В отдельных случаях, как например, для систем обыкновенных дифференциальных уравнений, обратный прогноз получают простой сменой знака временнóй переменной; существуют и стандартные методы восстановления пропущенных данных при статистической обработке временны́х рядов (Courtier et al., 1993). Однако в реальных экологических моделях рутинные методы обратного прогноза не применимы ни в идейном плане, ни в техническом (Logofet, 2019a).
Тем не менее идея обратного прогноза оказалась плодотворной в дискретных марковских цепях при обращении вспять оси времени не в уравнениях модели, а в данных наблюдений (Logofet, 2019a). Этот подход применен нами и в настоящей работе к матричной модели стадийно структурированной популяции проломника Androsace albana с целью подтвердить либо поставить под сомнение “неутешительный прогноз выживания ценопопуляции” (Логофет и др., 2019), полученный ранее через структурно-мультипликативное среднее ряда годичных ПМП.
МАТРИЧНАЯ МОДЕЛЬ ЦЕНОПОПУЛЯЦИИ A. ALBANA
Объект. По нашим данным, A. albana в условиях альпийских лишайниковых пустошей проявляет себя как травянистый хамефит,
летнезеленый стержнекорневой многолетний монокарпик (Казанцева, 2016; Логофет и др.,
2017б). Вид включен в “Красную книгу Краснодарского края” (2007) и “Красную книгу
Республики Адыгея” (2012) как редкий категории 3. Биология, экология и онтогенез вида
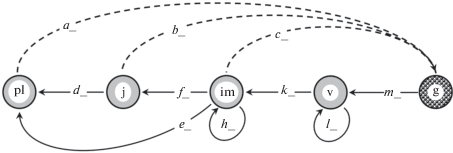
описаны ранее (Казанцева, 2016; Логофет и др., 2017б), и построен граф жизненного цикла по стадиям онтогенеза (рис. 1), которые различимы в поле по морфологии растения. Наличие в ГЖЦ нетривиальных задержек
 в стадиях im и v, а также ускоренного перехода pl
в стадиях im и v, а также ускоренного перехода pl 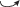 im есть проявление поливариантности онтогенеза A. albana в условиях альпийского пояса Северо-Западного Кавказа (Логофет и др., 2019).
im есть проявление поливариантности онтогенеза A. albana в условиях альпийского пояса Северо-Западного Кавказа (Логофет и др., 2019).
Рис. 1.
Граф жизненного цикла проломника Androsace albana по стадиям онтогенеза: pl – проростки, j – ювенильные растения, im – имматурные, v – взрослые вегетативные, g – генеративные; штриховые стрелки – пополнение популяции, обнаруженное в соответствующих стадиях (Логофет и др., 2017б, рис. 2).
Методы исследования. Исследования проводились в Карачаево-Черкесской Республике, на территории Тебердинского государственного природного биосферного заповедника, на постоянных площадках, заложенных в 2009 г. на лишайниковой пустоши, на горе Малая Хатипара, 2800 м над ур. м. Метод ежегодной переписи всех растений на площадках описан в работе Д.О. Логофета с соавт. (2017б). Мониторинг проводили каждый год в конце августа в течение 11 лет с 2009 по 2019 год включительно.
Собранные данные относятся к типу “идентифицированные особи” (“identified individuals”; Caswell, 2001, p. 134), т.е. содержат сведения о стадии каждого растения A. albana с момента его появления на площадке и до момента цветения с шагом в один год. Поэтому, наряду со структурой ценопопуляции в каждый год наблюдения, т.е. вектором(-столбцом)
Таблица 1.
Структура ценопопуляции A. albana по годам согласно данным учетов 2009–2019 гг. (продолжение табл. 1 из Логофет и др., 2019)
| Численность стадийных групп в год наблюдения | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Стадия | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
| pl | 37 | 30 | 19 | 49 | 19 | 16 | 4 | 10 | 3 | 12 | 13 |
| j | 110 | 48 | 45 | 86 | 137 | 98 | 19 | 29 | 8 | 23 | 38 |
| im | 99 | 55 | 43 | 87 | 95 | 34 | 10 | 13 | 12 | 13 | 2 |
| v | 35 | 26 | 57 | 58 | 73 | 50 | 20 | 22 | 28 | 23 | 23 |
| g | 13 | 1 | 1 | 4 | 6 | 3 | 4 | 2 | 1 | 2 | 1 |
Матричная модель и калибровка матриц. Наблюдаемые изменения вектора x(t) по годам описываются основным уравнением модели в векторно-матричной форме:
(1)
$x\left( {t + 1} \right) = L\left( t \right)x\left( t \right),~\,\,\,\,t = 2009,\,\,2010,\,\, \ldots ,\,\,2019,$(2)
$L = \left[ {\begin{array}{*{20}{c}} 0&0&0&0&a \\ d&0&0&0&b \\ e&f&h&0&c \\ 0&0&k&l&0 \\ 0&0&0&m&0 \end{array}{\text{ }}} \right];~\,\,\,\,a,\,\,b,\,\, \ldots ,\,\,l,\,\,m \geqslant {\text{ }}0,~$Таблица 2.
К вычислению параметров матричной модели: числа особей ежегодного пополнения популяции A. albana и переходов по дугам ГЖЦ (рис. 1) согласно данным учетов (продолжение табл. 2 из Логофет и др., 2019)
| Переход t → t + 1 |
Год переписи (момент t + 1) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | |
a: pl g g |
30 | 19 | 49 | 19 | 16 | 4 | 10 | 3 | 12 | 13 |
b: j g g |
40 | 31 | 85 | 136 | 98 | 19 | 29 | 8 | 23 | 38 |
c: im g g |
3 | 0 | 25 | 1 | 2 | 0 | 0 | 0 | 0 | 0 |
| d: pl→j | 8 | 14 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
e: pl im im |
2 | 4 | 6 | 10 | 2 | 2 | 0 | 2 | 3 | 1 |
| f: j→im | 22 | 22 | 35 | 45 | 16 | 2 | 10 | 5 | 2 | 1 |
h: im 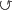 im im |
28 | 17 | 21 | 39 | 14 | 6 | 3 | 5 | 8 | 0 |
| k: im→v | 7 | 34 | 10 | 28 | 6 | 4 | 5 | 8 | 2 | 1 |
l: v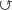 v v |
19 | 23 | 48 | 45 | 44 | 16 | 17 | 20 | 21 | 22 |
| m: v → g | 1 | 1 | 4 | 6 | 3 | 4 | 2 | 1 | 2 | 1 |
Таблица 3.
Результаты калибровки ПМП для A. albana по данным 2009–2019 гг. (продолжение табл. 2 из Логофет и др., 2019)
| Год переписи, t | Матрица L(t): t → t +1 |
λ1(L(t)) | Вектор x*, % |
|---|---|---|---|
| 2009 j = 0 | ${{L}_{0}} = \left[ {\begin{array}{*{20}{c}} 0&0&0&0&{{\raise0.7ex\hbox{${30}$} \!\mathord{\left/ {\vphantom {{30} {13}}}\right.\kern-0em} \!\lower0.7ex\hbox{${13}$}}} \\ {{\raise0.7ex\hbox{$8$} \!\mathord{\left/ {\vphantom {8 {37}}}\right.\kern-0em} \!\lower0.7ex\hbox{${37}$}}}&0&0&0&{{\raise0.7ex\hbox{${40}$} \!\mathord{\left/ {\vphantom {{40} {13}}}\right.\kern-0em} \!\lower0.7ex\hbox{${13}$}}} \\ {{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 {37}}}\right.\kern-0em} \!\lower0.7ex\hbox{${37}$}}}&{{\raise0.7ex\hbox{${22}$} \!\mathord{\left/ {\vphantom {{22} {110}}}\right.\kern-0em} \!\lower0.7ex\hbox{${110}$}}}&{{\raise0.7ex\hbox{${28}$} \!\mathord{\left/ {\vphantom {{28} {99}}}\right.\kern-0em} \!\lower0.7ex\hbox{${99}$}}}&0&{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 {13}}}\right.\kern-0em} \!\lower0.7ex\hbox{${13}$}}} \\ 0&0&{{\raise0.7ex\hbox{$7$} \!\mathord{\left/ {\vphantom {7 {99}}}\right.\kern-0em} \!\lower0.7ex\hbox{${99}$}}}&{{\raise0.7ex\hbox{${19}$} \!\mathord{\left/ {\vphantom {{19} {35}}}\right.\kern-0em} \!\lower0.7ex\hbox{${35}$}}}&0 \\ 0&0&0&{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {35}}}\right.\kern-0em} \!\lower0.7ex\hbox{${35}$}}}&0 \end{array}} \right]$ | 0.5661 | $\left[ {\begin{array}{*{20}{c}} {10.61} \\ {18.20} \\ {16.99} \\ {51.59} \\ {2.60} \end{array}} \right]$ |
| 2010 j = 1 | ${{L}_{1}} = \left[ {\begin{array}{*{20}{c}} 0&0&0&0&{{\raise0.7ex\hbox{${19}$} \!\mathord{\left/ {\vphantom {{19} 1}}\right.\kern-0em} \!\lower0.7ex\hbox{$1$}}} \\ {{\raise0.7ex\hbox{${14}$} \!\mathord{\left/ {\vphantom {{14} {30}}}\right.\kern-0em} \!\lower0.7ex\hbox{${30}$}}}&0&0&0&{{\raise0.7ex\hbox{${31}$} \!\mathord{\left/ {\vphantom {{31} 1}}\right.\kern-0em} \!\lower0.7ex\hbox{$1$}}} \\ {{\raise0.7ex\hbox{$4$} \!\mathord{\left/ {\vphantom {4 {30}}}\right.\kern-0em} \!\lower0.7ex\hbox{${30}$}}}&{{\raise0.7ex\hbox{${22}$} \!\mathord{\left/ {\vphantom {{22} {48}}}\right.\kern-0em} \!\lower0.7ex\hbox{${48}$}}}&{{\raise0.7ex\hbox{${17}$} \!\mathord{\left/ {\vphantom {{17} {55}}}\right.\kern-0em} \!\lower0.7ex\hbox{${55}$}}}&0&{{\raise0.7ex\hbox{$0$} \!\mathord{\left/ {\vphantom {0 1}}\right.\kern-0em} \!\lower0.7ex\hbox{$1$}}} \\ 0&0&{{\raise0.7ex\hbox{${34}$} \!\mathord{\left/ {\vphantom {{34} {55}}}\right.\kern-0em} \!\lower0.7ex\hbox{${55}$}}}&{{\raise0.7ex\hbox{${23}$} \!\mathord{\left/ {\vphantom {{23} {26}}}\right.\kern-0em} \!\lower0.7ex\hbox{${26}$}}}&0 \\ 0&0&0&{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {26}}}\right.\kern-0em} \!\lower0.7ex\hbox{${26}$}}}&0 \end{array}} \right]$ | 1.2283 | $\left[ {\begin{array}{*{20}{c}} {15.90} \\ {31.99} \\ {18.25} \\ {32.83} \\ {1.03} \end{array}} \right]$ |
| 2011 j = 2 | ${{L}_{2}} = \left[ {\begin{array}{*{20}{c}} 0&0&0&0&{{\raise0.7ex\hbox{${49}$} \!\mathord{\left/ {\vphantom {{49} 1}}\right.\kern-0em} \!\lower0.7ex\hbox{$1$}}} \\ {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {19}}}\right.\kern-0em} \!\lower0.7ex\hbox{${19}$}}}&0&0&0&{{\raise0.7ex\hbox{${85}$} \!\mathord{\left/ {\vphantom {{85} 1}}\right.\kern-0em} \!\lower0.7ex\hbox{$1$}}} \\ {{\raise0.7ex\hbox{$6$} \!\mathord{\left/ {\vphantom {6 {19}}}\right.\kern-0em} \!\lower0.7ex\hbox{${19}$}}}&{{\raise0.7ex\hbox{${35}$} \!\mathord{\left/ {\vphantom {{35} {45}}}\right.\kern-0em} \!\lower0.7ex\hbox{${45}$}}}&{{\raise0.7ex\hbox{${21}$} \!\mathord{\left/ {\vphantom {{21} {43}}}\right.\kern-0em} \!\lower0.7ex\hbox{${43}$}}}&0&{{\raise0.7ex\hbox{${25}$} \!\mathord{\left/ {\vphantom {{25} 1}}\right.\kern-0em} \!\lower0.7ex\hbox{$1$}}} \\ 0&0&{{\raise0.7ex\hbox{${10}$} \!\mathord{\left/ {\vphantom {{10} {43}}}\right.\kern-0em} \!\lower0.7ex\hbox{${43}$}}}&{{\raise0.7ex\hbox{${48}$} \!\mathord{\left/ {\vphantom {{48} {57}}}\right.\kern-0em} \!\lower0.7ex\hbox{${57}$}}}&0 \\ 0&0&0&{{\raise0.7ex\hbox{$4$} \!\mathord{\left/ {\vphantom {4 {57}}}\right.\kern-0em} \!\lower0.7ex\hbox{${57}$}}}&0 \end{array}} \right]$ | 1.5779 | $\left[ {\begin{array}{*{20}{c}} {17.20} \\ {30.40} \\ {39.29} \\ {12.45} \\ {0.55} \end{array}} \right]$ |
| 2012 j = 3 | ${{L}_{3}} = \left[ {\begin{array}{*{20}{c}} 0&0&0&0&{{\raise0.7ex\hbox{${19}$} \!\mathord{\left/ {\vphantom {{19} 4}}\right.\kern-0em} \!\lower0.7ex\hbox{$4$}}} \\ {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {49}}}\right.\kern-0em} \!\lower0.7ex\hbox{${49}$}}}&0&0&0&{{\raise0.7ex\hbox{${136}$} \!\mathord{\left/ {\vphantom {{136} 4}}\right.\kern-0em} \!\lower0.7ex\hbox{$4$}}} \\ {{\raise0.7ex\hbox{${10}$} \!\mathord{\left/ {\vphantom {{10} {49}}}\right.\kern-0em} \!\lower0.7ex\hbox{${49}$}}}&{{\raise0.7ex\hbox{${45}$} \!\mathord{\left/ {\vphantom {{45} {86}}}\right.\kern-0em} \!\lower0.7ex\hbox{${86}$}}}&{{\raise0.7ex\hbox{${39}$} \!\mathord{\left/ {\vphantom {{39} {87}}}\right.\kern-0em} \!\lower0.7ex\hbox{${87}$}}}&0&{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 4}}\right.\kern-0em} \!\lower0.7ex\hbox{$4$}}} \\ 0&0&{{\raise0.7ex\hbox{${28}$} \!\mathord{\left/ {\vphantom {{28} {87}}}\right.\kern-0em} \!\lower0.7ex\hbox{${87}$}}}&{{\raise0.7ex\hbox{${45}$} \!\mathord{\left/ {\vphantom {{45} {58}}}\right.\kern-0em} \!\lower0.7ex\hbox{${58}$}}}&0 \\ 0&0&0&{{\raise0.7ex\hbox{$6$} \!\mathord{\left/ {\vphantom {6 {58}}}\right.\kern-0em} \!\lower0.7ex\hbox{${58}$}}}&0 \end{array}} \right]$ | 1.2641 | $\left[ {\begin{array}{*{20}{c}} {6.01} \\ {43.15} \\ {29.67} \\ {19.56} \\ {1.60} \end{array}} \right]$ |
| 2013 j = 4 | ${{L}_{4}} = \left[ {\begin{array}{*{20}{c}} 0&0&0&0&{{\raise0.7ex\hbox{${16}$} \!\mathord{\left/ {\vphantom {{16} 6}}\right.\kern-0em} \!\lower0.7ex\hbox{$6$}}} \\ 0&0&0&0&{{\raise0.7ex\hbox{${98}$} \!\mathord{\left/ {\vphantom {{98} 6}}\right.\kern-0em} \!\lower0.7ex\hbox{$6$}}} \\ {{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 {19}}}\right.\kern-0em} \!\lower0.7ex\hbox{${19}$}}}&{{\raise0.7ex\hbox{${16}$} \!\mathord{\left/ {\vphantom {{16} {137}}}\right.\kern-0em} \!\lower0.7ex\hbox{${137}$}}}&{{\raise0.7ex\hbox{${14}$} \!\mathord{\left/ {\vphantom {{14} {95}}}\right.\kern-0em} \!\lower0.7ex\hbox{${95}$}}}&0&{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 6}}\right.\kern-0em} \!\lower0.7ex\hbox{$6$}}} \\ 0&0&{{\raise0.7ex\hbox{$6$} \!\mathord{\left/ {\vphantom {6 {95}}}\right.\kern-0em} \!\lower0.7ex\hbox{${95}$}}}&{{\raise0.7ex\hbox{${44}$} \!\mathord{\left/ {\vphantom {{44} {73}}}\right.\kern-0em} \!\lower0.7ex\hbox{${73}$}}}&0 \\ 0&0&0&{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 {73}}}\right.\kern-0em} \!\lower0.7ex\hbox{${73}$}}}&0 \end{array}} \right]$ | 0.6345 | $\left[ {\begin{array}{*{20}{c}} {7.76} \\ {47.54} \\ {14.34} \\ {28.51} \\ {1.85} \end{array}} \right]$ |
| 2014 j = 5 | ${{L}_{5}} = \left[ {\begin{array}{*{20}{c}} 0&0&0&0&{{\raise0.7ex\hbox{$4$} \!\mathord{\left/ {\vphantom {4 3}}\right.\kern-0em} \!\lower0.7ex\hbox{$3$}}} \\ 0&0&0&0&{{\raise0.7ex\hbox{${19}$} \!\mathord{\left/ {\vphantom {{19} 3}}\right.\kern-0em} \!\lower0.7ex\hbox{$3$}}} \\ {{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 {16}}}\right.\kern-0em} \!\lower0.7ex\hbox{${16}$}}}&{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 {98}}}\right.\kern-0em} \!\lower0.7ex\hbox{${98}$}}}&{{\raise0.7ex\hbox{$6$} \!\mathord{\left/ {\vphantom {6 {34}}}\right.\kern-0em} \!\lower0.7ex\hbox{${34}$}}}&0&{{\raise0.7ex\hbox{$0$} \!\mathord{\left/ {\vphantom {0 3}}\right.\kern-0em} \!\lower0.7ex\hbox{$3$}}} \\ 0&0&{{\raise0.7ex\hbox{$4$} \!\mathord{\left/ {\vphantom {4 {34}}}\right.\kern-0em} \!\lower0.7ex\hbox{${34}$}}}&{{\raise0.7ex\hbox{${16}$} \!\mathord{\left/ {\vphantom {{16} {50}}}\right.\kern-0em} \!\lower0.7ex\hbox{${50}$}}}&0 \\ 0&0&0&{{\raise0.7ex\hbox{$4$} \!\mathord{\left/ {\vphantom {4 {50}}}\right.\kern-0em} \!\lower0.7ex\hbox{${50}$}}}&0 \end{array}} \right]$ | 0.3988 | $\left[ {\begin{array}{*{20}{c}} {11.71} \\ {56.64} \\ {11.69} \\ {17.46} \\ {3.50} \end{array}} \right]$ |
| 2015 j = 6 | ${{L}_{6}} = \left[ {\begin{array}{*{20}{c}} 0&0&0&0&{{\raise0.7ex\hbox{${10}$} \!\mathord{\left/ {\vphantom {{10} 4}}\right.\kern-0em} \!\lower0.7ex\hbox{$4$}}} \\ 0&0&0&0&{{\raise0.7ex\hbox{${29}$} \!\mathord{\left/ {\vphantom {{29} 4}}\right.\kern-0em} \!\lower0.7ex\hbox{$4$}}} \\ 0&{{\raise0.7ex\hbox{${10}$} \!\mathord{\left/ {\vphantom {{10} {19}}}\right.\kern-0em} \!\lower0.7ex\hbox{${19}$}}}&{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 {10}}}\right.\kern-0em} \!\lower0.7ex\hbox{${10}$}}}&0&{{\raise0.7ex\hbox{$0$} \!\mathord{\left/ {\vphantom {0 4}}\right.\kern-0em} \!\lower0.7ex\hbox{$4$}}} \\ 0&0&{{\raise0.7ex\hbox{$5$} \!\mathord{\left/ {\vphantom {5 {10}}}\right.\kern-0em} \!\lower0.7ex\hbox{${10}$}}}&{{\raise0.7ex\hbox{${17}$} \!\mathord{\left/ {\vphantom {{17} {20}}}\right.\kern-0em} \!\lower0.7ex\hbox{${20}$}}}&0 \\ 0&0&0&{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {10}}}\right.\kern-0em} \!\lower0.7ex\hbox{${10}$}}}&0 \end{array}} \right]$ | 1.0679 | $\left[ {\begin{array}{*{20}{c}} {9.19} \\ {26.66} \\ {18.28} \\ {41.94} \\ {3.93} \end{array}} \right]$ |
| 2016 j = 7 | ${{L}_{7}} = \left[ {\begin{array}{*{20}{c}} 0&0&0&0&{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}} \\ 0&0&0&0&{{\raise0.7ex\hbox{$8$} \!\mathord{\left/ {\vphantom {8 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}} \\ {{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 {10}}}\right.\kern-0em} \!\lower0.7ex\hbox{${10}$}}}&{{\raise0.7ex\hbox{$5$} \!\mathord{\left/ {\vphantom {5 {29}}}\right.\kern-0em} \!\lower0.7ex\hbox{${29}$}}}&{{\raise0.7ex\hbox{$5$} \!\mathord{\left/ {\vphantom {5 {13}}}\right.\kern-0em} \!\lower0.7ex\hbox{${13}$}}}&0&0 \\ 0&0&{{\raise0.7ex\hbox{$8$} \!\mathord{\left/ {\vphantom {8 {13}}}\right.\kern-0em} \!\lower0.7ex\hbox{${13}$}}}&{{\raise0.7ex\hbox{${20}$} \!\mathord{\left/ {\vphantom {{20} {22}}}\right.\kern-0em} \!\lower0.7ex\hbox{${22}$}}}&0 \\ 0&0&0&{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {22}}}\right.\kern-0em} \!\lower0.7ex\hbox{${22}$}}}&0 \end{array}} \right]$ | 0.9611 | $\left[ {\begin{array}{*{20}{c}} {5.26} \\ {14.04} \\ {6.02} \\ {71.30} \\ {3.37} \end{array}} \right]$ |
| 2017 j = 8 | ${{L}_{8}} = \left[ {\begin{array}{*{20}{c}} 0&0&0&0&{{\raise0.7ex\hbox{${12}$} \!\mathord{\left/ {\vphantom {{12} 1}}\right.\kern-0em} \!\lower0.7ex\hbox{$1$}}} \\ 0&0&0&0&{{\raise0.7ex\hbox{${23}$} \!\mathord{\left/ {\vphantom {{23} 1}}\right.\kern-0em} \!\lower0.7ex\hbox{$1$}}} \\ {{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 3}}\right.\kern-0em} \!\lower0.7ex\hbox{$3$}}}&{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 8}}\right.\kern-0em} \!\lower0.7ex\hbox{$8$}}}&{{\raise0.7ex\hbox{$8$} \!\mathord{\left/ {\vphantom {8 {12}}}\right.\kern-0em} \!\lower0.7ex\hbox{${12}$}}}&0&0 \\ 0&0&{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 {12}}}\right.\kern-0em} \!\lower0.7ex\hbox{${12}$}}}&{{\raise0.7ex\hbox{${21}$} \!\mathord{\left/ {\vphantom {{21} {28}}}\right.\kern-0em} \!\lower0.7ex\hbox{${28}$}}}&0 \\ 0&0&0&{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 {28}}}\right.\kern-0em} \!\lower0.7ex\hbox{${28}$}}}&0 \end{array}} \right]$ | 1.1206 | $\left[ {\begin{array}{*{20}{c}} {12.93} \\ {24.78} \\ {42.13} \\ {18.95} \\ {1.21} \end{array}} \right]$ |
| 2018 j = 9 | ${{L}_{9}} = \left[ {\begin{array}{*{20}{c}} 0&0&0&0&{{\raise0.7ex\hbox{${13}$} \!\mathord{\left/ {\vphantom {{13} 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}} \\ 0&0&0&0&{{\raise0.7ex\hbox{${38}$} \!\mathord{\left/ {\vphantom {{38} 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}} \\ {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {12}}}\right.\kern-0em} \!\lower0.7ex\hbox{${12}$}}}&{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {23}}}\right.\kern-0em} \!\lower0.7ex\hbox{${23}$}}}&{{\raise0.7ex\hbox{$0$} \!\mathord{\left/ {\vphantom {0 {13}}}\right.\kern-0em} \!\lower0.7ex\hbox{${13}$}}}&0&0 \\ 0&0&{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {13}}}\right.\kern-0em} \!\lower0.7ex\hbox{${13}$}}}&{{\raise0.7ex\hbox{${22}$} \!\mathord{\left/ {\vphantom {{22} {23}}}\right.\kern-0em} \!\lower0.7ex\hbox{${23}$}}}&0 \\ 0&0&0&{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {23}}}\right.\kern-0em} \!\lower0.7ex\hbox{${23}$}}}&0 \end{array}} \right]$ | 0.9617 | $\left[ {\begin{array}{*{20}{c}} {13.22} \\ {38.66} \\ {2.89} \\ {43.27} \\ {1.96} \end{array}} \right]$ |
Прогноз выживания ценопопуляции дается величиной λ1(L) – доминантным собственным числом калиброванной ПМП L, которое показывает асимптотическую скорость роста популяции: если L(t) = L остается постоянной во времени, то при t → ∞ структура популяции x(t) сходится к равновесию – собственному вектору x*, отвечающему λ1(L), – а ее динамика x(t) ~ λ1(L)tx*, т.е. стремится к геометрическому росту (или убыли) с показателем λ1(L) > 0 (Logofet, 1993; Caswell, 2001; Логофет, Уланова, 2018). Поэтому прогноз положительный, если λ1(L) > 1, и отрицательный, если λ1(L) < 1. В неавтономной (т.е. с зависимостью параметров от времени) модели вместе с изменением матрицы L(t) в зависимости от t существенно меняется и величина λ1(L), оставляя результирующий прогноз неопределенным (Логофет и др., 2019, табл. 3).
Прогноз выживания через осреднение годичных ПМП. Чтобы зафиксировать онтогенетические переходы и пополнение популяции, необходимы данные двух последовательных переписей (в моменты t и t + 1), и потому число калиброванных ПМП всегда на единицу меньше числа лет наблюдений (11 лет наблюдений обеспечивают калибровку 10 матриц L(t)). Нет оснований полагать, что они окажутся одинаковыми, а практика калибровки показывает различия не только количественные, но и качественные: в отдельные годы прогноз выживания меняется на противоположный (Логофет и др., 2017а, б, 2019). Итог всего периода мониторинга способна отразить матрица G, найденная методом СМО неотрицательных матриц (Logofet, 2018; Логофет и др., 2019).
Логика СМО такова: согласно калиброванной модели (1) вектор, x(2009), структуры популяции в начальный момент наблюдений t = 2009 преобразуется в x(2019) – вектор структуры в последний момент t = 2019 – путем последовательного умножения на 10 годичных ПМП L(t), т.е. (после переобозначения L(t) = Lj , j = t – 2009)
(3)
$\begin{gathered} x\left( {2019} \right) = \\ = {{L}_{9}}\, \cdot \,{{L}_{8}}\, \cdot \,{{L}_{7}}\, \cdot \,{{L}_{6}}\, \cdot \,{{L}_{5}}\, \cdot \,{{L}_{4}}\, \cdot \,{{L}_{3}}\, \cdot \,{{L}_{2}}\, \cdot \,{{L}_{1}}\, \cdot \,{{L}_{0}}\, \cdot \,x\left( {2009} \right). \\ \end{gathered} $То же самое должна делать и средняя матрица G, т.е.
(4)
${{G}^{{10}}} = {{L}_{9}} \cdot {{L}_{8}} \cdot {{L}_{7}} \cdot {{L}_{6}} \cdot {{L}_{5}} \cdot {{L}_{4}} \cdot {{L}_{3}} \cdot {{L}_{2}} \cdot {{L}_{1}} \cdot {{L}_{0}}.$Уравнение (4) указывает на мультипликативный характер осреднения, а общее для всех усредняемых матриц строение (2) требует того же и от средней матрицы G. Логично потребовать, кроме того, чтобы все элементы средней матрицы не выходили за границы соответствующих элементов усредняемых матриц.
Данная логика приводит к математической задаче минимизации ошибки приближения в решении матричного уравнения (4) (Логофет и др., 2019, Приложение А). Положение доминантного собственного числа λ1(G) средней матрицы G относительно 1 позволяет сделать вывод о судьбе ценопопуляции в долговременной перспективе на основании нескольких лет наблюдений: рост, если λ1(G) > 1; убыль, если λ1(G) < 1; стабилизация, если λ1(G) = 1. Десять лет мониторинга ценопопуляции A. albana привели к значению λ1(G) = = 0.89262 < 1 у средней матрицы G, найденной с погрешностью в сотых долях (Логофет и др., 2019, табл. 3), т.е. к негативному прогнозу выживания ценопопуляции. Отметим, что предельный вектор, y*, матрицы G был весьма близок к вектору x(2019) – относительной структуре популяции в последний год наблюдения: мера несходства Кейфица (Keyfitz, 1968; Логофет и др., 2019) между ними составляла менее 1%. Итог 11 лет мониторинга, т.е. результат СМО 10 годичных ПМП, представлен в настоящей статье.
МЕТОД ОБРАТНОГО ПРОГНОЗА В МАТРИЧНОЙ МОДЕЛИ A. ALBANA
Обратный прогноз призван подтвердить или поставить под сомнение выводы прогноза прямого – в частности, по значению λ1(G–) структурно-мультипликативного среднего, G–, годичных матриц обратного прогноза и предельному вектору, $z_{{{{G}_{ - }}}}^{*}$, средней матрицы. Как отмечено выше, рутинные методы обратного прогноза работают лишь в специальных случаях, а для матричной модели формальное обращение уравнения (1), т.е.
(5)
$\begin{gathered} x\left( t \right) = L{{\left( t \right)}^{{--1}}}x\left( {t + 1} \right),~ \\ t = 2009,\,\,2010,\,\, \ldots ,\,\,2018, \\ \end{gathered} $Простой альтернативный подход к обратному прогнозу: получать наблюдавшиеся структуры ценопопуляции в обратном порядке, от 2019 к 2009 году, с помощью ПМП, B(t), отвечающих прежнему ГЖЦ (рис. 1), – наталкивается на неоднозначность решения задачи. В прямой модели все переходы между стадиями, состоявшиеся за один год, т.е. все изменения вектора x(t) = [p(t), j(t), im(t), v(t), g(t)]T во времени, известны из наблюдений, а обратных наблюдений в реальности нет. Основное уравнение обратной модели, которое связывает данные наблюдений в обратном порядке,
имеет при каждом t много разных решений даже в рациональных числах (лишь 5 скалярных уравнений для 10 неизвестных элементов матрицы B). Поэтому нужен специальный подход к реализации идеи обратного прогноза.Идея обратного прогноза через обращение вспять оси времени в наблюдениях была успешно реализована для дискретной марковской цепи (Logofet, 2019a), и в следующем разделе мы применяем ее для построения обратного прогноза в матричной модели популяции.
Обратный прогноз через “обращение” годичной ПМП. Как отмечено выше, обращение годичной ПМП в смысле вычисления обратной матрицы неприемлемо для обратного прогноза, и потому “обращение” приобретает в нашем случае специальный смысл. Данные ежегодных наблюдений содержат сведения не только о структуре ценопопуляции (табл. 1), но и обо всех переходах по стадиям онтогенеза, состоявшихся за прошедший год (табл. 2) согласно ГЖЦ (рис. 1). Представим эти данные в форме целочисленных таблиц TL(t), имеющих такое же строение, как и сами годичные ПМП, т.е. в соответствии с ГЖЦ (табл. 2), но показывавших не частоты или коэффициенты, а фактические числа переходов и пополнений. Тогда строчные суммы элементов TL(t) будут закономерно совпадать с размерами соответствующих стадийных групп (технические подробности в Приложении А).
Обратить время в этих данных значит изменить направления всех переходов жизненного цикла на противоположные или сделать то же самое с дугами ГЖЦ (рис. 2). При этом само количество переходов не изменяется, и в терминах таблицы TL(t) обращение означает транспонирование (т.е. перенос каждого элемента симметрично относительно главной диагонали) или, что эквивалентно, замену строк таблицы ее столбцами. Полученную таким образом таблицу TL(t – 1)T нужно превратить в матрицу B(t) обратного прогноза так, чтобы выполнялось условие калибровки (6). Для этого достаточно положить
(7)
$\begin{gathered} B(t) = {\text{diag\{ }}{{d}_{1}},\,\,{{d}_{2}},\,\, \ldots ,\,\,{{d}_{5}}\} {{T}_{L}}{{\left( {t--1} \right)}^{{\text{T}}}}, \\ t = 2019,\,\,2018,\,\, \ldots ,\,\,2010, \\ \end{gathered} $(8)
$\begin{gathered} {\text{diag}}\{ {{d}_{1}},\,\,{{d}_{2}},\,\, \ldots ,\,\,{{d}_{5}}\} {{T}_{L}}{{\left( {t--{\text{ }}1} \right)}^{{\text{T}}}}x\left( t \right) = x\left( {t--1} \right), \\ t = 2019,\,\,2018,\,\, \ldots ,\,\,2010 \\ \end{gathered} $Таким образом, каждая из 10 матриц (7) обратного прогноза неотрицательна, и ее строение соответствует сильно связному орграфу (рис. 2), т.е. матрица неразложима (irreducible; Horn, Johnson, 1990), и по теореме Перрона–Фробениуса (Гантмахер, 1967) она имеет доминантное собственное число, λ1(B(t)) > 0, и соответствующий ему положительный собственный вектор, y* > 0, который представляет собой устойчивое предельное распределение (Caswell, 2001; Логофет, Уланова, 2018) в модели (6) обратного прогноза. После калибровки матрицы B(t) все ее собственные числа и соответствующие им собственные векторы вычисляем стандартной процедурой, из результатов которой выбираем доминантное собственное число λ1 и нормируем соответствующий ему вектор (Приложение Б). По смыслу обратного прогноза ожидается, что λ1(B(t)) > 1 для тех лет, для которых λ1(L(t – 1)) < 1, т.е. результирующий обратный прогноз следует получать, как и прямой прогноз, через осреднение годичных матриц (Приложение В).
Обратный прогноз через осреднение годичных матриц. Логика осреднения годичных матриц обратного прогноза такая же, как и в прямой модели (Логофет и др., 2019): структура популяции, зафиксированная в первый год наблюдения, должна переходить в структуру последнего года путем ее умножения на последовательность годичных матриц в хронологическом порядке (от 2019 к 2010 году в данном случае), и такой же результат должна давать средняя матрица G– в степени, равной числу шагов. Формально
(9)
$G_{\_}^{{{\mathbf{10}}}} = B\left( {2010} \right)...\,\,B\left( {2018} \right)B\left( {2019} \right),$(10)
${{G}_{ - }} = \left[ {\begin{array}{*{20}{c}} 0&{{{d}_{ - }}}&{{{e}_{ - }}}&0&0 \\ 0&0&{{{f}_{ - }}}&0&0 \\ 0&0&{{{h}_{ - }}}&{{{k}_{ - }}}&0 \\ 0&0&0&{{{l}_{ - }}}&{{{m}_{ - }}} \\ {{{a}_{ - }}}&{{{b}_{ - }}}&{{{c}_{ - }}}&0&0 \end{array}} \right];\,\,\,\,{{a}_{ - }},\,\,{{b}_{ - }},\,\,...,\,\,{{l}_{ - }},\,\,{{m}_{ - }} \geqslant 0,$Условие (10) приводит к переопределенности (GUFO.ME, 2020) матричного уравнения (9) как системы из 25 скалярных уравнений для 10 неизвестных a–, b–, …, l–, m–, т.е. к отсутствию точного решения. Таким образом, поиск средней матрицы G– сводится к приближенному решению уравнения (9), т.е. к задаче ограниченной минимизации ошибки приближения (Приложение В).
РЕЗУЛЬТАТЫ
Калибровка годичных ПМП. Результаты калибровки матриц L(t) представлены в табл. 3. К девяти матрицам, калиброванным ранее (Логофет и др., 2019, табл. 3), последний, 2019-й, год наблюдений добавил матрицу L(2018) с доминантным собственным числом, меньшим 1 (последняя строка табл. 3).
Калиброванные матрицы обратного прогноза. Результаты вычисления годичных матриц B(t) по формулам (7), (8) представлены в табл. 4. Вариации меры приспособленности локальной популяции (доминантного собственного числа λ1(B(t)) по годам весьма значительны, как и в прямой модели. Как и ожидалось, λ1(B(t)) > 1 во всех тех случаях, когда прямая модель давала значение λ1(L(t – 1)) < 1 (табл. 3), и наоборот. Явной закономерности в предельных распределениях (векторах y*(t)) не наблюдается: в разные годы доминирование перемещается между стадиями j, im и v, и только при наименьшем значении λ1(t = 2011) доминирующей оказалась стадия p.
Таблица 4.
Результаты калибровки матриц обратного прогноза для A. albana по данным 2009–2019 гг.
| Год переписи, t | Матрица B(t) | λ1(B(t)) | Вектор y*, % |
|---|---|---|---|
| 2019 j = 9 | $\left\lfloor {\begin{array}{*{20}{c}} 0&0&{{\raise0.7ex\hbox{$6$} \!\mathord{\left/ {\vphantom {6 {77}}}\right.\kern-0em} \!\lower0.7ex\hbox{${77}$}}}&0&0 \\ 0&0&{{\raise0.7ex\hbox{${23}$} \!\mathord{\left/ {\vphantom {{23} 2}}\right.\kern-0em} \!\lower0.7ex\hbox{$2$}}}&0&0 \\ 0&0&{{\raise0.7ex\hbox{${52}$} \!\mathord{\left/ {\vphantom {{52} {31}}}\right.\kern-0em} \!\lower0.7ex\hbox{${31}$}}}&{{\raise0.7ex\hbox{${13}$} \!\mathord{\left/ {\vphantom {{13} {31}}}\right.\kern-0em} \!\lower0.7ex\hbox{${31}$}}}&0 \\ 0&0&0&{{\raise0.7ex\hbox{${437}$} \!\mathord{\left/ {\vphantom {{437} {438}}}\right.\kern-0em} \!\lower0.7ex\hbox{${438}$}}}&{{\raise0.7ex\hbox{${23}$} \!\mathord{\left/ {\vphantom {{23} {438}}}\right.\kern-0em} \!\lower0.7ex\hbox{${438}$}}} \\ {{\raise0.7ex\hbox{${15}$} \!\mathord{\left/ {\vphantom {{15} {479}}}\right.\kern-0em} \!\lower0.7ex\hbox{${479}$}}}&{{\raise0.7ex\hbox{${20}$} \!\mathord{\left/ {\vphantom {{20} {479}}}\right.\kern-0em} \!\lower0.7ex\hbox{${479}$}}}&{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 {958}}}\right.\kern-0em} \!\lower0.7ex\hbox{${958}$}}}&0&0 \end{array}} \right\rfloor $ | 1.6837 | $\left\lfloor {\begin{array}{*{20}{c}} {14.02} \\ {73.04} \\ {10.69} \\ {0.16} \\ {2.09} \end{array}} \right\rfloor $ |
| 2018 j = 8 | $\left\lfloor {\begin{array}{*{20}{c}} 0&0&{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 {13}}}\right.\kern-0em} \!\lower0.7ex\hbox{${13}$}}}&0&0 \\ 0&0&{{\raise0.7ex\hbox{$8$} \!\mathord{\left/ {\vphantom {8 {13}}}\right.\kern-0em} \!\lower0.7ex\hbox{${13}$}}}&0&0 \\ 0&0&{{\raise0.7ex\hbox{${16}$} \!\mathord{\left/ {\vphantom {{16} {25}}}\right.\kern-0em} \!\lower0.7ex\hbox{${25}$}}}&{{\raise0.7ex\hbox{$4$} \!\mathord{\left/ {\vphantom {4 {25}}}\right.\kern-0em} \!\lower0.7ex\hbox{${25}$}}}&0 \\ 0&0&0&{{\raise0.7ex\hbox{${588}$} \!\mathord{\left/ {\vphantom {{588} {487}}}\right.\kern-0em} \!\lower0.7ex\hbox{${487}$}}}&{{\raise0.7ex\hbox{${56}$} \!\mathord{\left/ {\vphantom {{56} {487}}}\right.\kern-0em} \!\lower0.7ex\hbox{${487}$}}} \\ {{\raise0.7ex\hbox{${12}$} \!\mathord{\left/ {\vphantom {{12} {673}}}\right.\kern-0em} \!\lower0.7ex\hbox{${673}$}}}&{{\raise0.7ex\hbox{${23}$} \!\mathord{\left/ {\vphantom {{23} {673}}}\right.\kern-0em} \!\lower0.7ex\hbox{${673}$}}}&0&0&0 \end{array}} \right\rfloor $ | 1.2080 | $\left\lfloor {\begin{array}{*{20}{c}} {3.63} \\ {9.67} \\ {18.98} \\ {67.39} \\ {0.33} \end{array}} \right\rfloor $ |
| 2017 j = 7 | $\left\lfloor {\begin{array}{*{20}{c}} 0&0&{{\raise0.7ex\hbox{$8$} \!\mathord{\left/ {\vphantom {8 5}}\right.\kern-0em} \!\lower0.7ex\hbox{$5$}}}&0&0 \\ 0&0&{{\raise0.7ex\hbox{${49}$} \!\mathord{\left/ {\vphantom {{49} 5}}\right.\kern-0em} \!\lower0.7ex\hbox{$5$}}}&0&0 \\ 0&0&{{\raise0.7ex\hbox{${51}$} \!\mathord{\left/ {\vphantom {{51} {35}}}\right.\kern-0em} \!\lower0.7ex\hbox{${35}$}}}&{{\raise0.7ex\hbox{${34}$} \!\mathord{\left/ {\vphantom {{34} {35}}}\right.\kern-0em} \!\lower0.7ex\hbox{${35}$}}}&0 \\ 0&0&0&{{\raise0.7ex\hbox{${50}$} \!\mathord{\left/ {\vphantom {{50} {21}}}\right.\kern-0em} \!\lower0.7ex\hbox{${21}$}}}&{{\raise0.7ex\hbox{${25}$} \!\mathord{\left/ {\vphantom {{25} {42}}}\right.\kern-0em} \!\lower0.7ex\hbox{${42}$}}} \\ {{\raise0.7ex\hbox{${12}$} \!\mathord{\left/ {\vphantom {{12} {377}}}\right.\kern-0em} \!\lower0.7ex\hbox{${377}$}}}&{{\raise0.7ex\hbox{${57}$} \!\mathord{\left/ {\vphantom {{57} {377}}}\right.\kern-0em} \!\lower0.7ex\hbox{${377}$}}}&0&0&0 \end{array}} \right\rfloor $ | 0.8071 | $\left\lfloor {\begin{array}{*{20}{c}} {13.72} \\ {39.80} \\ {13.29} \\ {20.99} \\ {12.20} \end{array}} \right\rfloor $ |
| 2016 j = 6 | $\left\lfloor {\begin{array}{*{20}{c}} {{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 5}}\right.\kern-0em} \!\lower0.7ex\hbox{$5$}}}&0&0&0&0 \\ 0&0&{{\raise0.7ex\hbox{${19}$} \!\mathord{\left/ {\vphantom {{19} {13}}}\right.\kern-0em} \!\lower0.7ex\hbox{${13}$}}}&0&0 \\ 0&0&{{\raise0.7ex\hbox{${30}$} \!\mathord{\left/ {\vphantom {{30} {149}}}\right.\kern-0em} \!\lower0.7ex\hbox{${149}$}}}&{{\raise0.7ex\hbox{${50}$} \!\mathord{\left/ {\vphantom {{50} {149}}}\right.\kern-0em} \!\lower0.7ex\hbox{${149}$}}}&0 \\ 0&0&0&{{\raise0.7ex\hbox{${170}$} \!\mathord{\left/ {\vphantom {{170} {189}}}\right.\kern-0em} \!\lower0.7ex\hbox{${189}$}}}&{{\raise0.7ex\hbox{${20}$} \!\mathord{\left/ {\vphantom {{20} {189}}}\right.\kern-0em} \!\lower0.7ex\hbox{${189}$}}} \\ {{\raise0.7ex\hbox{${40}$} \!\mathord{\left/ {\vphantom {{40} {941}}}\right.\kern-0em} \!\lower0.7ex\hbox{${941}$}}}&{{\raise0.7ex\hbox{${116}$} \!\mathord{\left/ {\vphantom {{116} {941}}}\right.\kern-0em} \!\lower0.7ex\hbox{${941}$}}}&0&0&0 \end{array}} \right\rfloor $ | 0.9104 | $\left\lfloor {\begin{array}{*{20}{c}} 0 \\ {32.53} \\ {20.26} \\ {42.81} \\ {4.40} \end{array}} \right\rfloor $ |
| 2015 j =5 | $\left\lfloor {\begin{array}{*{20}{c}} 0&0&{{\raise0.7ex\hbox{$8$} \!\mathord{\left/ {\vphantom {8 5}}\right.\kern-0em} \!\lower0.7ex\hbox{$5$}}}&0&0 \\ 0&0&{{\raise0.7ex\hbox{${49}$} \!\mathord{\left/ {\vphantom {{49} 5}}\right.\kern-0em} \!\lower0.7ex\hbox{$5$}}}&0&0 \\ 0&0&{{\raise0.7ex\hbox{${51}$} \!\mathord{\left/ {\vphantom {{51} {35}}}\right.\kern-0em} \!\lower0.7ex\hbox{${35}$}}}&{{\raise0.7ex\hbox{${34}$} \!\mathord{\left/ {\vphantom {{34} {35}}}\right.\kern-0em} \!\lower0.7ex\hbox{${35}$}}}&0 \\ 0&0&0&{{\raise0.7ex\hbox{${50}$} \!\mathord{\left/ {\vphantom {{50} {21}}}\right.\kern-0em} \!\lower0.7ex\hbox{${21}$}}}&{{\raise0.7ex\hbox{${25}$} \!\mathord{\left/ {\vphantom {{25} {42}}}\right.\kern-0em} \!\lower0.7ex\hbox{${42}$}}} \\ {{\raise0.7ex\hbox{${12}$} \!\mathord{\left/ {\vphantom {{12} {377}}}\right.\kern-0em} \!\lower0.7ex\hbox{${377}$}}}&{{\raise0.7ex\hbox{${57}$} \!\mathord{\left/ {\vphantom {{57} {377}}}\right.\kern-0em} \!\lower0.7ex\hbox{${377}$}}}&0&0&0 \end{array}} \right\rfloor $ | 2.5137 | $\left\lfloor {\begin{array}{*{20}{c}} {9.27} \\ {56.79} \\ {14.57} \\ {15.84} \\ {3.53} \end{array}} \right\rfloor $ |
| 2014 j = 4 | $\left\lfloor {\begin{array}{*{20}{c}} 0&0&{{\raise0.7ex\hbox{${19}$} \!\mathord{\left/ {\vphantom {{19} {34}}}\right.\kern-0em} \!\lower0.7ex\hbox{${34}$}}}&0&0 \\ 0&0&{{\raise0.7ex\hbox{${137}$} \!\mathord{\left/ {\vphantom {{137} {34}}}\right.\kern-0em} \!\lower0.7ex\hbox{${34}$}}}&0&0 \\ 0&0&{{\raise0.7ex\hbox{${665}$} \!\mathord{\left/ {\vphantom {{665} {388}}}\right.\kern-0em} \!\lower0.7ex\hbox{${388}$}}}&{{\raise0.7ex\hbox{${285}$} \!\mathord{\left/ {\vphantom {{285} {388}}}\right.\kern-0em} \!\lower0.7ex\hbox{${388}$}}}&0 \\ 0&0&0&{{\raise0.7ex\hbox{${3212}$} \!\mathord{\left/ {\vphantom {{3212} {2209}}}\right.\kern-0em} \!\lower0.7ex\hbox{${2209}$}}}&{{\raise0.7ex\hbox{${219}$} \!\mathord{\left/ {\vphantom {{219} {2209}}}\right.\kern-0em} \!\lower0.7ex\hbox{${2209}$}}} \\ {{\raise0.7ex\hbox{${12}$} \!\mathord{\left/ {\vphantom {{12} {1241}}}\right.\kern-0em} \!\lower0.7ex\hbox{${1241}$}}}&{{\raise0.7ex\hbox{${147}$} \!\mathord{\left/ {\vphantom {{147} {2482}}}\right.\kern-0em} \!\lower0.7ex\hbox{${2482}$}}}&{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 {2482}}}\right.\kern-0em} \!\lower0.7ex\hbox{${2482}$}}}&0&0 \end{array}} \right\rfloor $ | 1.7351 | $\left\lfloor {\begin{array}{*{20}{c}} {8.58} \\ {61.84} \\ {26.63} \\ {0.77} \\ {2.18} \end{array}} \right\rfloor $ |
| 2013 j = 3 | $\left\lfloor {\begin{array}{*{20}{c}} 0&{{\raise0.7ex\hbox{${49}$} \!\mathord{\left/ {\vphantom {{49} {1087}}}\right.\kern-0em} \!\lower0.7ex\hbox{${1087}$}}}&{{\raise0.7ex\hbox{${490}$} \!\mathord{\left/ {\vphantom {{490} {1087}}}\right.\kern-0em} \!\lower0.7ex\hbox{${1087}$}}}&0&0 \\ 0&0&{{\raise0.7ex\hbox{${86}$} \!\mathord{\left/ {\vphantom {{86} {95}}}\right.\kern-0em} \!\lower0.7ex\hbox{${95}$}}}&0&0 \\ 0&0&{{\raise0.7ex\hbox{${3393}$} \!\mathord{\left/ {\vphantom {{3393} {5749}}}\right.\kern-0em} \!\lower0.7ex\hbox{${5749}$}}}&{{\raise0.7ex\hbox{${2436}$} \!\mathord{\left/ {\vphantom {{2436} {5749}}}\right.\kern-0em} \!\lower0.7ex\hbox{${5749}$}}}&0 \\ 0&0&0&{{\raise0.7ex\hbox{${290}$} \!\mathord{\left/ {\vphantom {{290} {369}}}\right.\kern-0em} \!\lower0.7ex\hbox{${369}$}}}&{{\raise0.7ex\hbox{${116}$} \!\mathord{\left/ {\vphantom {{116} {1107}}}\right.\kern-0em} \!\lower0.7ex\hbox{${1107}$}}} \\ {{\raise0.7ex\hbox{${19}$} \!\mathord{\left/ {\vphantom {{19} {4772}}}\right.\kern-0em} \!\lower0.7ex\hbox{${4772}$}}}&{{\raise0.7ex\hbox{${34}$} \!\mathord{\left/ {\vphantom {{34} {1193}}}\right.\kern-0em} \!\lower0.7ex\hbox{${1193}$}}}&{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {4772}}}\right.\kern-0em} \!\lower0.7ex\hbox{${4772}$}}}&0&0 \end{array}} \right\rfloor $ | 0.7955 | $\left\lfloor {\begin{array}{*{20}{c}} {19.14} \\ {34.51} \\ {30.32} \\ {14.69} \\ {1.34} \end{array}} \right\rfloor $ |
| 2012 j = 2 | $\left\lfloor {\begin{array}{*{20}{c}} 0&{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {32}}}\right.\kern-0em} \!\lower0.7ex\hbox{${32}$}}}&{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 {16}}}\right.\kern-0em} \!\lower0.7ex\hbox{${16}$}}}&0&0 \\ 0&0&{{\raise0.7ex\hbox{${15}$} \!\mathord{\left/ {\vphantom {{15} {19}}}\right.\kern-0em} \!\lower0.7ex\hbox{${19}$}}}&0&0 \\ 0&0&{{\raise0.7ex\hbox{${903}$} \!\mathord{\left/ {\vphantom {{903} {2407}}}\right.\kern-0em} \!\lower0.7ex\hbox{${2407}$}}}&{{\raise0.7ex\hbox{${110}$} \!\mathord{\left/ {\vphantom {{110} {157}}}\right.\kern-0em} \!\lower0.7ex\hbox{${157}$}}}&0 \\ 0&0&0&{{\raise0.7ex\hbox{${171}$} \!\mathord{\left/ {\vphantom {{171} {175}}}\right.\kern-0em} \!\lower0.7ex\hbox{${175}$}}}&{{\raise0.7ex\hbox{${57}$} \!\mathord{\left/ {\vphantom {{57} {700}}}\right.\kern-0em} \!\lower0.7ex\hbox{${700}$}}} \\ {{\raise0.7ex\hbox{$7$} \!\mathord{\left/ {\vphantom {7 {1698}}}\right.\kern-0em} \!\lower0.7ex\hbox{${1698}$}}}&{{\raise0.7ex\hbox{${85}$} \!\mathord{\left/ {\vphantom {{85} {11886}}}\right.\kern-0em} \!\lower0.7ex\hbox{${11886}$}}}&{{\raise0.7ex\hbox{${25}$} \!\mathord{\left/ {\vphantom {{25} {11886}}}\right.\kern-0em} \!\lower0.7ex\hbox{${11886}$}}}&0&0 \end{array}} \right\rfloor $ | 0.9773 | $\left\lfloor {\begin{array}{*{20}{c}} {4.08} \\ {10.34} \\ {19.55} \\ {65.89} \\ {0.14} \end{array}} \right\rfloor $ |
| 2011 j = 1 | $\left\lfloor {\begin{array}{*{20}{c}} 0&{{\raise0.7ex\hbox{${210}$} \!\mathord{\left/ {\vphantom {{210} {401}}}\right.\kern-0em} \!\lower0.7ex\hbox{${401}$}}}&{{\raise0.7ex\hbox{${60}$} \!\mathord{\left/ {\vphantom {{60} {401}}}\right.\kern-0em} \!\lower0.7ex\hbox{${401}$}}}&0&0 \\ 0&0&{{\raise0.7ex\hbox{${48}$} \!\mathord{\left/ {\vphantom {{48} {43}}}\right.\kern-0em} \!\lower0.7ex\hbox{${43}$}}}&0&0 \\ 0&0&{{\raise0.7ex\hbox{${55}$} \!\mathord{\left/ {\vphantom {{55} {157}}}\right.\kern-0em} \!\lower0.7ex\hbox{${157}$}}}&{{\raise0.7ex\hbox{${110}$} \!\mathord{\left/ {\vphantom {{110} {157}}}\right.\kern-0em} \!\lower0.7ex\hbox{${157}$}}}&0 \\ 0&0&0&{{\raise0.7ex\hbox{${299}$} \!\mathord{\left/ {\vphantom {{299} {656}}}\right.\kern-0em} \!\lower0.7ex\hbox{${656}$}}}&{{\raise0.7ex\hbox{${13}$} \!\mathord{\left/ {\vphantom {{13} {656}}}\right.\kern-0em} \!\lower0.7ex\hbox{${656}$}}} \\ {{\raise0.7ex\hbox{${19}$} \!\mathord{\left/ {\vphantom {{19} {1756}}}\right.\kern-0em} \!\lower0.7ex\hbox{${1756}$}}}&{{\raise0.7ex\hbox{${31}$} \!\mathord{\left/ {\vphantom {{31} {1756}}}\right.\kern-0em} \!\lower0.7ex\hbox{${1756}$}}}&0&0&0 \end{array}} \right\rfloor $ | 0.4733 | $\left\lfloor {\begin{array}{*{20}{c}} {44.23} \\ {35.66} \\ {15.12} \\ {2.65} \\ {2.34} \end{array}} \right\rfloor $ |
| 2010 j = 0 | $\left\lfloor {\begin{array}{*{20}{c}} 0&{{\raise0.7ex\hbox{${148}$} \!\mathord{\left/ {\vphantom {{148} {247}}}\right.\kern-0em} \!\lower0.7ex\hbox{${247}$}}}&{{\raise0.7ex\hbox{${37}$} \!\mathord{\left/ {\vphantom {{37} {247}}}\right.\kern-0em} \!\lower0.7ex\hbox{${247}$}}}&0&0 \\ 0&0&2&0&0 \\ 0&0&{{\raise0.7ex\hbox{${66}$} \!\mathord{\left/ {\vphantom {{66} {41}}}\right.\kern-0em} \!\lower0.7ex\hbox{${41}$}}}&{{\raise0.7ex\hbox{${33}$} \!\mathord{\left/ {\vphantom {{33} {82}}}\right.\kern-0em} \!\lower0.7ex\hbox{${82}$}}}&0 \\ 0&0&0&{{\raise0.7ex\hbox{${133}$} \!\mathord{\left/ {\vphantom {{133} {99}}}\right.\kern-0em} \!\lower0.7ex\hbox{${99}$}}}&{{\raise0.7ex\hbox{$7$} \!\mathord{\left/ {\vphantom {7 {99}}}\right.\kern-0em} \!\lower0.7ex\hbox{${99}$}}} \\ {{\raise0.7ex\hbox{${26}$} \!\mathord{\left/ {\vphantom {{26} {199}}}\right.\kern-0em} \!\lower0.7ex\hbox{${199}$}}}&{{\raise0.7ex\hbox{${104}$} \!\mathord{\left/ {\vphantom {{104} {597}}}\right.\kern-0em} \!\lower0.7ex\hbox{${597}$}}}&{{\raise0.7ex\hbox{${134}$} \!\mathord{\left/ {\vphantom {{134} {995}}}\right.\kern-0em} \!\lower0.7ex\hbox{${995}$}}}&0&0 \end{array}} \right\rfloor $ | 1.6281 | $\left\lfloor {\begin{array}{*{20}{c}} {18.13} \\ {40.93} \\ {33.32} \\ {1.52} \\ {6.10} \end{array}} \right\rfloor $ |
Осреднение годичных матриц прямого и обратного прогноза. Структурно-мультипликативное среднее 10 годичных ПРМ L(t), полученное как приближенное решение уравнения (4), показано в первой строке табл. 5. Добавление 10-й матрицы с λ1(L(2018)) < 1 (табл. 3) к набору из 9 усредняемых ПМП (Логофет и др., 2019, табл. 3) закономерно снизило значение λ1(G) (в сотых долях), т.е. 10-летний мониторинг дает прогноз с более быстрым убыванием ценопопуляции, нежели 9‑летний. Ошибка приближения снизилась почти на порядок. Предельное распределение стадийных групп сохранило двугорбый характер с доминированием в стадиях j и v, и оно по-прежнему мало отличается от распределения x(2019) в последний год наблюдения (4.5%, см. последний столбец табл. 5).
Таблица 5.
Структурно-мультипликативное осреднение 10 годичных ПМП (табл. 3) и 10 матриц обратного прогноза (табл. 4)
| Средняя матрица | Погрешность осреднения† | λ1 | Вектор z*‡, % | $\Delta \left( {\frac{{100x{{{({{t}_{{{\text{fin}}}}})}}^{ \pm }}}}{{{{{\left\| {x({{t}_{{{\text{fin}}}}})} \right\|}}_{1}}}} - z{\text{*}}} \right)$ |
|---|---|---|---|---|
| $G = \left\lfloor {\begin{array}{*{20}{c}} 0&0&0&0&{8.5705} \\ {0.2791}&0&0&0&{22.5219} \\ {0.0900}&{0.0700}&{0.1173}&0&{0.3017} \\ 0&0&{0.2097}&{0.8390}&0 \\ 0&0&0&{0.0502}&0 \end{array}} \right\rfloor $ | 3.0153 × 10–3 | 0.8876 | $\left\lfloor {\begin{array}{*{20}{c}} {15.87} \\ {46.70} \\ {6.74} \\ {29.05} \\ {1.64} \end{array}} \right\rfloor $ | 4.48 |
| ${{G}_{ - }} = \left\lfloor {\begin{array}{*{20}{c}} 0&{0.1624}&{0.2543}&0&0 \\ 0&0&{1.2346}&0&0 \\ 0&0&{0.9151}&{0.4882}&0 \\ 0&0&0&{1.0308}&{0.0799} \\ {0.0687}&{0.1257}&{0.0066}&0&0 \end{array}} \right\rfloor $ | 0.020891 | 1.0724 | $\left\lfloor {\begin{array}{*{20}{c}} {13.48} \\ {37.76} \\ {32.72} \\ {10.55} \\ {5.49} \end{array}} \right\rfloor $ | 2.31 |
Приближенное решение уравнения (9) для 10 матриц из табл. 4, т.е. СМО годичных матриц обратного прогноза, с приемлемой точностью приближения дает матрица G–, представленная в последней строке табл. 5. Строение G–, очевидно, соответствует (10), т.е. обращенному ГЖЦ (рис. 2), а значения ее элементов не выходят из границ, заданных соответствующими элементами усредняемых матриц (Приложение В, условие (В.2)). Доминантное собственное число λ1(G–) матрицы обратного прогноза оказалось больше 1, подтвердив ожидания, а соответствующий доминантный собственный вектор z*, т.е. предельное распределение численности стадийных групп при движении назад, оказался весьма близким к фактическому в начальный год наблюдений: показатель несходства между ними по Кейфицу около 2% (табл. 5).
ОБСУЖДЕНИЕ И ЗАКЛЮЧЕНИЕ
Ежегодные наблюдения за ценопопуляцией проломника Androsace albana на постоянных площадках продолжаются с 2009 г. (Логофет и др., 2017б, 2019), и каждый очередной год добавляет новую матрицу в набор годичных ПМП, расширяя спектр вариаций условий среды, опосредованно отраженных в матрицах. Этот набор служит исходным пунктом в оценке жизнеспособности ценопопуляции по каждому из двух дальнейших альтернативных направлений. Оценка стохастической скорости роста, λS, популяции в случайно меняющейся среде (Tuljapurkar, 1986, 1990; Caswell, 2001) преобладает в англоязычной литературе (Caswell, 2010), а вычисление доминантного собственного числа λ1(G) средней матрицы G следует оригинальной концепции структурно-геометрического (структурно-мультипликативного в данной статье) осреднения неотрицательных матриц (Logofet, 2018, 2019b; Логофет и др., 2019). Оба подхода дают качественно одинаковый – отрицательный – прогноз выживания ценопопуляции A. albana (Логофет и др., 2019), хотя количественные результаты, т.е. скорости ежегодного снижения численности, заметно различаются (Логофет и др., 2019, табл. 3, 4).
Поскольку результат СМО годичных ПМП представляет собой приближенное решение уравнения (9) (Приложение В), причину вышеназванного различия можно усмотреть в неточности приближения, так как λ1 любой неотрицательной неразложимой матрицы весьма чувствительно к вариациям ее элементов (монотонно возрастает при увеличении любого элемента и наоборот; Гантмахер, 1967, §XIII.3, Теорема 6; Логофет, Уланова, 2018, утверждение (П7.1–2)). Это классическое положение имеет качественный характер и нуждается в дальнейшем теоретическом уточнении в связи с задачей СМО годичных ПМП. Несколько математических результатов были получены в этой связи (Protasov, 2019; Протасов, Широков, 2019), однако до практических рекомендаций дело еще не дошло.
В подобной ситуации возрастает роль альтернативных подходов к задаче прогноза, способных подтвердить выводы, полученные методом СМО, и обратный прогноз выступает одним из таких методов. Годичные матрицы, B(t), обратного прогноза (табл. 4) обнаружили не меньшее разнообразие характеристик, чем ПМП прямой модели (табл. 3), в зависимости от года наблюдения t. Примечательно, что мера, λ1(B(t)), “обратной” жизнеспособности ценопопуляции оказалась больше 1 во все те годы, когда “прямая” мера на предыдущем шаге, λ1(L(t – 1), была меньше 1, и наоборот, – подтверждая формально очевидное положение здравого смысла.
Как и в прямой модели, итоговый прогноз жизнеспособности дает структурно-мультипликативная средняя матрица, G–, ряда годичных матриц своим доминантным собственным числом λ1(G–). Оно закономерно оказалось больше 1 (табл. 5), указывая на рост ценопопуляции в обратном направлении времени, а предельное распределение, z*, размеров стадийных групп практически совпадает с финальным распределением, x(2009), при движении назад (различие менее 2%; табл. 5).
Предложенная методика обратного прогноза оказалась эффективной в матричной модели популяции A. albana со стадийной структурой, и она не специфична для A. albana: единственное принципиальное условие – неразложимость годичных матриц, т.е. сильная связность исходного ГЖЦ (рис. 1), – обеспечено непрерывностью онтогенеза, начальная стадия которого пополняется в результате репродукции. Поэтому методика обратного прогноза применима во всех случаях, где имеется временнóй ряд данных типа “идентифицированные особи” (“identified individuals”; Caswell, 2001, p. 134). В приложении к данным многолетнего мониторинга ценопопуляции A. albana данная методика подтвердила справедливость “неутешительного прогноза выживания ценопопуляции” на альпийской пустоши (Логофет и др., 2019).
Сбор и обработка полевого материала осуществлены при финансовой поддержке РФФИ (грант № 14-04-00214). Модельная часть исследований поддержана РФФИ, грант № 19-04-01227. Вычисления проделаны в среде MATLAB, версия R2019b.
Список литературы
Гантмахер Ф.Р., 1967. Теория матриц. М.: Наука. 576 с.
Казанцева Е.С., 2016. Популяционная динамика и семенная продуктивность малолетних альпийских растений северо-западного Кавказа. Дис. … канд. биол. наук. М.: МГУ. 165 с.
Красная книга Краснодарского края, 2007. Растения и грибы. Изд. 2-е / Отв. ред. Литвинская С.А. Краснодар: ООО “Дизайн Бюро № 1”. 640 с.
Красная книга Республики Адыгея, 2012. Редкие и находящиеся под угрозой исчезновения объекты животного и растительного мира: в 2 ч. Майкоп: Качество. 340 с.
Логофет Д.О, Белова И.Н., 2007. Неотрицательные матрицы как инструмент моделирования динамики популяций: классические модели и современные обобщения // Фунд. и прикл. математика. Т. 13. № 4. С. 145–164.
Логофет Д.О., Маслов А.А., 2018. Анализ мелкомасштабной динамики двух видов-доминантов в сосняке чернично-бруснично-долгомошном. II. Неоднородная марковская цепь и осредненные показатели // Журн. общ. биологии. Т. 79. № 2. С. 135–147.
Логофет Д.О., Уланова Н.Г., 2018. Матричные модели в популяционной биологии. Уч. пособие, 2-е изд. M.: МАКС Пресс. 128 с. https://elibrary.ru/item.asp?id=32701104
Логофет Д.О., Уланова Н.Г., Белова И.Н., 2015. Поливариантный онтогенез у вейников: новые модели и новые открытия // Журн. общ. биологии. Т. 76. № 6. С. 438–460.
Логофет Д.О., Уланова Н.Г., Белова И.Н., 2016а. От неопределенности к числу: развитие метода оценки приспособленности клонального вида с поливариантным онтогенезом // Журн. общ. биологии. Т. 77. № 5. С. 379–396.
Логофет Д.О., Белова И.Н., Казанцева Е.С., Онипченко В.Г., 2016б. Ценопопуляция незабудочника кавказского (Eritrichium caucasicum) как объект математического моделирования. I. Граф жизненного цикла и неавтономная матричная модель // Журн. общ. биологии. Т. 77. № 2. С. 106–121.
Логофет Д.О., Казанцева Е.С., Белова И.Н., Онипченко В.Г., 2017а. Ценопопуляция незабудочника кавказского (Eritrichium caucasicum) как объект математического моделирования. II. Сколько лет живет малолетник? // Журн. общ. биологии. Т. 78. № 1. С. 56–66.
Логофет Д.О., Казанцева Е.С., Белова И.Н., Онипченко В.Г., 2017б. Сколько лет живет альпийский малолетник? Модельный подход // Журн. общ. биологии. Т. 78. № 5. С. 63–80.
Логофет Д.О., Казанцева Е.С., Белова И.Н., Онипченко В.Г., 2018. Ценопопуляция незабудочника кавказского (Eritrichium caucasicum) как объект математического моделирования. III. Рост популяции в случайной среде // Журн. общ. биологии. Т. 79. № 4. С. 1–13.
Логофет Д.О., Казанцева Е.С., Белова И.Н., Онипченко В.Г., 2019. Androsace albana в случайно меняющейся среде // Журн. общ. биологии. Т. 80. № 3. С. 200–213.
На земле и под землёй: границы приспособленности для ценопопуляции клонального растения с поливариантным онтогенезом, 2015. Итоговый научный отчет по проекту РФФИ № 13-04-01836-а. https://istina.msu.ru/projects/8473479/
Протасов В.Ю., Широков М.Е., 2019. О взаимно-обратных преобразованиях функций на полупрямой // ДАН. Т. 489. № 5. С. 15–18.
Сколько лет живет малолетник, или задачи осреднения в неавтономных матричных моделях популяций, 2018. Итоговый научный отчет по проекту РФФИ № 16-04-00832-а. https://www.rfbr.ru/rffi/ru/project_search/o_2019899
Caswell H., 1989. Matrix Population Models: Construction, Analysis, and Interpretation. Sunderland, MA: Sinauer. 328 p.
Caswell H., 2001. Matrix Population Models: Construction, Analysis, and Interpretation. 2nd ed. Sunderland, MA: Sinauer. 722 p.
Caswell H., 2010. Life table response experiment analysis of the stochastic growth rate // J. Ecol. V. 98. № 2. P. 324–333.
COMADRE, 2020. https://www.compadre-db.org/Data/Comadre
COMPADRE, 2020. https://www.compadre-db.org/Data/Compadre
Courtier P., Derber J., Errico R., Louis J.-F., Vukićević T., 1993. Important literature on the use of adjoint, variational methods and the Kalman filter in meteorology // Tellus A. Dyn. Meteorol. Oceanogr. V. 45. № 5. P. 342–357.
GUFO.ME, 2020. https://gufo.me/dict/mathematics_encyclopedia/ Переопределенная_Система
Horn R.A., Johnson C.R., 1990. Matrix Analysis. Cambridge: Cambridge Univ. Press. 561 p.
Keyfitz N., 1968. Introduction to the Mathematics of Population. Reading, MA: Addison-Wesley. 450 p.
Logofet D.O., 1993. Matrices and Graphs: Stability Problems in Mathematical Ecology. Boca Raton, FL: CRC Press. 308 p.
Logofet D.O., 2018. Averaging the population projection matrices: Heuristics against uncertainty and nonexistence // Ecol. Complex. V. 33. № 1. P. 66–74.
Logofet D.O., 2019a. Bilberry vs. cowberry in a scots pine boreal forest: Exclusion or coexistence in a post-fire succession? II. Alternate modes of prediction // Ecol. Model. V. 401. P. 134–143.
Logofet D.O., 2019b. Does averaging overestimate or underestimate population growth? It depends // Ecol. Model. V. 411. P. 108744.
Logofet D.O., Maslov A.A., 2019. Bilberry vs. cowberry in a scots pine boreal forest: Exclusion or coexistence in a post-fire succession? // Ecol. Model. V. 401. P. 134–143.
Logofet D.O., Ulanova N.G., Belova I.N., 2014. Adaptation on the ground and beneath: Does the local population maximize its λ1? // Ecol. Complex. V. 20. P. 176–184.
MathWorks, 2020a. https://www.mathworks.com/help/ symbolic/index.html
MathWorks, 2020b. https://www.mathworks.com/help/ matlab/ref/eig.html
MathWorks, 2020c. https://www.mathworks.com/help/ matlab/ref/min.html
MathWorks, 2020d. https://www.mathworks.com/help/ matlab/ref/max.html
MathWorks, 2020e. https://www.mathworks.com/help/optim/ug/fmincon.html
MathWorks, 2020f. https://www.mathworks.com/help/ gads/globalsearch.html
McDonald J.J., Paparella P., Michae J., Tsatsomeros M.J., 2014. Matrix roots of eventually positive matrices // Linear Algebra Appl. V. 456. P. 122–137.
Politi T., Popolizio M., 2015. On stochasticity preserving methods for the computation of the matrix pth root // Math. Comput. Simul. V. 110. P. 53–68.
Protasov V.Yu., 2019. Comprehensive Lyapunov functions for linear switching systems // Automatica. V. 109. P. 108526.
Tuljapurkar S.D., 1986. Demography in stochastic environments. II. Growth and convergence rates // J. Math. Biol. V. 24. P. 569–581.
Tuljapurkar S.D., 1990. Population Dynamics in Variable Environments. N.Y.: Springer. 154 p.
Дополнительные материалы отсутствуют.
Инструменты
Журнал общей биологии