Журнал общей биологии, 2020, T. 81, № 5, стр. 374-386
Моделирование критических явлений в популяциях лесных насекомых
В. Г. Суховольский 1, 3, *, О. В. Тарасова 2, **, А. В. Ковалев 3, ***
1 Институт леса им. В.Н. Сукачева СО РАН
660036 Красноярск, Академгородок, 50/28, Россия
2 Сибирский федеральный университет
660049 Красноярск, пр. Свободный, 79, Россия
3 Федеральный исследовательский центр КНЦ СО РАН
660036 Красноярск, Академгородок, 50, Россия
* E-mail: soukhovolsky@yandex.ru
** E-mail: olvitarasova2010@yandex.ru
*** E-mail: sunhi.prime@gmail.com
Поступила в редакцию 27.04.2020
После доработки 23.06.2020
Принята к публикации 25.06.2020
Аннотация
Рассмотрены методы моделирования критических явлений в популяциях лесных насекомых, основанные на представлении процессов развития вспышек массового размножения как аналогов фазовых переходов первого и второго рода в физических системах. Предложены измеримые показатели, характеризующие процессы фазовых переходов. Для лесных насекомых р. Dendrolimus рассмотрены модели динамики конкретных популяций. Для описания долговременной динамики популяций лесных насекомых с учетом влияния на текущую плотность популяции ее значений в предыдущие годы и влияния модифицирующих факторов предложено использовать ADL (autoregressive distributed lag)-модели. Показана высокая степень согласованности предлагаемых моделей с данными наблюдений. Предлагаемый подход требует минимальных данных о состоянии экосистемы. Предполагается, что модели фазовых переходов и ADL-модели могут быть использованы для описания таких явлений, как вирусные и бактериальных эпидемии, подъемы численности млекопитающих и т.д.
Вспышка массового размножения насекомых – одно из первых критических явлений в экологических системах, описанных в мировой литературе (Библия, Исход 10:12 – цит. по: Библия, 1999, с. 77). Однако до настоящего времени задача прогнозирования и контроля численности насекомых-вредителей лесных насаждений и сельскохозяйственных культур полностью не решена. Ситуацию со вспышками массового размножения насекомых все еще можно описать словами Библии: “Настало утро, и восточный ветер нанес саранчу” (с. 77). В связи с этим для прогноза динамики численности вредителей и вспышек их массового размножения необходимы новые эффективные методы.
Согласно базовым положениям системного анализа, недостаточно изучать лишь один компонент экологической системы – в данном случае популяцию лесных насекомых. Анализ процессов, происходящих в сложной системе, должен быть основан на системном подходе и исследовании всех компонентов экосистемы. Однако постулаты системного анализа рушатся уже при первой встрече исследователя с изучаемым объектом – популяцией некоторого вида лесных насекомых-филлофагов. Если в теоретические модели динамики популяций можно ввести любые желательные исследователю переменные, то при моделировании реальной популяции лесных насекомых возникает проблема измерений соответствующих характеристик сообщества. При долгосрочных измерениях в лесу обычно удается регистрировать только показатели плотности популяции. Иногда (довольно редко) имеются данные о массе особей, окраске гусениц и имаго, плодовитости самок, степени зараженности особей паразитами (Тарасова и др., 2015; Пальникова, Суховольский, 2016). Но учет таких компонентов системы, как популяции хищников и доступные кормовые ресурсы, крайне затруднен. Таким образом, возможности натурных исследований динамики системы, в которую входит изучаемый вид лесных насекомых, ограничены, и в целом система “ускользает” от системного модельного анализа.
Если имеется информация только о плотности популяции изучаемого вида, то анализ динамики численности лесных насекомых можно проводить с помощью фазовых портретов для систем модельных уравнений (Исаев, Хлебопрос, 1973; Исаев и др., 2001). При этом влияние модифицирующих и регулирующих факторов динамики численности не изучается прямо, а оценивается по изменению формы фазового портрета популяции. Такой подход позволил дать классификацию типов динамики численности и типов вспышек массового размножения лесных насекомых. Однако в рамках такого подхода сложно получить прогноз развития вспышек в конкретных экологических условиях.
В настоящей работе предпринята попытка построения минималистских моделей динамики численности лесных насекомых, использующих только данные по плотности изучаемого вида без точного знания характеристик регулирующих и модифицирующих факторов. Для моделирования такого критического явления, как вспышка массового размножения насекомых, мы используем два подхода – описание экологических процессов как аналогов фазовых переходов в физических системах и как аналогов экономических процессов, в которых текущее состояние системы зависит от ее прошлых состояний (Исаев и др., 2015; Isaev et al., 2017).
ОБЪЕКТЫ И МЕТОДЫ ИССЛЕДОВАНИЯ
Объекты исследования
В настоящее время в энтомологии накоплен обширный материал по динамике численности большого числа видов лесных (Imperial Colledge, 2020). Для ряда видов существуют временны́е ряды более чем столетней длительности (Baltensweiler, 1964, 1991; Baltensweiler, Fischlin, 1988). Конечно, построение моделей всех видов, по которым имеются данные учетов, – задача неподъемная. В качестве примера моделирования критических явлений в лесных экосистемах в рамках настоящей работы мы использовали данные по динамике численности насекомых р. Dendrolimus, в частности по динамике таких видов, как сибирский шелкопряд Dendrolimus sibiricus Tschetv., Dendrolimus superans Butler и сосновый шелкопряд Dendrolimus pini L. (Прозоров, 1952; Ивлиев, 1961; Коломиец, 1962; Рожков, 1963; Надзор…, 1965; Болдаруев, 1969; Наконечный и др., 1974; Юрченко, Турова, 2007).
Несмотря на всю важность учетов такого опасного вредителя, как сибирский шелкопряд, для оценки рисков вспышек его массового размножения, достаточно длинные временны́е ряды численности популяций этого вида практически отсутствуют. Это связано с тем, что вспышки массового размножения возникают обычно в отдаленных таежных районах, где трудно проводить регулярные учеты численности вредителя. В нашем распоряжении имеется всего два достаточно продолжительных ряда динамики численности популяций видов из р. Dendrolimus – ряд с 1951 по 1969 год в темнохвойных лесах Красноярского края (Кондаков, 1974, 2002) и ряд с 1975 по 1996 год в лесах Хабаровского края (Юрченко, Турова, 2007). Кроме того, Центром защиты леса Красноярского края были предоставлены данные учетов сибирского шелкопряда на пробных площадках в очагах его массового размножения на территории Красноярского края в 2017 г.
Данные по многолетней динамике численности соснового шелкопряда в течение 1979–2015 гг. получены в ходе ежегодных учетов авторов (совместно с Е.Н. Пальниковой) в пяти местообитаниях на территории Краснотуранского соснового бора (Красноярский край, 54°16.315′ с.ш., 91°37.757′ в.д.). Детальные описания пробных площадей и данные учетов приведены в предыдущих работах (Пальникова и др., 2002; Исаева и др., 2015; Isaev et al., 2017).
Методы исследования
Популяция лесных насекомых может находиться в одной из двух фаз – в фазе стабильно разреженного состояния и фазе вспышки массового размножения. В фазе стабильно разреженного состояния плотность популяции предельно мала и ее особи осваивают лишь часть имеющихся кормовых объектов. Фаза вспышки массового размножения реализуется, когда плотность популяции вредителя превосходит некоторое критическое значение хr и популяция осваивает все доступные на данной территории кормовые объекты (Berryman, 1988; Исаев и др., 2001). Такое критическое явление, как вспышка массового размножения лесных насекомых, будем рассматривать как аналог фазовых переходов в физических системах. Важной особенностью моделей фазовых переходов, позволяющих использовать их для описания критических явлений в самых разных системах, является то, что в рамках теории фазовых переходов вводится принцип универсальности, согласно которому процессы фазовых переходов зависят только от некоторых основных свойств систем, таких как размерность, число компонентов параметра порядка, зависимость взаимодействия в системе от расстояния (Брус, Каули, 1984). Кроме того, характерной чертой простых статических моделей фазовых переходов является отсутствие в них зависимости от времени, что сильно упрощает построение моделей.
При фазовых переходах число факторов, влияющих на поведение системы вблизи точки фазового перехода, обычно сильно уменьшается и зависит только от двух переменных – так называемого параметра порядка, характеризующего некоторые общие свойства изучаемого объекта, и внешней переменной, такой, например, как температура Т в физических системах (Ландау, Лифшиц, 2002).
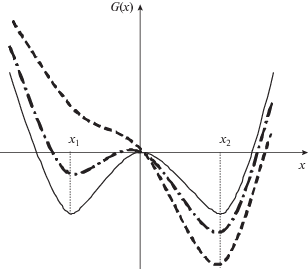
Возможные состояния популяции лесных насекомых могут быть описаны с помощью функции состояния G(х) – функции, обратной функции распределения популяции по плотности. Устойчивые состояния популяции характеризуются минимумами значений G(х). Действительно, если популяция будет находиться в стабильном или метастабильном состоянии с низкой или высокой плотностью достаточно часто, то значения функции состояния для этих плотностей будут малы. Напротив, пограничные состояния с плотностью между плотностями популяции в стабильно разреженном состоянии и в состоянии вспышки будут встречаться достаточно редко, и для таких плотностей значения потенциальной функции будут велики. На рис. 1 приведен общий вид функции состояния для бистабильной системы с двумя устойчивыми состояниями.
Влияние внешних факторов в модели фазовых переходов первого рода учитывается как некоторое постоянное внешнее поле h (например, температура окружающей среды Т или гидротермический коэффициент (ГТК) – отношение суммарных осадков за сезон к средней температуре воздуха в сезоне). Если величина внешнего поля велика, один из локальных минимумов исчезает, и популяция будет находиться вблизи оставшегося устойчивого состояния.
Для описания вспышек массового размножения наряду с описанием изменений плотности популяции важно оценить характеристики освоения насекомыми кормовых объектов (деревьев). Если N особей популяции распределены по n деревьям в насаждении достаточно равномерно, то даже при высокой плотности популяции нагрузка N/n на одно дерево может оказаться достаточно малой. Если же для особей вредителей характерно групповое распределение и заселяется n0 деревьев (n0$ \ll $ n), то плотность насекомых N/n0 на этих деревьях может оказаться высокой, и вероятность гибели таких деревьев возрастет. Для описания заселения дерева насекомыми целесообразно ввести аналог модели фазового перехода второго рода (Ландау, Лифшиц, 2002). С этой целью введем параметр порядка q как долю кормовых объектов (деревьев), не подвергшихся нападению вредителя:
где $A = \frac{{{{n}_{0}}}}{n}$ – относительная заселенность учетных единиц (деревьев, пробных площадок и т.п.) насекомыми, $n$ – общее число учетных единиц, n0 – число учетных единиц, заселенных насекомыми; 0 ≤ q ≤ 1. Если все деревья на пробной площади заселены вредителем, то q = 0. Если на пробной площади не найдено особей изучаемого вида, то q = 1.Функцию освоения деревьев ${{G}_{1}} = f(x,q)$ с достаточной точностью можно представить в виде ряда по степеням параметра порядка (Ландау, 1937; Ландау, Лифшиц, 2002). При этом фазовые переходы второго рода будут описываться разложением функции G1 только по четным степеням параметра порядка q:
где b = const, А есть линейная функция от внешней переменной x – плотности популяции, оцениваемой, например, по числу особей вида на учетную единицу (дерево).Коэффициент А в уравнении (2) запишем как линейно зависящий от плотности популяции:
Значение параметра порядка для фаз вспышки и разреженного состояния находим из решения уравнения $\frac{{\partial {{G}_{1}}}}{{\partial q}} = 0$, указывающего на возможные минимумы функции G1:
Уравнение (4) распадается на два:
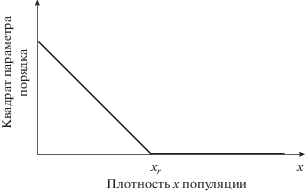
Решение $q = 0$ характеризует полное освоение насаждения насекомыми. Второе решение (частичное освоение насаждения) реализуется, когда плотность популяции меньше критического значения хr. Графически решения (5) представлены на рис. 2.
Наряду с использованием моделей фазовых переходов для моделирования динамики численности лесных насекомых в условиях, когда известны лишь данные учетов численности моделируемого вида и погодные условия на территории его обитания, можно использовать ADL (autoregressive distributed lag)-модели (Исаев и др., 2015; Сток, Уотсон, 2015; Isaev et al., 2017):
(6)
$lnx(i) = {{a}_{0}} + \sum\limits_{j = 1}^k {{{a}_{j}}ln\,} x(i - j) + \sum\limits_{m = 0}^u {{{b}_{m}}} W(i - m),$В уравнении (6) известны: в левой части – временной ряд {ln x(i)} численности, а в правой части – ряд {ln x(i – j)} (фактически тот же временной ряд численности моделируемого вида, взятый с некоторым сдвигом j) и ряд погодных показателей W(i), выбираемых из условия минимума невязок модельного ряда (3) по отношению к временнóму ряду {ln x(i)} данных учетов численности. Фактически это означает, что уравнение (6) следует рассматривать как линейное регрессионное уравнение, для которого нужно оценить порядки k и u членов в правой части, а затем с помощью стандартной процедуры нахождения коэффициентов линейных регрессионных уравнений вычислить коэффициенты aj и bm.
Для оценки порядка k AR-составляющей временных рядов можно использовать методы автокорреляционного анализа (Бокс, Дженкинс, 1974; Андерсон, 1976; Кендалл, Стьюарт, 1976) и вычислить парциальную автокорреляционную функцию. Однако такой расчет корректно выполняется только в случае, если изучаемый временной ряд стационарен и его средние значения и стандартное отклонение от среднего не изменяются во времени (Бокс, Дженкинс, 1974). Если эти условия не выполняются и наблюдается тренд значений плотности популяции и/или изменяющийся во времени размах колебаний плотности, то необходимо преобразовать наблюдаемый временной ряд так, чтобы без потери интересующих нас свойств ряда он трансформировался в LTI-ряд (linear time-invariant set). LTI-ряд должен иметь постоянное во времени среднее значение, постоянное во времени значение дисперсии среднего и постоянную во времени частоту колебаний переменной.
Для оценки качества модели используются четыре критерия: 1) значение коэффициента детерминации R2 должно быть близко к 1; 2) значения коэффициентов регрессионного уравнения (6) должны быть значимыми согласно t-критерию; 3) трансформированный ряд данных учетов и модельный ряд должны быть синхронны (синхронность оценивается по характеристикам кросс-корреляционной функции между этими рядами); и 4) ряд остатков между значениями ряда данных учетов и модельного ряда должен быть некоррелированным и обладать свойствами белого шума, что оценивается, например, по критерию Дики–Фуллера (Подкорытова, Соколов, 2016). Если модель отвечает всем этим критериям, можно говорить о том, что она адекватно описывает динамику изучаемой популяции.
Для построения ADL-моделей необходима трансформация данных учетов: переход в логарифмическую шкалу плотностей, низкочастотная фильтрация, позволяющая выделить долгосрочные тренды численности, и высокочастотная фильтрация, позволяющая уменьшить возможные ошибки учетов.
Таким образом, для моделирования динамики численности популяций на основе данных многолетних учетов численности можно использовать как модели фазовых переходов, так и ADL-модели.
РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ
Ранее (Эпова, Плешанов, 1995) считалось, что в Сибири и на Дальнем Востоке встречается один и тот же вид насекомых Dendrolimus sibiricus Tschetv. (синоним Dendrolimus superans Butler). Однако после анализа нуклеотидных последовательностей митохондриальных генов COI и COII и спейсера ITS2 ядерных рибосомных генов у насекомых из р. Dendrolimus было обнаружено, что можно выделить два кластера близкородственных видов. Первый кластер включает в себя D. pini, D. sibiricus (сибирские популяции) и D. superans (дальневосточные популяции); второй – D. spectabilis, D. punctatus и D. tabulaeformis. В связи с этим D. sibiricus и D. superans можно рассматривать как различные виды (Mikkola, Ståhls, 2008; Kononov et al., 2016). Далее в тексте виды в Сибири и на Дальнем Востоке рассматриваются как эволюционно близкие, но не идентичные.
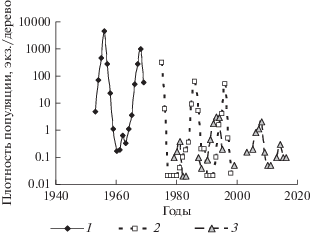
На рис. 3 приведены временны́е ряды численности D. sibiricus в бассейне р. Ангары (Мотыгинский район Красноярского края), D. superans на территории Хабаровского края (в 1975–1993 гг. в бассейне р. Синей в Кокшаровском лесхозе, в 1994–1998 гг. в смежных лесных массивах Арсеньевского и Чугуевского лесхозов) и D. pini в сосновых насаждениях Краснотуранского бора (Красноярский край).
Рис. 3.
Данные учетов численности D. sibiricus на территории Красноярского края (1), D. superans на территории Хабаровского края (2) и D. pini в Краснотуранском бору (3).
Для оценки влияния модифицирующих погодных факторов использованы данные с метеостанций, расположенных вблизи очагов массового размножения изучаемых популяций – метеостанции в Енисейске (58°27′00″ с.ш., 92°09′00″ в.д.), Елабуге (56°16′48″ с.ш., 90°30′00″ в.д.) и Минусинске (53°42′63″ с.ш., 91°41′24″ в.д.) (http://meteo-dv.ru/geospace/AverageMonthW).
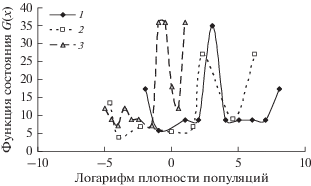
Используя данные многолетней динамики D. sibiricus в бассейне Ангары, D. superans на Дальнем Востоке и D. pini в Краснотуранском бору мы построили функции состояния G(x) (рис. 4). Все функции состояния имеют сходный вид с двумя локальными минимумами и максимумом между ними – потенциальным барьером. Однако высоты барьеров для этих видов достаточно близки, что указывает на близость характерных времен перехода из одного состояния в другое. Как видно, для D. sibiricus и D. superans критические плотности xr , по достижению которых популяция переходит в фазу вспышки, достаточно близки (xr = 20 особей на дерево для D. sibiricus и xr = 10 особей на дерево для D. superans). Для D. pini xr ≈ 0.4 особи на дерево, но значение х2 = 1.65 особи на дерево много меньше значений х2 для D. sibiricus (≈400 особей на дерево) и для D. superans (≈100 особей на дерево).
Рис. 4.
Функции состояния D. sibiricus в бассейне Ангары (1), D. superans на Дальнем Востоке (2) и D. pini в Краснотуранском бору (3).
По данным учетов численности популяций возможно вычислить величину q2 как функцию от ln x, характеризующую степень освоения деревьев насекомыми в ходе двух вспышек массового размножения сибирского шелкопряда на территории Красноярского края (рис. 5 и 6). Видно, что критические плотности хm освоения насаждения для популяций сибирского шелкопряда, по достижению которых q = 0 и происходит освоение вредителем всех деревьев в насаждении, в разные годы различаются. Так, для периода с 1953 по 1969 год. критическая плотность освоения хm ≈ 6.4 гусеницы на дерево (т.е. меньше критической плотности xr = 20 особей на дерево), а для 2017 г. – хm ≈ 100 гусениц на дерево. Таким образом, возможна ситуация, когда популяция осваивает все деревья в насаждении еще до достижения критической плотности и перехода в фазу вспышки. Различия в значениях xm для разных вспышек массового размножения показывают, что особи вредителя по-разному распределяются на деревьях и, возможно, это оказывает влияние на интенсивность изъятия хвои вредителями. Важно то, что, используя представленную модель и зная линейную связь между ln x и q2, критическую плотность можно оценить по данным учетов в разреженном состоянии или в начале вспышки, когда плотности популяции низки и много меньше критической плотности. Используя данные учетов на низких плотностях, такой расчет позволяет заблаговременно оценить риски повреждений деревьев в насаждении и долю освоенных деревьев при различных плотностях популяции вредителя.
Рис. 5.
Связь между квадратом доли неповрежденных деревьев q2 и логарифмом плотности х популяции сибирского шелкопряда в очагах массового размножения на территории Красноярского края в 2017 г.: 1 – плотности популяции ниже критической плотности освоения xm, 2 – плотности популяции выше критического плотности освоения xm.
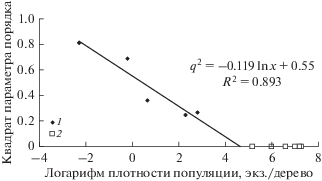
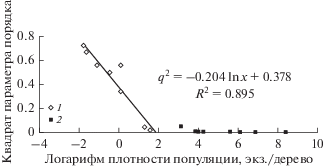
Рис. 6.
Связь между квадратом доли неповрежденных деревьев q2 и логарифмом плотности х популяций сибирского шелкопряда в очагах массового размножения в 1953–1969 гг.: 1 – плотности популяции ниже критической плотности освоения xm, 2 – плотности популяции выше критической плотности освоения xm.
По данным учетов построены модели динамики популяций сибирского шелкопряда. Для оценки порядка авторегрессии вычислены парциальные автокорреляционные функции (PACF) (расчеты производили с помощью статистического пакета Statistica 6.0). На рис. 7 и 8 приведены PACF трансформированных рядов динамики численности D. sibiricus в бассейне Ангары и D. superans на Дальнем Востоке. Как видно из рисунков, за пределами нулевого доверительного интервала находятся значения PACF со сдвигами k = 1 и k = 2. Это значит, что запаздывание в AR-составляющей рядов динамики этих видов составляет два года.
Рис. 7.
PACF трансформированного ряда динамики численности D. sibiricus в бассейне Ангары: 1 – значение PACF, 2 – границы нулевого доверительного интервала.
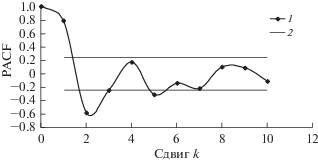
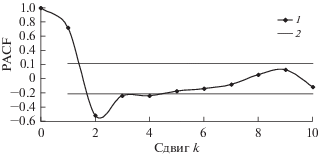
Рис. 8.
PACF трансформированного ряда динамики численности D. superans на Дальнем Востоке: 1 – значение PACF, 2 – границы нулевого доверительного интервала.
Зная величину k, далее выполняем расчет коэффициентов регрессионного уравнения $lnx(i)$ = $ = {{a}_{0}} + \sum\nolimits_{j = 1}^2 {{{a}_{j}}lnx} (i - j)$ + $\sum\nolimits_{m = 0}^u {{{b}_{m}}} W(i - m)$. Так как теоретические обоснования для выбора влияния того или иного периода сезона на динамику численности вида отсутствуют, ищем период сезона и погодный показатель (среднемесячная температура и осадки, гидротермический коэффициент отдельных месяцев), при которых величина R2 для ADL-модели максимальна, а коэффициенты погодных переменных модели значимы. В результате найдено, что наибольшее значение коэффициента детерминации достигается, если в качестве показателя погоды выбрана средняя температура воздуха T(5, i) мая i-го года. В табл. 1 приведены коэффициенты полученной ADL-модели динамики численности D. sibiricus в бассейне Ангары, показаны значения и стандартные ошибки значений коэффициентов уравнения (6), t-критерий и доверительная вероятность ошибки значимости коэффициентов. Как видно, значения всех коэффициентов превосходят критическое значение t = 2.04 и, следовательно, все они значимы с вероятностью ошибки не больше 0.025. Величина R2 = 0.90, т.е. найденное уравнение описывает 90% дисперсии переменной ln x(i). Важно обратить внимание на абсолютные значения и знаки коэффициентов уравнения. Абсолютное значение каждого коэффициента в уравнении (3) характеризует чувствительность величины логарифма плотности популяции к изменению значения соответствующей переменной. Текущая плотность популяции максимально чувствительна к плотноcти популяции предыдущего года. При этом знак а1 положителен, т.е. между ln x(i) и ln x(i – 1) существует положительная обратная связь. Знак же а2 отрицателен, т.е. между плотностями популяции в текущем и позапрошлом сезонах имеет место отрицательная обратная связь. Отрицательную обратную связь обычно объясняют запаздыванием во времени влияния паразитов на популяцию хозяина (Исаев и др., 2001). Коэффициент b положителен, т.е. чем теплее май, тем больше численность сибирского шелкопряда.
Таблица 1.
Статистические характеристики ADL-модели динамики численности D. sibiricus в бассейне Ангары
| Переменные | Коэффициенты | Статистические характеристики | |||
|---|---|---|---|---|---|
| значение | стандартная ошибка | t(11) | доверительный уровень, p | ||
| a0 | –4.962 | 1.834 | –2.705 | 0.020 | |
| T(5, i) | b | 0.622 | 0.240 | 2.590 | 0.025 |
| ln x(i – 2) | a2 | –0.684 | 0.179 | –3.812 | 0.003 |
| ln x(i – 1) | a1 | 1.427 | 0.168 | 8.502 | 0.000 |
| R2 | 0.90 | ||||
| F(3, 11) | 31.85 | ||||
| Средняя многолетняя плотность, экз./дерево | 386.5 | ||||
| Максимальная плотность, экз./дерево | 4380 | ||||
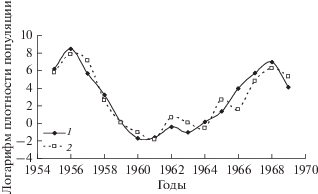
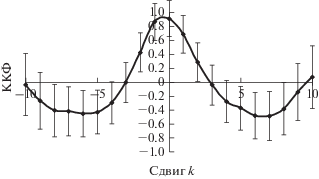
На рис. 9 приведены трансформированный ряд численности D. sibiricus в бассейне Ангары и модельный ряд. Как видно, модельный ряд хорошо описывает наблюдаемую динамику вредителя в течение 15 лет. Сравниваемые ряды синхронны, как это следует из кросс-корреляционной функции (ККФ) этих рядов (рис. 10). Максимальное значение ККФ, близкое к 1, наблюдается при нулевом сдвиге рядов (k = 0), т.е. оба ряда синхронны и максимумы и минимумы трансформированного и модельного рядов численности совпадают.
Рис. 10.
ККФ трансформированного ряда численности и модельного ряда для D. sibiricus в бассейне Ангары.
Сходные расчеты были выполнены для популяции D. superans на Дальнем Востоке (табл. 2, рис. 11).
Таблица 2.
Статистические характеристики ADL-модели динамики численности D. superans на Дальнем Востоке
| Переменные | Коэффициенты | Значения | Стандартная ошибка | t(16) | Доверительный уровень, р |
|---|---|---|---|---|---|
| a0 | 0.134 | 0.275 | 0.488 | 0.632 | |
| WS(i – 1) | b | –0.009 | 0.003 | –2.808 | 0.013 |
| ln x(i – 2) | a2 | –0.730 | 0.106 | –6.885 | 0.000 |
| ln x(i – 1) | a1 | 1.140 | 0.134 | 8.515 | 0.000 |
| R2 | 0.93 | ||||
| F(3, 16) | 70.49 | ||||
| Средняя многолетняя плотность, экз./дерево | 18.2 | ||||
| Максимальная плотность, экз./дерево | 300 |
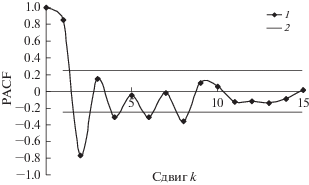
Аналогичные расчеты можно выполнить и для популяции соснового шелкопряда D. pini в условиях, когда вспышек это вида не происходит, а наблюдаются только регулярные продромальные подъемы численности. Порядок авторегрессии для популяции этого вида, так же как и для D. sibiricus и D. superans, оказался равен 2 (рис. 12).
Рис. 12.
PACF трансформированного ряда численности D. pini для урочища Дюна: 1 – значение PACF, 2 – границы нулевого доверительного интервала.
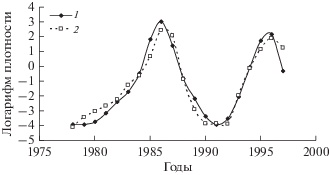
Трансформированный временной ряд данных учетов и модельный временной ряд численности D. pini для урочища Дюна представлены на рис. 13. Параметры уравнений (6) для популяций соснового шелкопряда в различных местообитаниях (урочищах) Краснотуранского бора приведены в табл. 3. Во всех случаях для популяций соснового шелкопряда, точно так же как для популяций D. sibiricus и D. superans, наблюдается положительная обратная связь между смежными учетами и отрицательная обратная связь между учетами в годах i и (i – 2). При отличающихся средних многолетних плотностях популяций соснового шелкопряда в различных местообитаниях Краснотуранского бора параметры уравнений (6) очень близки – коэффициенты вариации значений а1 и а2 близки к 0.03. Сравнивая значения коэффициентов ADL-моделей, можно заключить, что значения коэффициентов а2, характеризующих восприимчивость текущей плотности популяции к изменению значения плотности в год (i – 2), для всех изученных видов достаточно близки (от ‒0.68 до –0.80), а значения коэффициента а1, отражающего восприимчивость текущей плотности популяции к плотности в предыдущий год, близки для D. sibiricus и D. pini. Значения же коэффициентов а0 сильно различны для изученных видов насекомых.
Рис. 13.
Трансформированный ряд численности D. pini в Краснотуранском бору (урочище Дюна) (1) и модельный ряд (2).
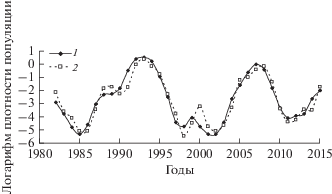
Таблица 3.
Характеристики модельных регрессионных уравнений динамики численности D. pini в различных местообитаниях Краснотуранского бора
| Переменная | Коэффициент | Местообитание | ||||
|---|---|---|---|---|---|---|
| Терраса | Дюна | Плакор | Озеро | Лысая гора | ||
| a0 | –0.283 | –0.561 | –0.452 | –1.275 | –0.565 | |
| ГТК(10, i – 1) | B1 | –0.279 | –0.152 | –0.402 | 0.000 | –0.374 |
| ГТК(5, i) | B2 | –0.417 | 0.000 | 0.000 | 0.215 | 0.000 |
| ln x(i – 2) | A2 | –0.763 | –0.798 | –0.748 | –0.750 | –0.782 |
| ln x(i – 1) | A1 | 1.416 | 1.536 | 1.479 | 1.446 | 1.488 |
| R2 | 0.860 | 0.905 | 0.906 | 0.860 | 0.901 | |
| Средняя многолетняя плотность, экз./дерево | 0.38 | 0.33 | 0.16 | 0.09 | 0.16 | |
| Максимальная плотность, экз./дерево | 3.08 | 2.96 | 1.20 | 0.65 | 1.30 | |
| Среднее по всем местообитаниям значение/коэффициент вариации а2 | 0.768/0.028 | |||||
| Среднее по всем местообитаниям значение/коэффициент вариации а1 | 1.473/0.031 | |||||
Для ответа на вопрос, являются ли такие значения коэффициентов специфичными для всего р. Dendrolimus, можно эти значения сопоставить со значениями приведенных в табл. 4 коэффициентов ранее рассмотренных нами ADL-моделей непарного шелкопряда Lymantria dispar L., Zeiraphera griseana L. и сосновой пяденицы Bupalus piniarius L. (Исаев и др., 2015).
Таблица 4.
Коэффициенты ADL-моделей нескольких видов насекомых-филлофагов, дающих вспышки массового размножения
| Коэффициент ADL-модели | Lymantria dispar L. | Zeiraphera griseana L. | Bupalus piniarius L. | |||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| a2 | –0.529 | –0.76 | –0.96 | –0.71 | –0.793 | –0.68 |
| a1 | 1.215 | 1.29 | 1.36 | 1.21 | 1.603 | 1.39 |
Как следует из табл. 4, для насекомых-филлофагов из других систематических групп значения коэффициентов ADL-модели достаточно близки к значениям этих коэффициентов для насекомых р. Dendrolimus, и поэтому нельзя говорить о специфичности коэффициентов для этих видов. Но можно говорить о сходстве коэффициентов ADL-моделей для видов, дающих вспышки массового размножения.
ЗАКЛЮЧЕНИЕ
Проведенные расчеты показали, что характер динамики популяций различных видов насекомых-филлофагов в далеко отстоящих друг от друга местообитаниях оказался сходным. Все изученные популяции характеризуются двухлетним запаздыванием динамики, положительной обратной связью между плотностями популяции в смежные годы и отрицательной обратной связью между значениями, отстоящими друг от друга на два года. Отличие популяции D. superans на Дальнем Востоке от популяции D. sibiricus в бассейне Ангары заключается в том, что текущая численность D. sibiricus зависит от температуры мая текущего года Т(5, i), тогда как текущая численность модельной популяции D. superans на Дальнем Востоке определялась значениями числа Вольфа WS(i – 1) в апреле–июне предыдущего года. Физический механизм влияния солнечной активности на динамику локальной популяции вредителя объяснить трудно, однако статистические расчеты указывают на наличие такой связи. Предложенные модели можно использовать для прогноза вспышек массового размножения по данным мониторинга численности популяций вредителя и значений модифицирующих факторов.
Представляется, что предложенный подход носит общий характер и модели фазовых переходов могут описывать критические явления не только в популяциях лесных насекомых, но и такие феномены, как эпидемии вирусных заболеваний (Суховольский, Ковалев, 2020).
В физике хорошо известно, что под влиянием изменений внешний среды (например, повышение температуры) могут происходить такие критические явления, как кипение и скачкообразный переход физической системы из жидкого в газообразное состояние (фазовый переход первого рода) и появление у вещества новых свойств – магнитного момента или сверхтекучести (фазовый переход второго рода). Биологические и экологические критические явления можно рассмотреть, используя те же подходы, которые были предложены для описания фазовых переходов в физических системах (Ландау, 1937; Паташинский, Покровский, 1982; Ландау, Лифшиц, 2002; Лифшиц, Питаевский, 2004).
В рамках теории фазовых переходов вводится принцип универсальности, согласно которому процессы фазовых переходов зависят только от некоторых основных свойств систем, таких как размерность, число компонентов у параметра состояния системы, зависимость взаимодействия в системе от расстояния (Брус, Каули, 1984). Характерной чертой простых статических моделей фазовых переходов является отсутствие в них зависимости от времени. Такое свойство существенно упрощает модель. Использование идеи универсальности фазовых переходов упрощает и унифицирует построение соответствующих моделей. Даже не зная точного вида функции состояния системы, все же можно описать процесс фазового перехода и найти критические значения внешнего фактора и значения параметров в устойчивых состояниях системы. Такой упрощенный подход заманчиво использовать для описания не только физических систем.
В анализе временны́х и пространственных колебаний состояния системы при реализации критических явлений можно выделить два типа флуктуаций состояния: высокочастотные и мелкомасштабные флуктуации, низкочастотные и крупномасштабные флуктуации. В первом случае состояния системы в пространстве и времени мало изменяются, и система бóльшую часть времени будет находиться вблизи одного из устойчивых состояний. Крупномасштабные и низкочастотные колебания состояния системы характеризуют ситуацию, когда происходят переходы из одного устойчивого состояния в другое, и характерное время таких флуктуаций – так называемое время Крамерса (Ван Кемпен, 1990) – соответствует среднему времени пребывания между двумя смежными критическими событиями.
Таким образом, можно говорить об общих системных свойствах критических явлений и сравнивать эти общие свойства для разных систем. За многие века существования науки очень многие явления были рассмотрены с точки зрения общего системного подхода, начиная с системного обобщения исторических процессов, проделанного Плутархом в его “Сравнительных жизнеописаниях” (2008). Представляется, что системный подход может быть использован и при описании критических явлений в биологических и экологических системах (Суховольский, 2004; Суховольский и др., 2008; Isaev et al., 2017). В частности, развитие онкозаболеваний было описано как модель фазового перехода второго рода (Суховольский и др., 2015). В цитируемых работах показано, что критические явления в биологических и экологических системах можно моделировать как аналоги моделей фазовых переходов в физических системах и как авторегрессионные модели. Это означает, что такие системы характеризуются наличием отрицательных обратных связей, позволяющих поддерживать систему в стабильном (метастабильном) состоянии, и положительных обратных связей, перебрасывающих систему из одного устойчивого состояния в другое. Существование критических явлений – обязательное свойство бистабильной системы. Если же критические явления не наблюдаются для какого-то вида, это может указывать не на то, что у изучаемого объекта только одно устойчивое состояние, а на то, что потенциальный барьер “жесткий”, а критическая плотность достаточно велика и редко достигается. При этом локальный минимум кривой G(x) вблизи плотности x1 существенно меньше локального минимума G(x) состояния при плотности x2. Это означает, что вероятность существования популяции вблизи состояния х1 существенно больше существования в состоянии вспышки. На состояние популяции могут влиять модифицирующие факторы, такие как погодные. Если погоду учитывать как некоторое внешнее поле h, то в уравнение (2) необходимо включить дополнительный член. Тогда ${{G}_{1}} = {{G}_{0}} + A{{q}^{2}} + b{{q}^{4}} - сhq,$ и при слабом воздействии внешнего поля решение с плотностью х1 исчезает, и система “выбрасывается” из состояния вблизи локального минимума с низкой плотностью в состояние вспышки вблизи х2 (Абаимов, 2013). При снятии же поля решение уравнения с х = х1 восстанавливается и система может вернуться в состояние х1.
Таким образом, можно говорить о пороговом характере возникновения критических явлений и наличии критических значений характеристик системы, при достижении которых начинаются качественные изменения в системе. Эти процессы можно описать как аналоги фазовых переходов первого рода в физических системах. Освоение внешней среды (отдельных территорий и стран в ходе эпидемии коронавируса, деревьев в насаждении в ходе вспышек массового размножения) можно описать как аналоги фазовых переходов второго рода в физических системах. Можно также говорить о существовании как минимум двух стабильных или метастабильных состояний систем, характеристики которых колеблются вблизи некоторого значения каждого из них, и о наличии потенциального барьера, препятствующего перебросу системы из одного состояния в другое. Чем выше значение потенциального барьера, тем меньше вероятность реализации критического явления. Если ввести понятие параметра порядка как некоторого обобщенного показателя состояния системы, то описать воздействие внешних факторов на систему можно, используя два подхода: представляя внешние воздействия как некоторые поля в уравнении Ландау для фазовых переходов, либо построив ADL-модели (Сток, Уотсон, 2015), в которых вместо описания воздействия регулирующих факторов использовано запаздывание реакции переменных системы на внешние воздействия.
При моделировании критических явлений важно корректно определить значение параметра порядка, функции состояния и величины внешнего поля, оказывающего влияние на фазовый переход. Но этот подход все же проще подхода к моделированию с использованием систем нелинейных дифференциальных или разностных уравнений (да еще когда не все переменные в модели измеримы) (Lotka, 1925; Volterra, 1931; Свирежев, Логофет, 1978; Базыкин, 2003). Использование предлагаемых моделей позволяет оценить риски возникновения критических явлений и вероятности реализации нового критического явления после окончания предыдущего.
Работа поддержана грантом РФФИ и ККФН № 19-44-240003. Авторы благодарят Центр защиты леса Красноярского края (директор В.В. Солдатов) за предоставление данных учетов вредителя в очагах его массового размножения.
Список литературы
Абаимов С.Г., 2013. Статистическая физика сложных систем. М.: Книжный дом “ЛИБРОКОМ”. 392 с.
Андерсон Т., 1976. Статистический анализ временных рядов. М.: Мир. 755 с.
Базыкин А.Д., 2003. Нелинейная динамика взаимодействующих популяций. М.; Ижевск: Ин-т комп. исследований. 368 с.
Библия, 1999. М.: Российское библейское общество. 303 с.
Бокс Дж., Дженкинс Г., 1974. Анализ временных рядов. Прогноз и управление. М.: Мир. Вып. 1. 406 с.
Болдаруев В.О., 1969. Динамика численности сибирского шелкопряда и его паразитов. Улан-Удэ: Бурят. кн. изд-во. 164 с.
Брус А., Каули Р., 1984. Структурные фазовые переходы. М.: Мир. 408 с.
Ван Кемпен Н.Г., 1990. Стохастические процессы в физике и химии. М.: Высш. шк. 375 с.
Ивлиев Л.А., 1961. Новые данные к познанию очагов сибирского шелкопряда на Амуре // Вопросы сельского и лесного хозяйства Дальнего Востока. Вып. 3. Владивосток. С. 3–19.
Исаев А.С., Хлебопрос Р.Г., 1973. Принцип стабильности в динамике численности лесных насекомых // ДАН СССР. Т. 208. № 1. С. 225–228.
Исаев А.С., Пальникова Е.Н., Суховольский В.Г., Тарасова О.В., 2015. Динамика численности лесных насекомых-филлофагов: модели и прогнозы. М.: Т-во науч. изд. КМК. 262 с.
Исаев А.С., Хлебопрос Р.Г., Кондаков Ю.П., Недорезов Л.В., Киселев В.В., Суховольский В.Г., 2001. Популяционная динамика лесных насекомых М.: Наука. 374 с.
Кендалл М.Дж., Стьюарт А., 1976. Многомерный статистический анализ и временные ряды. М.: Наука. 736 с.
Коломиец Н.Г., 1962. Паразиты и хищники сибирского шелкопряда. Новосибирск: Изд-во СО АН СССР. 174 с.
Кондаков Ю.П., 1974. Закономерности массовых размножений сибирского шелкопряда // Экология популяций лесных животных Сибири. Новосибирск: Наука. С. 206–265.
Кондаков Ю.П., 2002. Массовые размножения сибирского шелкопряда в лесах Красноярского края // Энтомологические исследования в Сибири. Вып. 2. Красноярск: РЭО. С. 25–74.
Ландау Л.Д., 1937. К теории фазовых переходов // ЖЭТФ. Т. 7. С. 19–32.
Ландау Л.Д., Лифшиц Е.М., 2002. Статистическая физика. М.: ФИЗМАТЛИТ. 616 с.
Лифшиц Е.М., Питаевский Л.П., 2004. Статистическая физика. Ч. 2. Теория конденсированного состояния. М.: ФИЗМАТЛИТ. 496 с.
Надзор, учет и прогноз массовых размножений хвое- и листогрызущих насекомых в лесах СССР, 1965. М.: Лес. пром. 528 с.
Наконечный В.И., Челышева Л.П., Малоквасова Т.С., Жарикова Н.А., Арефьев Ю.Ф. и др., 1974. О вспышке массового размножения сибирского шелкопряда в лиственничных лесах Хабаровского края // Тр. ДальНИИЛХ. Вып. 16. С. 170–179.
Пальникова Е.Н., Суховольский В.Г., 2016. Взаимодействие “фитофаг – энтомофаг” на разных фазах массового размножения лесных насекомых // Лесоведение. № 1. С. 15–24.
Пальникова Е.Н., Свидерская И.В., Суховольский В.Г., 2002. Сосновая пяденица в лесах Сибири. Новосибирск: Наука. 252 с.
Паташинский А.З., Покровский В.Л., 1982. Флуктуационная теория фазовых переходов. М.: Наука. 382 с.
Плутарх, 2008. Сравнительные жизнеописания. М.: Альфа-книга. 1264 с.
Подкорытова О.А., Соколов М.В., 2016. Анализ временных рядов. М.: Юрайт. 266 с.
Прозоров С.С., 1952. Сибирский шелкопряд в пихтовых лесах Сибири // Тр. СибЛТИ. Т. 7. № 3. С. 93–132.
Рожков А.С., 1963. Сибирский шелкопряд. М.: Изд-во АН СССР. 175 с.
Свирежев Ю.М., Логофет Д.О., 1978. Устойчивость биологических сообществ. М.: Наука. 352 с.
Сток Дж., Уотсон М., 2015. Введение в эконометрику. М.: “Дело” РАНХиГС. 864 с.
Суховольский В.Г., 2004. Экономика живого: оптимизационный подход к описанию процессов в экологических сообществах и системах. Новосибирск: Наука. 140 с.
Суховольский В.Г., Ковалев А.В., 2020. Методы моделирования пандемии коронавируса // Журн. общ. биологии. Т. 81. № 5. С. 362–373.
Суховольский В.Г., Исхаков Т.Р., Тарасова О.В., 2008. Оптимизационные модели межпопуляционных взаимодействий. Новосибирск: Наука. 162 с.
Суховольский В.Г., Иванова Ю.Д., Шульман K., Мажаров В.Ф., Тарасова И.В. и др., 2015. Популяционная динамика онкозаболеваний: модель фазового перехода второго рода // Биофизика. Т. 60. № 4. С. 777–786.
Тарасова О.В., Калашникова И.И., Кузнецова В.В., 2015. Энергетический баланс потребления корма насекомыми-филлофагами: оптимизационная модель // Сиб. лесн. журн. № 3. С. 83–92.
Эпова В.И., Плешанов А.С., 1995. Зоны вредоносности насекомых-филлофагов Азиатской России. Новосибирск: Наука. 147 с.
Юрченко Г.И., Турова Г.И., 2007. Сибирский и белополосый шелкопряды на Дальнем Востоке. Хабаровск: Изд-во ФГУ “ДальНИИЛХ”. 98 с.
Baltensweiler W., 1964. Zeiraphera griceana Hubner (Lepidoptera, Tortricedae) in the European Alps. A contribution to the problem of cycles // Can. Entomol. V. 96. № 5. P. 792–800.
Baltensweiler W., 1991. The folivore guild on larch (Larix decidua) in the Alps // Forest Insect Guilds: Patterns of Interaction with Host Trees / Eds Baranchikov Y., Mattson W., Hain F., Payne T. USDA Forest Service. Gen. Tech. Rep. NE-153. P. 145–164.
Baltensweiler W., Fischlin A., 1988. The larch budmoth in the Alps // Dynamics of Forest Insect Populations: Patterns, Causes, Implications. N.Y.: Plenum Press. P. 331–351.
Berryman A.A., 1988. Dynamics of Forest Insect Populations. N.Y.: Plenum Press. 603 p.
Imperial Colledge, 2020. The Global Population Dynamics Database. https://knb.ecoinformatics.org/view/doi:10.5063 /F1BZ63Z8.
Isaev A.S., Soukhovolsky V.G., Tarasova O.V., Palnikova E.N., Kovalev A.V., 2017. Forest Insect Population Dynamics, Outbreaks and Global Warming Effects. N.Y.: Wiley and Sons. 286 p.
Kononov A., Ustyantsev K., Wang B., Mastro V.C., Fet V. et al., 2016. Genetic diversity among eight Dendrolimus species in Eurasia (Lepidoptera: Lasiocampidae) inferred from mitochondrial COI and COII, and nuclear ITS2 markers // BMC Genet. V. 17. Suppl. 3. P. 157.
Lotka A.J., 1925. Elements of Physical Biology. Baltimore: Williams and Wilkins Company. 495 p.
Mikkola K., Ståhls G., 2008. Morphological and molecular taxonomy of Dendrolimus sibiricus Chetverikov stat. rev. and allied lappet moths (Lepidoptera: Lasiocampidae), with description of a new species // Entomol. Fennica. V. 19. P. 65–85.
Volterra V., 1931. Leçons sur la Théorie Mathématique de la Lutte pour la Vie. Paris: Gauthier-Villars. 214 p. Русский перевод: Вольтера В., 1976. Математическая теория борьбы за существование. М.: Наука. 288 с.
Дополнительные материалы отсутствуют.
Инструменты
Журнал общей биологии