Океанология, 2020, T. 60, № 1, стр. 37-48
Океанические приливные модели и гравиметрические приливные наблюдения
В. Ю. Тимофеев 1, *, М. Г. Валитов 2, Д. Г. Ардюков 1, А. В. Тимофеев 1, Б. Дюкарм 3, Р. Г. Кулинич 2, Т. Н. Колпащикова 2, З. Н. Прошкина 2, Е. В. Бойко 1, С. Б. Наумов 4
1 Институт нефтегазовой геологии и геофизики
им. А.А. Трофимука СО РАН
Новосибирск, Россия
2 Тихоокеанский океанологический институт
им. В.И. Ильичева ДВО РАН
Владивосток, Россия
3 Центр исследований Земли и климата
Католического Университета Лоувэйна
Лоувэйн, Бельгия
4 Региональный информационно-обрабатывающий центр сейсмической подсистемы службы
предупреждения о цунами Геофизической службы РАН
Владивосток, Россия
* E-mail: timofeevvy@ipgg.sbras.ru
Поступила в редакцию 14.03.2019
После доработки 12.05.2019
Принята к публикации 18.06.2019
Аннотация
Влияние приливных эффектов Мирового океана отражается в результатах высокоточных гравиметрических измерений. Эксперименты на станциях трансконтинентального земноприливного профиля позволяют проверить существующие приливные модели океана. В работе рассматриваются данные по станциям в зоне влияния Атлантического и Тихого океанов. Для станций, расположенных в центре Евразии, эффекты минимальны и хорошо описываются как широко известными моделями Швидерского, так и более современными моделями. Результаты изменяются при приближении к берегам океанов, где становятся значимыми океанические приливные нагрузки. В западной части профиля анализируются результаты наблюдений в Аквитании (Франция) в зоне влияния Бискайского залива. В восточной части профиля рассматриваются данные измерений в районе Хабаровска, на острове Сахалин и в Приморье на станциях Посьет и Мыс Шульца в зоне влияния Охотского и Японского морей. На юге Приморья получены многолетние серии уровнемерных и гравиметрических измерений. На основании полученных результатов проведен выбор приливных альтиметрических моделей океана и определен круг нерешенных вопросов.
ВВЕДЕНИЕ
Приливы – это планетарное явление, т.е. воздействие на все тело Земли от ее центра до поверхности, на океаны и поверхностные воды, создающее эффекты, отражающиеся на всех видах высокоточных измерений [1]. Известно, что приливы являются единственным геофизическим явлением, где априори, с очень высокой точностью известна сила воздействия. Отношение масс Земля–Луна и Земля–Солнце определено с точностью 2 × 10–6, а частота орбитального движения и ее вариации, такие как частота вращения Земли, известны до 7-й цифры. Если бы орбиты Земли и Луны были круговыми и лежали в одной плоскости, то имелись бы две приливные компоненты: одна лунная и одна солнечная полусуточная волна. Наклонение плоскостей орбит по отношению к экватору, эллиптичность обеих орбит, эвекция и вариация, обусловленные изменениями эллиптичности лунной орбиты Солнцем – все эти воздействия вызывают разделение основных спектральных линий и образование большого количества приливных компонент [6, 7]. В 1883 г. Д. Дарвин опубликовал первое гармоническое разложение приливного потенциала из 39 членов. В настоящее время имеется несколько новых разложений, содержащих 1200 волн. Приливный “гармонический” анализ, предложенный Кельвином в 1868 г., сейчас основывается на методе наименьших квадратов с использованием специальных цифровых фильтров для разделения трех лапласовых серий приливов перед выделением наибольшего количества спектральных линий в зависимости от длины записи. Максимальная величина гравиметрического прилива – 240 мкГал (~2 × 10–7 от нормального значения ускорения силы тяжести; 1 мкГал = 10 нм/с2). Приливный эффект для Земли описывается в рамках статической теории [6, 7, 17, 25], с учетом неупругости мантии – в рамках квазистатической теории [12], а с учетом эффекта жидкого ядра Земли – в рамках динамической теории жидкого ядра (резонанс на суточных периодах – до 2% в амплитуде) [6, 7, 12]. Современные модели приливной деформации рассчитываются путем численного интегрирования системы дифференциальных уравнений для всей Земли, состоящей из уравнений движения, уравнения Пуассона и реологического соотношения напряжение – деформация. Учитываются распределения по глубине: плотности, упругих модулей, притяжения и сжатия каждого слоя Земли [6, 7, 12, 25].
Исследование морских приливов в океанах и отдельных морях является сложной задачей [2–6, 8, 12]. Вклад эффекта океана в гравиметрические результаты на континентах и островах достигают 10% от эффекта приливной деформации Земли. Эти явления описываются в рамках динамической приливной теории Мирового океана. Здесь, помимо вынужденных приливных волн, появляются свободные колебания и резонансы, которые зависят от многих параметров (высота статического прилива на невозмущенной поверхности, трения на дне океана, вязкой турбулентной диссипации, глубины океана, вязкости воды, силы Кориолиса, высоты свободной поверхности океана и т.д.). Некоторые авторы полагают, что вихревая диссипация существенна в глубоких океанах, а донное трение важно в мелких морях. Известна важная роль приливной диссипации в Мировом океане в эволюции Земли, в частности, в изменении скорости вращения Земли. В последние десятилетия приливные модели Земли и Мирового океана активно используются в спутниковых технологиях для навигации (VLBI, GPS), в исследованиях климата и временных вариаций в параметрах гидросферы планеты (GRACE), для расчета поправок в высокоточные гравиметрические наблюдения, при газовой съемке и в других геофизических измерениях, где учитываются эффекты на уровне деформаций 10–8 или соответствующих напряжений в земной коре (0.01 бар).
Задача наших исследований – провести оценку существующих моделей приливной деформации Земли (WD93 и DDW99) и приливных моделей океана (SCW80, CSR3, FES95, ORI96, CSR4, FES02, GOT00, NAO99, TPX06 и FES04) на разных расстояниях от побережья, рассмотреть особенности приливной реакции в прибрежной зоне.
РЕЗУЛЬТАТЫ ГРАВИМЕТРИЧЕСКИХ ИЗМЕРЕНИЙ НА ПРОФИЛЕ
Высокоточные измерения современными приборами на профиле от Атлантического побережья Франции до Сахалина и Приморья выполнялись впервые. Наблюдения приливных вариаций силы тяжести проводились в полосе от 42 до 55° с.ш. и от 0° до 143° в.д. Исследовались волны суточного и полусуточного диапазонов. Известно, что амплитуды полусуточного прилива имеют максимум на экваторе, а на полюсах принимают нулевое значение. Суточные приливы принимают максимальные значения на широтах +45° и ‒45° при максимальном склонении возмущающего тела. Этими соображениями определяется среднеширотный выбор положения профиля (рис. 1, табл. 1). Высоты пунктов наблюдений составляли от 35 (мыс Шульца) до 550 м (Талая, Байкал).
Рис. 1.
Положение станций трансконтинентального приливного профиля. Профиль включает станции Западной Европы (Минипли (Франция) и Уикль (Бельгия)), две станции юга Сибири (Ключи и Талая) и три станции на Дальнем Востоке России (Забайкальское и Южно-Сахалинск, мыс Шульца).
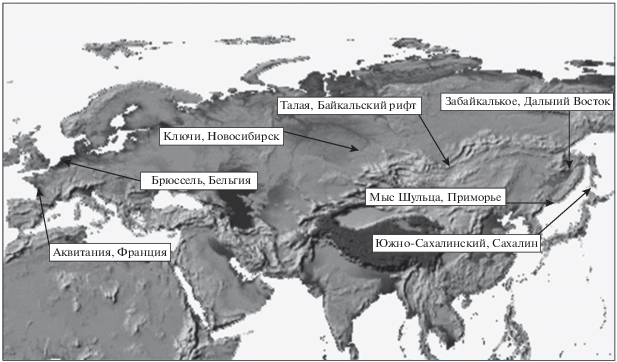
Таблица 1.
Положение пунктов гравиметрических измерений, периоды измерений, астрономические амплитуды главных приливных волн в нм/с2. 10 нм/с2 = 1 мкГал
| Станция | Координаты | Период наблюдений | Амплитуда в нм/с2 | ||
|---|---|---|---|---|---|
| с.ш. | в.д. | годы | волна О1 | волна М2 | |
| Минипли | 45°019′ | 0°105′ | 1995–2000 | 310.6 | 375.4 |
| Уикль | 50°799′ | 4°358′ | 1998; 2001; 2005 | 304.3 | 300.2 |
| Новосибирск | 54°842′ | 83°247′ | 1995–1996; 2003–2004 | 292.7 | 249.3 |
| Талая | 51°681′ | 103°644′ | 1996–1997 | 302.4 | 289.0 |
| Забайкальское | 47°630′ | 134°747′ | 2001–2003 | 309.4 | 341.3 |
| Южно-Сахалинск | 47°030′ | 142°717′ | 2004–2005 | 309.9 | 349.1 |
| Мыс Шульца | 42°650′ | 130°880′ | 2012–2014 | 309.4 | 407.2 |
Для измерений на трансконтинентальном профиле использованы мобильные цифровые гравиметры ЛаКоста-Ромберга различной модификации: LCR402, LCR906 и Gphone111 [1, 13]. На юге Приморья исследования дополнены измерениями уровня моря в заливе Посьета датчиком давления с разрешением в 1 см. Дискретизация цифровой записи на гравиметрах составляла – от 1 до 60 с. Продолжительность непрерывных измерений от 1 года до 3 лет, что позволяет надежно выделять и разделять более 10 волн приливного спектра. Анализ моделей проводился по наиболее сильным волнам полусуточного и суточного диапазонов. Почасовые данные обрабатывались приливными программами: ETERNA, ANALYSE-ETERNA и VAV03-VAV04 [22, 23, 26]. Тестирование гравиметров проводилось на базовой станции Международного приливного центра ICET (Королевская Обсерватория Бельгии, Уикль, Брюссель, координаты 50.7986° с.ш., 4.3581° в.д.). Уровнемерные данные обрабатывались по программам, используемым океанологами.
Анализ начинаем с результатов, полученных на внутриконтинентальных станциях, потом рассмотрим результаты, полученные на западе на побережье Атлантического океана. Далее двигаемся на восток до побережья Охотского и Японского морей. Проанализируем следующие приливные модели мирового океана: SCW80, CSR3, FES95, ORI96, CSR4, FES02, GOT00, NAO99, TPX06 [9–11, 15, 16, 18, 19, 21]. В расчетах океанической модели SCW80 [20] использована сетка с разрешением 1° × 1°. Позднее с широким применением спутниковых данных происходит постоянное уточнение моделей по сетке с ячейками размером до 10 км.
Остановимся на гравиметрических экспериментальных результатах и расчетах влияния океана для внутриконтинентальных станций Ключи (под г. Новосибирск) и Талая (в 6 км от берега озера Байкал), расположенных на расстояниях более трех тысяч километров от побережья Северного Ледовитого и Тихого океанов. В результате приливного анализа получаем два параметра: амплитудный фактор – это безразмерная величина, отношение амплитуд и фазовое запаздывание относительно приливной силы. Если бы Земля была абсолютно твердой, то гравиметр измерял бы только приливную силу – астрономический прилив, а приливный фактор, отношение измеренной амплитуды к астрономической, был бы равен единице. Реальная Земля дает увеличение приливного фактора на 15–16%. Теоретические значения амплитудного гравиметрического фактора (δ = A/Ath = Aтеоретическая-Земля/Aастрономическая) в средних широтах Евразии для главных приливных волн (суточная О1 и полусуточная М2) для статической упругой модели Земли WD [25] и квазистатической модели DDW99 [12] приведены в табл. 2.
Таблица 2.
Теоретические значения приливной деформации Земли для различных моделей Земли для средних широт
| Модель земных приливов | δ(O1) | δ(M2) |
|---|---|---|
| Упругая мантия на базе модели PREM | 1.1519 | 1.1567 |
| Упруго-вязкая с зависимостью добротности мантии от частоты вынуждающего воздействия Q ∼ ω0.15 | 1.1562 | 1.1608 |
Учет влияния океана можно проиллюстрировать, используя векторные соотношения [17] (рис. 2). В этом случае океаническая компонента – это приливный нагрузочный вектор L, при построении которого принимаются во внимание прямое притяжение водных масс, изгиб земной поверхности и соответствующее изменение потенциала. Приливным анализом, для главных приливных волн мы определяем амплитуду A и разность фаз α, т.е. вектор A(A, α). Амплитудный фактор δ определяем как отношение A/Ath [17], т.е. амплитуда A по отношению к астрономической приливной амплитуде Ath. Модельный приливный фактор строим на основе приливной амплитуды R(R = AthδDDW, 0), вычисленной по негидростатичной неупругой модели DDW99 [12], и океанического нагрузочного вектора L(L, λ), вычисляемого по приливным моделям океана для каждой волны. Модельный вектор Am (Am, αm) получаем как:
Модельный амплитудный фактор δm просто выражается через отношение Am/Ath. Таким путем моделируется вектор из выражения:(2)
${{{\mathbf{A}}}_{{\text{m}}}}({{\delta }_{{\text{m}}}}{{A}_{{{\text{theo}}}}},{{\alpha }_{{\text{m}}}}) = {\mathbf{R}}(R,0) + {\mathbf{L}}(L,\lambda ).$(3)
$\begin{gathered} {{{\mathbf{A}}}_{{\text{c}}}}({{\delta }_{{\text{c}}}}{{A}_{{{\text{theo}}}}},{{\alpha }_{{\text{c}}}}) = {\mathbf{A}}(\delta {{A}_{{{\text{theo}}}}},\alpha ) - {\mathbf{L}}(L,\lambda ) = \\ = {\mathbf{R}}(R,0) + {\mathbf{X}}(X,\chi ). \\ \end{gathered} $(4)
${\mathbf{B}}(B,\beta ) = {\mathbf{A}}(\delta {{A}_{{{\text{theo}}}}},\alpha ) - {\mathbf{R}}(R,0).$Рис. 2.
Соотношения между наблюдаемым приливным амплитудным вектором A(A, α), моделью для Земли R(R, 0), вычисленным океаническим приливным нагрузочным вектором L(L, λ), приливным остатком B(B, β) и откорректированным остатком X(X, χ): B = A – R; X = B – L.
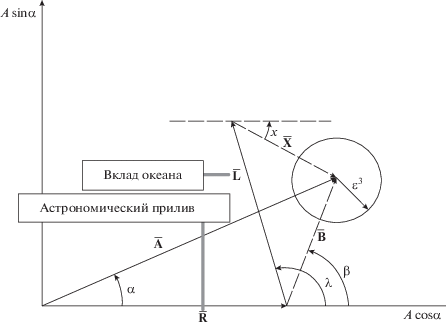
Рис. 3.
Приливные вариации силы тяжести, станция Южно-Сахалинск. Минутная запись с 20 по 30.08. 2005 г., масштаб: 0.039 мкГал на 1 деление вертикальной шкалы справа, гравиметр LCR402. 10 нм/с2 = 1 мкГал.

Экспериментальные результаты для суточной волны О1 и полусуточной волны М2, полученные по данным цифрового гравиметра ЛаКоста Ромберга G 402, приведены в табл. 3. Здесь же представлены модельные расчеты с использованием модели Земли DDW99 [11] и океанических моделей: SCW80 и FES02, CSR4, GOT00, TPX06 [9–11, 15, 16, 18–21]. В таблице показаны значения, средние для группы моделей океана, построенных по уровнемерным данным в портах: SCW80, и для групп моделей, построенных по альтиметрическим спутниковым данным: FES02, CSR4, GOT00, TPX06. Стандартное отклонение при расчете моделей океана в среднем составляет для всех станций профиля для амплитудного фактора 0.0012 (для фазового запаздывания 0.079°) для суточной волны О1 и, соответственно, 0.0018 (0.099°) для полусуточной волны М2.
Таблица 3.
Результаты приливного анализа экспериментальных результатов по станциям Ключи (Новосибирск), Талая (Байкал), теоретические значения, построенные по квазистатической модели приливной деформации Земли (DDW) с учетом динамического влияния океана по моделям SCW80, и среднее по моделям FES02, CSR4, GOT00, TPX06. О1 – суточная волна, М2 – полусуточная волна. δ – амплитудный фактор (отношение наблюдаемой амплитуды прилива к теоретической амплитуде), α – фазовый сдвиг (в градусах относительно теоретического прилива)
| Волна | O1 | M2 | ||
|---|---|---|---|---|
| Ключи, Новосибирск, периоды наблюдений 1995–1996 гг. и 2003–2004 гг. |
δ | α, град | δ | α, град |
| РЕЗУЛЬТАТ, программа ANALYZE | 1.1577 | 0.254 | 1.1599 | –0.230 |
| Ошибка измерений | ±.0039 | ±.193 | ±.0040 | ±.183 |
| Модель SCW80 | 1.1554 | 0.284 | 1.1560 | –0.318 |
| Среднее по моделям FES02, CSR4, GOT00,TPX0 | 1.1543 | 0.303 | 1.1606 | –0.275 |
| Талая, Байкальский регион, период наблюдений 1996–1997 гг. |
δ | α, град | δ | α, град |
| РЕЗУЛЬТАТ, программа ANALYZE | 1.1598 | 0.313 | 1.1585 | 0.106 |
| Ошибка измерений | ±.0051 | ±.270 | ±.0028 | ±.137 |
| Модель SCW80 | 1.1607 | 0.353 | 1.1592 | 0.153 |
| Среднее по моделям FES02, CSR4, GOT00,TPX0 | 1.1596 | 0.389 | 1.1627 | 0.052 |
В результате для внутриконтинентальных станций согласно экспериментальным данным по суточным (О1) и полусуточным волнам (М2), отклонение амплитуд от приливной модели составляет менее долей процента (табл. 3). Вклад океанического прилива в фазовое запаздывание составляет от 0.1° до 0.3°, а отклонение от моделей, учитывающих влияние океана, не превышает 0.05°–0.08° и находится в пределах ошибки наблюдений.
Рассмотрим результаты, полученные в прибрежной зоне на западе профиля. В сводной табл. 4 приведены данные анализа для станции Минипли в Аквитании (Menesplet, Франция, 110 км от берега Бискайского залива Атлантического океана, цифровой гравиметр LCR906).
Таблица 4.
Результаты приливного анализа данных для пункта в Аквитании на атлантическом побережье Франции (Aquitaine, Menesplet), Забайкальское (Хабаровск), Южно-Сахалинск (Сахалин). Теоретические модельные значения, построенные по модели приливной деформации Земли DDW, с учетом влияния океана, модели SCW80 и для групп моделей: CSR4, FES02, GOT00, NAO99 и FES02, CSR4, GOT00, TPX06
| Волна | O1 | M2 | ||
|---|---|---|---|---|
| станция измерений и результаты | ||||
| Минипли (Aquitaine, Menesplet, Франция) период наблюдений 1995–1999 гг. |
δ | α, град | δ | α, град |
| РЕЗУЛЬТАТ, программа ANALYZE | 1.1490 | –0.240 | 1.1896 | 6.020 |
| С ошибкой | ±.0018 | ±0.090 | ±.0004 | ±.020 |
| Модель SCW80 | 1.1461 | –0.210 | 1.1875 | 5.890 |
| Среднее по моделям CSR4, FES02, GOT00, NAO99 | 1.1458 | –0.130 | 1.1882 | 6.010 |
| Забайкальское, (юг Хабаровского края) период наблюдений 2001–2003 гг. |
δ | α, град | δ | α, град |
| РЕЗУЛЬТАТ, программы ANALYZE + VAV04 | 1.1850 | 0.767 | 1.1729 | 0.674 |
| С ошибкой | ±.0078 | ±.380 | ±.0055 | ±.270 |
| Модель SCW80 | 1.1868 | 0.870 | 1.1736 | 0.485 |
| Среднее по моделям FES02, CSR4, GOT00, TPX06 | 1.1837 | 0.813 | 1.1715 | 0.507 |
| Южно-Сахалинск, (остров Сахалин), период наблюдений 2004–2005 гг. |
δ | α, град | δ | α, град |
| РЕЗУЛЬТАТ, программа VAV04 | 1.2235 | 1.111 | 1.1752 | 1.531 |
| С ошибкой | ±.0034 | ±.162 | ±.0022 | ±.106 |
| Модель SCW80 | 1.2199 | 1.334 | 1.1811 | 1.697 |
| Среднее по моделям FES02, CSR4, GOT00, TPX06 | 1.2206 | 1.250 | 1.1768 | 1.453 |
В восточной части профиля рассмотрим данные по станциям: Забайкальское (Хабаровский край, в 290 км от берега Татарского пролива Японского моря, цифровой гравиметр LCR G 402) и Южно-Сахалинск (остров Сахалин, в 35 км от берега Охотского моря, цифровой гравиметр LCR G 402). Пример гравиметрической цифровой записи прилива на станции Южно-Сахалинск (ИМГ ДВО РАН, о. Сахалин) с 20 по 30 августа 2005 г. приведен на рис. 3.
В табл. 4 приведено сравнение модельных данных (модель DDW99 + модель Швидерского и современные приливные модели океана) с экспериментальными результатами, полученными с помощью цифровых гравиметров ЛаКоста Ромберга, по западной и восточной части трансконтинентального приливного профиля. Отметим, что наибольшее влияние на фазу (6°) получено в зоне влияния Бискайского залива в Атлантическом океане (Аквитания, Франция) для полусуточной волны М2. В восточной части профиля полученное влияние достигает полутора градусов, что в пределах ошибки (от 0.02 до 0.2°) хорошо соответствует модельным представлениям. Вклад в амплитуду достигает 5% и хорошо коррелирует с результатами моделирования. Различаются влияния океана для западной и восточной частей профиля. Так, в зоне влияния Атлантики сильнее вклад океана в полусуточный диапазон (см. табл. 3, по волне М2 сильное влияние для амплитуды и для фазы), а для восточных морей в зоне Тихого океана сильнее влияние в суточном диапазоне (см. табл. 4, значения амплитудного фактора δ).
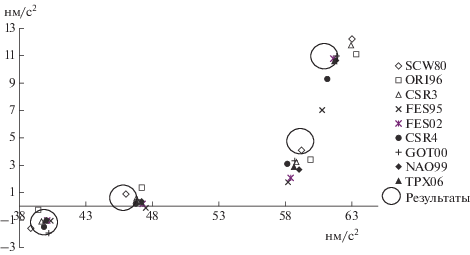
Используя векторные соотношения (1–5), можно оценить корректность выбора океанической компоненты (приливного нагрузочного вектора L), представительность котидальных карт и наземных измерений, проанализировав соотношение векторов B = A – R и L по косинусным и синусным компонентам: B cos β с L cos λ и B sin β с L sin λ. Графически результаты сравнения по отдельным станциям профиля представлены на рис. 4. Здесь мы имеем по осям значения в фазе: δ cos α (горизонтальная ось) и вне (вертикальная ось): δ sin α (динамический эффект, т.е. океанический вклад). По горизонтальной оси – сравнение амплитуды для волны М2 (полусуточная), а именно – разность относительно астрономической амплитуды Ath для каждой станции. Результаты такого анализа для восточной части профиля от Новосибирска до Южно-Сахалинска приведены на рис. 4. Показана остаточная часть амплитудной и фазовой реакции на приливную силу тяжести для станций профиля, расположенных в центре континента и далее к океану. Из анализа результатов, представленных на рис. 4, можно видеть увеличение вклада океанического прилива до 12 нм/с2 = 1.2 микрогал при смещении на восток к Тихому океану. При отсутствии влияния океана результаты располагались бы вдоль горизонтальной оси почти на нулевом значении вертикальной оси. Как видим из рис. 4, модельные оценки хорошо соответствуют экспериментальным результатам. Заметим, что, убирая все моделируемые эффекты (модель отклика Земли, модель океанической нагрузки и притяжения) из наблюдений, можно исследовать другие эффекты: неупругость коры и мантии, горизонтальные неоднородности, корреляцию с тепловым потоком, диссипацию в ядро-мантийном слое Земли.
Рис. 4.
Сравнение приливных моделей и экспериментальных результатов для полусуточной волны М2. По вертикальной оси – сдвиг по фазовой компоненте (около нуля для внутриконтинентальных станций, эффект увеличивается с приближением к океану). Слева направо: Новосибирск–Ключи (1289), Талая–Байкал (1301), Хабаровск–Забайкальское (1401), Южно-Сахалинск (1403). Приведены номера станций в мировой приливной сети. 10 нм/с2 = 1 мкГал.
Продолжением гравиметрических приливных исследований на Дальнем Востоке явились измерения на научном полигоне “Мыс Шульца” ТОИ ДВО РАН, которые проводятся здесь различными типами приборов с 2010 г. Цифровой гравиметр Gphone111 используется для мониторинга силы тяжести на полигоне с 2012 г. Станция гравиметрических наблюдений расположена на юге Приморья, мыс Шульца, полуостров Гамова (координаты пункта гравиметрических измерений – 42.58° с.ш., 131.16° в.д., пункт расположен в 130 м от берега бухты Витязь в заливе Посьет Японского моря, рис. 5). На пункте одновременно проводятся измерения смещений земной поверхности методом космической геодезии различными типами двухчастотных геодезических приемников [1]. Абсолютным гравиметром ГАБЛ здесь выполняются ежегодные измерения неприливных вариаций силы тяжести, в которых отражаются эффекты катастрофических землетрясений Дальнего Востока [1].
Рис. 5.
Станции наблюдений на побережье Японского моря. Положение пунктов приливных наблюдений (пункт Залив Посьет “LEVEL” – измерения уровня моря) и мыс Шульца на полуострове Гамова (пункт гравиметрических измерений “GORA” (номер в международной сети приливных станций 1406)).

Гравиметрические измерения проводятся на массивных постаментах в специальном подземном бункере с пассивной термостабилизацией. Цифровой комплекс гравиметра Gphone111 имеет 18 каналов при 1 – секундной записи. Для анализа использовался канал № 1 и канал № 8, т.е. прямая запись с маятника гравиметра и вариации атмосферного давления на пункте. Результаты анализа данных измерений за период с 2012 по 2014 гг. приведены в табл. 5. В табл. 6 показаны результаты сравнения экспериментальных результатов и модельных расчетов для 10 моделей океана. Приливный анализ данных гравиметрических измерений по программам приливного анализа ETERNA и VAV04 показал одинаковые результаты (табл. 5 и 6). Сравнение экспериментальных результатов с модельными оценками свидетельствует о значительном отличии как в амплитудном факторе, так и в фазовом запаздывании. Фазовое запаздывание достигает 0.5° при ошибке измерений в 0.01°, амплитудное – до 1% при ошибке в 0.02%.
Таблица 5.
Результаты приливного анализа по программе ETERNA пункт Мыс Шульца период измерений (2012–2014 гг.). Представлены суточные, полусуточные и треть суточные волны. В суточном диапазоне на частоте волны K1 в амплитуде проявляется динамический эффект жидкого ядра Земли (занижение амплитуды на 2%) [6]. Внизу приведено значение коэффициента связи с атмосферным давлением в нанометрах на килопаскаль
| Номер станции в международной приливной сети – 1406, станция “Мыс Шульца” – SHULTS CAPE | |||||||
|---|---|---|---|---|---|---|---|
| Период наблюдений: 20 120 623…20 141 224, 13 блоков. Всего суток в анализе: 558.875 | |||||||
| Потенциал Тамура – Tamura (1987) 1200 волн | |||||||
| Использована неупругая модель Земли WAHR-DEHANT-ZSCHAU | |||||||
| Интервал осреднения 3600 с | |||||||
| Использован цифровой фильтр Перцева с 51 коэффициентом | |||||||
| Приливные параметры: | |||||||
| диапазон от цикл/день | до цикл/день | волна | Аtheor в нм/с2 |
δ фактор | ошибка | фазовый сдвиг в ° | ошибка в ° |
| 0.501370 | 0.842147 | SGQ1 | 2.2857 | 1.18232 | 0.03073 | –0.6425 | 1.4893 |
| 0.842148 | 0.860293 | 2Q1 | 7.8394 | 1.18255 | 0.00929 | 0.2786 | 0.4498 |
| 0.860294 | 0.878675 | SGM1 | 9.4619 | 1.18949 | 0.00724 | 0.5278 | 0.3490 |
| 0.878676 | 0.896968 | Q1 | 59.2480 | 1.16760 | 0.00115 | 0.0344 | 0.0565 |
| 0.896969 | 0.911390 | RO1 | 11.2540 | 1.15715 | 0.00552 | –0.3253 | 0.2730 |
| 0.911391 | 0.931206 | O1 | 309.4501 | 1.16540 | 0.00021 | 0.0786 | 0.0103 |
| 0.931207 | 0.947991 | TAU1 | 4.0361 | 1.16113 | 0.01151 | 1.0458 | 0.5687 |
| 0.947992 | 0.967660 | NO1 | 24.3372 | 1.16301 | 0.00263 | 0.2132 | 0.1299 |
| 0.967661 | 0.981854 | CHI1 | 4.6545 | 1.16522 | 0.01395 | –1.0953 | 0.6863 |
| 0.981855 | 0.996055 | PI1 | 8.4170 | 1.14997 | 0.00698 | 0.3503 | 0.3491 |
| 0.996056 | 0.998631 | P1 | 143.9864 | 1.15901 | 0.00042 | –0.0251 | 0.0205 |
| 0.998632 | 1.001369 | S1 | 3.4031 | 1.27373 | 0.02547 | 9.4348 | 1.2513 |
| 1.001370 | 1.004107 | K1 | 435.2104 | 1.14574 | 0.00015 | 0.0221 | 0.0075 |
| 1.004108 | 1.006845 | PSI1 | 3.4033 | 1.19917 | 0.01780 | 0.0417 | 0.8528 |
| 1.006846 | 1.023622 | PHI1 | 6.1962 | 1.18309 | 0.00956 | 0.3540 | 0.4648 |
| 1.023623 | 1.035379 | TET1 | 4.6538 | 1.19043 | 0.01338 | –0.4087 | 0.6440 |
| 1.035380 | 1.057485 | J1 | 24.3365 | 1.16962 | 0.00280 | –0.2847 | 0.1374 |
| 1.057486 | 1.071833 | SO1 | 4.0368 | 1.16816 | 0.01718 | 0.6642 | 0.8435 |
| 1.071834 | 1.090052 | OO1 | 13.3137 | 1.14600 | 0.00762 | –0.1702 | 0.3810 |
| 1.090053 | 1.470243 | NU1 | 2.5491 | 1.14599 | 0.03879 | –1.0635 | 1.9400 |
| 1.470244 | 1.845944 | EPS2 | 3.0083 | 1.19326 | 0.01314 | 0.8468 | 0.6317 |
| 1.845945 | 1.863026 | 2N2 | 10.3175 | 1.17026 | 0.00412 | –0.1804 | 0.2018 |
| 1.863027 | 1.880264 | MU2 | 12.4513 | 1.15049 | 0.00303 | 0.6464 | 0.1508 |
| 1.880265 | 1.897351 | N2 | 77.9694 | 1.16617 | 0.00050 | 0.8083 | 0.0244 |
| 1.897352 | 1.914128 | NU2 | 14.8095 | 1.16561 | 0.00247 | 0.6537 | 0.1214 |
| 1.914129 | 1.950419 | M2 | 407.2364 | 1.17104 | 0.00009 | 1.0513 | 0.0043 |
| 1.950420 | 1.964767 | LAM2 | 3.0029 | 1.15759 | 0.01164 | 0.5610 | 0.5770 |
| 1.964768 | 1.984282 | L2 | 11.5106 | 1.17131 | 0.00195 | 0.9116 | 0.0954 |
| 1.984283 | 1.998996 | T2 | 11.0727 | 1.18991 | 0.00339 | 0.2730 | 0.1637 |
| 1.998997 | 2.002736 | S2 | 189.4678 | 1.18247 | 0.00020 | 0.4386 | 0.0105 |
| 2.002737 | 2.022488 | K2 | 51.4967 | 1.17979 | 0.00086 | 0.7745 | 0.0416 |
| 2.022489 | 2.057484 | ETA2 | 2.8792 | 1.21188 | 0.01929 | 0.9562 | 0.9131 |
| 2.057485 | 2.451943 | 2K2 | 0.7541 | 1.21485 | 0.07860 | 1.0617 | 3.7123 |
| 2.451944 | 2.881176 | MN3 | 1.6170 | 1.08708 | 0.01800 | 0.2331 | 0.9493 |
| 2.881177 | 3.381378 | M3 | 5.8932 | 1.07970 | 0.00458 | 0.5400 | 0.2432 |
| Метеорологический параметр, коэффициент связи с атмосферным давлением | |||||||
| значение коэффициент связи | ошибка | единица измерений | |||||
| –4.17964 | 0.01882 | нм/с2/КПа | |||||
Таблица 6.
Модели приливной реакции на пункте Мыс Шульца (1406) и результаты анализа измерений гравиметром Gphone111, период наблюдений 22.06.2012–25.12.2014 (для анализа выбрано 585.3 дня). Результаты счета по приливной программе VAV04
| ВОЛНА | O1 | M2 | ||
|---|---|---|---|---|
| амплитуда астрономическая, мкГал | 30.945 | 40.723 | ||
| МОДЕЛЬ | δm | αm | δm | αm |
| 1. SCW80 | 1.1834 | 0.550 | 1.1767 | 0.513 |
| 2 ORI96 | 1.1764 | 0.490 | 1.1777 | 0.587 |
| 3 CSR3 | 1.1747 | 0.585 | 1.1762 | 0.654 |
| 4 FES95 | 1.1760 | 0.307 | 1.1727 | 0.337 |
| 5 CSR4 | 1.1760 | 0.366 | 1.1736 | 0.474 |
| 6 GOT00 | 1.1760 | 0.387 | 1.1744 | 0.498 |
| 7 NAO99 | 1.1779 | 0.360 | 1.1745 | 0.464 |
| 8 FES02 | 1.1765 | 0.463 | 1.1744 | 0.453 |
| 9 TPX06 | 1.1772 | 0.413 | 1.1746 | 0.449 |
| 10 FES04 | 1.1749 | 0.390 | 1.1745 | 0.548 |
| Среднее по моделям 2–7 | 1.1761 | 0.416 | 1.1749 | 0.496 |
| Среднее по моделям 5–10 | 1.1764 | 0.397 | 1.1744 | 0.474 |
| Среднее по моделям 2–10 | 1.1762 | 0.418 | 1.1748 | 0.492 |
| РЕЗУЛЬТАТ | δo | α0 | δo | α0 |
| VAV04 | 1.16552 | 0.073 | 1.17106 | 1.048 |
| Ошибка | ±.00019 | ±.010 | ±.00008 | ±.004 |
С другой стороны, выбор приливной модели океана для расчета поправок в результаты может быть проведен на основании анализа данных уровнемерной приливной станции мониторинга цунами, расположенной в западной части залива Посьет (координаты пункта наблюдений – 42.65° с.ш., 130.88° в.д.). Измерения выполнялись с помощью датчика давления, разрешение составляет 1 см. Экспериментальная запись морских приливов представлена на (рис. 6). Приливный анализ данных уровнемерных наблюдений показал хорошую сходимость результатов с приливными моделями океана CSR4 и FES02 (табл. 7), хотя эти измерения менее точны по сравнению с гравиметрическими.
Рис. 6.
Запись приливных вариаций, станция регистрации уровня воды Посьет. Почасовые данные. Шкала времени с 00 ч 01.12.2012 г. до 23 ч 31.01. 2013 г. Вертикальная шкала – в сантиметрах.

Таблица 7.
Альтиметрические модели океана CSR4 и FES02 и экспериментальные результаты (уровнемерная станция в заливе Посьета), для суточных (Q1, O1, P1, K1) и полусуточных (N2, M2, S2, K2) приливных волн. Для каждой приливной волны приведена амплитуда волны в сантиметрах и фазовое запаздывание в градусах (океанологическая модель). Координаты (коширота (κφ) и долгота (λ)) в градусах, площадь ячейки в м2 (S). Период наблюдений – 23.11.2012–02.03.2015
| Приливная волна | Q1 | O1 | P1 | K1 | N2 | M2 | S2 | K2 | ||
|---|---|---|---|---|---|---|---|---|---|---|
| Результаты анализа данных | ||||||||||
| Амплитуда в см | 1.17 | 5.00 | 1.78 | 5.65 | 1.81 | 7.70 | 3.34 | 0.92 | ||
| Фаза в ° | 181.0 | 198.0 | 223.0 | 227.0 | 181.0 | 194.0 | 219.0 | 209.0 | ||
| N | κφ (°) | S ячейки в м2 | ||||||||
| λ (°) | ||||||||||
| CSR4 | ||||||||||
| 41 895 | 47.0 | .2260658 × 1010 | 1.520 | 4.280 | 1.850 | 6.010 | 1.210 | 5.970 | 2.860 | 0.790 |
| 131.50 | 197.87 | 195.52 | 222.28 | 224.19 | 191.08 | 184.77 | 202.48 | 205.09 | ||
| 42 297 | 47.5 | .2278969 × 1010 | 1.600 | 4.720 | 1.810 | 6.010 | 0.900 | 6.240 | 2.990 | 0.800 |
| 130.50 | 203.97 | 197.09 | 224.34 | 226.80 | 183.69 | 182.03 | 202.11 | 205.14 | ||
| 42 298 | 47.5 | .2278969 × 1010 | 1.560 | 4.780 | 1.830 | 6.010 | 1.020 | 6.010 | 2.940 | 0.800 |
| 131.00 | 201.48 | 196.04 | 223.57 | 225.94 | 187.38 | 183.98 | 202.88 | 205.57 | ||
| FES02 | ||||||||||
| 537 842 | 47.0 | .5651670 × 109 | 1.140 | 4.890 | 1.790 | 5.110 | 2.010 | 8.620 | 3.190 | 0.820 |
| 131.75 | 164.80 | 201.32 | 233.83 | 232.73 | 143.31 | 196.66 | 202.25 | 198.51 | ||
| 536 343 | 47.5 | .5697446 × 109 | 1.110 | 4.750 | 1.760 | 5.010 | 1.830 | 7.560 | 2.780 | 0.720 |
| 131.00 | 163.26 | 199.87 | 232.18 | 231.39 | 142.04 | 193.52 | 197.91 | 193.18 | ||
В итоге, имеем для результатов анализа уровнемерных данных хорошее соответствие модельным оценкам (приливные модели океана CSR4 и FES02) для главных (по амплитуде) суточных и полусуточных волн. Более точные гравиметрические результаты показывают расхождение с модельными оценками, значительно превышающее ошибки измерений.
ЗАКЛЮЧЕНИЕ
В заключение следует отметить, что результаты гравиметрических измерений, полученные на станциях трансконтинентального профиля на расстояниях от 3000 до 35 км от берега моря, показали хорошее соответствие современным приливным моделям океана NAO99, GOT00, FES02, CSR4, TPX06. Модели влияния Атлантического и Тихого океана на средних широтах в целом удовлетворяют требованиям высокоточных гравиметрических измерений, эффект рассчитывается до 0.1 микрогала (0.1 мкГал = 1 нм/с2). Расхождение с моделями обнаружено на юге Приморья, на пункте, расположенном в 130 м от берега бухты Витязь залива Посьет Японского моря, Тихого океана. Известно, что амплитуда полусуточных приливов в большинстве районов Тихого океана меньше, чем в Атлантическом. Эти закономерности отмечены в полученных нами экспериментальных результатах. Заметим, что из 13 морей, омывающих территорию Российской Федерации, только Берингово и Японское моря имеют средние глубины в полтора километра (1640 и 1539 м) и максимальные более 4 км (4420 и 4224 м). В Японском море шельф развит слабо, граница проходит в 30 км от суши, глубины до 200 м занимают 27% всей площади и приходятся в основном на Татарский пролив [5]. Наблюдения на станции, расположенной на берегу бухты Витязь (размеры бухты – 4 на 2 км, глубина 30 м, с островами на выходе из бухты), выявили расхождения с существующими модельными оценками для Японского моря. Природа расхождений может быть связана с особенностями собственных колебаний в бухте Витязь залива Посьет Японского моря, т.к. существующие модельные сетки (10 на 10 км) не могут точно отразить резонансы в небольшой бухте. С другой стороны, результаты могут быть проинтерпретированы в рамках реологических многослойных моделей земной коры, астеносферы, верхней мантии и, возможно, связаны с существованием астеносферы на границе континента. Так, есть представления, что кроме зоны субдукции, окаймляющей с востока Японские острова, существует вторая слабовыраженная субдукционная зона, простирающаяся от Японского моря и уходящая на запад под Приморье [14, 24]. Для районов, расположенных на окраине континентов в зоне субдукции эффекты запаздывания земных приливов по отношению к приливному потенциалу (0.5°) можно связать с наличием вязкой астеносферы. Различные реологические модели для фазовых запаздываний приливов на разных частотах рассматривались в работе [17]. В таком случае, используя реологическую модель Максвелла, получаем значение вязкости для астеносферы региона порядка η ~ 1017–1018 Па с. Заметим, что в этой области отмечается повышенный тепловой поток, а значения вязкости соответствуют расчетам, полученным для астеносферы в зоне Курильских островов [24]. В целом, остается задача интерпретации приливных параметров, полученных на полигоне мыс Шульца. Здесь требуется моделирование собственных колебаний по более мелкой сетке (минимум 1 на 1 км и менее) с учетом глубин, течений, изрезанности берегов и наличием островов. С другой стороны, для вычисления поправок в результаты гравиметрических, геофизических и геодезических измерений могут быть использованы эмпирические оценки (например, табл. 5 и 6).
Благодарности. Авторы выражают глубокую признательность сотрудникам полигона “Мыс Шульца” ТОИ ДВО РАН за постоянное содействие при проведении наблюдений.
Список литературы
Ардюков Д.Г., Калиш Е.Н., Носов Д.А. и др. Результаты абсолютных измерений ускорения силы тяжести на мысе Шульца // Гироскопия и навигация. 2015. № 3 (90). С. 13–18. https://doi.org/10.17285/0869-7035.2015.23.3.013-018
Богданов К.Т. Приливы Мирового океана. М.: Наука, 1975. 116 с.
Жуков Л.А. Общая океанология. Ленинград: Гидрометеоиздат, 1976. 376 с.
Каган Б.А. Гидродинамические модели приливных движений в море. Ленинград: Гидрометеорологическое издательство, 1968. 220 с.
Кузьмин В.И., Косарев Н.С. Антонович К.М. Физика Земли. Строение атмосферы и гидросферы Земли. Новосибирск: СГУГиТ, 2017. 268 с.
Мельхиор П. Земные приливы. М.: Мир, 1968. 482 с.
Молоденский С. М. Приливы, нутация и внутреннее строение Земли. М.: ИФЗ АН СССР, 1984. 215 с.
Перцев Б.П. Влияние морских приливов ближних зон на земноприливные наблюдения // Изв. АН СССР. Сер. Физика Земли. 1976. № 1. С. 30–38.
Baker T.F., Bos M.S. Validating Earth and ocean models using tidal gravity measurements // Geophys. J. Int. 2003. № 152. P. 468–485.
Boy J.P., Lubes M., Ray R. et al. Validation of long-period oceanic tidal models with superconducting gravimeters // J. of Geodynamics. 2006. № 41. P. 112–118.
Chen J.L., Wilson C.R. Low degree gravity changes from GRACE, Earth rotation, geophysical models and satellite laser ranging // J. of Geophys. Res. 2008. № 113. B066402. https://doi.org/10.1029/2007JB00597
Dehant V., Defraigne P., Wahr J.M. Tides for a convective Earth // J. of Geophys. Res. 1999. V. 104. № B1. January 10. P. 1035–1058.
Ducarme B., Timofeev V.Yu., Everaerts M. et al. A Trans-Siberian Tidal Gravity Profile (TSP) for the validation of the ocean tides loading corrections // J. of Geodynamics. 2008. V. 45. № 2–3. P. 73–82.
Gornov P. Yu. Relationship of the thermal conductivity of rocks in the Komsomol’sk ore district (Khabarovsk Territory) with minerageny and metasomatism // Russian Geology and Geophysics. 2015. V. 56. № 3. P. 493–499. https://doi.org/10.1016/ j.rgg.2015.02.010
Lyard F., Lefevre F., Letellice T., Francis O. Modeling the global ocean tides: Insights from FES2004 // Ocean. Dyn. 2006. V. 56. P. 394–415.
Matsumoto K., Takanezawa T., Ooe M. Ocean tide models developed by assimilating TOPEX/POSEIDON altimeter data // J. Oceanography. 2000. № 56. P. 567–581.
Melchior P. The Tides of the Planet Earth. 2nd Edition. Pergamon Press. Oxford. 1983. 641 p.
Neumeyer J., Barthelmes F., Dierks O. Combination of temporal gravity variations resulting from Superconducting Gravimeter recordings, GRACE satellite observations and global hydrology models // J. of Geodesy. 2006. https://doi.org/10.1007/S00190-005-0014-8
Ray R.D., Luthcke S.B., Boy J.-P. Qualitative comparisons of global ocean tide models by analysis of intersatellite ranging data // J. Geophys. Res. 2009. V. 114. C09017. https://doi.org/10.1029/2009JC005362
Schiwiderski E.W. Atlas of Ocean Tidal Charts and Maps // Marine Geodesy. 1983. V. 6. № 3–4. P. 219–265.
Shum C. K., Andersen O. B., Egbert G. Comparison of Newly Available Deep Ocean Tide Models by the TOPEX/POSEIDON Science Working Team // J. Geophys. Res. 1997. № 102 (C11). P. 25 173–25 194.
Van Camp M., Vauterin P. Tsoft: graphical and interactive software for the analysis of time series and Earth tides // Computer & Geosciences. 2005. № 31. P. 631–640.
Venedikov A., Arnoso J., Vieira R. VAV: A program for tidal data processing // Computers & Geosciences. 2003. № 29. P. 487–502.
Vladimirova I.S. Modelling of postseismic processes in subduction regions // Geodynamics & Tectonophysics. 2012. V. 3. № 2. P. 167–178.
Wahr J.M. Effect of the fluid core. A normal mode expansion for the forced response of rotating Earth, Body tides // Geophys. J. R. Astron. Soc. 1981. V. 64. № 3. P. 635–728. P. 747–765.
Wenzel H.G. The nanogal software: earth tide data processing package ETERNA 3.30 // Bull. Inf. Maréees Terrestres (BIM). 1996. V. 124. P. 9425–9439.
Дополнительные материалы отсутствуют.


