Океанология, 2020, T. 60, № 5, стр. 805-813

ВВЕДЕНИЕ

Береговые профили с подводными валами широко распространены на песчаных морских побережьях. Типы подводных валов, а также гипотезы и теории, объясняющие их формирование, рассматриваются во множестве работ, например, в [3–5, 12, 30]. Развитие этих мезоформ прибрежного рельефа и их поведение тесно связаны с процессом обрушения волн на береговом склоне. Одним из важных свойств подводных валов является цикличность их перемещений, которая обнаруживается на различных масштабах времени.

В данной работе нас интересует поведение валов в масштабе штормового цикла, характеризующегося размывом пляжа в период повышенной волновой активности и частичным его восстановлением при сравнительно низких волнах зыби во время затухания. Известно, что в фазе размыва валы имеют тенденцию смещаться в сторону моря, а в фазе аккумуляции – в противоположном направлении. В работе [15] рассмотрена модель, описывающая движение вала к берегу. Автором был предложен подход к оценке итоговых смещений валов за время всего шторма [6]. Вместе с тем, морфодинамический прогноз профиля с подводными валами в масштабе штормового цикла, по-прежнему, актуален. Он может основываться на так называемой модели процессов (process-based model), учитывающей главные механизмы транспорта наносов в береговой зоне.

Известно множество подобных моделей [5, 28, 29], симулирующих реальные процессы перемещения осадков на береговом профиле. С помощью закона сохранения массы градиенты вычисленных расходов наносов конвертируются в изменения локальных глубин, которые, в свою очередь, влияют на значения расходов на следующем шаге вычислений, что обеспечивает обратную связь между гидродинамикой и рельефом дна. В результате удается проследить эволюцию морфологии и предсказать ее итоговые изменения при данном волнении.

В идеале модель берегового профиля должна описывать размыв пляжа штормовыми волнами и его восстановление в периоды зыби, формирование соответствующего типа профиля, а также перемещение подводных валов при данных волновых условиях. Однако ввиду сложности и недостаточного понимания морфодинамических процессов до создания универсальной модели пока далеко, что стимулирует дальнейшие попытки в этом направлении [18].

В настоящей работе представлена новая модель CROSS-PB, созданная на базе прежней CROSS-P [5, 7], которая хорошо зарекомендовала себя, например, при прогнозировании размыва песчаных берегов в условиях экстремальных штормовых нагонов, в том числе и при переливе через гребень авандюны [7, 26, 27]. Новая версия CROSS-PB основывается на более детальной трактовке физических механизмов транспорта наносов, что в итоге позволяет расширить рамки применения модели и, в частности, описать смещения подводных валов в различные фазы шторма. Кардинально изменен подход к оценке расходов песчаных наносов в области трансформации волн и прибойной зоне. Результаты моделирования сравниваются с опубликованными лабораторными и натурными данными. Обсуждаются механизмы, контролирующие перемещение валов при изменении волновой активности.

ТРАНСПОРТ НАНОСОВ В ОБЛАСТИ ТРАНСФОРМАЦИИ ВОЛН И ПРИБОЙНОЙ ЗОНЕ

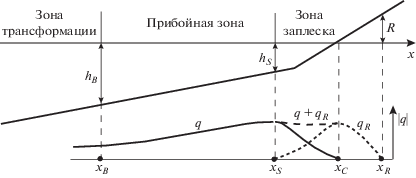
Формула расхода наносов. Область берегового профиля, включающая зону трансформации волн и прибойную зону (рис. 1), продолжается до зоны заплеска, условная граница которой маркируется глубиной ${{h}_{s}} = 0.04\sqrt {{{H}_{{s\infty }}}{{L}_{\infty }}} $, где ${{H}_{{s\infty }}}$ и ${{L}_{\infty }}$ – значимая высота и длина волн на глубокой воде. Поперечный объемный расход наносов $q$ на единицу длины берега (м³ м^–1 с^–1) определяем как [5, 7]

где ${{q}^{0}}$ – расход наносов над горизонтальным дном, выраженный в единицах погруженного веса твердых частиц, g – ускорение силы тяжести, ${{\rho }_{{\text{g}}}}$ и $\rho $ – плотности твердых частиц и воды, σ – пористость песчаного грунта, $\beta $ – локальный уклон дна, h – глубина, ось OX направлена к берегу (рис. 1).

Величина ${{q}^{0}}$ рассчитывается по известной формуле [9], основанной на энергетической концепции транспорта наносов:

где ${{f}_{w}}$ – коэффициент донного трения, $\rho $ – плотность воды, ${{\varepsilon }_{{\text{b}}}}$ и ${{\varepsilon }_{{\text{s}}}}$ – коэффициенты эффективности транспорта влекомых и взвешенных наносов (0.1 и 0.02), ${{\alpha }_{{\text{g}}}}$ – угол естественного откоса (около 30° для песка), ${{w}_{g}}$ – скорость осаждения твердых частиц в воде, $u$ – скорость течения вблизи дна, горизонтальная черта означает осреднение по времени. Коэффициент ${{f}_{w}}$ определяется по формулам [2, 23]: где ${{a}_{m}}$ – амплитуда колебаний частиц воды вдоль дна, ${{r}_{b}}$ – параметр донной шероховатости, ${{\theta }_{{2.5}}}$ – параметр Шилдса для условной шероховатости дна 2.5${{d}_{g}}$ (${{d}_{g}}$ – средний размер твердых частиц), ${{\eta }_{r}}$ и ${{\lambda }_{r}}$ – высота и длина донных рифелей (оцениваются по зависимостям [23]). Наносы перемещаются при ${{\theta }_{{2.5}}} > 0.05$.

Предполагаем, что величина $u$ включает вклады волновой орбитальной скорости ${{u}_{w}}$, переносной скорости $\bar {u}$, обусловленной противотечением, а также длинноволновой (инфрагравитационной) составляющей ${{u}_{L}}$, связанной с групповой структурой нерегулярных ветровых волн:

Волновую орбитальную скорость представляем суммой двух гармоник с амплитудами ${{u}_{m}}$ и ${{u}_{{m2}}}$ и сдвигом по фазе ${\Phi }$: После определения моментов скорости $\overline {u{{{\left| u \right|}}^{2}}} $ и $\overline {u{{{\left| u \right|}}^{3}}} $, а также некоторых аппроксимаций и упрощений формулу (2) можно записать в виде где ${{D}_{f}}$ – скорость диссипации энергии донным трением (амплитуда скорости ${{u}_{m}}$ рассчитывается по линейной теории), $~\Theta $ – угол между направлением волн и нормалью к берегу, а величины ${{A}_{u}}$, $U$ и ${{G}_{L}}$ представляют вклады асимметрии скоростей, противотечения и длинноволновых колебаний соответственно: где ${{u}_{{mL}}}$ – амплитуда длинноволновой составляющей скорости течения, ${{C}_{L}}$ – фактор корреляции между короткими (ветровыми) и инфрагравитационными волнами [25], ${{K}_{L}}$ – калибровочный коэффициент.

Вклад асимметрии волн. Асимметрия волновых скоростей является следствием двух типов асимметрии волнового профиля – относительно горизонтальной и вертикальной осей координат. Горизонтальная асимметрия (skewness) ${{A}_{x}}$ ассоциируется с узкими крутыми гребнями волн и широкими пологими ложбинами. Признаком вертикальной асимметрии (asymmetry) ${{A}_{z}}$ является пилообразный профиль волны (передний склон круче заднего), обусловленный сдвигом фазы второй гармоники ($\Phi \to - \frac{\pi }{2}$). В упрощенном представлении (7) перенос к берегу при этом должен затухать (${{A}_{u}} \to 0$). Однако в действительности ускорение течения в волнах с крутым фронтом увеличивает касательное напряжение под гребнями волн, что в итоге ведет к усилению транспорта наносов в сторону берега [10, 24]. Следовательно, при параметризации величины ${{A}_{u}}$ необходимо учитывать вклады обоих типов асимметрии:

где ${{K}_{x}}$ и ${{K}_{z}}$ – соответствующие калибровочные коэффициенты. Величины ${{A}_{x}}$ и ${{A}_{z}}$, как следует из результатов [29], могут быть представлены в виде функций числа Урселла, $Ur = \frac{3}{8}\frac{{k{{H}_{s}}}}{{{{{\left( {kh} \right)}}^{3}}}}$, где $k = \frac{{2\pi }}{L}$ – волновое число (L – длина ветровых волн):

Вклад противотечения. Скорость противотечения, компенсирующего стоксов перенос воды к берегу, определяется как [2]

где $E = \frac{1}{8}\rho gH_{{rms}}^{2}$ – энергия волн, ${{E}_{r}} = \frac{1}{2}{{K}_{r}}\rho \frac{{H_{{rms}}^{2}}}{{{{T}_{p}}}}C$ – энергия роллеров [11], ${{Q}_{b}}$ – доля обрушающихся волн, ${{H}_{{rms}}}$ – среднеквадратичная высота волн, ${{T}_{p}}$ – период пика спектра волн, C – скорость распространения волн, ${{K}_{r}}$ – калибровочный коэффициент порядка 1. С учетом определения ${{E}_{r}}$ второй член в правой части (10) можно представить как ${{a}_{r}} = {{K}_{r}}{{Q}_{b}}\frac{{~H_{{rms}}^{2}}}{{h{{T}_{p}}}}$.

Преобразование волновой энергии в турбулентную энергию роллера требует определенного времени. Соответствующий пространственный лаг ${\Delta }$ приводит к смещению пика противотечения в сторону берега [22]. В нашей модели этот лаг симулируется путем использования значений ${{a}_{r}}$, вычисленных не в данной точке профиля x, а в точке $x{\kern 1pt} ' = x - {\Delta }$. В качестве масштаба ${\Delta }$ принимается локальная глубина, т.е. ${\Delta } = {{K}_{{\Delta }}}h$, где ${{K}_{{\Delta }}}$ – калибровочный коэффициент.

Вклад длинноволновой составляющей. Инфрагравитационные волны, представленные величиной ${{G}_{L}}$ в формулах (6) и (7), трактуются как колебания среднего уровня, связанные с группами коротких (ветровых) волн. В зоне трансформации группам высоких волн соответствуют ложбины инфраграгравитационных колебаний, под которыми течение направлено от берега в море, тогда как в прибойной зоне средний уровень изменяется в фазе с группами высоких волн, и длинноволновая составляющая течения направлена к берегу [20]. Взаимодействие длинных и коротких волн характеризуется фактором корреляции ${{C}_{L}}$, который на основании результатов [25] может быть выражен эмпирической функцией:

где ${{H}_{{rms\infty }}}$ – значение ${{H}_{{rms}}}$ в открытом море. В зоне трансформации волн ${{H}_{{rms}}} \approx {{H}_{{rms\infty }}}$ и ${{C}_{L}} < 0$. Однако в зоне существенной диссипации энергии, где $H_{{rms}}^{2} \ll H_{{rms\infty }}^{2}$, имеем ${{C}_{L}} > 0$. Для рэлеевского распределения высот волн ${{H}_{{rms\infty }}} = \sqrt 2 {{H}_{{s\infty }}}$.

Отношение амплитуд скоростей ${{{{u}_{{mL}}}} \mathord{\left/ {\vphantom {{{{u}_{{mL}}}} {{{u}_{m}}}}} \right. \kern-0em} {{{u}_{m}}}}$ в выражении ${{G}_{L}}$ в (7), предположительно, пропорционально отношению соответствующих высот волн ${{{{H}_{{Lrms}}}} \mathord{\left/ {\vphantom {{{{H}_{{Lrms}}}} {{{H}_{{rms}}}}}} \right. \kern-0em} {{{H}_{{rms}}}}}$. При использовании зависимости для ${{H}_{{Lrms}}}$ [21] приходим к выражению

Необходимые для расчетов параметры волн ${{H}_{{rms}}}$, ${{Q}_{b}}$ и $\Theta $ определяются с помощью модели автора, основанной на уравнениях баланса энергии и рефракции волн [2, 5, 7], скорость распространения волн C рассчитывается по линейной теории.

ТРАНСПОРТ НАНОСОВ В ЗОНЕ ЗАПЛЕСКА

Здесь используется тот же подход, что и в модели CROSS-P [5, 7]. Предполагается, что максимум расхода наносов ${{\hat {q}}_{R}}$ в потоке заплеска достигается на береговой линии, $x = {{x}_{c}}$ (рис. 1),

где ${{K}_{R}}$ = 0.005 – масштабный коэффициент, ${{u}_{R}}$ – амплитуда скорости течения заплеска, ${{{\beta }}_{{eq}}}$ – равновесный уклон пляжа, $\bar {\beta } = {{\left( {{{h}_{s}} + R} \right)} \mathord{\left/ {\vphantom {{\left( {{{h}_{s}} + R} \right)} {\left( {{{x}_{R}} - {{x}_{s}}} \right)}}} \right. \kern-0em} {\left( {{{x}_{R}} - {{x}_{s}}} \right)}}$ – фактический средний уклон (рис. 1). Высота заплеска R и уклон равновесия ${{\beta }_{{eq}}}$ вычисляются по формулам где ${{\bar {H}}_{\infty }}$, ${{L}_{\infty }}$ и ${{\Theta }_{\infty }}$ – средняя высота, длина и угол подхода волн на глубокой воде, ${{S}_{D}}$ – параметр Дина. С приближением к границам зоны заплеска расход ${{q}_{R}}$ затухает [5, 7], а в нижней части зоны расходы ${{q}_{R}}$ и $q$ суммируются (рис. 1).

ДЕФОРМАЦИИ ПРОФИЛЯ ДНА

Изменения глубин на профиле определяются из закона сохранения массы,

где t – время, а величина ${{q}_{x}}$ принимает значения $q$, ${{q}_{R}}$ или $q + {{q}_{R}}$ в зависимости от положения данной точки (рис. 1). Уравнение (15) интегрируется с помощью численной схемы Лакса–Вендроффа [19] с шагом по времени порядка нескольких периодов волн. Шаг по пространству в зависимости от длины и уклона профиля составляет 10^–1–10⁰ м. Если в ходе расчетов локальный уклон дна достигает предельного значения ${\text{tg}}{{\alpha }_{{\text{g}}}}$, то включается алгоритм имитации обвала [2, 5, 17]. При расчетах принимаются во внимание изменения среднего уровня моря, включая штормовой нагон и приливные колебания.

ВЕРИФИКАЦИЯ МОДЕЛИ

Для тестирования модели вначале использовались данные трех экспериментов в волновом канале, приведенные в работе [13]. Опыты имели цель проследить изменения морфологии песчаного берегового профиля при последовательных воздействиях сравнительно высоких и низких волн, имитирующих режимы размыва при максимуме шторма и аккумуляции при его затухании. Песок в опытах имел средний размер ${{d}_{g}}$ = 0.25 мм (${{w}_{g}}$ = 0.034 м/с), уклон исходного профиля составлял ${{\beta }_{0}}$ = 0.067. Параметры волн в фазы размыва (E) и аккумуляции (A) для каждого теста приведены в табл. 1. Здесь ${{t}_{w}}$ – продолжительность волнения, а ${{S}_{D}}$ – параметр Дина, определенный в (14). Как известно, значения ${{S}_{D}}$ > 2 определяют режим размыва, а ${{S}_{D}}$ < 2 – аккумуляции [16]. При подсчете ${{S}_{D}}$ использовалось соотношение ${{H}_{{s\infty }}} = 1.6{{\bar {H}}_{\infty }}$, вытекающее из рэлеевского распределения высот волн.

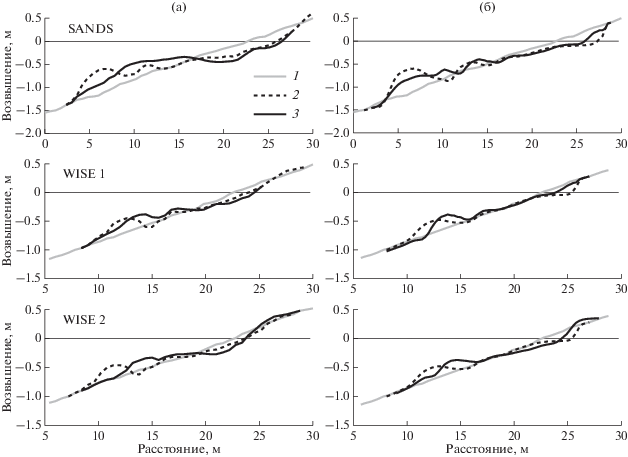
На рис. 2 показано сравнение результатов наблюдений (а) и расчетов (б) для соответствующих тестов. Как видно, по окончании фазы размыва во всех случаях формируется подводный вал, который затем в фазе аккумуляции перемещается к берегу. Отмечаются заметные расхождения результатов в прибрежной части профилей, особенно в опыте SANDS. Однако в тестах WISE 1 и WISE 2 наблюдаемые и расчетные тенденции поведения валов вполне аналогичны друг другу.

Дальнейшая проверка модели проводилась на базе опубликованных данных натурных наблюдений береговых профилей с подводными валами до и после прохождения штормового цикла. В табл. 2 отражены район и период наблюдений, средний размер песка на дне ${{d}_{g}}$, параметры волн и характерная высота штормового нагона ${\eta }$. Символом “T” отмечены условия воздействия прилива, амплитуда и период которого при расчетах аппроксимировались величинами 0.5 м и 12 ч соответственно.

Под величиной ${{H}_{s}}$ в табл. 2 подразумевается так называемая “эффективная” высота волн, учитывающая относительную продолжительность фазы затухания шторма [6]. Период волн ${{T}_{p}}$ и параметр Дина ${{S}_{D}}$ также представляют усредненные показатели шторма. В последней колонке таблицы указан средний уклон дна ${{\beta }_{0}}$ (отношение максимальной глубины профиля к расстоянию до уреза). Очевидно, в натурных условиях уклон профиля значительно меньше, а параметр Дина заметно больше величин, типичных для лабораторных экспериментов.

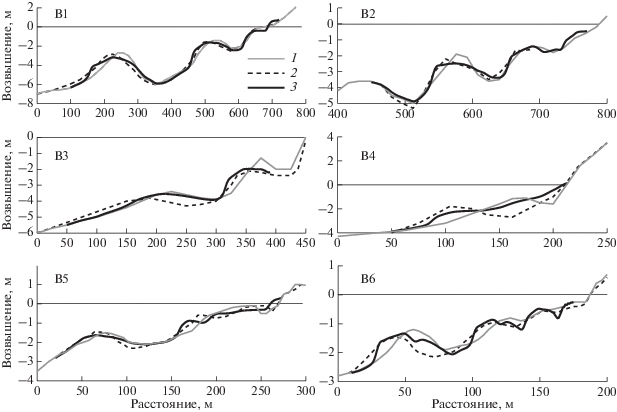
На рис. 3 наблюдавшиеся и расчетные изменения морфологии профилей сравниваются друг с другом. Как видно, воздействие шторма приводит к смещению подводных валов в сторону моря, что достаточно ясно демонстрирует и моделирование. В ряде случаев отмечаются значительные отклонения, но в целом результаты расчетов и наблюдений согласуются друг с другом.

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

В результате тестирования модели были оценены оптимальные значения ее калибровочных коэффициентов. Выяснилось, что значения ${{K}_{r}}$ и ${{K}_{L}}$, масштабирующие вклад роллеров и длинноволновой составляющей в транспорт наносов, могут быть приняты постоянными в исследованном диапазоне условий: ${{K}_{r}}$ = 1, ${{K}_{L}}$ = 0.5.

Остальные коэффициенты демонстрируют изменчивость при смене условий прибрежной среды. Так, ${{K}_{x}}$ и ${{K}_{z}}$, характеризующие вклады двух типов асимметрии волн, обнаруживают тенденцию к росту при уменьшении параметра Дина:

Это можно интерпретировать как возрастание роли асимметрии волн при транспортировке относительно более крупных наносов, что вполне отвечает общепринятой точке зрения.

Что касается коэффициента ${{K}_{{\Delta }}}$, определяющего лаг между началом обрушения волн и максимумом диссипации энергии, то для пологих природных берегов его значения заметно выше (более 10), чем для крутого профиля в волновом лотке (4.5). Различия, вероятно, связаны с тем, что изменения волнового поля в первом случае происходят медленнее, чем во втором. Исходя из имеющихся ограниченных данных, изменения ${{K}_{{\Delta }}}$ можно аппроксимировать как функцию среднего уклона профиля ${{\beta }_{0}}$:

Рисунок 4 дает представление о расчетных распределениях вкладов различных механизмов транспорта наносов при разных типах волновых воздействий в ходе эксперимента WISE 2. Главным фактором переноса к берегу во всех случаях оказывается асимметрия волн, причем доминирует вклад вертикальной асимметрии, что хорошо коррелирует с выводами исследования [10]. Хотя вынос от берега обусловливается, главным образом, противотечением, важную роль в этом процессе играют и длинноволновые колебания, особенно в режиме аккумуляции.

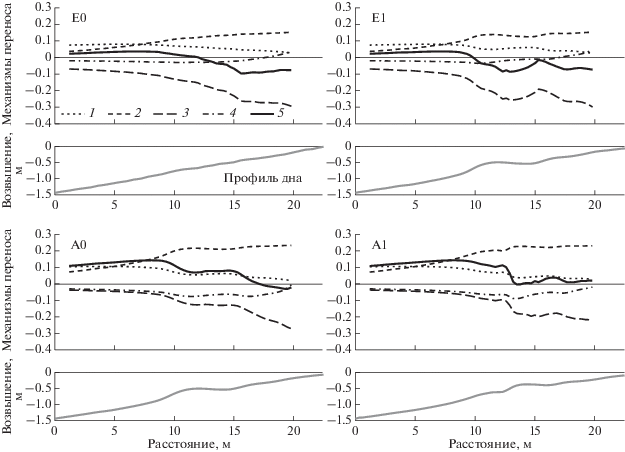
Результирующий транспорт в фазе размыва характеризуется конвергенцией встречных потоков. Максимум обратного потока приурочен к ложбине, точнее, к переднему склону формирующегося вала, что обусловливается лагом между обрушением волн и пиком противотечения. В режиме аккумуляции перемещение вала определяется доминирующим переносом в сторону берега и его резким уменьшением над гребнем вала.

В прибойной зоне результирующий поток испытывает осцилляции, которые конвертируются во вторичные волнообразные образования на профиле дна.

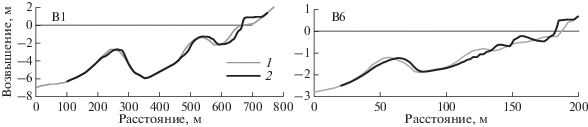
Модельные расчеты удовлетворительно воспроизводят перемещение подводного вала к берегу, зафиксированное в тестах WISE 1 и WISE 2 в условиях относительно слабого волнения (рис. 2). Для сравнения было проведено моделирование воздействия умеренной и слабой зыби на природные профили B1 и B6 (рис. 3). Полученные изменения морфологии показаны на рис. 5. Как видно, модель предсказывает тот же тренд – валы смещаются в сторону берега. Валы большего размера движутся медленнее, так как для этого требуется перемещение большего объема материала. Одновременно происходит нарастание пляжа.

ЗАКЛЮЧЕНИЕ

В представленной модели CROSS-PB принимаются во внимание вклады основных механизмов транспорта наносов, включая два вида асимметрии волн, противотечение и длинноволновые колебания (связанные с группами волн), что дает возможность более или менее реалистично описать морфодинамику берегового профиля в масштабе шторма, в том числе для берегов с системами подводных валов. Достоинства прежней версии CROSS-P при этом также сохраняются [18].

Сравнение расчетов с данными лабораторных экспериментов и натурных наблюдений показывает, что модель верно предсказывает тип формируемого берегового профиля, а также главные тренды поведения подводных валов при различных видах волновых воздействий. В частности, воспроизводятся перемещение валов в сторону моря во время шторма и движение их к берегу в периоды относительно слабого волнения. Первый процесс контролируется балансом транспортирующих механизмов, при котором максимум потока от берега приходится на передний склон вала. Второй процесс определяется доминирующим потоком наносов к берегу и резким его ослаблением над вершиной вала.

Модель включает пять калибровочных коэффициентов, два из которых, по результатам тестирования, сохраняют постоянство (${{K}_{r}}$ = 1, ${{K}_{L}}$ = 0.5), а остальные меняются вместе с внешними условиями. Так, величины ${{K}_{x}}$ и ${{K}_{z}}$, регулирующие вклады горизонтальной и вертикальной асимметрии скорости обнаруживают обратную зависимость от параметра Дина. Иначе говоря, роль асимметрии волн в перемещении относительно более крупных наносов возрастает. Вклад вертикальной асимметрии в перенос к берегу оказывается доминирующим, что согласуется с недавними исследованиями [10]. Коэффициент ${{K}_{{\Delta }}}$, определяющий лаг между началом обрушения волн и максимумом диссипации энергии, для пологих природных берегов оказывается выше, чем для крутых профилей в волновом лотке, что объясняется различием темпов трансформации волн при малых и больших уклонах дна.

В настоящее время сравнение результатов наблюдений и моделирования может быть проведено в основном на качественном уровне, так как имеющихся данных пока недостаточно для получения представительных статистических оценок в отношении изменчивости калибровочных коэффициентов и точности модельных расчетов. В дальнейшем предполагается уточнить параметры модели на основе дополнительных материалов наблюдений.

Источники финансирования. Работа выполнена в рамках государственного задания (тема № 0149-2019-0005) при частичной поддержке РФФИ (гранты № 18-55-34002 Куба_т и № 18-05-00741).