1. На главную
  2. Электронные версии
  3. Океанология
  4. T. 61, № 5, 2021

Океанология, 2021, T. 61, № 5, стр. 702-715

Усвоение данных альтиметрии в модели динамики вод в Южной Атлантике

И. Д. Дейнего 1, И. Ансорг 2, К. П. Беляев 1, 3, *

1 Институт океанологии им. П.П. Ширшова РАН (ИО РАН)
Москва, Россия

2 Университет Кейптауна, Факультет Океанографии
Кейптаун, ЮАР

3 Вычислительный Центр РАН им. А.А. Дородницына, ФИЦ ИУ РАН
Москва, Россия

* E-mail: kosbel55@gmail.com

Поступила в редакцию 19.05.2020
После доработки 11.09.2020
Принята к публикации 08.04.2021

Полный текст (PDF)

Аннотация

В работе усваиваются данные спутниковых наблюдений за уровнем океана из архива AVISO (Arc-hiving Validating and Interpolating Satellite Observations) в модель циркуляции океана INMOM (Institute of Numerical Mathematics Ocean Model). При усвоении используется оригинальный гибридный метод, обобщающий известный алгоритм Калмана, названный авторами обобщенным фильтром Калмана (Generalized Kalman filter, GKF). Строятся и анализируются различные поля модельных характеристик в районе Южной Атлантики, в частности, поля уровня, температуры поверхности океана (ТПО) и значений скорости течения на поверхности, и изучается их пространственно-временная изменчивость до и после ассимиляции данных наблюдений. Показано, что при усвоении данных увеличение уровня составляет примерно 0.05 м на 55° ю.ш., изменения в скоростях поверхностных течений достигают 30%, а в поле ТПО – 3°С. При этом поля уровня и ТПО до усвоения и после качественно похожи, а течения сонаправлены. Сопоставления с другими моделями подтверждают адекватность воспроизведения полей океана с помощью метода усвоения данных наблюдений.

Ключевые слова: численная модель, динамико-стохастическая и гибридная ассимиляция данных наблюдений, обобщенный фильтр Калмана, Южная Атлантика

1. ВВЕДЕНИЕ

Одним из наиболее актуальных направлений в современной океанологии и метеорологии является разработка и практическое применение методов усвоения (ассимиляции) данных наблюдений (АДН). Идея разработки и применения этих методов состоит в том, чтобы наиболее оптимальным способом совместить два подхода к описанию физической и/или технической системы, а именно ее математическое моделирование и непосредственное наблюдение за объектами или системами, их мониторинг. В последние годы методы АДН широко применяются в науках о Земле, обеспечивая взаимосвязь между двумя этими основными подходами с целью наилучшего анализа всей системы. Наибольшие приложения эти методы получили в метеорологии и океанографии, где наблюдения усваиваются в численные модели с целью получения новых граничных или начальных условий, промежуточной коррекции модельных результатов для дальнейшего моделирования и прогноза [8, 16, 20].

При усвоении данных решаются три задачи: инициализации, то есть нахождения оптимального начального и/или граничного условия, с использованием которого при повторном расчете модельная траектория будет проходить мимо заданного множества наблюдений на наиболее близком в смысле заданной метрики расстоянии; коррекции, когда построенное модельное решение изменяется так, чтобы наилучшим образом (в заданном смысле) соответствовать наблюдениям; настройки параметров модели, когда внутренние параметры модели, например, коэффициенты трения, подбираются таким образом, чтобы построенное новое решение наилучшим образом (опять же в заданном смысле) соответствовало наблюдениям. Как правило, в задачах инициализации используют так называемый вариационный метод, решающий обратную задачу нахождения начального условия. Оригинально это направление разрабатывалось Г.И. Марчуком и его школой [24, 1]. Современная версия этой схемы имеет название 4D-Var, активно разрабатывается и используется на практике [1, 23]. Задачи коррекции состоят в изменении (коррекции) модельного решения без нахождения начального и граничного условий, а только в текущий момент времени. Для решения этой задачи в основном используются вероятностно-статистические методы, представляя искомое решение как сумму неизвестного поля плюс случайный шум с заданными вероятностными характеристиками и решая задачу наилучшего оценивания (фильтрации). Оригинально это направление начало развиваться в метеорологии с работ Л.С. Гандина [4] и Р. Калмана [18]. Современная версия этого метода называется Ансамблевым Фильтром Калмана (EnKF) [15] и используется при решении задач оперативной океанографии, 4D-прогноза состояния океана в районах, представляющих особый интерес с точки зрения добычи и транспортировки полезных ископаемых, прежде всего углеводородов, а также в зонах экологического мониторинга, рыбного промысла, защитных сооружений и пр. На развитие и применение таких методов АДН направлены, в частности, проекты REMO (Бразилия [30, 31]), BlueLink (Австралия [29]), TOPAZ (Норвегия [28]) и ряд других. В России также активно разрабатывают и используют данный подход, например, для анализа динамики Черного моря [7]. Кроме этих основных подходов АДН есть также и ряд гибридных методов, сочетающих оба вышеприведенных подхода. К этим методам можно, например, отнести авторскую схему АДН [3], в которой минимизируется функционал, построенный по динамико-стохастической схеме. Задачи настройки параметров модели в океанологии и физике атмосферы практически не используются в связи с особой сложностью соответствующих численных моделей. В других областях техники примеры таких задач приведены в [12].

При применении динамико-стохастического метода АДН и большинства гибридных методов никак или почти никак не исследуется вопрос, за счет чего происходит передача информации от наблюдений к самой модели и как именно знание характеристик в одних точках меняет значение поля в других. На картах полей исследуемых модельных характеристик не показываются области, где данные наблюдений наиболее сильно влияют количественно на расчетные характеристики и как именно это происходит. Другими словами, количественно и физически не исследуются взаимосвязи между различными точками пространства-времени, которые задаются уравнениями модели и соответствующими передаточными функциями, а также между различными модельными характеристиками. В динамико-стохастическом подходе и в ряде гибридных методов эти взаимосвязи количественно выражаются через ковариационные функции или взаимно-ковариационные функции, построение которых представляет собой непростую задачу. Важно уметь не только строить такие функции и изучать их пространственно-временные свойства, но и научиться их визуализировать, разбивать на отдельные составляющие, оптимально решать линейные уравнения большого порядка, где в качестве известных матриц при неизвестных переменных будут именно ковариационные функции (матрицы).

В динамико-стохастических и гибридных схемах обычно такие матрицы строятся методом Монте-Карло, так как аналитическое построение этих функций практически невозможно даже для самых простых моделей. Поэтому производится модельный расчет с разных начальных условий (построение ансамбля модельных расчетов) и затем, имея выборку в каждой точке сетки, проводится статистическая оценка ковариационных матриц. Этот прием был предложен в [15]. Далее, исходя из построенных таким способом ковариационных матриц, строятся весовые функции, известные в литературе как весовые функции Калмана (Kalman gain), и уже по ним строится оптимальное усвоение. Такая техника хорошо работает и успешно применяется в разных практических задачах. Однако остается ряд как теоретических, так и практических вопросов. При усвоении данных происходит разрыв траекторий всех модельных переменных в момент усвоения, и в результате вся динамическая система испытывает “шок”, то есть мгновенный скачок значений переменных в фазовом пространстве модели. Если скачок достаточно большой и/или такое усвоение происходит часто, то в результате в процессе расчетов может возникнуть неустойчивость, возникнут нефизичные значения модельных переменных. Это, например, показано в работе [14]. Там же предложен метод “сглаживания”, который подавляет (демпфирует) принимаемые нереальные значения. Однако хотелось бы предложить и использовать такой метод АДН, в котором с самого начала траектории процесса были бы теоретически непрерывными даже в моменты усвоения.

В применяемом в настоящей статье методе АДН, названном авторами обобщенным фильтром Калмана (Generalized Kalman filter, GKF), показано, что это свойство справедливо. Метод введен и математически обоснован в [13], а в [2] показано, что этот метод имеет существенные преимущества перед стандартной схемой EnKF. Кроме того, построенная по методу GKF весовая матрица обладает свойством факторизации, то есть состоит из произведения двух матриц, одна из которых строится только в области модельного расчета, а другая – только в наблюдаемой области. Это позволяет судить о том, насколько та или иная наблюдаемая область влияет на изменчивость модели и как количественно расположение и значения наблюдаемых величин корректируют модельные расчеты. Такой подход обобщает известный в климатологии, океанологии и физике атмосферы метод Карунена-Лоэва (Karhunen-Loeve). Как самому методу, так и его применению в геофизике посвящена обширная литература (например, [5, 11]). Тем не менее, при ассимиляции данных этим методом почти не пользуются, хотя он позволяет понять, какие именно пространственно-временные взаимосвязи модельных и наблюдаемых характеристик используются при усвоении, а также чем модельные пространственно-временные взаимосвязи отличаются от наблюдаемых. Кроме того, использование этого метода может упростить чисто технически реализацию расчетов по динамико-стохастическому методу, так как этот метод позволяет редуцировать размер ковариационной матрицы. Это показано в [6].

Данная работа продолжает исследование, начатое в [6], для района Южной Атлантики. Причины выбора этого района для исследования следующие: важность изучения этого района для исследования климата и общей циркуляции океана и при этом его относительная слабая изученность. Кроме того, в рамках сотрудничества со странами БРИКС изучение этого региона весьма важно и для нас, и для сотрудничества с Бразилией и ЮАР. И, наконец, разработка и применение новых методов более интересны и полезны там, где мало данных и где их отсутствие или недостаток можно компенсировать разработкой более продвинутых и сложных методов исследования.

Термодинамика и структура течений в этом регионе изучалась разными авторами, в том числе и российскими, результаты опубликованы в ряде статей и монографий [17, 9, 10, 25, 19]. Тем не менее, моделирование динамики с усвоением данных наблюдений в этом районе проводилось недостаточно подробно в связи с отсутствием или недостоверностью реальных измерений, конкретных результатов мало.

Цели настоящей работы: (а) провести расчет термодинамических переменных в Южной Атлантике по модели INMOM с усвоением данных наблюдений за уровнем океана AVISO и таким образом скорректировать модельные расчеты данными наблюдений; (б) проанализировать полученные результаты и сравнить их с наблюдаемыми полями, а также с результатами моделирования по другим моделям, при этом анализе и сравнении использовать как непосредственно усваиваемые величины (уровень океана), так и те величины, которые наблюдаются, но не усваиваются (температура поверхности океана, ТПО) и не наблюдаются и не усваиваются (скорости течений). Детальный анализ самой схемы усвоения, в частности, пространственно-временная изменчивость ковариационной матрицы ошибки, на основе которой строится весовая матрица, представляет собой сложную задачу, и ее исследование выходит за рамки данной статьи. Этому будет посвящена отдельная работа.

2. ЧИСЛЕННАЯ МОДЕЛЬ, ДАННЫЕ НАБЛЮДЕНИЙ И МЕТОД УСВОЕНИЯ

2.1. Численная модель

Для расчетов циркуляции в южной части Атлантического океана была использована новая версия российской модели циркуляции океанов и морей INMOM, подробно описанная в работе [25]. Основные уравнения модели, использующие так называемую сигма-систему координат, сформулированы в концепции полной нелинейной свободной поверхности океана с учутом изменения объема акватории через кинематическое граничное условие на поверхности. Для операторов переноса используется явная схема по времени с пересчетом. Операторы горизонтальной диссипации рассчитываются по явной схеме Эйлера, а вертикальной – по неявной схеме Эйлера. Расчет внешнего воздействия на поверхности океана с предписанными характеристиками атмосферы производится по методике NCAR, предлагаемой для использования с данными CORE (Coordinated Ocean-ice Reference Experiments) [22], в которой для расчета коэффициентов турбулентных потоков применяется построение функций устойчивости по теории Монина–Обухова.

Для устранения сгущения линий сетки в районе Северного географического полюса для области совместной циркуляции Атлантики и Северного Ледовитого океана используется сферическая система координат с повернутой осью. Эйлеровы углы поворота – 45°, 93°, 0°. При такой конфигурации области модельный “экватор” проходит вдоль Атлантического и Северного Ледовитого океанов, что обеспечивает квазиравномерное разрешение в исследуемой акватории. Горизонтальное разрешение составляет 0.25°, в среднем 19 км, вертикальное разрешение задается 40 сигма-уровнями, неравномерно распределенными по глубине по аналитической формуле со сгущением возле поверхности.

Маска расчетной области была подготовлена с использованием океанографической базы данных полигонов береговых линий (как в Generic Mapping Tools). Топография дна строилась на основе глобального массива ETOPO5 с разрешением 5′ путем интерполяции на модельную область, фильтрации и ограничения глубины минимальным значением 10 м для корректной постановки задачи в сигма-системе координат. Исходными данными по температуре и солености являются данные объективного анализа EN4.2.1 с поправками В.В. Гурецкого [17]. В качестве начального состояния для расчета использовались данные за январь 1948 г. Данные интерполировались на модельную область по горизонтали, затем переводились на сигма-уровни. Для расчета граничных условий на поверхности океана использовались специально созданные для автономных расчетов моделей океана данные атмосферных характеристик CORE за период с 1948 по 2009 г. Расчетный шаг по времени составлял 1/2 ч.

Эксперимент проводился по следующему сценарию. Сначала был проведен адаптационный расчет на год, в котором в качестве начальных условий задавались исходные температура и соленость из данных EN4.2.1, состояние покоя и отсутствие льда. В результате этого расчета появилась циркуляция и образовался лед. Затем был запущен сквозной расчет с января 1948 г., в качестве начальных условий в котором использовались исходные температура и соленость из данных EN4.2.1 и результаты годового адаптационного расчета для остальных прогностических величин: скорости, уровня, характеристик льда. Более подробно с аналогичным запуском данной модели можно ознакомиться в работе [26].

2.2. Данные наблюдений

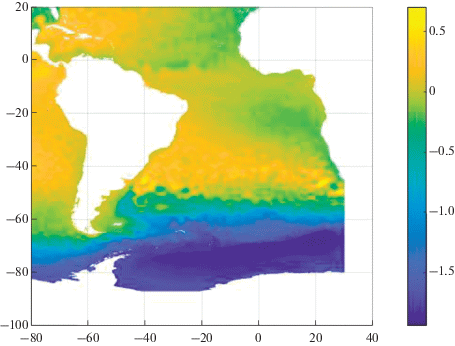
В качестве наблюдаемых данных использовались данные уровня океана из архива AVISO (www.aviso.altimetry.fr). Наблюдаемые ежесуточные значения уровня интерполировались в сетку модели. Соответствующее среднемесячное поле наблюдаемого уровня на климатический январь для расчетной области приведено на рис. 1. Это поле также будет использовано в дальнейшем для сравнения с модельными полями уровня до и после усвоения данных.

Рис. 1.

Наблюдаемый уровень поверхности океана (м) по данным Aviso Altimetry. Январь.

2.3. Метод усвоения

В этом разделе кратко описывается метод усвоения, используемый в данной работе. Полное его описание содержится в работах [2, 13]. Предполагается, что численная модель, в нашем случае модель INMOM, задается системой уравнений

(1)
$\frac{{\partial X}}{{\partial t}} = {{\Lambda }}\left( {X,{\text{\;}}t} \right)$
с начальным условием: $X\left( 0 \right) = {{X}_{0}}$.

Согласно предыдущим обозначениям [2], здесь и далее X обозначает состояние модели в фазовом пространстве, то есть множество значений модели, t – время. Символ ${{\Lambda }}$ обозначает вектор-функцию на том же фазовом пространстве и на временном интервале [t0, T]. Без потери общности можно считать t0 равным 0. В дискретной реализации модельный вектор состояний имеет размерность r, где r есть число точек сетки, умноженное на число независимых переменных модели. В данном эксперименте область исследования включала 106 016 расчетных точек и 5 независимых переменных модели (уровень, температуру, соленость и две компоненты скорости в каждой расчетной точке). То есть фазовое пространство модели будет подмножеством пространства Rr. Временной интервал [0, T] разбивается точками $0 = {{t}_{0}} < {{t}_{1}} < ... < {{t}_{N}} = T,$ в которых производится коррекция модельных расчетов, то есть АДН. Без ограничения общности все интервалы ${{\Delta }}~t = {{t}_{{n + 1}}} - {{t}_{n}}$ можно считать эквидистантными. На каждом из таких интервалов АДН происходит по формуле

(2)
${{X}_{{a,n + 1}}} = {{X}_{{b,n + 1}}} + {{K}_{{n + 1}}}\left( {{{Y}_{{n + 1}}} - H{{X}_{{b,n + 1}}}} \right).$

В формуле (2) обозначено: ${{X}_{{a,n}}},~{{X}_{{b,n}}},~\left( {n = 0,{\text{\;}}1,...,N} \right)$ – состояние модели после и до коррекции (the analysis and background), Yn – вектор наблюдений размерности m, где m – число наблюдений, умноженное на число независимо наблюдаемых величин. Например, если наблюдаются s независимых значений температуры и солености, то m = 2s. В нашем случае наблюдается только уровень, поэтому размерность m равна числу точек наблюдений на шаге n. Предполагается, что ${{X}_{{a,0}}} = {{X}_{{b,0}}} = {{X}_{0}}$ – известная величина (начальное значение). Далее, K – это так называемая весовая матрица (gain matrix) размерности r × m, а H – проекционная матрица размерности m × r. Требуется определить матрицу ${{K}_{{n + 1}}}$ на каждом шаге по времени. С учетом уравнения (1) можно увидеть, что

(3)
$\begin{gathered} {{X}_{{a,n + 1}}} = {{X}_{{a,n}}} + \Lambda ({{X}_{{a,n}}})\Delta t + \\ + \,\,{{K}_{{n + 1}}}({{Y}_{{n + 1}}} - H{{X}_{{a,n}}} - H\Lambda ({{X}_{{a,n}}})\Delta t), \\ \end{gathered} $
так как ${{X}_{{b,n + 1}}} = {{X}_{{a,n}}} + {{\Lambda }_{{n + 1}}}\Delta t$. Для краткости будем обозначать ${{\Lambda }_{{n + 1}}} = \Lambda ({{X}_{{a,n}}})$, нижние индексы “a”, “b” будем опускать, если это не вызовет недоразумений.

Уравнение (3) можно переписать в виде

(4)
$\begin{gathered} {{X}_{{n + 1}}} - {{X}_{n}} = \left( {I - {{K}_{{n + 1}}}H} \right){{\Lambda }_{{n + 1}}}\Delta t + \\ + \,\,{{K}_{{n + 1}}}({{Y}_{{n + 1}}} - H{{X}_{n}}), \\ \end{gathered} $
где I – единичная r × r матрица. Если предполагать, что наблюдения Yn – случайные величины, то процесс (2) можно рассматривать как случайный, и в [13] показано, что при общих и физически выполнимых условиях такой процесс может быть аппроксимирован как решение стохастического дифференциального уравнения
(5)
$d{{X}_{{n + 1}}} = {{C}_{{n + 1}}}dt + {{D}_{{n + 1}}}dW,$
где r – мерный вектор Сn+1 = (I – Kn + 1H)${{\Lambda }_{{n + 1}}}$, а Dn+1 – симметричная, положительно определенная матрица размера r × r, такая, что $D_{{n + 1}}^{2} = {{K}_{{n + 1}}}{{Q}_{{n + 1}}}K_{{n + 1}}^{T}$. Ковариационная матрица:
(6)
${{Q}_{{n + 1}}} = E({{Y}_{{n + 1}}} - H{{X}_{n}}){{({{Y}_{{n + 1}}} - H{{X}_{n}})}^{T}},$
где символом E обозначается математическое ожидание (осреднение) матрицы по ансамблю, а индекс “Т” наверху обозначает транспонирование вектора и/или матрицы. Обозначение dW – это принятое обозначение “белого шума” Гаусса, то есть случайного процесса, такого, что EdW = 0, E(dW)(dW)T = I.

Нахождение оптимального значения весовой матрицы представляет собой вариационную задачу нахождения минимума заданного функционала, а именно функционала действия, который для данной системы записывается в виде:

(7)
$L = \left| {\left| {(I - KH)\Lambda } \right|} \right| + \left| {\left| {KQ{{K}^{T}}} \right|} \right|,$
где ||·|| обозначает норму вектора или матрицы в Rr, а индексы в (7) опускаются. Ищется такое значение K, чтобы δL = 0 (принцип минимума действия, обращение в ноль вариации функционала). Это условие выполняется, если:
(8)
${{K}_{{n + 1}}} = {{(\sigma _{{n + 1}}^{2})}^{{ - 1}}}\left( {{{{{\Lambda }}}_{{n + 1}}} - {{C}_{{n + 1}}}} \right){{(H{{{{\Lambda }}}_{{n + 1}}})}^{T}}Q_{{n + 1}}^{{ - 1}},$
где

(9)
$\sigma _{{n + 1}}^{2} = {{(H{{{{\Lambda }}}_{{n + 1}}})}^{T}}Q_{{n + 1}}^{{ - 1}}\left( {H{{{{\Lambda }}}_{{n + 1}}}} \right).$

Сделаем анализ полученных формул (8) и (9). Во-первых, заметим, что величина $\sigma _{{n + 1}}^{2}$ представляет собой безразмерное число, то есть просто нормировочный множитель, определяемый однозначно при задании модели и параметров усвоения – тренда и ковариационной матрицы. Во-вторых, если Сn + 1 = 0, то формула (8) с точностью до множителя $\sigma _{{n + 1}}^{2}$ совпадает с известным выражением весовой матрицы Калмана в методе EnKF [15], где вместо среднего по ансамблю стоит анализ на предыдущий момент времени, ${{X}_{n}}$. Наконец, заметим, что матрица ${{K}_{{n + 1}}}$ обращается в ноль, если ${{{{\Lambda }}}_{{n + 1}}} = {{C}_{{n + 1}}}$, то есть если модельная тенденция совпадает с тенденцией системы при усвоении. Из выражения (6) видно, что физический смысл вектора ${{C}_{{n + 1}}}$ – это средняя тенденция всей системы, зависящяя как от модели, так и от данных наблюдений. Естественно ее выбрать таким образом, чтобы она совпадала со средней тенденцией наблюдаемых данных на том множестве, где есть наблюдения, и экстраполировалась на оставшуюся часть фазового пространства модели, то есть ${{C}_{{n + 1}}} = \frac{{E({{{\hat {Y}}}_{{n + 1}}} - {{{\hat {Y}}}_{n}})}}{{\Delta t}}$, где ${{\hat {Y}}_{n}}$ – случайный вектор, совпадающий с вектором ${{Y}_{n}}$ на фазовом пространстве наблюдений и продолженный на все фазовое пространство модели. Математическое ожидание здесь означает осреднение по ансамблю, описание которого приведено ниже. По принятой в схемах усвоения логике методом Монте-Карло создается ансамбль $\hat {X}_{n}^{i},i = 1,...M$ из М независимых модельных расчетов с различных начальных условий, и тогда

(10)
${{C}_{{n + 1}}} = \frac{{{{M}^{{ - 1}}}\sum\limits_{i = 1}^M {(\hat {X}_{n}^{i} - \hat {X}_{{n - 1}}^{i})} }}{{\Delta t}}.$

Можно отметить, что даже если модель имеет смещение (систематическую ошибку) относительно наблюдений, для определения вектора ${{C}_{{n + 1}}}$ это неважно, так как в формуле (10) стоит разность, а не сама величина среднего, то есть эта ошибка исчезает.

Соответственно, если анализ ${{X}_{n}}$ уже построен, то:

(11)
${{Q}_{{n + 1}}} = {{M}^{{ - 1}}}\mathop \sum \limits_{j = 1}^M (H\hat {X}_{{n + 1}}^{j} - H{{X}_{n}}){{(H\hat {X}_{{n + 1}}^{j} - H{{X}_{n}})}^{T}}.$

В литературе построение весовой матрицы K и представляет собой основную задачу АДН по динамико-стохастической схеме. Очень мало работ, в которых исследуются свойства этих матриц, а также делаются какие-либо сравнения модельных матриц с построенными по наблюдениям. Кроме вышеупомянутой работы [6], упомянем еще работы [2, 21], где исследуются числовые характеристики матрицы К для стандартной схемы Калмана (EnKF). Между тем, как видно из формул (8) и (9), структура матрицы $(\Lambda - C){{(H\Lambda )}^{T}}$ и спектр симметричной матрицы $Q$ будут определять свойства матрицы К, а затем и анализа ${{X}_{n}}$. При последовательном усвоении временные характеристики этих матриц будут давать основной вклад во временную изменчивость скорректированного поля. Более того, физические свойства полученного поля, например характеристики волн или течений, напрямую зависят от того, насколько хорошо эти матрицы учитывают физические взаимосвязи модельных и наблюдаемых параметров.

Из формулы (8) видно, что матрица $(\Lambda - C){{(H\Lambda )}^{T}}$ представляет собой произведение двух матриц размерности r × 1 и 1 × m соответственно. Причем первая матрица определена в точках сетки и представляет собой пространственное расположение разности модельного и наблюдаемого тренда на шаге n, а вторая матрица определена для точек наблюдений и представляет собой пространственное расположение спроектированного в точки наблюдений модельного тренда на шаге n. Поэтому их произведение дает наглядную картину влияния на конечный результат как чисто модельных характеристик, так и наблюдаемой информации.

Были записаны расчеты последних 8 лет модельных расчетов с климатическим форсингом на каждые сутки. По этим данным были построены средние по 8 годам и аномалии (разность между текущим и средним значениями). Затем строились наблюдаемые тренды и ковариационные матрицы аномалий от тренда по формулам (9)–(10). При этом на каждый климатический месяц выбиралось 15 число (среднее число месяца) и для увеличения длины выборки добавлялись 5, 10, 20, 25 числа этого же месяца, то есть длина выборки была 5 × 8 = 40. Итого было построено 12 среднемесячных ковариационных матриц аномалий, каждая по выборке длины 40.

3. ЧИСЛЕННЫЕ ЭКСПЕРИМЕНТЫ

Для усвоения были выбраны данные для всей поверхности Южной Атлантики южнее 20° с.ш. Следовательно, наибольший эффект от процедуры усвоения ожидался в центральной части исследуемого полигона, то есть в районе столкновения Бразильского и Фолклендского течений и далее вдоль границы субантарктического пояса. Структура водного переноса в этой зоне была подробно описана в работах [10, 25, 27].

В качестве основной физической характеристики для исследования был выбран уровень океана, обозначаемый через Yn на шаге расчета n – 1. Модель с усвоением стартовала с последнего расчетного поля Spin Up процедуры и форсировалась климатическими значениями потоков тепла и скорости ветра из Атласа [22]. Модельный расчет с усвоением осуществлялся на каждые сутки и затем проводилось осреднение полей на середину климатического месяца (январь, февраль и т.д.) по формулам (2). Так как локализация данных наблюдений совпадала с сеткой модели, оператор Н в формуле (2) был равен единичному для уровня океана и нулевому для всех остальных переменных. Таким образом, в качестве модельного решения выбирались значения модели на 15 число каждого месяца, обозначенные выше как ${{X}_{n}}$, и в качестве наблюдаемой величины значения уровня океана из ежемесячного климатического архива AVISO, интерполированного в точки сетки и обозначенного выше как ${{Y}_{n}}$. В нашем случае n – это один месяц, n = 1, 2…12.

4. АНАЛИЗ РЕЗУЛЬТАТОВ ЧИСЛЕННЫХ ЭКСПЕРИМЕНТОВ

4.1. Уровень океана

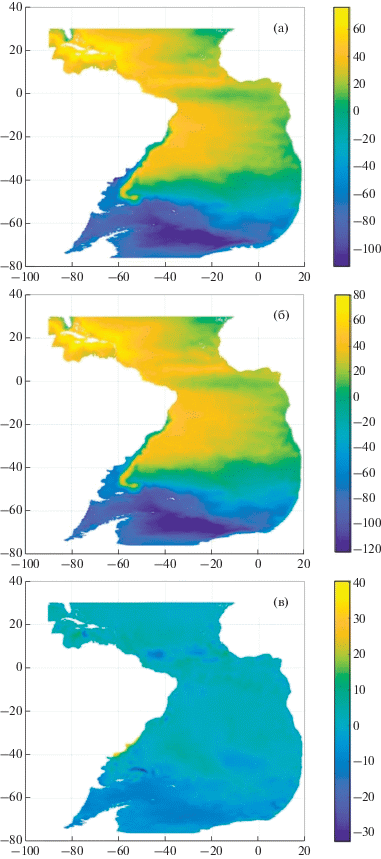
На рис. 2а показано значение модельного уровня в Южной Атлантике на 15 января. Значение уровня снижается от экватора к широте 80° ю.ш. примерно на 80 см, в то время как наблюдаемый уровень снижается в этом промежутке на 100 см, однако структурно поле уровня, рассчитанного моделью, соответствует наблюдаемому (рис. 1). Можно наблюдать четко выраженную зону Фолклендского течения с уровнем –40 см. В центральной части океана наблюдается небольшое понижение уровня (около 20 см) в районе пассатных течений, а также Бенгельского течения.

Рис. 2.

Модельное поле уровня (см) в январе. (а) – чисто модельное, (б) – после усвоения, (в) – разность: после усвоения минус модельное.

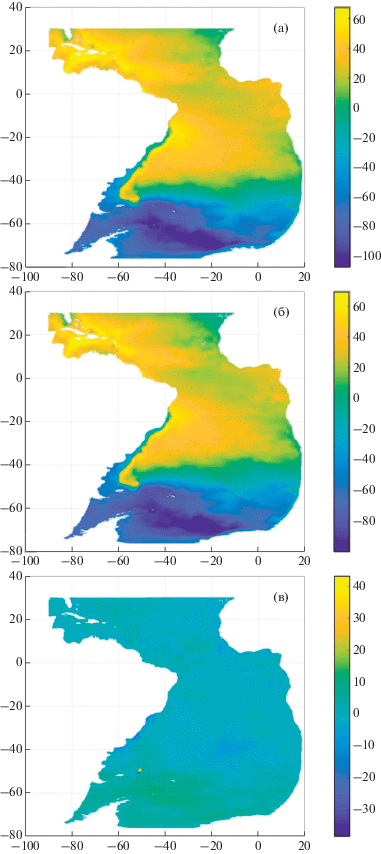
После усвоения данных (рис. 2б) заметно небольшое повышение уровня на широтах 70°–80° ю.ш., что несколько отдаляет абсолютное значение уровня модели от наблюдаемых результатов, однако делает их более схожими структурно, так как на рис. 1 видно, что наблюдаемый уровень имеет выраженный градиент в море Уэдделла и повышается примерно на 40 см к берегам Антарктиды. На рис. 2в, где приведена разность между модельным полем с усвоением и без него, заметна сильная разница уровней в самом центре антициклонического круговорота в Аргентинской котловине, где теплое Бразильское течение встречается с холодным Фолклендским, а также незначительное понижение уровня у берегов Южной Америки южнее 25° ю.ш.

При АДН уровня для августа (рис. 3) в том же прибрежном районе уровень, напротив, увеличивается, что, вероятно, компенсирует отсутствие воспроизведения сезонного изменения стока рек в используемой конфигурации модели, а также появляются значительные изменения в структуре антициклонического круговорота в Аргентинской котловине: несколько размывается резкий градиент высот и весь круговорот вытягивается на восток.

Рис. 3.

Уровень океана в Южной Атлантике на 15 августа (см). (а) – модель, (б) – модель после усвоения, (в) – разность: после усвоения минус до усвоения.

4.2. Воспроизведение поверхностных течений

В качестве усваиваемых данных использовался только массив наблюдений за уровнем моря, однако, согласно формуле (2), усвоение одной характеристики вносит поправки и в остальные чисто модельные поля. В этом разделе мы рассмотрим, как усвоение уровня повлияло на скорости поверхностных течений в августе.

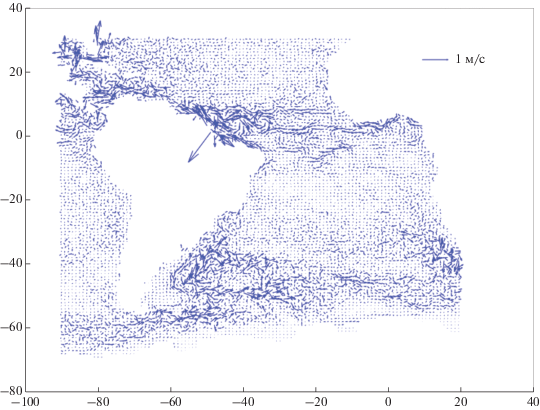
На рис. 4 показаны векторные поля поверхностных течений до и после коррекции и их разность. Усвоение увеличило скорость Антарктического циркумполярного течения (АЦТ) восточнее 20° з.д. и уменьшило ее в промежутке 40°–20° з.д., сделало АЦТ более меандрированным, усилило Бенгельское течение. Однако стоит заметить, что практически пропало Ангольское течение.

Рис. 4.

Скорости поверхностных течений в Южной Атлантике. Январь. (а) модель, (б) модель после усвоения, (в) разность: после усвоения минус до усвоения.

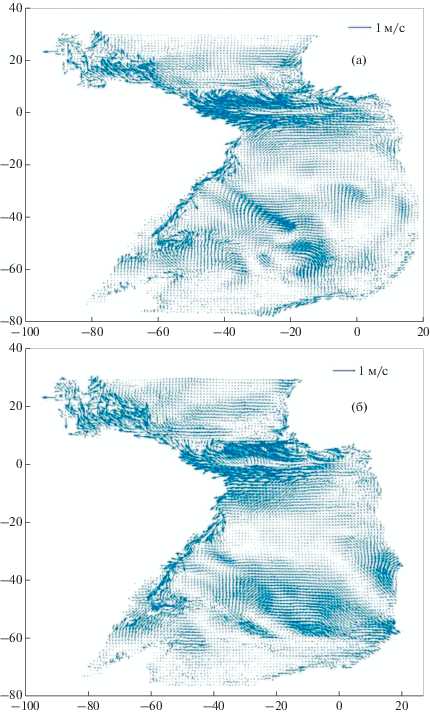
Рис. 4.

Окончание.

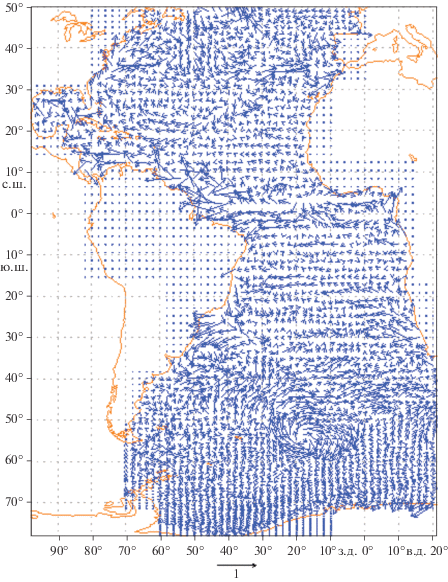
Для сравнения с нашими расчетами были взяты расчетные схемы течений по модели HYCOM, ранее подробно описанные в работе [27], примерно на тот же период времени (январь 2008 г.). На рис. 5 приведено поле поверхностных течений по модели HYCOM. Видно довольно хорошее качественное и даже количественное совпадение, при этом по модели HYCOM течения получаются больше, в частности, в тех участках АЦТ, где по модели HYCOM скорости превышают 60 см/с; в модели INMOM с тем же осреднением значения скорости на 17% меньше, и тем не менее, они хорошо совпадают по направлению. Отсюда можно сделать вывод, что наши расчеты соответствуют ранее проведенным расчетам в рассматриваемой области по другим моделям. На рис. 6 представлены среднесуточные данные спутникового наблюдения архива AVISO на ту же дату.

Рис. 5.

Скорости поверхностных течений по модели HYCOM на январь 2008 г.

Рис. 6.

Наблюдаемые скорости поверхностных течений океана по данным Aviso+.

Наблюдаемые поверхностные течения из архива AVISO+ выводятся из значений уровня моря при помощи геострофического соотношения, следовательно, не требуют дополнительного анализа. Качественные совпадения с модельными расчетами очевидны, хорошо видны все структурные особенности динамики вод Южной Атлантики (Бразильское течение, Бенгельское течение, АЦТ), которые адекватно воспроизводятся моделью. Коррекция в основном происходит количественно, и она соответствует тем данным наблюдений, которые мы используем.

5. ЗАКЛЮЧЕНИЕ И ВЫВОДЫ

В работе рассмотрена задача численного моделирования гидродинамики Южной Атлантики с усвоением данных наблюдений уровня океана и анализом структуры взаимосвязи характеристик полей наблюдаемого и модельного уровней. Показано, что при усвоении предложенным в статье методом вновь построенные (скорректированные) модельные поля имеют заметные отличия от исходных. В отдельных областях, в частности, поле уровня меняется до 0.05 м в сторону увеличения, а также структурно меняется в районе моря Уэдделла, делая модельный результат после усвоения более похожим на наблюдаемый. В полях течений происходит заметная (на 25–30%) интенсификация скоростей в районе Бенгельского течения, системе Экваториальных течений, в зоне Антарктического циркумполярного течения, но при этом заметно ослабевает Ангольское течение, что, по-видимому, соответствует наблюдаемому полю уровня океана.

Источник финансирования: работа выполнена по госзаданию ИО РАН № 0128-2021-0002 при поддержке гранта РФФИ № 19-57-60001 (модельные расчеты). Работа И. Ансорг была поддержана грантом UID 118901 Национальным Научным фондом Южно-Африканской Республики.

Список литературы

  1. Агошков В.И., Пармузин Е.И., Шутяев В.П. Численный алгоритм вариационной ассимиляции данных наблюдений о температуре поверхности океана // Журнал вычислительной математики и математической физики. 2008. Т. 48. № 8. С. 1371–1391. https://doi.org/10.1134/S0965542508080046

  2. Беляев К.П., Кулешов А.А., Смирнов И.Н., Танажура К.А. Сравнение методов усвоения данных в гидродинамических моделях циркуляции океана // Математическое моделирование. 2018. Т. 30. № 12. С. 39–54. https://doi.org/10.31857/S023408790001935-2

  3. Беляев К.П., Танажура К.А.С., Тучкова Н.П. Сравнительный анализ экспериментов с усвоением данных дрифтеров АРГО // Океанология. 2012. Т. 52. № 5. С. 643–653. https://doi.org/10.1134/S0001437012050025

  4. Гандин Л.С. Объективный анализ метеорологических полей. Л.: Гидрометиздат, 1963. 288 с.

  5. Гихман И., Скороход А. Введение в теорию случайных процессов. М.: МИР, 1977. 350 с.

  6. Дейнего И., Ансорг И., Беляев К., Дианский Н. Пространственно-временная изменчивость модельных характеристик в Южной Атлантике // Морской гидрофизический журн. 2019. Т. 35. № 6. С. 549–562. https://doi.org/10.22449/0233-7584-2019-6-572-584

  7. Кныш В.В., Демышев С.Г., Коротаев Г.К., Саркисян А.С. Методика и результаты ассимиляции климатических данных по температуре, солености и уровню в численной модели циркуляции Черного моря // Изв. РАН. Физика атмосферы и океана. 2007. Т. 43. № 3. С. 398–412. https://doi.org/10.1134/S0001433807030115

  8. Марчук Г.И., Патон Б.Е., Коротаев Г.К., Залесный В.Б. Информационно-вычислительные технологии – новый этап развития оперативной океанографии // Изв. РАН. Физика атмосферы и океана. 2013. Т. 49. № 6. С. 629–642. https://doi.org/10.7868/S0002351513060114

  9. Морозов Е.Г., Демидов А.Н., Тараканов Р.Ю. Перенос Антарктических вод в глубоководных каналах Атлантики // Докл. РАН. 2008. Т. 422. № 6. С. 815–818.

  10. Ремесло А.В., Морозов Е.Г., Нейман В.Г., Чернышков П.П. Структура и изменчивость Фолклендского течения // Докл. РАН. 2004. Т. 399. № 1. С. 110–113.

  11. Рожков В.А. Статистическая гидрометеорология, Ч1. СПГУ, 2013. 186 с.

  12. Самарский А.А., Михайлов А.П. Математическое моделирование. Идеи. Методы. Примеры. 2-е изд., испр. М.: Физматлит, 2001. 320 с. ISBN 5-9221-0120-X.

  13. Belyaev K., Kuleshov A., Tuchkova N., Tanajura C.A.S. An optimal data assimilation method and its application to the numerical simulation of the ocean dynamics // Mathematical and Computer Modelling of Dynamical Systems. 2018. V. 24. Iss. 1. P. 12–25.  https://doi.org/10.1080/13873954.2017.1338300

  14. Belyaev K., Tanajura C.A.S. On the correction of perturbations due to data assimilation in ocean circulation models // Applied Mathematical Modelling. 2005. V. 29. Iss. 7. P. 690–709. https://doi.org/10.1016/j.apm.2004.10.001

  15. Evensen G. Data Assimilation: The Ensemble Kalman Filter. Berlin: Springer, 2009. 307 p. https://doi.org/10.1007/978-3-642-03711-5.

  16. Ghil M., Malanotte-Rizzoli P. Data assimilation in meteorology and oceanography // Advances in Geophysics. 1991. V. 33. P. 141–266. https://doi.org/10.1016/S0065-2687(08)60442-2

  17. Gouretski V., Reseghetti F. On depth and temperature biases in bathythermograph data: Development of a new correction scheme based on analysis of a global ocean database // Deep-Sea Res. 2010. Iss. 57. P. 812–833. https://doi.org/10.1016/j.dsr.2010.03.011

  18. Kalman R. A New approach to linear filtering and prediction problems // ASME J. of Basic Engineering. 1960. V. 82. P. 35–45. https://doi.org/10.1115/1.3662552

  19. Kalnay E., Kanamitsu M., Kistler R. et al. The NCEP/NCAR 40-year reanalysis project // Bull. Am. Meteorol. Soc. 1996. V. 77. Iss. 3. P. 437–472. https://doi.org/10.1175/1520-0477(1996)077<0437: TNYRP>2.0.CO;2

  20. Kalnay E., Ota Y., Miyoshi T., Liu J. A simpler formulation of forecast sensitivity to observations: application to ensemble Kalman filters // Tellus A: Dynamic Meteorology and Oceanography. 2012. V. 64. Iss. 1. https://doi.org/10.3402/tellusa.v64i0.18462

  21. Kaurkin M., Ibraev R., Belyaev K. Assimilation of the AVISO altimetry data into the ocean dynamics model with a high spatial resolution using ensemble optimal interpolation (EnOI) // Izv., Atmos. Oceanic Phys. 2018. V. 54. Iss. 1. P. 56–64. https://doi.org/10.1134/S0001433818010073

  22. Large W.G., Yeager S.G. The global climatology of an interannually varying air–sea flux data set // Clim. Dyn. 2009. V. 33. P. 341–364. https://doi.org/10.1007/s00382-008-0441-3

  23. Marchuk G.I., Zalesny V.B. A numerical technique for geophysical data assimilation problem using Pontryagin’s principle and splitting-up method // Russ. J. Numer. Anal. Math. Modelling. 1993. V. 8. Iss. 4. P. 311–326. https://doi.org/10.1515/rnam.1993.8.4.311

  24. Marchuk G., Zalesny V. Modeling of the World Ocean circulation with the four-dimensional assimilation of temperature and salinity fields // Izv., Atmos. Oceanic Phys. 2012. V. 48. Iss. 1. P. 15–29. https://doi.org/10.1134/S0001433812010070

  25. Morozov E.G., Tarakanov R.Yu., Demidova T.A. et al. Velocity and transport of the Falkland Current at 46° S // Russ. J. Earth. Sci. 2016. V. 16. ES6005. https://doi.org/10.2205/2016ES000588

  26. Moshonkin S., Zalesny V., Gusev A. Simulation of the Arctic—North Atlantic ocean circulation with a two-equation K-omega turbulence parameterization // J. Mar. Sci. Eng. 2018. V. 6. Iss. 95. https://doi.org/10.3390/jmse6030095

  27. Piola A., Matano R. Ocean Currents: Atlantic Western Boundary—Brazil Current/Falkland (Malvinas) Current // Reference Module in Earth Systems and Environmental Sciences, Elsevier. 2017. https://doi.org/10.1016/B978-0-12-409548-9.10541-X

  28. Sakov P., Counillon F., Bertino L. et al. TOPAZ4: an ocean-sea ice data assimilation system for the North Atlantic and Arctic // Ocean Sci. 2012. V. 8. Iss. 4. P. 633–656. https://doi.org/10.5194/os-8-633-2012

  29. Schiller A., Brassington G.B. Operational Oceanography in the 21st Century. Dordrecht: Springer, 2011. 745 p. https://doi.org/10.1007/978-94-007-0332-2.

  30. Tanajura C.A.S., Mignac D, Santana A. et al. Observing system experiments over the Atlantic Ocean with the REMO ocean data assimilation system (RODAS) into HYCOM // Ocean Dynamics. 2019. V. 70. P. 115–138. https://doi.org/10.1007/s10236-019-01309-8

  31. Tanajura C.A.S., Santana A., Mignac D. et al. The R-EMO Ocean Data Assimilation System into HYCOM (RODAS_H): General Description and Preliminary Results // Oceanic Atmosphere Research Letters. 2014. V. 7. Iss. 5 P. 464–470. https://doi.org/10.3878/j.issn.1674-2834.14.0011

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Океанология

Архивы выпусков Информация о журнале Отправить рукопись в журнал